Second Law Analysis of a non-Newtonian Laminar Falling Liquid Film Along an Inclined Heated Plate
Abstract
:Introduction
Mathematical Formulation and Analysis
- ∆T = qδ/k = reference temperature difference
- X = dimensionless axial distance
- Y = dimensionless vertical distance
- U = dimensionless axial velocity
- Θ = dimensionless temperature
(2n+1)[1 / 6 – n3 / (2n+1)(3n + 1)(4n + 1)] }/ (n+1)
(3n + 1)(n+1) - (2n+1)[1 / 6 – n3 / (2n+1)(3n + 1)(4n + 1) – 1/2] / (n+1)
= k[(∂T(x, y)/∂x)2 + (∂T(x, y)/∂y)2] / T02 + μ[∂u(y)/∂y]n+1 / T0

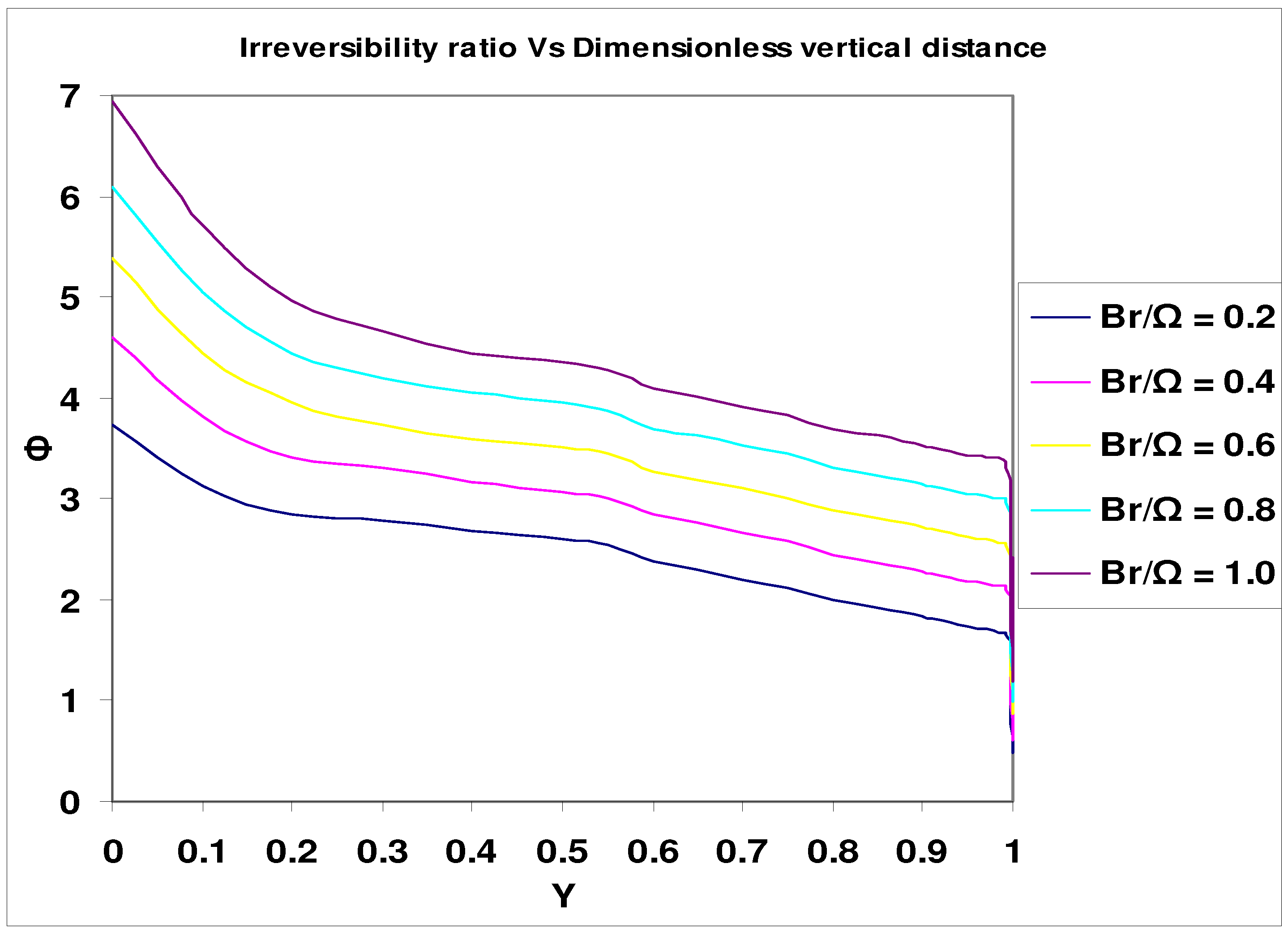
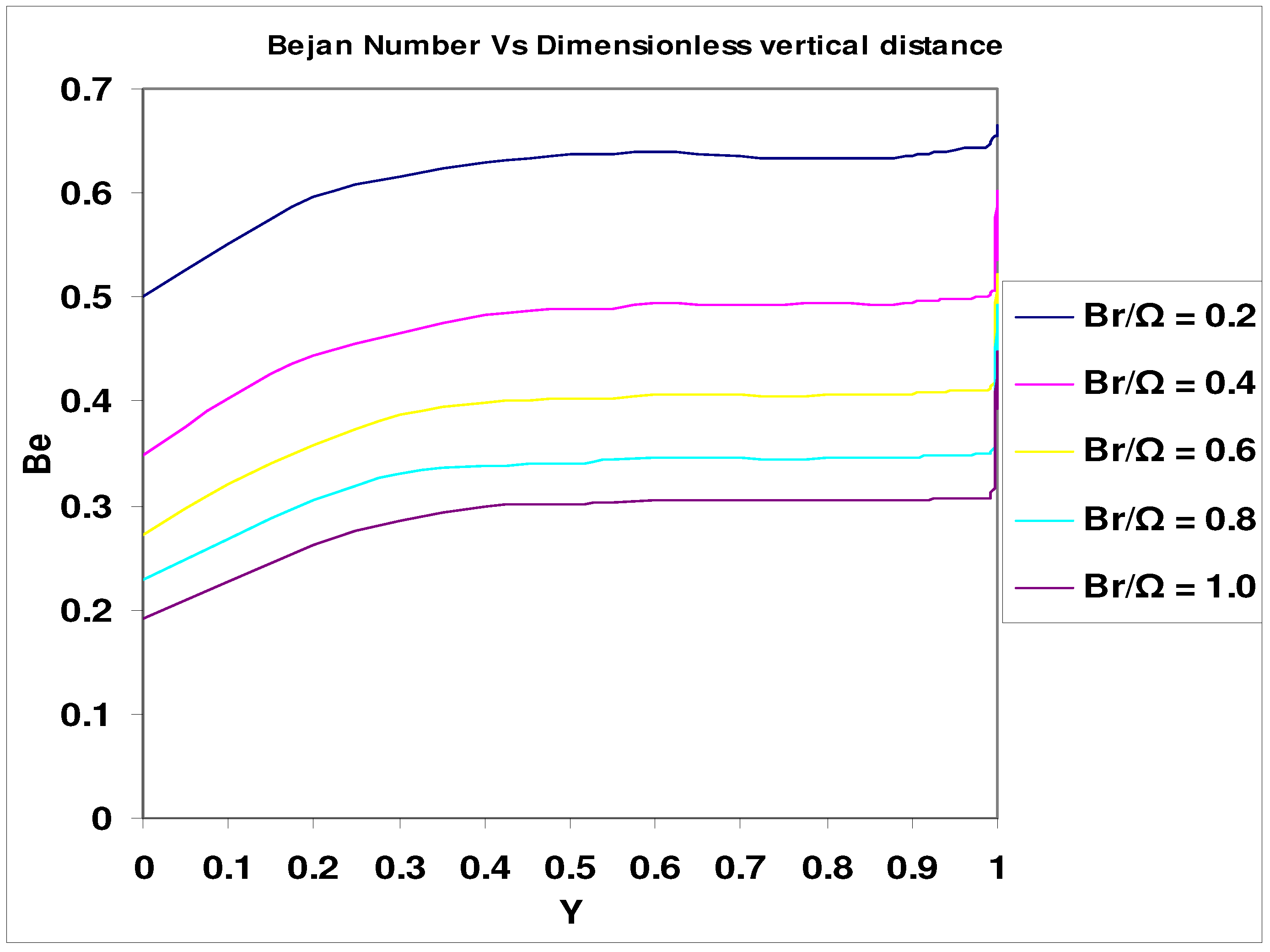
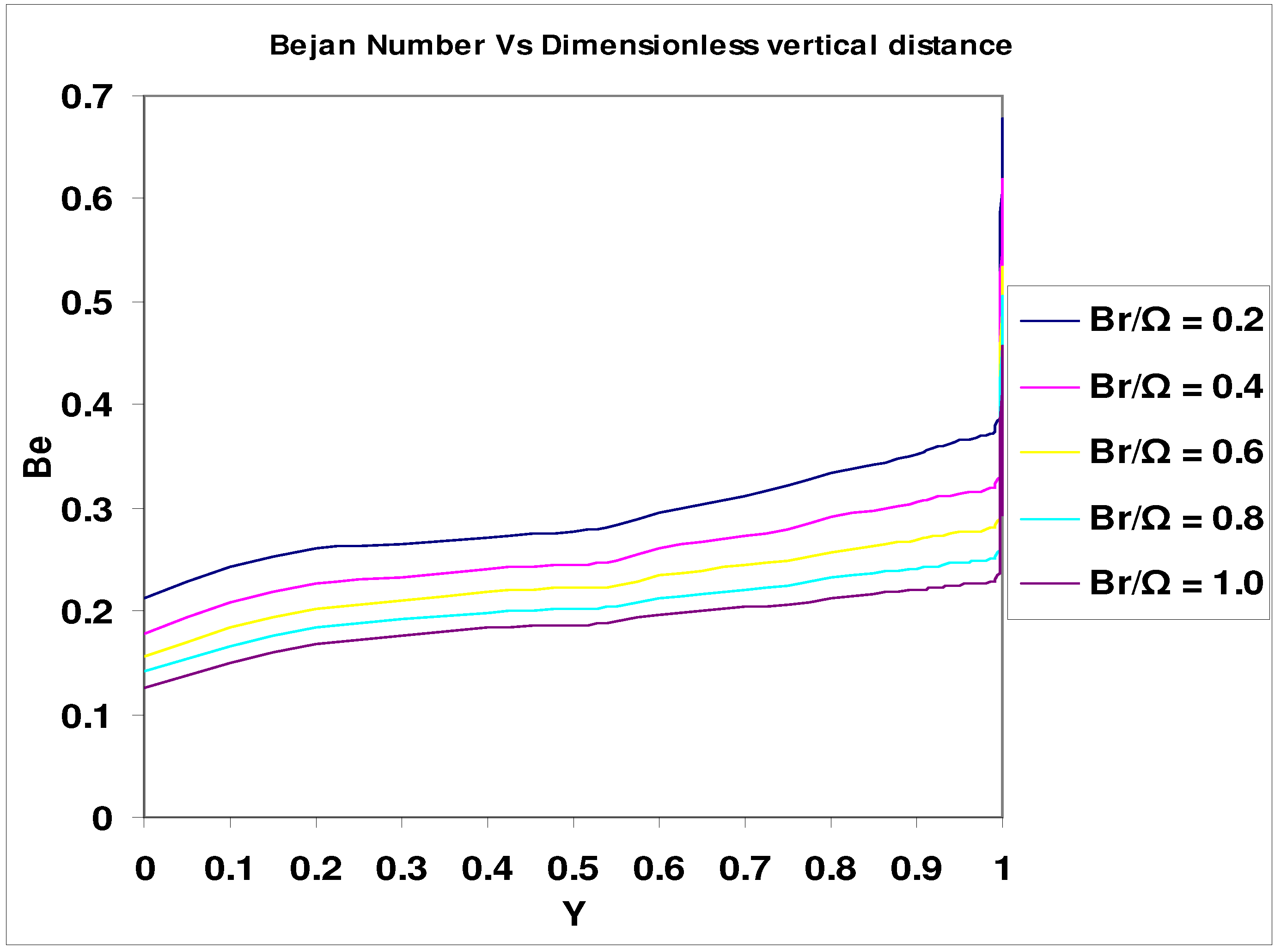
Results and Discussion
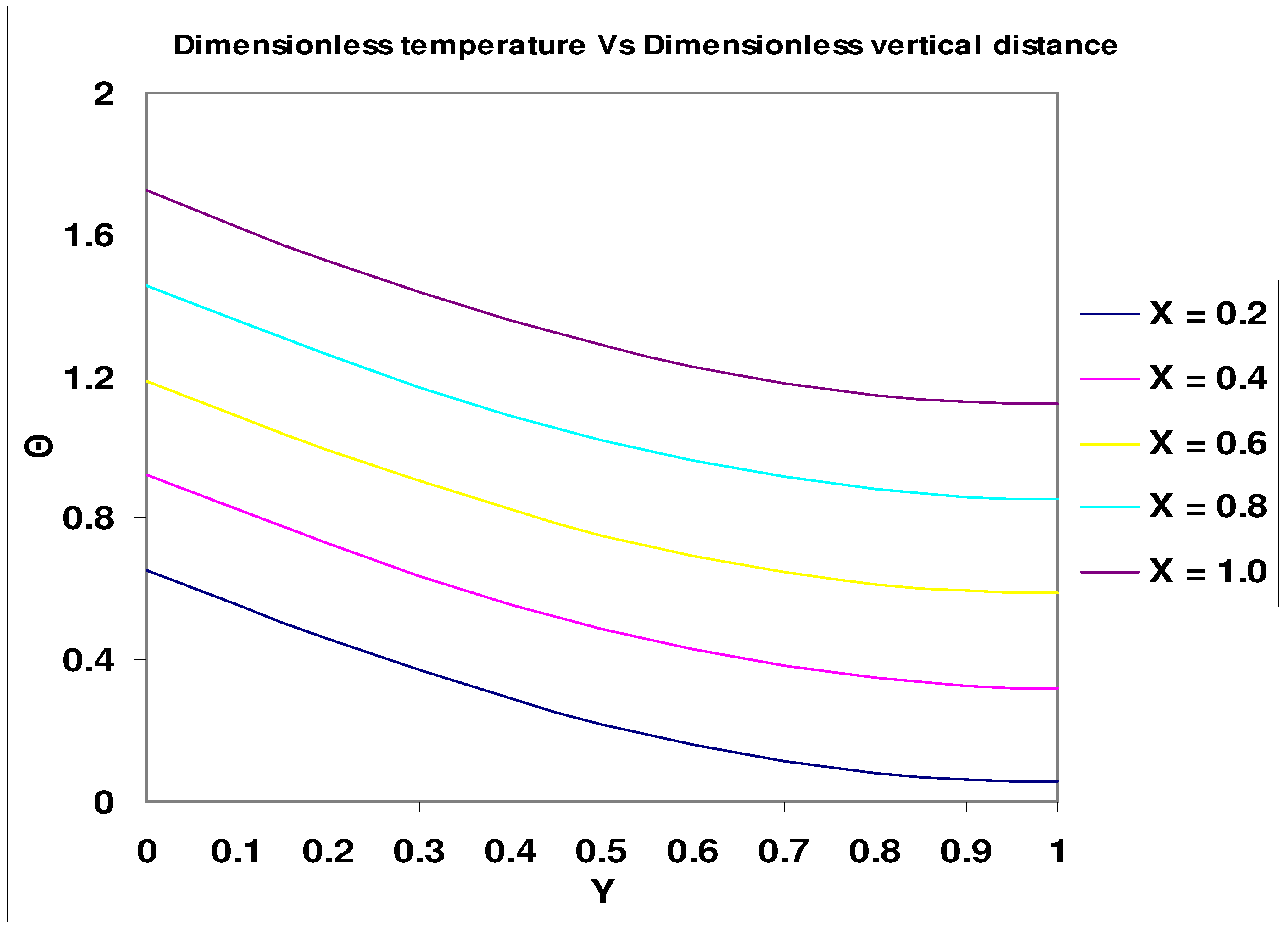
- Brinkman number (Br) = μu2m / k ΔT
- Dimensionless temperature difference Ω = ΔT / T0
- Viscous dissipation parameter (BrΩ-1) = μu2m T0 / k ΔT2
- Sg’’’ = k {[∂T(x, y)/∂x]2 + [∂T(x, y)/∂y]2} / T02+ μ [∂u(y)/∂y]n+1 / T0
- NS = kT02Sg’’’ / q2 = NC + NY + NF
- NC = {∂Θ(X, Y)/∂X} 2 / Pe2 = entropy generated due to heat transfer in the axial direction= {(2n+1) X / (n+1)} 2 / Pe2
- NY = {∂Θ(X, Y)/∂Y} 2 / Pe2 = entropy generated due to heat transfer in the transverse direction={(2n+1) [Y(Y/2-1)] / (n+1) – [n2 (1-Y) (3n+1)/n] / (3n + 1) (n+1) - (2n+1) [1 / 6 – n3 / (2n+1) (3n + 1) (4n + 1) – 1 / 2] / (n+1)} 2 / Pe2
- NF = (BrΩ-1)(∂U(Y)/∂Y) n+1 = entropy generation due to the fluid friction= (BrΩ-1)(∂U(Y)/∂Y) n+1 = (BrΩ-1)[(n+1) (1-Y) 1/ (n) / (n)] n+1
- Pe = umδ / α
- Br = μu2m / kΔT and
- Ω = ΔT / T0 = (TW - T0) / T0 are the Peclet number, Brinkman number and dimensionless temperature function, respectively.
- Bejan number = (NC + NY) / (NC + NY + NF)= 1 / (1 + Ф)
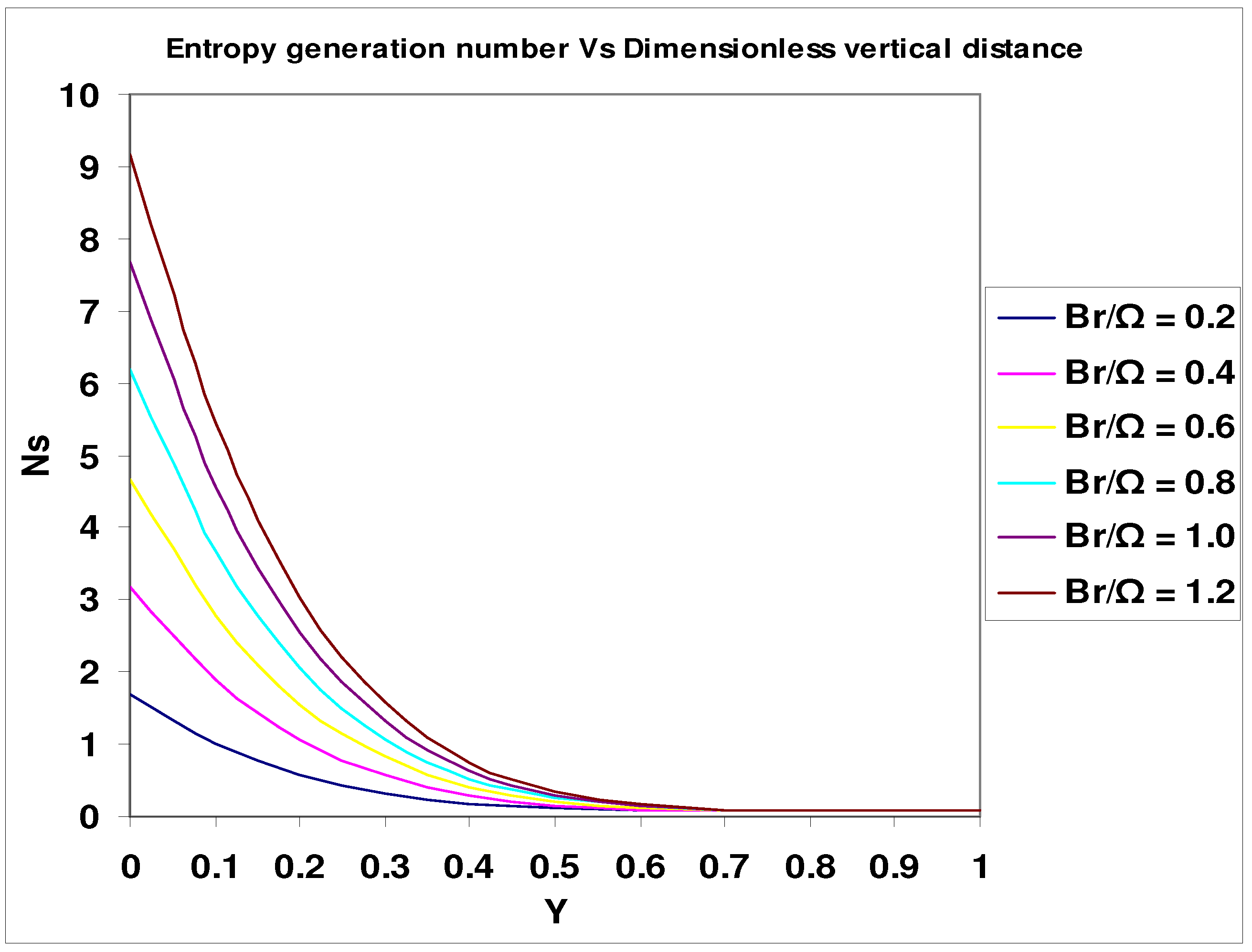
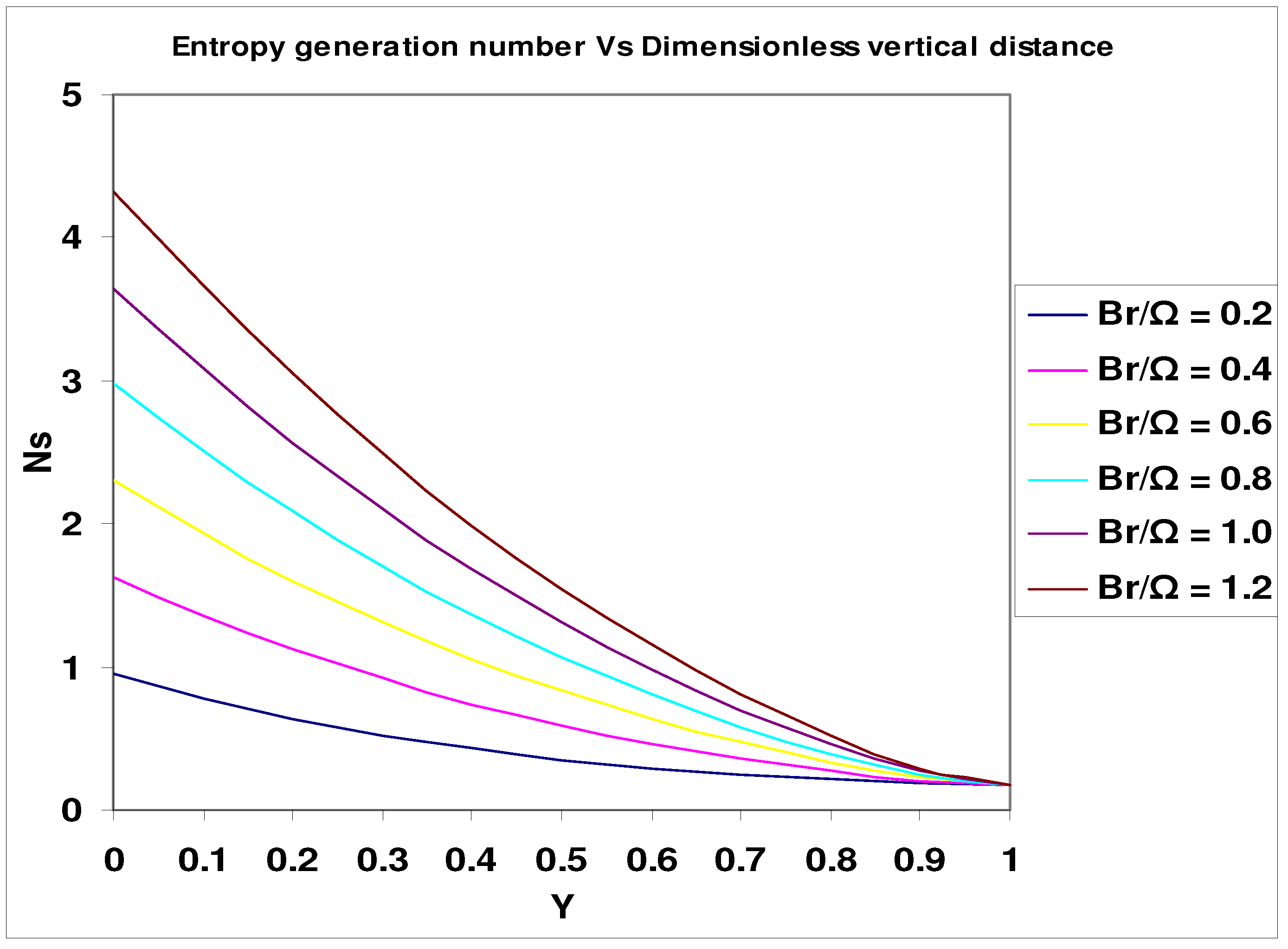
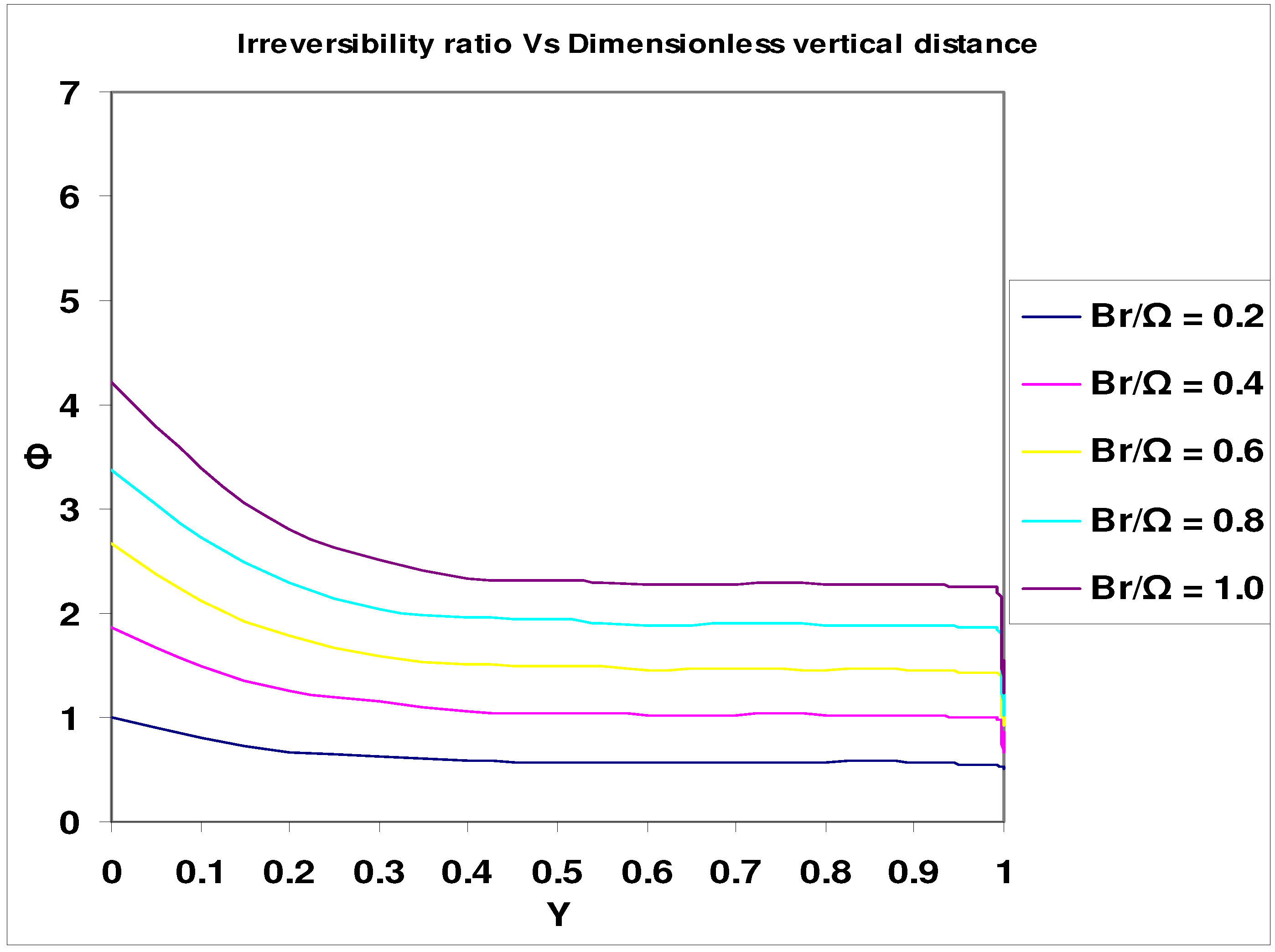
Concluding Remarks
Nomenclature
| Α | thermal diffusivity, m2 / s |
| Br | Brinkman Number, μu2m / λΔT |
| BrΩ-1 | viscous dissipation parameter |
| Be | Bejan Number |
| Cp | specific heat, J / kg K |
| G | gravitational acceleration, m / s2 |
| n | viscosity index |
| Ns | dimensionless entropy generation number |
| Pe | Peclet number, umδ / |
| q | constant heat flux at the wall, W / m2 |
| Q | mass flow rate, kg / m s |
| Sg | entropy generation rate, W / m3 k |
| T | temperature, K |
| u | axial velocity, m |
| U | dimensionless axial velocity |
| x | axial distance, m |
| X | dimensionless axial distance |
| y | vertical distance, m |
| Y | dimensionless vertical distance |
Greek Symbols
| δ | liquid film thickness, m |
| ΔT | reference temperature difference, K |
| θ | inclination angle, radian |
| Θ | dimensionless temperature |
| k | thermal conductivity, W / m K |
| μ | dynamic viscosity, Pa. s |
| Ω | dimensionlesstemperature difference, ΔT / T0 |
| Ф | irreversibility ratio |
| ρ | densityof the fluid, kg / m3 |
Subscripts
| m | maximum value |
| 0 | reference value |
References
- Makinde, O. D.; Osalusi, E. Second law analysis of laminar flow in a channel filled with saturated porous media. Entropy 2005, 7, 148–160. [Google Scholar]
- Bejan, A. Method of entropy generation minimization, or modeling and optimization based on combined heat transfer and thermodynamics. Revue Generale de Thermique 1996, 35, 637–646. [Google Scholar]
- Bejan, A. Entropy generation Minimization: The method of thermodynamic optimization of finite-size systems and finite-time processes. CRC Press: Boca Raton, New York, 1996. [Google Scholar]
- Bejan, A.; Tien, C.-L. Natural convection in horizontal space bounded by two concentric cylinders with different end temperatures. International Journal of Heat and Mass Transfer 1979, 22, 919–927. [Google Scholar]
- Bejan, A. A Study of Entropy Generation in Fundamental Convective Heat Transfer. Journal of Heat Transfer 1979, 101, 718–725. [Google Scholar]
- Erbay, L.B.; Ercan, M.Ş.; Sülüş, B.; Yalçın, M. M. Entropy generation during fluid flow between two parallel plates with moving bottom plate. Entropy 2003, 5, 506–518. [Google Scholar]
- Saouli, S.; Saouli-Aïboud, S. Second law analysis of laminar falling liquid film along an inclined heated plate. International Communications in Heat and Mass Transfer 2004, 31, 879–886. [Google Scholar]
- Saouli-Aïboud, S.; Saouli, S.; Settou, N.; Meza, N. Thermodynamic Analysis of Gravity-driven Liquid Film along an inclined heated plate with Hydromagnetic and Viscous Dissipation Effects. Entropy 2006, 8, 188–199. [Google Scholar]
- Sahin, A. Z. Thermodynamics of laminar viscous flow through a duct subjected to constant heat flux. Energy 1996, 21, 1179–1187. [Google Scholar]
- Sahin, A. Z. Entropy generation in turbulent liquid flow through a smooth duct subjected to constant wall temperature. International Journal of Heat and Mass Transfer 2000, 43, 1469–1478. [Google Scholar]
- Bejan, A. Second law analysis in heat transfer. Energy 1980, 5, 721–732. [Google Scholar]
- Narusawa, U. The second law analysis of mixed convection in rectangular ducts. Heat and Mass Transfer 2001, 37, 197–203. [Google Scholar]
- Mahmud, S.; Fraser, R. A. The second law analysis in fundamental convective heat transfer problems. International Journal of Thermal Sciences 2003, 42, 177–186. [Google Scholar]
- Mahmud, S.; Fraser, R. A. Thermodynamic analysis of flow and heat transfer inside channel with two parallel plates. Exergy 2002, 2, 140–146. [Google Scholar]
© 2007 by MDPI (http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Gorla, R.S.R.; Pratt, D.M. Second Law Analysis of a non-Newtonian Laminar Falling Liquid Film Along an Inclined Heated Plate. Entropy 2007, 9, 30-41. https://doi.org/10.3390/e9010030
Gorla RSR, Pratt DM. Second Law Analysis of a non-Newtonian Laminar Falling Liquid Film Along an Inclined Heated Plate. Entropy. 2007; 9(1):30-41. https://doi.org/10.3390/e9010030
Chicago/Turabian StyleGorla, Rama Subba Reddy, and David M. Pratt. 2007. "Second Law Analysis of a non-Newtonian Laminar Falling Liquid Film Along an Inclined Heated Plate" Entropy 9, no. 1: 30-41. https://doi.org/10.3390/e9010030
APA StyleGorla, R. S. R., & Pratt, D. M. (2007). Second Law Analysis of a non-Newtonian Laminar Falling Liquid Film Along an Inclined Heated Plate. Entropy, 9(1), 30-41. https://doi.org/10.3390/e9010030



