Abstract
Adiabatic and isothermal propagations of spherical blast wave produced due to a nuclear explosion have been studied using the Energy hypothesis of Thomas, in the nonuniform atmosphere of the earth. The explosion is considered at different heights. Entropy production is also calculated along with the strength and velocity of the shock. In both the cases; for adiabatic and isothermal flows, it has been found that shock strength and shock velocity are larger at larger heights of explosion, in comparison to smaller heights of explosion. Isothermal propagation leads to a smaller value of shock strength and shock velocity in comparison to the adiabatic propagation. For the adiabatic case, the production of entropy is higher at higher heights of explosion, which goes on decreasing as the shock moves away from the point of explosion. However for the isothermal shock, the calculation of entropy production shows negative values. With negative values for the isothermal case, the production of entropy is smaller at higher heights of explosion, which goes on increasing as the shock moves away from the point of explosion. Directional study of the shock motion and entropy production show that in both the cases of adiabatic and isothermal flow, shock strength and shock velocity are larger in upward motion of the shock, in comparison to the downward motion of the shock. For adiabatic flow, entropy production is larger in upward motion of the shock; whereas, with negative values, entropy production is smaller in upward motion of the isothermal shock. For the adiabatic case, the profiles of shock strength, shock velocity and entropy production are smooth and have the largest value in vertically upward direction and have the lowest value in vertically downward direction, forming the oval shape. For the isothermal case, the profiles of shock strength and shock velocity show similar trend as that for adiabatic case but the profile of entropy production shows opposite trend. The profiles maintain their shape as the shock moves away. Comparison with observed values of shock velocity shows that isothermal case produces better results in comparison to the adiabatic case.
| Nomenclature | Subscripts |
| h0 =height of explosion (m) | h = unshocked state at a height h |
| p = pressure of fluid (air) | 1 = state at the earth surface |
| g = defined in equation (2.2) | 2 = state just behind the shock front |
| gs= acceleration due to gravity at the surface of earth (m/s2) | |
| Re=radius of earth (m) | |
| t = time | |
| r = radial distance from the point of explosion | Greek letters |
| h =height of any point from the earth surface (m) | ρ =density of fluid (air) |
| u= radial component of fluid velocity (m/s) | θ = angle measured in vertical direction |
| v= transverse component of fluid velocity (m/s) | ε = total energy /unit mass (sum of internal and kinetic energies for unit mass = E+½ u2) |
| U =shock velocity (m/s) | |
| R=shock radius (m) | |
| γ =specific heat ratio of the gas | α =constant defined in equation (2.19) |
| ℜ=gas constant for unit mass of the gas | |
| T′=energy released during explosion (J) | |
| T=absolute temperature (K) | |
| E=internal energy/unit mass (J/kg) | |
| M=shock strength | |
| s =specific entropy (entropy /unit mass) (kJ/kg-K) | |
| c=local sound speed (m/s) | |
| A=function of entropy defined in (2.6) | |
| B=constant defined in (2.11) | |
| A′=constant defined in (3.4) | |
| B′=constant defined in (3.10) | |
| K, L, N, O=coefficients defined in (2.23), (2.24), (2.25) and (2.26) respectively |
1. Introduction
Propagation of spherical blast wave in nonuniform media is of immense importance in the field of shock dynamics, as almost all the naturally available media are nonuniform in nature. Nonuniformity in any medium can be due to various phenomena namely the gravitation, self gravitation, rotation, thermal conductivity, viscosity etc. The atmosphere on the earth surface is a commonly available example of the nonuniform medium produced due to the gravitational effect of the earth.
Adiabatic propagation of blast wave produced due to a sudden release of a large amount of energy has been first investigated by Taylor [,] and Sedov [,] using the similarity method. A detailed study of adiabatic shock propagation in air and nonuniform media has also been done by Zeldowitch and Raizer [,]. Other studies in this field are by Kopal [], Sakurai [,], Brode [], Hayes [,], Laumbach and Probestein [], Ojha [] and Nath [].
An atomic explosion or the burst of novae produces very strong Shocks and very high temperature. The assumption of adiabatic flow by Taylor [] in case of atomic explosion and by Parker [] in the case of novae burst is no more valid. In such cases, the assumption of isothermal flow gives more accurate description of the problem. The text by U.S. department of Defense [], Zel’dovich and Raizer [] and many other websites [,] describes the effect of atomic explosion in the air. Fission of Uranium or Plutonium in an Atomic bomb leads to the liberation of a large amount of energy (~ 1013 J) in a very small period, with in a limited space. The large amount of energy released, causes a temperature of more than a million degrees. Because of the extremely high temperature, there is an emission of energy by the electromagnetic radiations. Much of these radiations are absorbed by the air surrounding the bomb, with the results that air becomes heated. Since the radiation energy can travel rapidly between any two points, hence there is no appropriate temperature gradient. Because of the uniform temperature, the medium surrounding the explosive is referred to as an Isothermal sphere and the blast generated by the explosive propagates isothermally.
Self similar isothermal flow behind the spherical shock wave produced by a point explosion with their propagation in uniform and nonuniform atmosphere has been first investigated by Korbinikov [,]. Other studies in isothermal shock propagation are done by many using different methods [,,,,]. Isothermal blast wave model of Supernova Remnants are been developed by Solinger et.al. []. Ray and Bhomik [] studied the explosion in stars for isothermal shock conditions. The expansion of solar corona has been investigated by Bhomik [] using blast wave theory headed by an isothermal shock. Blast wave in inhomogeneous isothermal atmosphere, with real gas and heat transfer effects have been studied by Gretler []. Using isothermal shock conditions, cylindrical blast wave with radiation heat flux in self gravitating gas has been investigated by Singh et.al.[].
Thomas [] used energy hypothesis for spherical blast wave. This hypothesis was used by Bhutani [], Singh and coworkers [,,,] and Vishvakarma et al. [] used it for the case of water.
Change in entropy is an essential phenomenon of shock wave propagation. Change in entropy and temperature due to shock wave in different type of media are considered by Kopal [], Sakurai [,], Rosciszewshi [], Eschenroeder [], Strusmia [] In case of relativistic shock, Yadav and coworkers [,] and. Recently, rate of entropy production is investigated by Yadav et al. [] for the case of explosion in seawater.
In this paper, the adiabatic and isothermal propagation of spherical blast wave in the nonuniform media of earth’s atmosphere has been considered using energy hypothesis of Thomas []. Expressions for the shock strength, shock velocity and pressure, density and temperature ratios of shocked (downstream) and unshocked (upstream) fluid parameters are calculated numerically to achieve the variation of entropy production with propagation distance (r) in different directions (θ). Results are compared with those obtained by Taylor [].
2. Adiabatic propagation of the blast wave
Let us consider the nonuniform earth atmosphere, in which the explosion take place at point `O’ due to a spherical charge at a time t=0 and at a height h0 above the surface of earth. This point is considered as origin (r=0). (Figure 1).
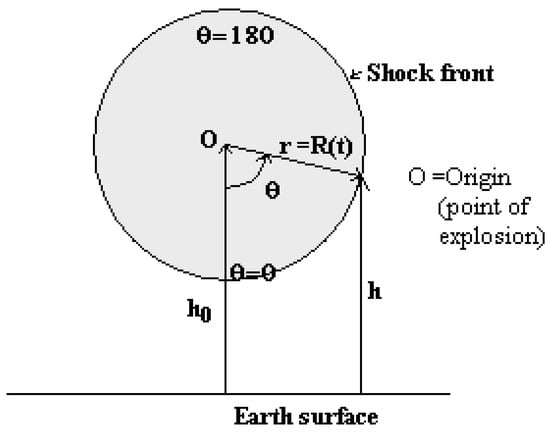
Figure 1.
Shock front in the earth’s atmosphere.
The explosion causes an immediate production of a spherical blast wave which propagates with a velocity U. At any time t, the radius of the spherical shock front is given as r=R (t). Variable θ represents the direction, which is taken as zero (θ=00) towards the earth surface and is 1800 in the vertical direction.
The partial differential equations governing the conservation of mass, momentum and energy of the adiabatic spherical flow under the effect of earth’s gravitation are given by:
Variation of the gravity with height is given by:
As h<< Re, then:
In the hydrostatic equilibrium condition:
The height h at any point on the spherical shock front of radius R, in the direction θ is given by:
Relationship between pressure and density for any gas particle is adiabatic, for which adiabatic equation of state is:
For the sake of simplicity it is assumed that γ does not vary with temperature. Differentiating equation (2.6) with respect to r and equating it with equation (2.3):
Differentiating equation (2.5) and substituting it in equation (2.7):
Substituting equation (2.2) in (2.8) and integrating for the limits ρ=ρ1 at h=0 and ρ=ρh for the height h:
Rearranging, we get density at a height h is:
And pressure at a height h is:
Where the constant B is given by:
Local sound velocity is
Relation (2.9), (2.10) and (2.12) denotes the undisturbed values of the density, pressure and local sound velocity at a height h, in front of the shock wave produced by the explosion.
2.1. Calculation of downstream fluid parameters
After the passage of the shock, the new values of pressure, density, particle velocity and temperature are p2, ρ2, u2 and T2 respectively. Using well known Rankine – Hugoniot conditions, these flow variables can be written in terms of the initial conditions of the air given by ph and ρh, by means of following equations:
Where shock strength
The Rankine- Hugoniot condition for the conservation of energy at the shock front is given by:
With the assumption that all the released energy is used in producing shock, then according to the Energy hypothesis, the change in total energy per unit mass is given by:
For the case of strong shock α is given by []:
From equation (2.17) and (2.18):
With the algebraic substitution of the values of p2, u2, ρ2 and α in (2.20) and on solving, we get the shock strength:
Shock velocity is given by:
U = ch.M
Where the coefficients K, L, N and O are given as:
Shock strength M is calculated at different shock positions (shock radius) in a particular direction (θ) given in equation (2.5). Then pressure ratio p2/p0 and density ratio ρ2/ρ0 at different shock positions in a particular direction θ, are calculated using equations (2.13) and (2.14) given below:
2.2. Calculation of entropy production
Assuming that no chemical reaction takes place, the entropy change in a gaseous medium is given by the relation []:
The first part of equation (2.29) is calculated using the gas equation as below:
On solving we get:
Substituting (2.31) and (2.28) in (2.29), the rate of change of entropy in a non dimensional form (as Δs is divided by ℜ, the gas constant) is given by:
Entropy production is calculated at different shock positions (shock radius R) in a particular direction θ and for different heights of explosion.
3. Isothermal propagation of the shock
Let us consider the isothermal propagation of the shock produced due to explosion at point O (Figure 1). The partial differential equations governing the conservation of mass, momentum and energy for the isothermal spherical flow under the effect of earth’s gravitation are given by:
Equation (3.1d) shows the absence of any temperature gradient.
The hydrostatic equilibrium conditions are given by:
Relationship between pressure and density of the fluid particle is given by the equation of state:
The fluid (air) particles are in a state of isothermal flow (T is constant), for which the equation of state is:
Where A′=ℜT. Differentiating equation (3.4) with respect to r, and dividing both sides by ρ, we get:
Equating equation (3.5) and (3.2):
Differentiating equation (2.5) and substituting it in equation (3.6):
Substituting equation (2.2) in (3.7) and integrating for the limits ρ=ρ1 at h=0 and ρ=ρh at a height h:
Rearranging, we get density at a height h is:
And pressure at a height h is:
Where the constant B is given by:
Local sound velocity is
Relation (3.8) and (3.9) denotes the undisturbed values of the density and pressure. Local sound velocity at a height h is given by equation (3.11) which is same everywhere as the medium is isothermal.
3.1. Calculation of downstream fluid parameters
After the passage of the shock, the new values of pressure, density, particle velocity and temperature are p2, ρ2, u2 and T2 respectively. The jump conditions for the fluid variables across the isothermal shock front are given by []:
Where shock strength
The Rankine- Hugoniot condition representing the conservation of energy at the shock front is given by:
With the assumption that all the released energy is used in producing shock, then according to the Energy hypothesis, the change in total energy per unit mass is given by:
For the case of strong isothermal shock, α is given by []:
From equation (3.17) and (3.18):
Substituting the values of p2, u2, ρ2 and α in (3.20), we get the shock strength as:
Shock velocity is given by:
Shock strength M is calculated at different shock positions (shock radius) in a particular direction (θ), given in equation (2.5).
The density ratio ρ2/ρh at different shock positions in a particular direction θ, are calculated using equation (3.13) and (3.21), given by:
3.2. Calculation of entropy production
Assuming that no chemical reaction takes place, the entropy change in a gaseous medium is given by the relation []:
For the isothermal case T2=Th, hence change in entropy is given by:
Substituting (3.23) in (3.25), the rate of entropy production in a non dimensional form is given by:
At different heights of explosion, entropy production is calculated at different shock positions in a particular direction θ.
4. Results and Discussion
The plots in Figure 2 and Figure 3 show the effect of height of explosion on the shock strength M and shock velocity U. Figure 2a,b shows the variation of shock strength (M) with propagation distance (R) for the adiabatic and isothermal flow respectively, at different heights of explosion h0 (=1km, 4km and 7km), as the shock moves in the horizontal direction (θ=900). Corresponding variation of shock velocity (U) with propagation distance (R), for the two cases, are shown in Figure 3a,b.
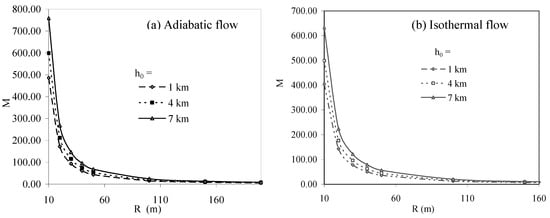
Figure 2.
Variation of Shock strength (M) with propagation distance (R) at different heights of explosion h0 in the direction θ = 900.
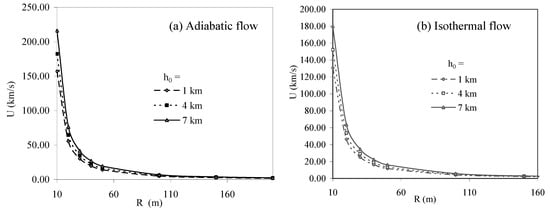
Figure 3.
Variation of shock velocity (U) with propagation distance (R) at different heights of explosion h0 in the direction θ = 900.
In both the cases of adiabatic and isothermal flow, shock strength and shock velocity have higher values at higher heights of explosion (i.e. M and U at 7km > at 4km > at 1km). However, for the isothermal case, the values of shock strength and shock velocity are smaller in comparison to the adiabatic case. The effect of earth gravitation on the motion of shock is dominantly shown by these plots.
These plots also show the characteristics properties of blast waves. Near the point of explosion, M and U are quite large. As the shock moves away from the point of explosion, M and U decrease initially very sharply. At a sufficiently large distance the shock strength approaches the value 1.0 and shock velocity approaches the value of local sound velocity.
Entropy production also depends on the height of explosion. Figure 4 give the corresponding variation of entropy production with propagation distance (R) for the adiabatic and isothermal case.
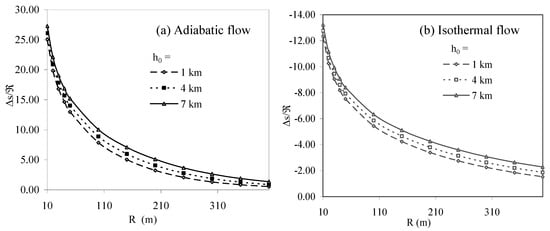
Figure 4.
Variation of entropy production (Δs/ℜ) with propagation distance (R) at different heights of explosion h0 in the direction θ = 900.
For the adiabatic case (Figure 4a), entropy production decreases as the shock moves away. In this manner the shock produces a non isentropic flow field behind it. However the decrease in entropy production is not so much sharp as shown by M and U. Also the entropy production is larger for higher height of explosion (i.e. Δs/ℜ at 7km > at 4km > at 1km). The plot also shows that the difference in entropy production at different heights of explosion is small near the point of explosion. Again the difference in Δs/ℜ at different h0’s decreases as the shock moves away.
At high altitudes, the shock faces a low value of initial pressure and initial density. At low pressure and density the air molecules are freer for motion. Hence the conversion of kinetic energy of the shock motion into the disordered motion of the air molecules (entropy) is larger for explosions at high altitudes [].
Figure 4b shows the corresponding variation of entropy production with propagation distance (R) for the isothermal case. It shows that variation in entropy production increases as the shock moves away (attention is to be made on the negative sign of entropy production. A decrease in negative value corresponds to the increase in the entropy. It looks strange to see the negative entropy production for the case of isothermal shock considered here. In the oncoming article, production of negative entropy has been discussed.). However the increase in entropy production is not so much sharp as shown by M and U. Also the entropy production is smaller for higher height of explosion (i.e. Δs/ℜ at 7km < at 4km < at 1km). The plot also shows that the difference in entropy production at different heights of explosion is small near the point of explosion. Again the difference in Δs/ℜ at different h0’s decreases as the shock moves away from the point of explosion.
Directional dependence of the shock motion is shown in Figure 5 and Figure 6. Figure 5a,b shows the variation of shock strength M with propagation distance R for the adiabatic and isothermal case respectively, in different directions at a fixed height of explosion h0= 4km.
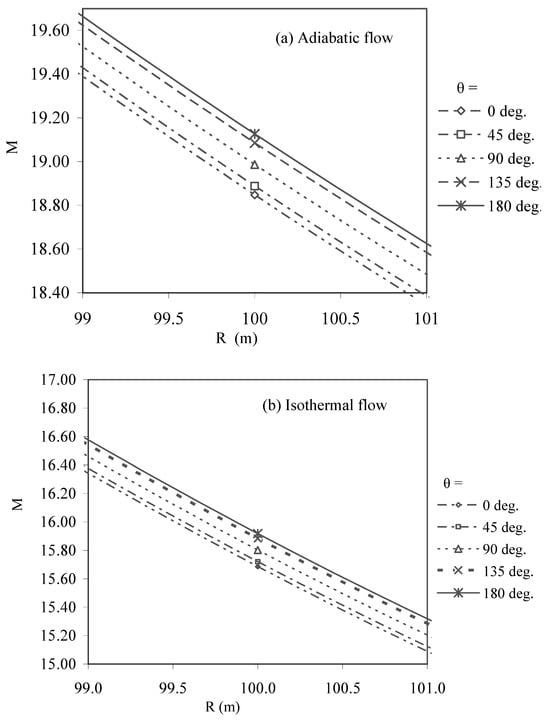
Figure 5.
Variation of shock strength (M) with propagation distance (R) in different directions (θ) at the height of explosion h0= 4 km.
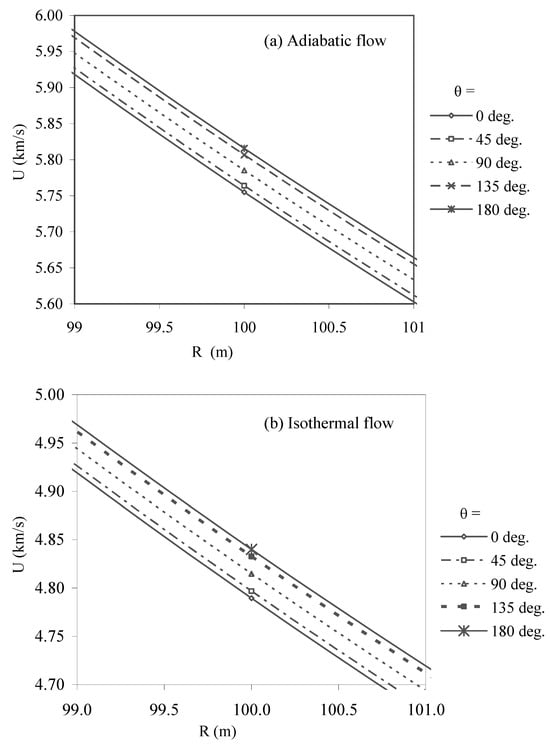
Figure 6.
Variation of shock velocity (U) with propagation distance (R) in different directions (θ) at the height of explosion h0= 4 km.
Plots in Figure 5 show that, in both the cases of adiabatic and isothermal flow, shock strength M is larger as the shock moves in upward direction (i.e. M in the direction θ = 1800 >θ = 900 >θ = 00). However, for the isothermal case, the value of shock strength is smaller in comparison to the adiabatic case.
Corresponding to Figure 5(a and b), Variation of shock velocity U with propagation distance R, in different directions at a fixed height of explosion h0= 4km is shown in Figure 6a (adiabatic case) and Figure 6b (isothermal case).
Plots in Figure 6 show that, in both the cases, shock velocity U is larger as the shock moves in upward direction (i.e. U in the direction θ = 1800 >θ = 900 >θ = 00). However, for the isothermal case, the values of shock velocity are smaller in comparison to the adiabatic case.
For the adiabatic and isothermal cases, the variations of entropy production Δs/ℜ with propagation distance R in different directions, at a fixed height of explosion h0= 4km is given in Figure 7a,b respectively. Figure 7a show that for the adiabatic case, entropy production is larger in upward motion of the shock, in comparison to the downward motion of the shock.
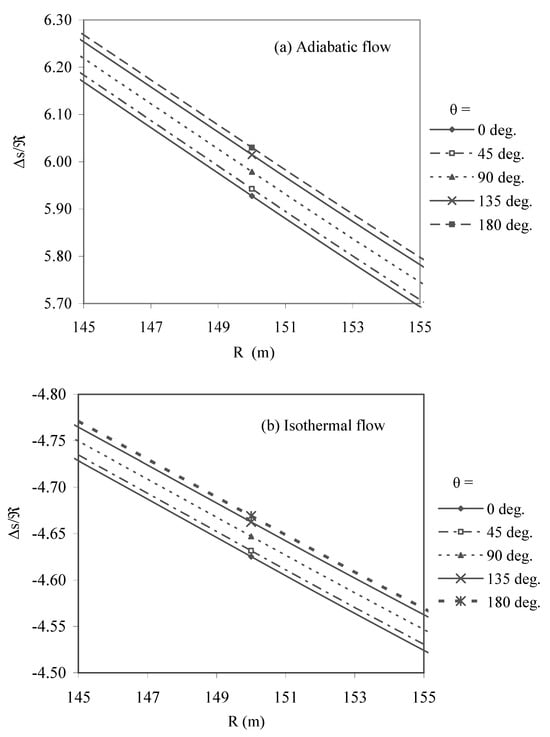
Figure 7.
Variation of entropy production (Δs/ℜ) with propagation distance (R) in different directions (θ) at the height of explosion h0= 4 km.
For the isothermal case (Figure 7b), the curves show that entropy production is smaller in upward motion of the shock, in comparison with the downward motion of the shock.
Figure 8a,b shows the variation of shock strength M with the direction (θ) at a fixed propagation distance R=10m and a constant height of explosion h0=7km, for the adiabatic and isothermal cases respectively. Axes, representing M are drawn at θ=900 (showing the horizontal direction, in which shock motion is unaffected by the gravity). The direction 1800> θ>900 signifies the upward motion of the shock and the direction 900> θ>00 show the downward motion of the shock.
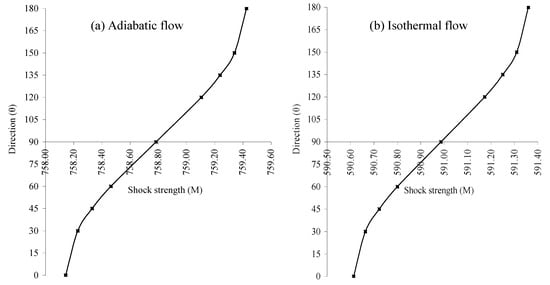
Figure 8.
Variation of shock strength (M) with direction (θ) at the height of explosion (h0) = 7 km and at propagation distance R=10m.
Figure 9a,b shows the variation of shock velocity U with the direction (θ), for the adiabatic and isothermal cases respectively, at a fixed propagation distance R=10m and a constant height of explosion h0=7km.
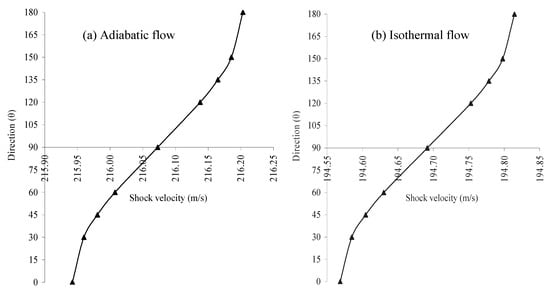
Figure 9.
Variation shock velocity (U) with direction (θ) at the height of explosion (h0) = 7 km and at propagation distance R=10m.
Figure 8 and Figure 9 show that in both the cases, shock strength and shock velocity are highest in vertical upward motion (θ=1800) of the shock. With a decreasing trend, M and U are lowest in downward motion of the shock (θ=00).
Figure 10a,b shows the corresponding variation of entropy production Δs/ℜ with the direction (θ) at a fixed propagation distance R=10m and at a height of explosion h0=7km, for the adiabatic and isothermal flow respectively.
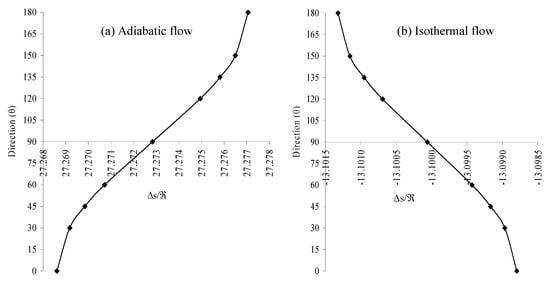
Figure 10.
Variation of entropy production (Δs/ℜ) with direction (θ) at the height of explosion (h0) = 7 km and at propagation distance R=10m.
For the adiabatic case, Figure 10a shows that entropy production is highest in vertical upward motion (θ=1800) of the shock. With a smoothly decreasing trend, entropy production Δs/ℜ is lowest in downward motion of the shock. However, the isothermal case (Figure 10b) shows that entropy production is lowest in vertical upward motion (θ=1800) of the shock.
A more enhanced view of the directional dependence of the shock motion for the adiabatic and isothermal flows are shown in radial plots in Figure 11, Figure 12 and Figure 13. Plots in Figure 11(a, b and c) show the shock strength profiles at propagation distances R= 10m, 20m and 30m respectively. Radial axes show the different directions, from 00 to 3600 and the shaded area gives the relative magnitude of shock strength in different direction. Corresponding profiles of shock velocity and entropy production are shown in Figure 12 (a, b, c) and Figure 13 (a, b, c).
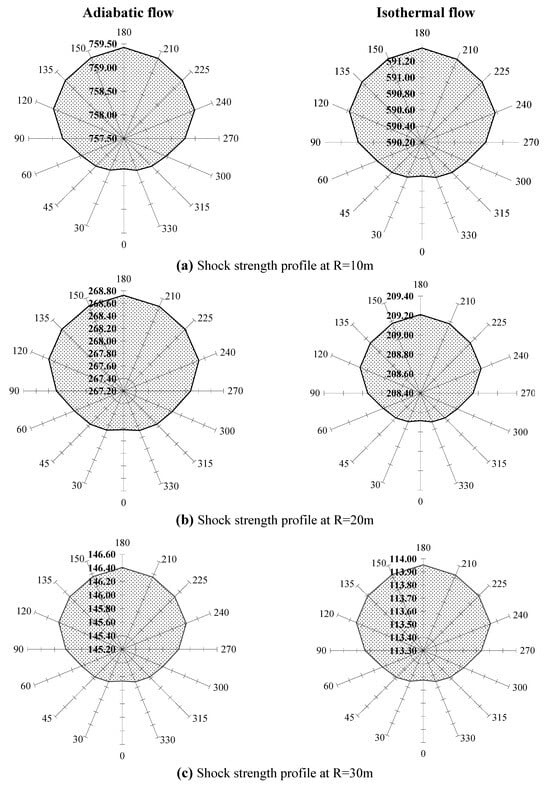
Figure 11.
Variation of shock strength (M) in different directions (shock strength profiles) at the height of explosion h0=7 km and at the propagation distances (a) R=10m (b) R=20m (c) R=30m.
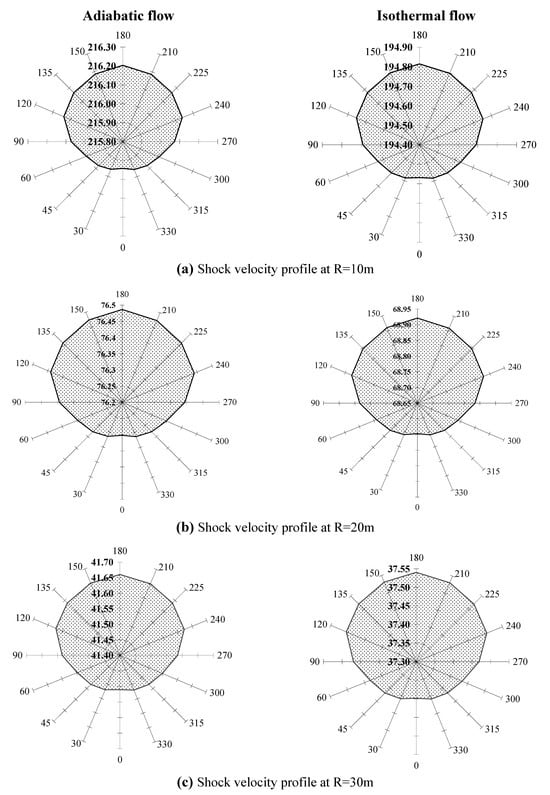
Figure 12.
Variation of shock velocity (U) in different directions (shock velocity profiles) at the height of explosion h0=7 km and at the propagation distances (a) R=10m (b) R=20m (c) R=30m.
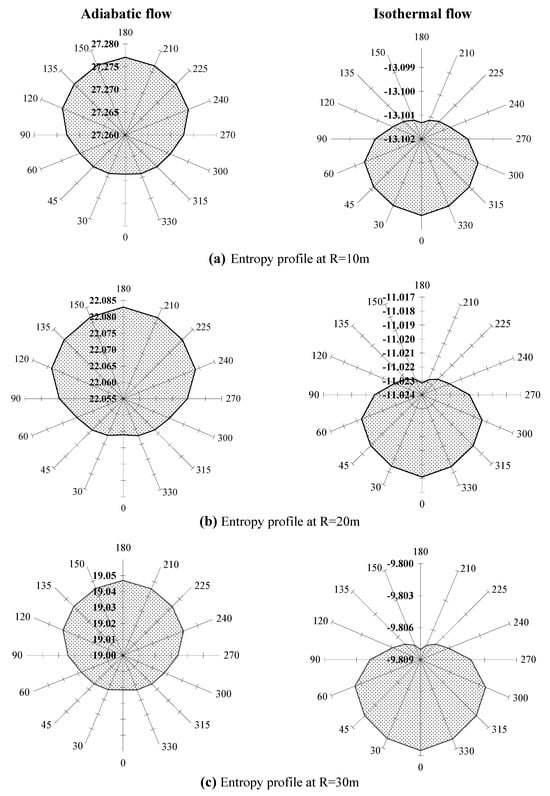
Figure 13.
Variation of entropy production (Δs/ℜ) in different directions (entropy profiles) at the height of explosion h0=7 km and at the propagation distances (a) R=10m (b) R=20m (c) R=30m.
In both the cases, the profiles of shock strength (M) and shock velocity (U) given in Figure 11(a, b and c) and Figure 12(a, b and c) show a smooth variation with direction, with the highest value in vertical upward direction and the lowest value in vertical downward direction, forming an oval shape. The profiles maintain their shape as the shock moves forward.
For adiabatic flow, the profiles of entropy production Δs/ℜ, given in Figure 13(a, b and c) show a smooth variation with direction, with the highest value in vertical upward direction and the lowest value in vertical downward direction, forming an oval shape. Whereas, for isothermal flow, the profiles of entropy production Δs/ℜ, show a smooth variation with direction, with the lowest value in vertical upward direction and the highest value in vertical downward direction, forming an oval shape. The profiles maintain their shape as the shock moves forward.
5. Comparison with observed results
Among the results, the most easily observable is the velocity of the shock U. All the other parameters can be calculated using shock velocity. I.e. why, in this work we have used the shock velocity for the comparison of our results. The commonly available experimental data is given in Taylor′s paper []. His work describes the New Mexico atomic bomb explosion, occurred in 1945 [Appendix]. The experimental points fit very well in the theoretical curve predicted by Taylor.
To make a comparison, we have used here the same values of γ=1.32, energy of explosion T′=8.45×1013 J and initial density ρ0=1.25 kg/m3 as given in []. The horizontal direction (θ=900) of shock propagation is taken for the height of explosion h0=100m.
In Figure 14, it can be seen that shock velocity U calculated using Energy hypothesis for both adiabatic and isothermal flow are higher then the shock velocity obtained using Taylor′s relation. Near the point of explosion the difference in the two is quite large, which decreases sharply as the shock moves away from the point of explosion. It can be seen that shock velocity U calculated using Energy hypothesis for isothermal flow give more accurate results in comparison to the adiabatic flow.
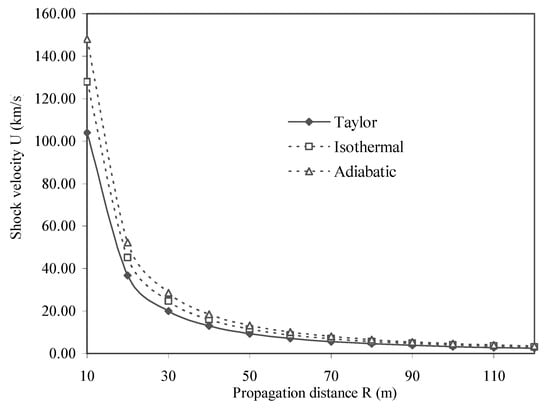
Figure 14.
Comparison of our results for shock velocity with those obtained using Taylor′s work.
In Figure 15, the comparison of density ratio (ρ2/ρh) for the isothermal and adiabatic flow shows that the post shock medium is largely compressed in the case of isothermal shock how ever for the adiabatic case the compression is limited only up to (γ+1)/(γ-1), as given in relation (2.19).
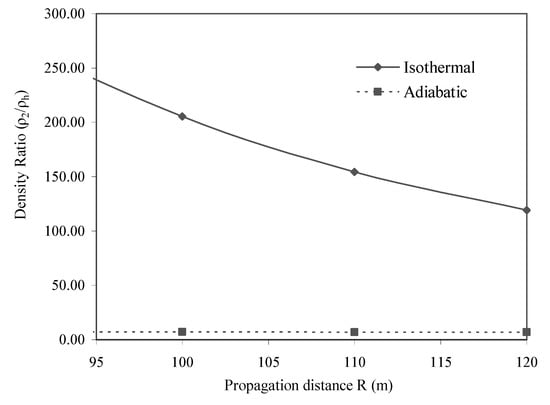
Figure 15.
Comparison of density ratio (ρ2/ρh) obtained for the adiabatic and isothermal flow.
6. Negative entropy production by isothermal shocks!!
Entropy production for a gas is simply given by:
For the isothermal compression process (created by the isothermal shock), Tinitial=Tfinal and ρfinal>ρinitial, we have the entropy production (Δs/ℜ) = - (ρfinal/ρinitial), which results a negative entropy production. This looks paradoxical, as if it is the violation of second law of thermodynamics. But it is not violating the second law of thermodynamics.
This can be explained on the basis of the entropy concept of Prigogine []. According to it, the change in entropy dS can be splitted into two parts, i.e.
dS = deS + diS
Where deS denotes the flow of entropy due to interaction with the exterior and diS is the contribution due to changes inside the system. Entropy change inside the system diS is never negative. i.e.
diS = 0 for reversible process
diS > 0 for irreversible process
The medium in which the shock propagates can be divided into two regions, namely the shocked region and the unshocked region. For the case of adiabatic shock, the shocked region behaves as an isolated system. At any moment, there is no coupling of energy between this isolated system and the surrounding unshocked region (i.e. deS = 0). In this case the change in entropy is,
dS = diS > 0
But in case of isothermal shock, the shocked region is no more an isolated system but it behaves as an open system. Isothermal conditions permit the coupling of energy through radiation between the shocked and unshocked region. In case of isothermal shock propagation, the first phase of the process started earlier, with the preheating of the gas molecules in the unshocked region by the radiation energy produced in the shocked region. The isothermal condition (T1 = T2) prevails due to the preheating of unshocked gas molecules in the presence of large amount of radiation energy. In the second phase of the process, the gas molecule crosses the shock front and enters in the shocked region where they are compressed, as well as radiates, to maintain the isothermality.
For an open system, entropy can change in both ways i.e. positive and negative. If the heat flows into the system, its entropy increases. But, entropy decreases if the heat flows out from the system. The first phase of the shock process (during preheating) leads to an increase in entropy of the gas molecules where as the second phase produces a decrease in entropy. Overall entropy increases because of the large increase in entropy in the first phase, in comparison to the decrease in entropy in the second phase. Hence, there is no violation of the second law of thermodynamics.
In our study we have considered only the equilibrium conditions for the isothermal case. From conservation of energy point of view, for the isothermal shock case, it is necessary to include the heat flow between the system (shocked region) and the surrounding (unshocked region), which happens in the form of radiations. Considering the heating of unshocked gas by the radiations, the shock process becomes very complex.
Conclusion
The results of this paper show that for both adiabatic and isothermal flow, explosion at higher altitudes on earth′s atmosphere produces higher shock velocity and shock strength. In both the cases, near the point of explosion, strength and velocity of the shock are quite large. As the shock moves away from the point of explosion, shock strength and shock velocity decrease initially very sharply. At a sufficiently large distance the shock strength approaches the value unity and shock velocity approaches the value of local sound velocity. However, for the isothermal case, the values of shock strength and shock velocity are smaller in comparison to the adiabatic case. For adiabatic flow, entropy production/unit mass of the gas is also higher for explosions at high altitudes in comparison to explosion at low altitude. This is due to the low initial pressure and density at high altitudes. The molecules of air are freer for random motion, due to low pressure and density. Hence, the shock produces higher entropy at high altitudes.
The results for isothermal assumption show that entropy production/unit mass of the gas is smaller for explosions at high altitudes in comparison to explosion at low altitude. With the isothermal assumption, entropy production is equal to the negative logarithm of the final and initial density. Due to the low density at high altitudes, such results are obtained. However, the variation of entropy production with propagation distance increases as the shock moves away from the point of explosion due to the decreasing isothermal compression.
The directional study of adiabatic shock propagation shows that upward moving shock has higher shock velocity and shock strength. For adiabatic shock, entropy production is also higher for upward moving shock in comparison to downward moving shock. The variations of shock strength, shock velocity and entropy production with direction (the profiles of shock strength, shock velocity and entropy production respectively) are also smooth, with the highest value in the vertical upward direction and lowest value in vertical downward direction, forming an oval shape. All the profiles maintain their shape as the shock moves forward. These results are different from those achieved in case of shock propagation in seawater []. In case of water, the profiles change their shape during the shock motion.
In contrast, the directional study of isothermal shock propagation shows that the entropy production is smaller in upward motion of the shock. The profiles of shock strength and shock velocity have the highest value in vertical upward direction and lowest value in the vertically downward direction, forming the shape of an oval. Where as, the profiles for entropy production Δs/ℜ show an opposite trend in comparison to the profiles of shock strength and shock velocity. The profiles maintain their shape as the shock moves forward.
Comparison with observed results show that shock velocity U calculated using Energy hypothesis for isothermal flow give more accurate results in comparison to the adiabatic flow.
Negative outcome of entropy in isothermal assumption shows that the state of the system (shocked medium) has changed from a relatively disorganized state to a more organized state (density of the medium is largely increased). It is the change in entropy that ultimately provides us with the answer to how systems will naturally evolve in one direction with time and not the other. Systems always evolve in time in such a way that the total entropy of the “system + surroundings” increases. If it is observed that entropy appears to decrease in a system, than compulsorily there is a change in the entropy of the surroundings large enough to make the total entropy change positive.
Our results show that blast wave produces a non-isentropic flow field behind it. In other words, the blast wave produces a flow field with entropy gradients. The present work is as such applicable to the case of explosions in stellar medium. An explosion in such type of medium produces entropy gradients, with decreasing value of entropy, away from the point of explosion. Due to many reasons, compression waves are generated in the stellar medium. The steepening of a normal compressive wave into a shock in the presence of entropy gradients have been studied by many [,,]. Hence, each compressive wave moving out from the interior of the stellar medium are steepened to form a shock, in the presence of entropy gradients created earlier. In this manner multiple shocks are presents in the non-isentropic stellar medium. This work is applicable as well, for the shock motion in interstellar mediums. The interstellar medium is dominated by the action of Supernovae, stellar wind and other violent activities. Shock waves are supposed to be an essential part in all the violent activities of the space. In this manner the study of shocks play an important role in the dynamic evolution, emission process and interpretation of many unsolved facts of the universe.
The physics of shock waves give a strong coupling between the fluid dynamics and the thermodynamics of the medium, in which they propagates. The thermodynamic state of the fluid molecules changes as they cross the shock front. Thermodynamic state is defined by many variables. Among them, entropy is the most powerful to define a thermodynamic state. For all type of processes, reversible or irreversible, entropy analysis can provide many such informations regarding the changes in energy and the matter [], which can not be given by other variables. Because of this, it becomes important to analyze the entropy production during shock propagation.
Data employed
The data employed for the calculation is given below:
Acceleration due to gravity at the earth surface gs = 9.81 m/s2
Radius of the earth Re = 6371.230 km
Pressure at the earth surface p1 = 1 b
Density of the air at the earth surface = 1.29 kg/m3
Specific heat ratio for air γ =1.4
Energy released during explosion = 8.45 x 1013 J
Appendix
The experimental results are based on the photographs of the explosion taken at different moments. The different photographs give the radius of the shock at different moments. These results fit very well in the theoretical curves of Taylor [], giving the relation between the shock radius and the time as:
Where β is a coefficient depending on specific heat ratio γ (note- β is denoted as α in []). From the relation between the radius of the shock and time, we get the relation for the shock velocity U as below:
For γ=1.32, the value of βT′=8.45×1013 J.
References
- Balasubramanian, K.; Sujith, R.I. Relativistic shock formation in the presence of radial entropy gradients. Phy. Fluids 2005, 17, 057105. [Google Scholar] [CrossRef]
- Bhatnagar, P.L.; Sachdev, P.L. Propagation of an isothermal shock in stellar envelopes. ILNuovo Cimento 1966, XLIV B(no. 1), 15–30. [Google Scholar] [CrossRef]
- Bhomik, J.B. A study of the expansion of the solar corona with radiation heat flux. Astrophy. Sp. Sci. 1980, 70, 433–439. [Google Scholar] [CrossRef]
- Bhutani, O.P. Propagation and attenuation of Cylindrical blast wave in Magneto hydrodynamics. J. Math. Anal. Applic. 1966, 13, 565–576. [Google Scholar] [CrossRef]
- Brode, H.L. Review of Nuclear weapons effects. Ann. Rev. Nuclear Science 1968, 18, 153. [Google Scholar] [CrossRef]
- Dincer, I.; Cengel, Y.A. Energy, Entropy and Exergy concepts and their role in thermal engineering. Entropy 2001, 3, 116–149. [Google Scholar] [CrossRef]
- Eschenroeder, A.Q. Entropy changes in nonequilibrium flows. Phy. Fluids 1963, 6, 1408–1419. [Google Scholar] [CrossRef]
- Gretler, W. Blast wave in inhomogeneous atmosphere including real gas and heat transfer effect. Flu. Dy. Res. 1994, 14, 191–216. [Google Scholar] [CrossRef]
- Hayes, W.D. Self similar strong shocks in an exponential medium. J. Fluid Mech 1968, 32(part 2), 305–315. [Google Scholar] [CrossRef]
- Hayes, W.D. The propagation upward of the shock wave from a strong explosion in the atmosphere. J. Fluid Mech. 1968, 32(part 2), 317–331. [Google Scholar] [CrossRef]
- Kopal, Z. The propagation of Shock waves in self-gravitating gas spheres. Ap. J. 1954, 120, 159–171. [Google Scholar] [CrossRef]
- Korobeinikov, V.P.; Melnikova, N.S.; Rjazanov, E.V. Theory of point explosion (in Russian). Fizmutgiz 1961, 201. [Google Scholar]
- Korobeinikov, V.P. The problem of a strong point explosion in a gas at zero temperature gradient (in Russian). Dokl. Akad. Nauk. SSSR 1956, 109(no. 2), 271–273. [Google Scholar]
- Laumbach, D.D.; Probestein, R.F. A point explosion in a cold exponential atmosphere. J. Fluid Mech. 1969, 35(part 1), 53–75. [Google Scholar] [CrossRef]
- Laumbach, D.D.; Probstein, R.F. A point explosion in a cold atmosphere. Part 2. Radiating flow. J. Fluid Mech. 1970, 40(part 4), 833–858. [Google Scholar] [CrossRef]
- Lin, H.; Szeri, A.J. Shock formation in the presence of entropy gradients. J. Fluid Mech 2001, 431, 161–188. [Google Scholar] [CrossRef]
- Melnikova, N.S. Unsteady motion of compressible media with blast wave. Proc. Of the Steklov Instt. Maths, American Math. Soc. 1967, 87, 109. [Google Scholar]
- Muralidharan, S.; Sujith, R.I. Shock formation in the presence of entropy gradients in fluid exhibiting mixed nonlinearity. Phy. Fluids 2004, 16, 4121–4128. [Google Scholar] [CrossRef]
- Nath, O. Self similar flow behind a spherical shock with varying strength in an inhomogeneous medium. Astrophy Sp. Sci. 1988, 146, 169–174. [Google Scholar] [CrossRef]
- Ojha, S.N. Self similar flow behind a spherical shock with varying strength in an inhomogeneous self gravitating medium. Astrophy Sp. Sci. 1987, 129, 11–17. [Google Scholar] [CrossRef]
- Parker, E.N. Interplanetary dynamical process; Intrscience: New York, 1963; pp. 107–111. [Google Scholar]
- Prigogine, I. Introduction to thermodynamics of irreversible process, 2nd ed.; Interscience Pub., 1955; pp. 14–36. [Google Scholar]
- Raizer, Yu.P. On the brightness of strong shock waves in the air. Soviet Phys. JETP (Eng. Transl.) 1958, 6, 77–84. [Google Scholar]
- Ranga Rao, M.P.; Purohit, S.C. Self similar flow with increasing energy-2 Isothermal flow. Int. J. Engg. Sci. 1972, 10, 963–973. [Google Scholar] [CrossRef]
- Ray, G.D.; Bhomik, J.B. Similarity solutions for explosions in radiating star. Ind. J. Pure App. Maths 1976, 7(no. 1), 96–103. [Google Scholar]
- Rosciszewshi, J. Calculations of the motion of non-uniform shock waves. J. Fluid Mech. 1960, 8, 337–367. [Google Scholar] [CrossRef]
- Sachdev, P.L.; Ashraf, S. Strong shock with radiation near the surface of star. Phy. Fluids 1971, 14(no. 10), 2107–2110. [Google Scholar] [CrossRef]
- Sakurai, A. On the propagation and structure of Blast wave -II J. Ph. Soc. Japan 1954, 9(no.2), 256–266. [Google Scholar] [CrossRef]
- Sakurai, A. On the propagation and structure of Blast wave-I. J. Ph. Soc. Japan 1953, 8(no.5), 662–669. [Google Scholar] [CrossRef]
- Sedov, L.I. On unsteady one dimensional motions of a gas near the centre of symmetry (in Russian). Dokl. Akad. Nauk. SSSR 1952, 87(no1), 4. [Google Scholar]
- Sedov, L.I. Propagation of strong explosion waves (in Russian). P M M 1946, 10(no.2), 241–250. [Google Scholar]
- Singh, J.B.; Singh, P.S. Cylindrical blast wave with radiation heat flux in self gravitating gas. IL Nuovo Cimento 1995, 17 D(no. 4), 343–349. [Google Scholar] [CrossRef]
- Singh, V.P. Modification of energy hypothesis for the case of explosive charge. Ind. J. Pure Appl. Math. 1976, 7(no.2), 147–150. [Google Scholar]
- Singh, V.P. On underwater explosions- A comparative study. Def. Sci. J. 1982, 32, 327–332. [Google Scholar] [CrossRef]
- Singh, V.P. Spherical shock wave in water. Ind. J. Phys. 1972, 46, 547–555. [Google Scholar]
- Singh, V.P.; Bola, M.S. A note on explosive shock in homogeneous water. Ind. J. Pure Appl. Math. 1976, 7(no. 12), 1405–1410. [Google Scholar]
- Solinger, A.; Rappaport, S.; Buff, J. Isothermal blast wave model of Supernova remnants. Astrophy. J. 1975, 201, 381–386. [Google Scholar] [CrossRef]
- Strusmia, A. A detailed study of entropy jump across shock waves in relativistic Fluid dynamics. IL Nuovo cimento 1986, 92B(no.1), 91–105. [Google Scholar] [CrossRef]
- Taylor, G.I. The formation of a blast wave by a very intense explosion.-I Theoretical discussion. Proc. Roy. Soc. 1950, A 201, 159–174. [Google Scholar]
- Taylor, G.I. The formation of a blast wave by a very intense explosion.-II The atomic explosion of 1945. Proc. Roy. Soc. 1950, A 201, 175–186. [Google Scholar]
- Thomas, T.Y. On the propagation and decay of spherical blast waves. J. Math. Mech. 1957, 6, 607–620. [Google Scholar] [CrossRef][Green Version]
- U.S. Department of Defense. The effect of Atomic weapons; Mc Graw Hill: New York, 1950. [Google Scholar]
- Vishvakarma, J.P.; Nagar, K.S.; Mishra, R.B. On the propagation of shock wave produced by explosion of a spherical charge in deep sea. Def. Sci. J. 1988, 38(no.1), 69–76. [Google Scholar] [CrossRef]
- Website www. nuclearweaponarchive.org/nwfaq/nfaq5.
- Website www.cddc.vt.edu/host/atomic/nukeffect/enw77b3.
- Yadav, R.P.; Rana, D.S.; Singh, A. Effect of overtaking disturbances on sound and temperature behind strong shock waves in non-uniform medium. J. Nat. Phy. Sci. 2000, 14(1-2), 49–58. [Google Scholar]
- Yadav, R.P.; Agarwal, P.K.; Sharma, A. On the entropy production due to explosion in sea water. Entropy 2005, 7(2), 134–147. [Google Scholar] [CrossRef]
- Yadav, R.P.; Gangwar, P.K. Change in entropy of the universe. Acta Cien. Indica 2002, 28(no.3), 121–128. [Google Scholar]
- Zel’dovich, Y.B.; Raizer, Y.P. Physics of shock wave and high temperature hydrodynamic phenomena; Academic press: New York, 1966; vol. II, p. 612. [Google Scholar]
- Zel’dowitch, Ya.B. Shock waves of large amplitude in air. Soviet Phys. JETP (Eng. Transl.) 1957, 5, 919–927. [Google Scholar]
- Zemansky, M.W.; Dittman, R.H. Heat and thermodynamics; Mc Graw Hill.: New York, 1997; pp. 194–196. [Google Scholar]
© 2006 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).