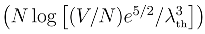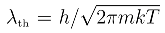Two-way thermodynamics: Could it really happen?
Abstract
:1. Context
2. Opposite arrows
3. Dialogue on opposite arrows
3.1 Solving the two-time boundary value problem
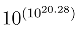 microstates, i.e., lives in a Hilbert space of that dimension. Squeezing them into 1/64 that volume (in coordinate space) changes the “20.28” to about 20.24. Squeezing them by only 1/8 and insisting that they reoccupy such a region again at a later time also brings the “20.28” to 20.24 [18]. There’s plenty of room in phase space.
microstates, i.e., lives in a Hilbert space of that dimension. Squeezing them into 1/64 that volume (in coordinate space) changes the “20.28” to about 20.24. Squeezing them by only 1/8 and insisting that they reoccupy such a region again at a later time also brings the “20.28” to 20.24 [18]. There’s plenty of room in phase space.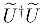 , where
, where 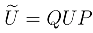 . The operator
. The operator 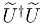 is Hermitian and has spectrum in the interval [0, 1]. Eigenvectors with eigenvalue 1 represent solutions to the boundary value problem. In [8] I report studies of this mathematical problem for several models of apparatus. Generally speaking there are many eigenvalues clustering around 1. (Interestingly, sometimes there can be none, and this gives rise to potential experimental tests of this theory. See [19].) As the size of the apparatus grows there are more and more near-unity eigenvalues as well [20]. Two remarks: (1.) For these special states there is no entanglement at the end of a measurement, particularly useful if one wants to think time-symmetrically about measurement. (2.) Apropos Zeh’s remarks about trial and error in the finding of solutions, when solutions of this problem were produced, the process consisted of finding the spectrum (including eigenvectors) of the particular operator mentioned above by standard operator techniques (usually numerical).
is Hermitian and has spectrum in the interval [0, 1]. Eigenvectors with eigenvalue 1 represent solutions to the boundary value problem. In [8] I report studies of this mathematical problem for several models of apparatus. Generally speaking there are many eigenvalues clustering around 1. (Interestingly, sometimes there can be none, and this gives rise to potential experimental tests of this theory. See [19].) As the size of the apparatus grows there are more and more near-unity eigenvalues as well [20]. Two remarks: (1.) For these special states there is no entanglement at the end of a measurement, particularly useful if one wants to think time-symmetrically about measurement. (2.) Apropos Zeh’s remarks about trial and error in the finding of solutions, when solutions of this problem were produced, the process consisted of finding the spectrum (including eigenvectors) of the particular operator mentioned above by standard operator techniques (usually numerical).3.2 Isolation
3.3 Closed timelike curves
3.4 Entropy calculation
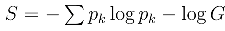 , with pk = nk/N, if all grains are of equal coordinate space volume. The “pk log pk” as usual arises from the logarithm of N!/(n1!...nG!) and represents the missing information associated with particle identity. The missing information associated with going from real numbers to finite volumes is the same for all (n1,..., nG), and is dropped, since in this study I am not concerned with comparing coarse grainings.
, with pk = nk/N, if all grains are of equal coordinate space volume. The “pk log pk” as usual arises from the logarithm of N!/(n1!...nG!) and represents the missing information associated with particle identity. The missing information associated with going from real numbers to finite volumes is the same for all (n1,..., nG), and is dropped, since in this study I am not concerned with comparing coarse grainings.4. Causality
Acknowledgments
References
- The direction of time: The role of reversibility/irreversibility in the study of nature, organized by Sergio Albeverio, Philippe Blanchard, Michael Drieschner, and Sylvie Paycha, Bielefeld. January 2002.
- Zeh, H.D. Remarks on the Compatibility of Opposite Arrows of Time, also posted on the arXiv as physics/0306083. 2003.
- Shakespeare, W. Hamlet, act III, scene 1.
- Zeh, H.D. The Physical Basis of The Direction of TimeSpringer: Berlin, 1989, 1st ed. [Google Scholar]
- Schulman, L.S. The Problem of Time. Book Review of “The Physical Basis of the Direction of Time” by H. Dieter Zeh. Science 1990, 249, 192. [Google Scholar]
- Gold, T. The Arrow of Time. Am. J. Phys. 1962, 30, 403–410. [Google Scholar]
- Schulman, L.S. Correlating Arrows of Time. Phys. Rev. D 1973, 7, 2868–2874. [Google Scholar]
- Schulman, L.S. Time’s Arrows and Quantum Measurement; Cambridge University Press: New York, 1997. [Google Scholar]
- Schulman, L.S. Opposite Thermodynamic Arrows of Time. Phys. Rev. Lett. 1999, 83, 5419–5422. [Google Scholar]
- Schulman, L.S. Resolution of causal paradoxes arising from opposing thermodynamic arrows of time. Phys. Lett. A 2001a, 280, 239–245. [Google Scholar]
- Schulman, L.S. Opposite Thermodynamic Arrows of Time. In Quantum Limits to the Second Law; Sheehan, D.P., Ed.; Amer. Inst. Phys.: Melville, New York, 2002a. [Google Scholar]
- Schulman, L.S. compromised arrows of time. In Hyperbolic Differential Operators and Related Problems; Ancona, V., Vaillant, J., Eds.; Marcel Dekker: New York, 2003; pp. 355–370. [Google Scholar]
- Schulman, L.S. Schulman Replies. Phys. Rev. Lett. 2000, 85, 897. [Google Scholar]
- The idea of having opposite arrows has been taken up by other authors as well. Wiener [37] speculated on this subject, and Creswick [38] has looked into the possibility physically producing systems that in a sense evolve backward in time. Finally there have been recent works of science fiction [39,40] that explored some of the consequences of these ideas.
- Schulman, L.S. Causality is an effect. In Time’s Arrows, Quantum Measurements and Superluminal Behavior; Mugnai, D., Ranfagni, A., Schulman, L.S., Eds.; Consiglio Nazionale delle Ricerche (CNR): Rome, 2001b; pp. 99–112, on the arXiv at cond-mat/0011507. [Google Scholar]
- The time separation used in any particular two-time problem depends on what is being studied. For looking at Gold’s proposal I generally think of the earlier time as being (approximately) the era of recombination, when our present cosmic background radiation was emitted. In a time-symmetric cosmology, I take the other time to be a corresponding time interval before the big crunch (or oscillation minimum). These are times for which matter should be distributed (roughly) uniformly, representing an entropy maximum for a system dominated by short-range forces. As the universe expands and gravitational forces dominate, uniformity becomes an extremely unlikely circumstance, so that what was a maximum becomes a minimum. This justifies two-time low entropy boundary conditions. For the opposite arrow boundary value problem, I have in mind a smaller time interval (later and “earlier” than recombination) and regions of space smaller than the entire universe. Finally, for the quantum problems associated with finding “special states” my time range is before and after the operation of a particular apparatus.
- Wheeler, J.A.; Feynman, R.P. Classical Electrodynamics in Terms of Direct Interparticle Action. Rev. Mod. Phys. 1949, 21, 425–433. [Google Scholar]
- The numbers given here differ slightly from those in [8]. Here I use the physically more realistic statistics of indistinguishable particles. These numbers also reflect more detailed state counting. Specifically, for an ideal gas the number of states is = exp(S/k) = exp
, using the standard expression [41] for the entropy of an ideal gas in three dimensions. N is computed from the pressure using PV = NkT, k is the Boltzmann constant, and
is the thermal wavelength. The formula for can also be used directly to see the effect of volume changes, as discussed in the text.
- Schulman, L.S. Jump time and passage time: the duration of a quantum transition. In Time in Quantum Mechanics; Muga, J.G., Sala Mayato, R., Egusquiza, I.L., Eds.; Springer-Verlag: Berlin, 2002b; pp. 99–120. [Google Scholar]
- The terms “apparatus” and “system” do not imply that this scheme holds only for laboratory experiments. Any situation that could lead to superpositions of macroscopically different states will have this feature. Again, the present paper is not about quantum measurement theory, and for the many questions that may come to mind please consult [8].
- Vugmeister, B.E.; Botina, J.; Rabitz, H. Nonstationary optimal paths and tails of prehistory probability density in multistable stochastic systems. Phys. Rev. E 1997, 55, 5338–5342. [Google Scholar]
- Vugmeister, B.E.; Rabitz, H. Cooperating with nonequilibrium fluctuations through their optimal control. Phys. Rev. E 1997, 55, 2522–2524. [Google Scholar]
- Judson, R.S.; Rabitz, H. Teaching Lasers to Control Molecules. Phys. Rev. Lett. 1992, 68, 1500–1503. [Google Scholar]
- Dykman, M.I.; Mori, E.; Ross, J.; Hunt, P.M. Large fluctuations and optimal paths in chemical kinetics. J. Chem. Phys. 1994, 100, 5735–5750. [Google Scholar]
- Dykman, M.I.; Luchinsky, D.G.; McClintock, P.V.E.; Smelyanskiy, V.N. Corrals and Critical Behavior of the Distribution of Fluctuational Paths. Phys. Rev. Lett. 1996, 77, 5229–5232. [Google Scholar]
- Palao, J.P.; Kosloff, R. Quantum Computing by an Optimal Control Algorithm for Unitary Transformations. Phys. Rev. Lett. 2002, 89, 188301. [Google Scholar]
- Palao, J.P.; Kosloff, R. Optimal control theory for unitary transformations. Phys. Rev. A. 2003, 68, 062308. [Google Scholar]
- Schulman, L.S. Illustration of Reversed Causality with Remarks on Experiment. J. Stat. Phys. 1977, 16, 217–231. [Google Scholar]
- Schulman, L.S. Normal and Reversed Causality in a Model System. Phys. Lett. A 1976, 57, 305–306. [Google Scholar]
- Schulman, L.S. Models for Intermediate Time Dynamics with Two-Time Boundary Conditions. Physica A 1991, 177, 373–380. [Google Scholar]
- Gell-Mann, M.; Hartle, J.B. Time Symmetry and Asymmetry in Quantum Mechanics and Quantum Cosmology. In Physical Origins of Time Asymmetry; Halliwell, J.J., Pérez-Mercader, J., Zurek, W.H., Eds.; Cambridge Univ. Press: New York, 1994; pp. 311–345. [Google Scholar]
- Bear in mind that this has meaning only with respect to a particular coarse graining.
- Zeh, H.D. The Physical Basis of The Direction of TimeSpringer: Berlin, 2001, 4th ed. [Google Scholar]
- Penrose, R. Singularities and time-asymmetry. In General Relativity: An Einstein Centenary Survey; Hawking, S.W., Israel, W., Eds.; Cambridge Univ. Press: New York, 1979. [Google Scholar]
- Penrose, R. Big Bangs, Black Holes and ‘Time’s Arrow’. In The Nature of Time; Flood, R., Lockwood, M., Eds.; Basil Blackwell: Oxford, 1986. [Google Scholar]
- Steinhardt, P.J.; Turok, N. Cosmic evolution in a cyclic universe. Phys. Rev. D 2002, 65, 126003. [Google Scholar]
- Wiener, N. Cybernetics or control and communication in the animal and the machineM.I.T. Press: Cambridge, Mass., 1961, 2nd ed. [Google Scholar]
- Creswick, R.J. Time-reversal and charge echo in an electron gas. Phys. Rev. Lett. 2004, 93, 100601. [Google Scholar]
- Wharton, K.B. Aloha. Analog Science Fiction and Fact, 2003. [Google Scholar]
- Wharton, K. Divine Intervention, Ace Books: New York, 2001.
- Baierlein, R. Thermal Physics, Cambridge Univ. Press: Cambridge, 1999.
© 2005 by MDPI (http://www.mdpi.org). Reproduction for noncommercial purposes permitted.
Share and Cite
Schulman, L.S. Two-way thermodynamics: Could it really happen? Entropy 2005, 7, 208-220. https://doi.org/10.3390/e7040208
Schulman LS. Two-way thermodynamics: Could it really happen? Entropy. 2005; 7(4):208-220. https://doi.org/10.3390/e7040208
Chicago/Turabian StyleSchulman, L. S. 2005. "Two-way thermodynamics: Could it really happen?" Entropy 7, no. 4: 208-220. https://doi.org/10.3390/e7040208
APA StyleSchulman, L. S. (2005). Two-way thermodynamics: Could it really happen? Entropy, 7(4), 208-220. https://doi.org/10.3390/e7040208