Introduction
The entropy generation plays an important role in the design and development of thermo-fluid components such as heat exchangers, pumps, turbine, and pipe networks. The optimal design of these components can be achieved by minimizing the entropy generation. Entropy generation is increased by the presence of high gradients in velocity and temperature. Such high gradients are found in very small scale devices which interact with the fluid flow such as microchannels. Entropy generation has undesirable impact on the performance of these thermal systems, which tends to destruct their exergy and as a result great efforts are made to reduce the effect of entropy generation. Examples of these efforts are found in references [
1,
2,
3,
4,
5].
In the recent years, the microfluidics or the micro-fluid mechanics became an attractive area of research. The importance of the microfluidics rises from the new applications of micro-scale electromechanical systems that encounter fluid flow, such as micro-pumps, micro-turbines and micro-robotics. Extensive experimental and theoretical studies were made in this area in order to understand the fluid behavior within these micro-devises [
6,
7,
8,
9]. An important dimensionless parameter in microflows is Knudsen number, which is the ratio of the mean free path length of the fluid to the characteristic length of the fluid domain. The macro Navier-Stokes and energy equations with no velocity slip and temperature jump boundary conditions are applicable for flows with Knudsen numbers less than 10
-3, whereas for Knudsen numbers range of 10
-3-10
-1, Navier-Stokes and energy equations are still applicable, but with velocity slip and temperature jump boundary conditions at the wall(s). For Knudsen numbers greater than 10
-1, the Navier-Stokes equations will not be valid. That is, the continuum approach will not be valid for this range of Knudsen number. For large Knudsen numbers (Knudsen number >10), the molecular approach is used to model the microfluidic systems [
10].
Unfortunately, the open literature shows very small number of papers that deal with entropy generation related problems in the field of microfluidics. On the other hand, the effect of viscous dissipation on the temperature field and on the friction factor of a microflow is investigated by [
11]. A criterion for the significance of viscous dissipation effects on microchannel flow is suggested by [
12]. In a previous work [
13], the authors have investigated the effect of fluctuation on some basic flow problems in microgeometries. In the present work, the entropy generation due to laminar incompressible forced convection fluid flow through parallel plates microchannel has been investigated numerically. For this purpose, the velocity and temperature profiles are found using the finite difference technique. The microflow regime considered in this study is the slip flow regime for which 10
-3<Kn<10
-1 [
10]. This flow regime is modeled by macro Navier-Stokes and energy equations with first order slip in velocity and jump in temperature at the wall(s) [
10]. According to the authors’ knowledge, the literature lacks for entropy generation results for microflows and thus the entropy generation for such flows needs to be investigated.
Numerical Method
The above system of four nonlinear-coupled partial differential equations is solved by adopting Kwon and Pletcher method for internal boundary layer flow. Details on this method can be found in [
14]. The equations are discretized by applying a space centered second order non-uniform finite difference grid in Y direction, and forward difference in X direction. The system of the finite difference equations are given as:
The above three FDE’s are nonlinear. The nonlinearity was resolved by applying Newton Raphson linearization. After that, the FDE’s are assembled in matrix form, which results in a banded matrix with band width equals to 7 at each x-station. The banded system is solved by making use of LSARB subroutine of IMSL library that solves real systems of linear equations in band storage mode with iterative refinement. After that, the numerical solution proceeds iteratively while the solution at the last previous x-station is used as an initial guess for the current x-station.
The number of grid points in Y direction, the grid’s expansion ratio in Y direction, the step size in X direction, and the tolerated relative error in solving the banded system are chosen very carefully in order to obtain a grid independent solutions. These values are given respectively as: 75, 1.05, 0.001, and 1x10-6.
Results and Discussions
The numerical solution is validated by comparing the obtained numerical results with the analytical solution of the special case when the left hand side of equations (1-2) is negligible at different values of Knudsen Number. The analytical solution for this case is obtained as:
where
, and
.
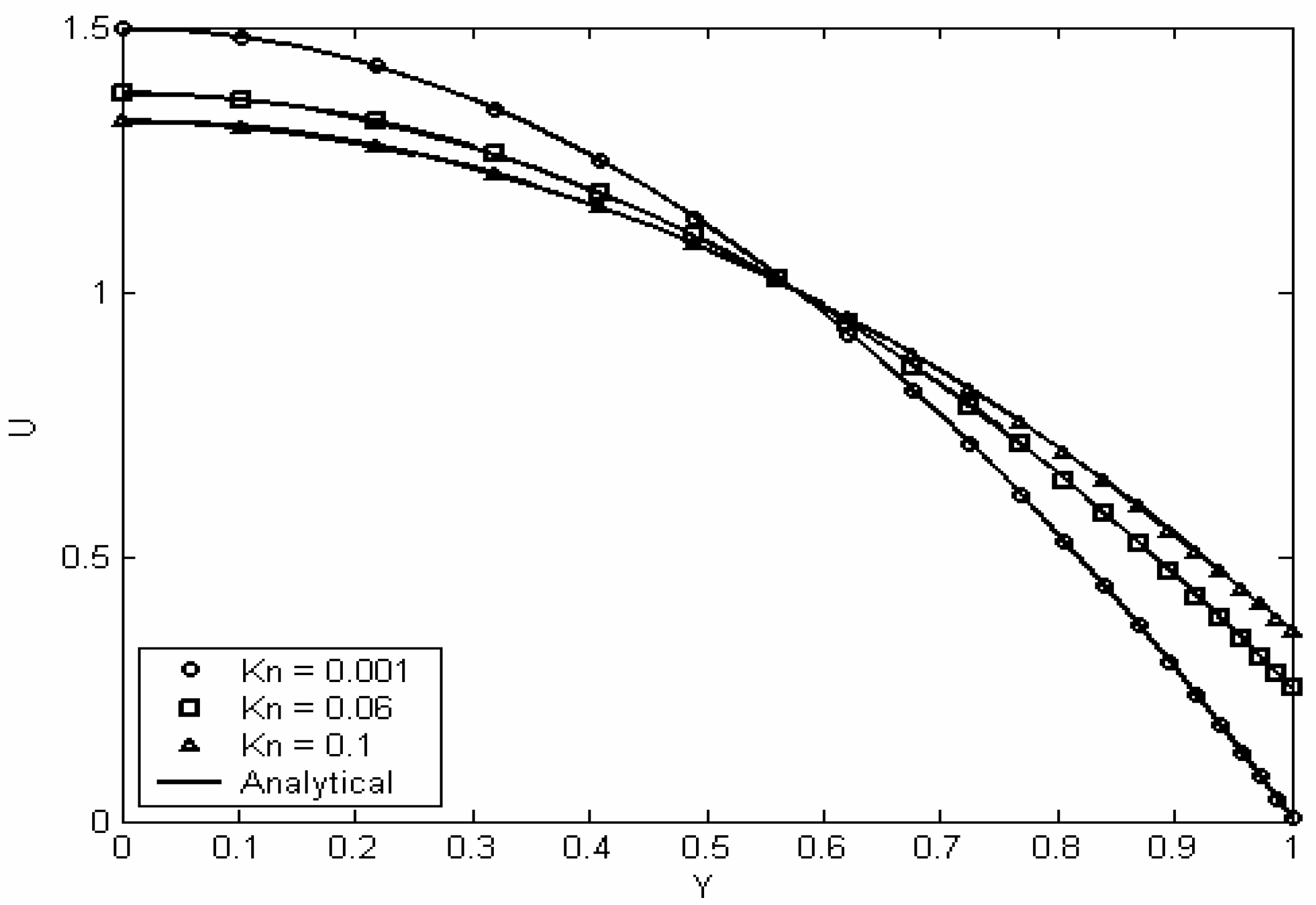
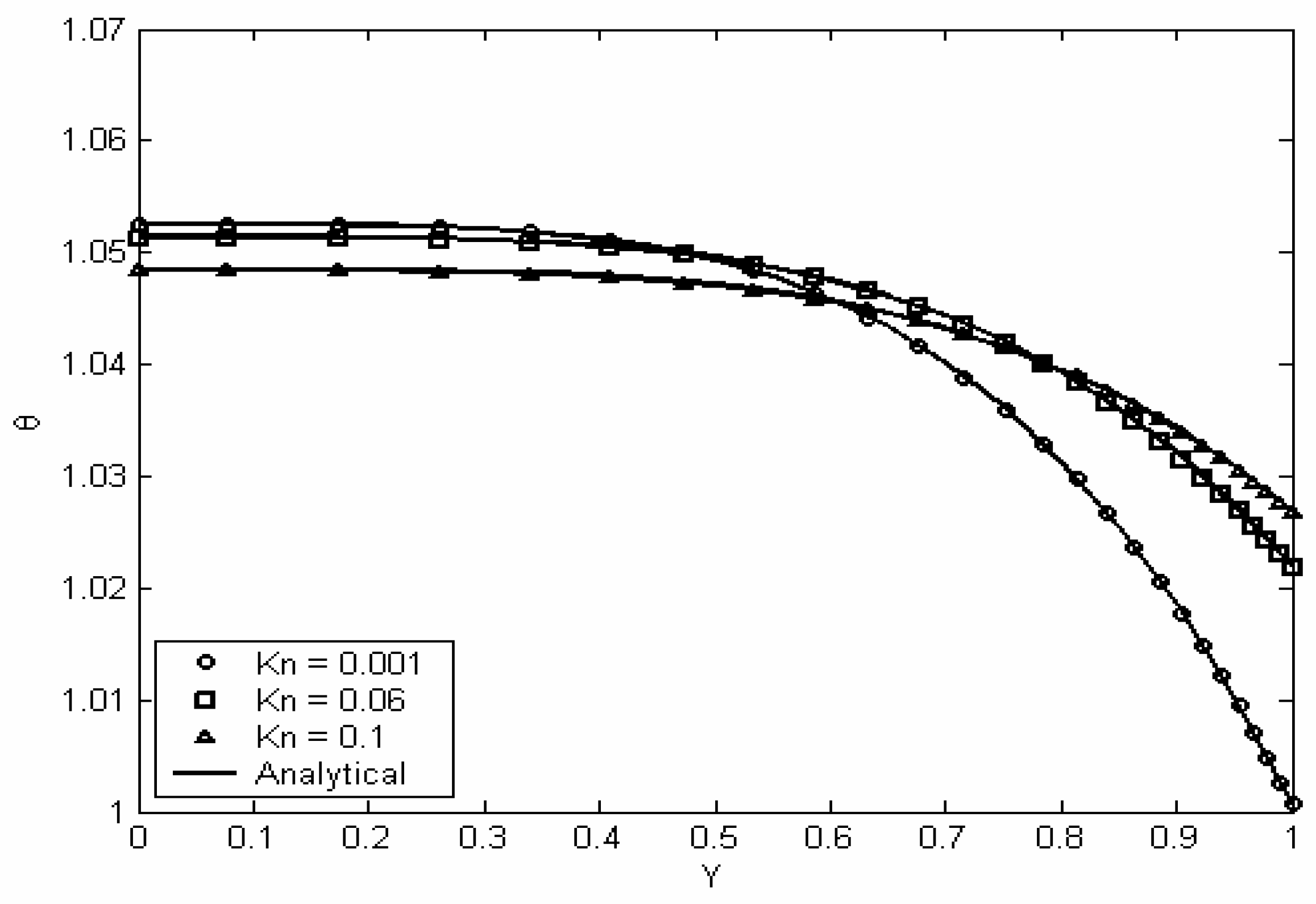
Figure 2 and
Figure 3 show a comparison between the numerical and the analytical velocity and temperature profiles at different values of Knudsen number. Obviously, the agreement between the two solutions is excellent. Also one can note that near the wall in
Figure 2, as Knudsen number increases the velocity slip increases, accordingly the flow velocity near the centerline of the channel decreases to satisfy the continuity equation. Similarly in
Figure 3, the fluid is heated under the effect of viscous dissipation and this leads to a temperature slightly above one, however since cooling occurs at the wall, the increase in temperature is not uniform between the wall and the centerline of the channel.
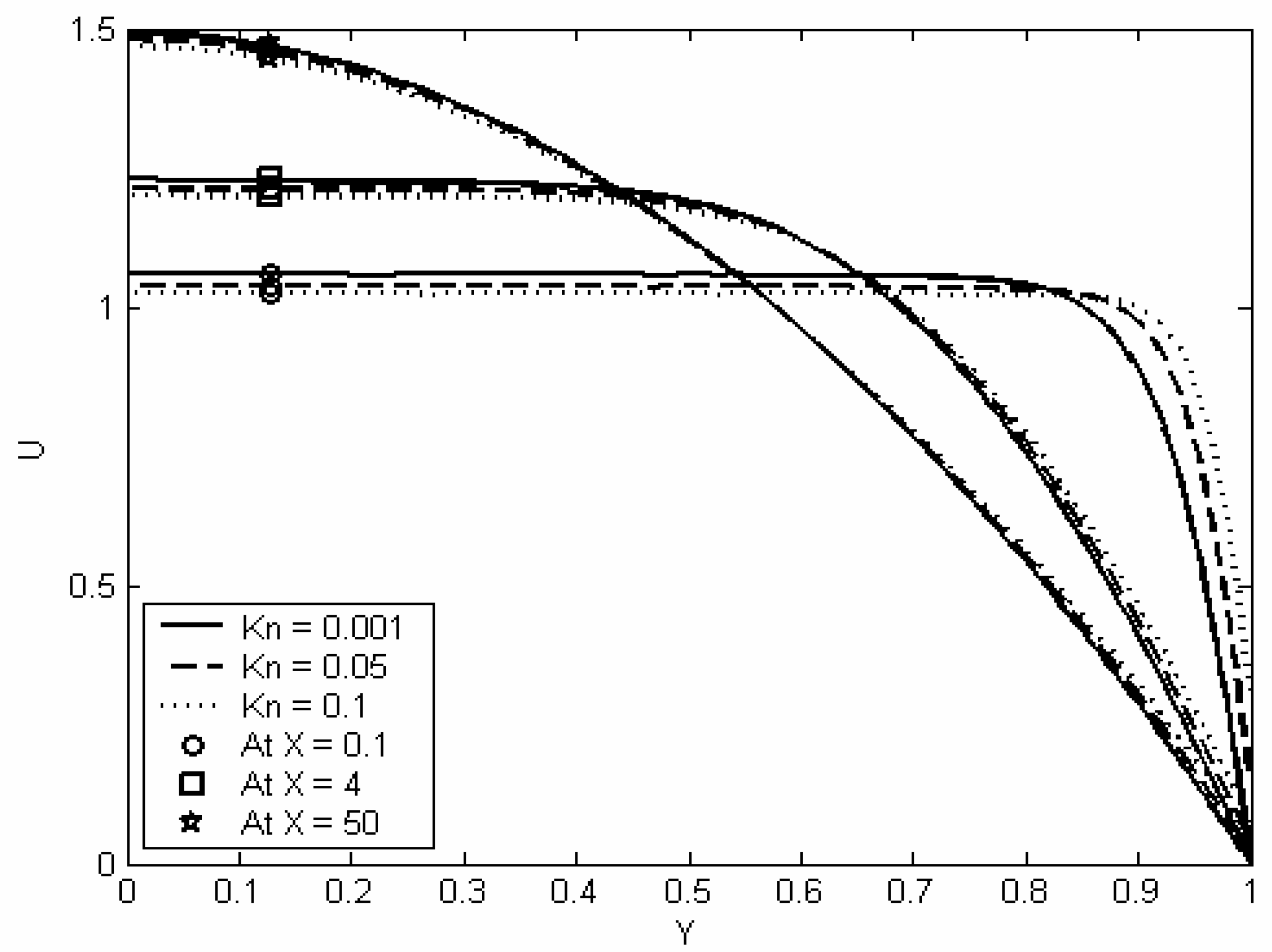
Figure (4) shows the spatial velocity profiles along the transverse direction of the channel at different Knudsen numbers. It is clear that the increase in Knudsen number causes an increase in the slip at the wall. Accordingly, the flow velocity decreases near the center of the channel in order to satisfy the continuity equation. The increase in the slip with Knudsen number results from the increase of the mean free path length of the fluid molecules, which in turn decreases the retardation effects at the walls and so increasing the slip at it. Also,
Figure (4) shows that the velocity slip at the entry region is larger than that at the fully developed region. The decrease in the velocity slip during the development of the flow results from the effect of the viscous diffusion, which tends to decrease the velocity gradient near the wall during the development of the flow.
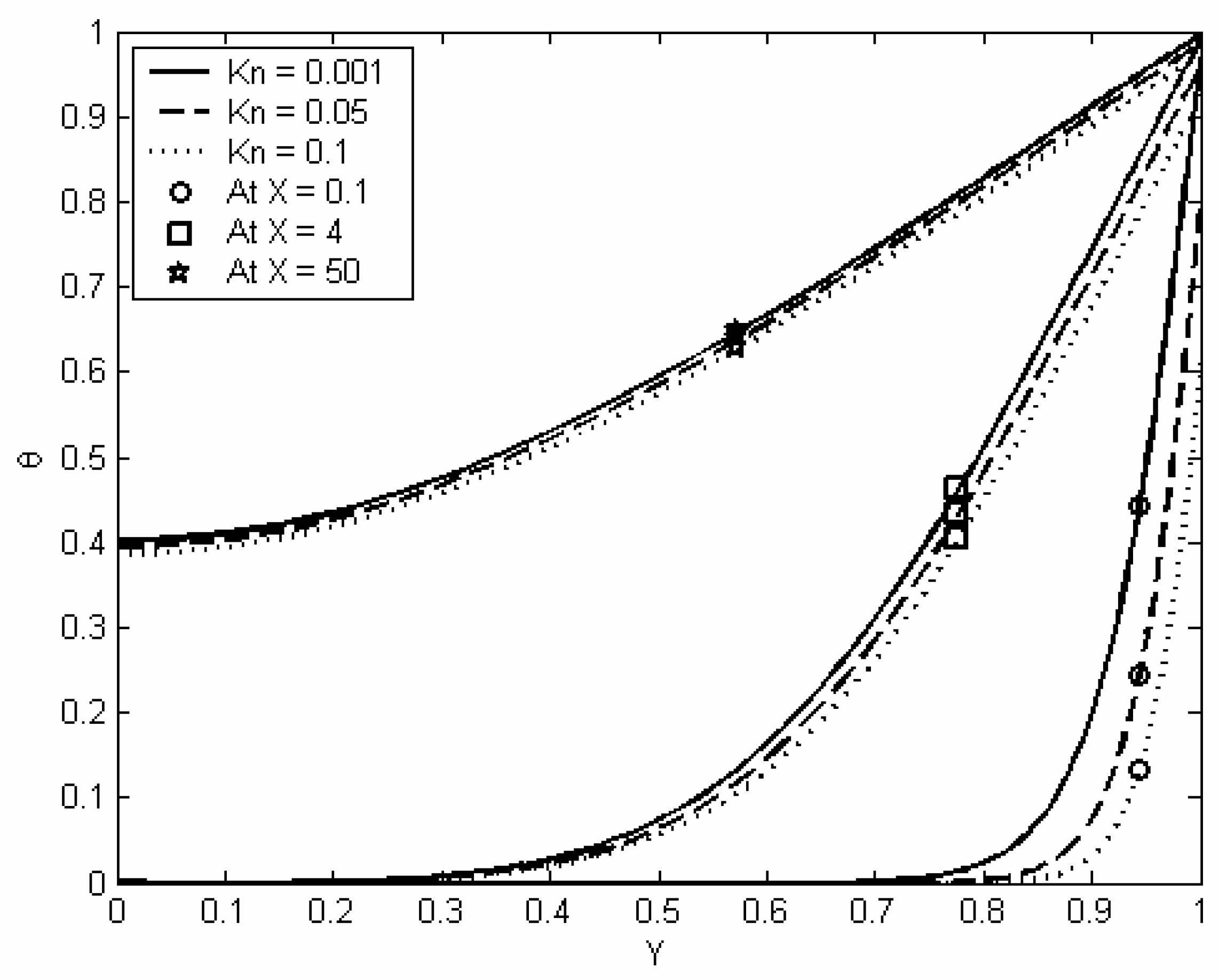
Figure (5) shows the development of the spatial fluid temperature distribution along the channel transverse direction and at different Knudsen numbers. From this figure it can be noted that as Knudsen number increases, the nondimensional temperature (θ) profiles shift down. This is due to the increase in temperature jump at the wall (i.e. less heat is transferred from the wall to the adjacent fluid). The figure also shows that the temperature jump is a maximum at the entry region of the channel. Within the entry region, the heat transfer rate is high and the temperature gradient is large. This in turns forces the temperature jump at the wall of the entry region to increase. However, as (X) increases, dissipation effect becomes more significant and this leads to a reduction in temperature jump at the wall.
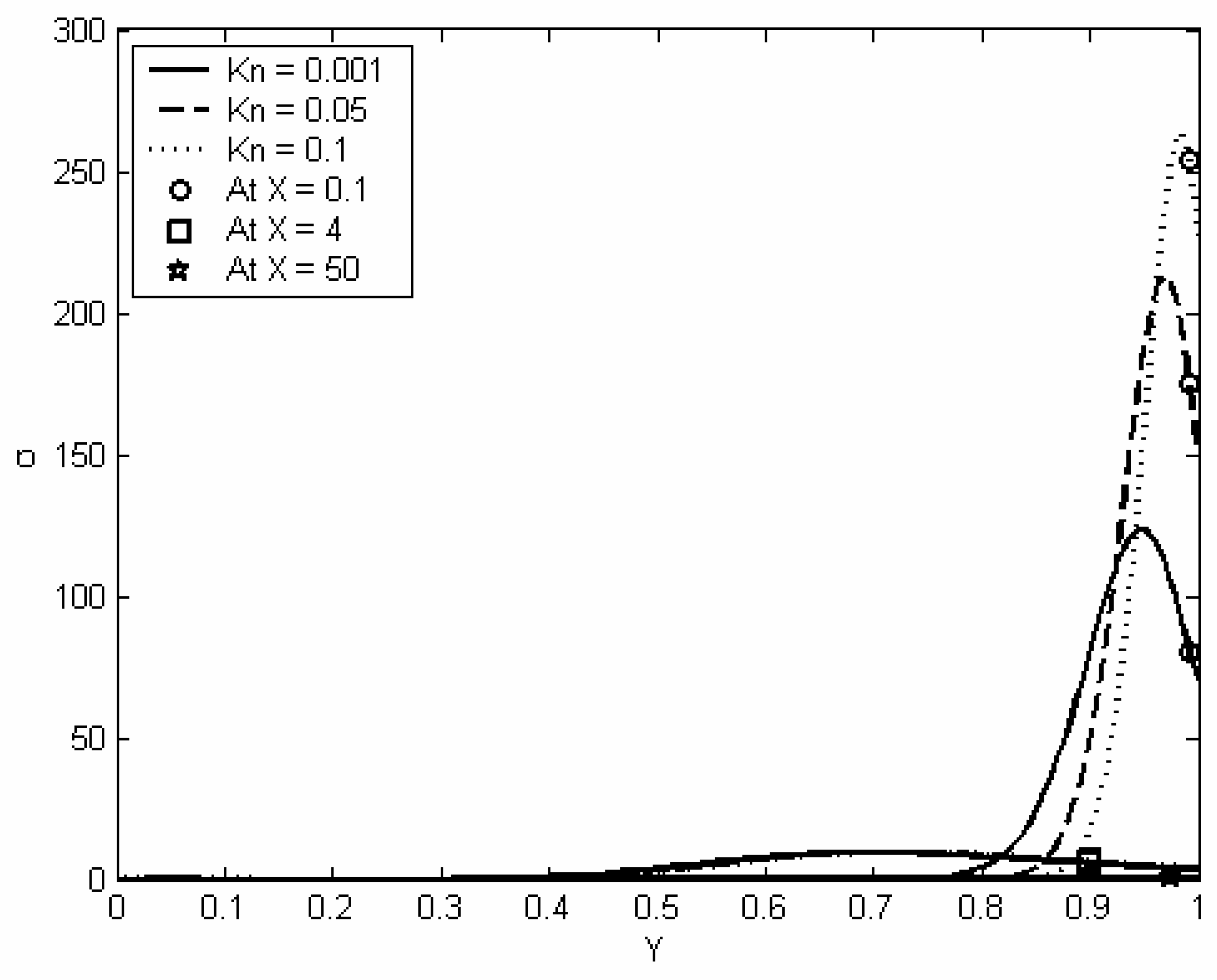
Figure (6) shows the spatial distribution of the local entropy generation within the channel at different axial locations and for different values of Knudsen numbers. This figure shows that as Knudsen number increases the local entropy generation near the wall increases, whereas far from the wall the effect of Knudsen number is just the opposite. Theoretically, the local entropy generation increases due to three factors [
15]: (1) the increase in local velocity gradient. (2) The increase in local temperature gradient. (3) The decrease in local temperature. As Knudsen number increases, both the temperature gradient and the velocity gradient decrease. This will cause a decrease in the local entropy generation. However, the increase in Knudsen number causes a decrease in the local temperature. This in turns causes an increase in the local entropy generation. Near the wall, the effect of the decrease in the local temperature will compensate the effect of the decrease in the local velocity and temperature gradients, and so the local entropy generation will increase as Knudsen number increases. Far from the wall, the effect of the decrease in local temperature is almost negligible, and so the effect of the decrease in the local velocity and temperature gradients is relatively more significant. That is, the local entropy generation at locations far from the wall decreases as Knudsen number increases. Also,
figure (6) shows that the local entropy generation has its maximum values at the entry region and as one marches toward the fully developed region the local entropy generation is going to decrease. This is attributed to three factors: (1) the high values of the local velocity and temperature gradients at the entry region. (2) The acceleration of the core fluid at the entry region; that is, the axial derivative of the fluid velocity is high at the entry region. (3) The low temperature of the fluid at the entry region. Finally,
Figure (6) shows that the effect of Knudsen number on entropy generation becomes insignificant as one marches along the axial direction far from the entry region. As shown previously in
Figure 4 and
Figure 5, the velocity slip and temperature jump at the wall are not significant at axial locations very far from the channel entrance. This is true over the entire range of Kn number which is covered by the present study (i.e. for slip flow: 10
-3 ≤ Kn ≤10
-1). When first order slip/jump conditions are considered, both the velocity slip and temperature jump are proportional to Kn multiplied by the velocity and temperature gradients, respectively. However, both the velocity and temperature gradients are very small at the walls of location very far from the channel entrance. As a result the effect of Kn on velocity and temperature gradients and hence on entropy generation is very weak. Lastly, (σ) is maximum near the wall where the velocity and temperature gradients are maximum, however, the value of (σ
max) decreases as Knudsen number increases due to the increase in slip/jump at the wall.
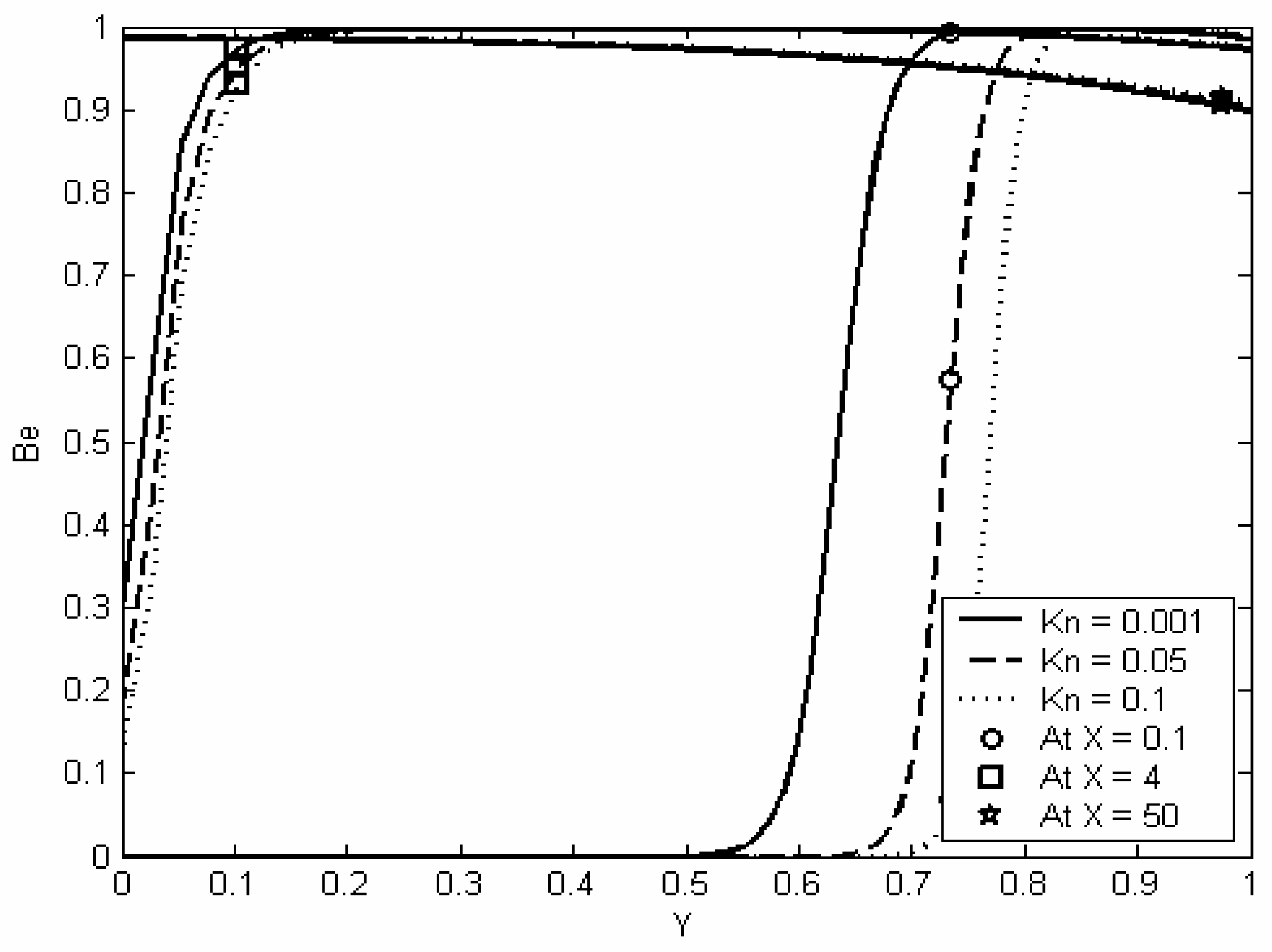
Figure (7) shows the spatial distribution of Bejan number within the channel at different axial locations and at different values of Knudsen numbers. This figure shows that Bejan number has large values near the wall, which means that near the wall most of the entropy is generated due to heat transfer. This is attributed to the high temperature gradient near the wall and the low temperature of the fluid. Also, from
Figure 6 and
Figure 7 one may conclude that at the entry region most of the entropy is generated due to heat transfer.
Figure (7) shows that as Knudsen number increases, Bejan number decreases. This is attributed to the decrease in the temperature gradient as Knudsen number increases which in turns causes a decrease in the thermal part of the entropy generation and hence causes a decrease in Bejan number.
Figure (8) shows the variation of the total entropy generation within the channel as a function of Knudsen number and at different values of Reynolds and Prandtl numbers. This figure shows that as Knudsen number increases the total entropy generation decreases due to the increase in velocity slip and temperature jump at the wall that lead to reduced heat transfer and momentum transfer from the wall to the fluid. This has been discussed and explained previously in
figure (6). Also,
figure (8) shows that as Reynolds number increases the total entropy generation increases. This is due to the increase in both the hydrodynamic and thermal entry lengths that in turn cause larger velocity and temperature gradients and thus would result in an increase in the total entropy generation. One can conclude from the same figure that as Prandtl number increases the total entropy generation increases. This can be attributed to two factors (1) the increase in thermal entry length (2) the reduction in temperature jump which increases the temperature gradient.
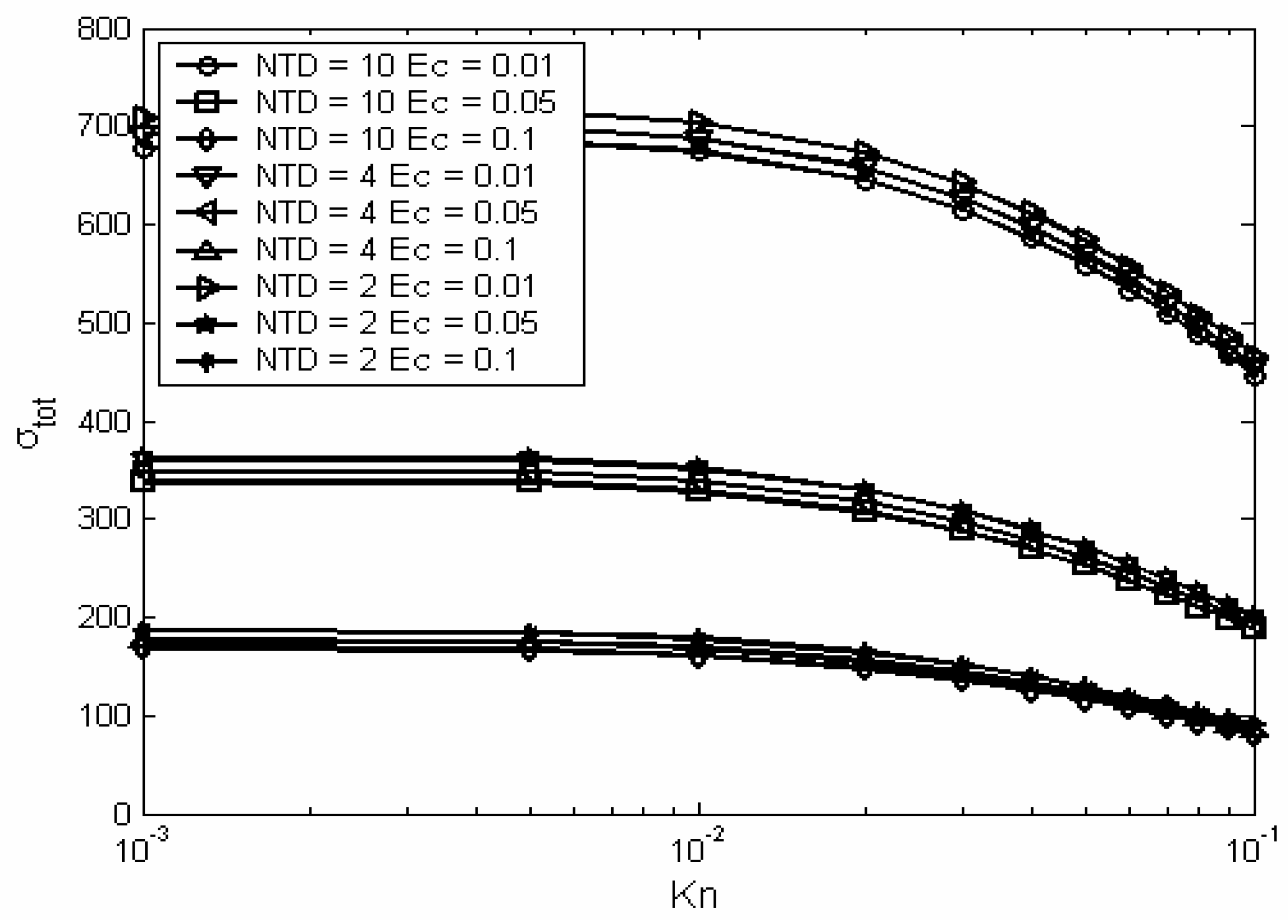
Figure (9) shows the total entropy generation as a function of Knudsen number and at different values of nondimensional temperature difference and Eckert numbers. The figure shows that as the nondimensional temperature difference increases the entropy generation increases. This is due to the increase in the driving temperature difference that would result in an increased temperature gradient and thus increased entropy generation from heat transfer. This effect (i.e. effect of NTD on σ) is mathematically obvious in equation (11). In addition,
Figure (9) shows that as Eckert number increases the entropy generation increases. This can be attributed to the increase in temperature gradient as Eckert number increases. Mathematically, the effect of (Ec) on (σ) is obvious in equation (7 and 11).
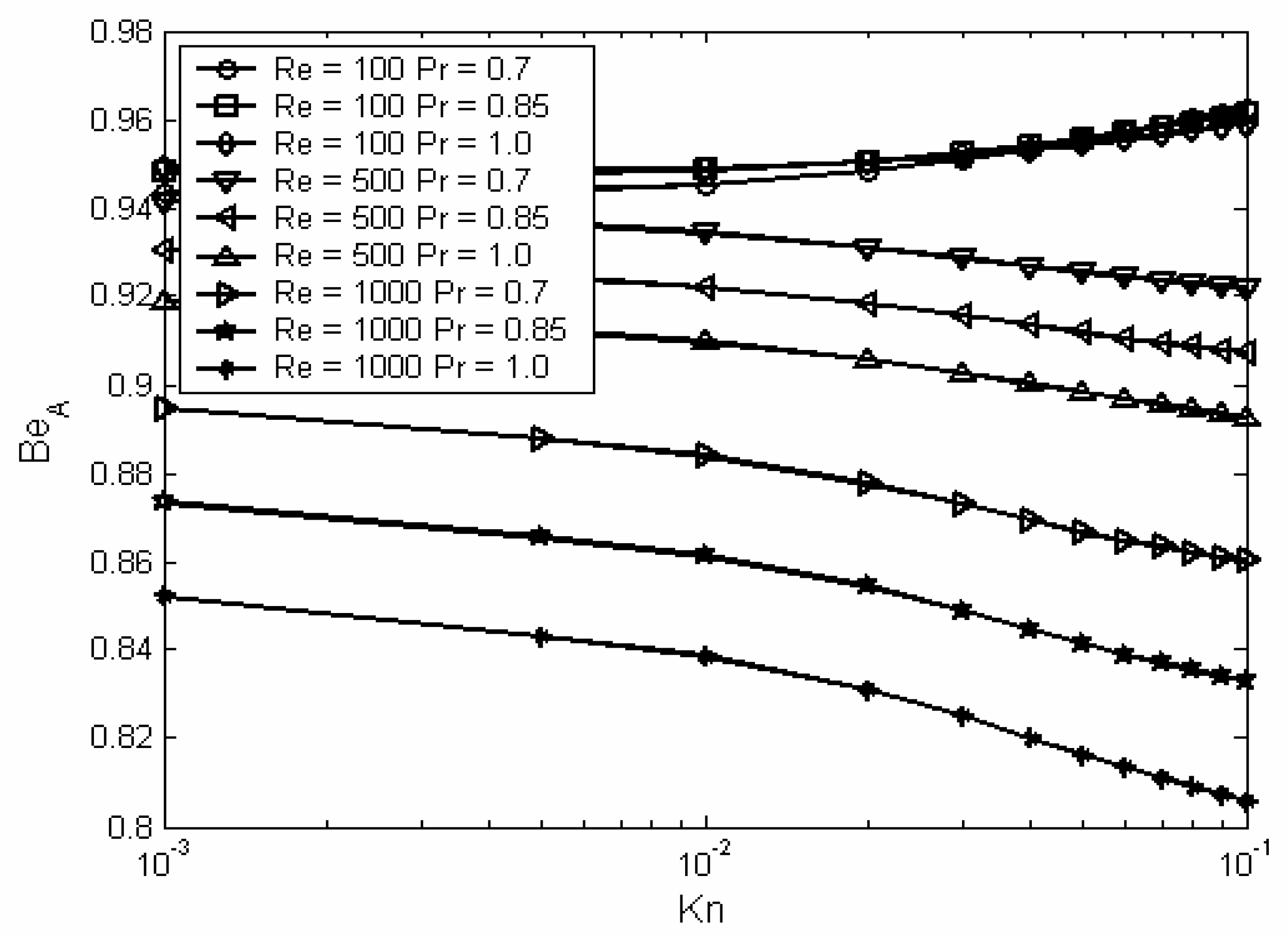
Figure (10) shows the average Bejan number as function of Knudsen number and at different values of Reynolds and Prandtl numbers. This figure shows that at high values of Reynolds number, as Knudsen number increases the average Bejan number decreases, whereas at low values of Reynolds number, as Knudsen number increases the average Bejan number increases. This behavior with Knudsen number can be attributed to two contradicting reasons: (1) The decrease in temperature gradient due to the increase in Knudsen number which in turn causes the average Bejan to decrease, (2) The decrease in velocity gradient due to the increase in Knudsen number which in turn causes the average Bejan number to increase. At low Reynolds number the effect of the decrease in velocity gradient compensate the effect of the decrease in temperature gradient. But at high Reynolds number the effect of the decrease in temperature gradient compensate the effect of the decrease in velocity gradient. Also,
Figure (10) shows that as Reynolds number increases the average Bejan number decreases. This is attributed to the increase in the thermal and hydrodynamic entry lengths due to the increase in Reynolds number. It is known that as the hydrodynamic and the thermal entry lengths increase, the local velocity and temperature gradients and the local temperature distributions decrease. The decrease in local velocity gradient and local temperature cause the local Bejan number to increase. But, the decrease in local temperature gradient causes the local Bejan number to decrease. The effect of the reduction in local temperature gradient on the local Bejan number dominates over the other effect and so the average Bejan number decreases as Reynolds number increases.
Figure (10) shows also the effect of Prandtl number on the average Bejan number. This figure shows that as Prandtl number increases the local entropy generation decreases. This can be attributed to the increase in thermal entry length as discussed previously. But, as Prandtl number increases the temperature jump decreases and this causes an increase in both the local temperature gradient and the local temperature distributions. These two effects lead to an increase in the local Bejan number.
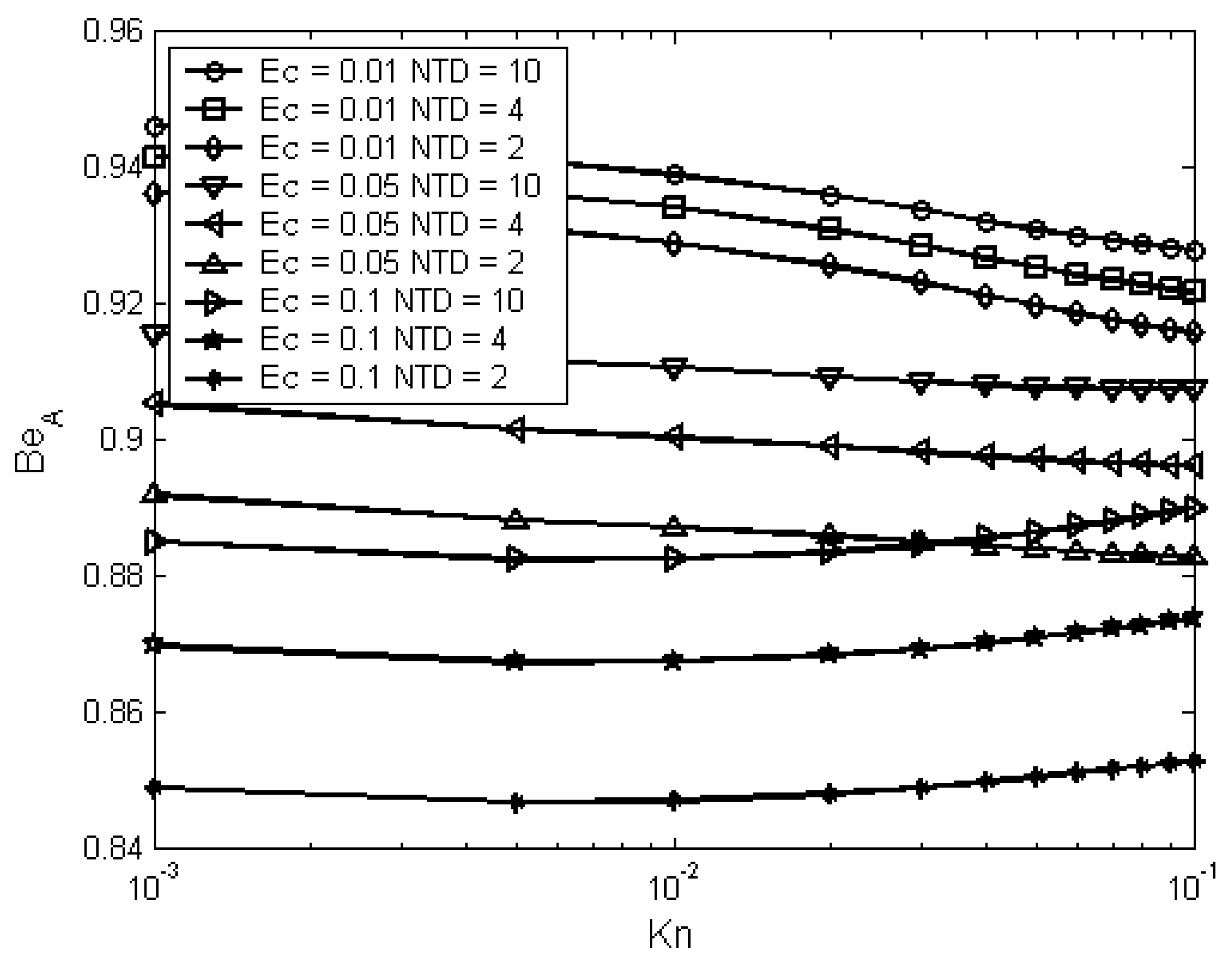
Figure (11) shows the variation of the average Bejan number as function of Knudsen number at different values of Eckert number and nondimensional temperature difference. At low values of Eckert number, this figure shows that as Knudsen number increases the average Bejan number decreases. This is because the entropy generation due to heat transfer decreases faster than that due to viscous dissipation and thus the net effect is to decrease Bejan number. On the other hand, at high values of Eckert number, as Knudsen number increases the average Bejan number increases. This is because the entropy generation due to dissipation decreases at much faster rate than that due to heat transfer and thus the net effect is to increase Bejan number. Also,
Figure (11) shows that the average Bejan number decreases as Eckert number increases. This is attributed mainly to the decrease in the entropy generation due to heat transfer with the increase in Eckert number. Furthermore,
figure (11) shows that as the nondimensional temperature difference decreases the average Bejan number decreases. This is related to the reduction in entropy generation due to heat transfer since heat transfer is reduced as the NTD is decreased.