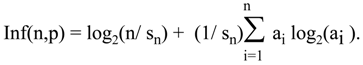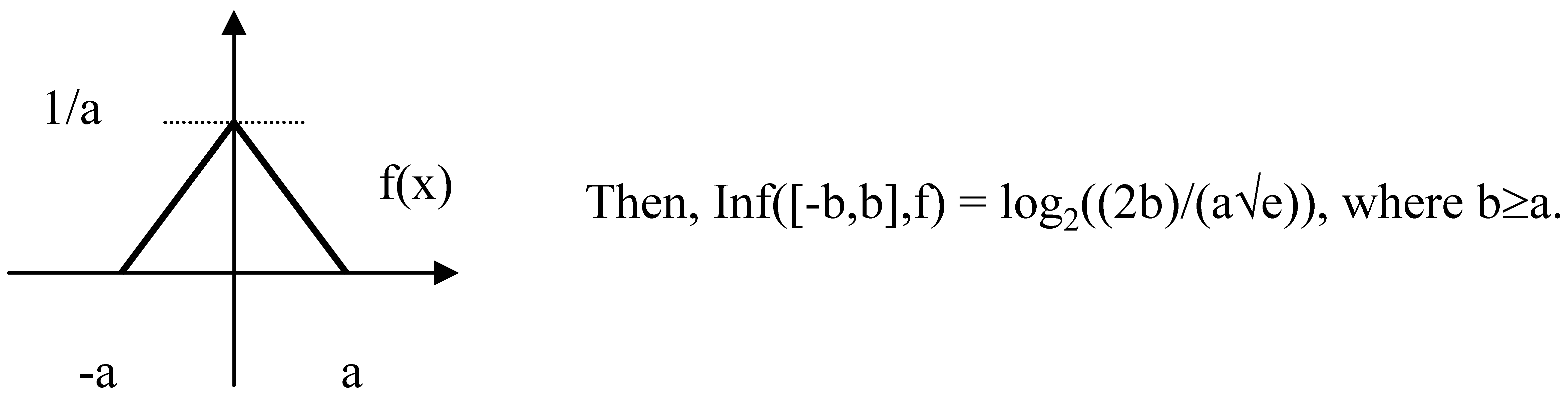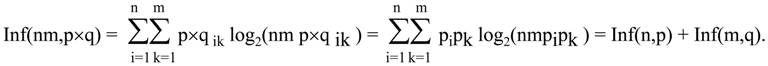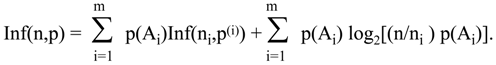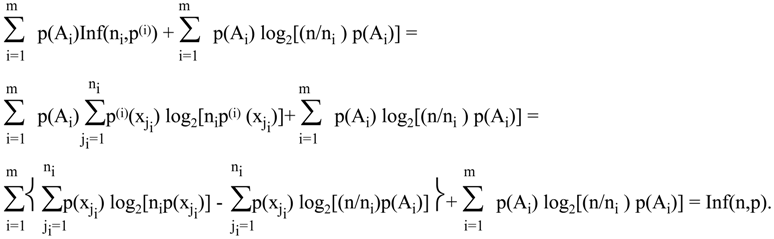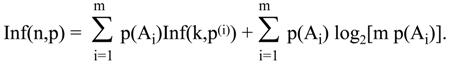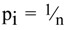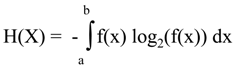Introduction
In this article an alternative to entropy measure of information is presented with the intention to contribute to the resolution of several open fundamental problems in the understanding of the concept of information. This alternative measure is not likely to provide new solutions to the technical problems in the analysis of communication systems. Its only superiority over entropy is, as I will try to demonstrate, in the fact that it actually measures information, while entropy gives account of the information deficit, and as such can be only indirectly used in the analysis of information transfer or change. For technical calculations of information transmission it does not matter whether the amount of information is calculated using entropy or any other compatible measure. For studying information outside of this “engineering problem,” especially when we want to establish connection between the meaning of information and information amount, what exactly is measured is of great importance.
It will take many pages to explain why seeking alternative measures of information is justified, in what sense entropy does not measure information, and what alternative measure can solve the problems which entropy could not. But how to compress it into a form suitable for introduction? The following commonly known historical anecdote will provide a short metaphorical description of the arguments presented in the article.
Shannon’s monumental work [
1] introducing entropy as a measure of information in the process of communication can be compared to the great achievement of Archimedes reported by Vitruvius in “On Architecture.” The goldsmith of the Syracuse ruler Hiero was accused of stealing part of the gold given to him for casting a crown and replacing it with silver. If the volume of the crown was known, it would have been possible to calculate the density of the metal, and from the known densities of gold and silver to find its composition. But the shape of the ornaments was way too complicated to make the measurement of volume feasible. As usual, when problems seemed hopelessly difficult, Archimedes was asked by Hiero for advice. The solution came to mind when he entered a barrel full of water in the public bath. The amount of spilled water in the overflow could be measured easily, thus giving the volume of the bather’s body. The same method could be used to measure the volume of the crown. Archimedes, overjoyed by finding the solution, ran naked through the streets of Syracuse shouting: Eureka! He put the crown in the vessel full of water and some of the water spilled out. After the crown was pulled out of the vessel, the missing amount of water could be added using calibrated cups. The volume of the water necessary to refill the vessel gave Archimedes the exact volume of the crown. Now, after measuring the weight of the crown, the density and, therefore the composition of the metal could be easily determined.
Well, the analogy between the approach of Archimedes and that of Shannon, and many other contributors to information theory actually ends with pulling the crown out of the water, and because of that it is not very close. It would have been closer, if Archimedes had tossed the crown aside, focused on the space left at the top of the vessel left after the water was spilled, and announced that the issues of the weight or density of materials, in particular of gold, are irrelevant to the engineering problem.
In spite of the limitations of the metaphor, the content of the article is probably now quite clear to an informed reader, and the remaining sections can be considered just footnotes. However, to do justice to the complications within information theory that caused the shift of focus from the crown to the spilled water and to the empty space left by it in the vessel, these “footnotes” must fill many pages.
1. Scandals and Paradoxes
If this article is intended as a contribution to resolving some fundamental problems in the understanding of the concept of information, the first question is whether there are any problems to solve, and if so, what are they? I share the belief of many others concerned with the issue, that there are several problems, and that they are of a really fundamental nature and of great importance.
Floridi, in his
Philosophy of Information manifesto patterned on the Hilbert Program and consisting of a review of the eighteen outstanding problems related to information, lists as Problem 1 - “the hardest and most central question”: What is information? [
2] His commentary on this question gives convincing evidence for the necessity to seek the answer: “Information is still an elusive concept. This is a scandal not by itself, but because so much basic theoretical work relies on a clear analysis and explanation of information and of its cognate concepts. We know that information ought to be quantifiable (at least in terms of partial ordering), additive, storable and transmittable. But apart from this, we still do not seem to have a much clearer idea about its specific nature.”
Twenty years earlier MacKay, in his recollections of the beginnings of information theory described similar feelings regarding the separation of the theory from semantic aspects of information: “As early as our 1950 Symposium on Information Theory, it was felt to be somewhat scandalous that the theory of information seemed to have so little working contact with such concepts as the
meaning and
relevance of information.” [
3]
To avoid the accusations of too much interest in tabloid themes, let’s move from the scandals to paradoxes which have a much better reputation in academic circles. And when we talk about the paradoxes within information science, we have to remember that information studies have one of their main origins in Maxwell’s Demon Paradox. Szillard’s attempts to exorcise this demon involve the first significant analysis of information outside of the communication context and one of the earliest in all this domain [
4]. The inclination to paradoxical, or at least counterintuitive, results in information theory cannot be blamed only on the “bad provenience” or “childhood disease” as it continues in the adult life of the theory.
Marijuan started his summary of the 2002 Foundations of Information Science e-conference “The Nature of Information: Conceptions, Misconceptions, and Paradoxes” by quoting a sentence from the presentation text of the FIS 2002: “Inconsistencies and paradoxes in the conceptualization of information can be found through numerous fields of natural, social and computer science.” [
5]
Indeed, there is an abundance of examples from which I will draw only the most relevant ones. One of more recent paradoxes (or more accurately, more recently brought to the attention of a wider audience) comes out of the study of reversible computing [
6,
7]. This surprising result, known now as Landauer’s Principle, states that the only unavoidable energy dissipation in the physical process of computer computation takes place when information is discarded. Thus, physical entropy is increasing when the amount of information is decreasing. In the various earlier discussions of Maxwell’s Demon, for instance by Szilard [
4] or Brillouin [
8], it was the acquisition of information in measuring speed of particles approaching the gate operated by the demon that explained the increase of entropy, not the forgetting of information. It is definitely a counterintuitive result that resetting the memory of a computer to zero is associated with the increase of entropy.
Even if we stay away from physical entropy and consider only mathematical information theory, we will encounter paradoxes at every corner. The very definition of information as a resolution or reduction of uncertainty, as it is formulated in the majority of books on the subject, involves a paradox (or just simply an error). Some authors [e.g.
9] do not hesitate to write first that uncertainty is a result of information deficiency, and then to explain the concept of information as uncertainty reduction. Those who claim that such a definition is not circular, meaning that uncertainty is not just the lack or shortage of information, try to convince us that it is not a psychological characteristic of one’s state of mind, but a legitimate and objective characteristic of any system which can make choices in a way which is not pre-determined. This argument would have been convincing if it were possible to distinguish clearly uncertainty from randomness and indeterminacy. After all, it seems more rational to explain randomness in terms of information, than information in terms of randomness.
But when somebody talks about “the paradox of information,” without doubt it is about the mysterious separation of information theory from the semantic aspects of information. Before the publication of Shannon’s paper [
1], and definitely until Hartley’s famous paper [
10] was published in 1928, it was natural to think that information is about something. Once the connection between information and thermodynamics had been established the meaning of information had to be reexamined to eliminate its simplistic identification with the psychological category of knowledge. But instead of such reexamination came the tendency to separate completely information theory from the semantics of information. First, Hartley declared his disinterest in the meaning carried by information and later, in more definite form Shannon made the divorce of information from meaning a programmatic principle, as stated in the frequently quoted passage from Shannon’s monumental work [
1]: “Frequently the messages have meaning; that is they refer to or are correlated according to some system with certain physical or conceptual entities. Those semantic aspects of communication are irrelevant to the engineering problem.”
Bar-Hillel [
14] has denounced several violations of such declarations, namely those committed by Hartley [
10] in his paper, by Weaver [
12] in the complementary text included in the book reprint of Shannon’s paper, and in the very influential paper written by Cherry for the general audience [
13]. Those violations of the declaration that the issues of meaning are strictly outside of the interest of information theory showed not only that the divorce from semantics was caused by the inability to build a connection between the measure of amount of information and its semantic characteristics rather than by actual irrelevance, but also that the apparent irrelevance of meaning was not so obvious for its propagators.
On the other side of the barricade, Carnap and Bar-Hillel [
14] attempted to formulate the first fully furnished with the formal apparatus, semantic theory of information in terms of logic and in separation from entropy which they despised, but were persuaded by von Neumann not to attack [
15]. The present author is convinced that the unconscious adaptation of Shannon’s paradigm of measuring information hidden in the method has had the major impact on the demise of this theory.
Carnap and Bar-Hillel started from the concept of the content of a statement (in the original notation “Cont”): “[W]e take
the content of a statement to be a class of those possible states of the universe which are excluded by this statement…” [
16] derived from “the scholastic dictum,
omnis determinatio est negatio” [
16]. Then they considered the logical probability of a statement (m(i)) as a complement to the value 1 of the measure of content (cont(i)). Up to this point their approach seems very promising. But in the next step they could not resist temptation to make their approach consistent with Shannon’s entropy, and they defined the semantic measure of information in a statement as the logarithm of reciprocal of the logical probability of the statement. This choice directed them towards an analogy to entropy, but that has not brought success to their theory. The theory was received without much interest and soon fell into oblivion. It seems that once more, the spilled water attracted more attention than the gold of the crown, to go back to the metaphor from the introduction to this article.
The efforts to develop an adequate semantic theory of information has been continued, but without any spectacular successes. The basic character of the four questions related to semantics of information out of the eighteen questions listed by Floridi [
2] shows that we are still far from a major breakthrough in this domain. Is it because the meaning of information is irrelevant to the concept of information? I doubt it, and probably not many information scientists would subscribe to such a view. There must be some fundamental obstacle which does not obstruct the rapid development of information theory in the context of communication, but which blocks even the simplest attempts to correlate the measure of information with its meaning. Later I will try to provide arguments for the view that the fault lies in the choice of entropy for the measure of information outside of a communication context.
2. Entropy Triumphant
There is no doubt that the most important moment in the history of information theory was the birth of Shannon’s measure of information which he chose to call entropy, apparently on advice from von Neumann [
17]. Its formula has become an icon for information theory:
Shannon’s entropy had a less influential predecessor in Hartley’s formula for the amount of information in the message consisting of d symbols selected from the alphabet of n symbols [
10]:
Frequently the relationship between these two measures is interpreted as a transition from the combinatorial to probabilistic analysis of information [
18], as the formula (2.1) becomes identical with (2.2) for classical probability
![Entropy 06 00388 i002]()
However it was Hartley who first introduced a probabilistic accent to the study in his observation that the message can equally well be generated by a chance event without influencing the measure of information [
19].
Shannon’s entropy has had three main sources of power giving it dominating position among all its contenders. First, it turned out to be an extremely useful and effective tool in the analysis of communication. In the United States, in the land where pragmatic trends in philosophy have long been dominant, this alone was enough to guarantee its central position. In Europe the fact that so much can be done using entropy as a measure of information was not an ultimate argument. However, the striking similarity to Boltzmann’s physical entropy gave Shannon’s measure strong support. Probably for that reason European critics of Shannon’s approach put forth so much effort to discredit that connection. For instance, even in the 1980’s, when Landauer [
6,
22], Bennet [
20,
21], and others were preparing to announce the conclusion that “information is inevitably physical” MacKay [
3] was still trying to ridicule the association of Boltzmann’s and Shannon’s concepts of entropy and insisted on the change of the name of Shannon’s measure to “mean unexpectedness or statistical variety.” Today, the attempts to dissociate information from physics have become an anachronism and the formal or factual association with physical entropy adds legitimacy to the priority of entropy as “the” measure of information.
The strongest support for this legitimacy has come from formal, mathematical analysis. It is a common or even universal belief (judging from the repeating statements in almost all introductory texts to information theory) that there are many different possible measures of information, but that Shannon’s entropy is the only one which satisfies apparently obvious axioms of the measure of information. Such a statement is already in Shannon’s paper [
1] in which the following “reasonable” postulates for any measure I(p
1,p
2,…,p
n) have been listed (originally with the symbol H, which we reserve for entropy, and therefore avoid when talking about any measure, and in the slightly more elaborate form):
Measure I(p1,p2,…,pn) should be continuous in the pi.
If all p
i are equal,
![Entropy 06 00388 i003]()
, then I should be a monotonic increasing function of n. With equally likely events there is more choice, or uncertainty, when there are more possible events.
If a choice be broken down into two successive choices, the original I should be the weighted sum of the individual values of I.
Then, Theorem 2 in Shannon’s paper asserts that the three postulates determine entropy uniquely. Later a simplified system of the postulates given by A. I. Khinchin due to D. K. Fadeev [
23,
24] (quoted here from Renyi [
25] with a slight simplification of the symbolic,) has been commonly accepted as the ultimate axiomatic characterization of the measure of information:
The information obtained depends only on the probability distribution p=(p1,p2,…,pn), consequently, it will be denoted by I(p) or I(p1,p2,…,pn). We suppose further that I(p1,p2,…,pn) is a symmetric function of its variables p1,p2,…,pn.
I(p,1-p) is a continuous function of p (0≤p≤1).
I(1/2,1/2)=1.
The following relation holds:
The last of the axioms usually is called the sub-additivity condition.
It is true that several other measures have been considered later, for instance by Renyi [
25], but not as an alternative, rather as a generalization. Some of them were considered inferior on a formal basis, for instance because they did not satisfy the fourth axiom [
24]. Neither of the generalizations has found important applications or provided a significant insight into the nature of information.
It is often concluded, that since it is difficult to imagine that any reasonable measure of information could fail to conform to the requirements described by Fadeev’s axioms, and that it can be demonstrated that the only measure that satisfies the axioms is Shannon’s entropy, it must be the ultimate measure. Case closed. Or is it?
3. The Case of Two Entropies
It is interesting that before Shannon developed “a mathematical theory of communication” [
1] which within one year has changed into “the mathematical theory of communication” [
12], in all sporadic attempts up to that point to associate information with physical entropy in its statistical form developed by Boltzmann, their mutual relationship seemed inversely proportional. Even in the book presenting Shannon’s work to the world [
12] Weaver referred to this type of relation: “Dr. Shannon’s work roots back, as von Neumann has pointed out, to Boltzmann’s observation, in some of his work on statistical physics (1894), that entropy is related to ‘missing information,’ inasmuch as it is related to the number of alternatives which remain possible to the physical system after all the macroscopically observable information concerning it has been recorded.” Tribus [
17] quotes a much stronger expression of this inverse relation from the 1930 work of Lewis [
26]: “Gain in entropy means loss of information – nothing more.”
This inverse proportionality suggested the existence of a hypothetical, if possibly only a theoretical, entity with the value opposite to that of entropy. Schroedinger, in his small, but very influential book “What is Life?” published in 1945 [
27], which has been acknowledged by Watson and Crick as a source of inspiration in their work on the structure of DNA, did not write explicitly about information, but he did write about the orderly structure of the “miniature code” of genetic inheritance, explained through the analogy to Morse code. In this context, he introduced the idea of negative entropy absorbed from the environment or sunshine by every living organism as a substrate for the order and the condition for its stability necessary for life in general, and “aperiodic crystals or solids” carrying functions of, at that time hypothetical, genes in particular.
The idea of negative entropy leads us straight to “negentropy” and another influential book, written by Brillouin, which appeared at a time when Shannon’s approach was already in full blossom. Its influence was of a different type, because when it happened to be mentioned as a source of inspiration for great achievements, it was sometimes done as a reaction “there must be better way to think about it.” [
22]
Indeed, it is a book full of inconsistencies and occasional bizarre statements that can cause a headache. But, it is also a good evidence for the need to reexamine connections between physical and information entropies. Brillouin was an enthusiastic propagator of Shannon’s approach on the pages of this book. It is clear that his loyalty to Shannon was stronger than his loyalty to physics or even logic. This can be seen for instance in his proposal on page 3 to measure temperature in energy units to make both types of entropy dimensionless. Where physics could not be bent to support Shannon’s views, Brillouin did not hesitate to express two contradictory statements almost next to each other.
On page 10, Brillouin subscribes to Shannon’s disinterest in the “meaning” of information (using words “meaning” and “value” as if they were synonyms): “Our definition of information…corresponds exactly to the problem of a communication engineer who must be able to transmit all the information contained in a given telegram, without paying any attention to the value of this information for the person receiving the telegram.” On page 9 he writes: “… we define ‘information’ as distinct from knowledge,’ for which we have no numerical measure…Our statistical definition of information is based on scarcity. If a situation is scarce, it contains information.” Also, on page 297 in the concluding remarks he writes: “We have also completely ignored another problem: that of meaning.”
But on page 159 we find a surprising (for several reasons) sentence: “Acquisition of information about a physical system corresponds to a lower state of entropy for this system.” On the next page he writes: “…entropy measures the lack of information about the actual structure of the system.” On page 293 we see: “Entropy is a measure of the lack of information about a physical system. The greater is the information, the smaller will be entropy.”
In all these statements the word “about” indicates reference to the semantic character of information which according to the earlier passages is irrelevant for the measure of the amount of information. We can find another puzzle on page 161: “The connection between entropy and information was rediscovered by Shannon, but he defined entropy with a sign just opposite to that of the standard thermodynamical definition. Hence what Shannon calls entropy of information actually represents negentropy. This can be seen clearly in two examples (pages 27 and 61 of Shannon’s book) where Shannon proves that in some irreversible processes (an irreversible transducer or a filter) his entropy of information is decreased. To obtain agreement with our conventions, reverse the sign and read negentropy.” And, we should add, forget about the annoying fact that both the standard thermodynamic definition and Shannon’s formula give only positive values.
The internal contradictions in the text of Brillouin’s book are frustrating, but there is some unexpected value in his lack of consistency. Being free from the bonds of logic he could introduce some interesting ideas which others who believed in the ultimate truth of Shannon’s approach could not, since they were paralyzed by the apparent inconsistency with the orthodox views of information theory. Thus, Brillouin could write in the same book in the spirit of Shannon’s approach, and against it. On page 8 we find: “Every type of constraints, every additional condition imposed on the possible freedom of choice immediately results in decrease of information.” Then on page 152 repeating the reasoning from page 3: “We considered a situation in which there were P0 different possible cases or events of equal a priori probability. Information I1 is required to reduce the number of possible cases to P1, and the logarithm of the ratio P0/P1 measures I1…
Initially: I0 = 0, P0 possibilities,
Finally: I1 > 0, P1 possibilities,
With I1 = K ln (P0 /P1).”
Brillouin unfortunately tried to be consistent this time, after all he was a great physicist, and in the next paragraphs diluted and lost the outcome in the attempt to restore agreement between the two types of entropy by introducing an unnecessary distinction between free and bound information of which only one could be compared to entropy. If not the return to orthodoxy, this section would have been the most valuable and interesting part of his book. Some more forgiving authors have recognized the value in this short passage and recognized it as an introduction of an independent measure of information in the process of reducing the number of answers to a problem: K ln (P
0 /P
1) defined by the comparison of the number of possible outcomes before and after information is available [
28].
In any case, publication of Brillouin’s book was an important event in the history of information theory. Many authors criticized him, some made use of his ideas, even if the applications were contrary to his intentions. In my opinion what was very important was his recognition of the fact that in order to restore agreement between physical entropy and information we have to modify the measure of information introduced by Shannon. This recognition of the problem carried a great potential. Also, as I will argue later, his measure of information in the form log2(P0/P1) can be considered an analog of Hartley’s measure for the alternative general measure of information. However, his firm belief in Shannon’s theory and following from that the adherence to the original formulation of information theory diverted his attention from the real meaning of his measure and dictated that he made the choice of a minimal modification of Shannon’s entropy, the change of sign. Using my metaphor from the introduction to this paper, Brillouin’s modification could be compared to the change in measuring the empty space in the barrel after the crown is removed and the level of the water lowers beneath the rim of the barrel. He has proposed to measure the amount of the empty space above the water considering the height of the surface of water to be given negative value. Then when we add water to the barrel we have the negative measure of the empty space above water increasing, even if the traditional measure tells us that the empty space is shrinking. This may give us an illusion that we have correct measure of the content of the barrel.
4. The Conduit Metaphor
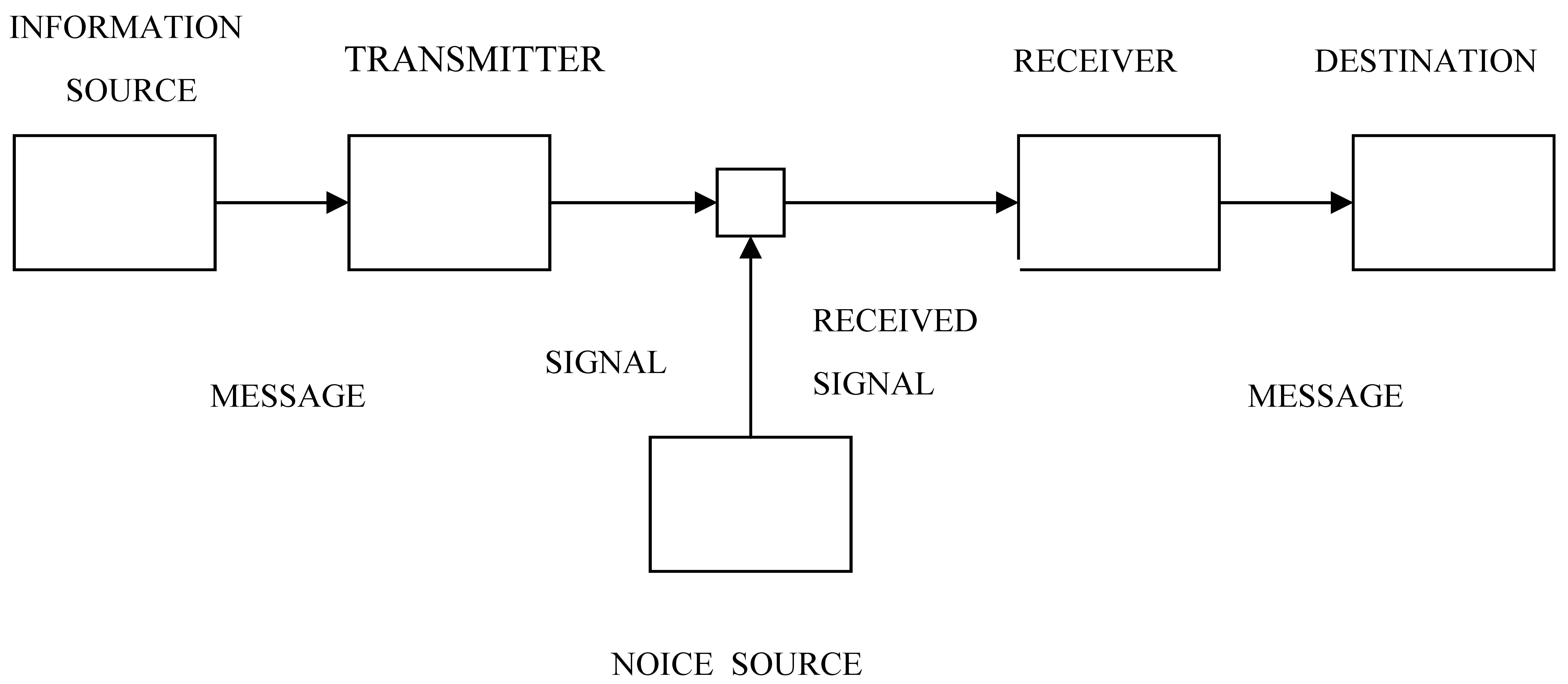
The last decade has brought the recognition of the degree in which the communication setting of information theory, utilized by Shannon and Wiener in their works, has influenced our modern way of understanding information (or I would argue, more the way we misunderstand it). However, the critical analyses in this spirit that have been published thus far were focused rather on the linguistic or sociological aspects of the phenomenon of information, not on the actual understanding of the concept of information as an object of philosophical study. The reflection on the influence of the setting on the understanding of information requires first a recollection of what the actual setting was. Then we can try to identify the influence.
The original diagram in Shannon’s paper [
1], used also by Weaver in his part of the book presentation of the mathematical theory of communication [
12] had several elements which were important for the “engineering problem,” but which were not necessary for conceptual analysis. Accidentally, the diagram does not include the distinction of the channel of communication out of the other parts of the communication system.
Now, we can ask about the elements of the communication system on the diagram which are necessary to understand Shannon’s explanation of information measure. The diagram can be simplified at least as follows.
In Shannon’s explanation of the concept of information and entropy we have simply the information source producing a message, the channel in which message is transmitted towards the destination, and the destination where the message arrives. It is worth observing that the word “information” is not frequent in Shannon’s text. More frequently Shannon is writing about the message, which most likely he understands as a synonym of “information.” Weaver in his part is referring to the word information much more frequently and explicitly.
The use of the word “channel” gives automatically an association with the flow of information, and Shannon is explicitly writing about such a flow in the first sentence in the first section of Part 1 of his paper: “Teletype and telegraphy are two simple examples of a discrete channel for transmitting information.“ [
1]
Shannon described in the introduction to his paper the fundamental problem of communication as reproduction in one place of the message selected in another place. But his model is quite specific about the fact that this reproduction is based on the flow of information between these two points. Therefore, we can assume that information, together with the message or as a message, is somewhere between the two places all the time. In other words information is an entity having its own existence, or at least that it is a persistent characteristic of the message which is carried between the information source and destination. This means that information cannot be considered a collective property of all communication system, incomprehensible at the level of the system’s components, nor as the momentary characteristic of the system or its parts.
Here we can find inconsistency with the popular interpretations of Shannon’s approach which have been developed later, namely that information is uncertainty or that information is the reduction of uncertainty, with the word “uncertainty” understood in the generic way. It is difficult to accept the idea of uncertainty moving within the communication channel in the former case, or in the latter case of reduction of uncertainty moving through the system. Certainly, we can consider the reduction of uncertainty as a product or effect of information, but any form of identification of uncertainty and information, or reduction of uncertainty and information is clearly incompatible with the model.
Uncertainty appears in Shannon’s work in
Section 6 (p.49) when he is talking about the amount of information produced by the source, or rather about the rate at which information is produced. It is in the context of the description of the information amount derived from the analysis of the source of information. There is here a hidden assumption that in normal situation the amount of information is conserved through the communication process, as otherwise characterizing information in terms of the process of information production does not make sense.
In the next step, Shannon introduces the measure of information production using his three postulates listed in our
Section 1. Information source is characterized exclusively by the probability distribution of the events within the source (p. 49), with indirect suggestion that each elementary event corresponds to selection of a message. Here the word “uncertainty” appears, along with another complication. In spite of the formulation of the initial question in terms of production of information by the source: “How much information is ‘produced’ by such a process, or better at what rate information is produced”, and in spite of the title of the next section “The Entropy of an Information Source” we can find the statement: “Quantities of the form
![Entropy 06 00388 i004]()
… play a central role in information theory as measures of information, choice and uncertainty.” (p. 50) Shannon suddenly jumps from the description of information production to information itself, choice, and uncertainty. Assuming consistency of his reasoning and the context, we can interpret it as follows. H measures the amount of information transmitted in the communication process as a product of the selection of one out of several possible messages, reflecting the occurrence of one event out of several events in the information source. The process of selection (choice) is characterized subjectively by our uncertainty regarding the outcome of selection. It is clear from the text on page 49 that he means subjective, psychological uncertainty: “Can we find a measure of how much ‘choice’ is involved in the selection of the event or how uncertain we are of the outcome?”
There is only one more concept involved in the general, non-technical considerations in his paper, the concept of redundancy. He writes: “The ratio of the entropy of the source to the maximum value it could have while still restricted to the same symbols will be called its relative entropy. This is the maximum compression possible when we encode into the same alphabet. One minus the relative entropy is the redundancy.”
Now, we can try to identify these specific characteristics of Shannon’s conduit metaphor that have determined our thinking about information. In the text written by Shannon there is one prominent element, the process of production of information, or of the message which carries it. This process cannot be eliminated from the consideration of information without eliminating that which gives us the measure of information. Shannon does not write anything about this production, except that it takes place in the information source and is described by the probability distribution.
At this point one critical remark is necessary. Shannon is talking about the probability distribution without much care for mathematical subtleties. Thus, for him the probability distribution is simply a sequence of nonnegative numbers adding to 1, nothing more. He doesn’t make any clear distinction between the case when we have n positive numbers, and another case of n+k numbers where n of them are positive and k are equal zero. It is easy to notice that in the expression for H only probabilities different from zero contribute non zero terms (he assumed, as it is always done in the context of information theory that the function x log2(x) is extended by the right side continuity to the argument x=0 by assigning for this argument the value of 0). We cannot be sure, but when he writes about n possible events, it looks like he means n events with non-zero probability. The difference is not purely academic. Entropy for the distribution of n “possible” events H(p1,p2,…,pn) is equal to H(p1,p2,…,pn,0,0,0,0,0), but the distributions are not identical, neither are the probability spaces in which they are defined. Is information for the two information sources identical?
It is clear that for Shannon the process of information transmission is crucial. For our analysis of information it was important to realize that, because due to the focus on information flow, we can assume that information is an entity, or at least persisting property of the message. Now, in order to measure information using entropy, we have to assume that there is some process with the initial and final stage (production of information extended or not to include the actual process of transmission). There is no way to talk about production without having “before” and “after.” And the essence of the conduit metaphor consists in this involvement of the two stages. We can find it in the works of Shannon, but also in works of probably all information theorists, including Brillouin. From this point of view, we can see that the conduit metaphor has in itself a seed of incompleteness. On one hand we have information as an entity, as something has to flow in the system, on the other hand we have its main characteristic given only in the relative form, in the comparison of “before” and “after.”
Coming back to the metaphor from the introduction to present paper, there is an inherent characteristic of Shannon’s approach which limits his analysis to the flow of water (adding or moving it to another vessel). In this approach it doesn’t matter whether we measure volume of water, or volume of the empty space above water. Additionally and more importantly, his approach does not allow for the absolute measurement of the volume of water, as it focuses on the empty space.
5. So, What is Wrong with Entropy?
The answer is obviously, that there is nothing wrong with entropy as long as we analyze communication systems and are interested in the “engineering problem.” It would be insane to try to question the value of entropy for measuring information in communication. The question is whether we can use entropy equally successfully for measuring information in different contexts. Here I believe the answer is in the negative. Actually, Shannon all his life has had doubts about the attempts to generalize his theory beyond the communication context.
So what is wrong with entropy when we want to use it for measuring information outside of the conduit metaphor. Before I talk about the objections, a few words are necessary about eliminating the conduit metaphor from our considerations.
Why should we eliminate the conduit metaphor? We want to find an appropriate methodology to study information as it is, not as it flows. We could see that the conduit metaphor required the continuing existence of information through all process of communication. But that was all about information as an entity. There was nothing about its nature. We could, and Shannon actually did, consider it equivalent to a message. When we want to study information without any reference to the specific context, such as a model of communication system, we have to provide means to identify the meaning of the term “information,” i.e. we have to define information using in the definiens only these concepts which have known meaning. Preferably, the concepts used in the explanation should have well established philosophical legitimacy. Any reference to the intuitive but vague terms such as “uncertainty” should be avoided, as they bring more confusion than insight into the meaning of definiendum.
I will provide my own definition without elaborate explanation or justification, which can be found elsewhere [
30]. Thus, information is the identification of variety. The identification is understood in terms of the one-many opposition studied for centuries in philosophy. The word “variety” can be considered as synonymous with the words “many, plurality, multiplicity, set”, etc. Identification of a variety means either the characteristic, or characteristics of the elements of the variety which select one out of many, or alternatively an internal structure that gives the variety its unity. The first is selective information, the second structural information. We are concerned here only with the first type, or rather with the first manifestation of information.
Now we are ready to look for the deficiencies of entropy as a measure of such a general concept of information. Our “bill of indictment” is as follows.
Entropy has its maximum value for the probability distribution in which all events are equi-probable, i.e. which does not provide any distinction of one outcome out of the others. Information understood in the general way should be minimal in such a case.
The value of entropy does not depend on the number of all elements in the variety, but only on the number of the elements which cannot be completely eliminated (those with the probability different from zero.) Thus, we do not have any increase of information when additional impossible outcomes are eliminated.
Entropy does not allow for a natural extension of the measure of information to the varieties of continuous character even in the case when the range of the variety is finite (i.e. the support of the random variable is bounded) [
31]. This would have been a death sentence for entropy in the context of continuous random variable, if not the conduit metaphor in which use of two random variables makes sense, and therefore information theory of continuous channels can be developed using mutual information between two random variables. Thus, those who prefer mathematical consistency do not consider any counterpart for discrete entropy in the continuous case [
32]. Others sacrifice consistency and introduce so called “differential entropy,” but after warning about the problem with the divergence and following from that dissociation of differential entropy from information, and after providing suitable interpretation, such as given by Reza [
31] “…in the limit when an infinite number of infinitesimal subintervals are considered, the entropy becomes infinitely large. The interpretation is that the continuous distribution can potentially convey infinitely large amounts of information. We have used the word ‘potentially’ since the information must be received by a receiver or an observer. The observer can receive information with a bounded accuracy….If the observer had an infinitely great level of accuracy, he could detect an infinitely large amount of information from a random signal assuming a continuum of values.” Finally, some (more recent) authors just jump without warning from the discrete entropy to differential entropy forgetting about the infinity separating them [
33].
Differential entropy
has several properties that make it a questionable candidate for the measure of information no matter how it is related to discrete entropy. Reza [
31] summarizes these difficulties as follows: “There are at least three basic points to be discussed:
The entropy of a random variable with continuous distribution may be negative.
The entropy of a random variable with continuous distribution may become infinitely large. Furthermore, if the probability scheme under consideration is ‘approximated’ by a discrete scheme, it can be shown that the entropy of the discrete scheme will always tend to infinity as the quantization is made finer and finer.
In contrast to the discrete case, the entropy of a continuous system does not remain invariant under the transformation of the coordinate systems.”
Our objective is to find a measure alternative to entropy, free from the deficiencies listed above. Does such alternative exist?
6. Eureka! An Alternative Measure for Information
Yes, there is an alternative measure of information that escapes all objections listed above, at least if we limit our considerations to linear transformations of the coordinate systems. But let’s start from heuristic considerations that demonstrate how natural its choice is. The conduit metaphor approach can be generalized to the form that does require all three elements of the communication system: information source, channel, and destination. If we disregard the issue of continuing existence of information in the process of transmission, it is enough to have just opposition of the type: source-destination, before-after, etc.
An example of such a generalization can be found in the famous article of Miller on the limitations of human information processing given by “the magical number seven” [
34]. He writes there: “The ‘amount of information’ is exactly the same concept that we have talked about for years under the name of ‘variance.’ The equations are different, but if we hold tight to the idea that anything that increases the variance also increases the amount of information we cannot go far astray…. The similarity of variance and amount of information might be explained this way: When we have a large variance, we are very ignorant about what is going to happen. If we are very ignorant, then when we make the observation it gives us a lot of information. On the other hand, if the variance is very small, we know in advance how our observation must come out, so we get little from making observation.”
Clearly, Miller’s approach is still within the conduit metaphor, as he refers implicitly to the probability distribution a priori, and an observation which changes information from that before the experiment to that after. Why is “before” in terms of probability distribution, but not “after”? Since the XIXth century, and in particular after the development of quantum mechanics in the first quarter of the XXth century the description of a physical systems in terms of probability distributions has become a standard method. Why don’t we apply this approach to our study of information?
Suppose our information source is a classical gambling “tool,” a die with the six equiprobable outcomes. The outcomes of casting a die are communicated to destination by the means whose nature is irrelevant. The probability distribution describing the die is uniform, all p
i are equal,
![Entropy 06 00388 i007]()
, so
Now, what is the probability distribution that describes the destination, or if somebody prefers, that describes the die after it is cast? It is the other extreme: if the outcome is j, pj = 1 and pi = 0, for every i≠j. In this case Hfin = 0. It is a strange result. When we do not know anything about the outcome, we have maximum amount of information, when we know exactly the outcome, the amount of information is minimum 0. Miller, and before and after him all defenders of Shannon’s measure of information would answer: It is because before the die is cast our ignorance is greatest, so we “can” learn a lot from the cast. After the die is cast we “cannot” learn anything more.
I was always extremely uncomfortable with this explanation. There must be a better way to think about it! We have to find different measure (let’s use for it the symbol “Inf,”) but of course, we have to make sure that the amount of information transmitted is the same as in Shannon’s calculations. What can we change in our analysis of the die’s cast? Maybe we should exchange the values of information measure, Inf
in = 0 and Inf
fin = log
2 6, and assume that information transmitted is the difference between amount of information before and after transmission. We have the amount of information transmitted exactly the same as in Shannon’s calculations. But also we have much more intuitive interpretation. Before the die is cast our information about the outcome is nill due to symmetry of the die. After cast we know exactly what the outcome is. How to get Inf(p), for arbitrary probability distribution p=(p
1,p
2,…,p
n)?
Then, we get desired values. But we wanted to have a measure of information free from the conduit metaphor, without any “before” or “after,” without any reference to arbitrarily selected level of reference such as maximum, minimum, or else. We want to have measure for information about selecting one element out of many in the variety of elements of known size provided by probability distribution. Even this is not a problem. We have two such measures, the second of them with the range of values between 0 an 1 is a result of normalization of the first.
The second measure (6.3), after closer look can be recognized as an old friend from Shannon’s paper, where, under its “maiden name” it was known as redundancy. It has several interesting properties, but it is the first measure (6.2) which is the object of our primary interest. This is the alternative measure announced before, free of many (if not all) blemishes of entropy.
This alternative measure has made some occasional public appearances in the last forty years, but never as contender for the priority over entropy, at most as an impoverished cousin whose very existence depended on entropy. Its formula appeared for the first (and probably last) time in Renyi’s exposition of information theory [
25] as an example of “information gain” in the transition from the uniform to an unspecified probability distribution. Renyi, who was writing his lecture in the convention of the conduit metaphor, considered the concept of information gain only in the context of the differences between different probability distributions. Therefore, he never considered the possibility to use the information gain, with the focus on transitions from the uniform distribution, as a measure for arbitrary single distribution.
To my best knowledge there were only two authors who, in their work in applications of information theory, explicitly considered the idea of using the difference between entropies as a measure of information within one system, Lewis [
35] and Gatlin [
36]. It is a mystery for me, why they have never went beyond the analog of the equality (6.1) in their conceptual analyses to establish an independent measure of information, and based on that measure, to consider entropy as a secondary concept describing the difference between information measures for different distributions:
The power of the conduit metaphor must have been paralyzing.
In
Section 3 above, I mentioned that Brillouin’s measure can be considered an analog of Hartley’s measure for the alternative measure of information presented here. Indeed, let’s consider the probability distribution p=(p
1,p
2,…,p
kp
k+1,p
2,…,p
k+m), where k+m = n and p
i = 1/k for I = 1,…,k, p
i=0 for i>k. Then
Thus, for the special case of probability distribution with n elementary events, such that n-k elementary events have vanishing probability, and the distribution is uniform for the remaining k events, we get Brillouin’s measure.
Let’s go back for the last time to the metaphor from the introduction to this paper. Based on the fact that entropy can be considered the difference between the maximum value of the alternative measure of information for the variety of n elements and the value of this measure for any probability distribution as described in (6.4) H(p) = Infmax – Inf(p), we can think about entropy as a difference between the volume of all barrel and the volume of water in the barrel, or simply as a measure of the volume of empty space above the water. It is the alternative measure which gives the direct measure of the volume of water.
7. Properties of the Alternative Measure for Information
We still have long way to go to demonstrate superiority of the alternative measure of information over entropy. After all, it may be considered irrelevant whether we say that the barrel is half empty, or that it is half full, which, as a popular anecdote has it, just helps to qualify the speaker as a pessimist or optimist. But, there are several reasons beyond intuitiveness and natural character of the alternative measure that make it superior. Unlike entropy, the alternative measure can be easily extended to the continuous distributions on the bound support, and such extension is (again, unlike differential entropy) always nonnegative and invariant with respect to transformations of the coordinate system.
Let’s start from more systematic review of the properties of the alternative measure. In the following we will use an elementary inequality:
Therefore,
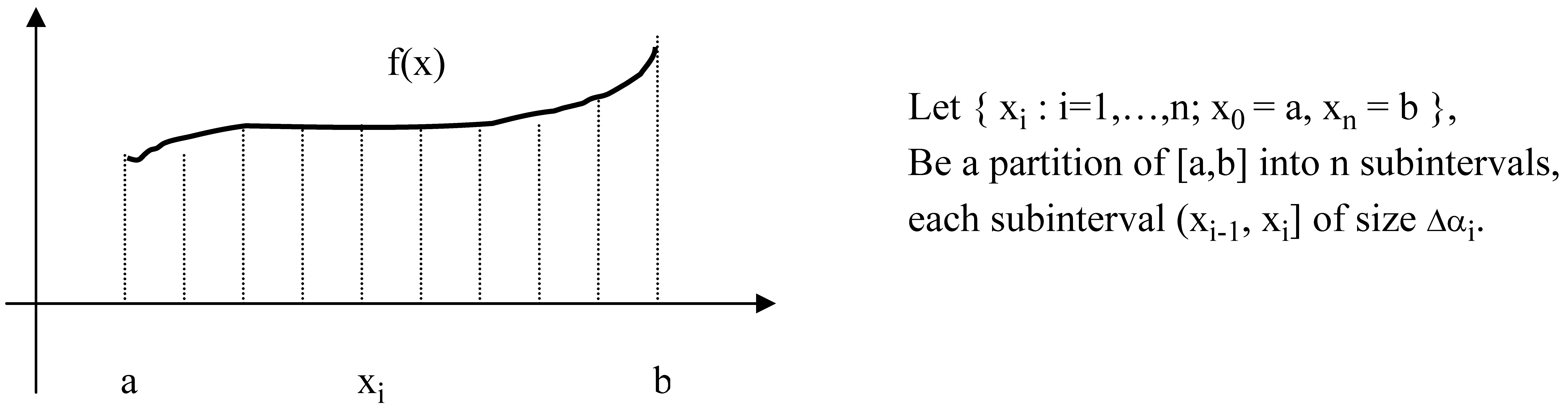
Now, let’s consider the alternative measure for a continuous distribution on interval [a,b] given by the density function f(x) integrable on [a,b].
For each partition into n sub-intervals we can consider a discrete probability distribution q with qi = p
i Δα
i, where:
Now, since f(x) is integrable function on [a,b], we don’t lose generality assuming that each partition is into subintervals of equal length Δα. Then we have:
Now, in the limit when n → +∞, Inf
n(n,q) converges to:
Thus, the alternative measure defined for the discrete probability distributions has a natural extension to the measure (7.5) for continuous distributions. Unlike for entropy, the sequence of partial sums for the alternative measure is convergent.
The interval of integration in (7.5) can be extended to the entire real line as the support for the density function is limited to finite interval. We have assumed that the support of the density function is interval [a,b]. Actually, in the formula (7.5) for the alternative measure the relationship between interval [a,b] and the support of density function is more general. We have to assume only that the support of f(x) is included in the interval [a,b]. Each choice of [a,b] is a choice of the range of the variety which is reduced to unity by information. Therefore, the expression (b-a) in the argument of the logarithmic function follows from the definition of the measure Inf([a,b],f(x)) not from the support of f(x). Thus, the two measures for the same density function f(x): Inf([a,b],f(x)) and Inf([c,d],f(x)) may be different, even if the support of f(x) is included in both intervals. The presence of the expression (b-a) which is the measure of length of the interval representing the range of values for all variety, is an analog of the presence of n in the formula for the discrete case.
Now when we have identified the continuous analog of alternative measure, it is easy to show that it is always nonnegative.
Since t log
2(t) ≥ (t-1) log
2(e) for every t>0,
Finally, we can show that the alternative measure for continuous distributions on the finite interval is invariant with respect to linear transformations of coordinate systems.
Let the random variable X is transformed into new variable Y by a differentiable one-to-one transformation Y = ϕ(X) = mX + c, m ≠ 0 The density function changes as follows g(y) = |1/m|f(x). Then we have [
31,
33]: H(Y) = H(X) + log
2|m|. Let’s assume that ϕ(a) ≤ ϕ (b).
Now, a < b if and only if m > 0, so for a < b we have - H(X) - log
2|m| + log
2m(b-a) = log
2(b-a) – H(X) =
If b<a, then m < 0, and - H(X) - log
2|m| + log
2m(b-a) = log
2(a-b) – H(X) =
From this we can conclude that, if a < b, then Inf([ϕ(a), ϕ (b)],g(y)) = Inf([a,b], f(x)), and if b < a, then Inf([ϕ(a), ϕ (b)],g(y)) = Inf([b,a], f(x)) for a linear transformation of coordinates ϕ.
Thus, the three major objections to entropy, the fact that differential entropy is different from entropy for discrete random variables (i.e. de facto that differential entropy is not an extension of the concept of entropy to the continuous probability distributions), that differential entropy can be negative, and that entropy is not invariant with respect to linear transformations of coordinates, do not apply to the alternative measure of information. The invariance with respect to linear transformations does not restore the property of invariance with respect to all bijective transformations shared by entropy [
33] and the alternative measure in the discrete case, but at least the alternative measure matches invariance properties of mutual information in the continuous case.
Actually, it is only through the alternative measure of information that the connection between entropy and differential entropy can be established. As we could see (6.4), entropy can be defined as the difference between the values of the alternative measure H(p) = Inf(n)max– Inf(n,p). Similarly, differential entropy for the random variable X with density function f(x) with the support on interval [a,b] can be defined as follows H(X) = log2(b-a) – Inf([a,b],f(x)), although in this case the role of the expression log2(b-a) is not so clear, as there is no maximum information on an interval [a,b]. The arbitrary value of log2(b-a) may be interpreted as a reflection of the arbitrary choice of differential entropy as a continuous counterpart of discrete entropy. It is an interesting open question whether the choice of log2(b-a) has any interpretation other than convenience.
8. Examples
We have had some examples of the alternative measures for very simple probability distributions in
Section 6. Thus, for the distribution with n elementary events with one value of probability 1 and all other 0, Inf(n,p) = 0. Then, we considered Brillouin’s measure as the measure for the probability distribution p=(p
1,p
2,…,p
kp
k+1,p
2,…,p
k+m), where k+m=n and p
i=1/k for i=1,…,k, p
i=0 for i>k.
Now, little bit more complicated example. Suppose {a
i: i=1,…,n} be a finite sequence of nonnegative real numbers. Then, when we define s
n as a sum of elements of the sequence
![Entropy 06 00388 i021]()
, and the sequence p
i = a
i/s
n defines probability distribution p for which
Then, the measure for the geometric probability distribution p
i= ar
i, for i=1,…,n, where the constant a = (1-r)/(1-r
n) to give the sum of probabilities equal 0, is
Inf(n,p) = log2(na) + [nrn/(rn -1)-r/(r-1)] log2(r).
It can be seen easily that with increase of n to infinity, Inf(n,p) for the geometric distribution is divergent to infinity. It can be shown, that Inf(n,p) is divergent to infinity with n, no matter what sequence of probability distributions we choose [
37].
Now let’s consider some examples of continuous probability distributions. Obviously, for the uniform distribution f(x) on interval [a,b], Inf([a,b],f) = 0. For the distribution f(x) on interval [a,b] uniform on the subinterval [c,d] (a < c < d <b), Inf([a,b],f) = log2((b-a)/(d-c)), a continuous analog of Brillouin’s measure.
Now, let’s consider Simpson’s distribution, i.e. the convolution of identical uniform distributions on the interval [-a,a]. The density function f(x) is given by: f(x) = 0, for x<-a or x>a; f(x) = (x+a)/a2 for –a ≤ x < 0; f(x) = (-x+a)/a2 for 0 ≤ x ≤ a.
Its graph is as follows.
From this value of the measure for Simpson distribution we get the infinite value of the measure for the probability distribution given by Dirac’s delta δ(x).
Lemma [
38]: Let f(x) be a piecewise continuous density function, f
a(x) = af(ax). Then f
a(x) is convergent to δ(x) as a → +∞, in a sense of distribution convergence.
Now, since any Simpson’s distribution on [-a,a] can be considered f1/a(x) for f(x) defined by f(x) = 0, for x<-1 or x>1; f(x) = x+1 for –1 ≤ x < 0; f(x) = -x+1 for 0 ≤ x ≤ 1, we can conclude a → 0, Simpson’s density functions approach δ(x). When we consider Inf([-b,b], f1/a) for constant b and a → 0, it is diverging to infinity. It is not a surprise, as differential entropy in this case is divergent to minus infinity.
Obviously, the alternative measure is not defined for the normal distribution, or any other distribution with unbounded support. It could be considered a great disadvantage in comparison to differential entropy which is defined for many such distributions, if we knew what exactly differential entropy measures. In any case, it is an interesting problem to clarify the mutual relationship between differential entropy and the alternative measure in the limit when the support of distribution increases to infinity. From the result for infinite discrete distributions mentioned above, it follows directly that we cannot expect that for any sequence of distributions with increasing size of support the alternative measure could be convergent.
9. More About Properties of the Alternative Measure
To complete this introductory study of the alternative measure for the discrete probability distributions, two more properties should be mentioned. The first, quite obvious, is that the measure on the direct product of probability spaces is the sum of measures.
Theorem 9.1
Let S = S1×S2 with the probability distribution given by p×q ik= pipk. Let S1 consists of n elements, S2 consists of m elements. Then Inf(nm,p×q) = Inf(n,p) + Inf(m,q).
The second property is much less obvious.
Theorem 9.2
Let S be a disjoint union of the family of probability spaces {Ai: i = 1,…,m; Ai∩Ak=∅, if i≠k}, each with probability distribution p(i). Let n indicates the number of elements in S, and ni of elements in Ai. We can define a probability distribution p(x) on S the following way.
For every x in S, p(x) = ai p(i)(x), where i is selected by the fact that x belongs to Ai and a1+…+am = 1. Of course, ai = p(Ai) and we can write p(x) = p(Ai) p(i)(x).
If all sets A
i have the same size k, then the formula for Inf(n,p) becomes much simpler:
We can interpret this theorem as an assertion that the total information amount Inf(n,p) can be separated into information identifying the element of the partition Ai, plus the average information identifying an element within subsets of the partition.
10. Conclusion
The alternative measure of information has a potential to provide a sound basis for the semantic theory of information. One of the possible approaches is to go back to the point where Carnap and Bar-Hillel, guided (or misguided) by the analogy with entropy made their choice of measure, and to look for the measure consistent with that presented above.
It is my belief, that even if the alternative measure presented here does not solve all conceptual problems in the study of information, it can help in finding solutions.

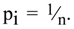 However it was Hartley who first introduced a probabilistic accent to the study in his observation that the message can equally well be generated by a chance event without influencing the measure of information [19].
However it was Hartley who first introduced a probabilistic accent to the study in his observation that the message can equally well be generated by a chance event without influencing the measure of information [19]., then I should be a monotonic increasing function of n. With equally likely events there is more choice, or uncertainty, when there are more possible events.

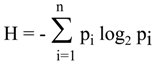 … play a central role in information theory as measures of information, choice and uncertainty.” (p. 50) Shannon suddenly jumps from the description of information production to information itself, choice, and uncertainty. Assuming consistency of his reasoning and the context, we can interpret it as follows. H measures the amount of information transmitted in the communication process as a product of the selection of one out of several possible messages, reflecting the occurrence of one event out of several events in the information source. The process of selection (choice) is characterized subjectively by our uncertainty regarding the outcome of selection. It is clear from the text on page 49 that he means subjective, psychological uncertainty: “Can we find a measure of how much ‘choice’ is involved in the selection of the event or how uncertain we are of the outcome?”
… play a central role in information theory as measures of information, choice and uncertainty.” (p. 50) Shannon suddenly jumps from the description of information production to information itself, choice, and uncertainty. Assuming consistency of his reasoning and the context, we can interpret it as follows. H measures the amount of information transmitted in the communication process as a product of the selection of one out of several possible messages, reflecting the occurrence of one event out of several events in the information source. The process of selection (choice) is characterized subjectively by our uncertainty regarding the outcome of selection. It is clear from the text on page 49 that he means subjective, psychological uncertainty: “Can we find a measure of how much ‘choice’ is involved in the selection of the event or how uncertain we are of the outcome?”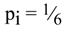 , so
, so
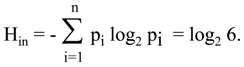
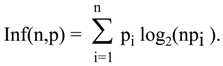
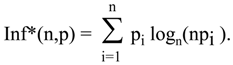
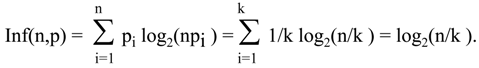
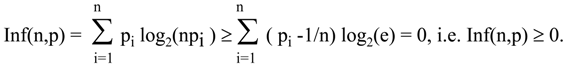
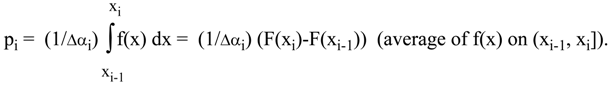
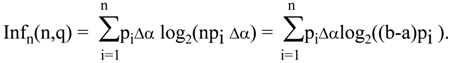
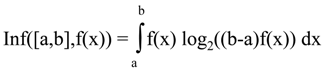
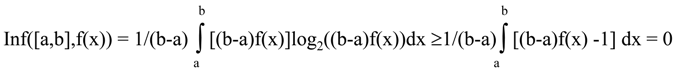
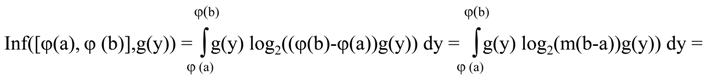
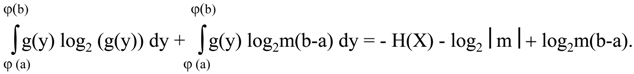
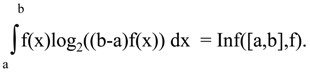
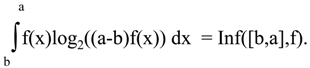
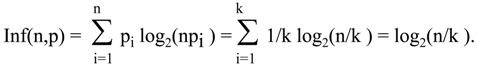
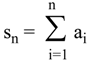 , and the sequence pi = ai/sn defines probability distribution p for which
, and the sequence pi = ai/sn defines probability distribution p for which