Abstract
A concept of entropy production associated with continuous topological evolution is deduced (without statistics) from the fact that Cartan-Hilbert 1-form of Action defines a non-equilibrium symplectic system of Pfaff Topological dimension 2n+2. The differential entropy, dS, is composed of the interior product of the non-canonical components of momentum with the components of the differential velocities. An irreversible process can describe entropy production in terms of continuous topological evolution to non-equilibrium but stationary states. An equilibrium system can be defined topologically as a Lagrange submanifold of the 2n+2 topological space, upon which the change in entropy by continuous topological evolution is zero, dS{equil}=0.
1 A Topological Perspective
In this article, non-equilibrium thermodynamics will be studied from the perspective of continuous topological evolution, using methods based upon Cartan’s theory of exterior differential forms. Discontinuous processes and statistical methods are, more or less, ignored, for a method has been found to distinguish between the dynamics of reversible and irreversible processes acting on non-equilibrium systems. The title emphasizes that this article describes a search for entropic thermodynamic features based upon, and applicable to, continuous topological evolution unfettered by geometrical constraints of metric and connection, and without the imposition of statistical constraints. Of particular utility are the topological concepts of Pfaff dimension, orientability, and that fact that continuous topological evolution can be used to describe topological change with respect to C1 maps without inverse.
It is remarkable that Cartan’s theory of exterior differential forms can be applied to this task, giving a local (differential) method of determining global (topological) features of a thermodynamic system. When local differential methods are constrained by limiting processes (that impose geometrical constraints such as metric and connection), then the induced local linearity of derivatives defeats (or suppresses) any ability to determine global (non-geometric) properties (such as stability) that might be associated with non-linear effects. Cartan’s methods permit an assessment of global features from local differential (not derivative) data. Derivatives require a limiting process to be prescribed; differentials do not. The assumed limiting processes for a derivative refine the topological structure of the more general differential physical system.
Non-equilibrium thermodynamics owes a lot to the work of C. Eckart [9] who imposed phenomenological geometrical constraints on hydrodynamic (Navier-Stokes) systems in order to incorporate "irreversible" processes into the classical laws of physics. (The Lagrange-Euler equations of hydrodynamics, which as Hamiltonian systems, have no thermodynamic irreversible solutions.) Such phenomenological methods ultimately led to the industry of TIP (Thermodynamic Irreversible Processes), which, when proved to be somewhat inadequate, were superseded by adding new geometric variables to the mathematical descriptions, a technique that led to the idea of "extended" thermodynamics. Such geometric methods led to more palatable ideas concerning entropy production, but the concept that change had to approach a maximum was axiomatically imposed.
Generally, the geometric methods presumed that entropy maintained its classical status as an extensive variable (homogenous of degree 1). That assumption should have given the clue that metric geometry was not of intrinsic importance, for homogeneity of degree 1 and additivity of extensive variables is a property of projective (not metric) transformations. Projective invariants are always composed of cross ratios, which are independent from scales. Indeed, an entropy based upon cross ratios has been suggested by Rodriguez [28]. Nowadays there have been concepts of entropy change that do away with the extensive property of classic entropy and lead to yet another industry of "Non - Extensive Entropy" [30].
Using Cartan’s methods, equivalence classes of solutions to the Navier-Stokes equations [19] can be defined which delineate between non-equilibrium chaotic and non-equilibrium turbulent solutions. I know of no other theory that permits such a determination to be made without ad hoc phenomenological additions. Similarly, given an electromagnetic field as solutions to Maxwell’s equations, can it be decided if the electrodynamic system is a non-equilibrium or equilibrium system from a thermodynamic point of view? The methods of continuous topological evolution based on exterior differential forms permit such decisions to be made in terms of the Pfaff topological dimension of that Action 1-form that encodes the potentials, and therefor the field intensities, of the electromagnetic system.
1.1 The fundamental axioms
The theory of non-equilibrium thermodynamics from the perspective of continuous topological evolution, as utilized in this article, is based on four axioms.
Axiom 1 Thermodynamic physical systems can be encoded in terms of a 1-form of covariant Action Potentials, Ak(x, y, z, t...), on a n ≥ 4 dimensional abstract variety of ordered independent variables, {x, y, z, t...}. The variety is pre-geometric in that a metric or connection has not been imposed. The variety, however, supports a volume element Ωn = dxˆdyˆdzˆdt...
Axiom 2 Thermodynamic processes are assumed to be encoded, to within a factor, ρ(x, y, z, t...), in terms of contravariant vector direction fields, Vn(x, y, z, t...).
Axiom 3 Continuous topological evolution of the thermodynamic system can be encoded in terms of Cartan’s magic formula (see p. 122 in [23]). The Lie differential, when applied to a exterior differential 1-form of Action, A = Akdxk, is equivalent abstractly to the first law of thermodynamics. For n = 4,
Cartan’s Magic Formula
L(ρV4)A = i(ρV4)dA + d(i(ρV4)A)
First Law of Thermodynamics : W + dU = Q,
Inexact 1-form of Heat L(ρV4)A = W + dU = Q
Inexact 1-form of Work W = i(ρV4)dA,
Internal Energy U = i(ρV4)A.
Axiom 4 Equivalence classes of systems and continuous processes can be defined in terms of the Pfaff topological dimension.
In effect, Cartan’s methods can be used to formulate precise mathematical definitions for many thermodynamic concepts in terms of topological properties - without the use of statistics or geometric constraints such as metric or connections. Moreover, the method applies to non-equilibrium thermodynamical systems and irreversible processes, again without the use of statistics or metric constraints. The fundamental tool is that of continuous topological evolution, which is distinct from the usual perspective of continuous geometric evolution. Such processes in non-equilibrium states (for which the Pfaff topological dimension is greater than 2) describe the evolution of non-homogeneous structures of multiple, topologically coherent, but disconnected, components.
In order to make the equations more suggestive to the reader, the symbolism for the variety of independent variables has been chosen to be of the format {x, y, z, t}, but be aware that no geometric constraints of metric or connection are imposed upon this variety. For instance, it is NOT assumed that the base variety is euclidean.
It is emphatically stated that geometric notions of scale and metric are to be avoided in favor of topological properties, some of which are invariants of continuous topological evolution, and some of which are not. Those classical thermodynamic features which are diffeomorphic invariants (and useful to many equilibrium applications) are ignored, while topological features which are invariants of continuous transformations (and therefore useful to non-equilibrium applications) are not. Topological evolution is understood to occur when topological features (not geometrical features of size and shape) change. The motivation for this perspective was based upon the goal of developing analytical methods which could decide if a given physical system was an equilibrium system or a non-equilibrium system, and, also, if a specific analytic process was applied to the physical system, was that process reversible or irreversible.
1.2 Notable Results
Remarkably, utilization of these (topological) axioms leads to notable results that are not obtained by geometric methods:
- Thermodynamics is a topological theory.
- Topological change is a necessary condition for thermodynamic irreversibility.
- When the Pfaff topological dimension of the 1-form of Action that encodes a physical system is 2, or less, the system is topologically isolated. The topological structure on domains of topological dimension n ≤ 2 never admit a continuous process which is thermodynamically irreversible. Non-equilibrium systems are of Pfaff topological dimension > 2.
- A 1-form of Action, A, with Pfaff topological dimension equal to 1, defines an equilibrium isolated system which has representation as a Lagrangian submanifold.
- The topological structure of physical systems on domains (contact manifolds) of odd topological dimension n = 3, 5, 7.. > 2 are non-equilibrium systems. On such systems there exists (to within a factor) a unique continuous extremal process, VE, which may be chaotic, but nevertheless is thermodynamically reversible, and has a Hamiltonian generator.
- The topological structure of physical systems on domains of even topological dimension n = 4, 6, 8... > 2 (symplectic manifolds) are non equilibrium systems. Such systems support (to within a factor) a unique continuous process, VT, related to the concept of Topological Torsion. Continuous evolution in the direction of the topological torsion vector is thermodynamically irreversible. In this sense, thermodynamic irreversibility is an artifact of topological dimension n ≥ 4.
- The change of the Pfaff topological dimension will produce topological defects and thermodynamic phase changes.
- The assumption of uniqueness of evolutionary solutions (which implies a Pfaff Topological dimension equal to 2 or less), and homeomorphic evolution, are different, but ubiquitous, constraints imposed upon classical mechanics that eliminate any time asymmetry.
- All Hamiltonian, Symplectic-Bernoulli and Helmholtz processes are thermodynamically reversible. In particular, the work 1-form, W, created by Hamiltonian processes is of Pfaff topological dimension 1 or less.
- The functional forms of tensor fields with arguments in terms of the base variables of the final state are not deterministically predictable in terms of the functional forms of tensor fields with arguments in terms of the base variables of the initial state, unless the map from initial to final state is a diffeomorphism (which preserves topology) [17] . On the other hand, the functional forms of those alternating tensor fields which are coefficients of exterior differential forms, and with arguments in terms of the base variables of the initial state, are well defined in terms of the functional forms of tensor fields with arguments in terms of the base variables of the final state, even when the (C1) map from initial to final state describes topological evolution. In other words, retrodiction of differential forms is possible when topology changes, but prediction is impossible. Hence an Arrow of Time asymmetry is a logical result [15] when topological evolution is admitted, but does not appear if the evolution is restricted to be a homeomorphism or a diffeomorphism, for then the topology is invariant.
- The topological structure of domains of Pfaff dimension 2 or less creates a connected, but not necessarily simply connected, topology. Evolutionary solution uniqueness is possible, to within a projective factor. Such a topological structure can be thought of as a topologically homogeneous object.
- The topological structure of domains of Pfaff dimension 3 or more creates a disconnected topology of multiple components. If solutions to a particular evolutionary problem exist, then the solutions are not unique. Envelope solutions, such as Huygen wavelets and propagating discontinuities (called signals) are classic examples of solution non-uniqueness. Such structures can be thought of as inhomogeneous topological objects.
- Cartan’s Magic formula, in terms of the Lie differential acting on exterior differential 1-forms establishes the long sought for combination of dynamics and thermodynamics, enabling non-equilibrium systems and many irreversible processes to be computed in terms of continuous topological evolution, without resort to probability theory and statistics. The technique goes beyond the usual constraints embedded in a variational principle.
- The Lie differential acting on differential forms is not necessarily the same as a linear affine covariant differential acting on differential forms. It is possible to demonstrate that if the process is locally adiabatic (no heat flow in the direction of the evolutionary process), then the Lie differential and the covariant differential can be made to coincide, as they both satisfy the Koszul axioms for an affine connection (see section 2.5). This is a surprising result, for, when the argument is reversed, the theorem implies that the ubiquitous affine covariant differential of tensor analysis, acting on a 1-form of Action, can always be cast into a form representing an adiabatic process. However, such adiabatic processes need not be reversible. Not all thermodynamic processes are adiabatic; the covariant derivative of tensor analysis does not capture such processes.
- The Lie differential can describe evolutionary processes which are not C2 differentiable, leading to a better understanding of wakes and shocks. On odd dimensional spaces, sequential C1 (translational) processes can be thermodynamically reversible, while intransitive C2 processes (rotation and expansion with a fixed point) will be thermodynamically irreversible.
- If the evolutionary process described by the Lie differential, affine equivalent or not, leaves the 1-form of Action invariant, then the process is thermodynamically reversible. If the affine covariant differential of tensor analysis induces parallel transport (the covariant differential is zero), then the affine process is adiabatic and reversible. Parallel transport does not encode irreversible processes.
- On spaces of Pfaff topological dimension 4, the Cayley-Hamilton theorem produces a characteristic polynomial with similarity invariant coefficients which will generate the format of the Gibbs function for a (universal) van der Waals gas, with a well defined critical point and binodal and spinodal lines. The same technique can be applied to dynamical systems. The fourth order polynomial indicates that the concept of phase change can be related to a 4th order "Higgs" potential.
These results, as they are determined from the perspective of continuous topological evolution, are summarized in section 2, but details appear elsewhere [18]. The notable missing thermodynamic feature in the list above is entropy. One objective of this article is determine how some of the concepts of classical entropy can be deduced from the perspective of continuous topological evolution of the Cartan topology.
Section 3 presents the details of how a concept of the entropy production, dS, of continuous topological evolution can be deduced (without statistics) from the fact that Cartan-Hilbert 1-form of Action (with topological fluctuations) is of Pfaff Topological dimension 2n+2 on a pre-geometric variety {qk, pk, vk, t} of dimension 3n+1. The entropy change can be put into correspondence with the concept of a space-time bulk viscosity, where dissipation is related to expansions and contractions, or otherwise intransitive motions. The requirement that the differential volume element of the 2n+2 dimensional symplectic space is non-zero implies the existence of a perfect differential of entropy change, dS, not included among the differentials of the functions that of the 2n+1 state space, {qk, pk, t}. The differential entropy change is composed of the interior product of the non-canonical components of momentum with the components of the differential velocities. The topological orientation of the 2n+2 volume element, coupled with a constraint of continuous evolution, requires that dS ≥ 0. Continuous topological processes preserve orientation, so once an orientation is decided, continuous transformations preserve that orientation.
Section 4 presents an everyday example of an irreversible process (a skidding - sliding bowling ball) that causes a thermodynamic system of Pfaff topological dimension 6 to decay to an excited state of Pfaff topological dimension 5, far from equilibrium, but where further continuous topological evolution is not thermodynamically irreversible. The coefficient of "bulk velocity" and its relationship to entropy production can be computed analytically.
1.3 Entropy and Topology
It must be remembered that many definitions of "topological" entropy put restrictions on the processes such that they are elements of some group. As Thomas Ward [32] states "For any automorphism α : X → X of a compact metrizable group X, the topological entropy h(α ) may be defined in several different ways. The most convenient formulation is that of Bowen [4], where the topological entropy is expressed as a local rate of volume growth." However, in this article the processes, X, are not restricted to be elements of a group, much less a compact metrizable group. The processes of interest are not homeomorphisms, much less, diffeomorphisms. The search is then for a definition of entropy that does not depend upon group properties and their inability to describe irreversible evolution.
In that which follows, a mechanism for defining an entropy production, dS, in terms of processes that express a local "space-time volume" growth will be established, and a certain amount of comparison can be made to the usual formulations of "topological entropy" and the phenomenological concept of "bulk viscosity". However, the irreversible processes described herein involve the concept of what has been defined as "Topological Torsion". Topological Torsion leads to concepts of entropy production related to "volumetric " expansion or contraction, but without the use of metrical geometric ideas. In engineering terms, the bottom line is that the phenomenological concept concept of "bulk viscosity" is a topological, not a geometric, idea. The bulk viscosity concept involves intransitive evolution of expansions and rotations with a projective fixed point (or origin) not at infinity, and therefor cannot be described by transitive affine assumptions (which do not preserve the origin). On the other hand, shear viscosity can be related to transitive affine assumptions.
Warning! The topology of interest to this article is that generated by Cartan’s Topological structure based on a 1-form of Action, A, and Cartan’s theory of exterior differential forms [2]. The Cartan topology is NOT a metric topology, NOT a Hausdorf topology, and even does NOT satisfy the separation axioms required to be a T1 topology [22]. Yet all of the pertinent topological ideas, including the non-intuitive ones, are easy to grasp from the simple example of the T4 point set topology. Of utmost importance, for physical systems of topological dimension greater than 2, is the fact that the Cartan topology is not a connected topology. This idea implies that such systems are topologically inhomogeneous. As will be discussed below, when the topological dimension is greater than 2, the physical system is a non-equilibrium physical system. Non-equilibrium systems are a consequence of a disconnected topology. Irreversible processes are artifacts where the Pfaff topological dimension is ≥ 4. The importance of this result resides with the topological theorem that mappings from a disconnected topology to a connected topology can be continuous, but continuous maps from a connected topology to a disconnected topology are impossible. In other words continuous maps can be used to describe the irreversible decay of a Turbulent state, but not its creation [14].
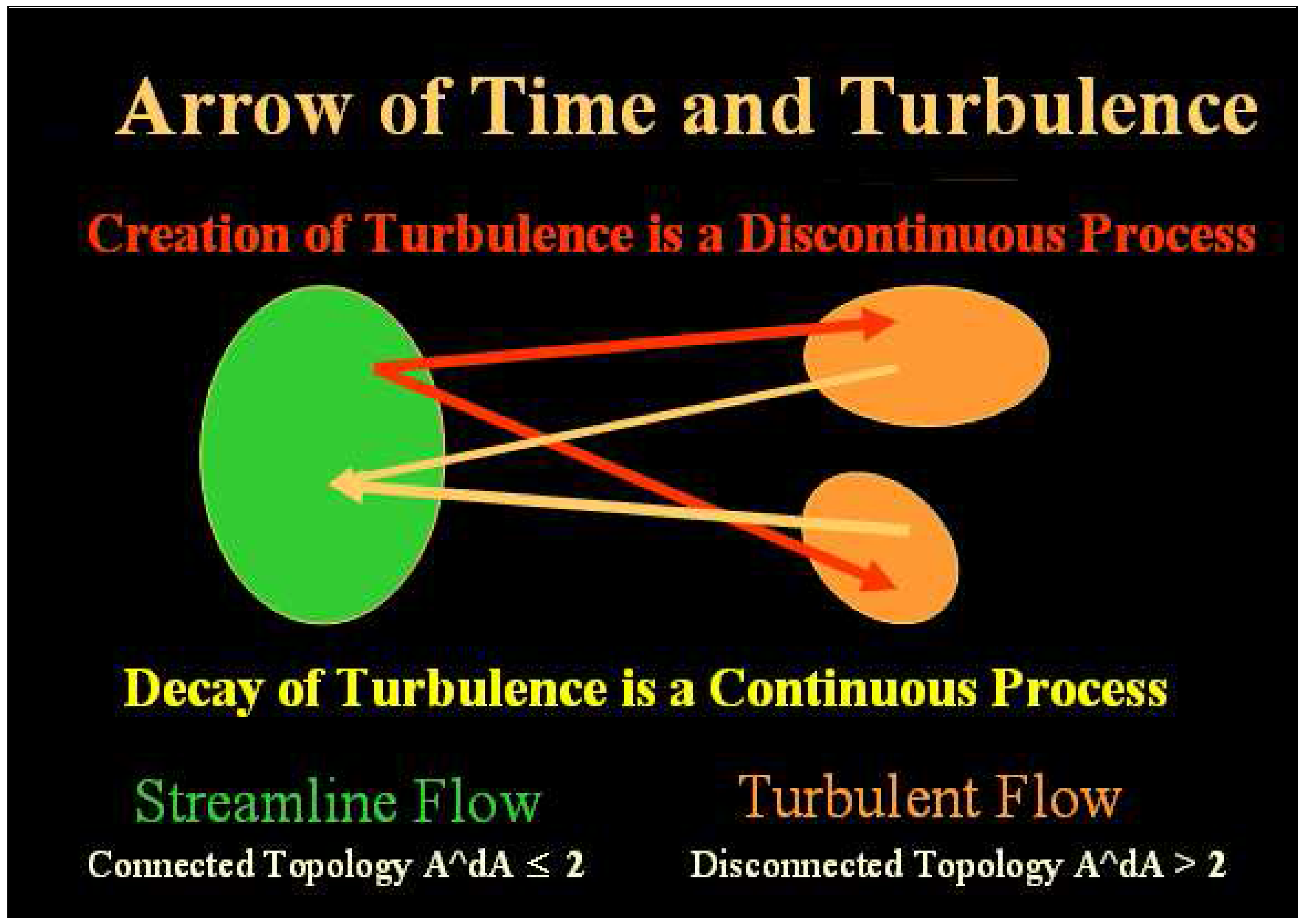
1.4 Topological Torsion
One of the major achievements of a thermodynamics expressed in terms of continuous topological evolution is that it is possible to define the concept of Topological Torsion on symplectic manifolds (of even Pfaff topological dimension > 2) in terms of a vector direction field, say T4 (on a space of Pfaff topological dimension 4). The components of the topological torsion direction field are uniquely defined in terms of the C1 coefficient functions used to encode the physical system as a 1-form of Action, A. On the symplectic manifold, the "divergence" of this vector field, T4, is not zero (implying that symplectic manifold is not compact without boundary, and is either open or with boundary). It section 2.3 it is demonstrated that a process with a component in the direction of the topological torsion vector, T4, is an irreversible process in a thermodynamic sense. The heat 1-form, Q, generated by such a process, T4, is of Pfaff dimension 3 or greater, and does not admit an integrating factor.
If the divergence of the topological torsion tensor is zero, then the Pfaff topological dimension of such a domain is not even. The domain no longer has a symplectic structure, but the does admit a contact structure. It is noteworthy fact that the contact structure (a non-equilibrium state space of odd topological dimension > 2 ) does support "stationary" states in a Hamiltonian sense. This result lends credence to the Prigogine conjecture of "stationary states far from equilibrium". Such "excited - stationary" states are far from equilibrium, for their Pfaff dimension is greater than 2. These excited states represent self organized topologically coherent complexes which are representative of the topological inhomogeneities in the thermodynamic system. On a state space of topological dimension 2n+1 embedded in a space of topological dimension, 2n+2, the topological torsion vector is not zero, but has a zero divergence. Evolution in the direction of the divergence free topological torsion vector is no longer thermodynamically irreversible. In fact, the topological torsion vector represents a characteristic process which is both extremal and associated, in the sense of the calculus of variations, and can be related to Hamilton-Jacobi theory.
2 Fundamentals of non-equilibrium thermodynamics from a perspective of continuous topological evolution.
2.1 The Pfaff Topological Dimension
Perhaps one of the most important topological tools to be used within the theory of continuous topological evolution is the concept of Pfaff topological dimension. The maximum Pfaff dimension is equal to number of independent variables in a given pre-geometric base variety, which in this section has been limited (for reasons of simplicity, and unless otherwise stated) to n = 4. For a given 1-form of Action, A = Ak(x, y, z, t)dxk defined on the base variety of independent variables, {x, y, z, t}, it is possible to ask what is the irreducible minimum number of independent functions θ(x, y, z, t) required to describe the topological features that can be generated by the specified 1-form, A. This irreducible number of functions is defined herein as the "Pfaff topological dimension" of the 1-form, A. For example, if
then only one C1 function θ(x, y, z, t) is required to describe the Action, not four. In this example the irreducible Pfaff topological dimension of the 1-form, A, is 1, although the dimension of the base variety is 4. In a sense, the Pfaff topological dimension defines the existence of a domain of "topological" base variables (topological coordinates) as submersions from the original base variety (pre- geometric coordinates) to the irreducible base variety (topological coordinates). Differential forms constructed on the irreducible topological base variety of functions, are functionally well defined on the original pre-geometric base variety, even though the submersion is not invertible.
A = Akdxk ⇒ dθ(x, y, z, t)irreducible,
such that Ak = ∂θ(x, y, z, t)/∂xk,
Relative to the Cartan topology [2], the "Pfaff topological dimension" can be generated for each of the Pfaffian forms associated with any thermodynamic system. The irreducible Pfaff topological dimension for any given 1-form A is readily computed by constructing the Pfaff sequence of forms:
In this 4D example the Top Pfaffian is the term dAˆdA, which is exact, and has a preimage as the 3-form AˆdA. The Pfaff topological dimension is equal to the number of non-zero terms in the Pfaff sequence. If dAˆdA is not equal to zero, then the Pfaff topological dimension is 4.
Pfaff sequence: {A, dA, AˆdA, dAˆdA}.
As another example, if the Pfaff sequence for a given 1-form A is {A, dA, 0, 0} in a region U ⊂ {x, y, z, t}, then the Pfaff topological dimension of A is 2 in that region, U. The 1-form A, in the region U, then admits description in terms of only two, but not less than 2, independent variables, say {u1, u2}. For a differentiable map ϕ from {x, y, z, t} ⇒ {u1, u2}, the exterior differential 1-form defined on the target variety U of 2 pre-geometry dimensions as
has a functionally well defined pre-image A(x, y, z, t) on the base variety {x, y, z, t} of 4 pregeometric dimensions. This functionally well defined pre-image is obtained by functional substitution of u1, u2, du1, du2 in terms of {x, y, z, t} as defined by the mapping ϕ. The process of functional substitution is called the pull-back:
A(u1, u2) = A1(u1, u2)du1 + A2(u1, u2)du2,
A(x, y, z, t) = Akdxk = ϕ∗(A(u1, u2)) = ϕ∗(Aσduσ).
It may be true that the functional form of A yields a Pfaff topological dimension equal to 2 globally over the domain {x, y, z, t}, except for sub regions where the Pfaff dimension of A is 3 or 4. These sub regions represent topological defects in the almost global domain of Pfaff dimension 2. Conversely, the Pfaff dimension of A could be 4 globally over the domain, except for sub regions where the Pfaff dimension of A is 3, or less. These sub regions represent topological defects in the almost global domain of Pfaff dimension 4. Applications of both viewpoints have merit. The important concept of Pfaff topological dimension also can be used to define equivalence classes of both physical systems and processes.
The concept of "Pfaff topological dimension" was developed more than 110 years ago (see page 290 of Forsyth [11] ), and has been called the "class"1 of a differential 1-form in the mathematical literature. More recent mathematical developments can be found in [29]. The method and its properties have been little utilized in the applied world of physics and engineering. Of key importance (in 4 dimensions) is the fact that the non-zero existence of the 3-form AˆdA = AˆF of Topological Torsion, and the 4-form of Topological Parity, dAˆdA = FˆF implies that the Pfaff topological dimension of the region is 3 or 4, respectively. Either value is an indicator that the physical system (in the sub region) is NOT in thermodynamic equilibrium. The concept of Topological Parity, FˆF, has its foundations in the theory of Pfaff’s problem, with a recognizable 4 dimensional formulation appearing in Forsyth [11] page 100. The idea of Topological Torsion, AˆF, is associated with the idea of magnetic helicity density, a concept that apparently had its electromagnetic genesis with the study of plasmas in WWII. However, the concept of helicity density is but one component of the four dimensional Topological Torsion 4 vector.
Recall that a space curve with non-zero Frenet - Serret torsion does not reside in a two dimensional plane. Non-zero Frenet - Serret torsion of a space curve is an indicator that the geometrical dimension of the space curve is at least 3. The fact that the Pfaff topological dimension of the 1-form, A, is at least 3, when AˆF is non-zero, is the reason why the 3-form, AˆF, was called "Topological Torsion". The idea of non-zero AˆF also appears in the theory of the Hopf Invariant [5].
2.2 Physical Systems: Equilibrium, Isolated, Closed and Open
Physical systems and processes are elements of topological categories determined by the Pfaff topological dimension (or class) of the 1-forms of Action, A, Work, W, and Heat, Q. For example, the Pfaff topological dimension of the exterior differential 1-form of Action, A, determines the various species of thermodynamic systems in terms of distinct topological categories. There are two topological thermodynamic categories that are determined by the closure (or differential ideal) of the 1-form of Action, A∪dA, and the closure of the 3-form of topological torsion, AˆdA∪dAˆdA. The first category is represented by a connected Cartan topology, while the second category is represented by a disconnected Cartan topology.
2.2.1 Connected Topology: Topological Torsion = AˆdA = 0
- Equilibrium physical systems are elements such that the Pfaff topological dimension is 1.
- Isolated physical systems are elements such that the Pfaff topological dimension is 2, or less [22]. Isolated systems of Pfaff dimension 2 need not be in equilibrium, but do not exchange radiation or mass with the environment.Systems : Pfaff topological dimension when: AˆdA = 0dA = 0 Equilibrium - Pfaff dimension 1AˆdA = 0 Isolated - Pfaff dimension 2Both systems have a connected topology, but these domains need not be simply connected.
2.2.2 Disconnected Topology: Topological Torsion = AˆdA ≠ 0
- Closed physical systems are elements such that the Pfaff topological dimension is 3. Closed systems can exchange radiation, but not mass, with the environment.
- Open physical systems are such that the Pfaff topological dimension is 4. Open physical systems can exchange both radiation and mass with the environment.Systems : Pfaff topological dimension when: AˆdA ≠ 0d(AˆdA) = 0 Closed - Pfaff topological dimension 3dAˆdA ≠ 0. Open - Pfaff topological dimension 4.
2.3 Reversible and Irreversible Processes
The Pfaff topological dimension of the exterior differential 1-form of Heat, Q, determines important topological categories of processes. From classical thermodynamics "The quantity of heat in a reversible process always has an integrating factor" [12] [25] . In the language of exterior differential forms, the existence of an integrating factor requires that the Frobrenius unique integrability theorem, QˆdQ = 0, must be statisfied. Hence all reversible processes are such that the Heat 1-form, Q, is of Pfaff dimension 2 or less. Irreversible processes are such that the Pfaff dimension of Q is greater than 2. A dissipative irreversible topologically turbulent process is defined when the Pfaff dimension of Q is 4.
Processes defined by the Pfaff dimension of Q
Processes : as defined by the Pfaff dimension of Q
QˆdQ = 0 Reversible - Pfaff dimension 2
d(QˆdQ) ≠ 0. Turbulent - Pfaff dimension 4.
Note that the Pfaff dimension of Q depends on both the choice of a process, V4, and the system, A, upon which it acts. As reversible thermodynamic processes are such that QˆdQ = 0, and irreversible thermodynamic processes are such that QˆdQ ≠ 0, Cartan’s formula of continuous topological evolution can be used to determine if a given process, V4, acting on a physical system, A, is thermodynamically reversible or not:
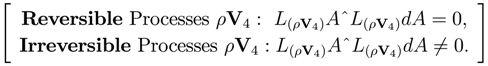
Processes defined by the Lie differential of A
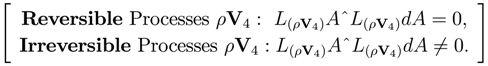
Remarkably, Cartan’s magic formula can be used to describe the continuous dynamic possibilities of both reversible and irreversible processes, in equilibrium or non-equilibrium systems, even when the evolution induces topological change, transitions between excited states, and changes of phase, such as condensations. It should be noted that all classic Hamiltonian, Bernoulli-Casimir, and Helmholtz dynamical processes satisfy the topological constraint [20] such that
Hence, it follows that all such processes are thermodynamically reversible, as QˆdQ = 0.
di(ρV4)dA = dW = dQ = 0.
It is also important to note that the direction field, V4, need not be topologically constrained such that it is singularly parameterized. That is, the evolutionary processes described by Cartan’s magic formula are not necessarily restricted to vector fields that satisfy the topological constraints of kinematic perfection, dxk − V kdt = 0. A discussion of topological fluctuations, where dxk − Vkdt = ∆k ≠ 0, and an example fluctuation process is described below. Topological fluctuations are related to the differences between the concept of a derivative and the concept of a differential.
2.4 A Non-Equilibrium Physical System
2.4.1 Topological Torsion
For maximal, non-equilibrium, turbulent systems in a 4D variety of independent variables (space-time), the maximal element in the Pfaff sequence generated by the three 1-forms, A, W, or Q, is a 4-form. On the geometric space of 4 independent variables, every 4-form is globally closed, in the sense that its exterior differential vanishes everywhere. It follows that every 4-form is exact and can be generated by the exterior differential of a 3-form. The exterior differential of the 3-form is related to the concept of a divergence of a contravariant vector direction field. At first, the development in this article will be devoted to the study of such 3-forms and 4-forms, whose existence imply that the associated thermodynamic system is a non-equilibrium system. It is a remarkable fact that all 3-forms (in general, N-1 forms) admit integrating denominators, such that the exterior differential of a rescaled 3-form is zero almost everywhere. Space time points upon which the integrating denominator has a zero value produce singularities defined as topological defect structures. In sections 3 and 4, these methods will be extended to spaces of higher Pfaff topological dimension.
When the Action for a 4D physical system is of Pfaff dimension 4, there exists a unique direction field, T4, defined as the Topological Torsion 4-vector, that can be evaluated entirely in terms of those component functions of the 1-form of Action, A, which define the physical system. To within a factor, this direction field2 has the four components of the 3-form AˆdA, with the following properties:
Properties of the Topological Torsion vector T4
i(T4)Ω4 = AˆdA
W = i(T4)dA = σ A,
U = i(T4)A = 0,
L(T4)A = σ A = Q,
QˆdQ = L(T4)AˆL(T4)dA = σ2AˆdA ≠ 0
dAˆdA = 2 σ Ω4.
Hence, by equation (26 ) evolution in the direction of T4 is thermodynamically irreversible, when σ ≠ 0 and A is of Pfaff topological dimension 4. The kernel of this vector field is defined as the zero set under the mapping induced by exterior differentiation. In engineering language, the kernel of this vector field are those point sets upon which the divergence of the vector field vanishes. The Pfaff topological dimension of the Action 1-form is 3 in the defect regions defined by the kernel of T4. The coefficient σ can be interpreted as a measure of space-time volumetric expansion or contraction. It follows that both expansion and contraction processes (of space-time) are related to irreversible processes. It is here that contact is made with the phenomenological concept of "bulk" viscosity.
Note that if QˆdQ = 0, then the thermodynamic process is reversible. In a qualitative sense, if the 3-form is non-zero, then its fluctuation away from zero yields information as to the "measure" of irreversibility. More precisely, if the initial conditions of QˆdQ are not zero, then equation (26) indicates that the measure of irreversibility is proportional to σ2. It is tempting to identify σ2 with the concept of entropy production, for the implication is that both expansions and contractions of the volume element, as indicated by the factor, σ, cause the 3-form to change in the same manner. The approach to reversibility leads to entropy production and an entropy maximum.
2.4.2 An Electromagnetic Example
For purposes of more rapid comprehension, consider a 1-form of Action given by the expression in terms of electromagnetic potentials,
The exterior differential, dA, leads to an electromagnetic interpretation (E = −∂A/∂t−∇φ, and B = ∇ × A)3. The explicit format of the Electromagnetic Topological Torsion 4 vector, T4, becomes [16]:
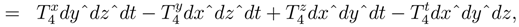
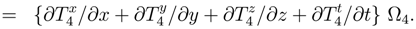 When the 3-form AˆdA is not zero, then the thermodynamic system is a non-equilibrium thermodynamic system. Note that a non-zero magnitude of helicity density, A ◦ B ≠ 0, is sufficient, but not necessary, for the electromagnetic system to represent a non-equilibrium thermodynamic system. Even systems without a magnetic field B can be non-equilibrium systems. Systems without an electric E field, but with non-zero B fields (such as found in certain plasmas) can also represent non-equilibrium thermodynamic systems.
When the 3-form AˆdA is not zero, then the thermodynamic system is a non-equilibrium thermodynamic system. Note that a non-zero magnitude of helicity density, A ◦ B ≠ 0, is sufficient, but not necessary, for the electromagnetic system to represent a non-equilibrium thermodynamic system. Even systems without a magnetic field B can be non-equilibrium systems. Systems without an electric E field, but with non-zero B fields (such as found in certain plasmas) can also represent non-equilibrium thermodynamic systems.
A = Ak(x, y, z, t)dxk = A ◦ dr − φdt.
T4 = −[E × A + Bφ, A ◦ B]
AˆdA = i(T4)Ω4
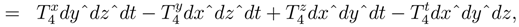
dAˆdA = 2 (E ◦ B]) Ω4 = KΩ4
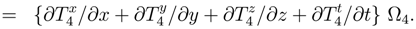
When the divergence of the topological torsion vector is not zero, σ = (E ◦ B) ≠ 0,and A is of Pfaff dimension 4, W is of Pfaff dimension 4, and Q is of Pfaff dimension 4. The process generated by T4 is thermodynamically irreversible, as
The evolution of the volume element relative to the irreversible process T4 is given by the expression,
Hence, the differential volume element Ω4 is expanding or contracting depending on the sign and magnitude of σ = E ◦ B, a useful fact when topological thermodynamics is applied to cosmology. A cosmology on 4D can have an expanding volume element, Ω4, but with embedded 3D defect structures (the galaxies) which are not "expanding".
QˆdQ = L(T4)AˆL(T4)dA = σ2AˆdA ≠ 0.
L(T4)Ω4 = i(T4)dΩ4 + d(i(T4)Ω4)
= 0 + d(AˆdA) = 2(E ◦ B) Ω4.
If A is (or becomes) of Pfaff dimension 3, then dAˆdA ⇒ 0 which implies that σ2⇒ 0, but AˆdA ≠ 0. The differential geometric volume element Ω4 is subsequently an evolutionary invariant, and evolution in the direction of the topological torsion vector is thermodynamically reversible. The physical system is not in equilibrium, but the divergence free T4 evolutionary process forces the Pfaff dimension of W to be zero, and the Pfaff dimension of Q to be at most 1. Indeed, a divergence free T4 evolutionary process has a Hamiltonian representation. In the domain of Pfaff dimension 3 the subsequent continuous evolution of the system, A, relative to the process T4, proceeds in an energy conserving manner, representing a "stationary" or "excited" state far from equilibrium. These excited states can be interpreted as the evolutionary topological defects in the Turbulent dissipative system of Pfaff dimension 4. The Topological Torsion vector becomes an adiabatic, extremal, characteristic direction field in the space of geometric dimension 4, but where the Pfaff dimension of the physical system, A, is of Pfaff topological dimension 3.

On a pre-geometric domain of 4 dimensions, assume that the evolutionary process generated by T4 starts from an initial condition (or state) where the Pfaff topological dimension of A is also 4. Depending on the sign of the divergence of T4, the process follows an irreversible path for which the divergence represents an expansion or a contraction. If the irreversible evolutionary path is attracted to a region (or state) where the Pfaff topological dimension of the 1-form of Action is 3, then E ◦ B becomes (or has decayed to) zero. The zero set of the function E ◦ B defines a hypersurface in the 4 dimensional space. If the process remains trapped on this hypersurface of Pfaff dimension 3, E ◦ B remains zero, and the T4 process becomes an extremal, adiabatic, characteristic direction field. Such extremal fields are such that the virtual work 1-form vanishes, W = i(T4)dA = 0. The direction field that represented an irreversible process, in domains where the divergence goes to zero, becomes a representation for a reversible conservative extremal Hamiltonian process. Although the process is conservative in a Hamiltonian sense, the physical system can be in a "excited" state on the hypersurface that is far from equilibrium, for the Pfaff dimension of the 1-form of Action is 3, and not 2. (If the path is attracted to a region where the function E ◦ B is oscillatory, the system evolutionary path defines a limit cycle, or what has been called a "breather" in soliton theory.)
2.5 The Lie differential L(V) and the Covariant differential ∇(V)
The covariant derivative of tensor analysis, as used in General Relativity, is often defined in terms of isometric diffeomorphic processes (that preserve the differential line element) and can be used to describe rigid body motions and isometric bendings, but not deformations and shear processes associated with convective fluid flow. Another definition of the covariant derivative is based on the concept of a connection, such that the differential process acting on a tensor produces a tensor. The definition of the covariant derivative usually depends upon the additional structure (or constraint) of a metric or a connection placed on a given variety, while the Lie differential does not. As the Lie differential is not so constrained, it may be used to describe non-diffeomorphic processes for which the topology changes continuously. The covariant derivative is avoided in this article.
Koszul ( see p. 262 in [13]) has given a set of axioms that can be used to define an affine connection and a covariant derivative. The covariant derivative axioms require that
This axiomatic representation of a covariant derivative and an affine connection should be compared to the Lie differential,
Only if the last term in the expansion of the Lie differential, df (i(V )A), is zero does the formula for the Lie differential have an equivalent representation as a covariant derivative in terms of an affine connection. Suppose that i(V)A = 0, such that the Lie differential and the covariant differential are equivalent.
Then it follows that
∇(fV)ω = f ∇(V)ω,
∇(V)fω = (∇(V)f)ω + f ∇(V)ω.
L(fV)A = f L(V)A + df (i(V)A),
L(V)fA = (L(V)f)A + f L(V)A.
L(fV)A = f L(V)A = f ∇(V)A.
L(fV)A = f L(V)A + df (i(V )A)
= f L(V)A = f Q.
But i(V)Q = f i(V)i(V )dA = 0 ⇒ i(V)Q,
where i(V)Q = 0 defines an adiabatic process.
Conclusion 5 Hence, all covariant derivatives with respect to an affine connection have an equivalent representation as an adiabatic process!!! Such covariant adiabatic processes need not be thermodynamically reversible.
Suppose that the adiabatic process is such that
Then
and it follows that the adiabatic process is reversible. However, the condition that Q be zero is the equivalent to the condition of parallel transport:
L(V)A = Q = 0.
dL(V)A = L(V)dA = dQ = 0,
L(V)ω⇒ ∇(V)ω = 0.
Conclusion 6 The remarkable conclusion is that the concept of parallel transport in tensor analysis is - in effect - an adiabatic, reversible process!!!
As it is apparent that not all evolutionary processes are adiabatic, much less reversible, it seems sensible to conclude that theories (such as general relativity) that invoke the use of a covariant derivative, and or parallel transport, to describe evolutionary processes have allowed irreversible phenomena, in the words of Sir Arthur Eddington, "to slip through the net".
3 The basic idea: Topological Fluctuations lead to a concept of an entropy production relative to continuous topological evolution.
3.1 Extensions of the Cartan-Hilbert Action 1-form
This subsection considers those physical systems that can be described by a Lagrange function L(q, v,t) and a 1-form of Action given by:
A = L(qk,vk, t)dt + pk·(dqk − vkdt),
The classic Action, L(qk,vk, t)dt, is extended to included topological fluctuations in the kinematic variables. It is no longer assumed that the equation of Kinematic perfection is satisfied. That is, fluctuations of the topological constraint of kinematic perfection are permitted:
Topological Fluctuations :
in position ∆q = (dqk − vkdt) ≠ 0,
in velocity ∆v = (dvk − akdt) ≠ 0,
in momenta ∆p = (dpk − fkdt) ≠ 0.
These topological fluctuations are not merely functions of time, but can be fluctuations in space and perhaps other parametric variables. Note that the topological fluctuations are not derivatives, but are differentials - the limit process has not been explicitly stated. One particular fluctuation problem is related to the choice of an "observers" origin. For example, in mechanics it is often assumed that the origin is located at the center of mass. Such an approach can lead to imprecision and fluctuations of parameters, such as mass. The only origin that is free from such defects is a singular barycentric system, but that cannot be defined with parameters that are positive definite (such as mass). In the singular barycentric system of projective systems, any point can be used as the "origin" for all other points in an equivalent manner.
When dealing with topological fluctuations, the pre-geometric dimension will not be constrained to only 4 independent variables. At first glance it appears that the domain of definition for the Cartan-Hilbert Action 1-form, above, is a 3n+1 dimensional variety of independent base variables, {pk, qk, vk, t}. The reader is warned that p is NOT constrained to be a jet; e.g., pk ≠ ∂L/∂vk. Instead, the pk are considered to be a (set of) Lagrange multiplier(s) to be determined later. Note that the Action 1-form has the format used in the Cartan-Hilbert invariant integral [8], except that herein it is not assumed that the pk are canonical; that is, pk ≠ ∂L/∂vk necessarily. Also, it is NOT assumed at this stage that the vector field, v, is a kinematic velocity function, such that (dqk − vkdt) ⇒ 0. A classical inference is to assert that topological fluctuations in kinematic velocity, ∆q, are related to pressure, and topological fluctuations in kinematic acceleration, ∆v, are related to temperature.
For the given Lagrangian and its Action, construct the Pfaff sequence
in order to determine the Pfaff dimension or class of the 1-form [27]. The top Pfaffian is defined as the non-zero p-form of largest degree p in the sequence. The top Pfaffian for the Cartan-Hilbert Action can be explicitly evaluated, and is given by the formula,
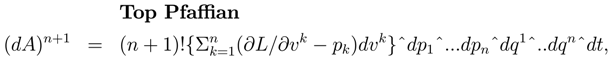 The formula is a bit surprising in that it indicates that the Pfaff topological dimension of the Cartan-Hilbert 1-form is 2n + 2, and not the expected "geometrical" dimension 3n + 1. For n = 3 degrees of freedom, the top Pfaffian indicates that the Pfaff topological dimension of the 2-form, dA is 2n + 2 = 8, and not the pre-geometrical dimension equal to 3n + 1 = 10. The implication is that there exists an irreducible number of independent variables equal to 2n+2 which completely characterize the differential topology of the first order system described by the Cartan-Hilbert Action. It follows that the exact two form, dA, satisfies the equations
As the top Pfaffian represents a 2n + 2 volume element,
then the bracketed expression in the formula for the top Pfaffian must reduce to an exact differential, dS :
The formula is a bit surprising in that it indicates that the Pfaff topological dimension of the Cartan-Hilbert 1-form is 2n + 2, and not the expected "geometrical" dimension 3n + 1. For n = 3 degrees of freedom, the top Pfaffian indicates that the Pfaff topological dimension of the 2-form, dA is 2n + 2 = 8, and not the pre-geometrical dimension equal to 3n + 1 = 10. The implication is that there exists an irreducible number of independent variables equal to 2n+2 which completely characterize the differential topology of the first order system described by the Cartan-Hilbert Action. It follows that the exact two form, dA, satisfies the equations
As the top Pfaffian represents a 2n + 2 volume element,
then the bracketed expression in the formula for the top Pfaffian must reduce to an exact differential, dS :
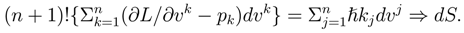
Pfaff Sequence {A, dA, AˆdA, dAˆdA, AˆdAˆdA, dAˆdAˆdA, ..}
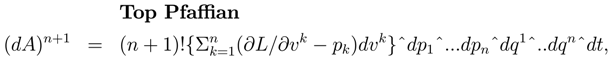
(dA)n+1 ≠ 0, but Aˆ(dA)n+1 = 0.
(dA)n+1 ⇒ Ω2n+2 = dSˆdp1ˆ...dpnˆdq1ˆ..dqnˆdt,
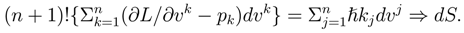
Conclusion 7 As the 2n+2 form represents a volume element, the coefficient of the top Pfaffian has a representation (to within a factor) as a perfect differential of a function, S, which is independent from the {pk, qk, t}. The differential change of the function S is explicitly dependent upon the differentials of velocity dvk and the non-canonical components of momentum (∂L/∂vk − pk).
Definition 8 The change in entropy due to continuous topological evolution is defined as dS, and is given by the expression
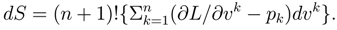
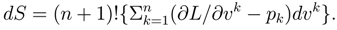
Definition 9 The function S whose differential is the 1-form given in eq. ( 58) is defined as the entropy of continuous topological evolution.
The even dimensional 2n+2 form represents an orientable volume element, and once an orientation has been fixed (say +1), then as continuous evolution is constrained to maintain the volume element and its sign, the change in the entropy, dS, must be of one sign. So entropy of topological evolution, if it changes globally, can be only of one sign (chosen to be positive in the historic literature). Also, as dA is presumed to be non-degenerate, then the differential, dS, can not change sign by continuous topological evolution on the 2n+2 dimensional space.
Conclusion 10 Hence the fact that global changes in entropy of continuous topological evolution must be of one sign ≥ 0 is an artifact of topological orientability.
Next consider subspaces of the Symplectic 2n+2 space. In particular consider a Lagrangian submanifold, which must be dimension n+1. By definition, on the Lagrangian submanifold (of dimension n+1) of the Symplectic space (of dimension 2n+2), the 2-form dA must vanish [3]. The 2-form can be written as:
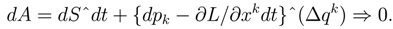
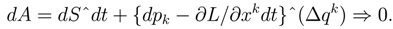
Observe that the immersion ψ of the configuration space with differentials {dq1ˆ..dqnˆdt} into the top Pfaffian space {dSˆdp1ˆ...dpnˆdq1ˆ..dqnˆdt}, defines a Lagrangian submanifold when the pullback of the 2-form dA vanishes. The 2-form dA has expression given by the equation above. Consider the case where the immersion into the 3n+1 space is such that the pullback of (∆qk ) ⇒ 0.
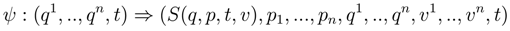 Then the 2-form has a pullback realization such that
Then the 2-form has a pullback realization such that
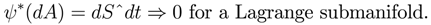 The Pfaff topological dimension of the constrained 1-form of Action is then 2 on configuration space, and induces a connected Cartan Topology. The 2-form vanishes when the entropy is a constant:
The Pfaff topological dimension of the constrained 1-form of Action is then 2 on configuration space, and induces a connected Cartan Topology. The 2-form vanishes when the entropy is a constant:
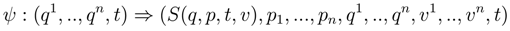
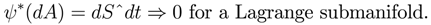
Conclusion 11 Equilibrium implies dSequil(q, p, t, v) ⇒ dSequil(t) ⇒ 0.
It is also remarkable to note that if the momenta are canonically defined, such that
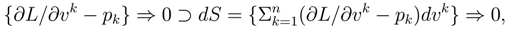 then the entropy production, dS,vanishes.The concept of an entropy of continuous topological evolution is explicitly dependent upon the existence of non-canonical momenta. It is important to remember that the differential production of entropy, dS, is not necessarily representable as derivative with respect to time, except on the Lagrangian equilibrium submanifold. If the Lagrange multipliers are constrained to be canonical momenta, as is done in the classical theory of Hamiltonian mechanics, then the entropy production vanishes, the Pfaff topological dimension becomes odd, and the Action 1-form admits extremal processes which have a Hamiltonian solution. All such Hamiltonian processes are thermodynamically reversible.
then the entropy production, dS,vanishes.The concept of an entropy of continuous topological evolution is explicitly dependent upon the existence of non-canonical momenta. It is important to remember that the differential production of entropy, dS, is not necessarily representable as derivative with respect to time, except on the Lagrangian equilibrium submanifold. If the Lagrange multipliers are constrained to be canonical momenta, as is done in the classical theory of Hamiltonian mechanics, then the entropy production vanishes, the Pfaff topological dimension becomes odd, and the Action 1-form admits extremal processes which have a Hamiltonian solution. All such Hamiltonian processes are thermodynamically reversible.
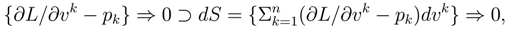
4 An Irreversible Example: The Sliding Bowling Ball
4.1 The Observation
To give substance to the methods described above, an example of an irreversible process, decaying from a set of initial conditions in a domain of Pfaff dimension 2n+2, will be given. The irreversible process continues until the system reaches a point where the Pfaff topological dimension decays to the value 2n+1. Once the evolutionary orbit enters the domain of Pfaff topological dimension 2n+1, further motion can be described by a Hamiltonian process without further irreersible dissipation. The physical system is not an equilibrium system, for the Pfaff topological dimension is 2n+1, yet the evolution is stationary in the sense of a Hamiltonian extremal field.
Consider a bowling ball given an initial amount of translational energy and rotational energy. Assume the angular momentum and the linear momentum are orthogonal to themselves and also orthogonal to the ambient gravitational field. Then place the bowling ball, subject to these initial conditions, in contact with the bowling alley. Initially, it is observed that the ball slips or skids, dissipating its linear and angular momentum, until the No-Slip condition is achieved. Note that it is possible for the angular momentum or the linear momentum to change sign during the irreversible phase of the evolution. The dynamical system representing the evolutionary process is irreversible until the No-Slip condition is reached. Thereafter, the dynamical system is reversible, and momentum is conserved.
4.2 The Analysis
Assume that the physical system may be represented by a 1-form of Action constructed from a Lagrange function:
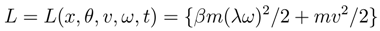 The constants are: m=mass, β = moment of inertial factor (2/5 for a sphere), λ = effective ”radius” of the object, the moment of inertia = βmλ2.
The constants are: m=mass, β = moment of inertial factor (2/5 for a sphere), λ = effective ”radius” of the object, the moment of inertia = βmλ2.
Let the topological constraints be defined anholonomically by the Pfaffian system:
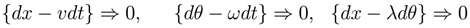
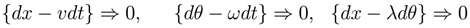
Define the constrained 1-form of Action as
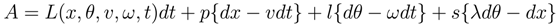 where {p, l, s} are Lagrange multipliers. Rearrange the variables to give (in the language of optimal control theory) a pre-Hamiltonian action:
where {p, l, s} are Lagrange multipliers. Rearrange the variables to give (in the language of optimal control theory) a pre-Hamiltonian action:
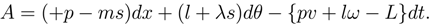 Computation of the Pfaff sequence leads to the apparent realization that the Pfaff dimension of this Action 1-form is 2n+2 = 6. The Action defines a symplectic manifold of dimension 6.
Computation of the Pfaff sequence leads to the apparent realization that the Pfaff dimension of this Action 1-form is 2n+2 = 6. The Action defines a symplectic manifold of dimension 6.
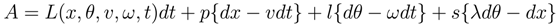
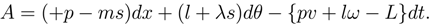
For algebraic simplicity, assume initially that two of the Lagrange multipliers (momenta) are defined canonically; e.g.,
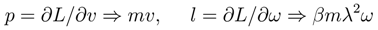 which implies that the 1-form of Action can be expressed as,
which implies that the 1-form of Action can be expressed as,
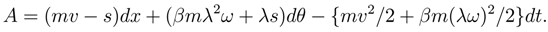 The 6-dimensional volume element of the symplectic manifold (the top Pfaffian) is given by the expression
The 6-dimensional volume element of the symplectic manifold (the top Pfaffian) is given by the expression
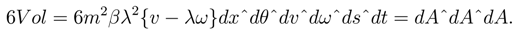 The 6D volume element is either expanding or contracting (irreversibly) with a coefficient 6m3βλ2{v − λω}. This dissipative coefficient is related to the concept of "bulk" viscosity.
The 6D volume element is either expanding or contracting (irreversibly) with a coefficient 6m3βλ2{v − λω}. This dissipative coefficient is related to the concept of "bulk" viscosity.
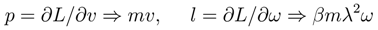
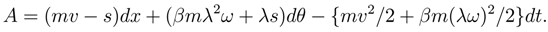
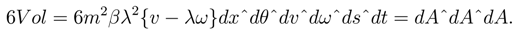
The symplectic manifold has a singular subset upon which the Pfaff dimension of the Action 1-form is 2n+1 = 5. The constraint for such a contact manifold is precisely the no-slip condition (when the "bulk viscosity" goes to zero):
This condition is the analogue of the zero divergence condition in incompressible hydrodynamics, only the divergence is that associated with the topological torsion vector, d(AˆdAˆdA) in a six dimensional (2n+2) space.
{v − λω} ⇒ 0.
On the 5 dimensional contact manifold there exists a unique extremal (Hamiltonian) field which (to within a projective factor) defines the conservative reversible part of the evolutionary process. As this unique extremal vector satisfies the equation
it is easy to show that dynamical systems defined by such vector fields must be reversible in the thermodynamic sense. (As dQ = d(i(V)dA) = 0 for all Hamiltonian or symplectic processes, it follows that QˆdQ = 0.)
i(V)dA = 0,
However, on the 6 dimensional symplectic manifold, there does not exist a unique extremal field, nor a unique stationary field, that can be used to define the dynamical system. The symplectic manifold does support vector fields, S, that leave the Action integral invariant, but these vector fields are not unique in the sense that that they depend on an arbitrary gauge addition to the 1-form of Action that may be required to satisfy initial conditions.
There does exist a unique torsion field (or current) defined (to within a projective factor, σ) by the 6 components of the 5 form,
Relative to the topological coordinates [dx, dθ, dt, dv, dω, ds], the Topological Torsion vector has the components
If the three non-zero components of the Topological Torsion vector are treated as a dynamical system, then it is to be noted that the dynamical system is a Volterra system generated on a Finsler space (see p.205 [1]).
Topological Torsion = AˆdAˆdA
T6 = [0, 0, 0, Tv, Tω, Ts],
AˆdAˆdA = i(T6)Ω6,
Tv = m2βλ2{+βλ2ω2+ 2λvω − v2}
Tω = m2λ{+βλ2ω2− 2βλvω − v2}
Ts = m2βλ2{+βmλ2ω2+ mv2+ 2(λω − v)s}
This unique Topological Torsion vector, T6, independent of gauge additions, has the properties that
This ”Torsion” vector field satisfies the equation
Hence a dynamical system having a component constructed from this unique Torsion vector field becomes a candidate to describe the initial irreversible decay of angular momentum and kinetic energy.
L(T)A = Γ · A and i(T)A = 0.
L(T)AˆL(T)dA = QˆdQ = (6m2βλ2{v − λω})2AˆdA ≠ 0.
It is to be noted that the non-canonical ”symplectic momentum” variables, defined by inspection from the constrained 1-form of Action lead to the momentum map:
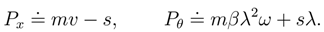
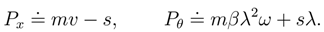
Substitution in terms of the momentum variables leads to the generic form (p. 31 [31], also see [24]) for the 1-form of Action:
where H is an independent variable on the 6-dimensional manifold. The H map is given by the expression for energy where v and ω are eliminated in terms of the Px and the Pθ.
Note that v = ∂H/∂Px and ω = ∂H/∂Pθ. Each component of ”canonical momenta” decays with the same rate in the canonical domain.
A = Pxdx + Pθdθ − Hdt
H = (mv2/2 + βm(λω)2/2) ⇒ (1/2m)[(Px + s)2 + (1/β)(Pθ/λ − s)2]
5 Summary
A fundamental problem of thermodynamics (that has been the subject of much discussion) is why canonical Hamiltonian mechanics (without additional and sometimes controversial constraints and modifications) is not able, from first principles, to describe the decay to an equilibrium state, or why the usual (extremal) methods of Hamiltonian mechanics (see eq. (21))do not give any insight into the concept of irreversibility. It is extraordinary that answers to these 150 year old Boltzmann - Loschmidt - Zermelo paradoxes of physics seem to follow (without recourse to statistics) if one utilizes a perspective of continuous topological evolution. The methods of continuous topological evolution lead to a precise evolutionary definition of entropy production, dS, (see eq. (58)). The entropy production differential 1-form, dS, is used to define the volume element of the 2n+2 dimensional symplectic manifold generated by the Cartan-Hilbert Action. For a continuous process that is initiated in the topological domain of Pfaff topological dimension 2n+2, the sign of the volume (representing its orientation) cannot change. However, continuous topological evolution can cause the 2n+2 dimensional volume element to expand or contract irreversibly (giving credence to concept of "bulk viscosity") until a topological change takes place, such that the Pfaff topological dimension becomes 2n+1. The continuous change of entropy dS during a process can never be negative, a requirement necessary if the orientation of the 2n+2 symplectic manifold (generated by the 2-form, dA) is continuously preserved. The 2-form dA represents the limit points of the Action 1-form. Equilibrium is defined by the n+1 dimensional Lagrangian submanifold of the 2n+2 dimensional symplectic space, upon which dA, hence dS,is zero.
References
- Antonelli, P. L.; Ingarden, R.S.; Matsumoto, M. The Theory of Sprays and Finsler Spaces with applications to Biology and Physics; Kluwer: Dordrecht, Nd, 1993. [Google Scholar]
- Baldwin, P.; Kiehn, R. M. Cartan’s Topological Structure, Poster presented at the summer workshop. In Topology in Fluid Dynamics, Inst. for Th. Phy. UCSB, August 1991. Also see arXiv math-ph/0101033, or http://www22.pair.com/csdc/pdf/topstru4.pdf.
- Bamberg, P.; Sternberg, S. A Course in Mathematics for students of Physics, 2; Cambridge University press: Cambridge, 1992; pp. 775–780. [Google Scholar]
- Bowen, Rufus. Entropy for group endomorphisms and homogeneous spaces. Trans. Amer. Math. Soc. 1971, 153, 401–414, MR 43 #469. [Google Scholar] [CrossRef]
- Bott, R; Tu, L. W. Differential Forms in Algebraic Topology; Springer Verlag, N.Y, 1994. [Google Scholar]
- Cartan, E. Systems Differentials Exterieurs et leurs Applications Geometriques; Hermann: Paris, 1922. [Google Scholar]
- Cartan, E. Sur certaines expressions differentielles et le systeme de Pfaff. Ann Ec. Norm. 1899, 16, 329+. [Google Scholar]
- Chern, S. S. Annals of Math 1944, 45, 747–752, also Science Reports Nat. Tsing Hua Univ. 1948, 5; pp 95-121..
- Eckart, C. The thermodynamics of irreversible processes I: The simple fluid, II: Fluid mixtures, III: Relativistic theory of the simple fluid”. Phys. Rev 1940, 58. [Google Scholar]
- Flanders, H. Differential Forms; Academic Press: New York, 1963; p. 126. [Google Scholar]
- Forsyth, A.R. Theory of differential equations V1 and V2; Dover, N.Y., 1959. [Google Scholar]
- Goldenblat, I.I. Some problems of the mechanics of continuous media; Noordhoff: Holland, 1962; p. 193, “The quantity of heat in a reversible process always has an integrating factor”. [Google Scholar]
- Hermann, R. Differential Geometry and the Calculus of Variations. Academic Press: New York, 1968. [Google Scholar]
- Kiehn, R. M. D turbulence is a Myth, (invited speaker EGS XXIV General Assembly IUTAM, the Hague, 1999). http://www22.pair.com/csdc/pdf/hague6.pdf.
- Kiehn, R. M. Thermodynamic Irreversibility and the Arrow of Time. In The Nature of Time: Geometry, Physics and Perception; Bucher, R., et al., Eds.; Kluwer: Dordrecht, Netherland, 2003; pp. 243–250, (http://www22.pair.com/csdc/pdf/arwfinal.pdf). [Google Scholar]
- Kiehn, R. M. Topological evolution of classical electromagnetic fields and the photon. In Photon and Poincaré Group; Dvoeglazov, V., Ed.; Nova Science Publishers, Inc.: Commack, New York, 1999; pp. 246–262, ISBN 1-56072-718-7. Also see (http://www22.pair.com/csdc/pdf/photon5.pdf). [Google Scholar]
- Kiehn, R.M. Retrodictive Determinism. Int. J. of Eng. Sci. 1976, 4, 749+, (http://www22.pair.com/csdc/pdf/retrodic.pdf). [Google Scholar] [CrossRef]
- Kiehn, R. M. ...3.5 Mb). see the forthcoming book “Non-equilibrium thermodynamics and Irrversible Processes — from the Perspective of Topological Evolution” (pre-publication copy is available at http://www22.pair.com/csdc/download/topthermo.pdf.
- Kiehn, R. M. Some Closed Form Solutions to the Navier Stokes Equations, LANL arXiv/physics/0102002. 1991; (http://www22.pair.com/csdc/pdf/nvsol.pdf). [Google Scholar]
- Kiehn, R. M. Coherent Structures in Fluids are Topological Torsion Defects. In IUTAM Symposium on Simulation and Identification of Organized Structures in Flows; Sørensen, N., et al., Eds.; Kluwer Academic Publishers: Dordrecht, 1999; pp. 239–248, See (http://www22.pair.com/csdc/pdf/copen5.pdf). Presented at the IUTAMSIMFLO Conference at DTU, Denmark, May 25-29, (1997). [Google Scholar]
- Kiehn, R.M. Topological evolution of classical electromagnetic fields and the photon. In Photon and Poincaré Group; Dvoeglazov, V., Ed.; Nova Science Publishers, Inc.: Commack, New York, 1999; pp. 246–262, ISBN 1-56072-718-7. Also see (http://www22.pair.com/csdc/pdf/photon5.pdf). [Google Scholar]
- Lipschutz, S. General Topology; Schaum: New York, 1965; p. 88. [Google Scholar]
- Marsden, J.E.; Riatu, T. S. ntroduction to Mechanics and Symmetry; Springer-Verlag, 1994; p. 122. [Google Scholar]
- Martinet, J. On the Singularities of Differential Forms. Ann. Inst. Fourier, Grenoble 1970, 20(1), 95–178. [Google Scholar] [CrossRef]
- Morse, P. M. Thermal Physics, Benjamin, NY. 1964; 60.
- Pittie, H. V. Characteristic classes of Foliations; Res Notes in Math; Ditman: London, 1976. [Google Scholar]
- Libermann, P.; Marle, C.-M. Symplectic Geometry and Analytical Mechanics. Riedel, Dordrecht/Boston. 1987; 65. [Google Scholar]
- Rodriguez, C. C. From Euclid to Entropy. In Maximum Entropy and Bayesian Methods; Grandy, W. T., Jr., Ed.; Kluwer Academic Publishers, 1991; pp. 1–6. [Google Scholar]
- Schouten, J. A.; Van der Kulk, W. Pfaff’s Problem and its Generalizations; Oxford Clarendon Press, 1949. [Google Scholar]
- Abe, S. Tsallis entropy: How Unique? arXiv: cond-mat/0305087.
- Zhitomirski, M. Typical Singularities and Differential 1-forms and Pfaffian Equations, Translations of Mathematical Monographs, 113, AMS Rhode Island 1991.
- Ward, T. Valuations and Hyperbolicity in Dynamics, PROYDYN Summer School June-July 2001. Georg-August-University at Göttingen. http://www.mth.uea.ac.uk/~h720/lecture_notes/valuations.pdf.
- 1The term "Pfaff topological dimension" (instead of class) was introduced by the present author in order to emphasize the topological foundations of the concept.
- 2A direction field is defined by the components of a vector field which establish the "line of action" of the vector in a projective sense. An arbitrary factor times the direction field defines the same projective line of action, just reparameterized. In metric based situations, the arbitrary factor can be interpreted as a renormalization factor.
- 3The bold letter A represents the first 3 components of the 4 vector of potentials, with the order in agreement with the ordering of the independent variables. The letter A represents the 1-form of Action.
© CSDC Inc. CSDC gives MDPI (http://www.mdpi.org) the right to publish and distribute the article freely for non commercial purposes. CSDC retains the right to publish the article on the web and to use all or part of the contents in future publications created by or for CSDC.