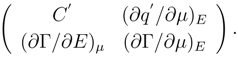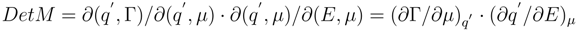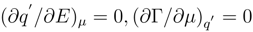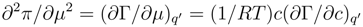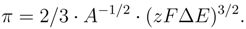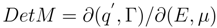The Stability Limits of the Surface Phases at the Polarized Interface of a Liquid Electrode with an Electrolyte Solution

Abstract

The thermodynamic stability limits of specific adsorption at the polarized liquid metal/electrolyte solution interface are studied. Here the reversible starting and disappearance of the electroadsorption effects at a threshold potential are revealed, which are the result of Gibbs stability violation. The stability limits are determined by the bi-furcation manifold of the critical states for which determinant of matrix of a second differential of the surface pressure equals zero.  The equations of the critical states are equivalent to the spinodal equations used in the theory of phase transitions. The conception developed beneath will help provide to interpretate the anomalies of electrocapillary effects through the catastrophe theory.

1 Overview

Different kinds of the surface phenomena can be examined at the liquid-liquid interface when one of they serves as an idealy polarisable electrode. The adsorption of surface-active anions is the best-understood [1,2,3,4,5]. The degree of development of their surface activity continuously depends on the electrode potential and their concentration in solution. Starting and vanishing of the effects in question at the particular values of the electrode potential, each of which have threshold character, also deserve attention [6].

Thus the interface characteristics (interface tension, differential capacity, etc.) undergo qualitative changes, permitting to presume a peculiar wetting transition. The explanation to the observed class of phenomena should be sought in the interconnection between the problems of the solution components’ surface activity and adsorptive phases’ stability at the polarized interface.

The stability criterion of the thermodynamic systems was first presented by Gibbs [7]. The general solution to a problem of stability limits of macroscopic phases in the volume was found within the phase transition theory [8] and later within the framework of modern analysis - the Theory of catastrophes [9]. The problems of stability of surface phases were studied in connection with wetting transitions [4,10] within the framework of the model functional’s methods.

The matter of stability of surface phases on the polarized interface of the liquids has its own specificity, connected with the main role of electrode potential. The problems of stability of electro-adsorptive phases and their influence on electro-capillary relations have not been esteemed, even in the primary way - single surfactant component in any of bordering phases.

The purposes of this research are to carry on an investigation of the ranges of stability of an adsorptive state at the polarized interface of metal - electrolyte solution, to examine the interface tension and other measured qualities close to them, to establish the connection with the wetting transitions, and to formulate the proper criteria.

2 Stability condition of surface phases

The necessary and sufficient condition for stability of thermodynamic system is availability of minimality of its free energy in conformity with Klausius inequality [8]. Applied to the interface it can be represented in such a way

$$\delta f_s>0,$$

(1)

where f_s is exceed free energy, combined with the interface. In physical chemistry the following expression f_s [11] is used at presence of a surfactant component in one of contacting phases

$$f_s=\gamma +\mathrm{\Gamma }·\mu .$$

(2)

In formula (2) γ is interfacial tension, Γ - an adsorption of a surfactant component, µ - its chemical potential. In electrochemical systems γ(E, c, T) depends on electrode potential E, concentration c and temperature T .

At a constant temperature the finite increment of the function (1) can be submitted as series of differentials of the ascendant order. The first differential is equal to zero strictly under thermodynamic equilibrium conditions. As a result we have the Lippman-Gibbs equation [12]. In passive electrolytes it expresses the connection between the changes of the interface tension γ₀ and the electrode potential E

$$-d{\gamma }_0=q_{0}dE,$$

where q₀ is the density of charge on an electrode. In the electrolytes including surfactant components it describes a relation of surface pressure π=γ₀−γ on electrode potential and c - concentration of surfactant component [13]. In presence of surface active anion in solution of fixed ionic strength Lippman-Gibbs equation will be have next form

$$d\pi =q\prime dE+\mathrm{\Gamma }d\mu ,$$

(3)

where q′ = q − q₀ is a change of charge density on an electrode in a surfactant electrolyte, E is electrode potential mesuring relative cation reversible reference electrode, Γ is an adsorption of a surfactant component at the interface and µ is its chemical potential. The equation (3) gives an adequate description of the stable state of the polarized interface.

According to Gibbs [7], the stability of the thermodynamic state is determined by the sign of the second differential of thermodynamical potential. Therefore analysis of stability range of polarized interface and the refinement of the singularities dependence of interface tension on the parameters of state close to them also requires consideration of the second order differential properties of the function π(E, µ)

(4)

According to physical sense of a partial derivative, being differential capacitance of the interface, it introduces the identification (∂q′/∂E)_µ = C′. The properties of a differential d²π are determined by its quadratic form (4) and, in particular, by its matrix M_ik

(5)

The matrix (5), by definition, - is real and symmetric. The fulfilment of an inequality

$$d^2\pi >0.$$

(6)

is sufficient for the stability of the interface. This will be executed, if

$$DetM>0,C\prime >0.$$

(7)

3 Gibbs stability limits

The properties of a surface activity of the solvent components become apparent reversibly, as a rule, in the restricted interval of the electrode potentials that depends on the active component concentration in volume. The inequalities (6) and (7) will be executed within this interval. The differential form (4) degenerates at the border of this reversibility interval, and the effects of a surface activity disappear. The transformation of a system from one state to another (e.g. adsorption or desorption process, and etc. at the reaching the electrode potential threshold) is associated with the transition from the unstable initial state to a new steady one. Determinant matrix M turn equal to zero in the indicated manifold of the transient states

$$DetM=0.$$

(8)

Differential form of the determinant of M in the form [8]

(9)

permits to present the value of the determinant as a product of two quantities. As a result we shall express it through directly measurable quantities

(10)

The stability condition and its limits according to Gibbs can be given a following view

(11)

4 Bifurcation equation

The surface phase stability will be broken for the system’s states satisfying equations

(12)

Either of the equations (12) or both of them determine the limits of an interface stability region in the relation to the specific adsorption. The function π(E,c) will display the bifurcation nature’s singularities resulted from this phenomenon. The equations (12) express the degeneration of the quadratic form (4) on the bifurcation manifold of the critical points [9].

In the case of vanishing of the second differential the formula (1) will be performed by the means of the next higher order differential.

5 Severel examples

For example, thiourea’s adsorption on the electrode [14], changes a charge on the value q′= q − q₀, in comparison with the case of organic’s absence in the solution. From the first equation (12) it follows the effective capacitance C′ = C −C₀ is zero at the vanishing of the adsorption process, and accordingly equality of the differential capacitances of the electrodes in solution with an organic and without it (C = C₀ [13]) below the threshold potential.

The influence of specific adsorption of anions is exhibited, in particular, in the next change of the effective inverse differential capacity of the interface: $C_a^{-1}=C^{-1}-C_0^{-1}$. At the desorption $C_a^{-1}$ will vanish. As a result the equality $C^{-1}=C_0^{-1}$ [13] is fulfilled.

Equalities of the capacitive factors obtained above one uses in a method of inverse integrating used at the analysis of experimental data [13,15].

6 Catastrophe equilibrium stability of surface phases

The second of the formulae (12) is executed, at any events, when c is equal to 0. It is evident from the fact that the second partial derivate of the surface pressure

(13)

vanishes at zero concentration. Thus the indicated concentration is a critical point for the function π(E,c). This circumstance has usually been missed in the analysis of a specific adsorption data at low concentrations of a surfactant component in electrolyte but it may be important for the adequate interpretation of experimental results. In the vicinity of the critical point the role of fluctuation at the interface increases.

Effects of surface active anions Br ⁻, I⁻, $N_3^{-}$ on electrocapillary curves of mercury electrode has been studied in [14,16,17,18]. We have re-examined the data from these studies related to low concentrations and have remade new analysis of the dependence of both the electrocapillary curves maxima and of the potential zero charge (pzc) displacements ∆E on the surfactant anion’s concentration. Analising the character of the data in limit of the low concentrations we have concluded that both relations may be presented by the power dependences on the concentration: π ∼ c^α, ∆E ∼ c^β with the indices α ≃ 1/2 and β ≃ 1/3.

Excluding c as a parameter from these expressions we will get the next dependence π on ∆E

$$\pi \sim \mathrm{∆}{E}^{3/2}.$$

(14)

To test conformity of our assumption we have re-counted the data of [14,16,17,18] in coordinates [(∆π/γ₀)^2/3,∆E/E₀], where E₀ is the pzc at c = 0.

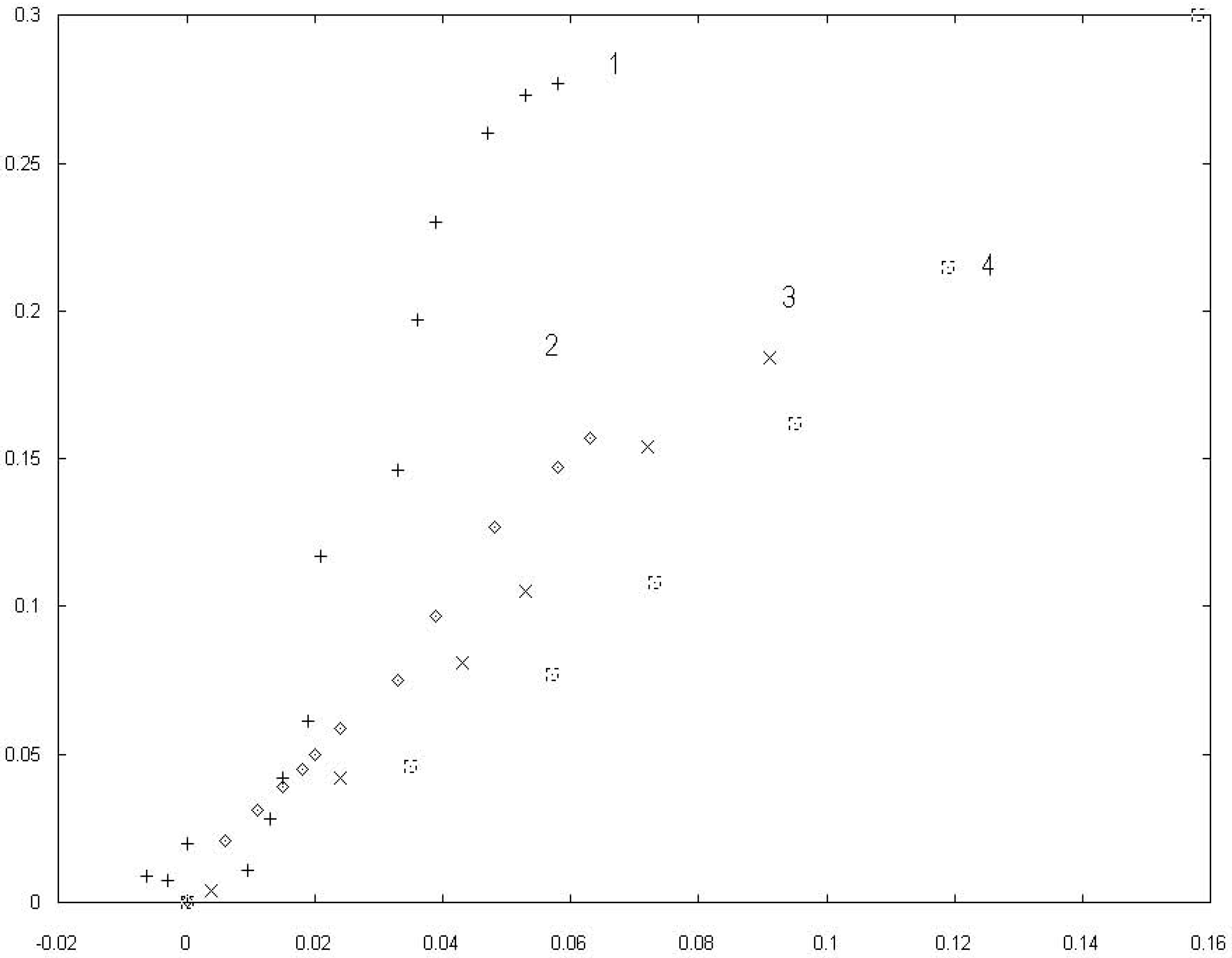
The experimental values of the changes of electrocapillary maxima vs. the pzc displacements obtained at the different concentrations of the surfactant component are presented in a fig. 1.

The data is pended in coordinates [(∆π)^2/3,∆E]. The option of axes was determined by supposed analytical feature of the function π(∆E) according to the formula (14). The sets of points 2, 3, 4 describe the diminution of the surface tention at the pzc on the potential displacment of the pzc for mercury electrode in water solutions of salts with surface active anions Br⁻, I⁻, $N_3^{-}$. In these coordinats we observe a linear behavior at low concentration limit which means a nonlinear behavior for π versus ∆E coordinates.

The set of points 1 is presented the dependence of the changes of surface pressure at the pzc versus displacements the pzc beacause of adsorption Br⁻ at the interface mercury and water solution ammonium bromine-fluoride at a constant ionic strengh. The linear trend characterises examining dependence at a low bromide concentration. There is a substential increasing scatter in the data while c is decreasing to c = 0.

The growth of the fluctuation near c = 0 is evident physically. Although it is not been related to a critical unstability. The nearness of the critical point explains the power dependence of the data in vicinity c = 0.

Having the violation of Gibbs stability conditiont in view it is necessary to use methods of the modern analysis - the Catastrophe theory [9] for the mathematical description of the surface pressure in the vicinity of c = 0. On the basis of Thom splitting theorem [9], the function π in the neighborhood of the critical point c = 0 should be presented as the catastrophe germ depicting influence of surface-active agents. Keeping in mind that function π depends only a single thermodynemical parameter near c = 0 and bifurcation manifold consists of a single point c = 0 we employ the fold catastrophe for its description

$$\pi =a\mathrm{\Gamma }-(A/3){\mathrm{\Gamma }}^3.$$

(15)

The fold catastrophe [9] is defined by a set of functions dependent on a control parameter a. In the studied case we have a = ∆µ where ∆µ is the change of the chemical potential’s values caused by variations in concentration of the surfactant anion. The augend is a usual Gibbs term. From the principle of the electrochemical potential conservation [12] it may be caused ∆µ = zF∆E at

Figure 1. Relation between the decreases of electrocapillary maxima ((γ₀ − γ)/γ₀)^2/3 and displacements of the potential zero charge ∆E/E₀ for a mercury electrode in salt solutions with different concentration of surface active anions: 1. Br⁻ according to the data [17], 2. $N_3^{-}$ - [16], 3. I⁻ - [18], 4. Br⁻ − [14].

Figure 1. Relation between the decreases of electrocapillary maxima ((γ₀ − γ)/γ₀)^2/3 and displacements of the potential zero charge ∆E/E₀ for a mercury electrode in salt solutions with different concentration of surface active anions: 1. Br⁻ according to the data [17], 2. $N_3^{-}$ - [16], 3. I⁻ - [18], 4. Br⁻ − [14].

the thermodynamical equilibrium and at absence of charge’s exchange with environment, where z is the anion’s charge and F is Faraday number.

The necessity of the inclusion in (15) the next term of expansion into series is cosequence of the vanishing a at c = 0. The factor A is setting to demand dimension of the second addend.

Adsorption Γ in (15) serves as an order parameter which may be received from the function’s stationary condition [8,9]

$$\partial \pi /\partial \mathrm{\Gamma }=0.$$

(16)

Replacing ∆µ by the last expression in the formula (15) and (16) we get

$$\mathrm{\Gamma }=\sqrt{zF{A}^{-1}E}.$$

(17)

The exclusion of Γ in the formula (15) gives the following expression to the surface pressure

(18)

The expression (18) determines the dependence of the electrocapillary maximum reduction on the displacement of a zero charge potential at the different concentrations of surfactant component in solution that is similar to the formula (14) received earlier from the analysis of the data [14,16,17,18].

It permits to confirm the adequacy of the description of the features of the electrocappilary effects in the terms of the catastrophe theory.

It can be marked, that the equation (12) is similar to the spinodal equation, formed the foundation for the phase transformation description in the volume [10, 17]. In the study of the polarized interface properties the equations (12) determine a bifurcation manifold of the critical points of the function π(E,c) in the coordinates (E,c) or, according to physics, a line of wetting transitions [9,17].

7 Conclusion

This research shows that the observed features of the analytical behaviour of the interface tension, together with other characteristics of the interface (as an example, differential capacity) vs. a potential and surfactant component concentration in the volume are connected with the critical points of these functions. Gibbs stability condition of the thermodynamical states is disturbed on the manifold of the critical points. The adequate mathematical description of an equilibrium system in this case may be given through the catastrophe theory. The indicated states correspond to the wetting transitions at the interface at the appropriate threshold values of the electrode potentials. The catastrophe theory in respect to the analysis of the experimental data, obtained at the polarized interface, permits not only explaining the observed electrocapillary relations anomalies, but forecasting new properties, and also the studing of the dynamics of other interface properties changes.

The analysis of stability limits of surface phases gives the relevant information on the nature of the factors deciding interactions between solvent components and the interface. The proposed approach gives the method for regular selfconsistent description of the interface characteristic anomalies and seems to be perspective at the analysis of any effect related to the indicated interactions.