Introduction
One of the fundamental flow geometries encountered in engineering processes is the channel between two parallel plates. When a viscous fluid flows in a parallel plate channel, a velocity boundary layer develops along the inner surfaces of the channel. If the plates have different thermal conditions the heat transfer starts from the inlet of the channel and temperature profile develops simultaneously along the inside duct surfaces. The convection is treated as the combined hydrodynamic and thermal entry length problem which can be also referred to as the simultaneously developing region problem in the literature. Although the analysis of the heat transfer in such a flow system is more complex due to the variation of the velocity distribution in all directions, the problem has attracted attention and investigators have given numerical solutions under various constraints. A comprehensive review of such solutions is addressed by Kays and Crawford [
1], Kakaç and Yener [
2,
3] and Bejan [
4].
The improvement of thermal systems has gained a growing interest due to the relations with the problems of material processing, energy conversion and environmental effects. Efficient energy utilization during the convection in any fluid flow is one of the fundamental problems of the engineering processes to improve the system. One of the methods used for the prediction of performance of the engineering processes has been the second law analysis. The second law of the thermodynamics is applied to investigate the irreversibilities in terms of the generation of entropy. The method was introduced by Bejan [
5,
6,
7] and followed by many investigators. Studies on the entropy generation rates and the irreversibilities for the basic convective heat transfer arrangements can be found in the literature [
8,
9,
10,
11]. Since the entropy generation is the measure of the destruction of the available work of the system, the determination of the active sites motivating the entropy generation is also important in upgrading the system performances.
Due to the interest to the efficient utilization of energy and the wide applications of the flows in the parallel plate channel, related studies can be found in the literature. Nag and Kumar [
12] carried out a second law analysis on convective heat transfer from a fluid flowing in a duct with constant heat flux and found an optimum value of the initial temperature difference for minimum entropy generation. The thermodynamics of laminar viscous flow through a duct subjected to constant heat flux was studied analytically by Şahin [
13]. To determine the optimum duct geometry, Şahin [
13] used entropy generation for laminar viscous flow through various geometries subjected to constant heat flux. He considered hydraulic diameters for square, equilateral triangular, rectangular and sinusoidal geometries and made comparisons with respect to the dimensionless entropy generation and the pumping power to heat transfer ratio with respect to Reynolds number. The entropy generation in turbulent liquid flow through a smooth duct subjected to constant temperature was studied by Şahin [
14]. Narusawa [
15] examined the rate of entropy generation both theoretically and numerically for forced and mixed convection in a rectangular duct heated at the bottom. Şahin [
16] made a thermodynamic analysis of turbulent fluid flow through a smooth duct subjected to constant heat flux and considered the temperature dependence of the viscosity. Mahmud and Fraser [
17] investigated analytically the first and the second law characteristics of fluid flow and heat transfer inside a channel having two parallel plates with finite gap between them and considered fully developed forced convection and non- Newtonian fluid. Mahmud and Fraser [
18] analyzed the mechanism of entropy generation and its distribution through fluid flows in basic channel configurations including two fixed plates and one fixed and one moving plates by considering simplified or approximate analytical expressions for temperature and velocity distributions and derived analytically general expressions for the number of entropy generation and Bejan number.
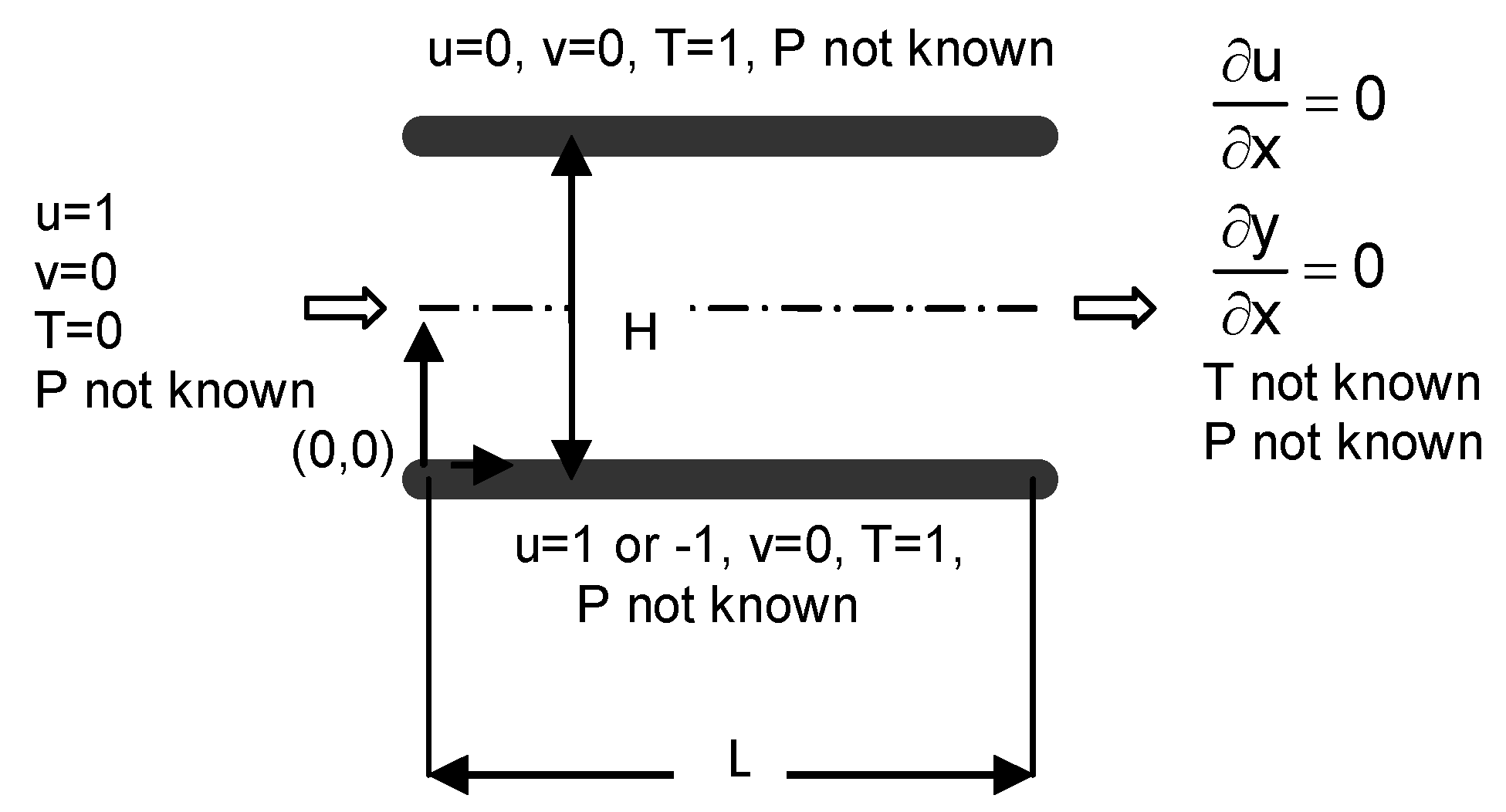
In this study, the second law analysis is applied to the simultaneously developing transient laminar flow between two parallel plates. The irreversibilities within the channel are presented by the entropy generation number. The transient solutions of the set of the governing equations for mass, momentum, energy, and entropy generation for two-dimensional Cartesian coordinates are obtained numerically. Special attention has been given to the effect of the motion of the bottom plate on the entropy generation by considering the Prandtl number of 1.0 and the Reynolds numbers 100, 500 and 1000. Three cases were considered at the bottom plate; stationary plate, moving plate in the parallel and reverse directions with the flow. The plates are held at equal constant temperature.
The results of the study provide valuable fundamental information on the physics of the simultaneously developing transient laminar convection in a parallel plate channel with moving bottom plate to improve the corresponding engineering applications. The designers under the responsibilities for the design and optimization of corresponding thermal systems can employ the results given about the entropy generation to reduce the loss of available work.
Results And Discussion
The irreversibility contours have been derived by using Equation (7) concerning the effect of the Reynolds and Prandtl numbers. The study is restricted to the fluids of Prandtl number 1.0 and studied for Reynolds (Re) numbers of 102, 5x102 and 103. The effect of Br/Ω on the entropy generation in the combined entrance length was investigated by solving the problem for Br/Ω =0.1, 1, and 10. Limited number of contours was used to describe the structure of the flow and temperature fields. The variations of the average number of entropy generation were drawn on the NSL-y coordinates for easy understanding.
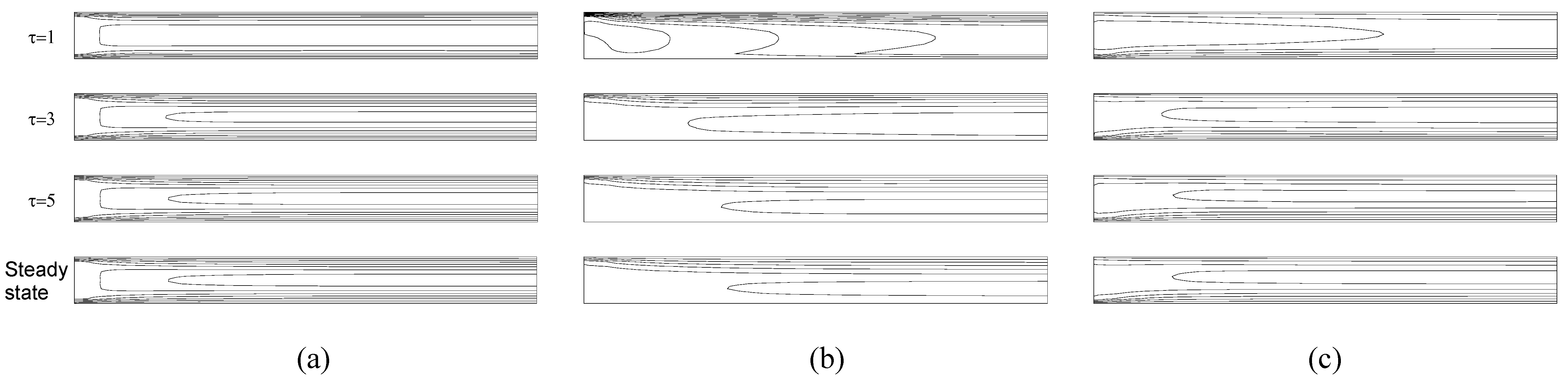
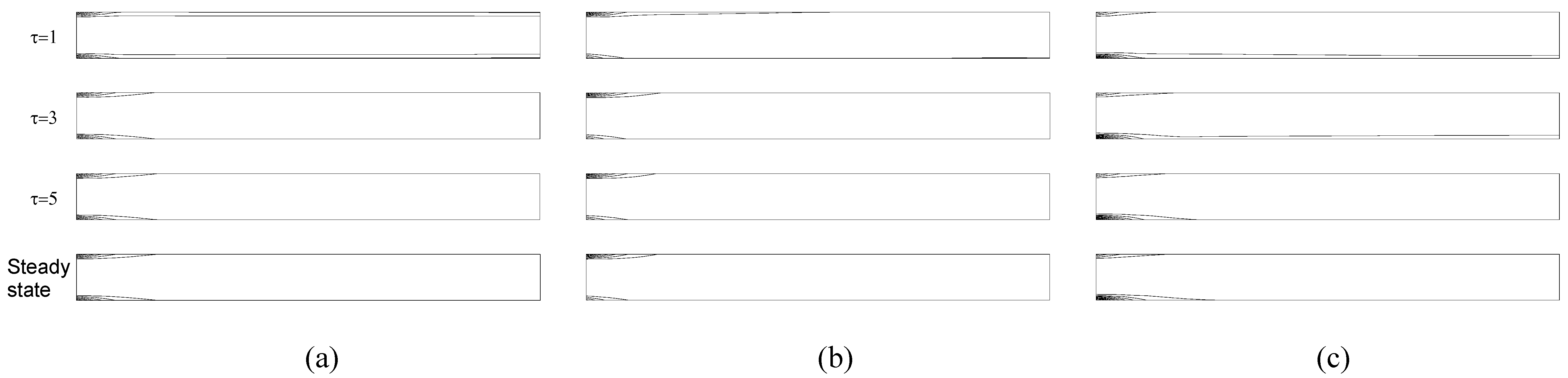
Figure 2 illustrates the time vise variation of the velocity contours for each case corresponding to τ=1, 3, 5, and the steady-state considering the Reynolds number 10
2. The formation of the symmetric structure observed with respect to mid-plane is only observed in the fixed plate case as it is seen in
Fig.2a. At the entire flow channel the stratified structure of the velocity contours are observed. When the lower plate moves in parallel to the flow direction, the contours place heavily inside the upper plate. The maximum is obtained below the symmetry axis at the lower half of the channel as seen in
Fig.2b.
Fig.2c summarizes the effect of counter motion of the lower plate on the velocity distribution. The dense structure of the velocity contours on the inner surface of the lower plate yields the result of increased friction, high shear stresses, and hence disturbed symmetry.
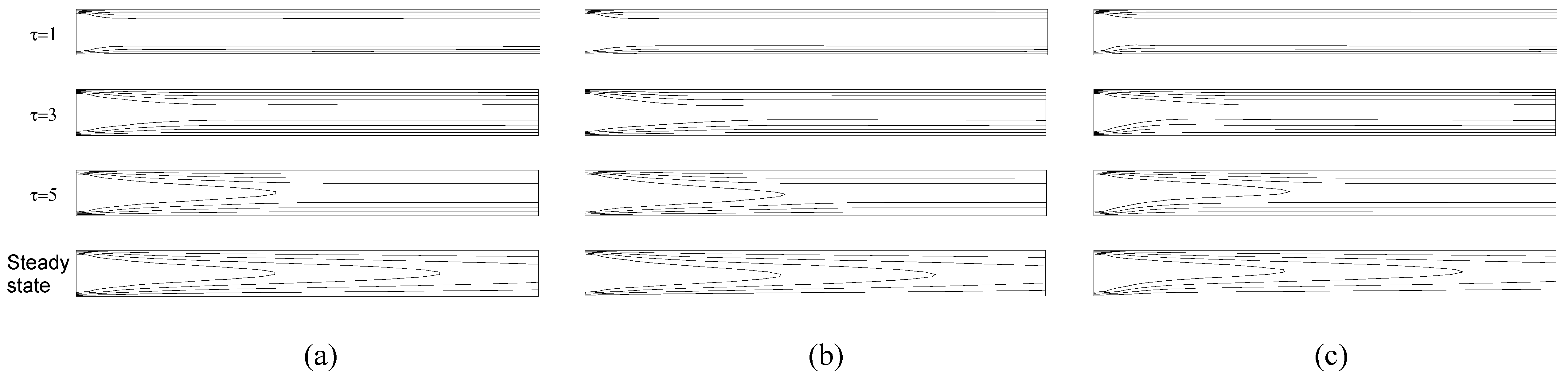
The distribution of the isotherms considering all cases at initial steps of transient process for τ=1, 3, 5, and at the steady-state are shown in
Fig.3. The combination of Pr=1.0 and Re=10
2 is used. At the initial step, thermal boundary layer is created immediately on the inner surfaces of the plates having the same characteristic distribution at all cases. The isotherms remain attached on the inner plate surfaces throughout the process. At the stationary case given in
Fig.3a, the imposed thermal boundary condition induces symmetric thermal boundary layers along the inner surfaces of the parallel plate channel, and covers the entire channel in time.
Fig.3b yields the structure of the contours heavily inside the upper plate in the flow direction due to the effect of velocity profile obtained at the parallel motion of the lower plate. It seen in
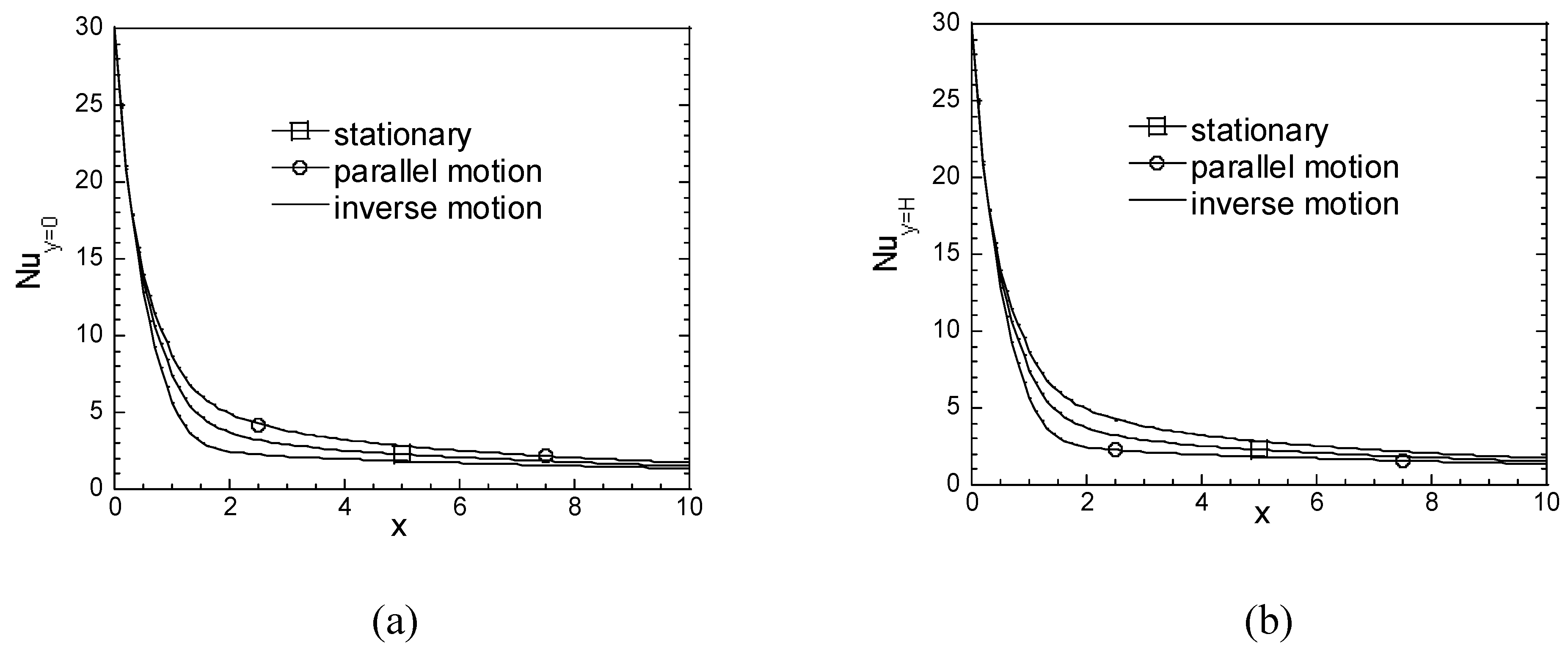
Fig.3c since the flows in the case of counter motion of the bottom plate create high shear stresses and enlarge the velocity profile inside the channel, the flow tend to lift the isotherms far from the lower plate. The average Nusselt numbers, NuL, at the steady- state are calculated 7.866, 7.871, and 7.603 for the parallel plate channel with stationary, forward and backward moving lower plates, respectively (see
Fig.4).
Figure 5 shows the contours of the predicted entropy generation numbers at different time steps for the combination of Reynolds number 10
2 and Br/Ω=1. The effect of transient changes up to the steady state is observed on the entropy generation number. The figure yields clearly the place of the active cites representing the spots of triggering irreversibilities in the parallel plate channel under consideration. It is seen that the structure of the contours of the entropy generation number follows the velocity and temperature contours and is affected by the transient changes in the combined developing region.
Fig.5 yields a general idea about the active cites representing the spots of triggering irreversibilities in the channel under consideration. The maximum value of N
SL is 450 at the entrance corners of the channel plates at the fixed case. For the motion parallel in the flow direction the maximum N
SL is 225 at the entrance corner of the moving bottom plate whereas 450 at the upper entrance. During the counter motion of the lower plate the maximum entropy generation number is obtained as 1125 at the entrance corner of the plate.
Figure 6 demonstrates the partitioning of the number of entropy generation according to the sources of irreversibilities. The contours of N
s dT/dx account the entropy generation due to the axial conductive heat transfer. The contours of N
s dT/dy represent the entropy generation due to the heat transfer in normal direction. The entropy generation values calculated from the terms in the second bracket on the RHS of the Eq.(7) illustrate the contribution of fluid friction, N
s friction which is presented at the third line of the
Fig.6. The contours of N
s friction stretch along the inside surface of the upper and the lower plates in the similar manner with the velocity contours. The N
s friction values are very small under the present conditions. At the last lines of the
Fig.6 (a), (b), and (c), the contours of the total value of the entropy generation number are given. Their values, the last line of the
Fig.6, is much the same with the results shown in the second line.
Figure 7 summarizes the effect of Br/Ω on the problem considered. It is seen that an increase in the Brinkman number which determines the relative importance between dissipation effects and fluid conduction yield strong increase in the entropy generation number. The relative motion of the lower plate with respect to the upper plate causes a deviation from the symmetric structure of N
SL. The shifted profile through upper plate is obtained in the case of parallel motion. The highest values of the number of entropy generation are realized in the last case.
Figure 8 is prepared to show the effect of Reynolds number on the entropy generation during the developing flow under consideration. Three values of the Reynolds number 10
2, 5x10
2, and 10
3 are considered for Pr=1 and Br/Ω =1. The number of the entropy generation increases with increasing Reynolds number. The strong effect of Re number is realized on the inside surfaces of the channel plates. In
Fig.8a, the symmetric distribution is clearly observed at the fixed channel case. The parallel motion of the bottom plate not only reduced the highest N
SL value but also decreased the entropy generation on the upper plate (
Fig 8b) with respect to fixed case. It is seen in
Fig.8c the highest value of N
SL is obtained at the highest Re number on the surface of the lower plate moving in counter direction to the flow.
The obtained results addressing all cases are as follows: The formation of the parallel structure of the entropy generation as well as the velocity and thermal boundary layers is obtained at the stationary plate case. Close thermal layers are found on the heated surfaces. The structure of the Ns contours keeps the same distribution at the transient steps. The Ns has its highest value at the highest Re and Br/Ω values, which is obtained at counter motion of the lower plate. The lowest average number of the entropy generation on the bottom plate is obtained at the case of the plate moving in parallel direction to the flow. The upper and the lower corners of the channel plates at the entrance play the role of active sites where the generation of entropy is triggered.