Fault Diagnosis of Planetary Gearboxes Based on LSTM Improved via Feature Extraction Using VMD, Fusion Entropy, and Random Forest
Abstract
1. Introduction
2. Methodology
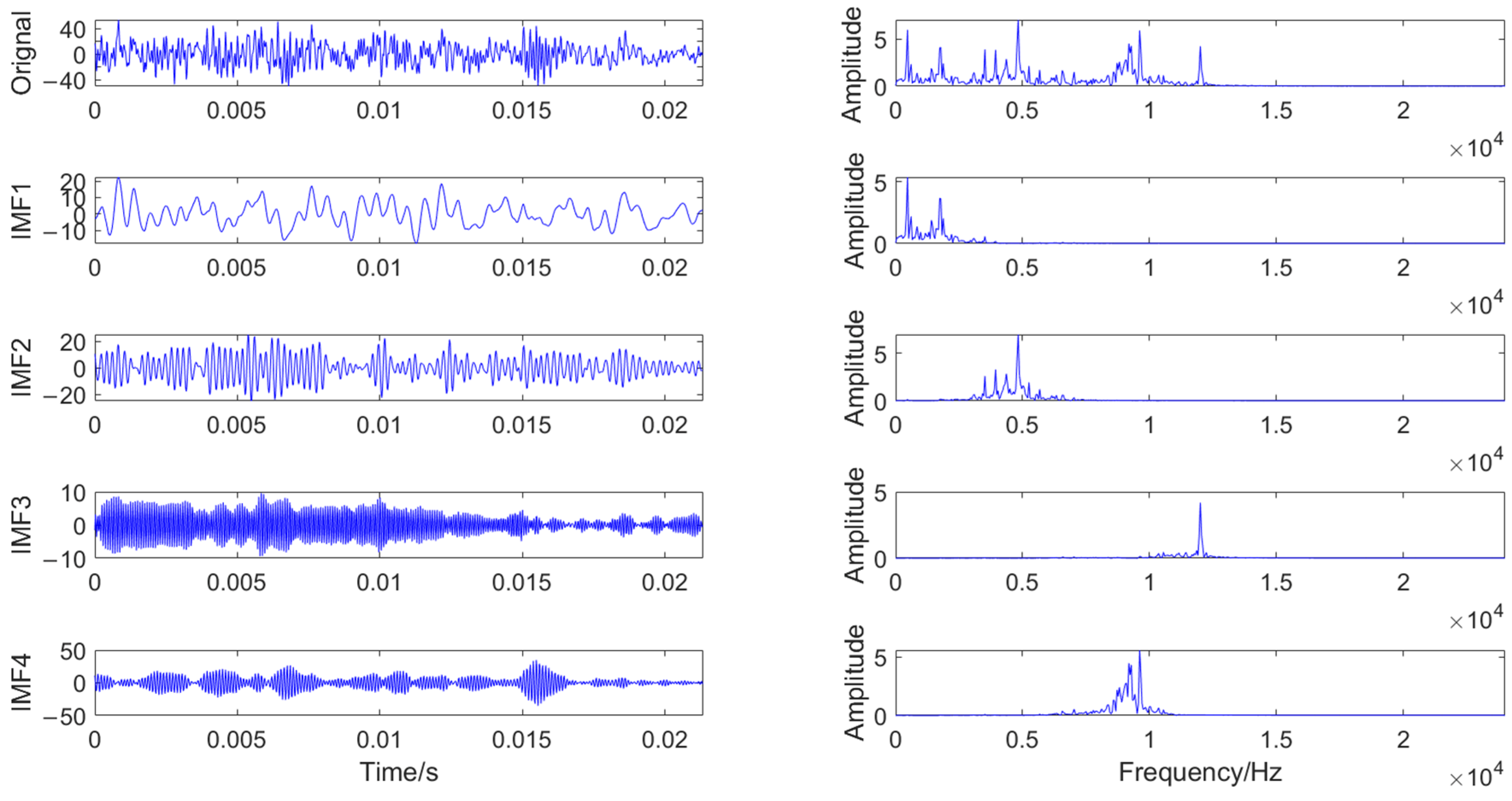
2.1. VMD-Based Signal Processing
2.2. Fusion Entropy
2.3. Feature Selection Utilizing RF
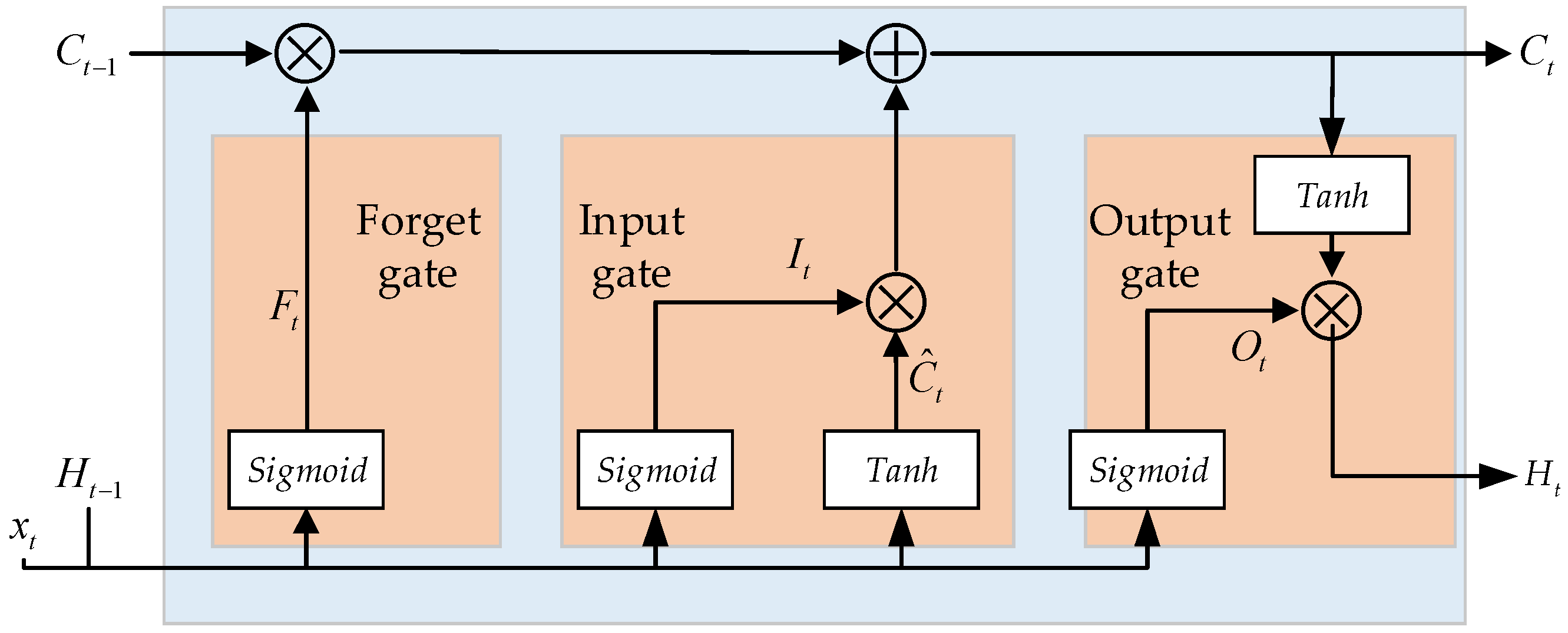
2.4. LSTM
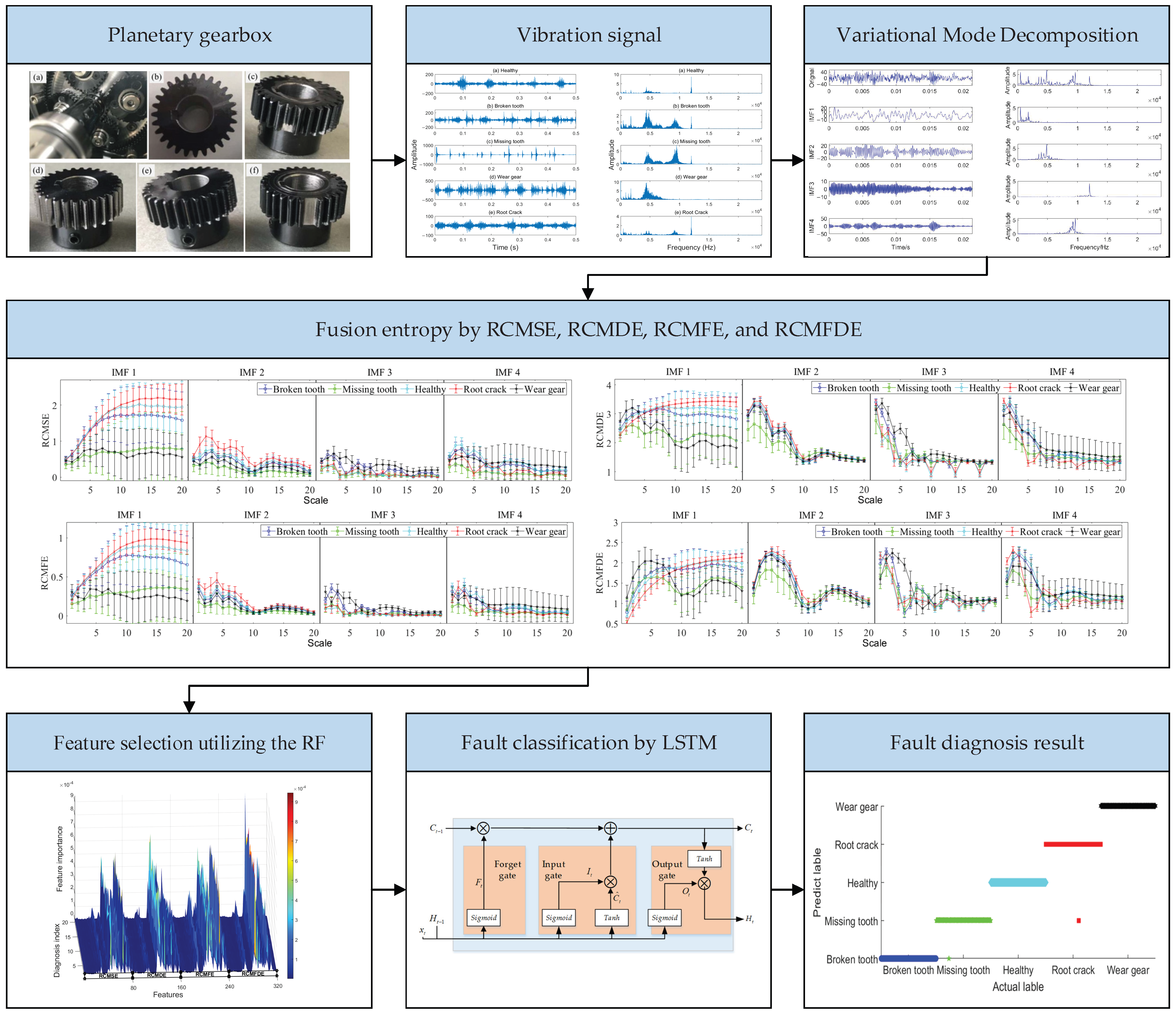
3. The Structure of the Proposed Method
4. Experimental Study
4.1. Experimental Description
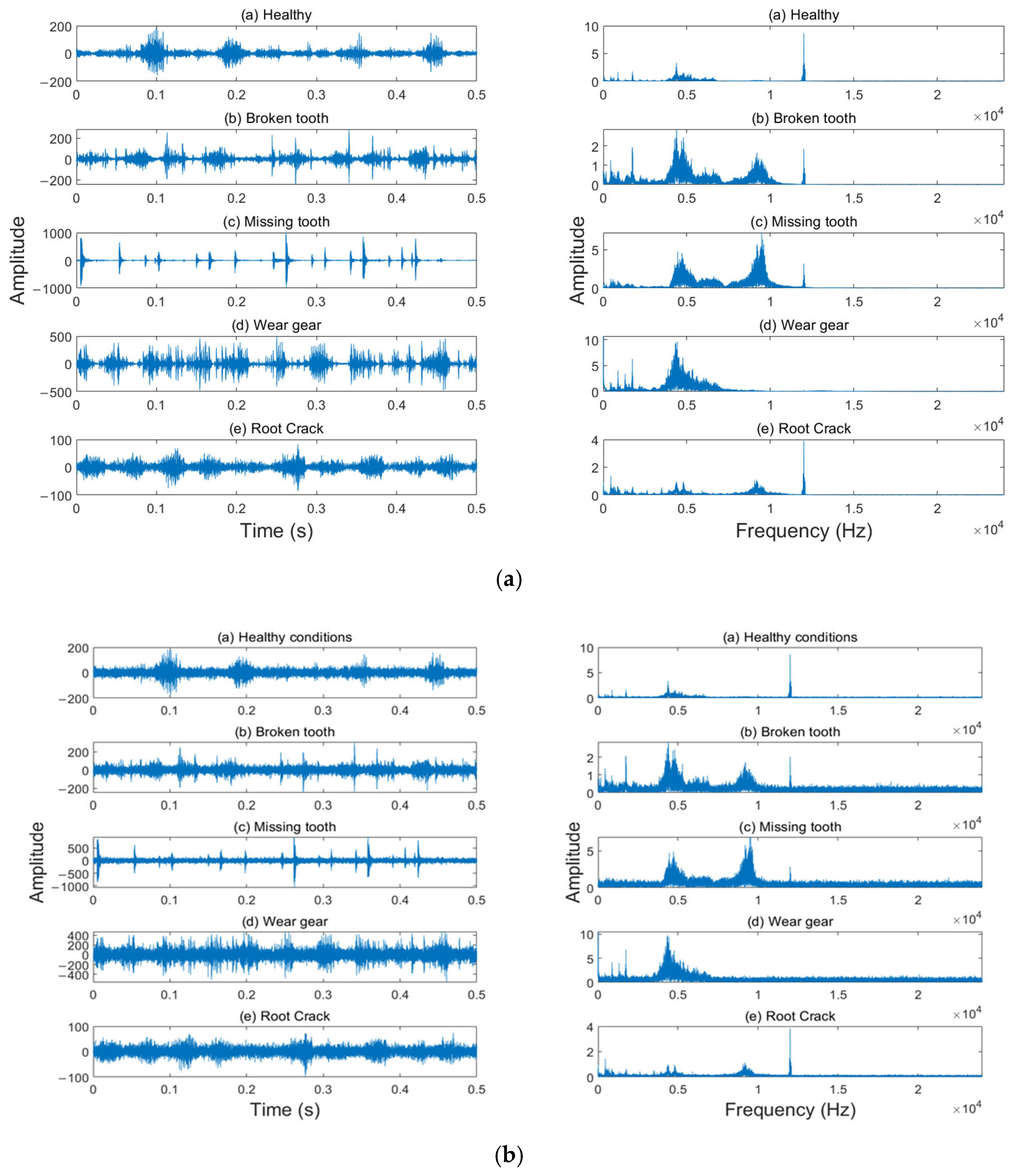
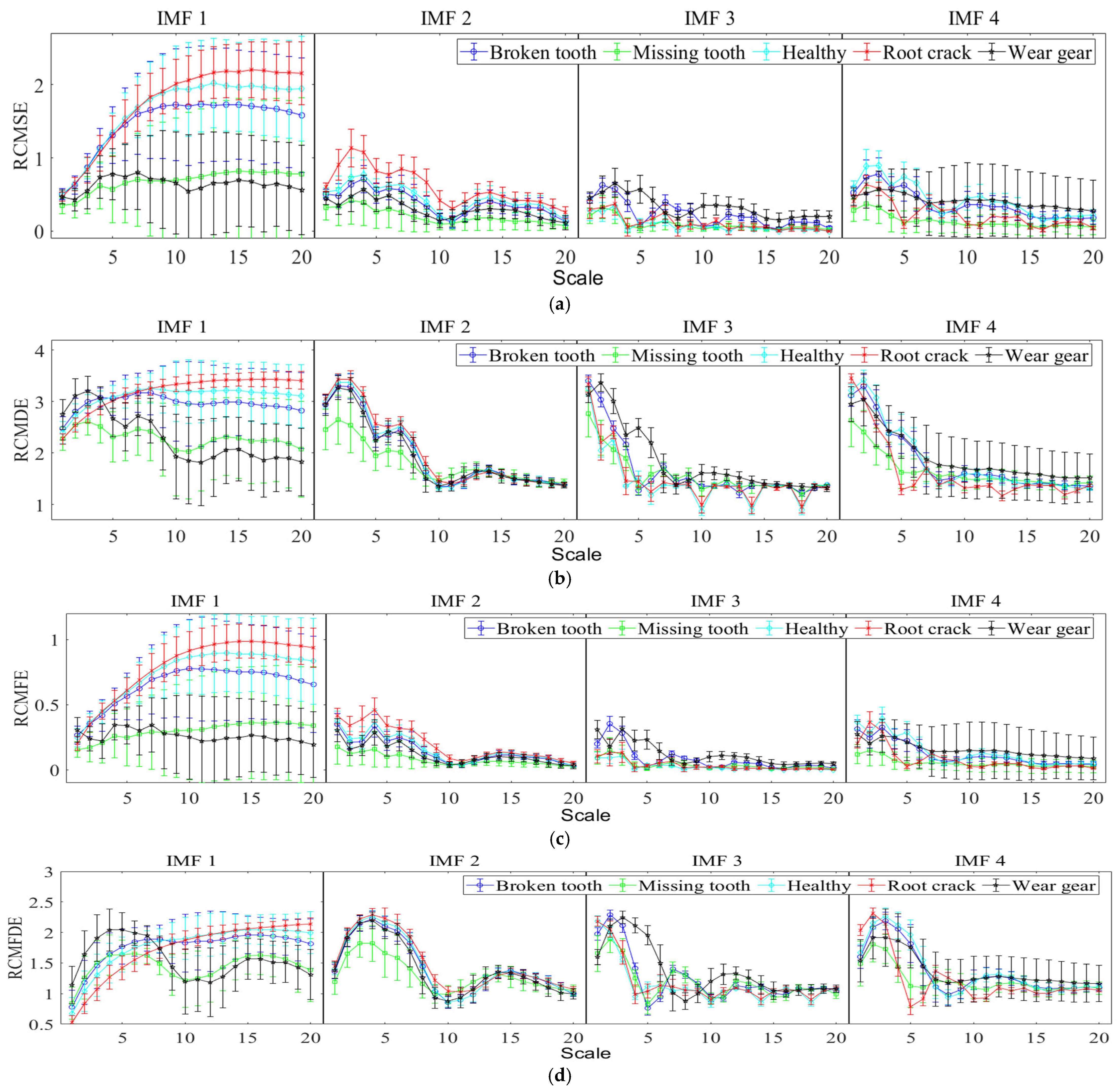
4.2. Signal Processing
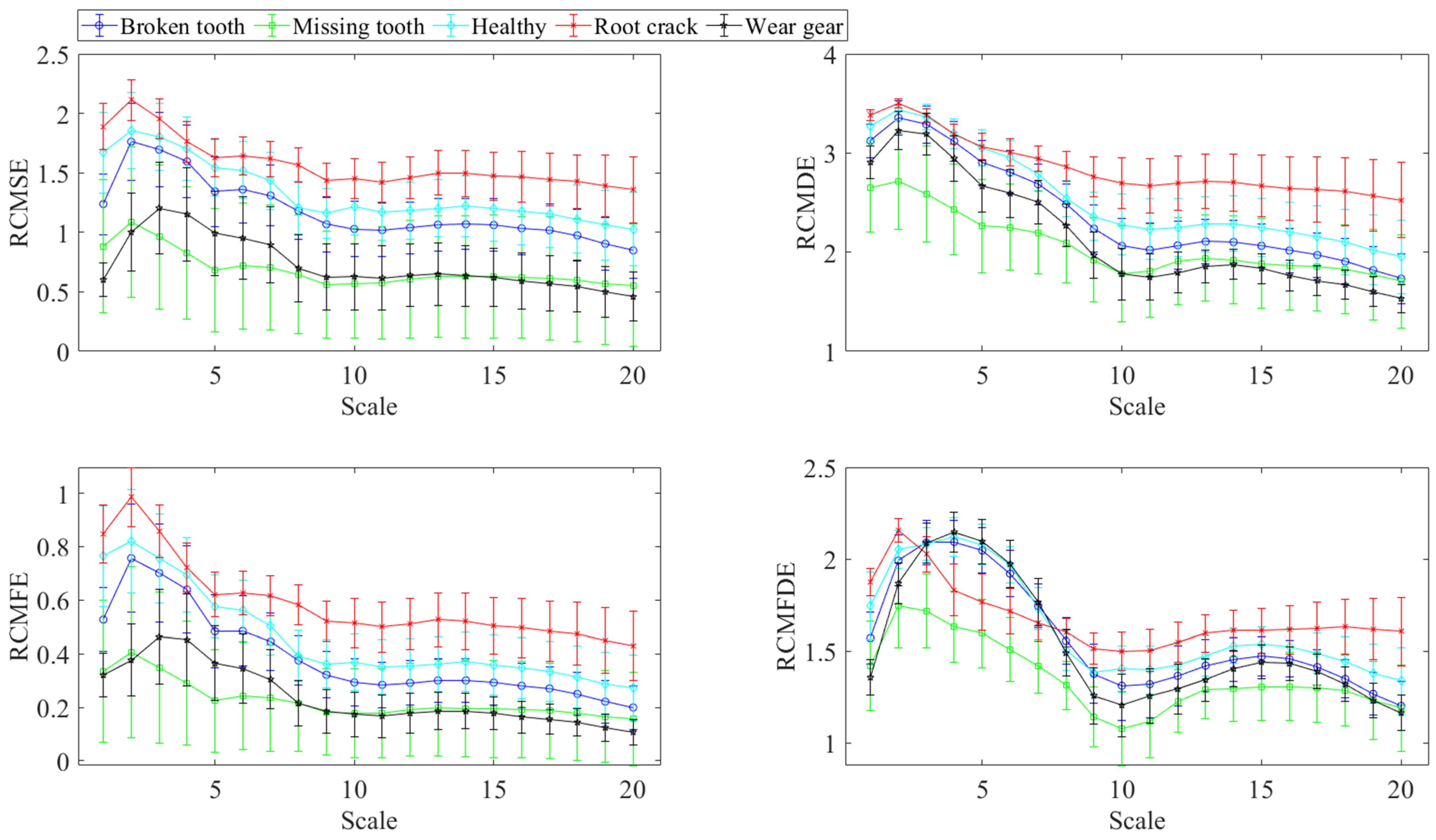
4.3. Feature Extraction and Fusion
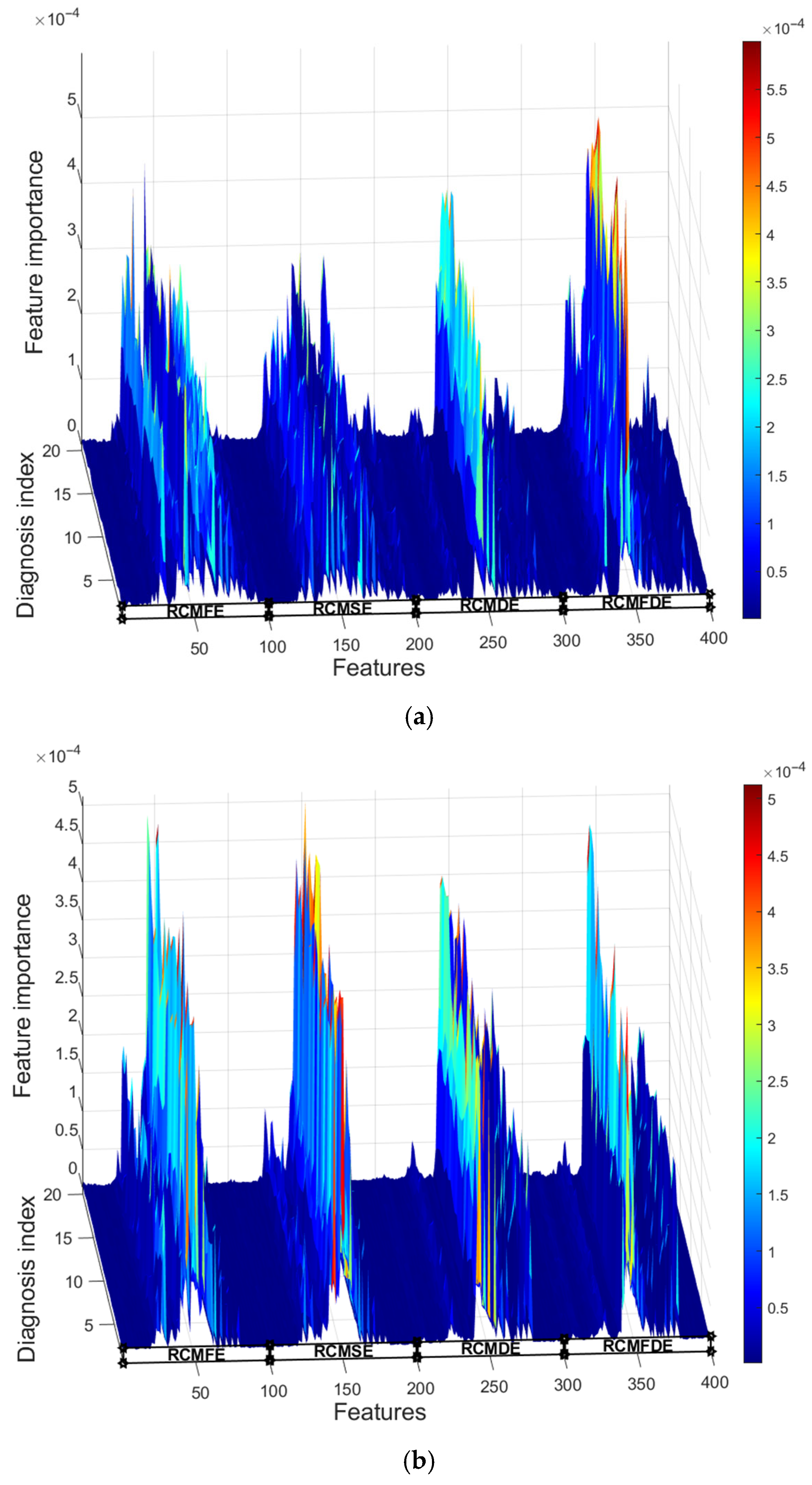
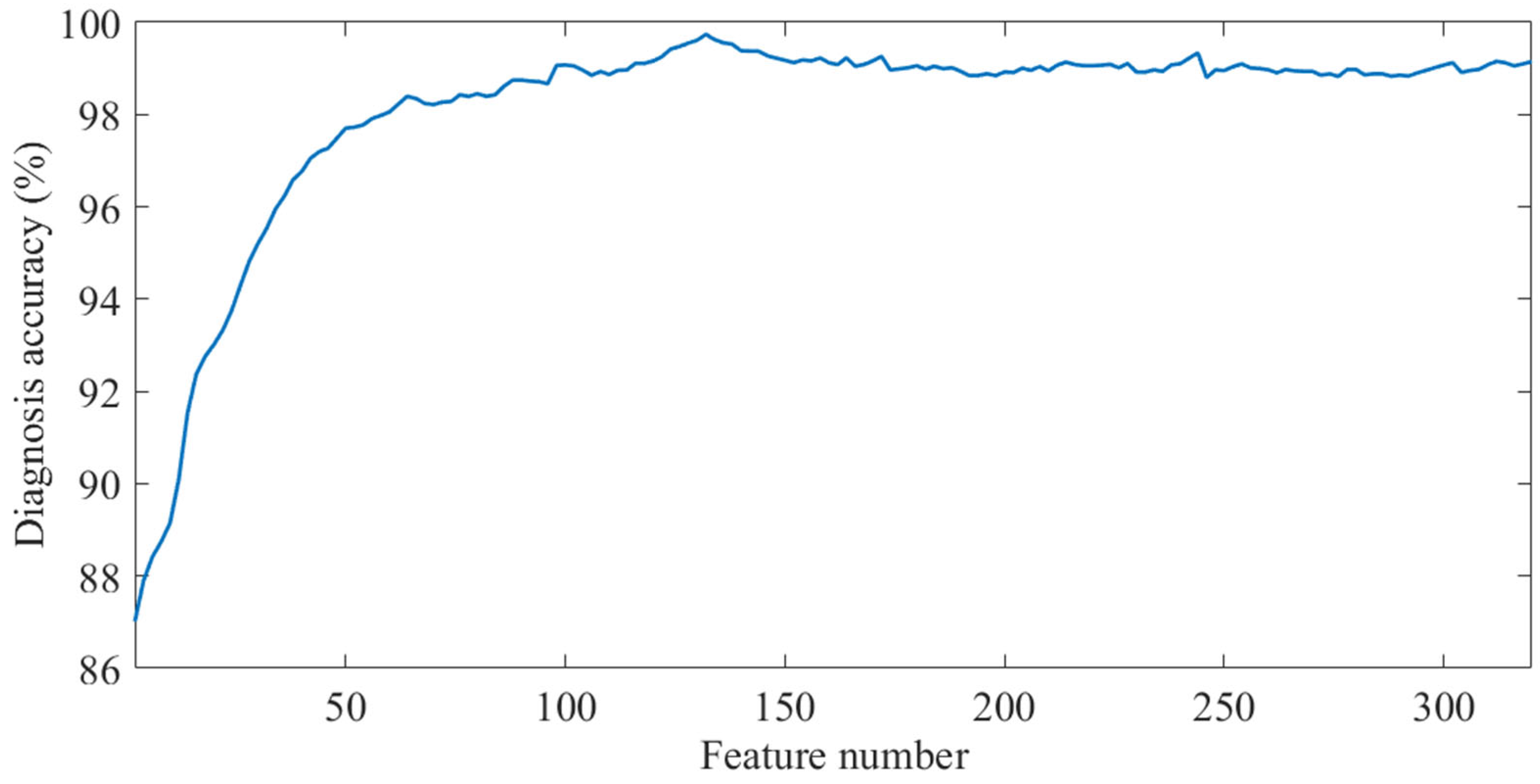
4.4. Feature Selection
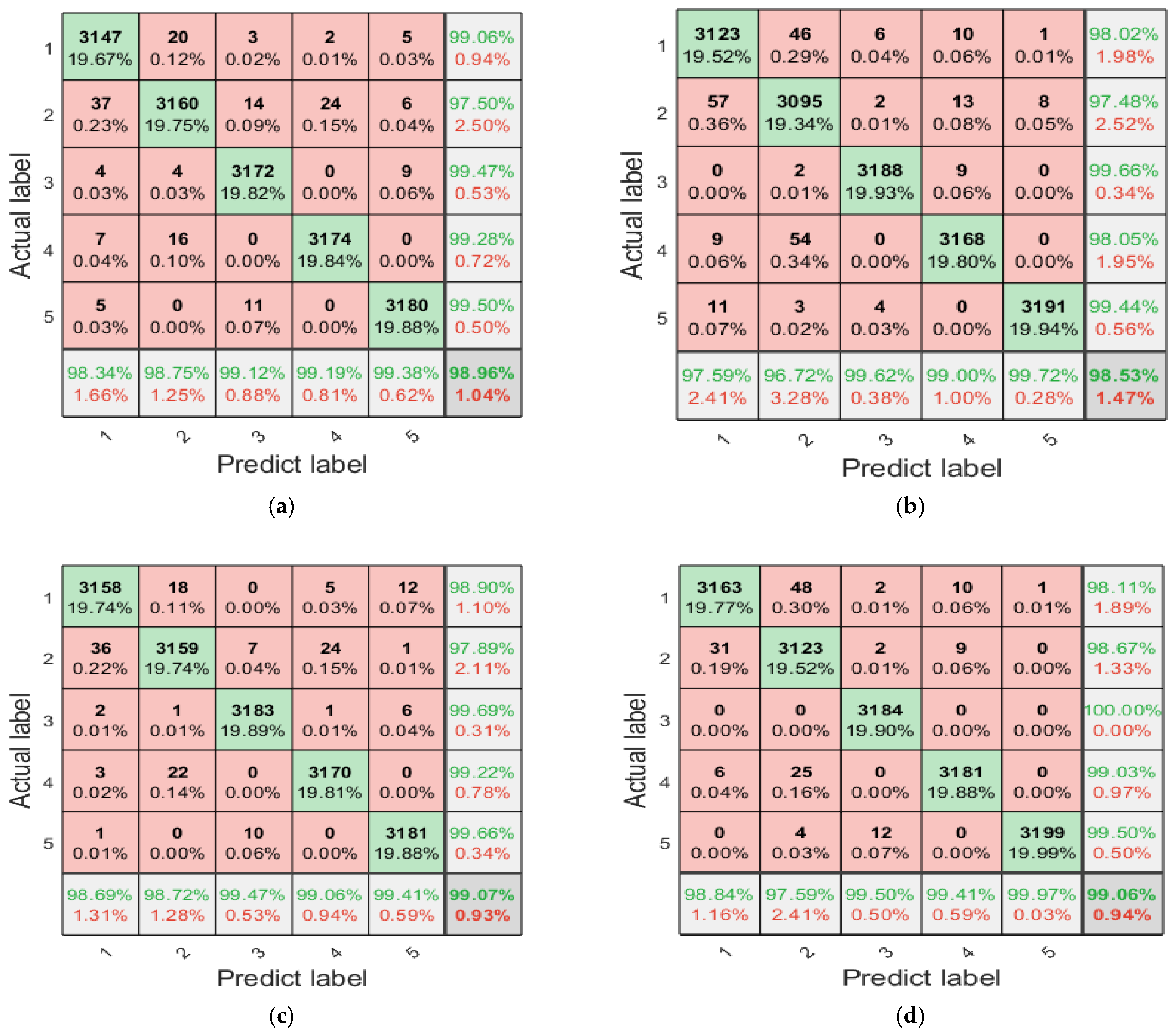
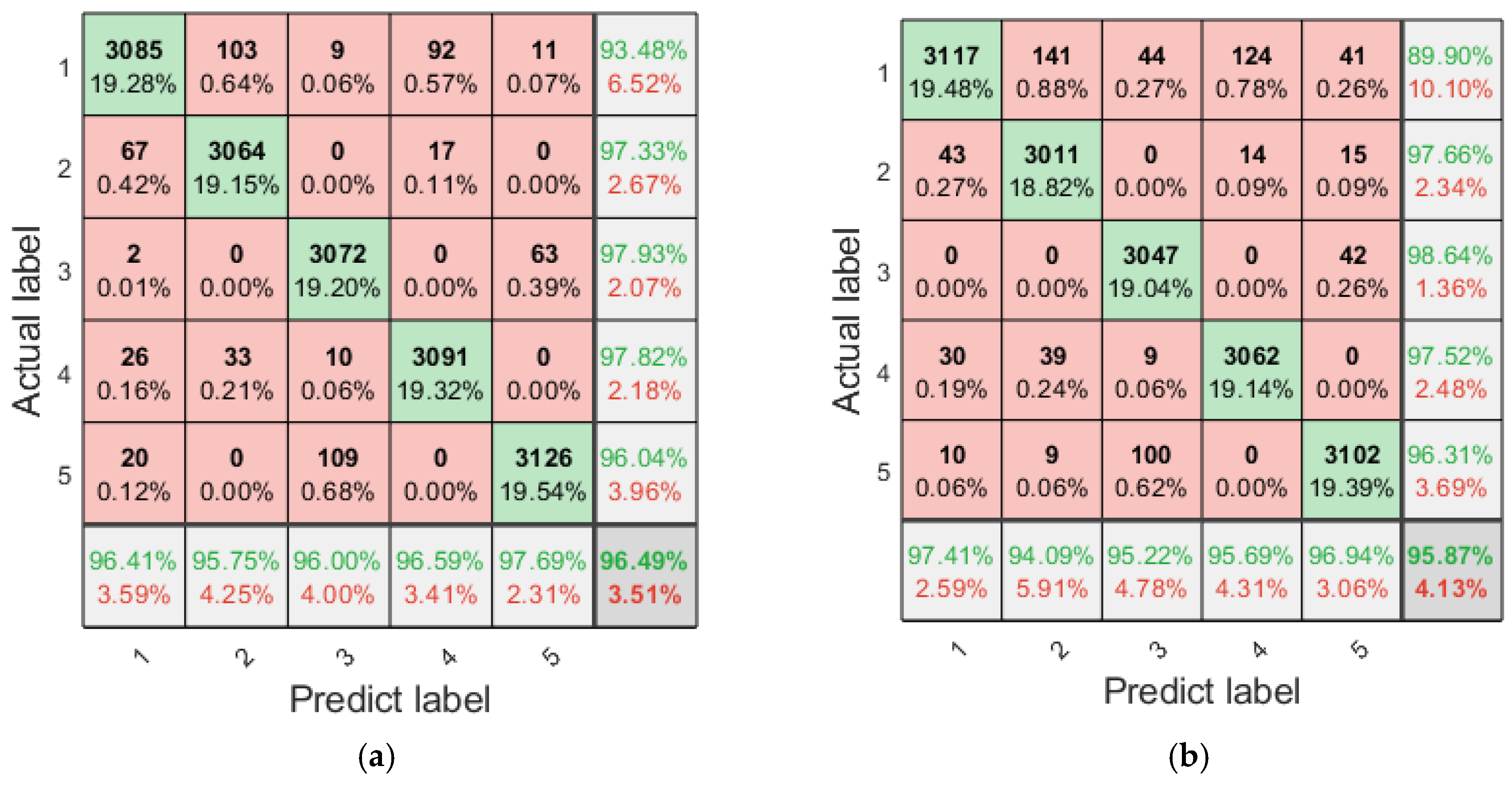
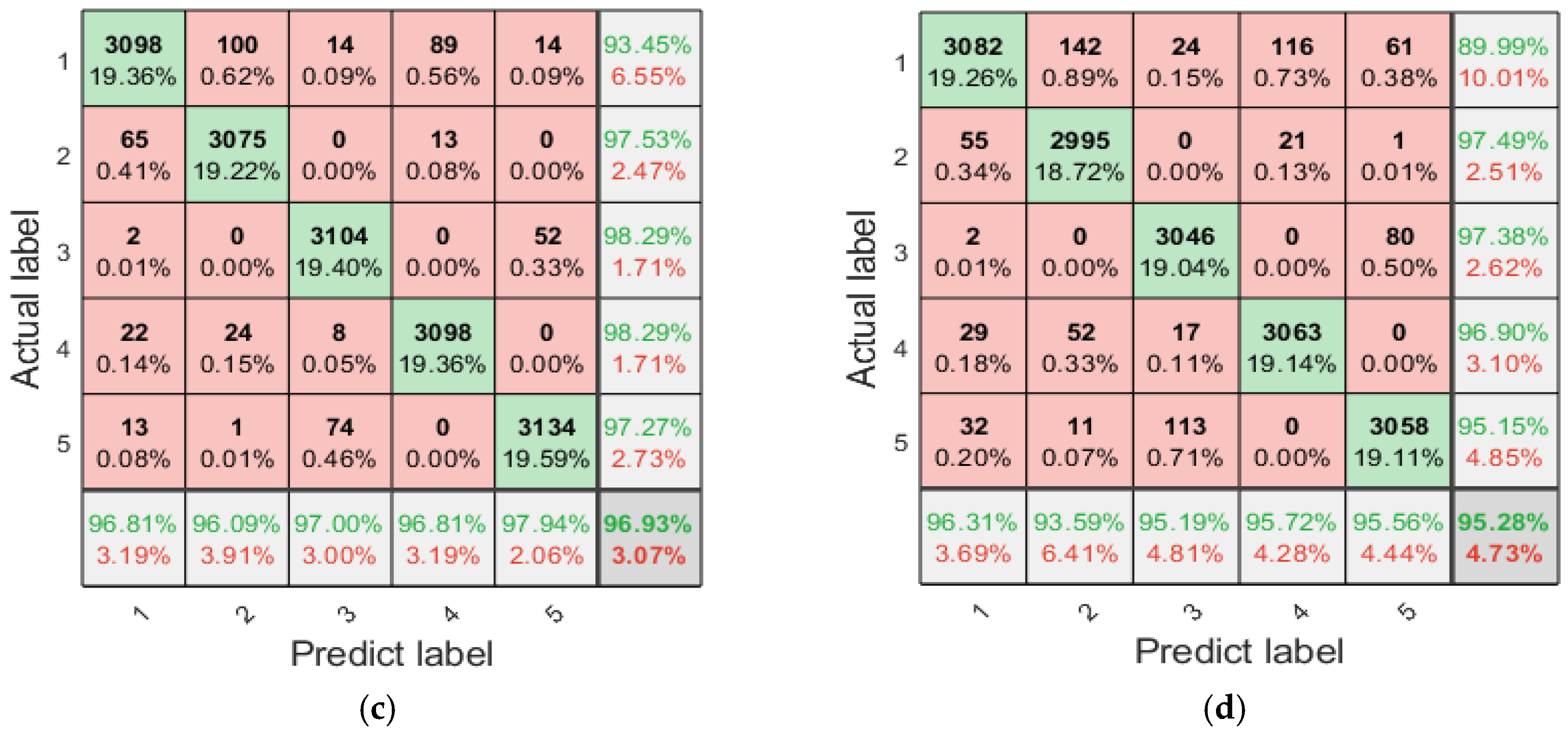
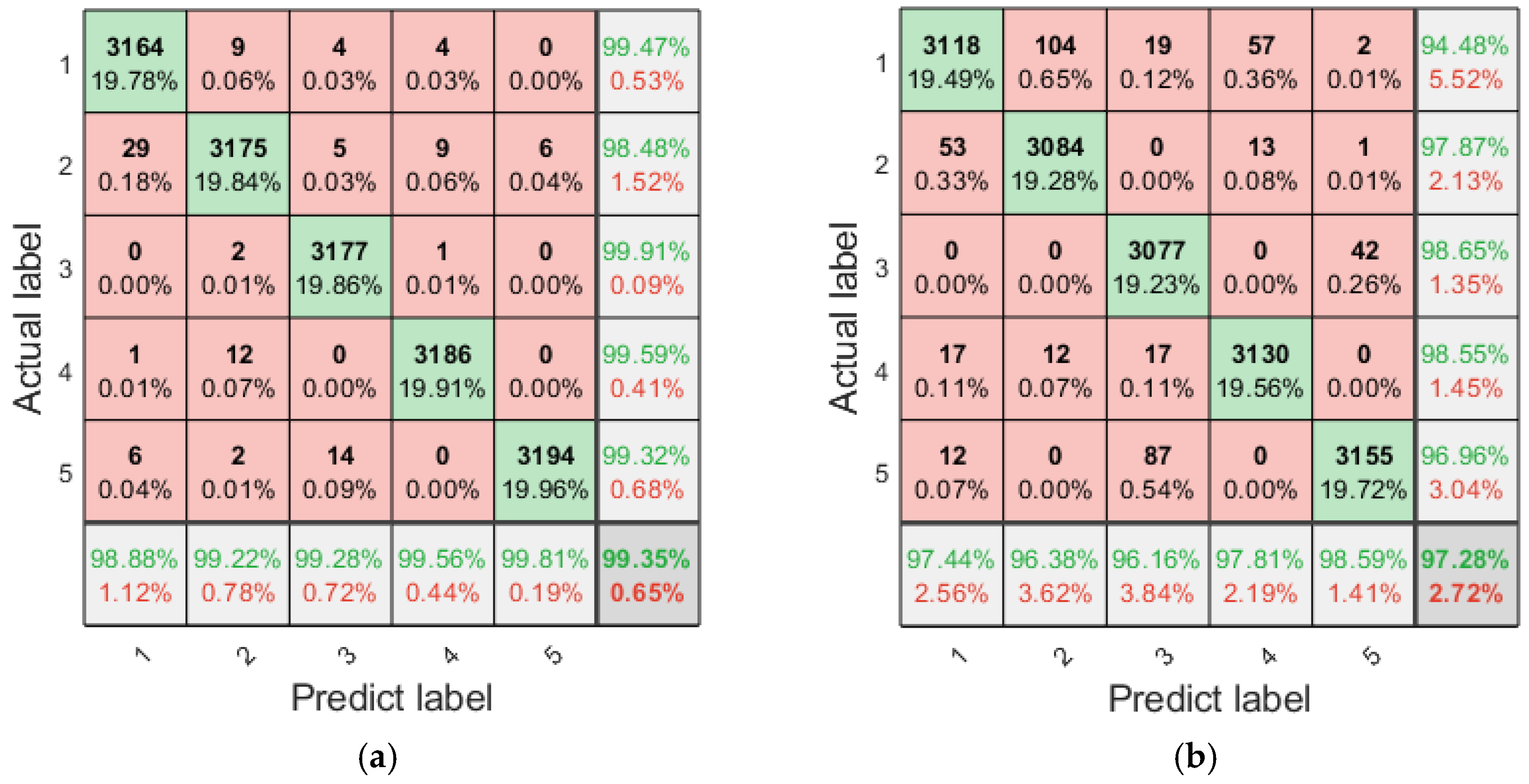
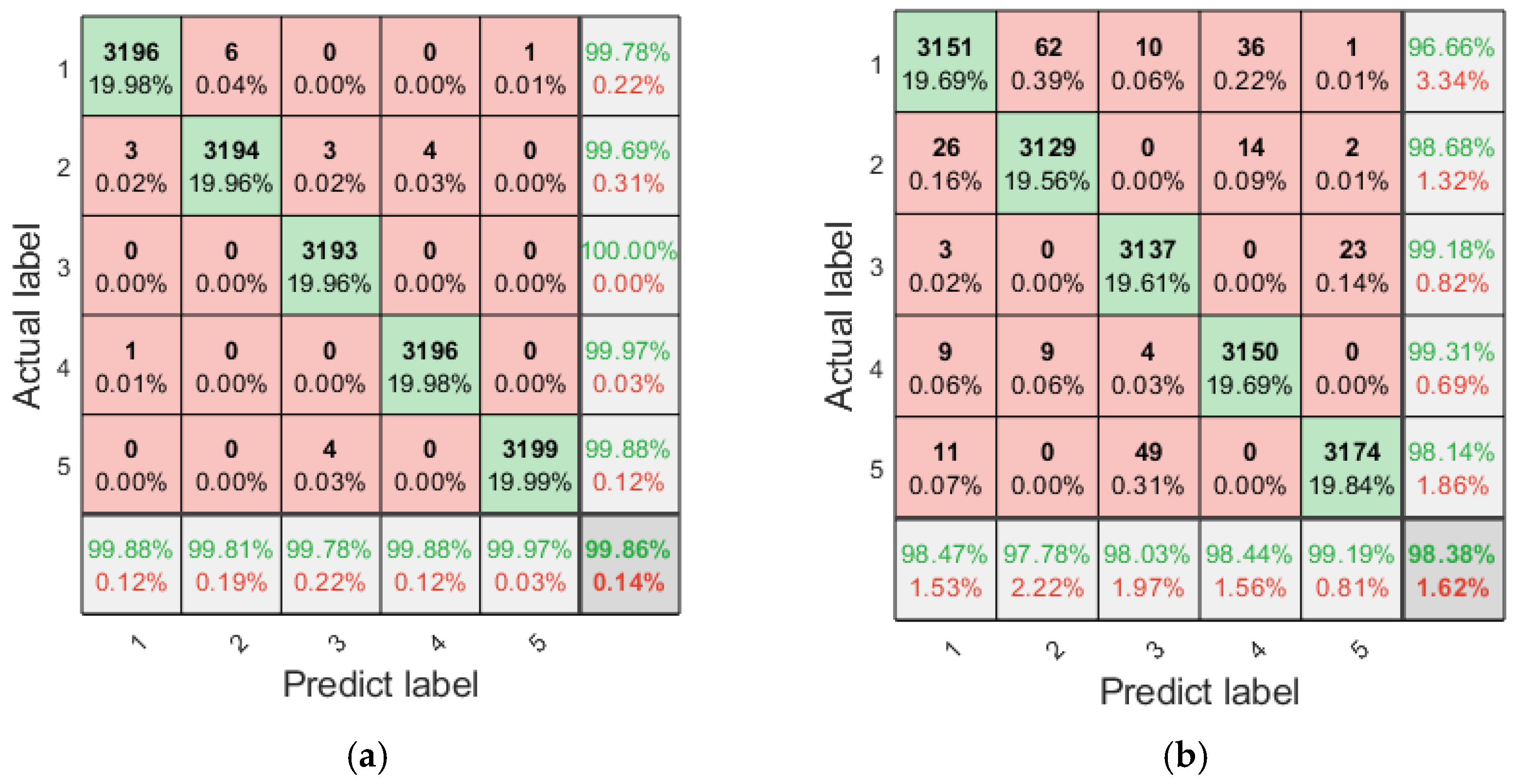
4.5. Fault Diagnosis Analysis
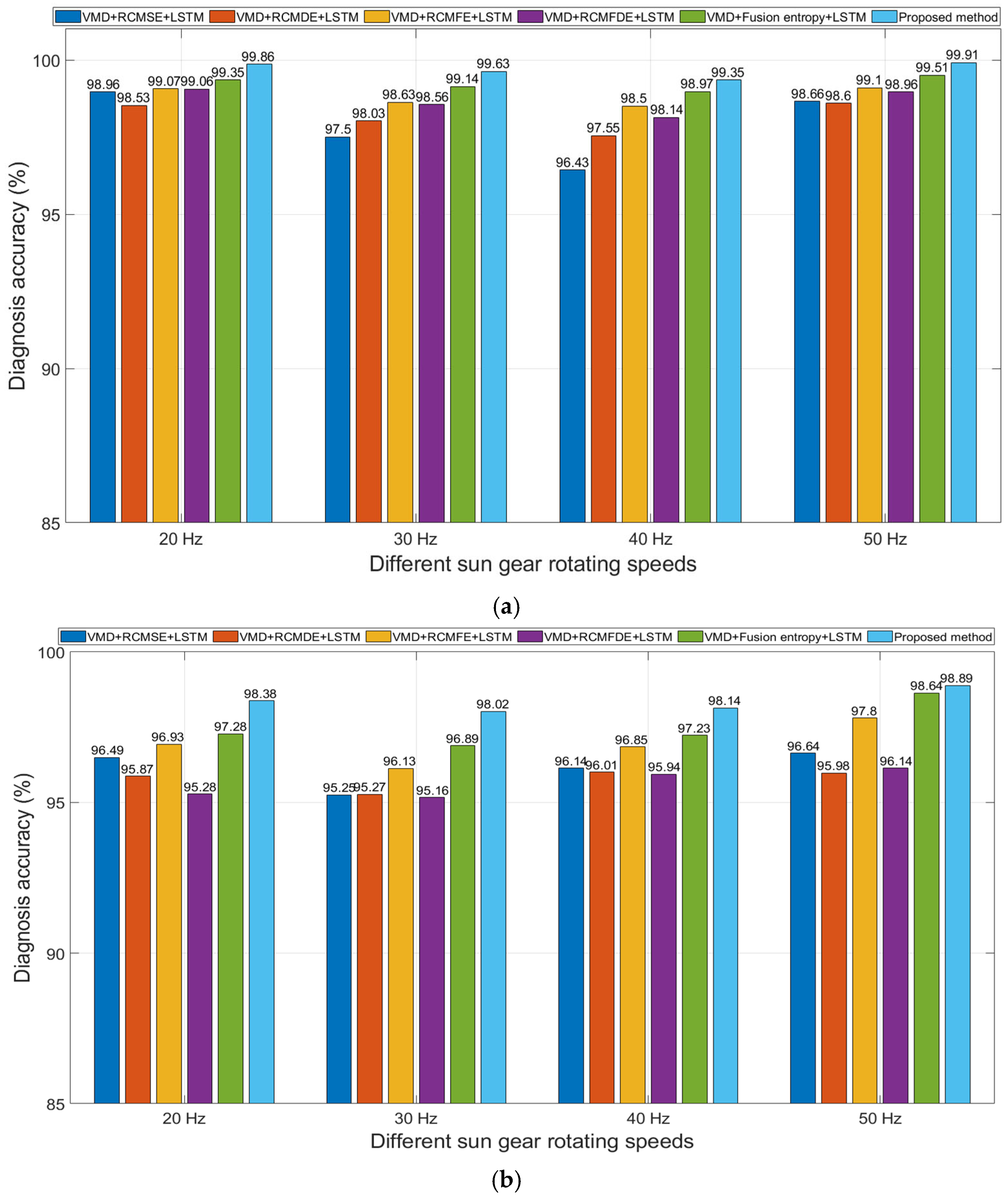
4.6. Fault Diagnosis Under Different Rotational Speeds
5. Conclusions
- (1)
- The experimental results show that feature extraction methods based on various entropy values differ in the aspects of signals they reflect. Different entropy values, when used as fault features, exhibit varying efficiencies in diagnosing different types of faults, with each entropy value having certain advantages. The use of fusion entropy as a fault feature can effectively improve the accuracy of fault diagnosis.
- (2)
- There exists a large number of redundant features in fusion entropy. Through the evaluation of feature importance by RF, it is found that there are significant differences in the importance of different features. Features with higher importance are selected to reconstruct the fault diagnosis feature vector.
- (3)
- The feature vectors processed by VMD, fusion entropy, and RF feature selection are used as inputs to the LSTM classifier for fault diagnosis of planetary gearboxes. The diagnosis results indicate that the proposed method has good diagnostic capability for planetary gearbox and also excellent performance and noise suppression capability.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, R.; Liu, C.; Han, T.; Yao, J.; Jiang, D. A planetary gearbox fault diagnosis method based on time-series imaging feature fusion and a transformer model. Meas. Sci. Technol. 2022, 34, 024006. [Google Scholar] [CrossRef]
- Yang, Y.; Hu, N.; Li, Y.; Cheng, Z.; Shen, G. Dynamic modeling and analysis of planetary gear system for tooth fault diagnosis. Mech. Syst. Signal Process. 2024, 207, 110946. [Google Scholar] [CrossRef]
- Ha, J.M.; Fink, O. Domain knowledge-informed synthetic fault sample generation with health data map for cross-domain planetary gearbox fault diagnosis. Mech. Syst. Signal Process. 2023, 202, 110680. [Google Scholar] [CrossRef]
- Amin, A.; Bibo, A.; Panyam, M.; Tallapragada, P. Vibration based fault diagnostics in a wind turbine planetary gearbox using machine learning. Wind Eng. 2023, 47, 175–189. [Google Scholar] [CrossRef]
- Dong, Y.; Jiang, H.; Wang, X.; Mu, M.; Jiang, W. An interpretable multiscale lifting wavelet contrast network for planetary gearbox fault diagnosis with small samples. Reliab. Eng. Syst. Saf. 2024, 251, 110404. [Google Scholar] [CrossRef]
- Meng, R.; Zhang, J.; Chen, M.; Chen, L. Fault Diagnosis Method of Planetary Gearboxes Based on Multi-Scale Wavelet Packet Energy Entropy and Extreme Learning Machine. Entropy 2025, 27, 782. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, H.; Cheng, W.; Xing, J.; Wang, W.; Du, S.; Li, L.; Zhang, R.; Chen, X.; Lu, J. Deep learning-based fault diagnosis of planetary gearbox: A systematic review. J. Manuf. Syst. 2024, 77, 730–745. [Google Scholar] [CrossRef]
- Huang, N.Q.; Song, M.M.; Tang, Y.H.; Huang, L.X.; Chen, Z.W. Research on fault diagnosis method for variable condition planetary gearbox based on SKN attention mechanism and deep transfer learning. Sci. Rep. 2025, 15, 22921. [Google Scholar] [CrossRef] [PubMed]
- Qian, Q.; Luo, J.; Qin, Y. Heterogeneous federated domain generalization network with common representation learning for cross-load machinery fault diagnosis. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 5704–5716. [Google Scholar] [CrossRef]
- Qian, Q.; Zhang, B.; Li, C.; Mao, Y.; Qin, Y. Federated transfer learning for machinery fault diagnosis: A comprehensive review of technique and application. Mech. Syst. Signal Process. 2025, 223, 111837. [Google Scholar] [CrossRef]
- Qian, Q.; Wen, Q.; Tang, R.; Qin, Y. DG-Softmax: A new domain generalization intelligent fault diagnosis method for planetary gearboxes. Reliab. Eng. Syst. Saf. 2025, 260, 111057. [Google Scholar] [CrossRef]
- Chen, L.; Feng, G.; Zhen, D.; Jing, H.; Liang, X.; Gu, F. Cross-Condition Fault Diagnosis of Planetary Gearboxes Driven by Data-Model Fusion Based on Improved Domain-Adversarial Transfer Learning. Shock. Vib. 2025, 2025, 9982177. [Google Scholar] [CrossRef]
- Liu, X. Vibration modelling and fault evolution symptom analysis of a planetary gear train for sun gear wear status assessment. Mech. Syst. Signal Process. 2022, 166, 108403. [Google Scholar] [CrossRef]
- Chen, R.; Huang, X.; Yang, L.; Xu, X.; Zhang, X.; Zhang, Y. Intelligent fault diagnosis method of planetary gearboxes based on convolution neural network and discrete wavelet transform. Comput. Ind. 2019, 106, 48–59. [Google Scholar] [CrossRef]
- Wang, J.; Li, J.; Wang, H.; Guo, L. Composite fault diagnosis of gearbox based on empirical mode decomposition and improved variational mode decomposition. J. Low Freq. Noise Vib. Act. Control 2021, 40, 332–346. [Google Scholar] [CrossRef]
- Li, Y.; Cheng, G.; Liu, C.; Chen, X. Study on planetary gear fault diagnosis based on variational mode decomposition and deep neural networks. Measurement 2018, 130, 94–104. [Google Scholar] [CrossRef]
- Pan, H.; Zheng, J.; Yang, Y.; Cheng, J. Nonlinear sparse mode decomposition and its application in planetary gearbox fault diagnosis. Mech. Mach. Theory 2021, 155, 104082. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Liu, Z.; Liang, X.; Si, S. The entropy algorithm and its variants in the fault diagnosis of rotating machinery: A review. IEEE Access 2018, 6, 66723–66741. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, H.; Yao, L.; Chen, X.; Qi, X.; Zhang, J. An effective multi-channel fault diagnosis approach for rotating machinery based on multivariate generalized refined composite multi-scale sample entropy. Nonlinear Dyn. 2021, 106, 2107–2130. [Google Scholar] [CrossRef]
- Azami, H.; Rostaghi, M.; Abásolo, D.; Escudero, J. Refined composite multiscale dispersion entropy and its application to biomedical signals. IEEE Trans. Biomed. Eng. 2017, 64, 2872–2879. [Google Scholar] [CrossRef]
- Minhas, A.S.; Singh, G.; Singh, J.; Kankar, P.K.; Singh, S. A novel method to classify bearing faults by integrating standard deviation to refined composite multi-scale fuzzy entropy. Measurement 2020, 154, 107441. [Google Scholar] [CrossRef]
- Rostaghi, M.; Khatibi, M.M.; Ashory, M.R.; Azami, H. Refined composite multiscale fuzzy dispersion entropy and its applications to bearing fault diagnosis. Entropy 2023, 25, 1494. [Google Scholar] [CrossRef]
- Xu, P.; Liu, J.; Zhang, W.; Wang, H.; Huang, Y. Multiscale kernel entropy component analysis with application to complex industrial process monitoring. IEEE Trans. Autom. Sci. Eng. 2023, 21, 3757–3772. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, J.; Yang, C.; Xu, D.; Ge, J. Remaining useful life prediction of rolling bearings based on Pearson correlation-KPCA multi-feature fusion. Measurement 2022, 201, 111572. [Google Scholar] [CrossRef]
- Zheng, K.; Wang, X. Feature selection method with joint maximal information entropy between features and class. Pattern Recognit. 2018, 77, 20–29. [Google Scholar] [CrossRef]
- Sylvester, E.V.; Bentzen, P.; Bradbury, I.R.; Clément, M.; Pearce, J.; Horne, J.; Beiko, R.G. Applications of random forest feature selection for fine-scale genetic population assignment. Evol. Appl. 2018, 11, 153–165. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhou, H.; Li, T. Cost-sensitive feature selection using random forest: Selecting low-cost subsets of informative features. Knowl.-Based Syst. 2016, 95, 1–11. [Google Scholar] [CrossRef]
- Huang, T.; Zhang, Q.; Tang, X.; Zhao, S.; Lu, X. A novel fault diagnosis method based on CNN and LSTM and its application in fault diagnosis for complex systems. Artif. Intell. Rev. 2022, 55, 1289–1315. [Google Scholar] [CrossRef]
- Zhao, L.; Li, Z.; Qu, L.; Zhang, J.; Teng, B. A hybrid VMD-LSTM/GRU model to predict non-stationary and irregular waves on the east coast of China. Ocean. Eng. 2023, 276, 114136. [Google Scholar] [CrossRef]
- Zheng, J.; Pan, H.; Tong, J.; Liu, Q. Generalized refined composite multiscale fuzzy entropy and multi-cluster feature selection based intelligent fault diagnosis of rolling bearing. ISA Trans. 2022, 123, 136–151. [Google Scholar] [CrossRef]
- Yi, M.; Zhou, C.; Yang, L.; Yang, J.; Tang, T.; Jia, Y.; Yuan, X. bearing fault diagnosis method based on RCMFDE-SPLR and ocean predator algorithm optimizing support vector machine. Entropy 2022, 24, 1696. [Google Scholar] [CrossRef] [PubMed]
- Iranzad, R.; Liu, X. A review of random forest-based feature selection methods for data science education and applications. Int. J. Data Sci. Anal. 2024, 20, 197–211. [Google Scholar] [CrossRef]
- Zhao, S.; Duan, Y.; Roy, N.; Zhang, B. A deep learning methodology based on adaptive multiscale CNN and enhanced highway LSTM for industrial process fault diagnosis. Reliab. Eng. Syst. Saf. 2024, 249, 110208. [Google Scholar] [CrossRef]
- Xia, X.; Wang, X. Fault Diagnosis of Planetary Gearbox Based on Hierarchical Refined Composite Multiscale Fuzzy Entropy and Optimized LSSVM. Entropy 2025, 27, 512. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Cui, L.; Cheng, W. Fault diagnosis of wind turbines under nonstationary conditions based on a novel tacho-less generalized demodulation. Renew. Energy 2023, 206, 645–657. [Google Scholar] [CrossRef]
| Parameter Description | Values | |
|---|---|---|
| Tooth number | Sun gear | 28 |
| Ring gear | 100 | |
| Planet gear (number) | 36 (4) | |
| Sun gear rotating frequency | 20 Hz, 30 Hz, 40 Hz, 50 Hz | |
| Sampling frequency | 48,000 Hz | |
| Operation State | Sample Length | Number of Samples | The Division Ratio of the Training Set and Test Set | Operation Label |
|---|---|---|---|---|
| Healthy | 1024 points | 400 | 6:4 (The samples were randomly selected) | 1 |
| Broken tooth | 400 | 2 | ||
| Missing tooth | 400 | 3 | ||
| Root crack | 400 | 4 | ||
| Wear gear | 400 | 5 |
| Parameter Description | Values |
|---|---|
| Scale factors, | 20 |
| Scalar embedding, | 2 |
| Scalar time lag, | 1 |
| Number of classes, | 6 |
| Scalar threshold, | 0.15 |
| Fuzzy power, | 2 |
| Methods | Fault Diagnosis Accuracy (Original Signal) | Fault Diagnosis Accuracy (SNR = 3 dB) |
|---|---|---|
| Fusion entropy + RF + LSTM | 98.15% | 92.42% |
| VMD + RCMSE + RF + LSTM | 99.07% | 97.18% |
| VMD + RCMFE+ RF + LSTM | 98.93% | 96.81% |
| VMD + RCMDE + RF + LSTM | 99.37% | 97.58% |
| VMD + RCMFDE + RF + LSTM | 99.31% | 96.31% |
| VMD + fusion entropy + LSTM | 99.35% | 97.28% |
| VMD + fusion entropy + RF + LSTM | 99.86% | 98.38% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, X.; Sun, H.; Wang, A. Fault Diagnosis of Planetary Gearboxes Based on LSTM Improved via Feature Extraction Using VMD, Fusion Entropy, and Random Forest. Entropy 2025, 27, 956. https://doi.org/10.3390/e27090956
Xia X, Sun H, Wang A. Fault Diagnosis of Planetary Gearboxes Based on LSTM Improved via Feature Extraction Using VMD, Fusion Entropy, and Random Forest. Entropy. 2025; 27(9):956. https://doi.org/10.3390/e27090956
Chicago/Turabian StyleXia, Xin, Haoyu Sun, and Aiguo Wang. 2025. "Fault Diagnosis of Planetary Gearboxes Based on LSTM Improved via Feature Extraction Using VMD, Fusion Entropy, and Random Forest" Entropy 27, no. 9: 956. https://doi.org/10.3390/e27090956
APA StyleXia, X., Sun, H., & Wang, A. (2025). Fault Diagnosis of Planetary Gearboxes Based on LSTM Improved via Feature Extraction Using VMD, Fusion Entropy, and Random Forest. Entropy, 27(9), 956. https://doi.org/10.3390/e27090956







