Ascertaining Susceptibilities in Smart Contracts: A Quantum Machine Learning Approach
Abstract
1. Introduction
- Presently, no research has been attempted to detect smart contract vulnerabilities using QML algorithms. To fill this existing gap, the current study employs four well known QML algorithms to detect vulnerabilities.
- Compared to classical ML algorithms, QML algorithms were able to process knowledge within smart contracts by consuming less memory and by utilizing the benefits of quantum mechanics. In addition to liability detection, the current work also implies prospects of network security implications from outcomes of QML approaches.
- Employing QML models for detecting liabilities in smart contracts on a larger scale would be beneficial. Non-uniform lengths of contracts were analyzed effectively using QML algorithms, especially by the quantum neural network (QNN) approach, thus solving the problem of inconsistent input lengths. Also, vulnerabilities were detected in batches using these QML algorithms, reflecting the capability of batch processing.
- Experimentations revealed that the QNN model outperformed other QML algorithms in detecting vulnerabilities with a performance accuracy of 81.78%. This accuracy was further improved to 97.63% on a test dataset. The average accuracy of the model on small-scale smart contracts datasets derived from splitting the test dataset was found to be 89.96%.
2. Literature Survey
2.1. Significance of Security in Smart Contracts
2.2. Conventional Static Techniques
2.3. ML Approaches Towards Vulnerability Detection
2.4. Recent Advances
3. Methodology
3.1. Notation and Assumptions
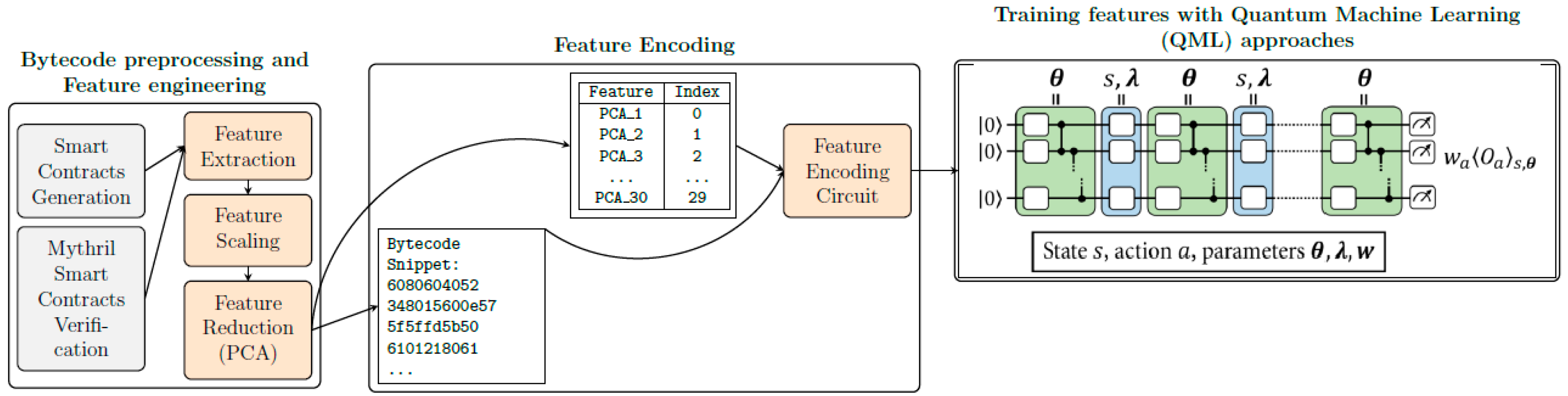
3.2. Data Collection and Preprocessing
3.3. Data Cleaning and Splitting
3.4. Opcode Processing and Feature Extraction
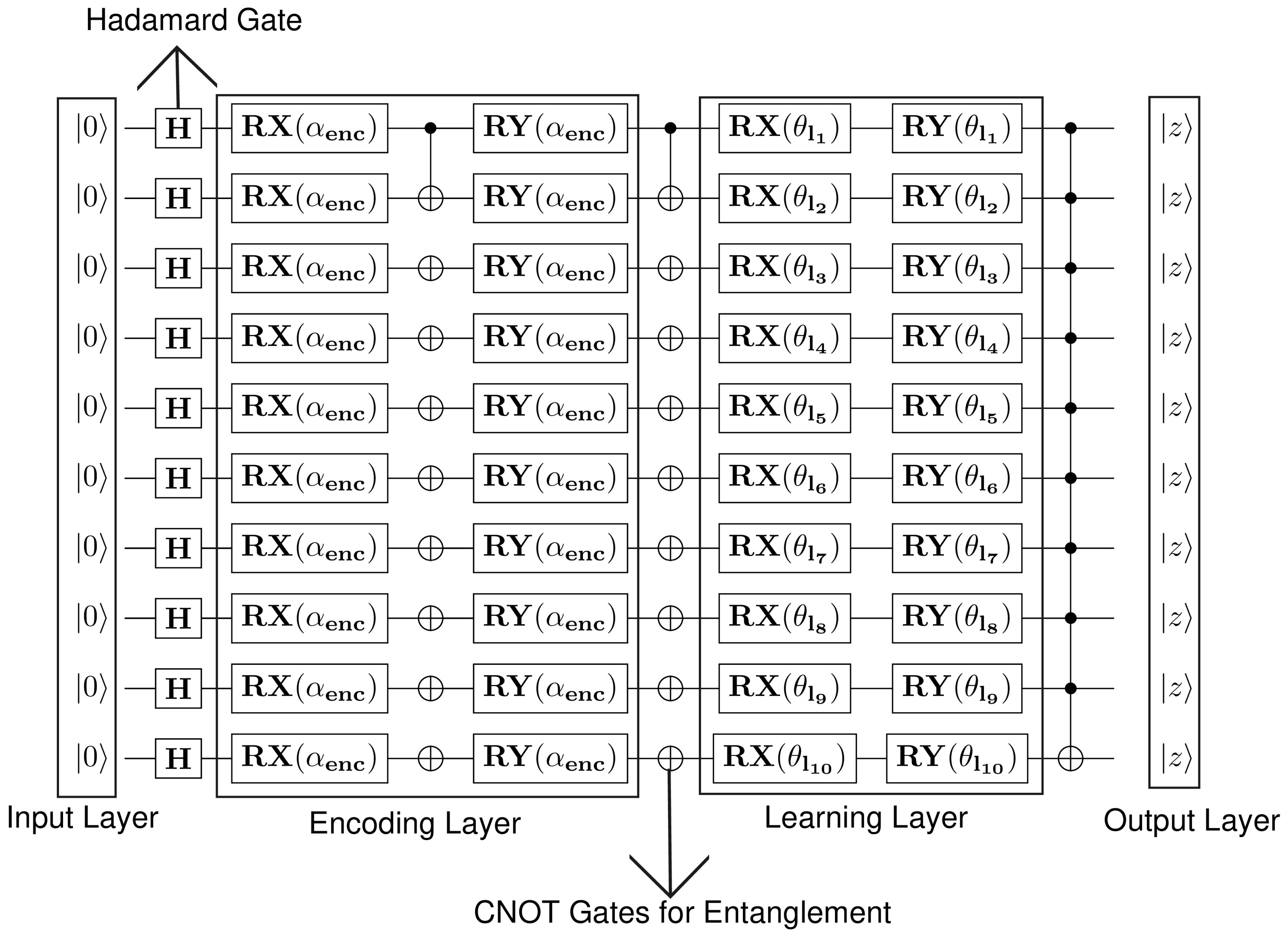
3.5. Quantum Encoding and Circuit Design
- A k-qubit register for G binary instances.
- A 2-qubit ancillary register .
- Selectively reverse qubits for matching the binary encoded instance a(b) on k qubits. This operation was performed by employing the CNOT (i.e., controlled NOT gate) controlled on |c1⟩ = 0, which targeted the qubits correlating to the bit that is equal to one of the (b + 1)th instance a(b).
- Reverse qubit supposing the state of . Also, apply the controlled rotation gate CG as defined below:Here, in Equation (1), α = G − b denotes the count of instances, along with the present one, which is yet to be determined. The gate acts as control qubits and acts as target qubits, respectively. This partition of qubits is intended to divide the quantum state across two branches d1 and d2. Branch d1 included primary (b + 1) occurrences in superposition, each of which had an amplitude of , while the branch d2 included new occurrences , with an amplitude of Here, branch d1 perpetually encoded binary occurrences until (b + 1)th.
- Finally, branch d2 is restored such that .
- Repeat from Step 1, to load subsequent instances to be encoded.
3.6. Detecting Vulnerabilities Using QML Approaches
- QNN: As the name suggests, QNN is centered on the concepts of neural network (NN) grounded on the fundamentals of quantum mechanics. The model accelerates learning towards better computation. Here, qubits portray the brain neurons [86]. Neuron models engross the quantum states for interpreting information. |0⟩ and |1⟩ are the quantum states representing classical bit information. The qubit state |γ⟩ sustains coherent superposition of quantum states |0⟩ and |1⟩.
- ii.
- QSVM: Using a kernel for quantum computing is the basis of QSVM. QSVM is the quantum variant of the classical SVM algorithm used in multiple ML tasks [87]. The quantum kernel is often estimated as an inner product of quantum states derived from two data coordinates. It can be mathematically defined as follows:
- iii.
- VQC: VQC is a variant of QNN employed for supervised learning. It optimizes the quantum circuit and minimizes the loss metric represented in triplet notation [89]:
- QRF: RF is a variant of the decision tree (DT) algorithm used for regression and classification tasks [90,91]. RF is composed of U discrete quantum DTs (QDTs), which form a group of weak ensembles, which is input for QRF. Given training data with V instances, , with class labels vc, , to be trained from interpreted data, and , from underlying distribution E. Every tree is trained using the partition size (i.e., Vp ≤ V). These instances are sampled from data V. When every classifier is trained, the model is evaluated on a separate dataset Vtrain, by linking the distribution of forecasted class labels. The overall predictions are derived by averaging predictions from every QDT, which in turn yields a probabilistic distribution.
3.7. Architecture of QML Models
- QNN: The model is implemented as a layered variational circuit with L blocks. Each block comprises a data encoding layer, parameterized rotation layer and entangling layer. The unitary block l is given byThe expected value of the first qubit was estimated and mapped to probability via . The network was trained using the parameter-shift rule and Adam optimizer.
- QSVM: The model utilized an entangling feature map , where each qubit undergoes rotation operation followed by CNOT entanglement. The quantum kernel between two feature vector x and x’ is computed using the SWAP test:The resulting kernel matrix is passed to a classical SVM solver with a precomputed kernel.
- VQC: VQC employs angle encoding followed by a strongly entangling ansatz. Each layer of the model comprises a rotation block and entanglement block. The output obtained from expectation values of designated qubits would be mapped to class probabilities of susceptibility, where cross-entropy was utilized for training.
- QRF: The ensemble of Quantum Decision Tree (QDT) is QRF. Each QDT encodes a random subset of features using RY rotations, followed by applying a shallow entangling circuit, and measures a decision qubit. Further, predictions from T QDTs are aggregated using the majority voting approach. Also, random feature selection and bootstrap sampling were applied to enhance diversity among trees.
4. Experiments
4.1. Hyperparameter Settings
4.2. Metrics for Performance Evaluation
- Precision, also known as positive predicted instances, estimates the ratio of accurately forecasted positive instances (i.e., true positives) to total count of instances predicted positive.
- Accuracy indicates the inclusive amount of perfection in a mathematical model. It is the ratio of correctly predicted values (i.e., True negative, True positive) to the total count of data instances.
- Recall estimates the capability of a mathematical model to ascertain all positive occurrences. It is also called sensitivity and estimated as the ratio of accurately forecasted positive occurrences to all positive occurrences in data.
- F1 score is a significant estimate that combines recall and precision metrics. It finds out the balance and trade-off their estimates. The estimate is essential when the dataset is unbalanced.
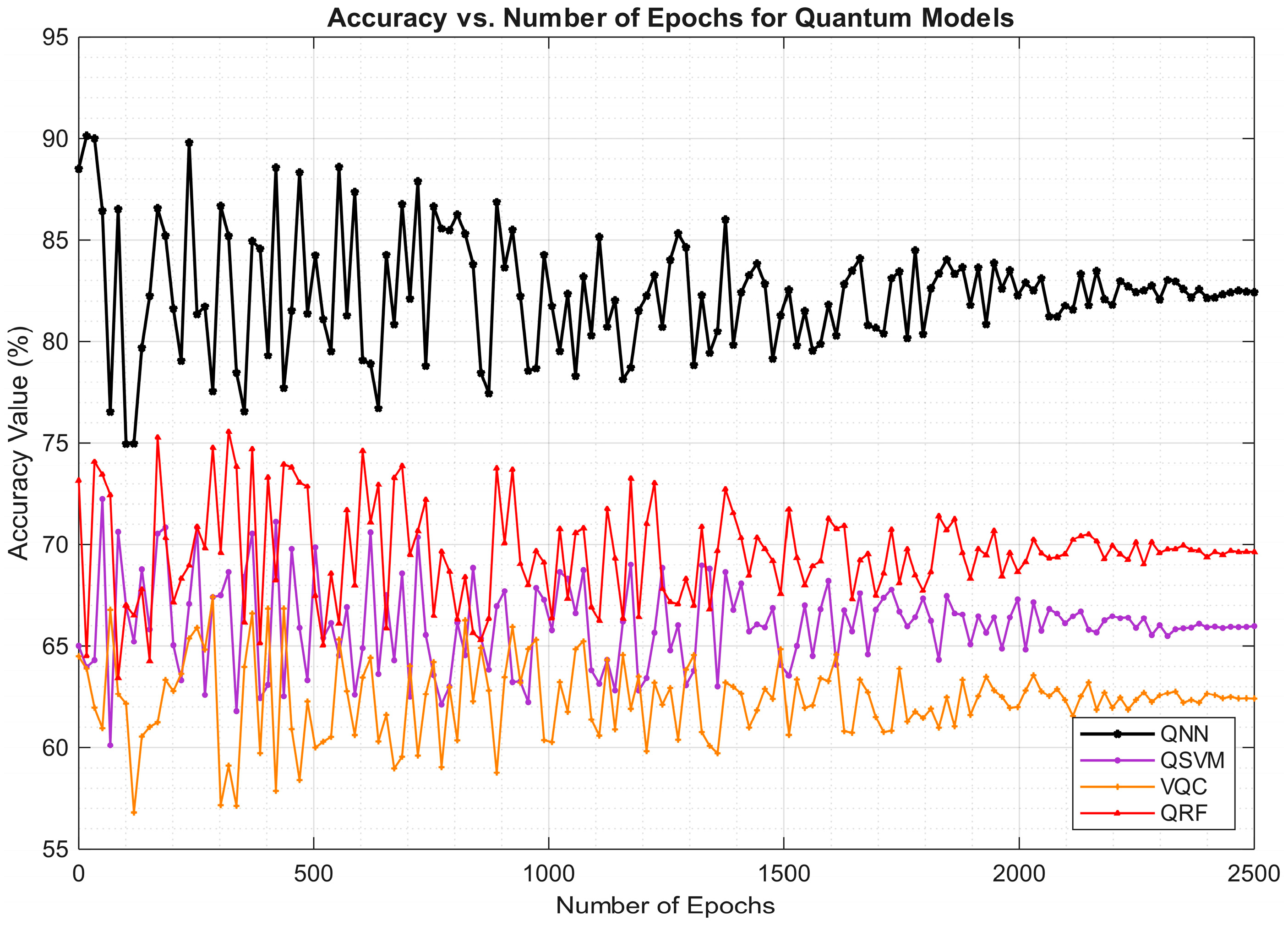
5. Results and Discussion
McNemar’s Test
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| QML | Quantum Machine Learning |
| QNN | Quantum Neural Network |
| QSVM | Quantum Support Vector Machine |
| QRF | Quantum Random Forest |
References
- Besley, T.; Coate, S. Centralized versus decentralized provision of local public goods: A political economy approach. J. Public Econ. 2003, 87, 2611–2637. [Google Scholar] [CrossRef]
- Aggarwal, S.; Kumar, N. Cryptographic Consensus Mechanisms. In Advances in Computer; Elsevier: Amsterdam, The Netherlands, 2021; pp. 211–226. [Google Scholar] [CrossRef]
- Arooj, A.; Farooq, M.S.; Umer, T. Unfolding the Blockchain Era: Timeline, Evolution, Types and Real-World Applications. J. Netw. Comput. Appl. 2022, 207, 103511. [Google Scholar] [CrossRef]
- Sunyaev, A. Distributed Ledger Technology. In Internet Computing; Springer Nature: Cham, Switzerland, 2024; pp. 239–272. [Google Scholar] [CrossRef]
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System; United Staes Sentencing Commission (USSC): Washington, DC, USA, 2008. Available online: https://www.ussc.gov/sites/default/files/pdf/training/annual-national-training-seminar/2018/Emerging_Tech_Bitcoin_Crypto.pdf (accessed on 12 June 2025).
- Szabo, N. Smart Contracts: Building Blocks for Digital Markets. 1996. Available online: https://www.truevaluemetrics.org/DBpdfs/BlockChain/Nick-Szabo-Smart-Contracts-Building-Blocks-for-Digital-Markets-1996-14591.pdf (accessed on 12 June 2025).
- Zou, W.; Lo, D.; Kochhar, P.S.; Le, X.-B.D.; Xia, X.; Feng, Y.; Chen, Z.; Xu, B. Smart Contract Development: Challenges and Opportunities. IEEE Trans. Softw. Eng. 2021, 47, 2084–2106. [Google Scholar] [CrossRef]
- Onifade, M.; Adebisi, J.A.; Zvarivadza, T. Recent Advances in Blockchain Technology: Prospects, Applications and Constraints in the Minerals Industry. Int. J. Min. Reclam. Environ. 2024, 38, 497–533. [Google Scholar] [CrossRef]
- Zamani, E.; He, Y.; Phillips, M. On the Security Risks of the Blockchain. J. Comput. Inf. Syst. 2020, 60, 495–506. [Google Scholar] [CrossRef]
- Atzei, N.; Bartoletti, M.; Cimoli, T. A Survey of Attacks on Ethereum Smart Contracts (SoK). In Principles of Security and Trust; Springer: Berlin/Heidelberg, Germany, 2017; pp. 164–186. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, F.R.; Li, X.; Ji, H.; Leung, V.C.M. Blockchain and Machine Learning for Communications and Networking Systems. IEEE Commun. Surv. Tutor. 2020, 22, 1392–1431. [Google Scholar] [CrossRef]
- Wang, S.; Ouyang, L.; Yuan, Y.; Ni, X.; Han, X.; Wang, F.-Y. Blockchain-Enabled Smart Contracts: Architecture, Applications, and Future Trends. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 2266–2277. [Google Scholar] [CrossRef]
- Kaulartz, M.; Heckmann, J. Smart Contracts—Anwendungen Der Blockchain-Technologie. Comput. Recht. 2016, 32, 618–624. [Google Scholar] [CrossRef]
- Ghaleb, A.; Rubin, J.; Pattabiraman, K. ETainter: Detecting Gas-Related Vulnerabilities in Smart Contracts. In Proceedings of the 31st ACM SIGSOFT International Symposium on Software Testing and Analysis, Virtual, Republic of Korea, 18–22 July 2022; ACM: New York, NY, USA, 2022; pp. 728–739. [Google Scholar] [CrossRef]
- Schär, F. Decentralized Finance: On Blockchain- and Smart Contract-Based Financial Markets. Review 2021, 103, 22. [Google Scholar] [CrossRef]
- Mehar, M.I.; Shier, C.L.; Giambattista, A.; Gong, E.; Fletcher, G.; Sanayhie, R.; Kim, H.M.; Laskowski, M. Understanding a Revolutionary and Flawed Grand Experiment in Blockchain. In Research Anthology on Blockchain Technology in Business, Healthcare, Education, and Government; IGI Global: Hershey, PA, USA, 2021; pp. 1253–1266. Available online: https://www.igi-global.com/gateway/chapter/268659 (accessed on 12 June 2025).
- bZx Protocol Token (BZRX). Etherscan. Available online: https://etherscan.io/token/0x56d811088235f11c8920698a204a5010a788f4b3 (accessed on 12 June 2025).
- Tang, X.; Du, Y.; Lai, A.; Zhang, Z.; Shi, L. Deep Learning-Based Solution for Smart Contract Vulnerabilities Detection. Sci. Rep. 2023, 13, 20106. [Google Scholar] [CrossRef]
- Park, D.; Zhang, Y.; Saxena, M.; Daian, P.; Roşu, G. A Formal Verification Tool for Ethereum VM Bytecode. In Proceedings of the 2018 26th ACM Joint Meeting on European Software Engineering Conference and Symposium on the Foundations of Software Engineering, Lake Buena Vista, FL, USA, 4–9 November 2018; ACM: New York, NY, USA, 2018; pp. 912–915. [Google Scholar] [CrossRef]
- Jiang, B.; Liu, Y.; Chan, W.K. ContractFuzzer: Fuzzing Smart Contracts for Vulnerability Detection. In Proceedings of the 33rd ACM/IEEE International Conference on Automated Software Engineering, Montpellier, France, 3–7 September 2018; ACM: New York, NY, USA, 2018; pp. 259–269. [Google Scholar] [CrossRef]
- Kalra, S.; Goel, S.; Dhawan, M.; Sharma, S. ZEUS: Analyzing Safety of Smart Contracts. In Proceedings of the 2018 Network and Distributed System Security Symposium, San Diego, CA, USA, 18–21 February 2018; Internet Society: Reston, VA, USA, 2018. [Google Scholar] [CrossRef]
- Durieux, T.; Ferreira, J.F.; Abreu, R.; Cruz, P. Empirical Review of Automated Analysis Tools on 47,587 Ethereum Smart Contracts. In Proceedings of the ACM/IEEE 42nd International Conference on Software Engineering, Seoul, Republic of Korea, 27 June–19 July 2020; ACM: New York, NY, USA, 2020; pp. 530–541. [Google Scholar] [CrossRef]
- Luu, L.; Chu, D.-H.; Olickel, H.; Saxena, P.; Hobor, A. Making Smart Contracts Smarter. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, New York, NY, USA, 24–28 October 2016; ACM: New York, NY, USA, 2016; pp. 254–269. [Google Scholar] [CrossRef]
- Feist, J.; Grieco, G.; Groce, A. Slither: A Static Analysis Framework for Smart Contracts. In Proceedings of the 2019 IEEE/ACM 2nd International Workshop on Emerging Trends in Software Engineering for Blockchain (WETSEB), Montreal, QC, Canada, 27 May 2019; IEEE: New York, NY, USA, 2019; pp. 8–15. [Google Scholar] [CrossRef]
- Jiao, J.; Wei Lin, S.; Sun, J. A Generalized Formal Semantic Framework for Smart Contracts. In Proceedings of the 2020 International Conference on Fundamental Approaches to Software Engineering, Dublin, Ireland, 25 April 2020; pp. 75–96. [Google Scholar] [CrossRef]
- Tsankov, P.; Dan, A.; Drachsler-Cohen, D.; Gervais, A.; Bünzli, F.; Vechev, M. Securify: Practical Security Analysis of Smart Contracts. In Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security, Toronto, ON, Canada, 15–19 October 2018; ACM: New York, NY, USA, 2018; pp. 67–82. [Google Scholar] [CrossRef]
- Tikhomirov, S.; Voskresenskaya, E.; Ivanitskiy, I.; Takhaviev, R.; Marchenko, E.; Alexandrov, Y. SmartCheck. In Proceedings of the 1st International Workshop on Emerging Trends in Software Engineering for Blockchain, Gothenburg, Sweden, 27 May 2018; ACM: New York, NY, USA, 2018; pp. 9–16. [Google Scholar] [CrossRef]
- Grimmelmann, J. All Smart Contracts Are Ambiguous. J. Law Innov. 2019, 2, 1–22. [Google Scholar]
- Singh, U.K.; Joshi, C.; Kanellopoulos, D. A Framework for Zero-Day Vulnerabilities Detection and Prioritization. J. Inf. Secur. Appl. 2019, 46, 164–172. [Google Scholar] [CrossRef]
- Kiani, R.; Sheng, V.S. Ethereum Smart Contract Vulnerability Detection and Machine Learning-Driven Solutions: A Systematic Literature Review. Electronics 2024, 13, 2295. [Google Scholar] [CrossRef]
- Gaur, R.; Prakash, S.; Kumar, S.; Abhishek, K.; Msahli, M.; Wahid, A. A Machine-Learning–Blockchain-Based Authentication Using Smart Contracts for an IoHT System. Sensors 2022, 23, 4793. [Google Scholar] [CrossRef]
- Wang, M.; Xie, Z.; Wen, X.; Li, J.; Zhou, K. Ethereum Smart Contract Vulnerability Detection Model Based on Triplet Loss and BiLSTM. Electronics 2023, 12, 2327. [Google Scholar] [CrossRef]
- Shafay, M.; Ahmad, R.W.; Salah, K.; Yaqoob, I.; Jayaraman, R.; Omar, M. Blockchain for Deep Learning: Review and Open Challenges. Clust. Comput. 2023, 26, 197–221. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, W.; Wang, W.; Jin, Z.; Zhao, C.; Cai, Z.; Chen, H. CBGRU: A Detection Method of Smart Contract Vulnerability Based on a Hybrid Model. Sensors 2022, 22, 3577. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, J.; Wang, W.; Jin, Z.; Zhao, C.; Cai, Z.; Chen, H. A Novel Smart Contract Vulnerability Detection Method Based on Information Graph and Ensemble Learning. Sensors 2022, 22, 3581. [Google Scholar] [CrossRef]
- Zhang, L.; Li, Y.; Jin, T.; Wang, W.; Jin, Z.; Zhao, C.; Cai, Z.; Chen, H. SPCBIG-EC: A Robust Serial Hybrid Model for Smart Contract Vulnerability Detection. Sensors 2022, 22, 4621. [Google Scholar] [CrossRef]
- Liu, Z.; Jiang, M.; Zhang, S.; Zhang, J.; Liu, Y. A Smart Contract Vulnerability Detection Mechanism Based on Deep Learning and Expert Rules. IEEE Access 2023, 11, 77990–77999. [Google Scholar] [CrossRef]
- Huang, T.T.H.-D. Hunting the Ethereum Smart Contract: Color-inspired Inspection of Potential Attacks. arXiv 2018, arXiv:1807.01868v1. [Google Scholar] [CrossRef]
- Liao, J.-W.; Tsai, T.-T.; He, C.-K.; Tien, C.-W. SoliAudit: Smart Contract Vulnerability Assessment Based on Machine Learning and Fuzz Testing. In Proceedings of the 2019 Sixth International Conference on Internet of Things: Systems, Management and Security (IOTSMS), Granada, Spain, 22–25 October 2019; IEEE: New York, NY, USA, 2019; pp. 458–465. [Google Scholar] [CrossRef]
- Yu, X.; Zhao, H.; Hou, B.; Ying, Z.; Wu, B. DeeSCVHunter: A Deep Learning-Based Framework for Smart Contract Vulnerability Detection. In Proceedings of the 2021 International Joint Conference on Neural Networks (IJCNN), Shenzhen, China, 18–22 July 2021; IEEE: New York, NY, USA, 2021; pp. 1–8. [Google Scholar] [CrossRef]
- Zhou, X.; Pang, J.; Yue, F.; Liu, F.; Guo, J.; Liu, W.; Song, Z.; Shu, G.; Xia, B.; Shan, Z. A New Method of Software Vulnerability Detection Based on a Quantum Neural Network. Sci. Rep. 2022, 12, 8053. [Google Scholar] [CrossRef]
- Menon, P.S.; Ritwik, M. A Comprehensive but Not Complicated Survey on Quantum Computing. IERI Procedia 2014, 10, 144–152. [Google Scholar] [CrossRef]
- Hassanien, A.E.; Elhoseny, M.; Kacprzyk, J. Quantum Computin: An Environment for Intelligent Large Scale Real Application; Springer International Publishing: Cham, Switzerland, 2018; Volume 33. [Google Scholar] [CrossRef]
- Biamonte, J.; Wittek, P.; Pancotti, N.; Rebentrost, P.; Wiebe, N.; Lloyd, S. Quantum Machine Learning. Nature 2017, 549, 195–202. [Google Scholar] [CrossRef] [PubMed]
- Schuld, M.; Petruccione, F. Machine Learning with Quantum Computers; Springer International Publishing: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Abbaszade, M.; Salari, V.; Mousavi, S.S.; Zomorodi, M.; Zhou, X. Application of Quantum Natural Language Processing for Language Translation. IEEE Access 2021, 9, 130434–130448. [Google Scholar] [CrossRef]
- Di Sipio, R.; Huang, J.-H.; Chen, S.Y.-C.; Mangini, S.; Worring, M. The Dawn of Quantum Natural Language Processing. In Proceedings of the ICASSP 2022–2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 23–27 May 2022; IEEE: New York, NY, USA, 2022; pp. 8612–8616. [Google Scholar] [CrossRef]
- Bikku, T.; Thota, S.; Shanmugasundaram, P. A Novel Quantum Neural Network Approach to Combating Fake Reviews. Int. J. Netw. Distrib. Comput. 2024, 12, 195–205. [Google Scholar] [CrossRef]
- Li, F.; Zhao, S.; Zheng, B. Quantum Neural Network in Speech Recognition. In Proceedings of the 6th International Conference on Signal Processing, Beijing, China, 26–30 August 2002; IEEE: New York, NY, USA, 2002; pp. 1267–1270. [Google Scholar] [CrossRef]
- Tang, E. A Quantum-Inspired Classical Algorithm for Recommendation Systems. In Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing, Phoenix, AZ, USA, 23–26 June 2019; ACM: New York, NY, USA, 2019; pp. 217–228. [Google Scholar] [CrossRef]
- Xiong, H.; Duan, X.; Yu, Y.; Zhang, J.; Yin, H. Image Classification Based on Quantum Machine Learning. In Proceedings of the 2023 5th International Conference on Intelligent Control, Measurement and Signal Processing (ICMSP), Chengdu, China, 19–21 May 2023; IEEE: New York, NY, USA, 2023; pp. 891–895. [Google Scholar] [CrossRef]
- Chen, Y. A Novel Image Classification Framework Based on Variational Quantum Algorithms. Quantum Inf. Process. 2024, 23, 362. [Google Scholar] [CrossRef]
- Li, R.Y.; Di Felice, R.; Rohs, R.; Lidar, D.A. Quantum Annealing versus Classical Machine Learning Applied to a Simplified Computational Biology Problem. npj Quantum Inf. 2018, 4, 14. [Google Scholar] [CrossRef]
- Satuluri, V.K.R.R.; Ponnusamy, V. Quantum-Enhanced Machine Learning. In Proceedings of the 2021 Smart Technologies, Communication and Robotics (STCR), Sathyamangalam, India, 9–10 October 2021; IEEE: New York, NY, USA, 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Durgut, S.; Küçüksille, E.U.; Tokmak, M. Hybrid Quantum–Classical Deep Neural Networks Based Smart Contract Vulnerability Detection. Appl. Sci. 2025, 15, 4037. [Google Scholar] [CrossRef]
- Feng, X.; Liu, H.; Wang, L.; Zhu, H.; Sheng, V.S. An Interpretable Model for Large-Scale Smart Contract Vulnerability Detection. Blockchain Res. Appl. 2024, 5, 100209. [Google Scholar] [CrossRef]
- Wu, C.; Xiong, J.; Xiong, H.; Zhao, Y.; Yi, W. A Review on Recent Progress of Smart Contract in Blockchain. IEEE Access 2022, 10, 50839–50863. [Google Scholar] [CrossRef]
- Liu, B. Two-Thirds of EVM Smart Contract Deployments in 2024 Are from Optimism: Report, Blockworks. Available online: https://blockworks.co/news/evm-smart-contract-deployments-optimism (accessed on 12 June 2025).
- Abdelhamid, M.; Hassan, G. Blockchain and Smart Contracts. In Proceedings of the 2019 8th International Conference on Software and Information Engineering, Cairo, Egypt, 9–12 April 2019; ACM: New York, NY, USA, 2019; pp. 91–95. [Google Scholar] [CrossRef]
- Wu, G.; Wang, H.; Lai, X.; Wang, M.; He, D.; Chan, S. A Comprehensive Survey of Smart Contract Security: State of the Art and Research Directions. J. Netw. Comput. Appl. 2024, 226, 103882. [Google Scholar] [CrossRef]
- Cernera, F.; La Morgia, M.; Mei, A.; Sassi, F. Token Spammers, Rug Pulls, and Sniper Bots: An Analysis of the Ecosystem of Tokens in Ethereum and in the Binance Smart Chain (BNB). In Proceedings of the SEC’ 23: 32nd USENIX Conference on Security Symposium, Anaheim, CA, USA, 9–11 August 2023; pp. 3349–3366. Available online: https://www.usenix.org/system/files/usenixsecurity23-cernera.pdf (accessed on 25 August 2025).
- Kirlappos, I.; Sasse, M.A.; Harvey, N. Why Trust Seals Don’t Work: A Study of User Perceptions and Behavior. In Trust and Trustworthy Computing; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; pp. 308–324. [Google Scholar] [CrossRef]
- Turing, A.M. Computing Machinery and Intelligence. 1950. Available online: https://web.iitd.ac.in/~sumeet/Turing50.pdf (accessed on 12 June 2025).
- Momeni, P.; Wang, Y.; Samavi, R. Machine Learning Model for Smart Contracts Security Analysis. In Proceedings of the 2019 17th International Conference on Privacy, Security and Trust (PST), Fredericton, NB, Canada, 26–28 August 2019; IEEE: New York, NY, USA, 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Surucu, O.; Yeprem, U.; Wilkinson, C.; Hilal, W.; Gadsden, S.A.; Yawney, J.; Alsadi, N.; Giuliano, A. A Survey on Ethereum Smart Contract Vulnerability Detection Using Machine Learning. In Disruptive Technologies in Information Sciences VI; Blowers, M., Hall, R.D., Dasari, V.R., Eds.; SPIE: Bellingham, WA, USA, 2022; p. 12. Available online: https://www.spiedigitallibrary.org/conference-proceedings-of-spie/12117/2618899/A-survey-on-ethereum-smart-contract-vulnerability-detection-using-machine/10.1117/12.2618899.short (accessed on 12 June 2025).
- Huang, J.; Zhou, K.; Xiong, A.; Li, D. Smart Contract Vulnerability Detection Model Based on Multi-Task Learning. Sensors 2022, 22, 1829. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Wang, J.; Wang, W.; Jin, Z.; Su, Y.; Chen, H. Smart Contract Vulnerability Detection Combined with Multi-Objective Detection. Comput. Netw. 2022, 217, 109289. [Google Scholar] [CrossRef]
- Deng, W.; Wei, H.; Huang, T.; Cao, C.; Peng, Y.; Hu, X. Smart Contract Vulnerability Detection Based on Deep Learning and Multimodal Decision Fusion. Sensors 2023, 23, 7246. [Google Scholar] [CrossRef]
- Nguyen, H.H.; Nguyen, N.-M.; Xie, C.; Ahmadi, Z.; Kudendo, D.; Doan, T.-N.; Jiang, L. MANDO-HGT: Heterogeneous Graph Transformers for Smart Contract Vulnerability Detection. In Proceedings of the 2023 IEEE/ACM 20th International Conference on Mining Software Repositories (MSR), Melbourne, Australia, 15–16 May 2023; IEEE: New York, NY, USA, 2023; pp. 334–346. [Google Scholar] [CrossRef]
- Colin, L.S.H.; Mohan, P.M.; Pan, J.; Keong, P.L.K. An Integrated Smart Contract Vulnerability Detection Tool Using Multi-Layer Perceptron on Real-Time Solidity Smart Contracts. IEEE Access 2024, 12, 23549–23567. [Google Scholar] [CrossRef]
- Wang, W.; Song, J.; Xu, G.; Li, Y.; Wang, H.; Su, C. ContractWard: Automated Vulnerability Detection Models for Ethereum Smart Contracts. IEEE Trans. Netw. Sci. Eng. 2021, 8, 1133–1144. [Google Scholar] [CrossRef]
- Narayana, K.L.; Sathiyamurthy, K. Automation and Smart Materials in Detecting Smart Contracts Vulnerabilities in Blockchain Using Deep Learning. Mater. Today Proc. 2023, 81, 653–659. [Google Scholar] [CrossRef]
- Pour, F.G.; Costa, G.; Galletta, L. Welcome back: A systematic literature review of smart contract reentrancy and countermeasures. Blockchain Res. Appl. 2025, in press. [Google Scholar] [CrossRef]
- Liao, S.; Grishman, R. Using Document Level Cross-Event Inference to Improve Event Extraction. In Proceedings of the 48th Annual Meeting of the Association for Computational Linguistics (ACL ’10), Uppsala, Sweden, 11 July 2010; pp. 789–797. [Google Scholar]
- Zhang, Y.; Ge, C.; Hong, S.; Tian, R.; Dong, C.; Liu, J. DeleSmell: Code Smell Detection Based on Deep Learning and Latent Semantic Analysis. Knowl. Based Syst. 2022, 255, 109737. [Google Scholar] [CrossRef]
- Pearson, K. LIII. On Lines and Planes of Closest Fit to Systems of Points in Space. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1901, 2, 559–572. [Google Scholar] [CrossRef]
- Li, T.; Luo, Y.; Wan, X.; Li, Q.; Liu, Q.; Wang, R.; Jia, C.; Xiao, Y. A Malware Detection Model Based on Imbalanced Heterogeneous Graph Embeddings. Expert Syst. Appl. 2024, 246, 123109. [Google Scholar] [CrossRef]
- Nguyen, H.H.; Nguyen, N.M.; Xie, C.; Ahmadi, Z.; Kudendo, D.; Doan, T.N.; Jiang, L. MANDO: Multi-Level Heterogeneous Graph Embeddings for Fine-Grained Detection of Smart Contract Vulnerabilities. arXiv 2022, arXiv:2208.13252v2. [Google Scholar]
- Liang, C.; Wei, Q.; Du, J.; Wang, Y.; Jiang, Z. Survey of Source Code Vulnerability Analysis Based on Deep Learning. Comput. Secur. 2025, 148, 104098. [Google Scholar] [CrossRef]
- Rossini, M. Slither Audited Smart Contracts Dataset. Hugging Face. Available online: https://huggingface.co/datasets/mwritescode/slither-audited-smart-contracts (accessed on 12 June 2025).
- Ferreira, J.F. Smartbugs-Wild. GitHub. Available online: https://github.com/smartbugs/smartbugs-wild (accessed on 12 June 2025).
- Li, J.; Lu, G.; Gao, Y.; Gao, F. A Smart Contract Vulnerability Detection Method Based on Multimodal Feature Fusion and Deep Learning. Mathematics 2023, 11, 23. [Google Scholar] [CrossRef]
- Sun, Y.; Gu, L. Attention-Based Machine Learning Model for Smart Contract Vulnerability Detection. J. Phys. Conf. Ser. 2021, 1820, 012004. [Google Scholar] [CrossRef]
- Berti, A.; Bernasconi, A.; Del Corso, G.M.; Guidotti, R. The Role of Encodings and Distance Metrics for the Quantum Nearest Neighbor. Quantum Mach. Intell. 2024, 6, 62. [Google Scholar] [CrossRef]
- Ventura, D. Quantum Associative Memory. Inf. Sci. 2000, 124, 273–296. [Google Scholar] [CrossRef]
- Kak, S. On Quantum Neural Computing. Inf. Sci. 1995, 83, 143–160. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Dema, B.A.; Arai, J.; Horikawa, K. Support Vector Machine for Multiclass Classification Using Quantum Annealers. Proceedings of the DEIM Forum 2020, Online, 2–4 March 2020; pp. 1–6. Available online: https://proceedings-of-deim.github.io/DEIM2020/papers/F3-4.pdf (accessed on 22 April 2025).
- Blance, A.; Spannowsky, M. Quantum Machine Learning for Particle Physics Using a Variational Quantum Classifier. J. High Energy Phys. 2021, 2021, 212. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Srikumar, M.; Hill, C.D.; Hollenberg, L.C.L. A Kernel-Based Quantum Random Forest for Improved Classification. Quantum Mach. Intell. 2024, 6, 10. [Google Scholar] [CrossRef]
- Lachenbruch, P.A. McNemar Test. In Wiley StatsRef: Statistics Reference Online; John Wiley and Sons: Hoboken, NJ, USA, 2014. [Google Scholar] [CrossRef]
- Chandolu, S.B.; Praveen, S.P.; Tirumalasetti, N.R.; Swathi, K.; Sirisha, U. Enhancing Real-Time Malware Analysis with Quantum Neural Networks. J. Intell. Syst. Internet Things 2024, 12, 57–69. [Google Scholar] [CrossRef]
- Srinidhi, S.K.; Vishal, K.S.; Shashank, U.S.; Belwal, M. Quantum Machine Learning Compiler for Hybrid Quantum-Classical Models. In Proceedings of the 2024 15th International Conference on Computing Communication and Networking Technologies (ICCCNT), Kamand, India, 24–28 June 2024; IEEE: New York, NY, USA, 2024; pp. 1–9. [Google Scholar] [CrossRef]


| Symbol | Meaning | Dimension/Type |
|---|---|---|
| n | Number of smart contracts | Integer |
| m | Number of extracted opcode-level features | Integer |
| k | Number of principal components derived from PCA | Integer |
| X | Original feature matrix | |
| Feature mean vector | ||
| Xc | Mean-centered feature matrix | |
| Ʃ | Covariance matrix | |
| Eigenvalue, Eigenvector | ||
| W | PCA Projection matrix | |
| Z | Reduced feature matrix | |
| q | Number of qubits | Integer |
| θ | Trainable quantum circuit parameters | Real vector |
| Predicted output | Scalar | |
| yi | True label | Binary |
| TP, TN, FP, FN | Confusion matrix terms | Integer |
| Data | Dataset | Instances | Susceptibilities Included | ||||
|---|---|---|---|---|---|---|---|
| Gas Limit | Uninitialized Pointers | Access Control | Reentrancy | Overflow | |||
| Training | Slither dataset | 10,000 | Yes | Yes | Yes | Yes | Yes |
| Smartbugs dataset | 20,000 | Yes | Yes | Yes | Yes | Yes | |
| Audited dataset | 5000 | Yes | Yes | Yes | Yes | Yes | |
| Test | SolidiFI dataset | 9369 | No | Yes | No | Yes | Yes |
| Contract_ID | Bytecode | Susceptibility Identified |
|---|---|---|
| Contract_33 | 6080604052348015600e575f5ffd5b5060d580601a5f395ff3fe6080604052348015600e5..................................00081c0033 | Normal |
| Contract_390 | 6080604052348015600e575f5ffd5b5060ba80601a5f395ff3fe6080604052348015600e57...........................................634300081c0033 | Access control |
| Contract_959 | 6080604052348015600e575f5ffd5b506102268061001c5f395ff3fe60806040526004361061003....................................................4300081c0033 | Reentrancy |
| Contract_2854 | 6080604052348015600e575f5ffd5b50610219861001c5f395ff3fe608060405234801561000f57.........................................................00081c0033 | Gas limit |
| Contract_3750 | 6080604052348015600e575f5ffd5b506101218061001c5f395ff3fe6080604052348015600e57................................................634300081c0033 | Overflow |
| Parameters | Optimal Configuration |
|---|---|
| Layers of network | 3 |
| Optimizer | Adam |
| Batch size | 128 |
| Learning rate | 1 × 10−5 |
| Dropout estimate | 0.1 |
| Decay of learning rate | 0.97 |
| L2 regularization | 1 × 10−3 |
| Loss metric | Cross entropy |
| Parameters | Optimal Configuration |
|---|---|
| Regularization constant, C | 0.8 |
| No. of support vectors | 14 |
| Parameters | Optimal Configuration |
|---|---|
| Layers of network | 2 |
| Quantum gate | CNOT |
| Batch size | 64 |
| Number of qubits | 10 |
| Optimizer | Adam |
| Loss metric | Cross entropy |
| Parameters | Optimal Configuration |
|---|---|
| Number of decision trees | 220 |
| Maximum depth | 9 |
| Qubit count | 20 |
| Quantum gate | CNOT |
| Learning rate | 1 × 10−5 |
| QML Approach | Precision (%) | Accuracy (%) | Recall (%) | F1 Score (%) |
|---|---|---|---|---|
| QNN | 83.50 | 82.43 | 81.17 | 81.20 |
| QSVM | 68.20 | 65.98 | 63.00 | 64.50 |
| VQC | 61.00 | 62.41 | 63.30 | 55.50 |
| RF | 70.10 | 69.63 | 63.50 | 60.20 |
| Vulnerability | QML Model | Precision (%) | Accuracy (%) | Recall (%) |
|---|---|---|---|---|
| Gas limit | QNN | 82.90 | 81.55 | 79.80 |
| QSVM | 67.12 | 65.50 | 62.50 | |
| VQC | 60.50 | 61.12 | 61.80 | |
| QRF | 69.50 | 68.15 | 66.80 | |
| Uninitialized storage pointers | QNN | 83.20 | 82.10 | 81.00 |
| QSVM | 66.20 | 64.00 | 61.80 | |
| VQC | 62.50 | 61.90 | 60.00 | |
| QRF | 70.20 | 68.90 | 68.00 | |
| Access control | QNN | 84.00 | 82.80 | 81.00 |
| QSVM | 68.00 | 66.50 | 63.20 | |
| VQC | 62.50 | 61.90 | 60.00 | |
| QRF | 70.20 | 68.90 | 68.00 | |
| Reentrancy | QNN | 83.50 | 82.43 | 81.50 |
| QSVM | 67.50 | 66.00 | 63.00 | |
| VQC | 62.80 | 62.10 | 60.50 | |
| QRF | 70.50 | 69.20 | 68.20 | |
| Overflow | QNN | 83.40 | 82.25 | 81.20 |
| QSVM | 68.50 | 67.90 | 63.50 | |
| VQC | 63.00 | 62.41 | 60.20 | |
| QRF | 70.80 | 69.63 | 68.50 |
| Vulnerability Detector | Gas Limit | Uninitialized Storage Pointers | Access Control | Reentrancy |
|---|---|---|---|---|
| Mythril | 9 | 35 | 108 | 101 |
| Smartcheck | 0 | 28 | 92 | 82 |
| Slither | 35 | 66 | 198 | 300 |
| QNN | 65 | 89 | 225 | 351 |
| QSVM | 29 | 48 | 104 | 229 |
| VQC | 22 | 39 | 94 | 194 |
| QRF | 32 | 51 | 145 | 254 |
| Vulnerabilities | Models | Discordant Pairs, i.e., B | Continuity Correction, i.e., C | Chi-Square Estimate | p-Value | Difference in Accuracy |
|---|---|---|---|---|---|---|
| Gas limit | QNN and other QML variants | 3981 | 1 | 1873.92 | 0 | Most significant |
| Uninitialized storage pointer | 998 | 1 | 289.93 | 0 | Most significant | |
| Access control | 783 | 1 | 209.62 | 0 | Most significant | |
| Reentrancy | 2673 | 1 | 2341.89 | 0 | Extremely significant | |
| Overflow | 3 | 1 | 0 | 1 | Not significant |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sridhar, A.; Nagaraj, K.; Bangalore Ravi, S.; Kurup, S. Ascertaining Susceptibilities in Smart Contracts: A Quantum Machine Learning Approach. Entropy 2025, 27, 933. https://doi.org/10.3390/e27090933
Sridhar A, Nagaraj K, Bangalore Ravi S, Kurup S. Ascertaining Susceptibilities in Smart Contracts: A Quantum Machine Learning Approach. Entropy. 2025; 27(9):933. https://doi.org/10.3390/e27090933
Chicago/Turabian StyleSridhar, Amulyashree, Kalyan Nagaraj, Shambhavi Bangalore Ravi, and Sindhu Kurup. 2025. "Ascertaining Susceptibilities in Smart Contracts: A Quantum Machine Learning Approach" Entropy 27, no. 9: 933. https://doi.org/10.3390/e27090933
APA StyleSridhar, A., Nagaraj, K., Bangalore Ravi, S., & Kurup, S. (2025). Ascertaining Susceptibilities in Smart Contracts: A Quantum Machine Learning Approach. Entropy, 27(9), 933. https://doi.org/10.3390/e27090933






