Post-Quantum Security of COPA
Abstract
1. Introduction
- Post-quantum security demands joint guarantees for both privacy (IND-qCPA) and integrity (EUF-qCMA);
- NIST’s migration guidelines explicitly require quantum-resistant confidentiality;
- No prior work has established whether COPA’s encryption mechanism resists quantum plaintext recovery attacks.
- The first IND-qCPA security analysis of COPA in quantum settings, establishing its confidentiality guarantees under quantum chosen-plaintext attacks.
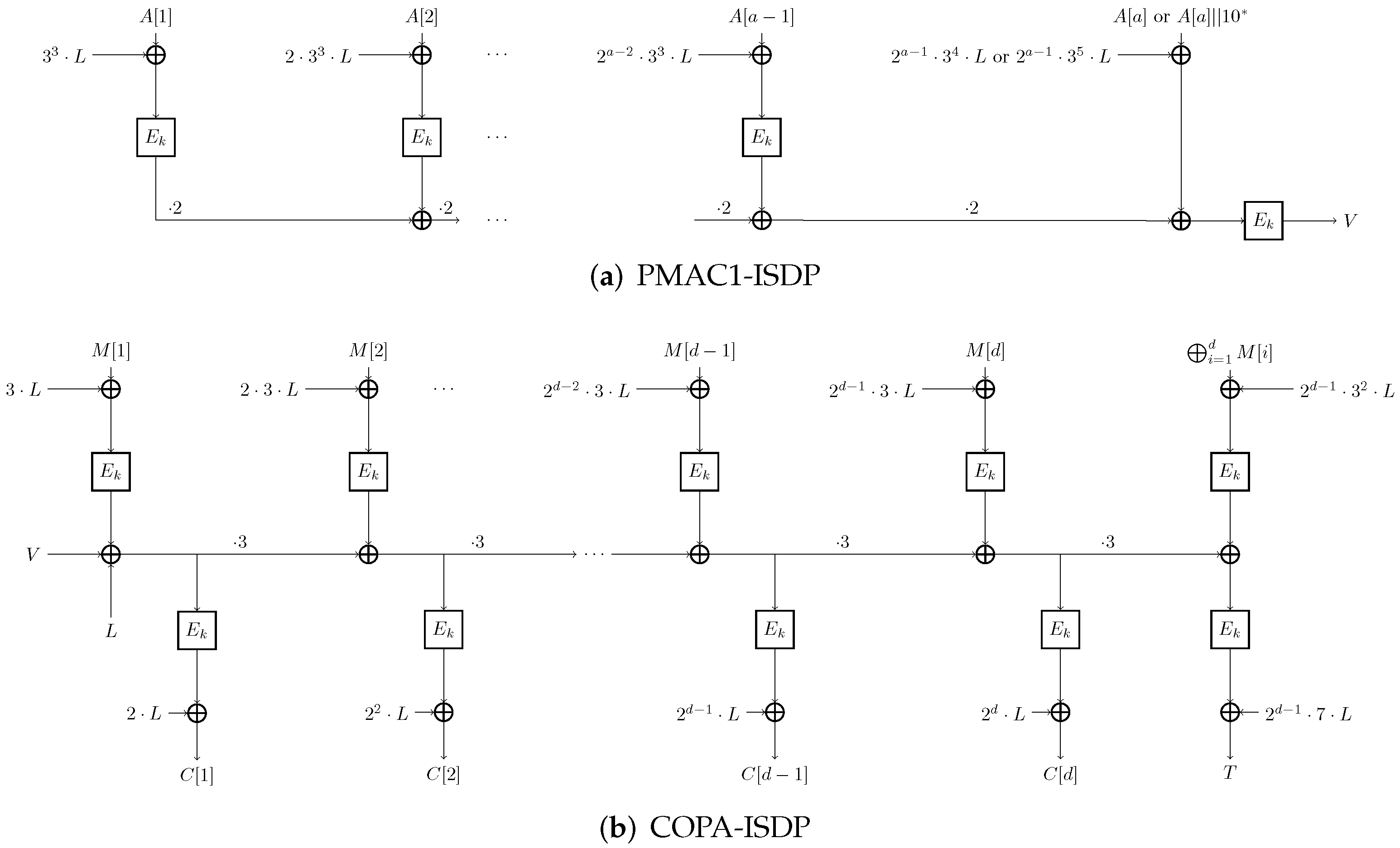
- COPA-ISDP: An enhanced variant achieving joint IND-qCPA and EUF-qCMA security via a mandatory non-empty associated data and a novel intermediate state doubling-point technique.
- Efficient security hardening that
- Preserves COPA’s parallelizability and efficiency.
- Breaks input/tag invariance using finite field double-multiplication.
- Mitigates quantum attacks (e.g., Simon’s algorithm).
- Distinct Security Goals: Confidentiality vs. Authenticity—Xu et al. (2021) [26] focused exclusively on EUF-qCMA security (authenticity), demonstrating how Simon’s algorithm can forge authentication tags via superposition queries. Our work addresses the critical gap they left: IND-qCPA security (confidentiality). We provide the first formal proof that COPA’s encryption mechanism fails to achieve IND-qCPA under quantum chosen-plaintext attacks. This establishes that COPA leaks plaintext information in quantum settings—a vulnerability that has not been addressed by prior work.
- Formalized Security Framework vs. Concrete Attacks—Xu et al. employed an attack-driven approach: They designed a specific quantum forgery attack but did not generalize COPA’s security properties. Our work develops a rigorous reductionist framework: We prove IND-qCPA insecurity via a game-based reduction to the quantum pseudorandom permutation (qPRP) security of the underlying block cipher (Section 3).
- Constructive Remedy with Provable Guarantees—Xu et al. exposed a vulnerability (authenticity), but they proposed no solution. In contrast, we introduce COPA-ISDP, an enhanced variant that achieves both IND-qCPA and EUF-qCMA security via intermediate state doubling-point and mandatory non-empty associated data. In addition, we provide joint security proofs for IND-qCPA and EUF-qCMA in the quantum random oracle model.
- Broader Impact: A Design Paradigm—Our work transcends COPA-specific analysis. The ISDP technique offers a generic countermeasure against quantum invariance attacks, and this is validated in our repair of COPA and can be extended to symmetric primitives.
2. Preliminaries
2.1. Basic Syntax
2.2. Quantum Circuit Models
2.3. Simon’s Algorithm
2.4. Quantum Security Models
- Key generation stage. and are randomly drawn by the challenge.
- Query stage. The quantum adversary is allowed to make two types of queries in any order.
- Encryption queries. The challenge first randomly chooses a nonce N and forwards it to . The adversary chooses a plaintext-AD pair in superposition, and the challenger encrypts with the classical nonce N and returns the output to .
- Challenge query. The challenger picks a random nonce N once more and forwards it to . Afterwards, chooses two same size classical plaintext-AD pairs and forwards them to the challenger, which in turn encrypts with the previous chosen classical nonce N. The output is returned to .
- Guess stage. The adversary decides whether is encrypted from or , outputs a bit , and wins if .
- Key generation stage. is randomly drawn by the challenge.
- Query stage. The quantum adversary is allowed to make encryption queries.
- Encryption queries. The challenge first randomly chooses a nonce N and forwards it to . The adversary chooses a plaintext–AD pair in superposition, and the challenger encrypts with the classical nonce N and returns the output to .
- Forgery stage. After making q encryption queries, produces classical tuples with any nonce N of its choice, and wins if, for each tuple, we have .
3. Quantum Attacks on COPA
3.1. Specifications of COPA
| Algorithm 1 PMAC1 Algorithm: |
Input: Key K and associated data A Output: MAC tag V if A is empty return else Partition A into , where for for to if else return V |
| Algorithm 2 The encryption algorithm: |
Input: Key K, associated data A, and plaintext M Output: Ciphertext C and tag T Partition M into , where for to d return |
| Algorithm 3 The decryption algorithm: |
Input: Key K, associated data A, ciphertext C, and tag T Output: Plaintext M or ⊥ Partition C into , where for to d if return M else return ⊥ |
3.2. IND-qCPA Security Analysis of COPA
3.3. EUF-qCMA Security Analysis of COPA
4. COPA-ISDP: COPA with Intermediate-State Doubling Point
| Algorithm 4 PMAC1-ISDP Algorithm: |
Input: Key K and associated data A Output: MAC tag V Partition A into , where for to if else return V |
| Algorithm 5 The encryption algorithm: |
Input: Key K, associated data A, and plaintext M Output: Ciphertext C and tag T Partition M into , where for to d return |
| Algorithm 6 The decryption algorithm: |
Input: Key K, associated data A, ciphertext C, and tag T Output: Plaintext M or ⊥ Partition C into , where for to d if return M else return ⊥ |
5. Conclusions and Future Work
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shor, P.W. Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. SIAM J. Comput. 1997, 26, 1484–1509. [Google Scholar] [CrossRef]
- Simon, D.R. On the Power of Quantum Computation. SIAM J. Comput. 1997, 26, 1474–1483. [Google Scholar] [CrossRef]
- Xie, H.; Yang, L. Using Bernstein-Vazirani algorithm to attack block ciphers. Des. Codes Cryptogr. 2019, 87, 1161–1182. [Google Scholar] [CrossRef]
- Qiu, D.; Zheng, S. Revisiting Deutsch-Jozsa algorithm. Inf. Comput. 2020, 275, 104605. [Google Scholar] [CrossRef]
- Leander, G.; May, A. Grover Meets Simon—Quantumly Attacking the FX-construction. In Proceedings of the Advances in Cryptology—ASIACRYPT 2017—23rd International Conference on the Theory and Applications of Cryptology and Information Security, Hong Kong, China, 3–7 December 2017; Proceedings, Part II, Lecture Notes in Computer Science. Takagi, T., Peyrin, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; Volume 10625, pp. 161–178. [Google Scholar] [CrossRef]
- Guo, T.; Wang, P.; Hu, L.; Ye, D. Attacks on Beyond-Birthday-Bound MACs in the Quantum Setting. In Proceedings of the Post-Quantum Cryptography—12th International Workshop, PQCrypto 2021, Daejeon, Republic of Korea, 20–22 July 2021; Proceedings, Lecture Notes in Computer Science. Cheon, J.H., Tillich, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2021; Volume 12841, pp. 421–441. [Google Scholar] [CrossRef]
- Kuperberg, G. A Subexponential-Time Quantum Algorithm for the Dihedral Hidden Subgroup Problem. SIAM J. Comput. 2005, 35, 170–188. [Google Scholar] [CrossRef]
- Bonnetain, X.; Hosoyamada, A.; Naya-Plasencia, M.; Sasaki, Y.; Schrottenloher, A. Quantum Attacks Without Superposition Queries: The Offline Simon’s Algorithm. In Proceedings of the Advances in Cryptology—ASIACRYPT 2019—25th International Conference on the Theory and Application of Cryptology and Information Security, Kobe, Japan, 8–12 December 2019; Proceedings, Part I, Lecture Notes in Computer Science. Galbraith, S.D., Moriai, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; Volume 11921, pp. 552–583. [Google Scholar] [CrossRef]
- Dong, X.; Wang, X. Quantum key-recovery attack on Feistel structures. Sci. China Inf. Sci. 2018, 61, 102501:1–102501:7. [Google Scholar] [CrossRef]
- Dong, X.; Dong, B.; Wang, X. Quantum attacks on some feistel block ciphers. Des. Codes Cryptogr. 2020, 88, 1179–1203. [Google Scholar] [CrossRef]
- Cui, J.; Guo, J.; Ding, S. Applications of Simon’s algorithm in quantum attacks on Feistel variants. Quantum Inf. Process. 2021, 20, 117. [Google Scholar] [CrossRef]
- Ni, B.; Ito, G.; Dong, X.; Iwata, T. Quantum Attacks Against Type-1 Generalized Feistel Ciphers and Applications to CAST-256. In Proceedings of the Progress in Cryptology—INDOCRYPT 2019—20th International Conference on Cryptology in India, Hyderabad, India, 15–18 December 2019; Proceedings, Lecture Notes in Computer Science. Hao, F., Ruj, S., Gupta, S.S., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; Volume 11898, pp. 433–455. [Google Scholar] [CrossRef]
- Alagic, G.; Bai, C.; Katz, J.; Majenz, C. Post-quantum security of the Even-Mansour cipher. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Trondheim, Norway, 30 May–3 June 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 458–487. [Google Scholar]
- Alagic, G.; Bai, C.; Katz, J.; Majenz, C.; Struck, P. Post-quantum Security of Tweakable Even-Mansour, and Applications. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zurich, Switzerland, 26–30 May 2024; Springer: Berlin/Heidelberg, Germany, 2024; pp. 310–338. [Google Scholar]
- Bai, C.; Esmaili, M.; Mantri, A. Quantum Security Analysis of the Key-Alternating Ciphers. IACR Cryptology ePrint Archive 2025, 945. [Google Scholar]
- Hosoyamada, A.; Iwata, T. Provably Quantum-Secure Tweakable Block Ciphers. IACR Trans. Symmetric Cryptol. 2021, 2021, 337–377. [Google Scholar] [CrossRef]
- Kaplan, M.; Leurent, G.; Leverrier, A.; Naya-Plasencia, M. Breaking Symmetric Cryptosystems Using Quantum Period Finding. In Proceedings of the Advances in Cryptology—CRYPTO 2016—36th Annual International Cryptology Conference, Santa Barbara, CA, USA, 14–18 August 2016; Proceedings, Part II, Lecture Notes in Computer Science. Robshaw, M., Katz, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; Volume 9815, pp. 207–237. [Google Scholar] [CrossRef]
- Bhaumik, R.; Bonnetain, X.; Chailloux, A.; Leurent, G.; Naya-Plasencia, M.; Schrottenloher, A.; Seurin, Y. QCB: Efficient quantum-secure authenticated encryption. In Proceedings of the Advances in Cryptology–ASIACRYPT 2021: 27th International Conference on the Theory and Application of Cryptology and Information Security, Singapore, 6–10 December 2021; Proceedings, Part I 27. Springer: Berlin/Heidelberg, Germany, 2021; pp. 668–698. [Google Scholar]
- Maram, V.; Masny, D.; Patranabis, S.; Raghuraman, S. On the quantum security of OCB. IACR Trans. Symmetric Cryptol. 2022, 2022, 379–414. [Google Scholar] [CrossRef]
- Zhang, M.; Wu, W.; Sui, H. Quantum IND-CPA Security Notions for AEAD. In Proceedings of the Post-Quantum Cryptography—16th International Workshop, PQCrypto 2025, Taipei, Taiwan, 8–10 April 2025; Proceedings, Part II, Lecture Notes in Computer Science. Niederhagen, R., Saarinen, M.O., Eds.; Springer: Berlin/Heidelberg, Germany, 2025; Volume 15578, pp. 195–230. [Google Scholar] [CrossRef]
- Hosoyamada, A. Post-Quantum Security of Keyed Sponge-Based Constructions through a Modular Approach. IACR Cryptology ePrint Archive 2025, 1059. [Google Scholar]
- Lang, N.; Lucks, S. On the Post-quantum Security of Classical Authenticated Encryption Schemes. In Proceedings of the Progress in Cryptology—AFRICACRYPT 2023—14th International Conference on Cryptology in Africa, Sousse, Tunisia, 19–21 July 2023; Proceedings, Lecture Notes in Computer Science. Mrabet, N.E., Feo, L.D., Duquesne, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2023; Volume 14064, pp. 79–104. [Google Scholar] [CrossRef]
- Anand, M.V.; Targhi, E.E.; Tabia, G.N.; Unruh, D. Post-Quantum Security of the CBC, CFB, OFB, CTR, and XTS Modes of Operation. In Proceedings of the Post-Quantum Cryptography—7th International Workshop, PQCrypto 2016, Fukuoka, Japan, 24–26 February 2016; Proceedings, Lecture Notes in Computer Science. Takagi, T., Ed.; Springer: Berlin/Heidelberg, Germany, 2016; Volume 9606, pp. 44–63. [Google Scholar] [CrossRef]
- Nan, J.; Hu, H.; Zhang, P.; Luo, Y. Quantum attacks against BBB secure PRFs or MACs built from public random permutations. Quantum Inf. Process. 2023, 22, 26. [Google Scholar] [CrossRef]
- Andreeva, E.; Bogdanov, A.; Luykx, A.; Mennink, B.; Tischhauser, E.; Yasuda, K. Parallelizable and Authenticated Online Ciphers. In Proceedings of the Advances in Cryptology—ASIACRYPT 2013—19th International Conference on the Theory and Application of Cryptology and Information Security, Bengaluru, India, 1–5 December 2013; Proceedings, Part I, Lecture Notes in Computer Science. Sako, K., Sarkar, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 8269, pp. 424–443. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, W.; Yu, W. Quantum forgery attacks on COPA, AES-COPA and marble authenticated encryption algorithms. Quantum Inf. Process. 2021, 20, 131. [Google Scholar] [CrossRef]
- Zhandry, M. A note on the quantum collision and set equality problems. Quantum Inf. Comput. 2015, 15, 557–567. [Google Scholar] [CrossRef]
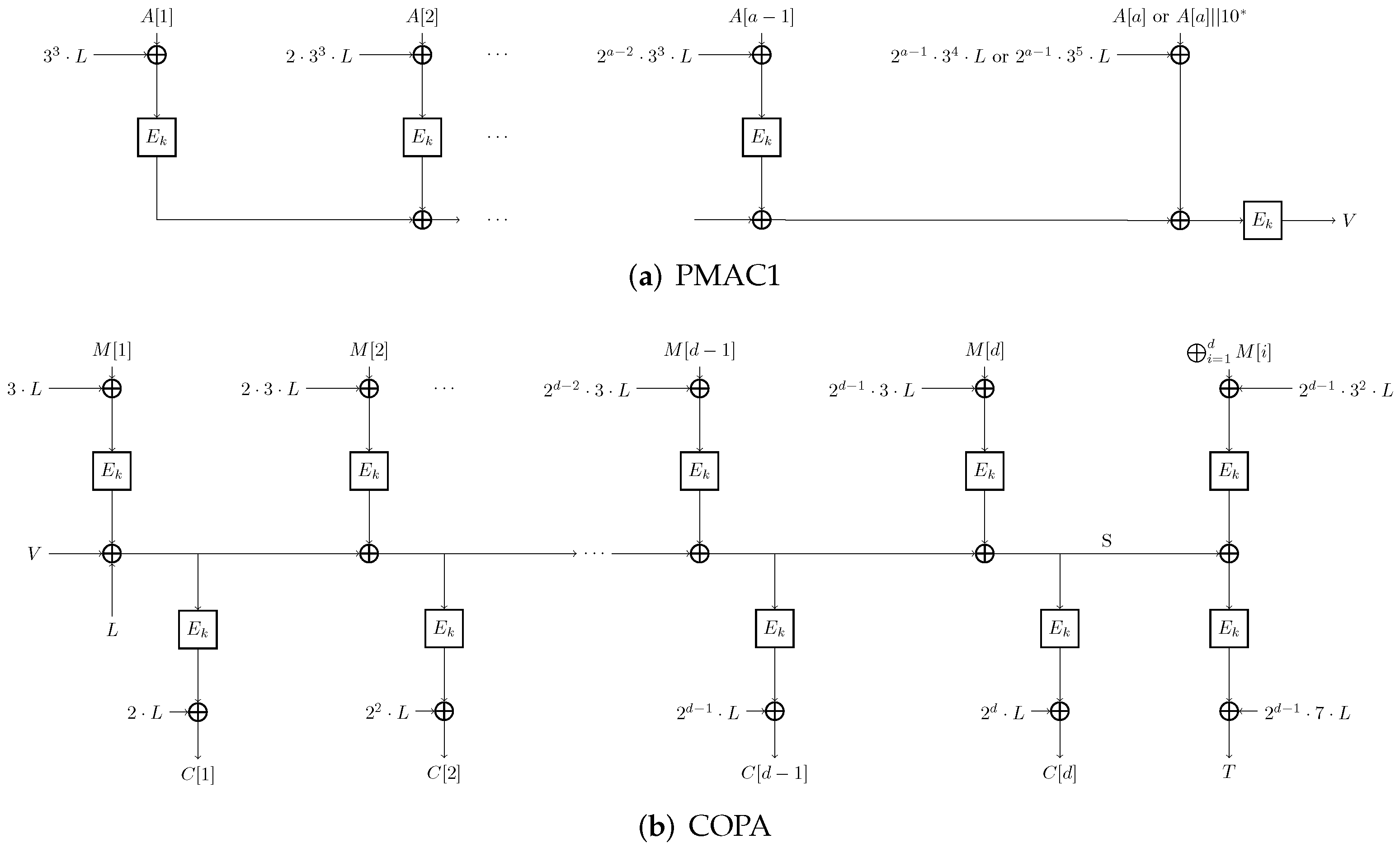
| Aspect | Xu et al.’s Work [26] | Our Work |
|---|---|---|
| Security Focus | EUF-qCMA only | IND-qCPA + EUF-qCMA |
| Methodology | Concrete attack | Formal reduction proofs |
| Technical Contribution | Vulnerability demonstration | Provably secure construction |
| Security Guarantees | Attack-specific | Generalized bounds |
| Practical Impact | Highlighted problem | Solution + design paradigm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Wang, Y. Post-Quantum Security of COPA. Entropy 2025, 27, 890. https://doi.org/10.3390/e27090890
Zhang P, Wang Y. Post-Quantum Security of COPA. Entropy. 2025; 27(9):890. https://doi.org/10.3390/e27090890
Chicago/Turabian StyleZhang, Ping, and Yutao Wang. 2025. "Post-Quantum Security of COPA" Entropy 27, no. 9: 890. https://doi.org/10.3390/e27090890
APA StyleZhang, P., & Wang, Y. (2025). Post-Quantum Security of COPA. Entropy, 27(9), 890. https://doi.org/10.3390/e27090890






