1. Introduction
In the field of statistical distribution theory, the practice of introducing additional parameters to existing distribution families has become widespread and highly valuable. By adding an extra parameter, statisticians are able to significantly enhance the flexibility of the underlying models, allowing them to better capture complex data patterns and provide improved fits to a variety of real-world phenomena. This approach not only enriches the mathematical structure of distributions but also extends their practical applications across numerous scientific and engineering disciplines.
Since the 1980s, the development of new probability distributions has largely focused on two principal strategies: one is the combination of existing distributions to create entirely new families and the other is the extension of classical distributions by introducing one or more extra parameters. The former method offers a way to blend the strengths of different models, while the latter provides a systematic enhancement of a given model’s flexibility without altering its core characteristics.
Adding new parameters often allows distributions to adapt to a broader range of shapes, including skewed, heavy-tailed or multi-modal data structures, which are frequently encountered in practice. Such improvements make the extended models particularly useful for applications in fields like survival analysis, reliability engineering, finance, environmental studies and biomedical research. Moreover, these extended families maintain a close connection to the baseline distributions, ensuring that the original models remain special or limiting cases within the new, more general, framework.
Overall, the introduction of additional parameters into existing distribution families continues to be a powerful and essential technique in statistical modeling. It not only broadens the theoretical landscape of probability distributions but also significantly enhances their practical utility in analyzing and interpreting real-world data.
One of the earliest and most fundamental techniques for generating new probability distributions was introduced in Reference [
1], which proposed the exponentiated family of distributions. This approach enhances a baseline distribution by introducing an additional shape parameter, thereby increasing its flexibility to model a wider variety of data patterns. It is widely acknowledged that no single probability model consistently provides the best fit across all real-world scenarios. As a result, various fields in statistics continually seek to develop new probability models tailored to specific needs. Modified or newly developed distributions often offer better fitting capabilities compared to existing models, which motivates researchers to explore novel distributions applicable across diverse areas. The cumulative distribution function (CDF) of the exponentiated family is given by
Here,
serves as an additional shape parameter and
represents the CDF of the baseline random variable with parameter vector
. The inclusion of this extra parameter enhances the classical distributions’ ability to better capture complex real-world phenomena.
Building on this idea, Reference [
2] introduced the Marshall–Olkin family of distributions, aimed at further improving the flexibility of existing models. Their transformation modifies the baseline CDF using the parameter
, resulting in the following CDF:
This transformation offers better control over the tail behavior of distributions, making it particularly useful in reliability and risk analysis.
To introduce greater flexibility in probability modeling, Reference [
3] proposed the alpha-power transformation (APT), which incorporates a new parameter
into the baseline distribution
. The properties of the exponential distribution under this transformation were discussed as a special case. The CDF of the APT family is given by
Further enhancing flexibility, Reference [
4] introduced the MIT transformation, which modifies a given baseline CDF by introducing a shape parameter
. Under the MIT framework, the transformed CDF is expressed as
Additionally, Reference [
5] applying the T-X family methodology from [
6], proposed the new exponent power-X (NGEP-X) family of distributions to generate more flexible probability models. The cumulative distribution function (CDF) of the NGEP-X family is given by
In recent developments, researchers have increasingly explored trigonometric transformations in constructing new distributions. For instance, Reference [
7] introduced a trigonometric function-based family of distributions, where a trigonometric function inside the exponent transforms the baseline distribution. The corresponding CDF is given by
Continuing in this direction, Reference [
8] introduced a flexible family of distributions designed to better model skewed and heavy-tailed data, offering robust alternatives to classical models, especially in engineering and medical sciences. The corresponding CDF is given by
Moreover, Reference [
9] introduced the Zubair-G family of distributions, with the CDF defined as
Similarly, Reference [
10] proposed the modified alpha-power exponential (MAPE) distribution, with the CDF given by
The extended alpha-power-transformed (Ex-APT) family, introduced in [
11], has its CDF expressed as
Finally, Reference [
12] proposed the alpha–beta power-E (ABPE) transformation method, with the CDF given by
Extending recent developments in probability distribution generation, this study proposes the novel and versatile novel alpha-power X (NAP-X) family. Traditional enhancement techniques often introduce additional shape parameters, potentially leading to parameter redundancy, increased complexity and difficulties in interpretation and implementation. The NAP-X framework strategically overcomes these limitations by providing enhanced distributional flexibility without unnecessary parameter inflation.
The NAP-X family is a transformation-based framework that systematically modifies baseline distributions to achieve superior adaptability. Unlike conventional methods relying on direct parameter expansion, it employs a controlled transformation mechanism to adjust shape and tail behavior. This enables the efficient modeling of both symmetric and asymmetric data patterns, making it a powerful tool for complex real-world phenomena across diverse fields.
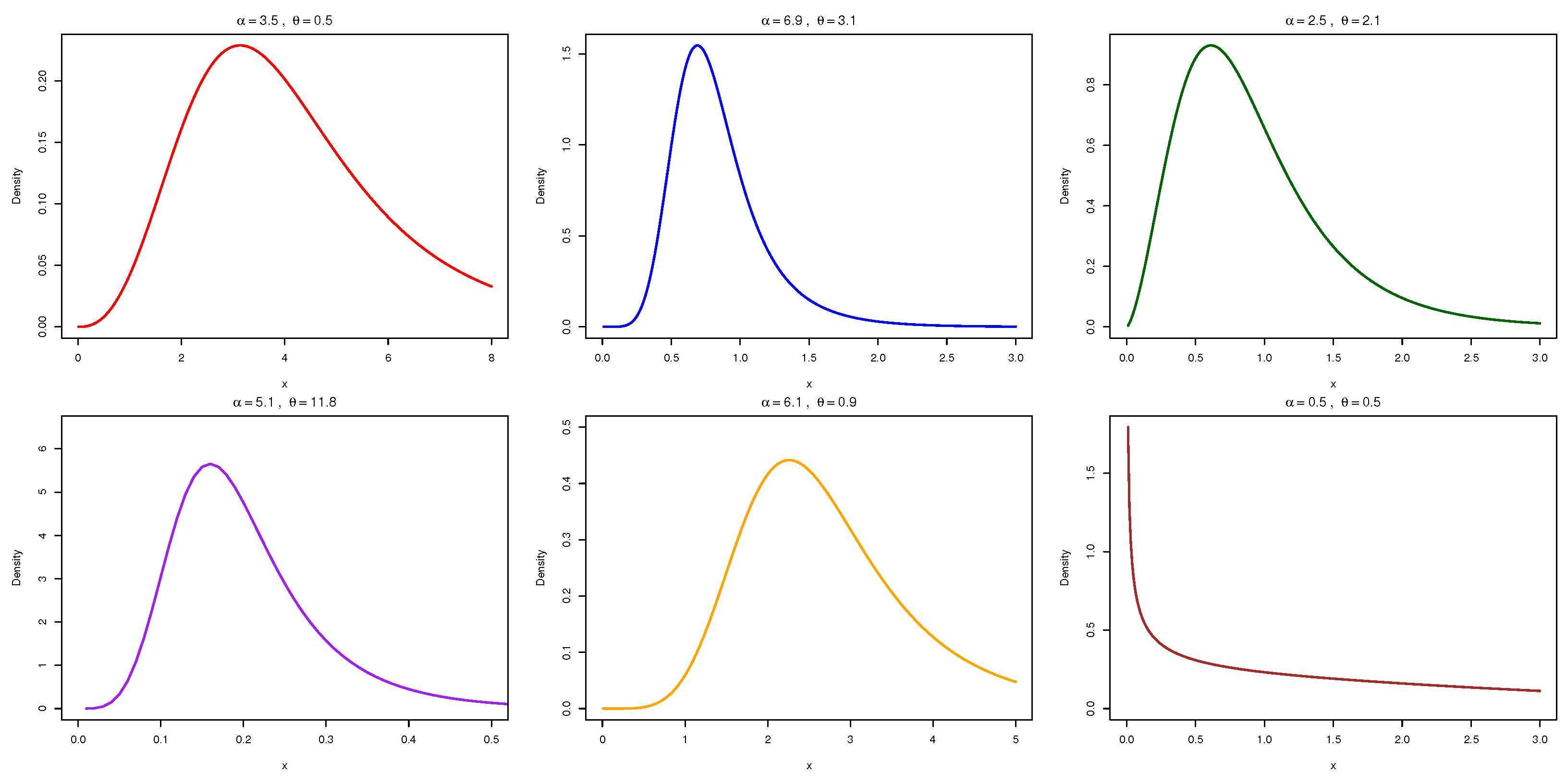
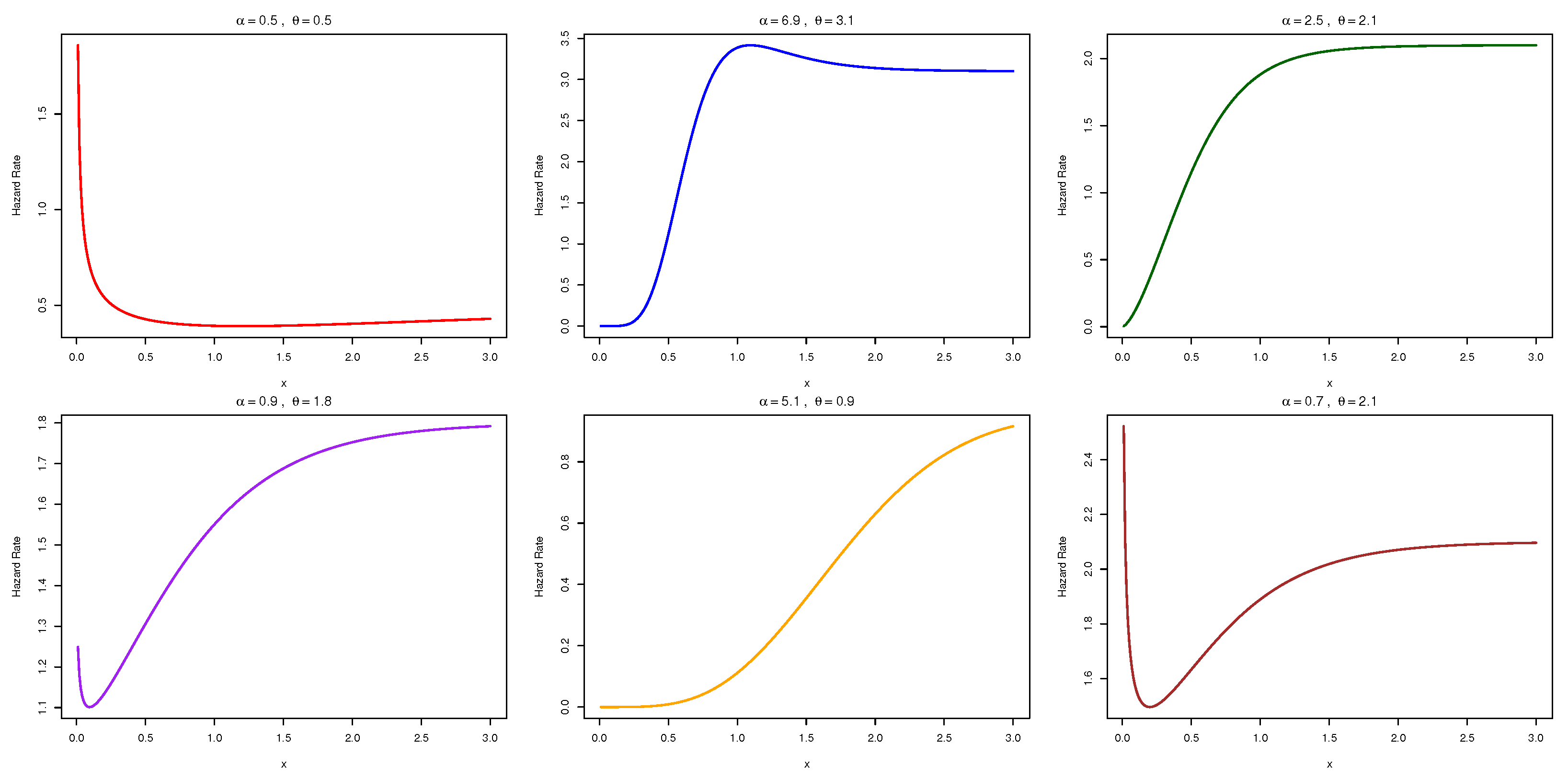
As a specific illustration, we derive a modified half-logistic distribution via the NAP-X transformation. This model demonstrates enhanced performance, particularly in its probability density function (PDF) and hazard rate function (HRF). Comprehensive comparisons with established models—including the alpha-power exponential and Marshall–Olkin exponential distributions—using standard metrics (AIC, BIC, AICC, HQIC, K-S statistics) consistently show the superior flexibility and goodness of fit of the NAP-X model, detailed in the applications sections.
Overall, the NAP-X family preserves the theoretical elegance of classical distributions while offering a robust mechanism for capturing diverse data patterns. Its effective handling of symmetry and asymmetry renders it highly suitable for reliability analysis, survival studies, biomedical research and engineering systems.
The manuscript is structured as follows:
Section 2: Presents the motivation behind this study and highlights the research gap addressed by the proposed NAP-X family of distributions.
Section 3: Introduces the novel alpha-power X (NAP-X) family of distributions and its special case, the NAP-HL model, along with key mathematical properties.
Section 4: Discusses parameter estimation using seven classical estimation techniques.
Section 5: Conducts a comprehensive Monte Carlo simulation study to evaluate and compare the performance of the proposed estimators across varying sample sizes.
Section 6: Validates the practical applicability of the NAP-HL model through real-world datasets.
Section 7: Concludes the manuscript with major contributions, findings and directions for future research.
A defining feature of the NAP-X family is its introduction of a shape parameter to generalize baseline distributions. This parameter enables the modeling of diverse behaviors such as skewness, varying tail weights and flexible hazard rate shapes, often inadequately captured by standard models. Crucially, the baseline distribution is retained as the special case when , ensuring the NAP-X family is a true generalization that preserves baseline properties while offering enhanced flexibility. This makes it particularly valuable for survival analysis, reliability studies and industrial data modeling.
2. Motivation and Research Gap
The advancement of statistical modeling, particularly in reliability and survival analysis, has led to the creation of numerous flexible probability distributions. These models aim to better capture real-world data behavior, especially in terms of skewness, kurtosis and hazard rate dynamics. A popular method to achieve flexibility involves transforming existing baseline distributions using functional techniques such as the exponentiated, Marshall–Olkin, alpha-power, beta-generated and transmutation approaches.
While these approaches have yielded substantial improvements in model fitting, they often come at the cost of excessive parameterization. The addition of multiple parameters can lead to interpretational difficulties, overfitting, numerical instability in estimation and challenges in model selection. Furthermore, many classical transformations lack the ability to simultaneously control symmetry and tail behavior in a simple yet effective manner.
In particular, the alpha-power transformation, despite its wide applicability, has limited structural flexibility when applied directly. It modifies tail behavior but does not consistently enhance hazard rate shapes or allow symmetric modeling. Moreover, transformations such as the Marshall–Olkin method tend to create abrupt changes in distribution structure, which may not be suitable for gradual changes observed in empirical data.
To address these limitations, there is a need for a new transformation technique with the following properties:
Enhances baseline distributions while maintaining parsimony (i.e., minimal parameter addition);
Improves flexibility in modeling both symmetric and asymmetric data;
Provides a wide variety of hazard rate shapes;
Is adaptable to various fields such as bio-statistics, engineering and economics.
This motivates the development of the novel alpha-power X (NAP-X) family of distributions, which generalizes the alpha-power transformation in a more structurally sound and application friendly manner. Unlike conventional methods, the NAP-X transformation introduces a shape control mechanism that modifies the baseline distribution with minimal structural disruption and parameter inflation. The resulting family offers significant improvements in terms of fitting ability, interpretability and applicability to real-life datasets.
7. Concluding Remarks
Continuous data in many disciplines demand more flexible lifetime models than those offered by the classical half-logistic law. We introduce the NAP-HL (novel alpha-power half-logistic) distribution, a three-parameter extension that embeds a shape control into the standard half-logistic form. By adjusting this shape parameter, the NAP-HL model can produce increasing, decreasing, or bathtub-shaped hazard rates, thus capturing a wide range of real-world aging and failure behaviors.
We derive closed-form expressions for the main characteristics of the NAP-HL model—moments, quantile function, and hazard function—highlighting how the added flexibility emerges from the exponentiation mechanism. A comprehensive Monte Carlo study compares seven estimation methods revealing their relative performance under different sample sizes and true parameter settings.
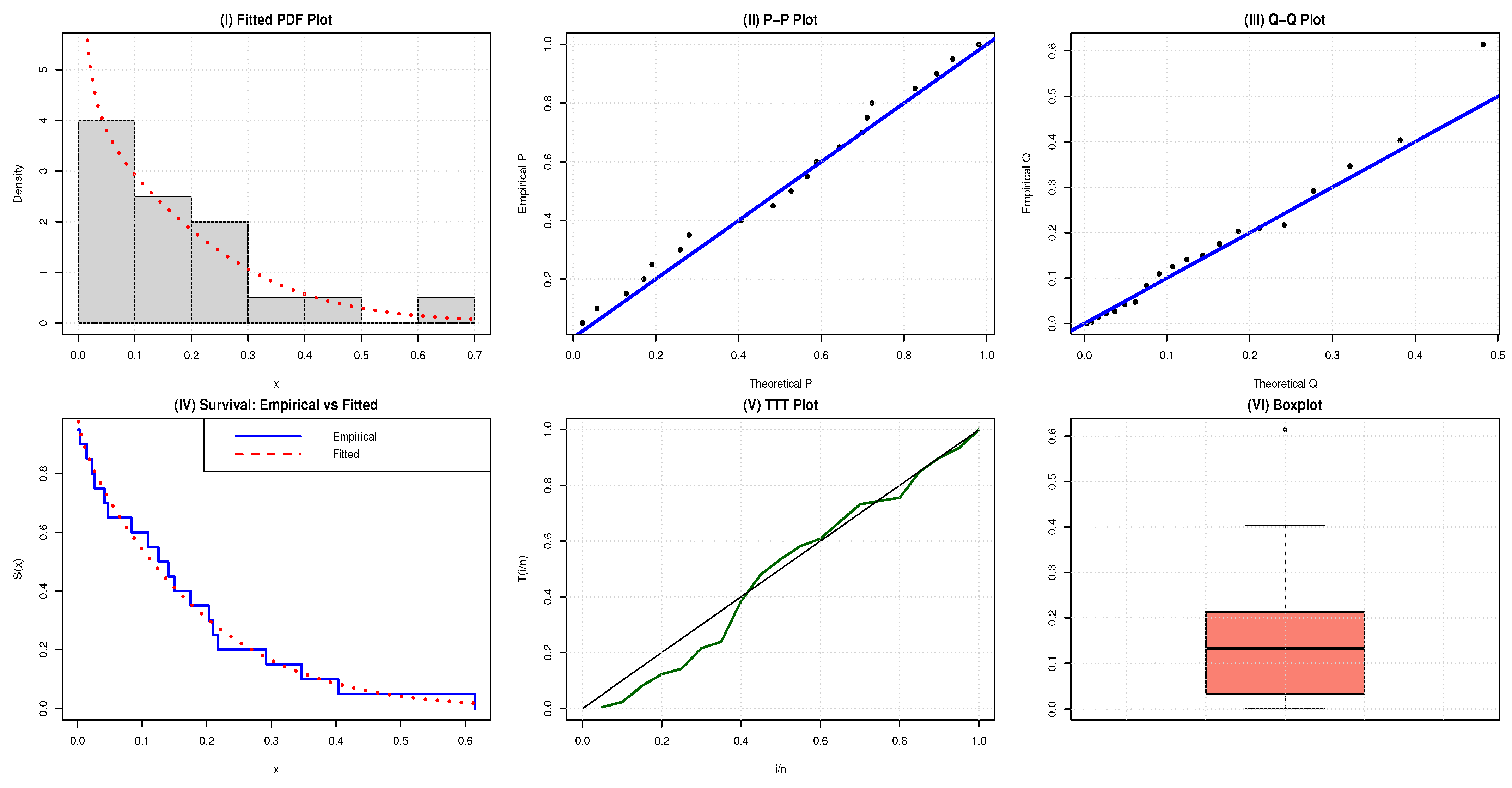
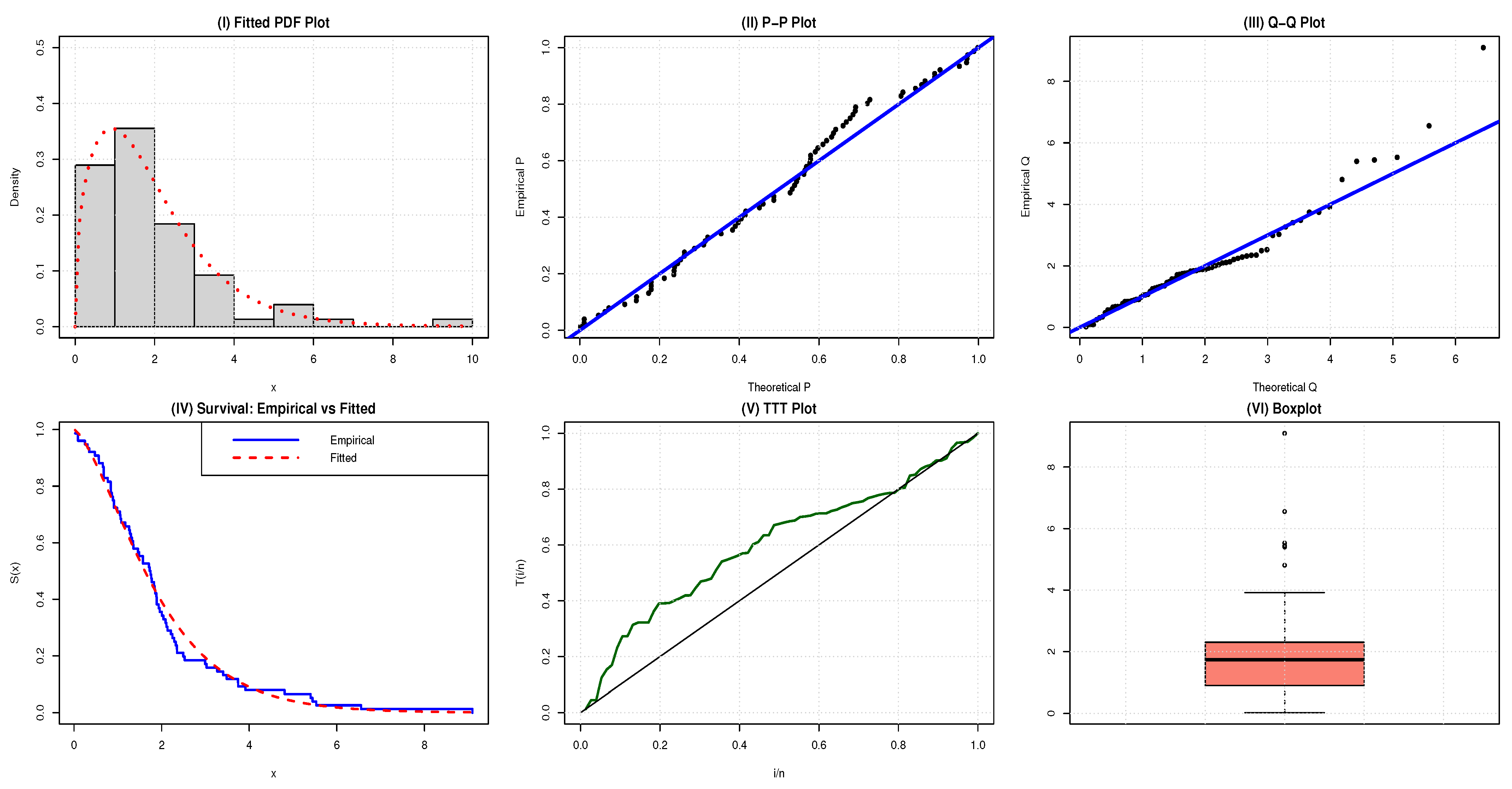
To assess empirical usefulness, we fit the NAP-HL model to two benchmark datasets: a metrology and an engineering dataset. In every case, the NAP-HL model achieves lower AIC and BIC and superior goodness-of-fit statistics (AD, CvM, K-S) than its half-logistic precursor and several competing families.
Future work will extend the NAP-HL model into regression frameworks, accommodate censored and truncated data streams, explore Bayesian estimation for small samples, and integrate with machine learning pipelines for large-scale predictive analytics. Such enhancements promise to make the NAP-HL model a go-to model for complex reliability and survival analysis tasks.