Quasi-Discrete Time Crystals in the Quasiperiodically Driven Lipkin–Meshkov–Glick Model
Abstract
1. Introduction
2. Model and DTC Dynamics
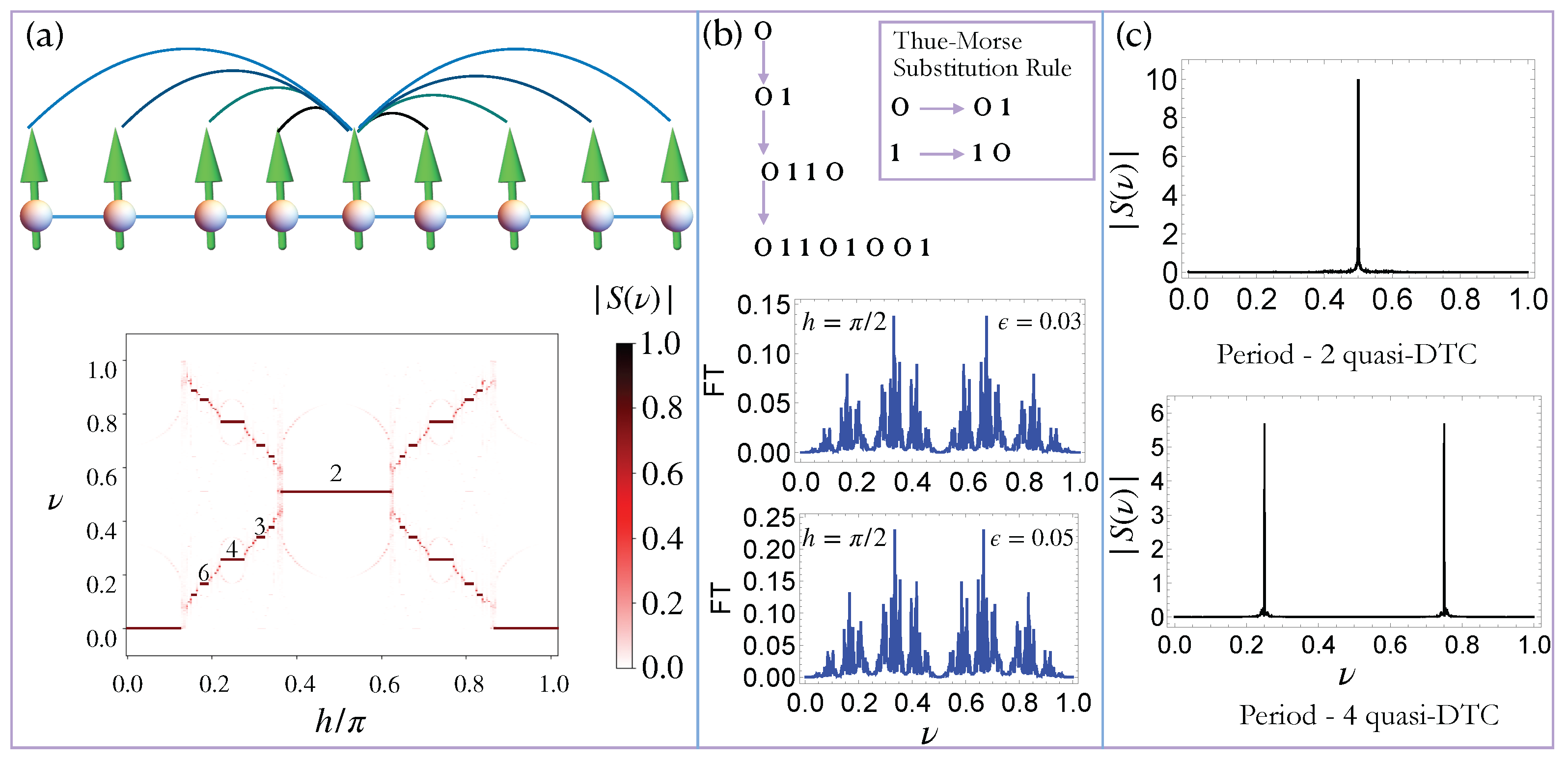
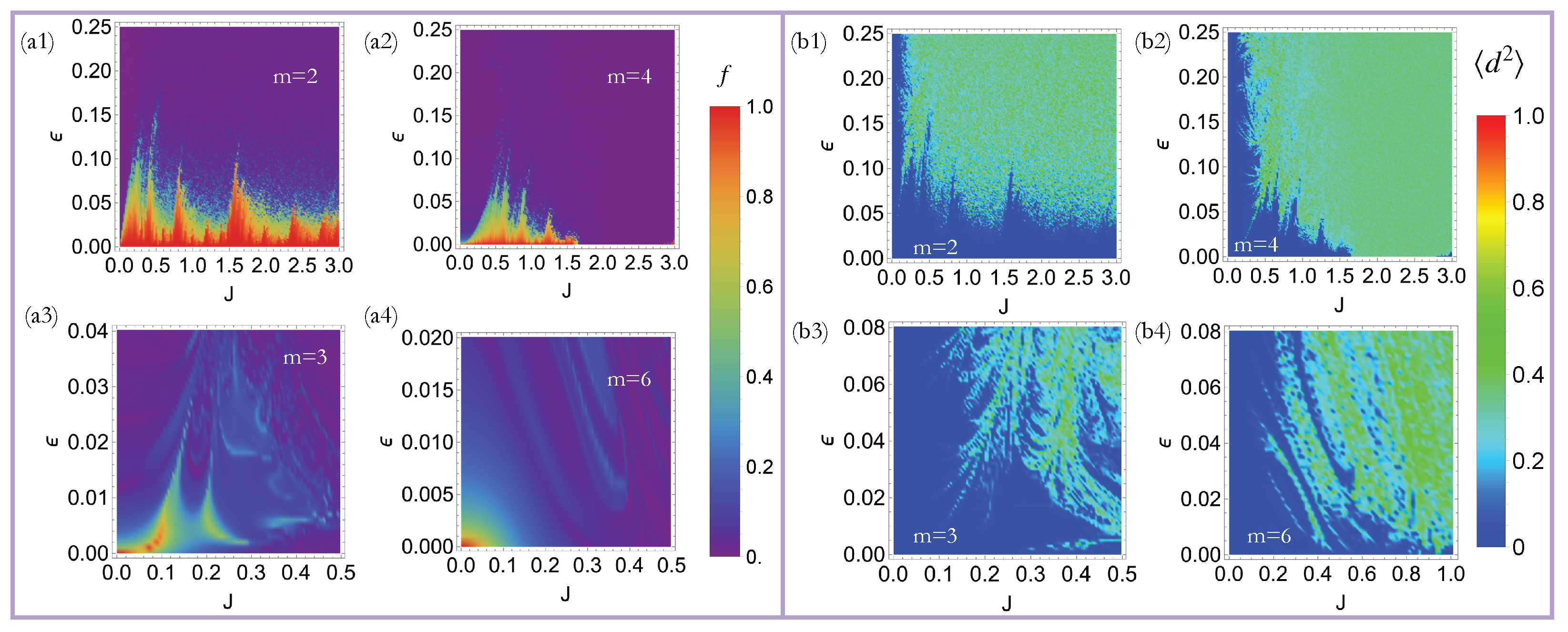
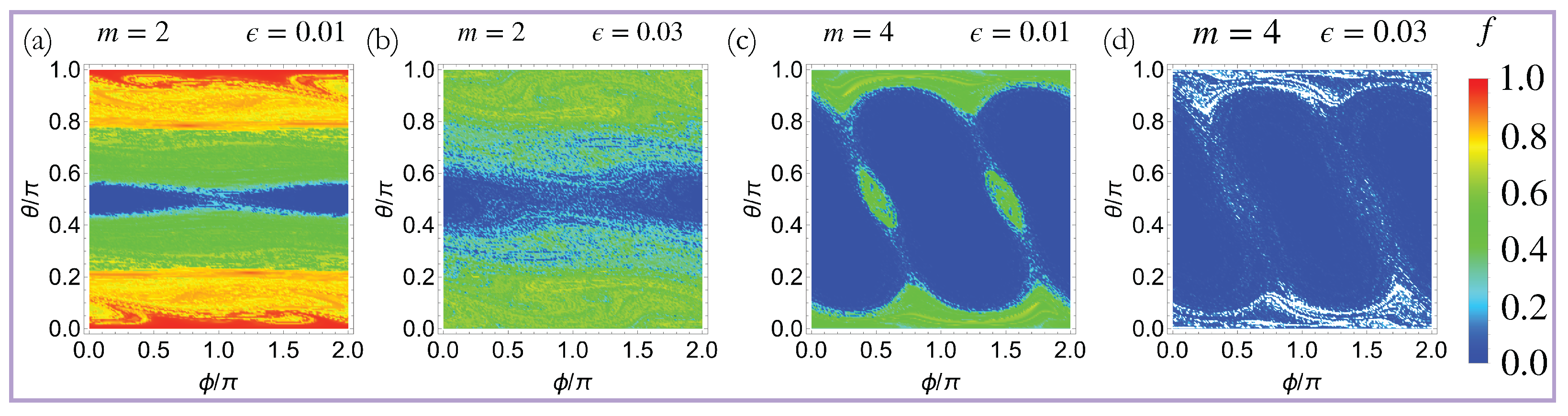
3. Thue–Morse Driving and Quasi-DTC Dynamics
4. Potential Experimental Realizations
5. Summary and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Eckardt, A.; Weiss, C.; Holthaus, M. Superfluid-insulator transition in a periodically driven optical lattice. Phys. Rev. Lett. 2005, 95, 260404. [Google Scholar] [CrossRef] [PubMed]
- Holthaus, M. Floquet engineering with quasienergy bands of periodically driven optical lattices. J. Phys. B 2015, 49, 013001. [Google Scholar] [CrossRef]
- Bukov, M.; D’Alessio, L.; Polkovnikov, A. Universal high-frequency behavior of periodically driven systems: From dynamical stabilization to Floquet engineering. Adv. Phys. 2015, 64, 139–226. [Google Scholar] [CrossRef]
- Oka, T.; Kitamura, S. Floquet engineering of quantum materials. Annu. Rev. Condens. Matter Phys. 2019, 10, 387–408. [Google Scholar] [CrossRef]
- Moessner, R.; Sondhi, S.L. Equilibration and order in quantum Floquet matter. Nat. Phys. 2017, 13, 424–428. [Google Scholar] [CrossRef]
- Eckardt, A. Colloquium: Atomic quantum gases in periodically driven optical lattices. Rev. Mod. Phys. 2017, 89, 011004. [Google Scholar] [CrossRef]
- Rudner, M.S.; Lindner, N.H. Band structure engineering and non-equilibrium dynamics in Floquet topological insulators. Nat. Rev. Phys. 2020, 2, 229–244. [Google Scholar] [CrossRef]
- Sacha, K.; Zakrzewski, J. Time Crystals: A Review. Rep. Prog. Phys. 2017, 81, 016401. [Google Scholar] [CrossRef]
- Sacha, K. Time Crystals; Springer Series on Atomic, Optical, and Plasma Physics; Springer: Cham, Switzerland, 2020; Volume 114. [Google Scholar]
- Khemani, V.; Moessner, R.; Sondhi, S.L. A Brief History of Time Crystals. arXiv 2019, arXiv:1910.10745. [Google Scholar]
- Else, D.V.; Monroe, C.; Nayak, C.; Yao, N.Y. Discrete Time Crystals. Annu. Rev. Condens. Matter Phys. 2020, 11, 467–499. [Google Scholar] [CrossRef]
- Sacha, K. Modeling Spontaneous Breaking of Time-Translation Symmetry. Phys. Rev. A 2015, 91, 033617. [Google Scholar] [CrossRef]
- Khemani, V.; Lazarides, A.; Moessner, R.; Sondhi, S.L. Phase Structure of Driven Quantum Systems. Phys. Rev. Lett. 2016, 116, 250401. [Google Scholar] [CrossRef]
- von Keyserlingk, C.W.; Khemani, V.; Sondhi, S.L. Absolute Stability and Spatiotemporal Long-Range Order in Floquet Systems. Phys. Rev. B 2016, 94, 085112. [Google Scholar] [CrossRef]
- Else, D.V.; Bauer, B.; Nayak, C. Floquet Time Crystals. Phys. Rev. Lett. 2016, 117, 090402. [Google Scholar] [CrossRef]
- Yao, N.Y.; Potter, A.C.; Potirniche, I.D.; Vishwanath, A. Discrete Time Crystals: Rigidity, Criticality, and Realizations. Phys. Rev. Lett. 2017, 118, 030401. [Google Scholar] [CrossRef]
- Zhang, J.; Hess, P.; Kyprianidis, A.; Becker, P.; Lee, A.; Smith, J.; Pagano, G.; Potirniche, I.D.; Potter, A.C.; Vishwanath, A.; et al. Observation of a discrete time crystal. Nature 2017, 543, 217–220. [Google Scholar] [CrossRef] [PubMed]
- Choi, S.; Choi, J.; Landig, R.; Kucsko, G.; Zhou, H.; Isoya, J.; Jelezko, F.; Onoda, S.; Sumiya, H.; Khemani, V.; et al. Observation of discrete time-crystalline order in a disordered dipolar many-body system. Nature 2017, 543, 221–225. [Google Scholar] [CrossRef]
- Rovny, J.; Blum, R.L.; Barrett, S.E. Observation of discrete-time-crystal signatures in an ordered dipolar many-body system. Phys. Rev. Lett. 2018, 120, 180603. [Google Scholar] [CrossRef]
- Pal, S.; Nishad, N.; Mahesh, T.; Sreejith, G. Temporal order in periodically driven spins in star-shaped clusters. Phys. Rev. Lett. 2018, 120, 180602. [Google Scholar] [CrossRef]
- O’Sullivan, J.; Lunt, O.; Zollitsch, C.W.; Thewalt, M.L.W.; Morton, J.J.L.; Pal, A. Signatures of discrete time crystalline order in dissipative spin ensembles. New J. Phys. 2020, 22, 085001. [Google Scholar] [CrossRef]
- Keßler, H.; Cosme, J.G.; Georges, C.; Mathey, L.; Hemmerich, A. From a continuous to a discrete time crystal in a dissipative atom-cavity system. New J. Phys. 2020, 22, 085002. [Google Scholar] [CrossRef]
- Randall, J.; Bradley, C.; Van Der Gronden, F.; Galicia, A.; Abobeih, M.; Markham, M.; Twitchen, D.; Machado, F.; Yao, N.; Taminiau, T. Many-body–localized discrete time crystal with a programmable spin-based quantum simulator. Science 2021, 374, 1474–1478. [Google Scholar] [CrossRef] [PubMed]
- Keßler, H.; Kongkhambut, P.; Georges, C.; Mathey, L.; Cosme, J.G.; Hemmerich, A. Observation of a dissipative time crystal. Phys. Rev. Lett. 2021, 127, 043602. [Google Scholar] [CrossRef] [PubMed]
- Mi, X.; Ippoliti, M.; Quintana, C.; Greene, A.; Chen, Z.; Gross, J.; Arute, F.; Arya, K.; Atalaya, J.; Babbush, R.; et al. Time-crystalline eigenstate order on a quantum processor. Nature 2022, 601, 531–536. [Google Scholar] [CrossRef]
- D’Alessio, L.; Rigol, M. Long-time behavior of isolated periodically driven interacting lattice systems. Phys. Rev. X 2014, 4, 041048. [Google Scholar] [CrossRef]
- Lazarides, A.; Das, A.; Moessner, R. Equilibrium states of generic quantum systems subject to periodic driving. Phys. Rev. E 2014, 90, 012110. [Google Scholar] [CrossRef]
- Gopalakrishnan, S.; Parameswaran, S.A. Dynamics and transport at the threshold of many-body localization. Phys. Rep. 2020, 862, 1–62. [Google Scholar] [CrossRef]
- Abanin, D.A.; Altman, E.; Bloch, I.; Serbyn, M. Colloquium: Many-body localization, thermalization, and entanglement. Rev. Mod. Phys. 2019, 91, 021001. [Google Scholar] [CrossRef]
- Morningstar, A.; Colmenarez, L.; Khemani, V.; Luitz, D.J.; Huse, D.A. Avalanches and many-body resonances in many-body localized systems. Phys. Rev. B 2022, 105, 174205. [Google Scholar] [CrossRef]
- Kiefer-Emmanouilidis, M.; Unanyan, R.; Fleischhauer, M.; Sirker, J. Slow delocalization of particles in many-body localized phases. Phys. Rev. B 2021, 103, 024203. [Google Scholar] [CrossRef]
- Huang, B.; Wu, Y.H.; Liu, W.V. Clean Floquet time crystals: Models and realizations in cold atoms. Phys. Rev. Lett. 2018, 120, 110603. [Google Scholar] [CrossRef] [PubMed]
- Pizzi, A.; Knolle, J.; Nunnenkamp, A. Period-n discrete time crystals and quasicrystals with ultracold bosons. Phys. Rev. Lett. 2019, 123, 150601. [Google Scholar] [CrossRef] [PubMed]
- Kshetrimayum, A.; Eisert, J.; Kennes, D. Stark time crystals: Symmetry breaking in space and time. Phys. Rev. B 2020, 102, 195116. [Google Scholar] [CrossRef]
- Choudhury, S. Route to Extend the Lifetime of a Discrete Time Crystal in a Finite Spin Chain without Disorder. Atoms 2021, 9, 25. [Google Scholar] [CrossRef]
- Pizzi, A.; Malz, D.; De Tomasi, G.; Knolle, J.; Nunnenkamp, A. Time crystallinity and finite-size effects in clean Floquet systems. Phys. Rev. B 2020, 102, 214207. [Google Scholar] [CrossRef]
- Russomanno, A.; Iemini, F.; Dalmonte, M.; Fazio, R. Floquet time crystal in the Lipkin-Meshkov-Glick model. Phys. Rev. B 2017, 95, 214307. [Google Scholar] [CrossRef]
- Lyu, C.; Choudhury, S.; Lv, C.; Yan, Y.; Zhou, Q. Eternal discrete time crystal beating the Heisenberg limit. Phys. Rev. Res. 2020, 2, 033070. [Google Scholar] [CrossRef]
- Pizzi, A.; Knolle, J.; Nunnenkamp, A. Higher-order and fractional discrete time crystals in clean long-range interacting systems. Nat. Commun. 2021, 12, 2341. [Google Scholar] [CrossRef] [PubMed]
- Giachetti, G.; Solfanelli, A.; Correale, L.; Defenu, N. Fractal nature of high-order time crystal phases. Phys. Rev. B 2023, 108, L140102. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, L.H.; Wang, Q.F.; Ma, Y.; Han, T.Y.; Zhang, J.; Zhang, Z.Y.; Shao, S.Y.; Li, Q.; Chen, H.C.; et al. Higher-order and fractional discrete time crystals in Floquet-driven Rydberg atoms. Nat. Commun. 2024, 15, 9730. [Google Scholar] [CrossRef]
- Cosme, J.G.; Skulte, J.; Mathey, L. Bridging closed and dissipative discrete time crystals in spin systems with infinite-range interactions. Phys. Rev. B 2023, 108, 024302. [Google Scholar] [CrossRef]
- Lipkin, H.J.; Meshkov, N.; Glick, A. Validity of many-body approximation methods for a solvable model: (I). Exact solutions and perturbation theory. Nucl. Phys. 1965, 62, 188–198. [Google Scholar] [CrossRef]
- Pilatowsky-Cameo, S.; Dag, C.B.; Ho, W.W.; Choi, S. Complete Hilbert-space ergodicity in quantum dynamics of generalized Fibonacci drives. Phys. Rev. Lett. 2023, 131, 250401. [Google Scholar] [CrossRef]
- Dumitrescu, P.T.; Vasseur, R.; Potter, A.C. Logarithmically slow relaxation in quasiperiodically driven random spin chains. Phys. Rev. Lett. 2018, 120, 070602. [Google Scholar] [CrossRef]
- Zhao, H.; Mintert, F.; Knolle, J. Floquet time spirals and stable discrete-time quasicrystals in quasiperiodically driven quantum many-body systems. Phys. Rev. B 2019, 100, 134302. [Google Scholar] [CrossRef]
- Haake, F.; Kuś, M.; Scharf, R. Classical and quantum chaos for a kicked top. Z. Phys. B Condens. Matter 1987, 65, 381–395. [Google Scholar] [CrossRef]
- Biswas, H.; Choudhury, S. The Floquet central spin model: A platform to realize eternal time crystals, entanglement steering, and multiparameter metrology. arXiv 2025, arXiv:2501.18472. [Google Scholar]
- He, G.; Ye, B.; Gong, R.; Yao, C.; Liu, Z.; Murch, K.W.; Yao, N.Y.; Zu, C. Experimental realization of discrete time quasicrystals. Phys. Rev. X 2025, 15, 011055. [Google Scholar] [CrossRef]
- Dutta, P.; Choudhury, S.; Shukla, V. Prethermalization in the PXP model under continuous quasiperiodic driving. Phys. Rev. B 2025, 111, 064303. [Google Scholar] [CrossRef]
- Nandy, S.; Sen, A.; Sen, D. Aperiodically driven integrable systems and their emergent steady states. Phys. Rev. X 2017, 7, 031034. [Google Scholar] [CrossRef]
- Zhao, H.; Mintert, F.; Moessner, R.; Knolle, J. Random multipolar driving: Tunably slow heating through spectral engineering. Phys. Rev. Lett. 2021, 126, 040601. [Google Scholar] [CrossRef] [PubMed]
- Mori, T.; Zhao, H.; Mintert, F.; Knolle, J.; Moessner, R. Rigorous bounds on the heating rate in Thue-Morse quasiperiodically and randomly driven quantum many-body systems. Phys. Rev. Lett. 2021, 127, 050602. [Google Scholar] [CrossRef] [PubMed]
- Tiwari, V.; Bhakuni, D.S.; Sharma, A. Dynamical localization and slow dynamics in quasiperiodically driven quantum systems. Phys. Rev. B 2024, 109, L161104. [Google Scholar] [CrossRef]
- Tiwari, V.; Bhakuni, D.S.; Sharma, A. Periodically and aperiodically Thue-Morse driven long-range systems: From dynamical localization to slow dynamics. Phys. Rev. B 2025, 111, 205109. [Google Scholar] [CrossRef]
- Mukherjee, B.; Sen, A.; Sen, D.; Sengupta, K. Restoring coherence via aperiodic drives in a many-body quantum system. Phys. Rev. B 2020, 102, 014301. [Google Scholar] [CrossRef]
- Zhao, H.; Knolle, J.; Moessner, R. Temporal disorder in spatiotemporal order. Phys. Rev. B 2023, 108, L100203. [Google Scholar] [CrossRef]
- Moon, L.J.I.; Schindler, P.M.; Sun, Y.; Druga, E.; Knolle, J.; Moessner, R.; Zhao, H.; Bukov, M.; Ajoy, A. Experimental observation of a time rondeau crystal: Temporal disorder in spatiotemporal order. arXiv 2024, arXiv:2404.05620. [Google Scholar]
- Ma, Z.; Yan, J.; Zhao, H.; Peng, L.Y. Stable time rondeau crystals in dissipative many-body systems. arXiv 2025, arXiv:2502.16999. [Google Scholar]
- Kumar, S.; Choudhury, S. Prethermalization in aperiodically driven classical spin systems. Phys. Rev. E 2024, 110, 064150. [Google Scholar] [CrossRef]
- Pilatowsky-Cameo, S.; Choi, S.; Ho, W.W. Critically slow Hilbert-space ergodicity in quantum morphic drives. arXiv 2025, arXiv:2502.06936. [Google Scholar]
- Thue, A. Uber unendliche zeichenreihen. Norske Vid. Selsk. Skr. I Mat.-Nat. Kl. 1906, 7, 1–22. [Google Scholar]
- Morse, H.M. Recurrent geodesics on a surface of negative curvature. Trans. Am. Math. Soc. 1921, 22, 84–100. [Google Scholar] [CrossRef]
- Yao, N.; Laumann, C.; Cirac, J.I.; Lukin, M.D.; Moore, J. Quasi-many-body localization in translation-invariant systems. Phys. Rev. Lett. 2016, 117, 240601. [Google Scholar] [CrossRef]
- Barbiero, L.; Menotti, C.; Recati, A.; Santos, L. Out-of-equilibrium states and quasi-many-body localization in polar lattice gases. Phys. Rev. B 2015, 92, 180406(R). [Google Scholar] [CrossRef]
- Bukov, M.; Gopalakrishnan, S.; Knap, M.; Demler, E. Prethermal floquet steady states and instabilities in the periodically driven, weakly interacting bose-hubbard model. Phys. Rev. Lett. 2015, 115, 205301. [Google Scholar] [CrossRef]
- Lellouch, S.; Bukov, M.; Demler, E.; Goldman, N. Parametric instability rates in periodically driven band systems. Phys. Rev. X 2017, 7, 021015. [Google Scholar] [CrossRef]
- Lemm, M.; Rademacher, S. Out-of-time-ordered correlators of mean-field bosons via Bogoliubov theory. Quantum 2025, 9, 1587. [Google Scholar] [CrossRef]
- Mivehvar, F.; Piazza, F.; Donner, T.; Ritsch, H. Cavity QED with quantum gases: New paradigms in many-body physics. Adv. Phys. 2021, 70, 1–153. [Google Scholar] [CrossRef]
- Li, Z.; Braverman, B.; Colombo, S.; Shu, C.; Kawasaki, A.; Adiyatullin, A.F.; Pedrozo-Peñafiel, E.; Mendez, E.; Vuletić, V. Collective spin-light and light-mediated spin-spin interactions in an optical cavity. PRX Quantum 2022, 3, 020308. [Google Scholar] [CrossRef]
- Muniz, J.A.; Barberena, D.; Lewis-Swan, R.J.; Young, D.J.; Cline, J.R.; Rey, A.M.; Thompson, J.K. Exploring dynamical phase transitions with cold atoms in an optical cavity. Nature 2020, 580, 602–607. [Google Scholar] [CrossRef]
- Jurcevic, P.; Shen, H.; Hauke, P.; Maier, C.; Brydges, T.; Hempel, C.; Lanyon, B.; Heyl, M.; Blatt, R.; Roos, C. Direct observation of dynamical quantum phase transitions in an interacting many-body system. Phys. Rev. Lett. 2017, 119, 080501. [Google Scholar] [CrossRef] [PubMed]
- Lanyon, B.P.; Hempel, C.; Nigg, D.; Müller, M.; Gerritsma, R.; Zähringer, F.; Schindler, P.; Barreiro, J.T.; Rambach, M.; Kirchmair, G.; et al. Universal digital quantum simulation with trapped ions. Science 2011, 334, 57–61. [Google Scholar] [CrossRef]
- Xu, K.; Sun, Z.H.; Liu, W.; Zhang, Y.R.; Li, H.; Dong, H.; Ren, W.; Zhang, P.; Nori, F.; Zheng, D.; et al. Probing dynamical phase transitions with a superconducting quantum simulator. Sci. Adv. 2020, 6, eaba4935. [Google Scholar] [CrossRef]
- Shin, Y.; Saba, M.; Pasquini, T.; Ketterle, W.; Pritchard, D.; Leanhardt, A. Atom interferometry with Bose-Einstein condensates in a double-well potential. Phys. Rev. Lett. 2004, 92, 050405. [Google Scholar] [CrossRef]
- Albiez, M.; Gati, R.; Fölling, J.; Hunsmann, S.; Cristiani, M.; Oberthaler, M.K. Direct observation of tunneling and nonlinear self-trapping in a single bosonic Josephson junction. Phys. Rev. Lett. 2005, 95, 010402. [Google Scholar] [CrossRef]
- Carr, L.D.; Dounas-Frazer, D.; Garcia-March, M. Dynamical realization of macroscopic superposition states of cold bosons in a tilted double well. Europhys. Lett. 2010, 90, 10005. [Google Scholar] [CrossRef][Green Version]
- Norcia, M.A.; Lewis-Swan, R.J.; Cline, J.R.; Zhu, B.; Rey, A.M.; Thompson, J.K. Cavity-mediated collective spin-exchange interactions in a strontium superradiant laser. Science 2018, 361, 259–262. [Google Scholar] [CrossRef]
- Blatt, R.; Roos, C.F. Quantum simulations with trapped ions. Nat. Phys. 2012, 8, 277–284. [Google Scholar] [CrossRef]
- Monroe, C.; Campbell, W.C.; Duan, L.M.; Gong, Z.X.; Gorshkov, A.V.; Hess, P.W.; Islam, R.; Kim, K.; Linke, N.M.; Pagano, G.; et al. Programmable quantum simulations of spin systems with trapped ions. Rev. Mod. Phys. 2021, 93, 025001. [Google Scholar] [CrossRef]
- Kyprianidis, A.; Machado, F.; Morong, W.; Becker, P.; Collins, K.S.; Else, D.V.; Feng, L.; Hess, P.W.; Nayak, C.; Pagano, G.; et al. Observation of a prethermal discrete time crystal. Science 2021, 372, 1192–1196. [Google Scholar] [CrossRef]
- Zhu, B.; Marino, J.; Yao, N.Y.; Lukin, M.D.; Demler, E.A. Dicke time crystals in driven-dissipative quantum many-body systems. New J. Phys. 2019, 21, 073028. [Google Scholar] [CrossRef]
- Ray, S.; Sinha, S.; Sen, D. Dynamics of quasiperiodically driven spin systems. Phys. Rev. E 2019, 100, 052129. [Google Scholar] [CrossRef] [PubMed]
- Schütz, S.; Jäger, S.B.; Morigi, G. Dissipation-assisted prethermalization in long-range interacting atomic ensembles. Phys. Rev. Lett. 2016, 117, 083001. [Google Scholar] [CrossRef] [PubMed]
- Yousefjani, R.; Sacha, K.; Bayat, A. Discrete time crystal phase as a resource for quantum-enhanced sensing. Phys. Rev. B 2025, 111, 125159. [Google Scholar] [CrossRef]
- Carollo, F.; Brandner, K.; Lesanovsky, I. Nonequilibrium many-body quantum engine driven by time-translation symmetry breaking. Phys. Rev. Lett. 2020, 125, 240602. [Google Scholar] [CrossRef]
- Estarellas, M.; Osada, T.; Bastidas, V.; Renoust, B.; Sanaka, K.; Munro, W.; Nemoto, K. Simulating complex quantum networks with time crystals. Sci. Adv. 2020, 6, eaay8892. [Google Scholar] [CrossRef]
- Engelhardt, G.; Choudhury, S.; Liu, W.V. Unified light-matter Floquet theory and its application to quantum communication. Phys. Rev. Res. 2024, 6, 013116. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anisur, S.; Liu, W.V.; Choudhury, S. Quasi-Discrete Time Crystals in the Quasiperiodically Driven Lipkin–Meshkov–Glick Model. Entropy 2025, 27, 609. https://doi.org/10.3390/e27060609
Anisur S, Liu WV, Choudhury S. Quasi-Discrete Time Crystals in the Quasiperiodically Driven Lipkin–Meshkov–Glick Model. Entropy. 2025; 27(6):609. https://doi.org/10.3390/e27060609
Chicago/Turabian StyleAnisur, Sk, Wensheng Vincent Liu, and Sayan Choudhury. 2025. "Quasi-Discrete Time Crystals in the Quasiperiodically Driven Lipkin–Meshkov–Glick Model" Entropy 27, no. 6: 609. https://doi.org/10.3390/e27060609
APA StyleAnisur, S., Liu, W. V., & Choudhury, S. (2025). Quasi-Discrete Time Crystals in the Quasiperiodically Driven Lipkin–Meshkov–Glick Model. Entropy, 27(6), 609. https://doi.org/10.3390/e27060609






