A Monte Carlo Study of Dynamic Phase Transitions Observed in the Kinetic S = 1 Ising Model on Nonregular Lattices
Abstract
1. Introduction
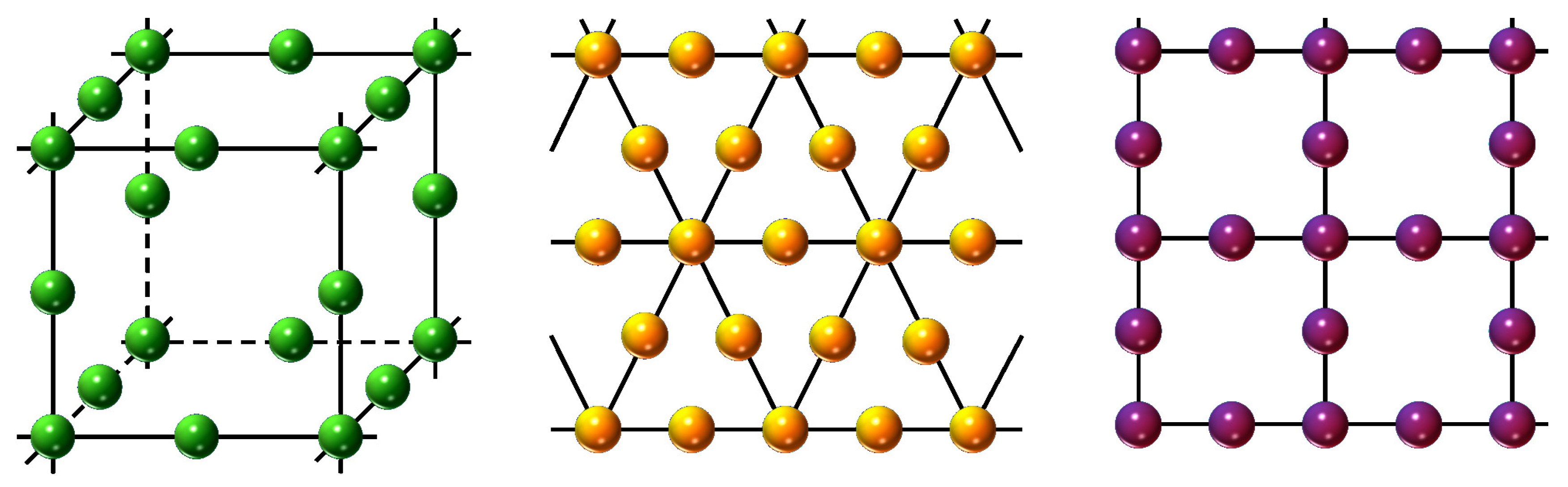
2. Model and Simulation Details
- Spontaneous magnetization,
- Longitudinal magnetic susceptibility,
3. Results
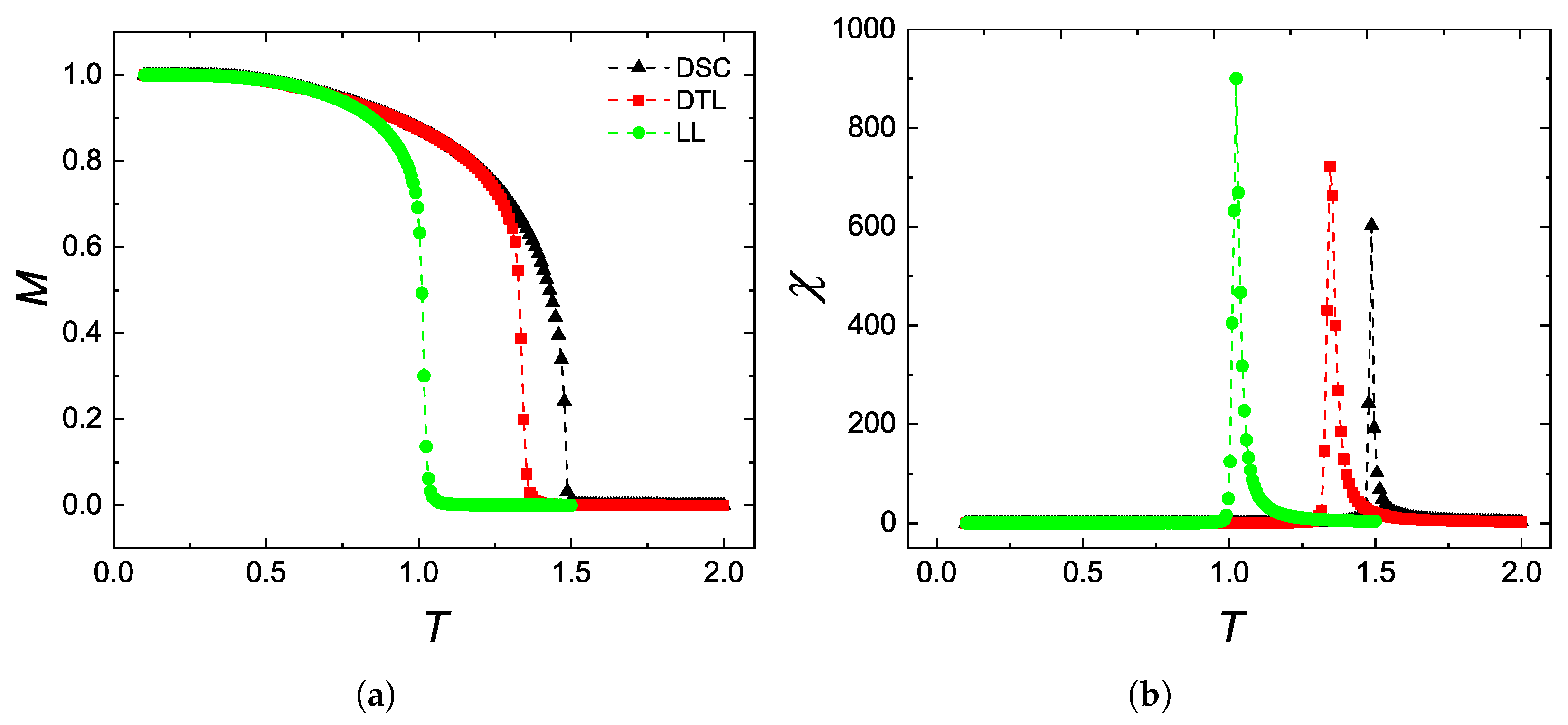
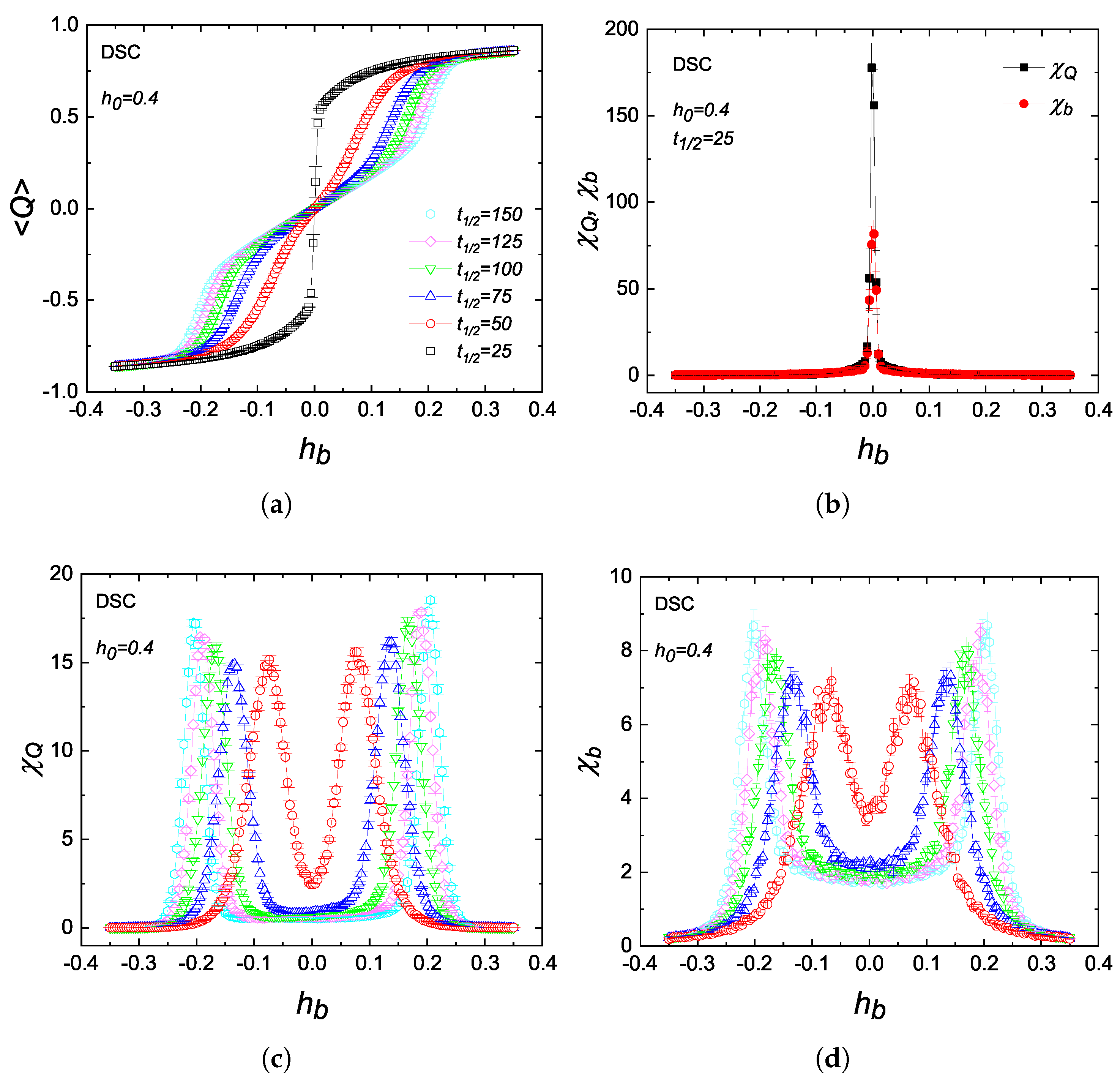
3.1. TPT Properties
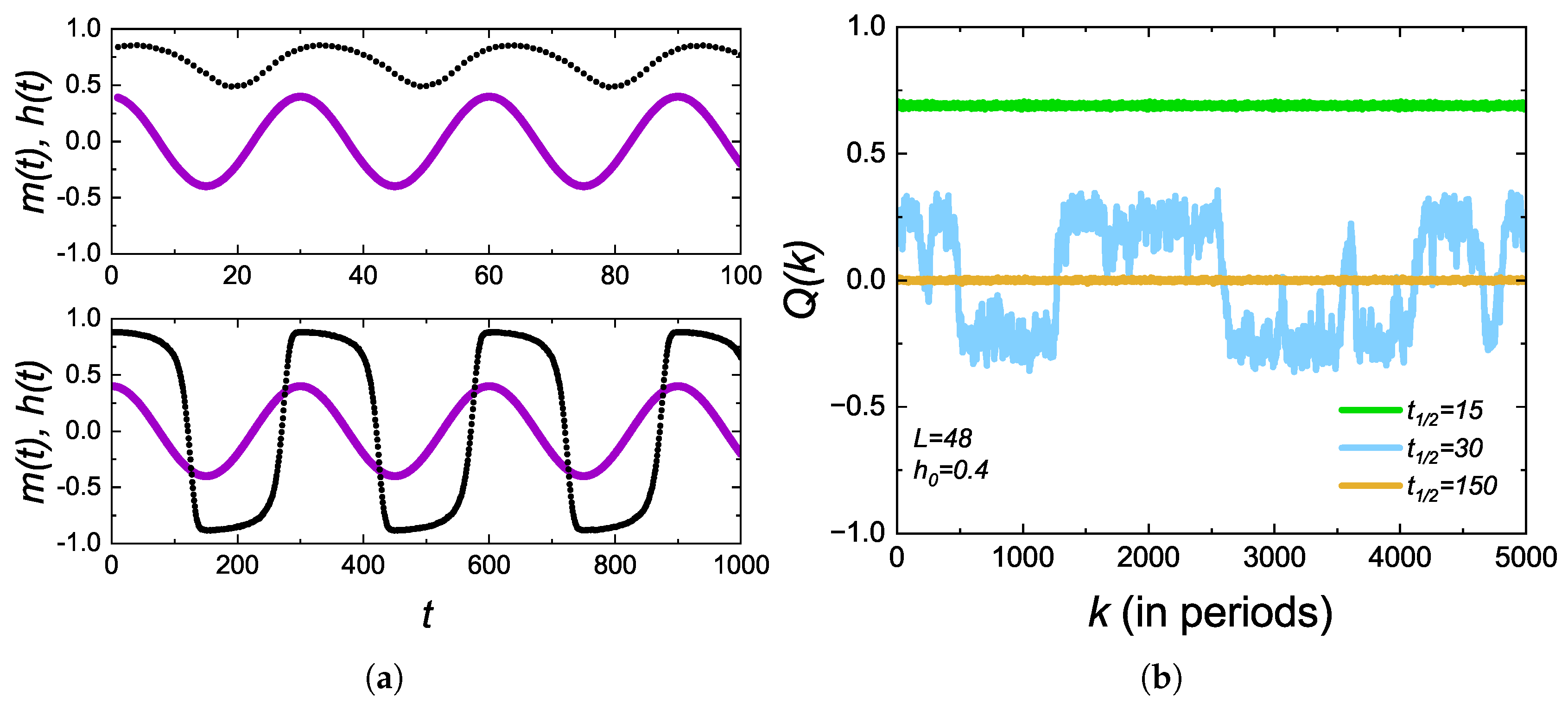
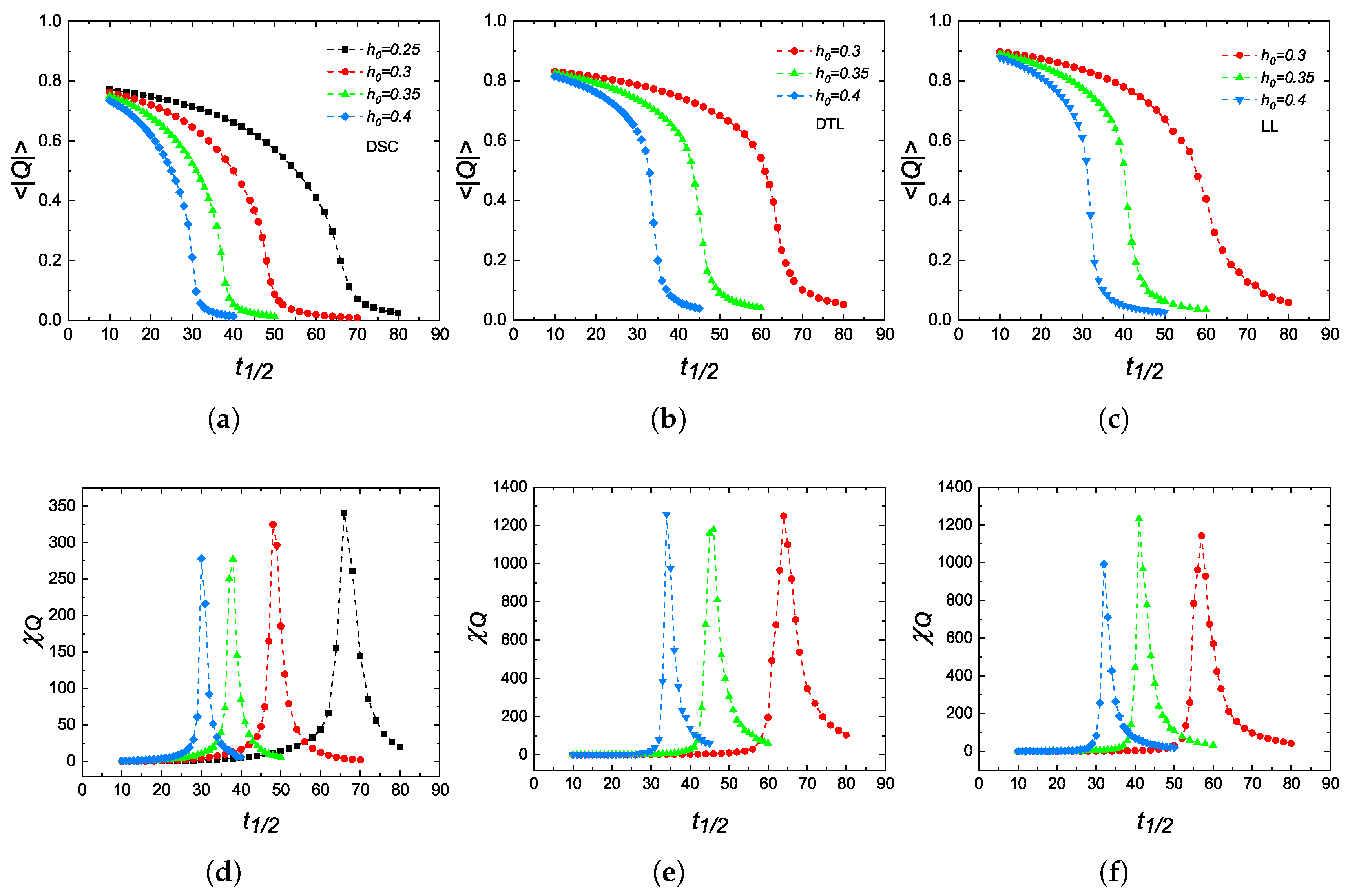
3.2. DPT Properties
3.3. Metamagnetic Anomalies
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chakrabarti, B.K.; Acharyya, M. Dynamic transitions and hysteresis. Rev. Mod. Phys. 1999, 71, 847. [Google Scholar] [CrossRef]
- Tomé, T.; de Oliveira, M.J. Dynamic phase transition in the kinetic Ising model under a time-dependent oscillating field. Phys. Rev. A 1990, 41, 251. [Google Scholar] [CrossRef] [PubMed]
- Lo, W.S.; Pelcovits, R.A. Ising model in a time-dependent magnetic field. Phys. Rev. A 1990, 42, 7471. [Google Scholar] [CrossRef]
- Yüksel, Y.; Vatansever, E. Dynamic phase transition in classical Ising models. J. Phys. D Appl. Phys. 2022, 55, 073002. [Google Scholar] [CrossRef]
- Berger, A.; Idigoras, O.; Vavassori, P. Transient Behavior of the Dynamically Ordered Phase in Uniaxial Cobalt Films. Phys. Rev. Lett. 2013, 111, 190602. [Google Scholar] [CrossRef] [PubMed]
- Robb, D.T.; Xu, Y.H.; Hellwig, O.; McCord, J.; Berger, A.; Novotny, M.A.; Rikvold, P.A. Evidence for a dynamic phase transition in [Co/Pt]3 magnetic multilayers. Phys. Rev. B 2008, 78, 134422. [Google Scholar] [CrossRef]
- Riego, P.; Vavassori, P.; Berger, A. Towards an understanding of dynamic phase transitions. Phys. B 2018, 549, 13. [Google Scholar] [CrossRef]
- Quintana, M.; Berger, A. General existence and determination of conjugate fields in dynamically ordered magnetic systems. Phys. Rev. E 2021, 104, 044125. [Google Scholar] [CrossRef]
- Quintana, M.; Berger, A. Verification of scaling behavior near dynamic phase transitions for nonantisymmetric field sequences. Phys. Rev. E 2024, 109, 054112. [Google Scholar] [CrossRef]
- Korniss, G.; White, C.J.; Rikvold, P.A.; Novotny, M.A. Dynamic phase transition, universality, and finite-size scaling in the two-dimensional kinetic Ising model in an oscillating field. Phys. Rev. E 2000, 63, 016120. [Google Scholar] [CrossRef]
- Buendía, G.M.; Rikvold, P.A. Dynamic phase transition in the two-dimensional kinetic Ising model in an oscillating field: Universality with respect to the stochastic dynamics. Phys. Rev. E 2008, 78, 051108. [Google Scholar] [CrossRef] [PubMed]
- Park, H.; Pleimling, M. Dynamic phase transition in the three-dimensional kinetic Ising model in an oscillating field. Phys. Rev. E 2013, 87, 032145. [Google Scholar] [CrossRef]
- Berger, A.; Mitchell, J.F.; Miller, D.J.; Bader, S.D. Evidence for competing order parameters in the paramagnetic phase of layered manganites (invited). J. Appl. Phys. 2001, 89, 6851. [Google Scholar] [CrossRef]
- Riego, P.; Vavassori, P.; Berger, A. Metamagnetic Anomalies near Dynamic Phase Transitions. Phys. Rev. Lett. 2017, 118, 117202. [Google Scholar] [CrossRef]
- Quintana, M.; Valderrama, C.M.; Berger, A. Metamagnetic fluctuation characteristics near dynamic phase transitions. Phys. Rev. E 2023, 108, 064121. [Google Scholar] [CrossRef]
- Ramírez, J.M.M.; Oblak, E.; Riego, P.; Campillo, G.; Osorio, J.; Arnache, O.; Berger, A. Experimental exploration of dynamic phase transitions and associated metamagnetic fluctuations for materials with different Curie temperatures. Phys. Rev. E 2020, 102, 022804. [Google Scholar] [CrossRef]
- Buendía, G.M.; Rikvold, P.A. Fluctuations in a model ferromagnetic film driven by a slowly oscillating field with a constant bias. Phys. Rev. B 2017, 96, 134306. [Google Scholar] [CrossRef]
- Mendes, C.; Buendía, G.M.; Rikvold, P.A. Numerical simulation of a two-dimensional Blume-Capel ferromagnet in an oscillating magnetic field with a constant bias. Phys. Rev. E 2024, 110, 044133. [Google Scholar] [CrossRef]
- Shi, X.; Liu, P. Metamagnetic anomalies in the kinetic Ising model. Phys. A 2019, 536, 120998. [Google Scholar] [CrossRef]
- Yüksel, Y. Unveiling the similarities and dissimilarities between dynamic and thermodynamic phase transitions in a magnetic binary alloy system: A Monte Carlo study. Phys. Scr. 2023, 96, 035832. [Google Scholar] [CrossRef]
- Azhari, M.; Yu, U. Monte Carlo studies of the Blume–Capel model on nonregular two- and three-dimensional lattices: Phase diagrams, tricriticality, and critical exponents. J. Stat. Mech. 2022, 033204. [Google Scholar] [CrossRef]
- Yüksel, Y. Exploring the equilibrium and dynamic phase transition properties of the Ising ferromagnet on a decorated triangular lattice. Phys. Rev. E 2023, 108, 034125. [Google Scholar] [CrossRef] [PubMed]
- Blume, M.; Emery, V.J.; Griffiths, R.B. Ising model for the λ transition and phase separation in He3-He4 mixtures. Phys. Rev. A 1971, 4, 1071. [Google Scholar] [CrossRef]
- Capel, H.W. On the possibility of first-order phase transitions in Ising systems of triplet ions with zero-field splitting. Physica 1966, 32, 966. [Google Scholar] [CrossRef]
- Newman, M.E.J.; Barkema, G.T. Monte Carlo Methods in Statistical Physics; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Sides, S.W.; Rikvold, P.A.; Novotny, M.A. Kinetic Ising Model in an Oscillating Field: Finite-Size Scaling at the Dynamic Phase Transition. Phys. Rev. Lett. 1998, 81, 834. [Google Scholar] [CrossRef]
- Rikvold, P.A.; Tomita, H.; Miyashita, S.; Sides, S.W. Metastable lifetimes in a kinetic Ising model: Dependence on field and system size. Phys. Rev. E 1994, 49, 5080. [Google Scholar] [CrossRef]
- Vatansever, E.; Fytas, N.G. Dynamic phase transition of the Blume-Capel model in an oscillating magnetic field. Phys. Rev. E 2018, 97, 012122. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yüksel, Y. A Monte Carlo Study of Dynamic Phase Transitions Observed in the Kinetic S = 1 Ising Model on Nonregular Lattices. Entropy 2025, 27, 530. https://doi.org/10.3390/e27050530
Yüksel Y. A Monte Carlo Study of Dynamic Phase Transitions Observed in the Kinetic S = 1 Ising Model on Nonregular Lattices. Entropy. 2025; 27(5):530. https://doi.org/10.3390/e27050530
Chicago/Turabian StyleYüksel, Yusuf. 2025. "A Monte Carlo Study of Dynamic Phase Transitions Observed in the Kinetic S = 1 Ising Model on Nonregular Lattices" Entropy 27, no. 5: 530. https://doi.org/10.3390/e27050530
APA StyleYüksel, Y. (2025). A Monte Carlo Study of Dynamic Phase Transitions Observed in the Kinetic S = 1 Ising Model on Nonregular Lattices. Entropy, 27(5), 530. https://doi.org/10.3390/e27050530







