Bias Reduction of Modified Maximum Likelihood Estimates for a Three-Parameter Weibull Distribution
Abstract
1. Introduction
2. Preliminaries
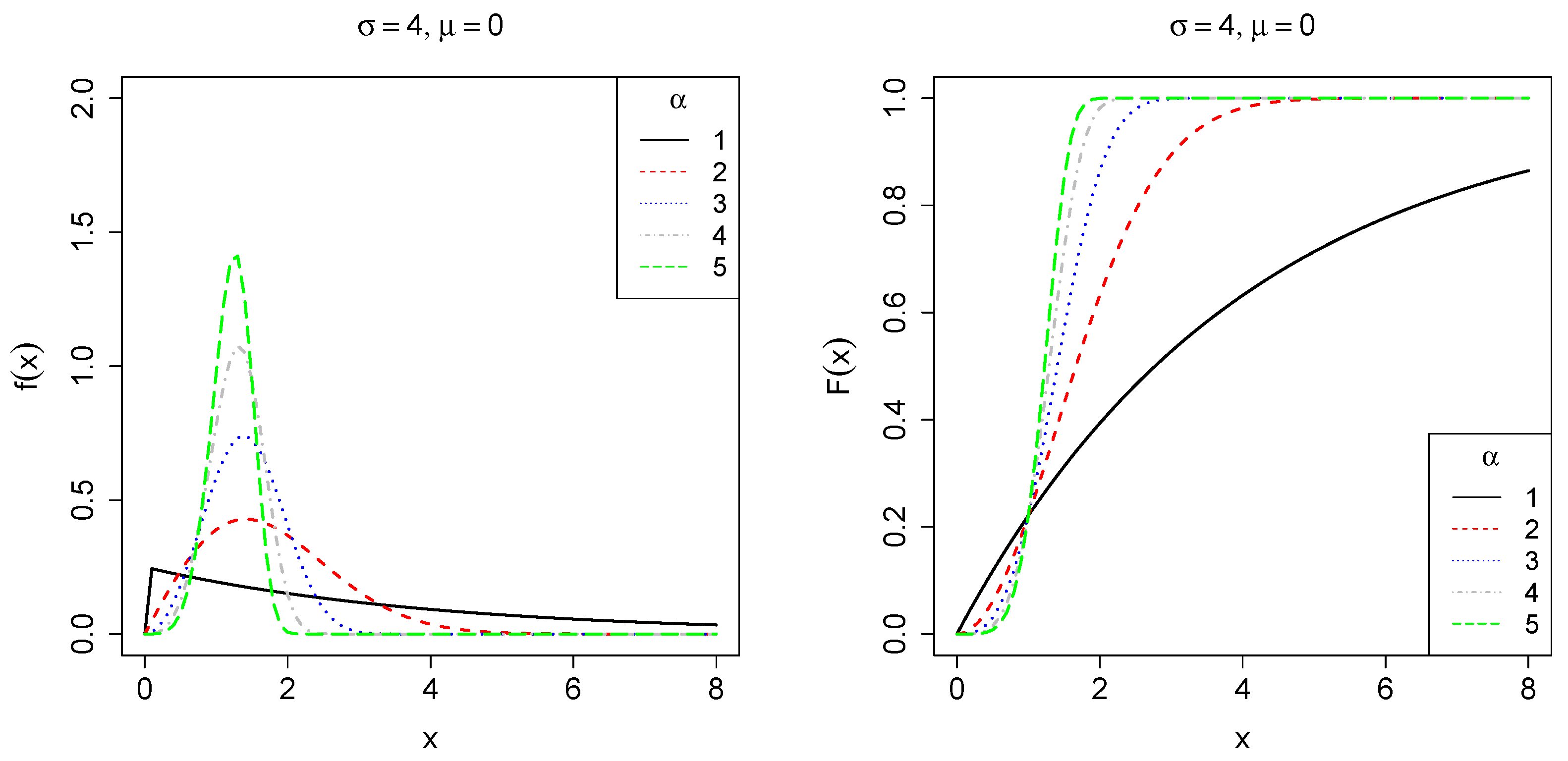
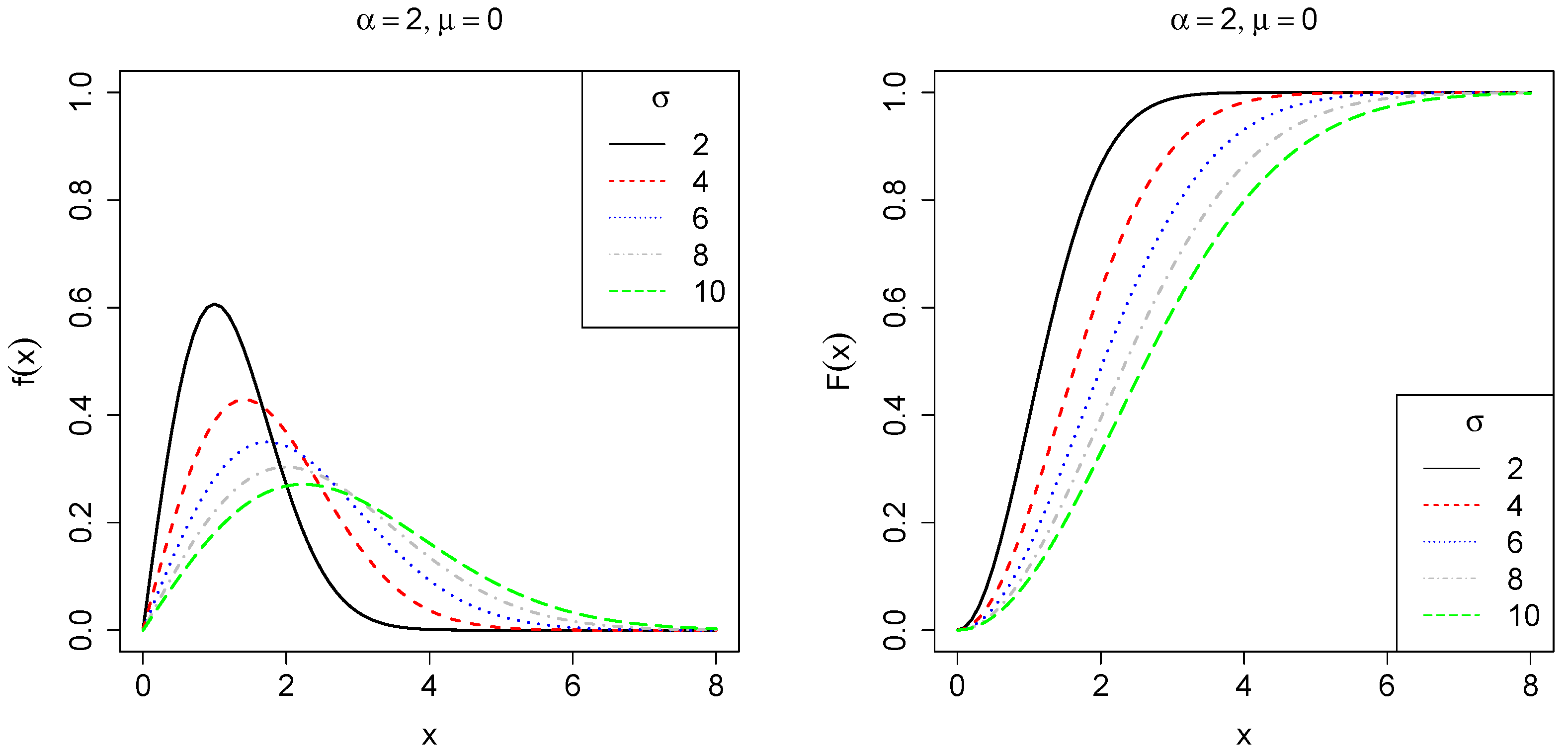
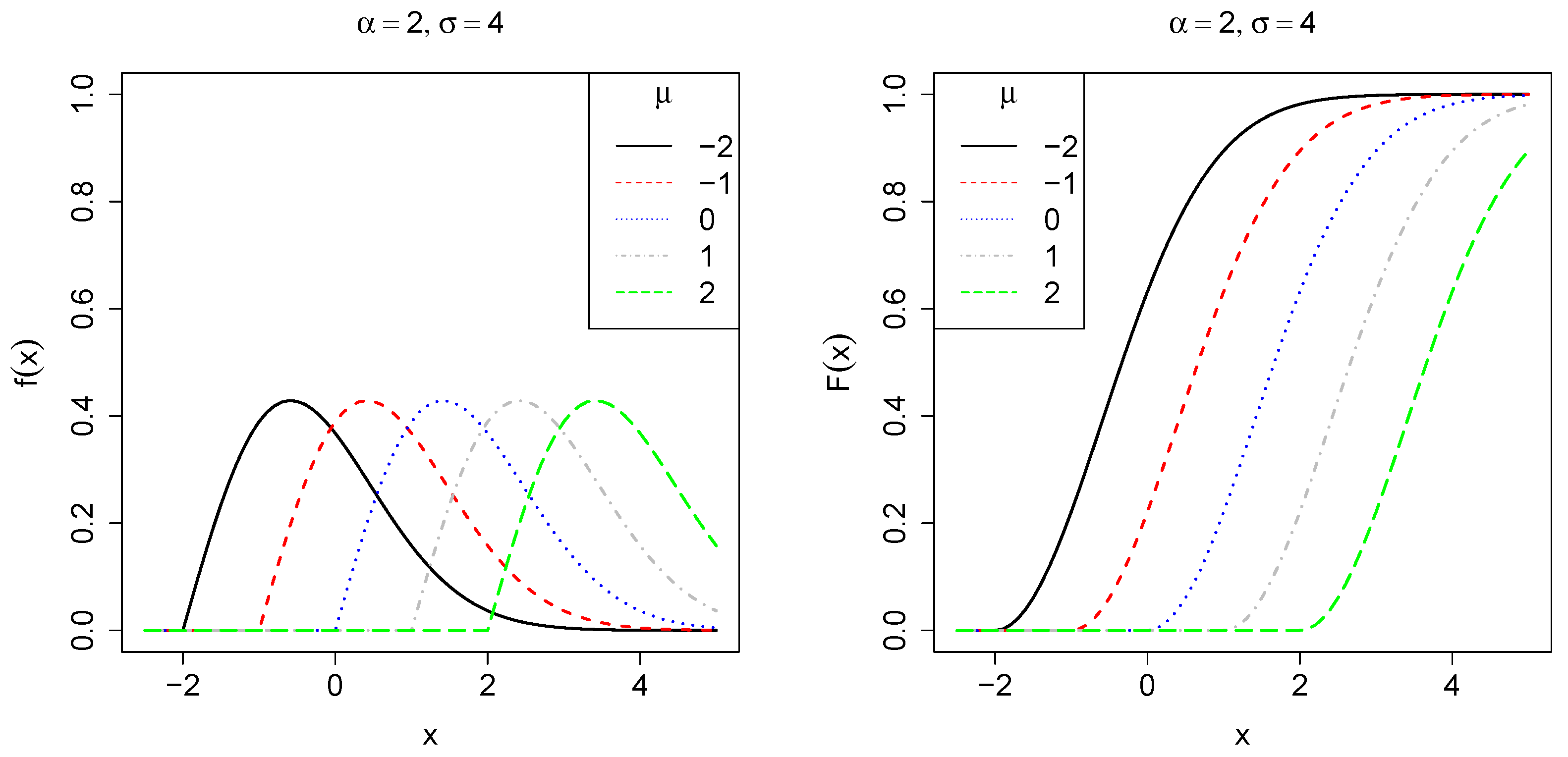
2.1. The Three-Parameter Weibull Distribution
2.2. Modified Log-Likelihood Function
3. Doubly Modified Likelihood Function
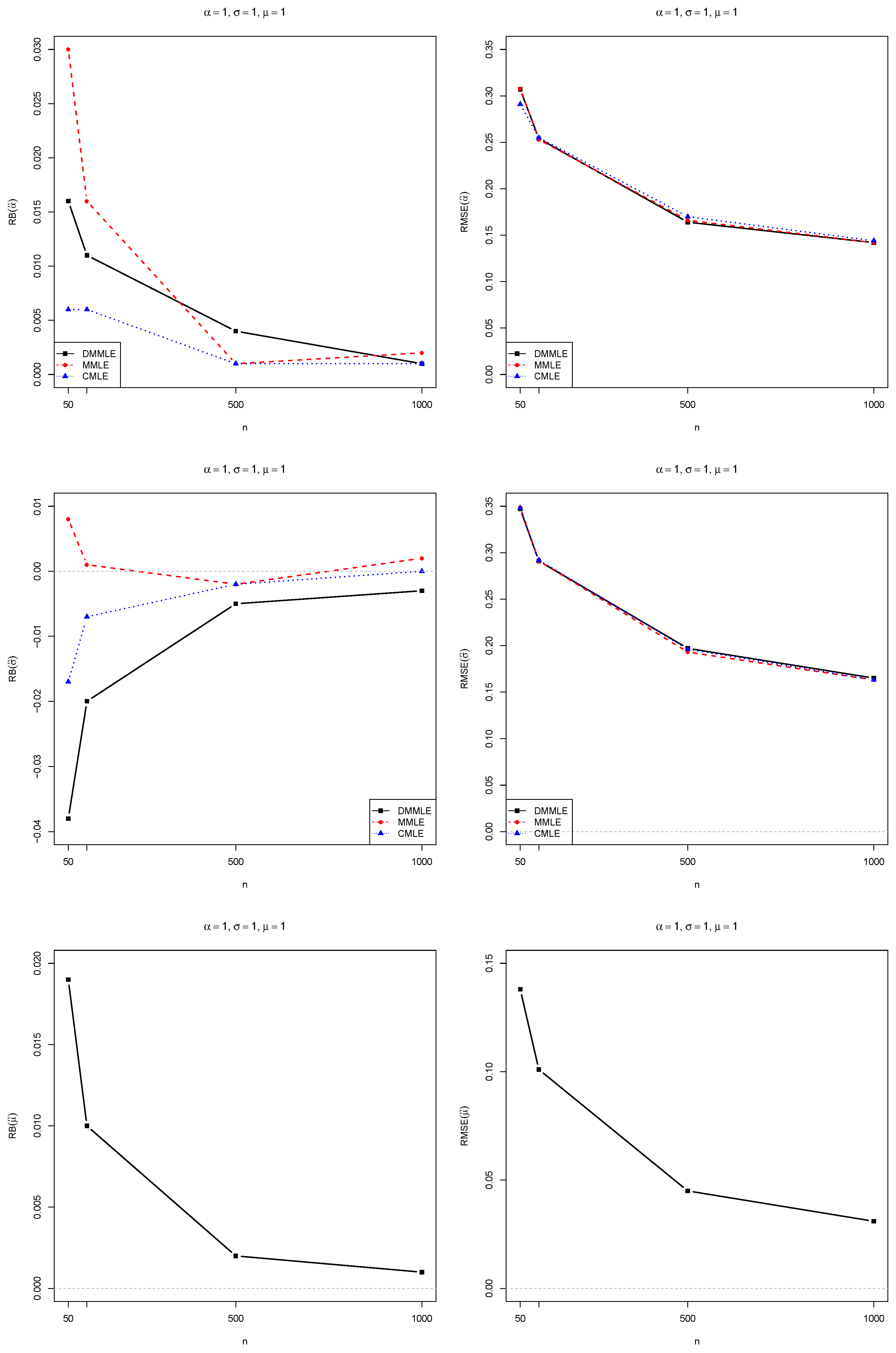
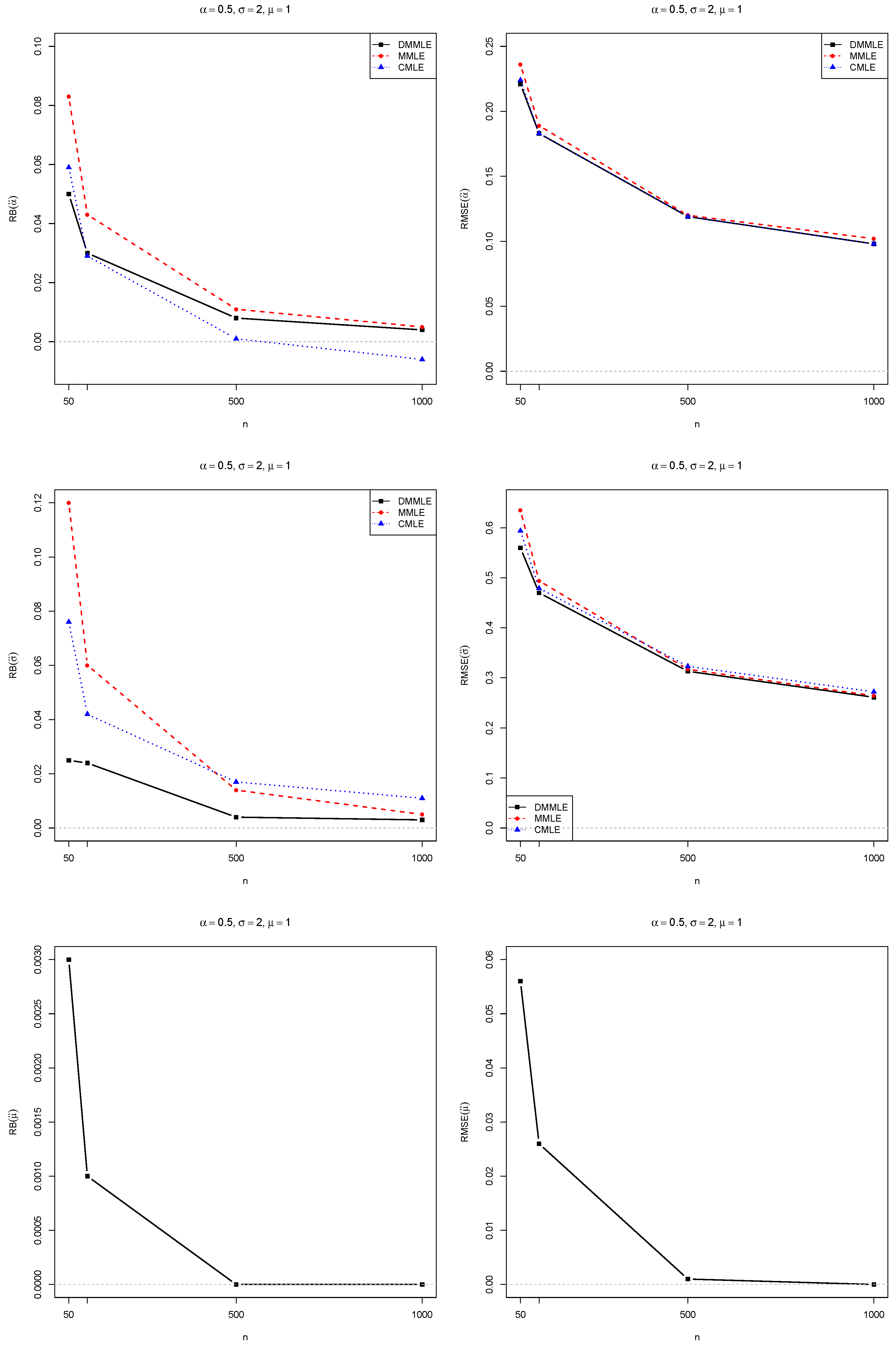
4. Monte Carlo Simulations
- true population’s parameters .
- Monte Carlo replications of samples directly sampled from true distributions since the parameters are known;
- sample size ;
5. Applications
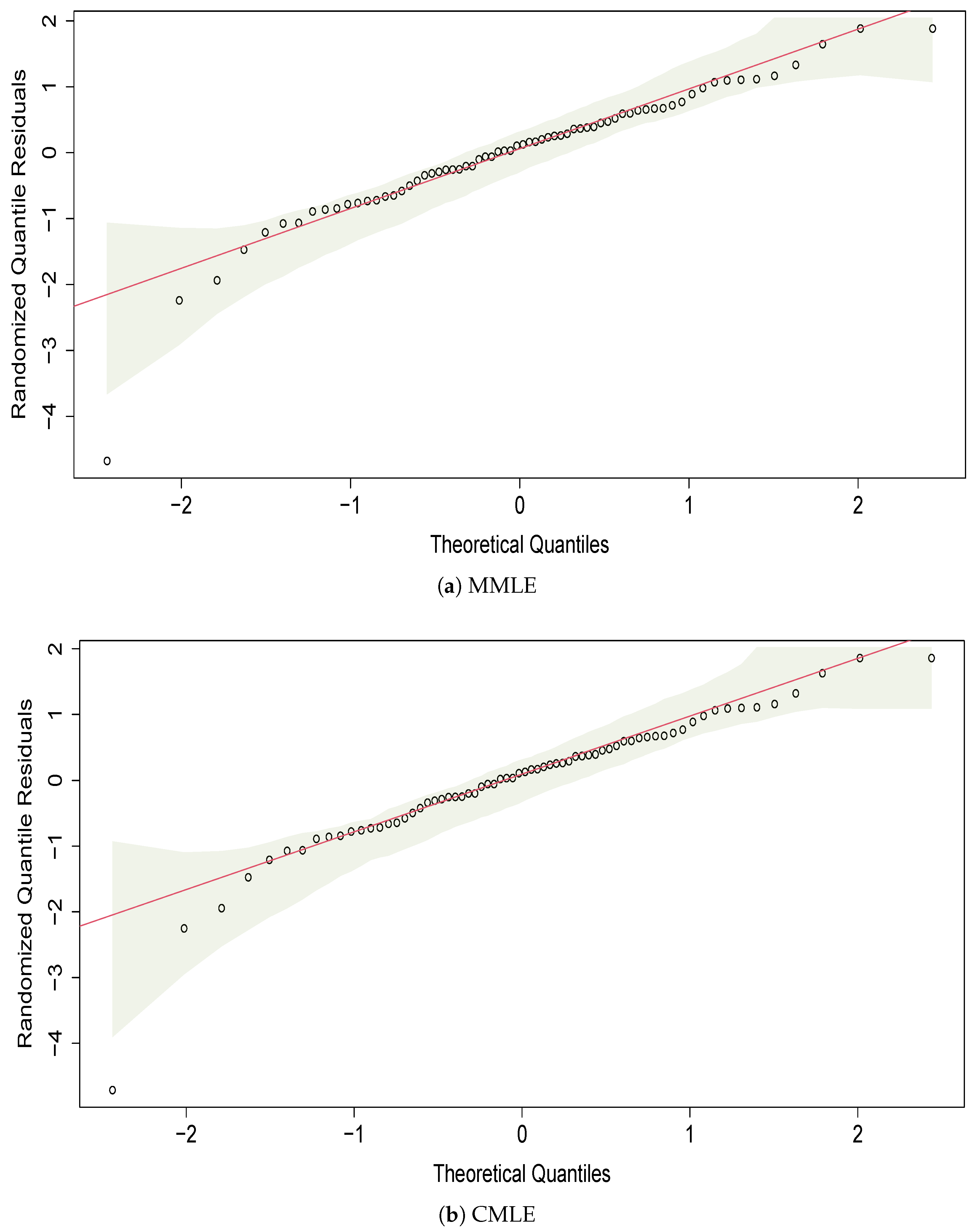
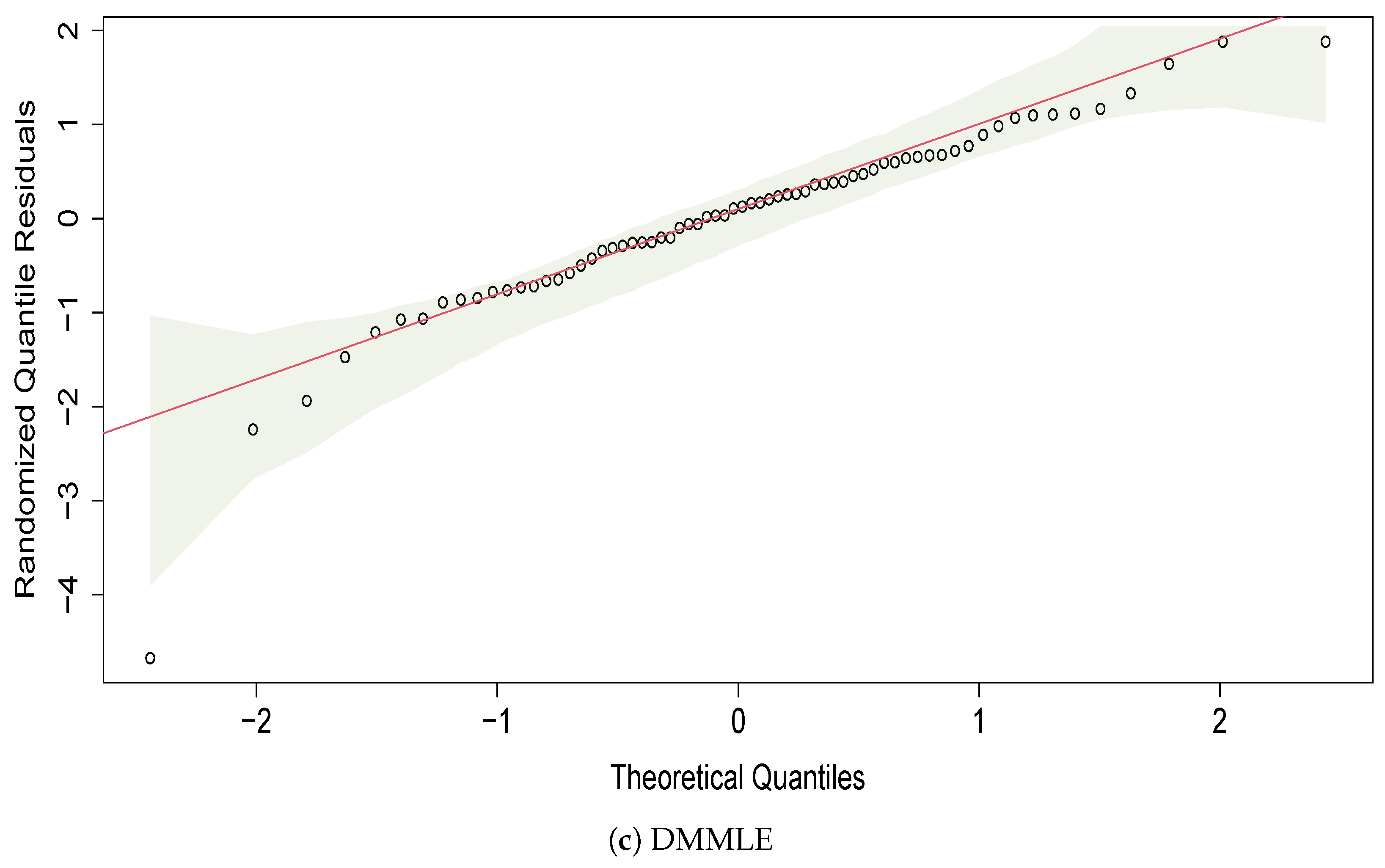
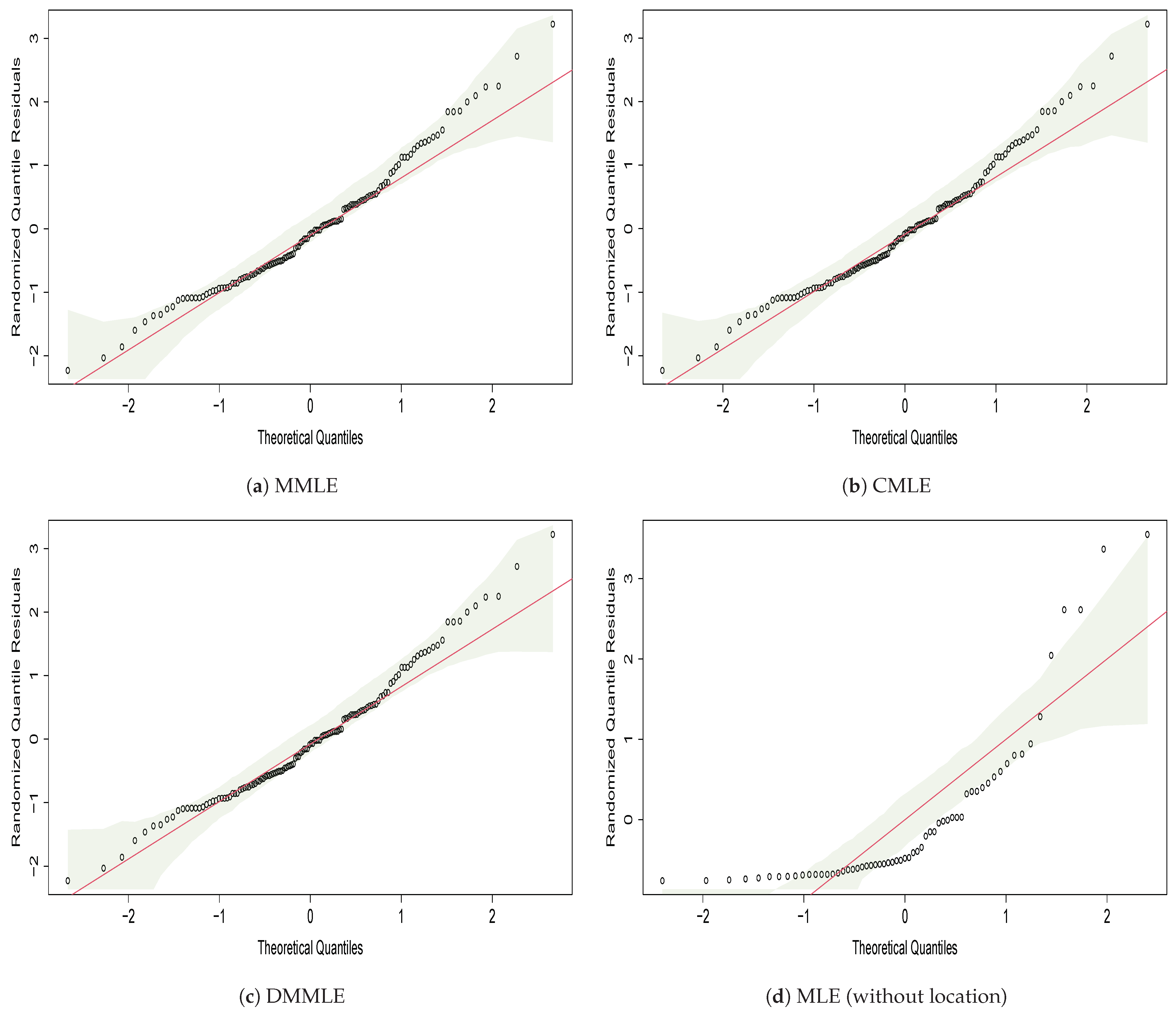
5.1. Carbon Fiber Strength
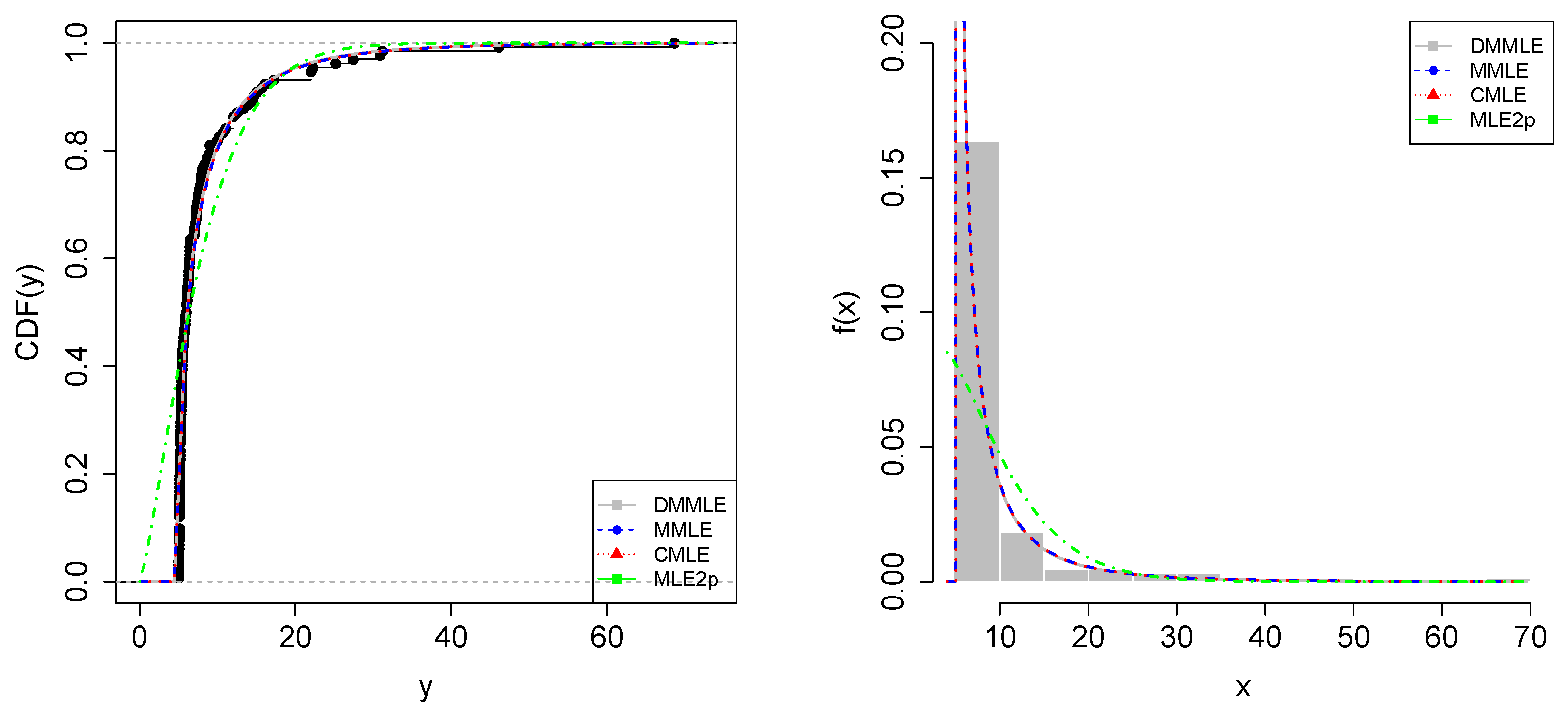
5.2. Foreign Investment in Brazil
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| 1.312 | 1.314 | 1.479 | 1.552 | 1.700 |
| 1.803 | 1.861 | 1.865 | 1.944 | 1.958 |
| 1.966 | 1.997 | 2.006 | 2.021 | 2.027 |
| 2.055 | 2.063 | 2.098 | 2.140 | 2.179 |
| 2.224 | 2.240 | 2.253 | 2.270 | 2.272 |
| 2.274 | 2.301 | 2.301 | 2.359 | 2.382 |
| 2.382 | 2.426 | 2.434 | 2.435 | 2.478 |
| 2.490 | 2.511 | 2.514 | 2.535 | 2.554 |
| 2.566 | 2.570 | 2.586 | 2.629 | 2.633 |
| 2.642 | 2.648 | 2.684 | 2.697 | 2.726 |
| 2.770 | 2.773 | 2.800 | 2.809 | 2.818 |
| 2.821 | 2.848 | 2.880 | 2.954 | 3.012 |
| 3.067 | 3.084 | 3.090 | 3.096 | 3.128 |
| 3.233 | 3.433 | 3.585 | 3.585 |
| 8.958070 | 25.150000 | 5.015640 | 11.006760 | 5.279225 | 5.013624 | 6.435200 |
| 5.835900 | 7.000000 | 30.801862 | 7.266010 | 5.019073 | 8.000000 | 22.000000 |
| 5.514300 | 5.302930 | 7.968871 | 6.000000 | 7.058850 | 15.000000 | 5.155455 |
| 5.243266 | 5.219835 | 9.950000 | 12.041000 | 7.300000 | 5.743445 | 6.272980 |
| 5.070780 | 6.529300 | 6.000000 | 8.697271 | 46.067600 | 17.171580 | 6.098290 |
| 10.166405 | 5.445229 | 7.281530 | 7.757070 | 6.413050 | 5.331970 | 6.225743 |
| 14.399190 | 5.850000 | 5.653820 | 5.484998 | 5.257000 | 5.841250 | 8.265000 |
| 27.373000 | 5.412000 | 5.099400 | 5.145000 | 5.344151 | 7.064000 | 7.608040 |
| 6.346600 | 5.052410 | 5.623980 | 14.615000 | 5.358124 | 5.210000 | 68.570220 |
| 5.097540 | 5.400696 | 5.959290 | 5.148630 | 7.860000 | 5.104935 | 22.000000 |
| 8.985627 | 5.176840 | 5.177960 | 5.040000 | 7.419586 | 15.634430 | 5.146730 |
| 5.131308 | 7.153940 | 6.105075 | 5.100000 | 5.202800 | 6.371200 | 5.477140 |
| 5.309140 | 5.776270 | 6.301900 | 5.100000 | 12.041000 | 5.123362 | 5.133710 |
| 5.225000 | 5.030000 | 6.508635 | 5.012000 | 5.064560 | 5.500000 | 12.041000 |
| 5.115196 | 13.318230 | 5.147040 | 7.895000 | 5.050000 | 5.400000 | 6.441160 |
| 5.090940 | 5.369000 | 8.607168 | 5.455010 | 22.230579 | 5.376720 | 7.275880 |
| 13.920000 | 5.225000 | 31.122660 | 12.499400 | 5.342750 | 5.177051 | 7.556150 |
| 5.390042 | 6.433160 | 7.514053 | 10.695323 | 8.985627 | 5.247600 | 6.287972 |
| 16.052030 | 5.659609 | 5.100000 | 6.098817 | 6.101590 | 5.281640 |
References
- Smith, R. Maximum likelihood estimation in a class of nonregular cases. Biometrika 1985, 72, 67–90. [Google Scholar] [CrossRef]
- Cheng, R.; Iles, T. Corrected maximum likelihood in non-regular problems. J. R. Stat. Soc. Ser. B Stat. Methodol. 1987, 49, 95–101. [Google Scholar] [CrossRef]
- Lemon, G. Maximum likelihood estimation for the three parameter Weibull distribution based on censored samples. Technometrics 1975, 17, 247–254. [Google Scholar] [CrossRef]
- Cohen, C.; Whitten, B. Modified maximum likelihood and modified moment estimators for the three-parameter Weibull distribution. Commun. Stat.-Theory Methods 1982, 11, 2631–2656. [Google Scholar] [CrossRef]
- Zanakis, S.; Kyparisis, J. A review of maximum likelihood estimation methods for the three-parameter Weibull distribution. J. Stat. Comput. Simul. 1986, 25, 53–73. [Google Scholar] [CrossRef]
- Panchang, V.; Gupta, R. On the Determination of Three–Parameter Weibull MLE’s. Commun. Stat.-Simul. Comput. 1989, 18, 1037–1057. [Google Scholar] [CrossRef]
- Qiao, H.; Tsokos, C. Estimation of the three parameter Weibull probability distribution. Math. Comput. Simul. 1995, 39, 173–185. [Google Scholar] [CrossRef]
- Tsionas, E. Posterior analysis, prediction and reliability in three-parameter Weibull distributions. Commun. Stat.-Theory Methods 2000, 29, 1435–1449. [Google Scholar] [CrossRef]
- Abbasi, B.; Rabelo, L.; Hosseinkouchack, M. Estimating parameters of the three-parameter Weibull distribution using a neural network. Eur. J. Ind. Eng. 2008, 2, 428–445. [Google Scholar] [CrossRef]
- Kundu, D.; Raqab, M. Estimation of R = P(Y < X) for three-parameter Weibull distribution. Stat. Probab. Lett. 2009, 79, 1839–1846. [Google Scholar]
- Cousineau, D. Fitting the three-parameter Weibull distribution: Review and evaluation of existing and new methods. IEEE Trans. Dielectr. Electr. Insul. 2009, 16, 281–288. [Google Scholar] [CrossRef]
- Ng, H.; Luo, L.; Hu, Y.; Duan, F. Parameter estimation of three-parameter Weibull distribution based on progressively Type-II censored samples. J. Stat. Comput. Simul. 2012, 82, 1661–1678. [Google Scholar] [CrossRef]
- Nagatsuka, H.; Kamakura, T.; Balakrishnan, N. A consistent method of estimation for the three-parameter Weibull distribution. Comput. Stat. Data Anal. 2013, 58, 210–226. [Google Scholar] [CrossRef]
- Yang, F.; Yue, Z. Kernel density estimation of three-parameter Weibull distribution with neural network and genetic algorithm. Appl. Math. Comput. 2014, 247, 803–814. [Google Scholar] [CrossRef]
- Örkcü, H.; Aksoy, E.; Dogan, M. Estimating the parameters of 3-p Weibull distribution through differential evolution. Appl. Math. Comput. 2015, 251, 211–224. [Google Scholar] [CrossRef]
- Nagatsuka, H.; Balakrishnan, N. Existence, uniqueness and consistency of estimation of life characteristics of three-parameter Weibull distribution based on Type-II right censored data. J. Stat. Comput. Simul. 2016, 86, 1248–1279. [Google Scholar] [CrossRef]
- Montoya, J.; Díaz-Francés, E.; Figueroa, G. Estimation of the reliability parameter for three-parameter Weibull models. Appl. Math. Model. 2019, 67, 621–633. [Google Scholar] [CrossRef]
- Garrido, A.; Caro-Carretero, R.; Jimenez-Octavio, J.; Carnicero, A.; Such, M. A new approach to fitting the three-parameter Weibull distribution: An application to glass ceramics. Commun. Stat.-Theory Methods 2021, 50, 3403–3420. [Google Scholar] [CrossRef]
- Fonseca, T.; Quintino, F.; Ozelim, L.; Rathie, P. Estimation of P(X < Y) for Fréchet, reversed Weibull and Weibull distributions: Analytical expressions, simulations and applications. Netw. Heterog. Media 2024, 19, 4. [Google Scholar]
- Gu, J.; Kong, X.; Guo, J.; Qi, H.; Wang, Z. Parameter estimation of three-parameter Weibull distribution by hybrid gray genetic algorithm with modified maximum likelihood method with small samples. J. Mech. Sci. Technol. 2024, 38, 5363–5379. [Google Scholar] [CrossRef]
- Matsushita, S.; Hagiwara, K.; Shiota, T.; Shimada, H.; Kuramoto, K.; Toyokura, Y. Lifetime data analysis of disease and aging by the Weibull probability distribution. J. Clin. Epidemiol. 1992, 45, 1165–1175. [Google Scholar] [CrossRef] [PubMed]
- Gebizlioglu, O.; Şenoğlu, B.; Kantar, Y. Comparison of certain value-at-risk estimation methods for the two-parameter Weibull loss distribution. J. Comput. Appl. Math. 2011, 38, 3304–3314. [Google Scholar] [CrossRef]
- Clarke, R. Estimating trends in data from the Weibull and a generalized extreme value distribution. Water Resour. Res. 2002, 38, 25-1–25-10. [Google Scholar] [CrossRef]
- Papalexiou, S.; AghaKouchak, A.; Foufoula-Georgiou, E. A Diagnostic Framework for Understanding Climatology of Tails of Hourly Precipitation Extremes in the United States. Water Resour. Res. 2018, 54, 6725–6738. [Google Scholar] [CrossRef]
- Mittnik, S.; Rachev, S. Modeling asset returns with alternative stable distributions. Econom. Rev. 1993, 12, 261–330. [Google Scholar] [CrossRef]
- Kohout, J. Three-parameter Weibull distribution with upper limit applicable in reliability studies and materials testing. Microelectron. Reliab. 2022, 137, 114769. [Google Scholar] [CrossRef]
- Murthy, D.; Prabhakar, M.; Jiang, R. Weibull Models; John Wiley & Son: Hoboken, NJ, USA, 2004. [Google Scholar]
- Johnson, N.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions; John Wiley & Son: Hoboken, NJ, USA, 1994. [Google Scholar]
- Pantcheva, E. Limit theorems for extreme order statistics under nonlinear normalization. Stab. Probl. Stoch. Models 1985, 12, 284–309. [Google Scholar]
- Mohan, N.; Ravi, S. Max domains of attraction of univariate and multivariate p-max stable laws. Theory Probab. Its Appl. 1993, 37, 632–643. [Google Scholar] [CrossRef]
- Quintino, F.; Rathie, P.; Ozelim, L.; Fonseca, T. Estimation of P(X < Y) Stress–Strength Reliability Measures for a Class of Asymmetric Distributions: The Case of Three-Parameter p-Max Stable Laws. Symmetry 2024, 16, 837. [Google Scholar] [CrossRef]
- Firth, D. Bias reduction of maximum likelihood estimates. Biometrika 1993, 80, 27–38. [Google Scholar] [CrossRef]
- Heinze, G.; Schemper, M. A solution to the problem of monotone likelihood in Cox regression. Biometrics 2001, 57, 114–119. [Google Scholar] [CrossRef] [PubMed]
- Arrué, J.; Arellano-Valle, R.; Gómez, H. Bias reduction of maximum likelihood estimates for a modified skew-normal distribution. J. Stat. Comput. Simul. 2016, 86, 2967–2984. [Google Scholar] [CrossRef]
- Almeida, F.; Colosimo, E.; Mayrink, V. Modified score function for monotone likelihood in the semiparametric mixture cure model. Biometr. J. 2022, 64, 635–654. [Google Scholar] [CrossRef] [PubMed]
- Arrué, J.; Arellano-Valle, R.; Calderín-Ojeda, E.; Venegas, O.; Gómez, H. Likelihood Based Inference and Bias Reduction in the Modified Skew-t-Normal Distribution. Mathematics 2023, 11, 3287. [Google Scholar] [CrossRef]
- Lima, V.; Cribari-Neto, F. Penalized maximum likelihood estimation in the modified extended Weibull distribution. Commun. Stat.-Simul. Comput. 2019, 48, 334–349. [Google Scholar] [CrossRef]
- Ali, M.; Pal, M.; Woo, J. Estimation of P(Y < X) in a four-parameter generalized gamma distribution. Austrian J. Stat. 2012, 41, 197–210. [Google Scholar]
- Kundu, D.; Raqab, M. Journal of Statistical Computation and Simulation. J. Stat. Comput. Simul. 2015, 85, 725–739. [Google Scholar] [CrossRef]
- Kohansal, A.; Rezakhah, S. Inference of R = P(Y < X) for two-parameter Rayleigh distribution based on progressively censored samples. Statistics 2019, 53, 81–100. [Google Scholar]
- Cheng, R.; Traylor, L. Non-regular maximum likelihood problems. J. R. Stat. Soc. Ser. B Stat. Methodol. 1995, 57, 3–24. [Google Scholar] [CrossRef]
- Almeida, F.; Colosimo, E.; Mayrink, V. Prior specifications to handle the monotone likelihood problem in the Cox regression model. Stat. Its Interface 2018, 11, 687–698. [Google Scholar] [CrossRef]
- Almeida, F.; Colosimo, E.; Mayrink, V. Firth adjusted score function for monotone likelihood in the mixture cure fraction model. Lifetime Data Anal. 2021, 27, 131–155. [Google Scholar] [CrossRef] [PubMed]
- Bull, S.; Mak, C.; Greenwood, C. A modified score function estimator for multinomial logistic regression in small samples. Comput. Stat. Data Anal. 2002, 39, 57–74. [Google Scholar] [CrossRef]
- Heinze, G.; Ploner, M. Fixing the nonconvergence bug in logistic regression with SPLUS and SAS. Comput. Methods Programs Biomed. 2003, 71, 181–187. [Google Scholar] [CrossRef] [PubMed]
- Cox, D.; Hinkley, D. Theoretical Statistics; CRC Press: Boca Raton, FL, USA, 1979. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2025; Available online: https://www.R-project.org/ (accessed on 2 March 2025).
- Bader, M.; Priest, A. Statistical Aspects of Fiber and Bundle Strength in Hybrid Composites. In Progress in Science and Engineering Composites; Hayashi, T., Kawata, S., Umekawa, S., Eds.; ICCM-IV: Tokyo, Japan, 1982; pp. 1129–1136. [Google Scholar]
- Dunn, P.; Smyth, G. Randomized quantile residuals. J. Comput. Graph. Stat. 1996, 10, 236–244. [Google Scholar] [CrossRef]




| Estimation Method | AIC | BIC | ||||
|---|---|---|---|---|---|---|
| MMLE | 2.380 (0.225) | 1.801 (0.278) | 1.312 | −51.674 | 109.349 | 116.051 |
| CMLE | 2.275 (0.215) | 1.705 (0.258) | 1.312 | −55.987 | 117.974 | 124.677 |
| DMMLE | 2.342 (0.221) | 1.714 (0.260) | 1.312 | −51.729 | 109.458 | 116.160 |
| Country of Origin | Value (×BRL 100,000) |
|---|---|
| France | 209.65 |
| Italy | 174.58 |
| China | 169.68 |
| Germany | 133.79 |
| Netherlands | 73.64 |
| United Kingdom | 48.64 |
| Portugal | 47.05 |
| Belgium | 42.19 |
| Spain | 38.09 |
| Romania | 33.45 |
| Estimation Method | AIC | BIC | ||||
|---|---|---|---|---|---|---|
| MMLE | 0.569 (0.039) | 1.535 (0.161) | 5.012 | −250.815 | 507.630 | 516.280 |
| CMLE | 0.565 (0.039) | 1.516 (0.158) | 5.012 | −252.279 | 510.558 | 519.206 |
| DMMLE | 0.565 (0.039) | 1.498 (0.156) | 5.012 | −250.842 | 507.684 | 516.333 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
da Silva, A.; Quintino, F.; Almeida, F.; Aguiar, D. Bias Reduction of Modified Maximum Likelihood Estimates for a Three-Parameter Weibull Distribution. Entropy 2025, 27, 485. https://doi.org/10.3390/e27050485
da Silva A, Quintino F, Almeida F, Aguiar D. Bias Reduction of Modified Maximum Likelihood Estimates for a Three-Parameter Weibull Distribution. Entropy. 2025; 27(5):485. https://doi.org/10.3390/e27050485
Chicago/Turabian Styleda Silva, Adriana, Felipe Quintino, Frederico Almeida, and Dióscoros Aguiar. 2025. "Bias Reduction of Modified Maximum Likelihood Estimates for a Three-Parameter Weibull Distribution" Entropy 27, no. 5: 485. https://doi.org/10.3390/e27050485
APA Styleda Silva, A., Quintino, F., Almeida, F., & Aguiar, D. (2025). Bias Reduction of Modified Maximum Likelihood Estimates for a Three-Parameter Weibull Distribution. Entropy, 27(5), 485. https://doi.org/10.3390/e27050485





