Chandrasekhar’s Conditions for the Equilibrium and Stability of Stars in a Universal Three-Parameter Non-Maxwell Distribution
Abstract
1. Introduction
2. The Gas Pressure in the Non-Maxwell Distribution
3. Generalized Chandrasekhar Condition of a Gas Star
4. Generalized Chandrasekhar Condition of a Centrally Condensed Star
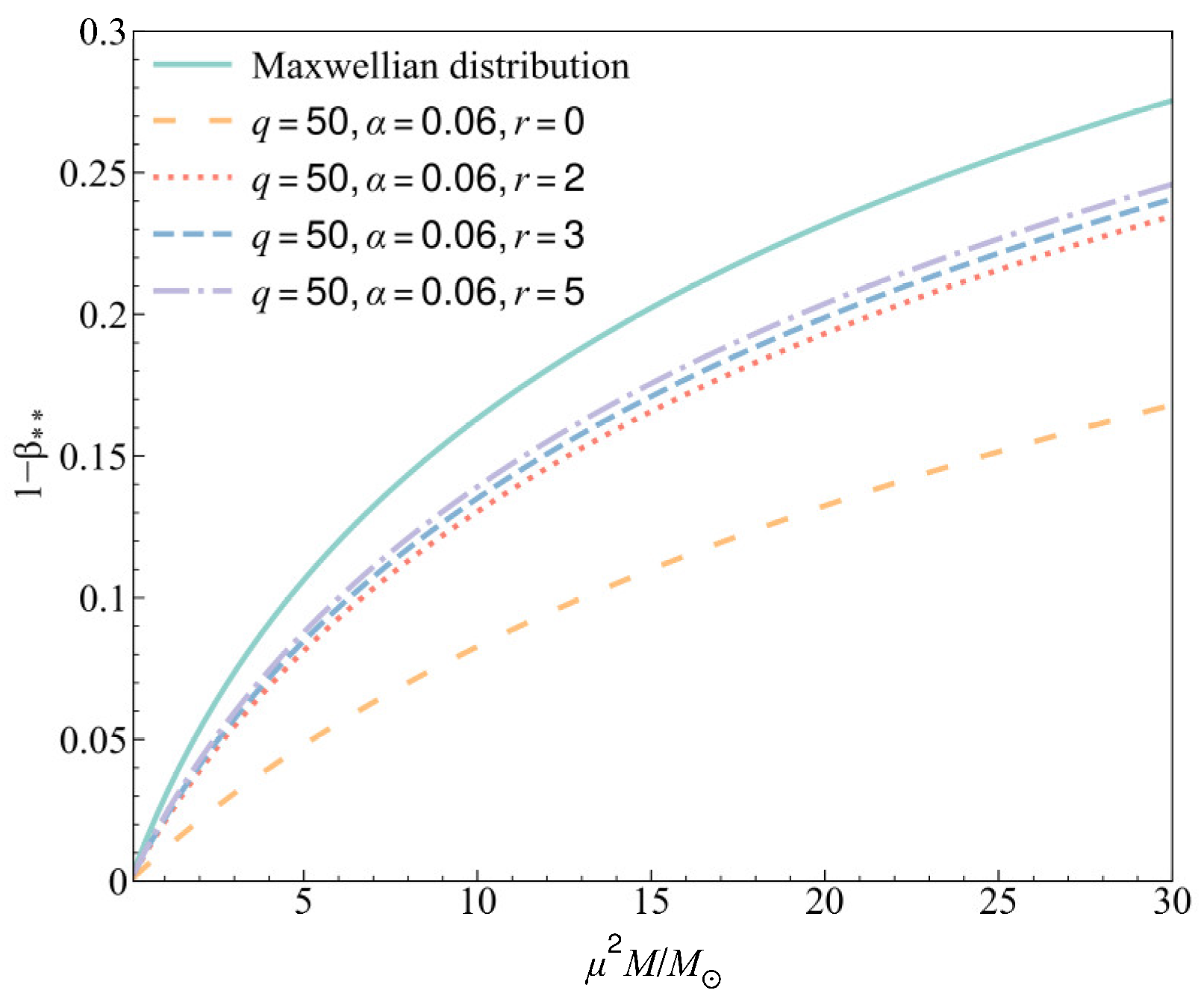
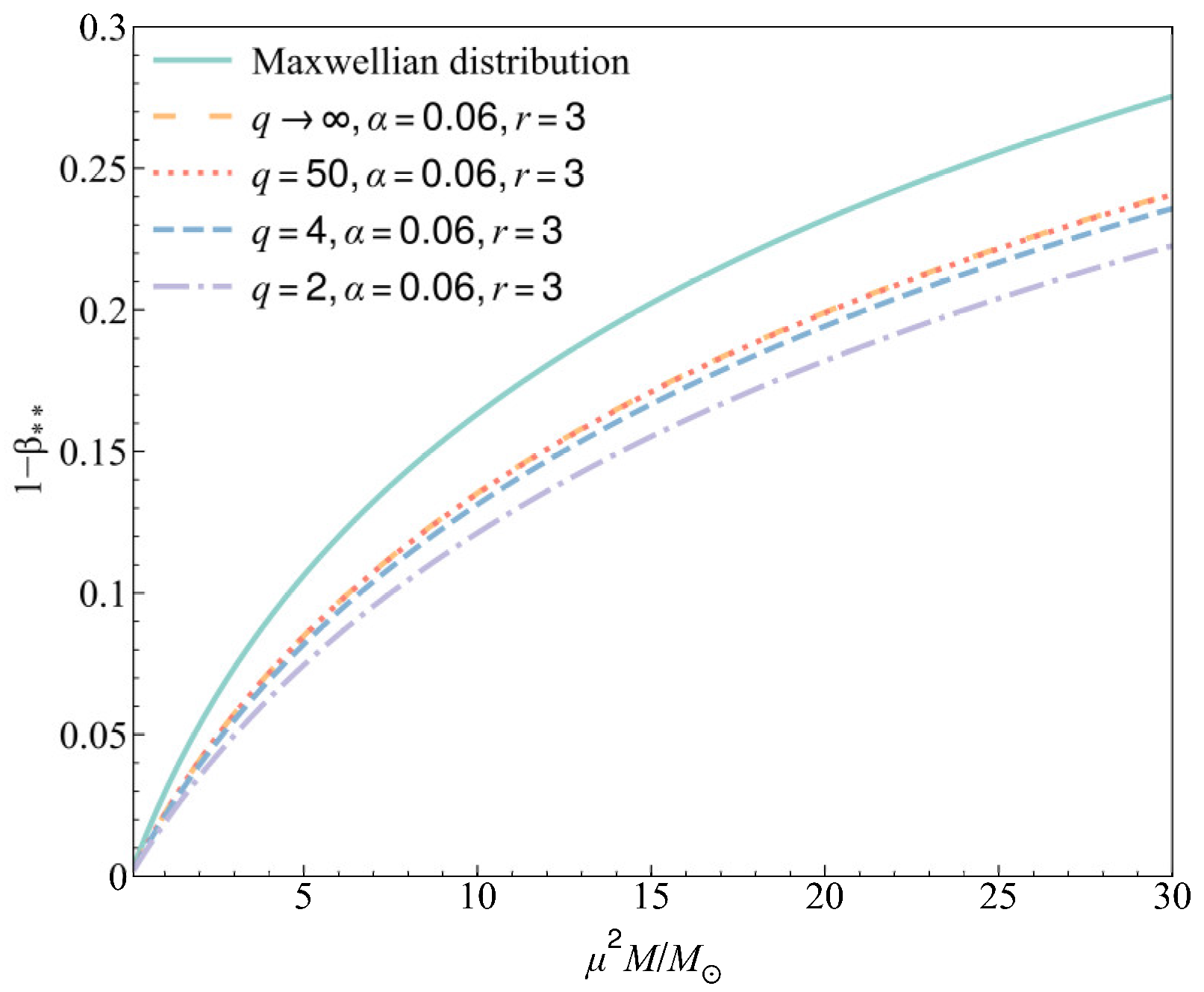
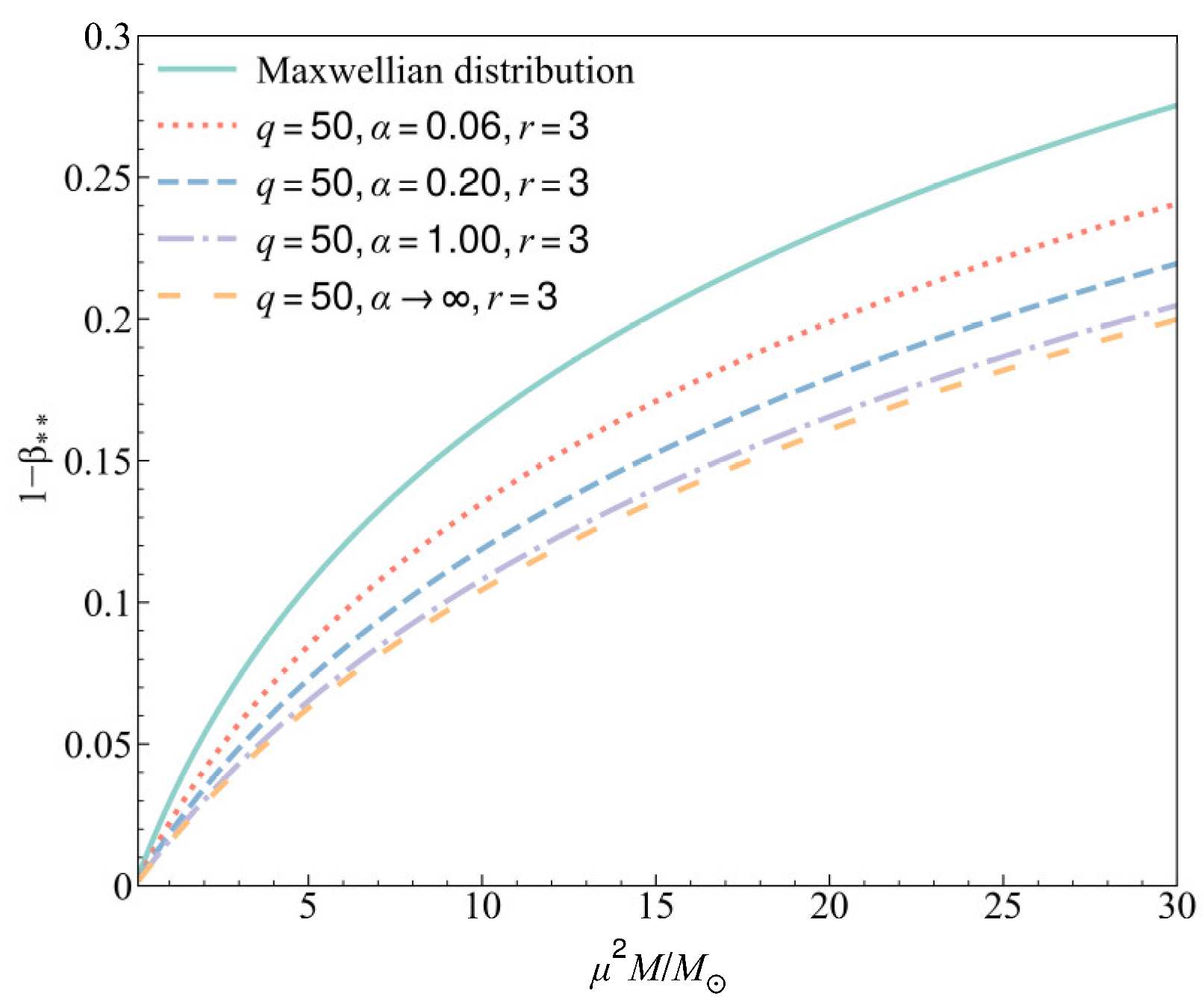
5. Numerical Analyses
6. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Eddington, A.S. Further Notes on the Radiative Equilibrium of the Stars. Mon. Not. R. Astron. Soc. 1917, 77, 596–612. [Google Scholar] [CrossRef][Green Version]
- Eddington, A.S. A Source Book in Astronomy and Astrophysics, 1900–1975; Kenneth, R.L., Owen, G., Eds.; Harvard University Press: Cambridge, UK, 1979; pp. 281–290. [Google Scholar]
- Chandrasekhar, S. The pressure in the interior of a star. Mon. Not. R. Astron. Soc. 1936, 96, 644–647. [Google Scholar] [CrossRef]
- Chandrasekhar, S. On stars, their evolution and their stability. Rev. Mod. Phys. 1984, 56, 137–147. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Some remarks on the state of matter in the interior of stars. J. Astrophys. Astron. 1994, 15, 119–125. [Google Scholar] [CrossRef]
- Vasyliunas, V.M. A survey of low-energy electrons in the evening sector of the magnetosphere with OGO 1 and OGO 3. J. Geophys. Res. 1968, 73, 2839–2884. [Google Scholar] [CrossRef]
- Cairns, R.A.; Mamum, A.A.; Bingham, R.; Boström, R.; Dendy, R.O.; Nairn, C.M.C.; Shukla, P.K. Electrostatic solitary structures in non-thermal plasmas. Geophys. Res. Lett. 1995, 22, 2709–2712. [Google Scholar] [CrossRef]
- Ali, S.; Abid, A.A.; Du, J.; Mamun, A.A. Dust surface potential in a generalized (r, q)-distributed multi-ion dusty plasma. Contrib. Plasma Phys. 2018, 58, 976–984. [Google Scholar] [CrossRef]
- Abid, A.A.; Ali, S.; Du, J.; Mamun, A.A. Vasyliunas-Cairns distribution function for space plasma species. Phys. Plasmas 2015, 22, 084507. [Google Scholar] [CrossRef]
- Cranmer, S.R. Non-Maxwellian redistribution in solar coronal Lyα emission. Astrophys. J. 1998, 508, 925. [Google Scholar] [CrossRef]
- Tao, J.; Wang, L.; Zong, Q.; Li, G.; Salem, C.S.; Wimmer-Schweingruber, R.F.; He, J.; Tu, C.; Bale, S.D. Quiet-time suprathermal (~0.1-1.5keV) electrons in the solar wind. Astrophys. J. 2016, 820, 22. [Google Scholar] [CrossRef]
- Wei, N.; Liu, Y. Small amplitude dust ion-acoustic solitons in dusty plasma with regularized kappa distributed electron. Eur. Phys. J. Plus 2024, 139, 1–11. [Google Scholar] [CrossRef]
- El-Taibany, W.F.; El-Siragy, N.M.; Behery, E.E.; El-Bendary, A.A.; Taha, R.M. Dust acoustic waves in a dusty plasma containing hybrid Cairns–Tsallis-distributed electrons and variable size dust grains. Chin. J. Phys. 2019, 58, 151–158. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Y. Small-amplitude kinetic Alfven solitons for hot electrons taking regularized kappa distribution in Earth’s inner magnetosphere. Contrib. Plasma Phys. 2023, 63, e202300009. [Google Scholar] [CrossRef]
- Alharthi, N.S. Nonlinear wave phenomena in Jupiter’s magnetosphere: Cnoidal waves and shock-like waves. Results Phys. 2024, 58, 107462. [Google Scholar] [CrossRef]
- Abid, A.A.; Khan, M.Z.; Lu, Q.; Yap, S.L. A generalized AZ-non-Maxwellian velocity distribution function for space plasmas. Phys. Plasmas 2017, 24, 033702. [Google Scholar] [CrossRef]
- Yao, G.; Du, J. Dust surface potential for the dusty plasma with negative ions and with a three-parameter non-Maxwell velocity distribution. Europhys. Lett. 2021, 132, 40002. [Google Scholar] [CrossRef]
- Pierrard, V.; Lazar, M. Kappa distributions: Theory and applications in space plasmas. Sol. Phys. 2010, 267, 153–174. [Google Scholar] [CrossRef]
- Paquette, C.; Pelletier, C.; Fontaine, G.; Michaud, G. Diffusion coefficients for stellar plasmas. Astrophys. J. Suppl. Ser. 1986, 61, 177–195. [Google Scholar] [CrossRef]
- Kosovichev, A.G. Probing plasma properties and dynamics inside the Sun. Adv. Space Res. 2006, 37, 1455–1466. [Google Scholar] [CrossRef]
- Sabry, R.; Moslem, W.M.; Shukla, P.K. Freak waves in white dwarfs and magnetars. Phys. Plasmas 2012, 19, 122903. [Google Scholar] [CrossRef]
- Van Horn, H.M. Dense astrophysical plasmas. Science 1991, 252, 384–389. [Google Scholar] [CrossRef]
- Du, J. Test of nonextensive statistical mechanics by solar sound speeds. Europhys. Lett. 2006, 75, 861. [Google Scholar] [CrossRef]
- Ko, Y.K.; Fisk, L.A.; Gloeckler, G.; Geiss, J. Limitations on suprathermal tails of electrons in the lower solar corona. Geophys. Res. Lett. 1996, 23, 2785–2788. [Google Scholar] [CrossRef]
- Ayaz, S.; Li, G.; Khan, I.A. Solar coronal heating by kinetic alfvén waves. Astrophys. J. 2024, 970, 140. [Google Scholar] [CrossRef]
- Ayaz, S.; Zank, G.P.; Khan, I.A.; Li, G.; Rivera, Y.J. Alfvén waves in the solar corona: Resonance velocity, damping length, and charged particles acceleration by kinetic Alfvén waves. Sci. Rep. 2024, 14, 27275. [Google Scholar] [CrossRef]
- Pinfield, D.J.; Keenan, F.P.; Mathioudakis, M.; Phillips, K.J.H.; Curdt, W.; Wilhelm, K. Evidence for non-Maxwellian electron energy distributions in the solar transition region: Si III line ratios from SUMER. Astrophys. J. 1999, 527, 1000. [Google Scholar] [CrossRef]
- Du, J. The Chandrasekhar’s condition of the equilibrium and stability for a star in the nonextensive kinetic theory. New Astron. 2006, 12, 60–63. [Google Scholar]
- Yu, H.; Du, J. The nonextensive parameter for the rotating astrophysical systems with power-law distributions. Europhys. Lett. 2016, 116, 60005. [Google Scholar] [CrossRef][Green Version]
- Bryant, D.A. Debye length in a kappa-distribution plasma. J. Plasma Phys. 1996, 56, 87–93. [Google Scholar] [CrossRef]
- Hellberg, M.A.; Mace, R.L.; Baluku, T.K.; Kourakis, I.; Saini, N.S. Comment on “Mathematical and physical aspects of Kappa velocity distribution”. Phys. Plasmas 2009, 16, 094701. [Google Scholar] [CrossRef]
| r | q | α | Zr,q,α | |
|---|---|---|---|---|
| 0 | ∞ | 0 | 1.00 | 9.21% |
| 0 | 50 | 0.06 | 1.69 | 1.24% |
| 2 | 50 | 0.06 | 1.21 | 4.54% |
| 3 | 50 | 0.06 | 1.17 | 5.06% |
| 5 | 50 | 0.06 | 1.15 | 5.55% |
| ∞ | 50 | 0.06 | 1 | 9.21% |
| r | Q | α | Zr,q,α | |
|---|---|---|---|---|
| 0 | ∞ | 0 | 1.00 | 9.21% |
| 3 | ∞ | 0.06 | 1.17 | 5.09% |
| 3 | 50 | 0.06 | 1.17 | 5.06% |
| 3 | 4 | 0.06 | 1.20 | 4.63% |
| 3 | 2 | 0.06 | 1.28 | 3.64% |
| r | q | α | Zr,q,α | |
|---|---|---|---|---|
| 0 | ∞ | 0 | 1.00 | 9.21% |
| 3 | 50 | 0.06 | 1.17 | 5.06% |
| 3 | 50 | 0.20 | 1.30 | 3.44% |
| 3 | 50 | 1.00 | 1.40 | 2.60% |
| 3 | 50 | ∞ | 1.43 | 2.36% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, W.; Du, J. Chandrasekhar’s Conditions for the Equilibrium and Stability of Stars in a Universal Three-Parameter Non-Maxwell Distribution. Entropy 2025, 27, 470. https://doi.org/10.3390/e27050470
Hu W, Du J. Chandrasekhar’s Conditions for the Equilibrium and Stability of Stars in a Universal Three-Parameter Non-Maxwell Distribution. Entropy. 2025; 27(5):470. https://doi.org/10.3390/e27050470
Chicago/Turabian StyleHu, Wei, and Jiulin Du. 2025. "Chandrasekhar’s Conditions for the Equilibrium and Stability of Stars in a Universal Three-Parameter Non-Maxwell Distribution" Entropy 27, no. 5: 470. https://doi.org/10.3390/e27050470
APA StyleHu, W., & Du, J. (2025). Chandrasekhar’s Conditions for the Equilibrium and Stability of Stars in a Universal Three-Parameter Non-Maxwell Distribution. Entropy, 27(5), 470. https://doi.org/10.3390/e27050470






