Multiscale Simplicial Complex Entropy Analysis of Heartbeat Dynamics
Abstract
1. Introduction
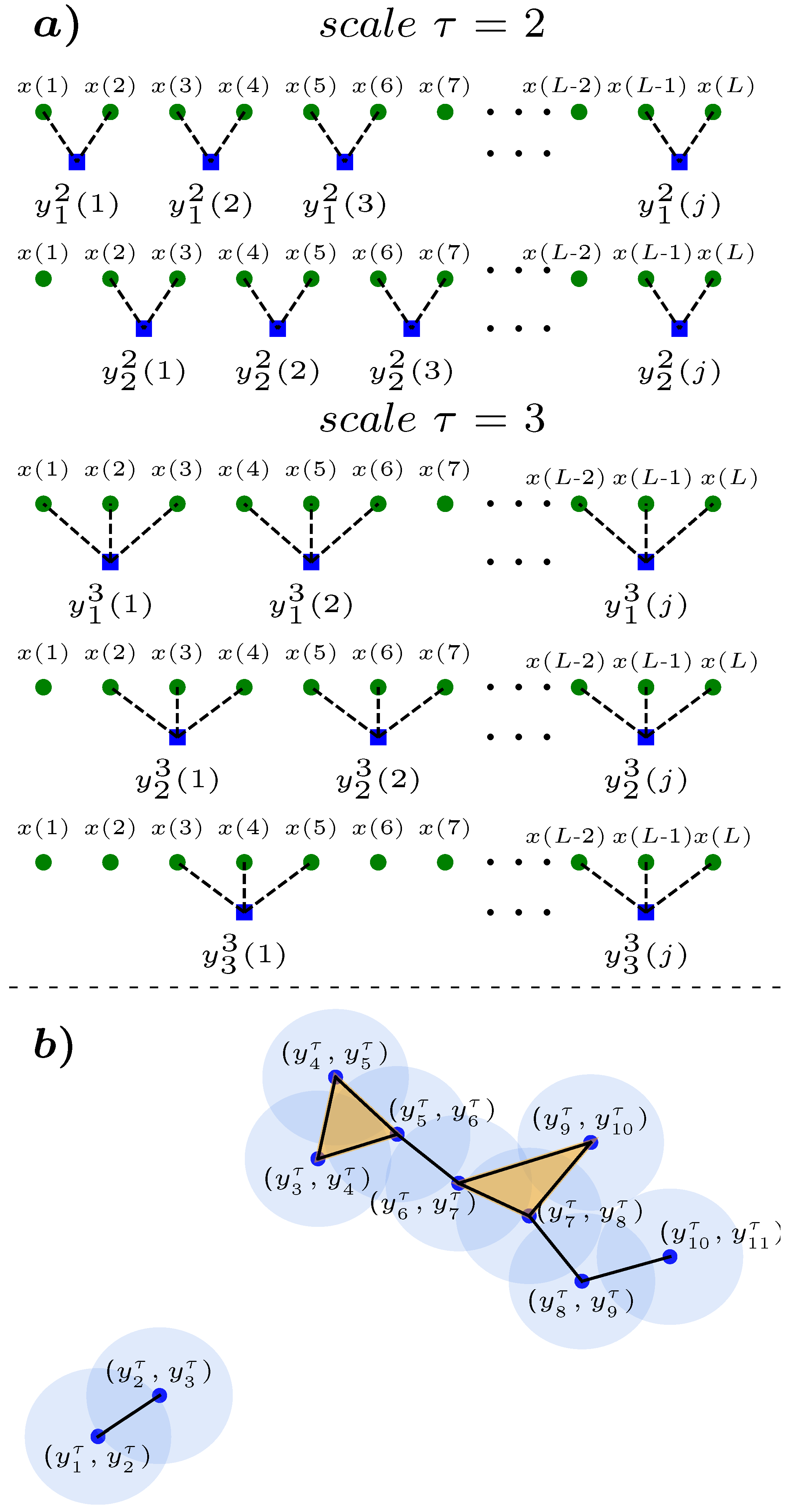
2. Methods and Database
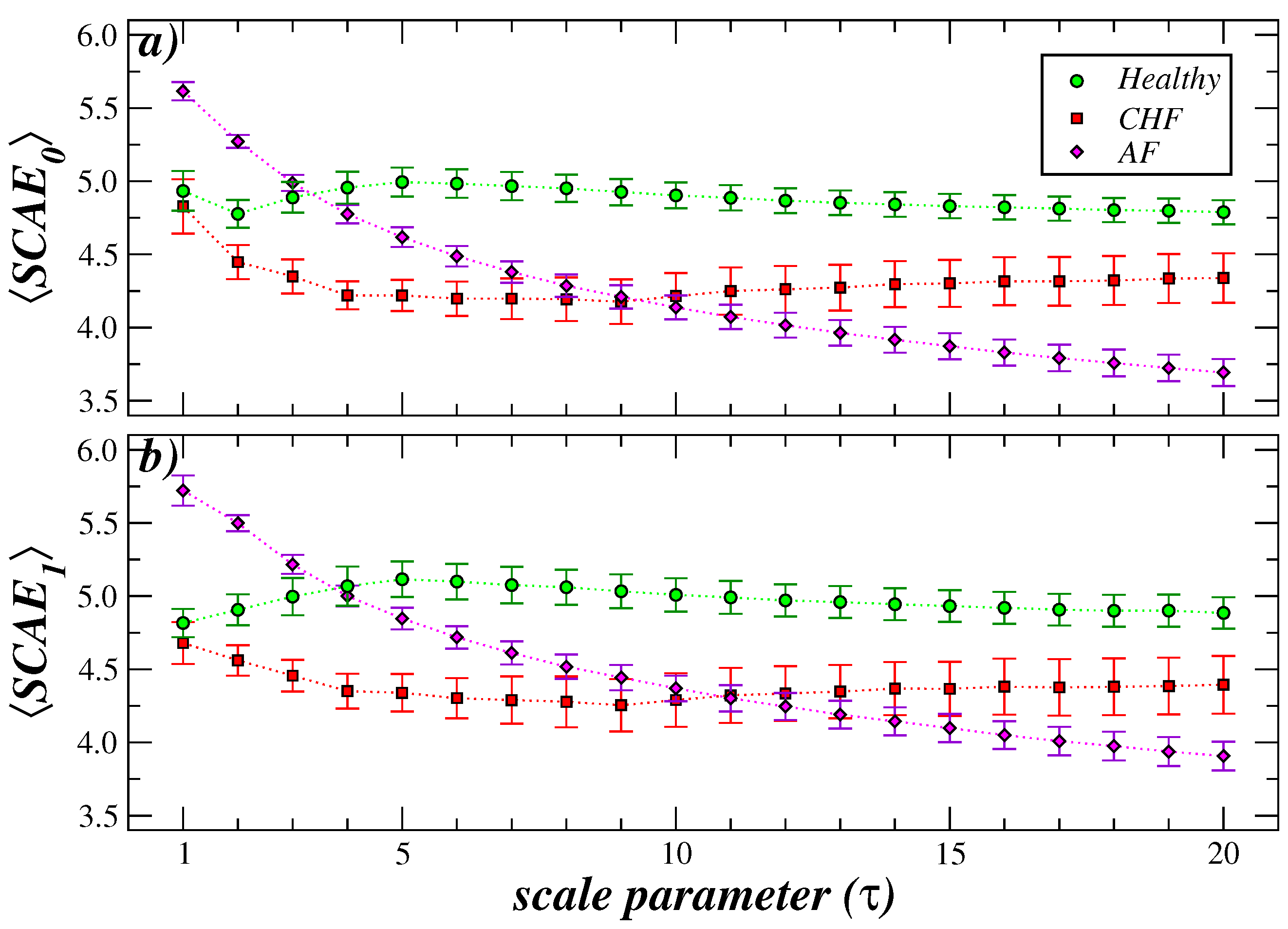
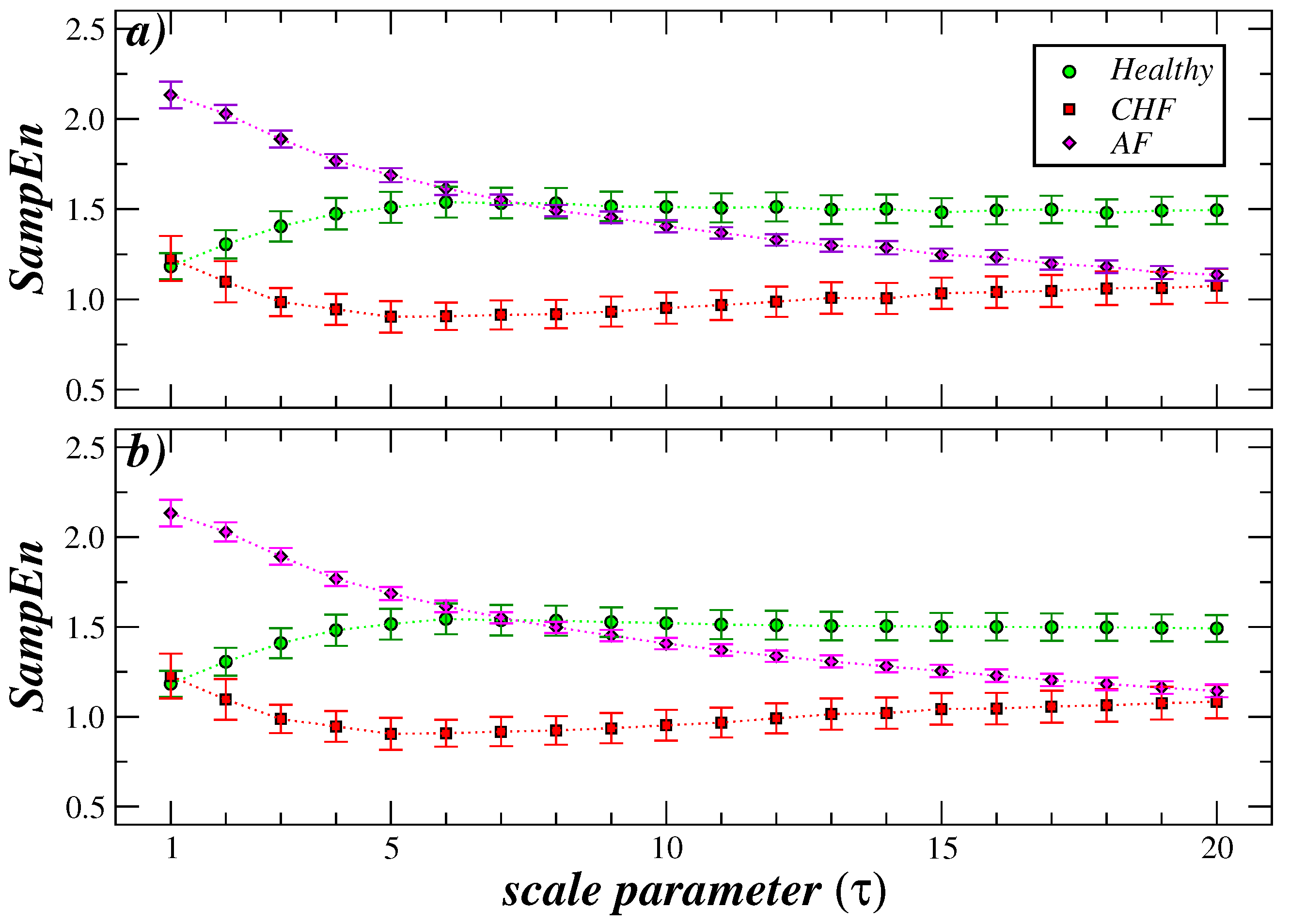
3. Results
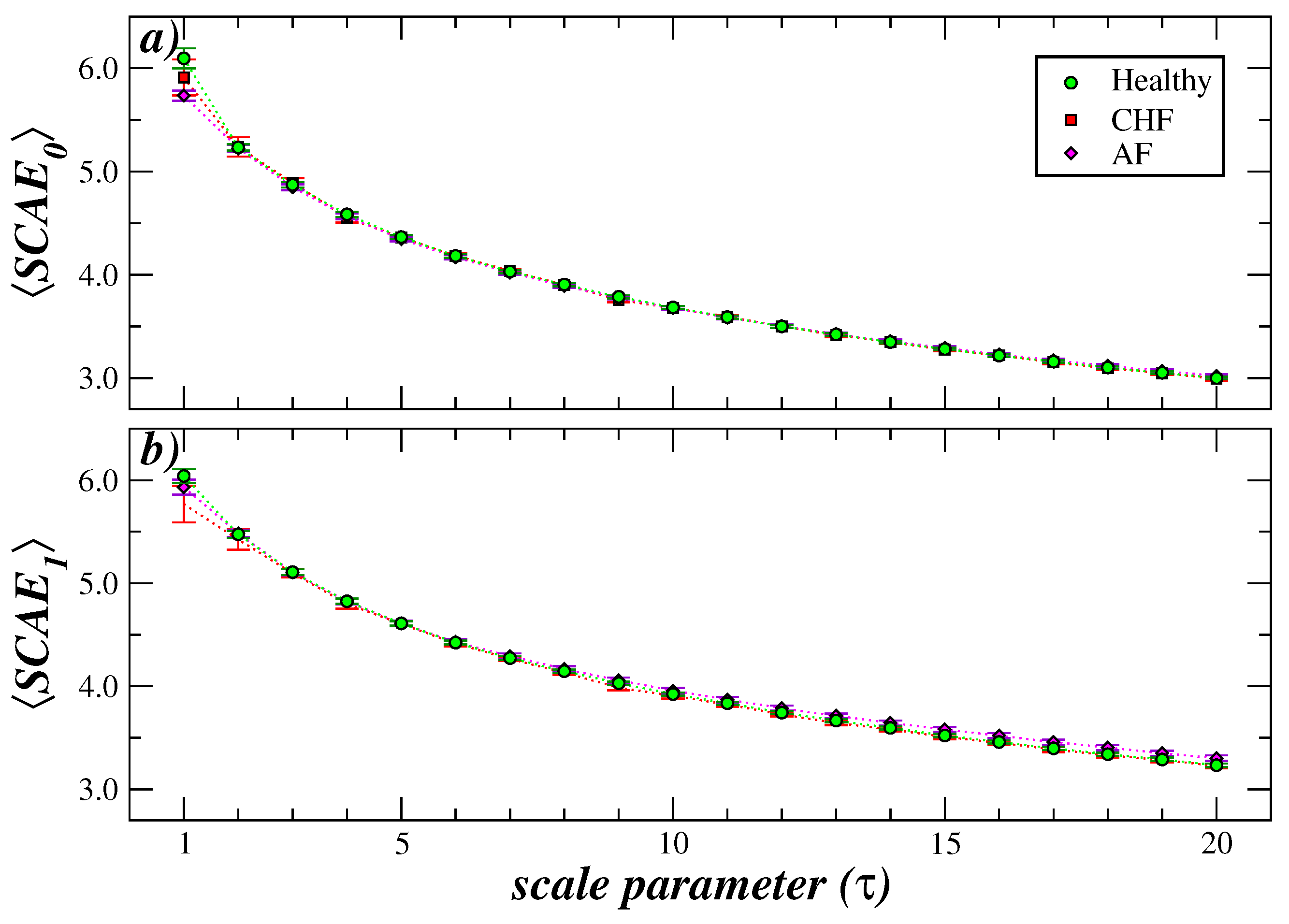
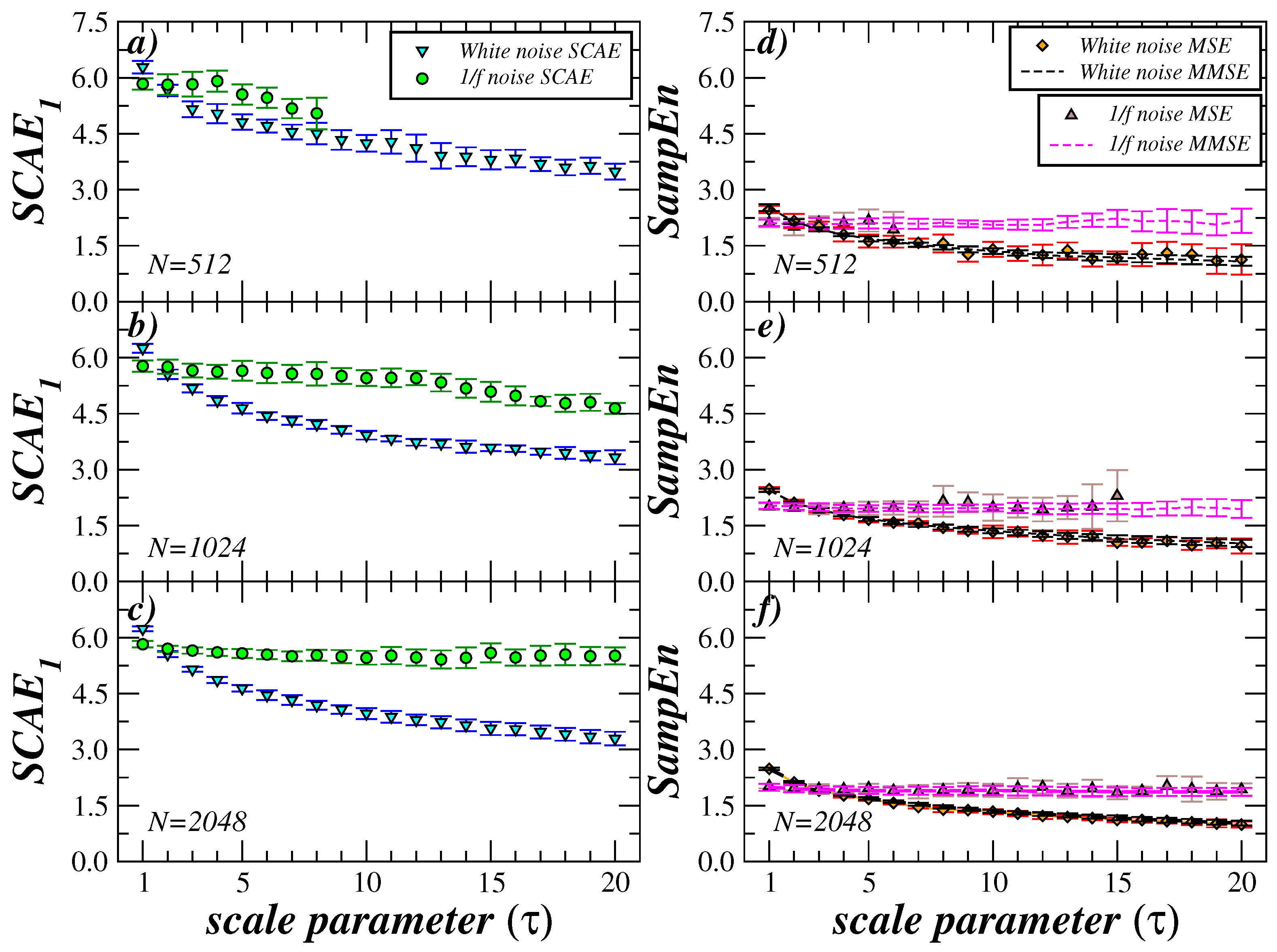
4. Comparison with Other Multiscale Methods and Length of the Time Series
5. Discussion and Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bassingthwaighte, J.B.; Liebovitch, L.S.; West, B.J. Fractal Physiology; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Eckmann, J.P.; Ruelle, D. Ergodic theory of chaos and strange attractors. Rev. Mod. Phys. 1985, 57, 617–656. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol.-Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed]
- Pincus, S. Approximate entropy (ApEn) as a complexity measure. Chaos Interdiscip. J. Nonlinear Sci. 1995, 5, 110–117. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71, 021906. [Google Scholar] [CrossRef]
- Lake, D.E.; Richman, J.S.; Griffin, M.P.; Moorman, J.R. Sample entropy analysis of neonatal heart rate variability. Am. J. Physiol.-Regul. Integr. Comp. Physiol. 2002, 283, R789–R797. [Google Scholar] [CrossRef]
- Zhang, T.; Yang, Z.; Coote, J.H. Cross-sample entropy statistic as a measure of complexity and regularity of renal sympathetic nerve activity in the rat. Exp. Physiol. 2007, 92, 659–669. [Google Scholar] [CrossRef]
- Xie, H.B.; Guo, J.Y.; Zheng, Y.P. Fuzzy approximate entropy analysis of chaotic and natural complex systems: Detecting muscle fatigue using electromyography signals. Ann. Biomed. Eng. 2010, 38, 1483–1496. [Google Scholar] [CrossRef]
- Faust, O.; Bairy, M.G. Nonlinear analysis of physiological signals: A review. J. Mech. Med. Biol. 2012, 12, 1240015. [Google Scholar] [CrossRef]
- Terrien, J.; Germain, G.; Marque, C.; Karlsson, B. Bivariate piecewise stationary segmentation; improved pre-treatment for synchronization measures used on non-stationary biological signals. Med. Eng. Phys. 2013, 35, 1188–1196. [Google Scholar] [CrossRef]
- Liang, Z.; Wang, Y.; Sun, X.; Li, D.; Voss, L.J.; Sleigh, J.W.; Hagihira, S.; Li, X. EEG entropy measures in anesthesia. Front. Comput. Neurosci. 2015, 9, 16. [Google Scholar] [CrossRef] [PubMed]
- Aguilar-Velázquez, D.; Guzmán-Vargas, L. Critical synchronization and 1/f noise in inhibitory/excitatory rich-club neural networks. Sci. Rep. 2019, 9, 1258. [Google Scholar] [CrossRef] [PubMed]
- Delgado-Bonal, A.; Marshak, A. Approximate Entropy and Sample Entropy: A Comprehensive Tutorial. Entropy 2019, 21, 541. [Google Scholar] [CrossRef] [PubMed]
- Jamin, A.; Duval, G.; Annweiler, C.; Abraham, P.; Humeau-Heurtier, A. Study of the influence of Age: Use of Sample Entropy and CEEMDAN on Navigation Data Acquired from a Bike Simulator. In Proceedings of the 2020 Tenth International Conference on Image Processing Theory, Tools and Applications (IPTA), Paris, France, 9–12 November 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Kleinbub, J.R.; Talia, A.; Palmieri, A. Physiological synchronization in the clinical process: A research primer. J. Couns. Psychol. 2020, 67, 420. [Google Scholar] [CrossRef]
- Peng, C.K.; Mietus, J.; Hausdorff, J.M.; Havlin, S.; Stanley, H.E.; Goldberger, A.L. Long-range anticorrelations and non-Gaussian behavior of the heartbeat. Phys. Rev. Lett. 1993, 70, 1343–1346. [Google Scholar] [CrossRef]
- Ivanov, P.C. Long-range dependence in heartbeat dynamics. In Processes with Long-Range Correlations: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2003; pp. 339–372. [Google Scholar] [CrossRef]
- Platisa, M.M.; Gal, V. Correlation properties of heartbeat dynamics. Eur. Biophys. J. 2008, 37, 1247–1252. [Google Scholar] [CrossRef]
- Costa, M.D.; Goldberger, A.L. Generalized Multiscale Entropy Analysis: Application to Quantifying the Complex Volatility of Human Heartbeat Time Series. Entropy 2015, 17, 1197–1203. [Google Scholar] [CrossRef]
- Guzmán-Vargas, L.; Angulo-Brown, F. Simple model of the aging effect in heart interbeat time series. Phys. Rev. E 2003, 67, 052901. [Google Scholar] [CrossRef]
- Guzmán-Vargas, L.; Muñoz-Diosdado, A.; Angulo-Brown, F. Influence of the loss of time-constants repertoire in pathologic heartbeat dynamics. Phys. A Stat. Mech. Its Appl. 2005, 348, 304–316. [Google Scholar] [CrossRef]
- Amaral, L.A.N.; Ivanov, P.C.; Aoyagi, N.; Hidaka, I.; Tomono, S.; Goldberger, A.L.; Stanley, H.E.; Yamamoto, Y. Behavioral-independent features of complex heartbeat dynamics. Phys. Rev. Lett. 2001, 86, 6026. [Google Scholar] [CrossRef]
- Ivanov, P.C.; Amaral, L.A.N.; Goldberger, A.L.; Havlin, S.; Rosenblum, M.G.; Struzik, Z.R.; Stanley, H.E. Multifractality in human heartbeat dynamics. Nature 1999, 399, 461–465. [Google Scholar] [CrossRef] [PubMed]
- Nardelli, M.; Lanata, A.; Bertschy, G.; Scilingo, E.P.; Valenza, G. Heartbeat complexity modulation in bipolar disorder during daytime and nighttime. Sci. Rep. 2017, 7, 17920. [Google Scholar] [CrossRef] [PubMed]
- Bian, C.; Qin, C.; Ma, Q.D.; Shen, Q. Modified permutation-entropy analysis of heartbeat dynamics. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2012, 85, 021906. [Google Scholar] [CrossRef] [PubMed]
- Shi, B.; Zhang, Y.; Yuan, C.; Wang, S.; Li, P. Entropy analysis of short-term heartbeat interval time series during regular walking. Entropy 2017, 19, 568. [Google Scholar] [CrossRef]
- Li, P.; Liu, C.; Li, K.; Zheng, D.; Liu, C.; Hou, Y. Assessing the complexity of short-term heartbeat interval series by distribution entropy. Med. Biol. Eng. Comput. 2015, 53, 77–87. [Google Scholar] [CrossRef]
- Lake, D.E. Renyi entropy measures of heart rate Gaussianity. IEEE Trans. Biomed. Eng. 2005, 53, 21–27. [Google Scholar] [CrossRef]
- Porta, A.; Guzzetti, S.; Montano, N.; Furlan, R.; Pagani, M.; Malliani, A.; Cerutti, S. Entropy, entropy rate, and pattern classification as tools to typify complexity in short heart period variability series. IEEE Trans. Biomed. Eng. 2002, 48, 1282–1291. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale Entropy Analysis of Complex Physiologic Time Series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef]
- Guzman-Vargas, L.; Ramírez-Rojas, A.; Angulo-Brown, F. Multiscale entropy analysis of electroseismic time series. Nat. Hazards Earth Syst. Sci. 2008, 8, 855–860. [Google Scholar] [CrossRef]
- Xia, J.; Shang, P. Multiscale entropy analysis of financial time series. Fluct. Noise Lett. 2012, 11, 1250033. [Google Scholar] [CrossRef]
- Silva, L.E.; Duque, J.J.; Felipe, J.C.; Murta, L.O., Jr.; Humeau-Heurtier, A. Two-dimensional multiscale entropy analysis: Applications to image texture evaluation. Signal Process. 2018, 147, 224–232. [Google Scholar] [CrossRef]
- Borowiec, M.; Litak, G.; Hunicz, J.; Koszałka, G.; Niewczas, A. Vertical Vibrations of a Vehicle Excited by Real Road Profiles. In PAMM: Proceedings in Applied Mathematics and Mechanics; Wiley Online Library: Hoboken, NJ, USA, 2008; Volume 8, pp. 10713–10714. [Google Scholar]
- Costa, M.; Goldberger, A.; Peng, C.K. Multiscale entropy to distinguish physiologic and synthetic RR time series. In Proceedings of the Computers in Cardiology, Memphis, TN, USA, 22–25 September 2002; Volume 19, pp. 137–140. [Google Scholar] [CrossRef]
- Wu, S.D.; Wu, C.W.; Lin, S.G.; Wang, C.C.; Lee, K.Y. Time Series Analysis Using Composite Multiscale Entropy. Entropy 2013, 15, 1069–1084. [Google Scholar] [CrossRef]
- Valencia, J.F.; Porta, A.; Vallverdu, M.; Claria, F.; Baranowski, R.; Orlowska-Baranowska, E.; Caminal, P. Refined multiscale entropy: Application to 24-h holter recordings of heart period variability in healthy and aortic stenosis subjects. IEEE Trans. Biomed. Eng. 2009, 56, 2202–2213. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Lin, Y.; Wang, J.; Shang, P. Refined generalized multiscale entropy analysis for physiological signals. Phys. A Stat. Mech. Its Appl. 2018, 490, 975–985. [Google Scholar] [CrossRef]
- Lee, D.Y.; Choi, Y.S. Multiscale Distribution Entropy Analysis of Short-Term Heart Rate Variability. Entropy 2018, 20, 952. [Google Scholar] [CrossRef]
- Shi, M.; Shi, Y.; Lin, Y.; Qi, X. Modified multiscale Renyi distribution entropy for short-term heart rate variability analysis. BMC Med. Inform. Decis. Mak. 2024, 24, 346. [Google Scholar] [CrossRef]
- Humeau-Heurtier, A. The Multiscale Entropy Algorithm and Its Variants: A Review. Entropy 2015, 17, 3110–3123. [Google Scholar] [CrossRef]
- Wu, S.D.; Wu, C.W.; Lee, K.Y.; Lin, S.G. Modified multiscale entropy for short-term time series analysis. Phys. A Stat. Mech. Its Appl. 2013, 392, 5865–5873. [Google Scholar] [CrossRef]
- Guzman-Vargas, L.; Zabaleta-Ortega, A.; Guzman-Saenz, A. Simplicial complex entropy for time series analysis. Sci. Rep. 2023, 13, 22696. [Google Scholar] [CrossRef]
- Edelsbrunner, H.; Letscher, D.; Zomorodian, A. Topological Persistence and Simplification. Discret. Comput. Geom. 2002, 28, 511–533. [Google Scholar] [CrossRef]
- Zomorodian, A.; Carlsson, G. Computing Persistent Homology. In Proceedings of the Twentieth Annual Symposium on Computational Geometry, New York, NY, USA, 8–11 June 2004; pp. 347–356. [Google Scholar] [CrossRef]
- Carlsson, G.; Zomorodian, A.; Collins, A.; Guibas, L.J. Persistence barcodes for shapes. Int. J. Shape Model. 2005, 11, 149–187. [Google Scholar] [CrossRef]
- Edelsbrunner, H.; Harer, J. Persistent homology-a survey. Contemp. Math. 2008, 453, 257–282. [Google Scholar] [CrossRef]
- Edelsbrunner, H.; Morozov, D. Persistent Homology: Theory and Practice; California Digital Library: Oakland, CA, USA, 2013. [Google Scholar]
- Carlsson, G. Topology and data. Bull. Am. Math. Soc. 2009, 46, 255–308. [Google Scholar] [CrossRef]
- Zomorodian, A. Topological Data Analysis. Adv. Appl. Comput. Topol. 2012, 70, 39. [Google Scholar] [CrossRef]
- Wasserman, L. Topological Data Analysis. Annu. Rev. Stat. Its Appl. 2018, 5, 501–532. [Google Scholar] [CrossRef]
- Pincus, S.M.; Huang, W.M. Approximate entropy: Statistical properties and applications. Commun. Stat.—Theory Methods 1992, 21, 3061–3077. [Google Scholar] [CrossRef]
- Dey, T.K.; Wang, Y. Computational Topology for Data Analysis; Cambridge University Press: Cambridge, UK, 2022. [Google Scholar] [CrossRef]
- Munkres, J. Elements of Algebraic Topology, 2nd ed.; Library of Congress Cataloguing in Publication Data, Addison-Wesley Publishing Company: White Plains, NY, USA, 1984. [Google Scholar]
- Hatcher, A. Algebraic Topology, 1st ed.; Cornell University Press: Ithaca, NY, USA, 2001. [Google Scholar]
- Munkres, J. Topology, 2nd ed.; British Library Cataloguing-in-Publication Data, Pearson Education Limited: Harlow, UK, 2014. [Google Scholar]
- Goldberger, A.; Amaral, L.; Glass, L.; Hausdorff, J.; Ivanov, P.C.; Mark, R.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a new research resource for complex physiologic signals. Circulation 2000, 101, e215–e220. [Google Scholar] [CrossRef]
- Baim, D.S.; Colucci, W.S.; Monrad, E.S.; Smith, H.S.; Wright, R.F.; Lanoue, A.; Gauthier, D.F.; Ransil, B.J.; Grossman, W.; Braunwald, E. Survival of patients with severe congestive heart failure treated with oral milrinone. J. Am. Coll. Cardiol. 1986, 7, 661–670. [Google Scholar] [CrossRef]
- Mietus, J.; Peng, C.; Henry, I.; Goldsmith, R.; Goldberger, A. The pNNx files: Re-examining a widely used heart rate variability measure. Heart 2002, 88, 378–380. [Google Scholar] [CrossRef]
- Goldsmith, R.L.; Bigger, J.; Bloomfield, D.M.; Krum, H.; Steinman, R.C.; Sackner-Bernstein, J.; Packer, M. Long-term carvedilol therapy increases parasympathetic nervous system activity in chronic congestive heart failure. Am. J. Cardiol. 1997, 80, 1101–1104. [Google Scholar] [CrossRef]
- Reyes-Ramírez, I.; Guzmán-Vargas, L. Scaling properties of excursions in heartbeat dynamics. Europhys. Lett. 2010, 89, 38008. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zabaleta-Ortega, A.; Carrizales-Velazquez, C.; Obregón-Quintana, B.; Guzmán-Vargas, L. Multiscale Simplicial Complex Entropy Analysis of Heartbeat Dynamics. Entropy 2025, 27, 467. https://doi.org/10.3390/e27050467
Zabaleta-Ortega A, Carrizales-Velazquez C, Obregón-Quintana B, Guzmán-Vargas L. Multiscale Simplicial Complex Entropy Analysis of Heartbeat Dynamics. Entropy. 2025; 27(5):467. https://doi.org/10.3390/e27050467
Chicago/Turabian StyleZabaleta-Ortega, Alvaro, Carlos Carrizales-Velazquez, Bibiana Obregón-Quintana, and Lev Guzmán-Vargas. 2025. "Multiscale Simplicial Complex Entropy Analysis of Heartbeat Dynamics" Entropy 27, no. 5: 467. https://doi.org/10.3390/e27050467
APA StyleZabaleta-Ortega, A., Carrizales-Velazquez, C., Obregón-Quintana, B., & Guzmán-Vargas, L. (2025). Multiscale Simplicial Complex Entropy Analysis of Heartbeat Dynamics. Entropy, 27(5), 467. https://doi.org/10.3390/e27050467






