The Intrinsic Dimension of Neural Network Ensembles
Abstract
1. Introduction
2. Methods
2.1. Neural Networks
2.2. Calculation of the Intrinsic Dimension
2.2.1. TwoNN
2.2.2. MLE
2.2.3. MiNDML
2.2.4. DANCo
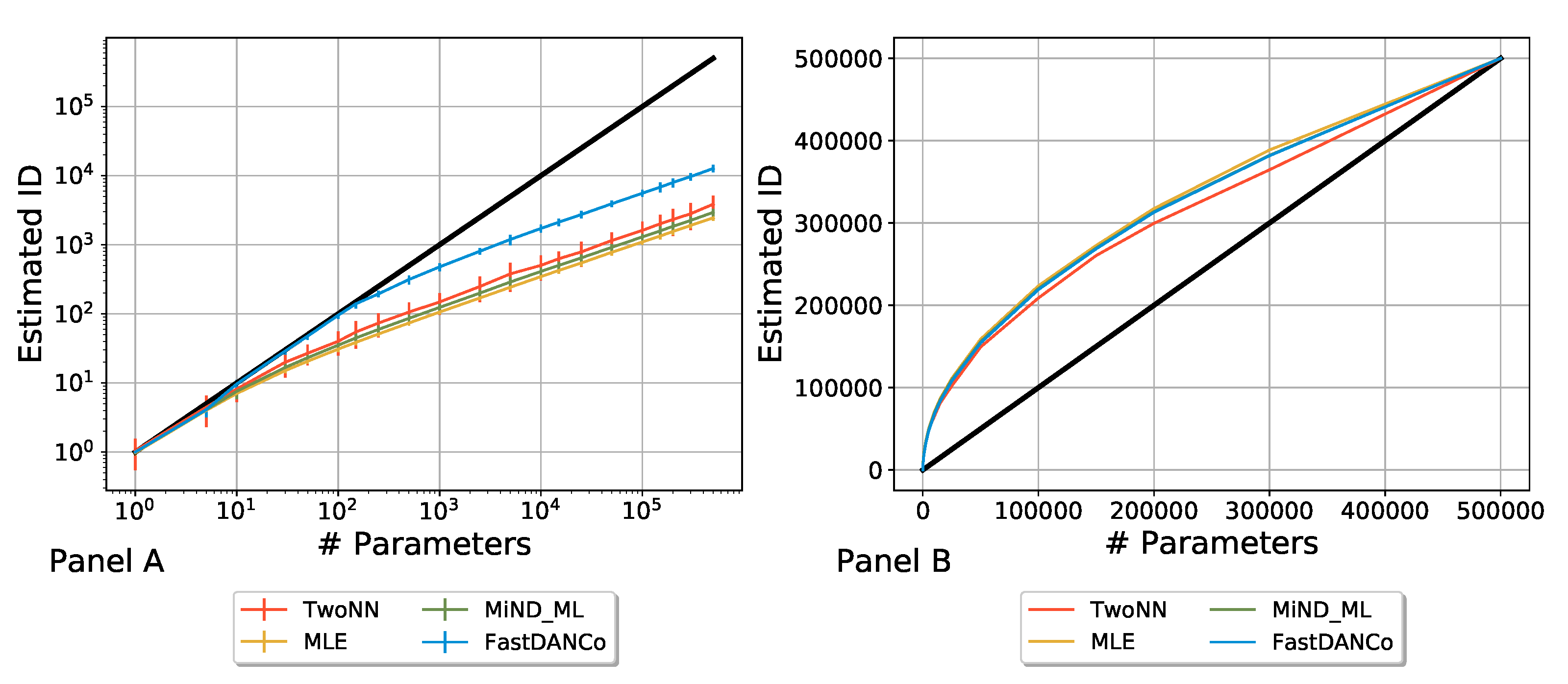
2.3. Rescaling the Algorithms
3. Results
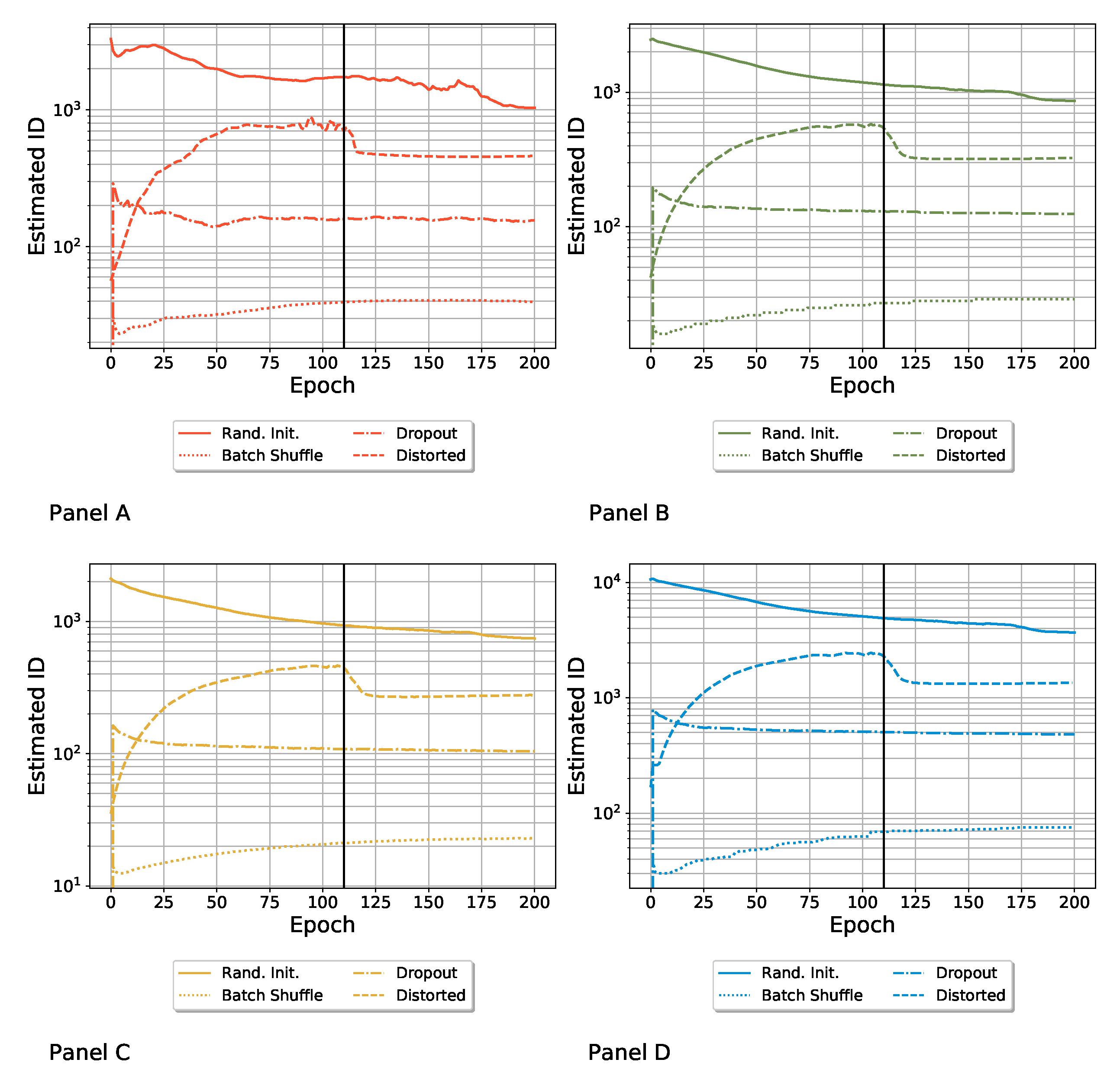
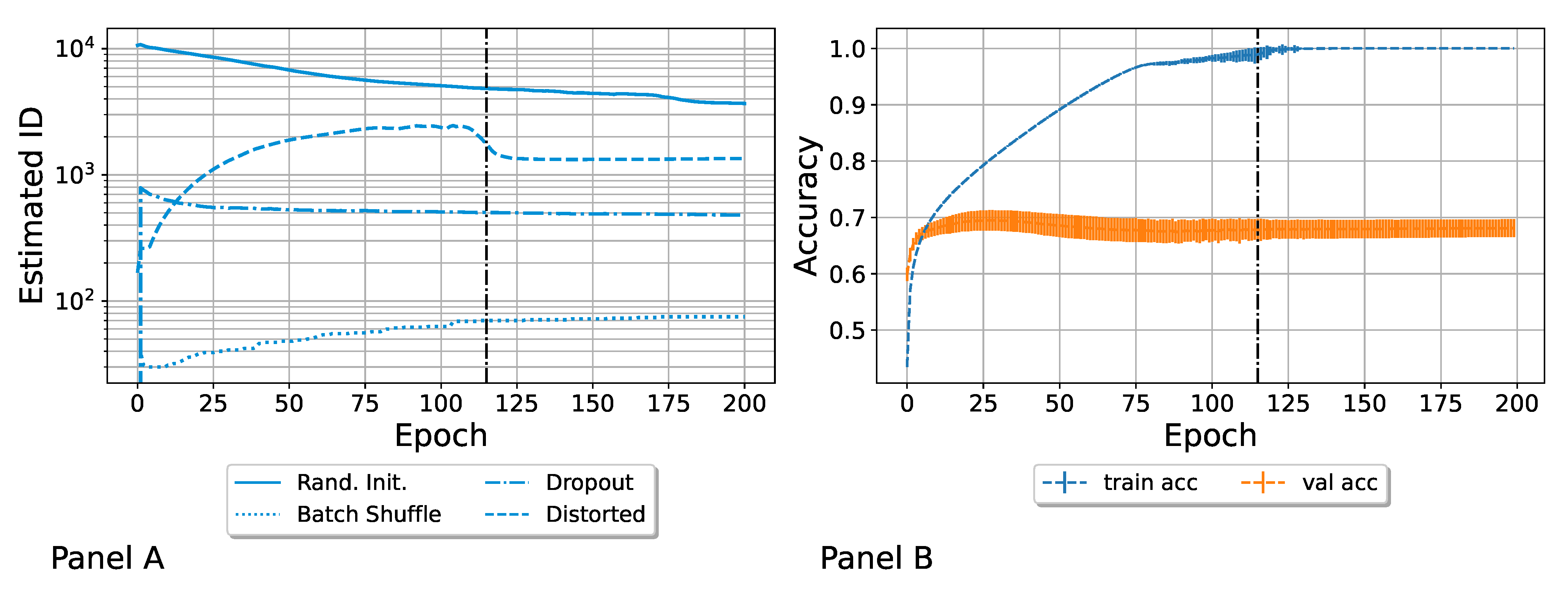
3.1. Computation of the ID Induced by Different Variability Sources
- Random parameter initialization. Each network was initialized with random parameters. Note that in this case, the starting (i.e., epoch zero) ID was the highest possible, and it was equal to the embedding dimension D. We refer to this ensemble as “Rand. Init.”;
- Random shuffling of the batches during the training. The order in which the SGD saw batches of the training set was random for each network. We refer to this ensemble as “Batch Shuffle”;
- Random exclusion of neurons during the training. We applied a dropout with a dropout rate of . We refer to this set as “Dropout”;
- Random distortion of the training set images. The images of the training set were randomly distorted, so each model was trained on slightly different data. We refer to this ensemble as “Distorted”, as was done by Ciregan et al. in [50]. See Appendix B for more details.
- Random initialization + Batch Shuffle. Each network was initialized with random parameters, and the order in which batches were presented was randomized for each network differently. We refer to this ensemble in the figure as “Rand. Init. + BS”;
- Random initialization + Batch Shuffle + Dropout. Each network was initialized with random parameters, the batch order was random, and the dropout rate equal was 0.5. We refer to this ensemble as “Rand. Init. + BS + Drop.”;
- Random initialization + Batch Shuffle + Distortion. Each network was initialized with random parameters, the batch order was random, and the images were randomly distorted (for each network in a different way). We refer to this ensemble as “Rand. Init. + BS + Dist.”;
3.2. Accuracy of Heterogeneous Ensembles
- Identify the best architecture for a given problem;
- Build a suitable ensemble of networks for the analysis;
- Keep track of the evolution of the ID of the ensemble to fine-tune the training strategy to explore a large portion of the solution manifold and identify the optimal ID for the specific problem;
- Average the prediction of the network ensemble and compare its accuracy to a benchmark, for example, a single model, and see if the ensemble forecasting outperforms single model forecasting.
3.3. Comparison with Hidden Representation
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ID | Intrinsic Dimension |
| NN | Neural Network |
| SGD | Stochastic Gradient Descent |
| Rand. Init. | Random Initialization |
| BS | Batch Shuffle |
| Drop. | Dropout |
| Dist. | Distortion |
Appendix A. Comparing Algorithms
Appendix B. Dataset Distortion
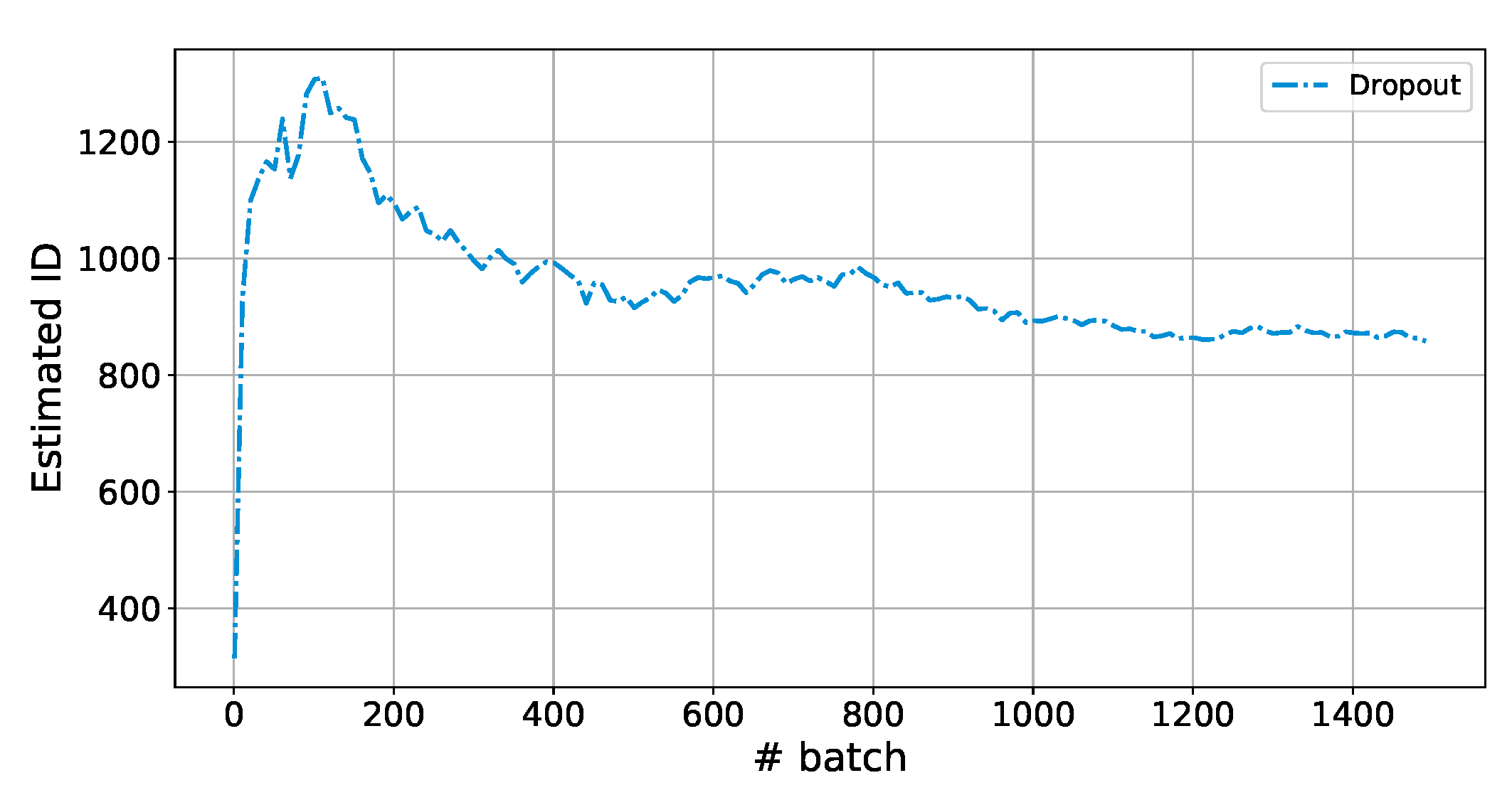
Appendix C. Zoom in the First Epoch
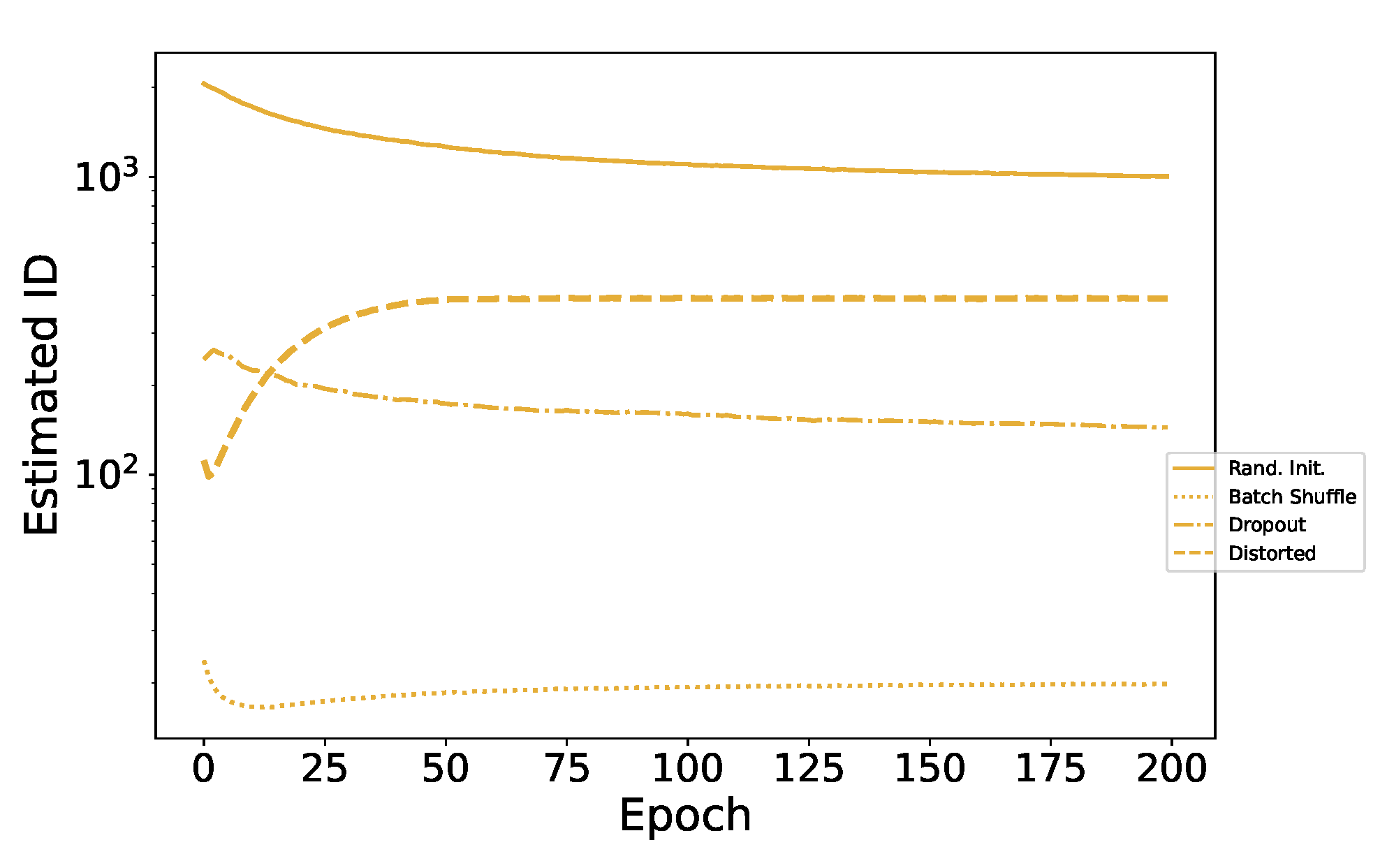
Appendix D. MNIST
Appendix E. Numerical Comparison of Loss and Accuracy
| Train Loss | Val Loss | |
|---|---|---|
| Rand. Init | 0.004 ± 0.001 | 0.644 ± 0.018 |
| Rand. Init. + BS | 0.003 ± 0.001 | 0.553 ± 0.009 |
| Rand. Init. + BS + Drop | 0.382 ± 0.002 | 0.321 ± 0.002 |
| Rand. Init. + BS + Dist | 0.003 ± 0.0001 | 2.318 ± 0.157 |
| Train Acc | Val Acc | |
|---|---|---|
| Rand. Init | 1.0000 ± 0.0002 | 0.892 ± 0.002 |
| Rand. Init. + BS | 1.0000 ± 0.0003 | 0.897 ± 0.001 |
| Rand. Init. + BS + Drop | 0.858 ± 0.001 | 0.882 ± 0.001 |
| Rand. Init. + BS + Dist | 1.0000 ± 0 | 0.690 ± 0.014 |
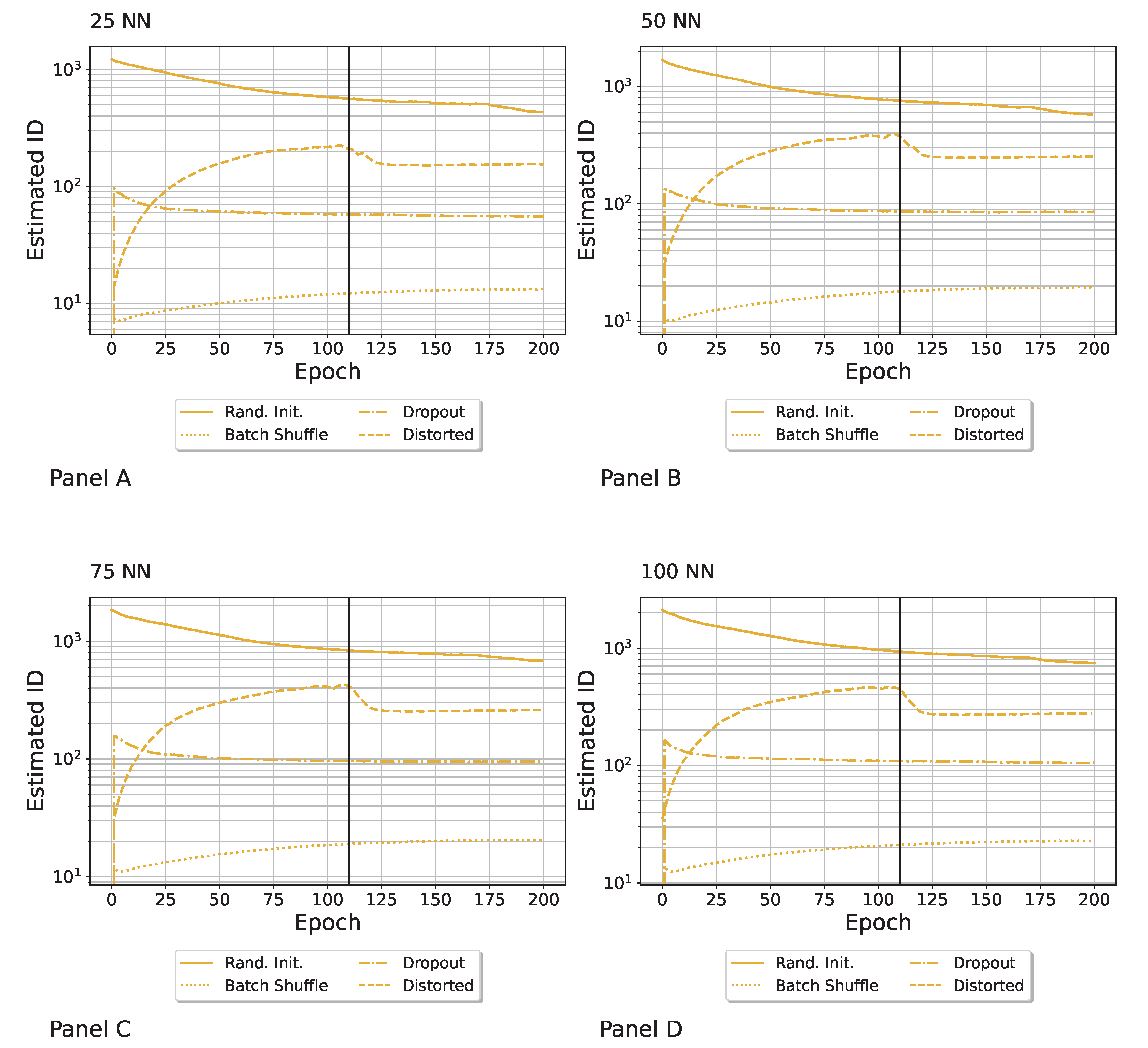
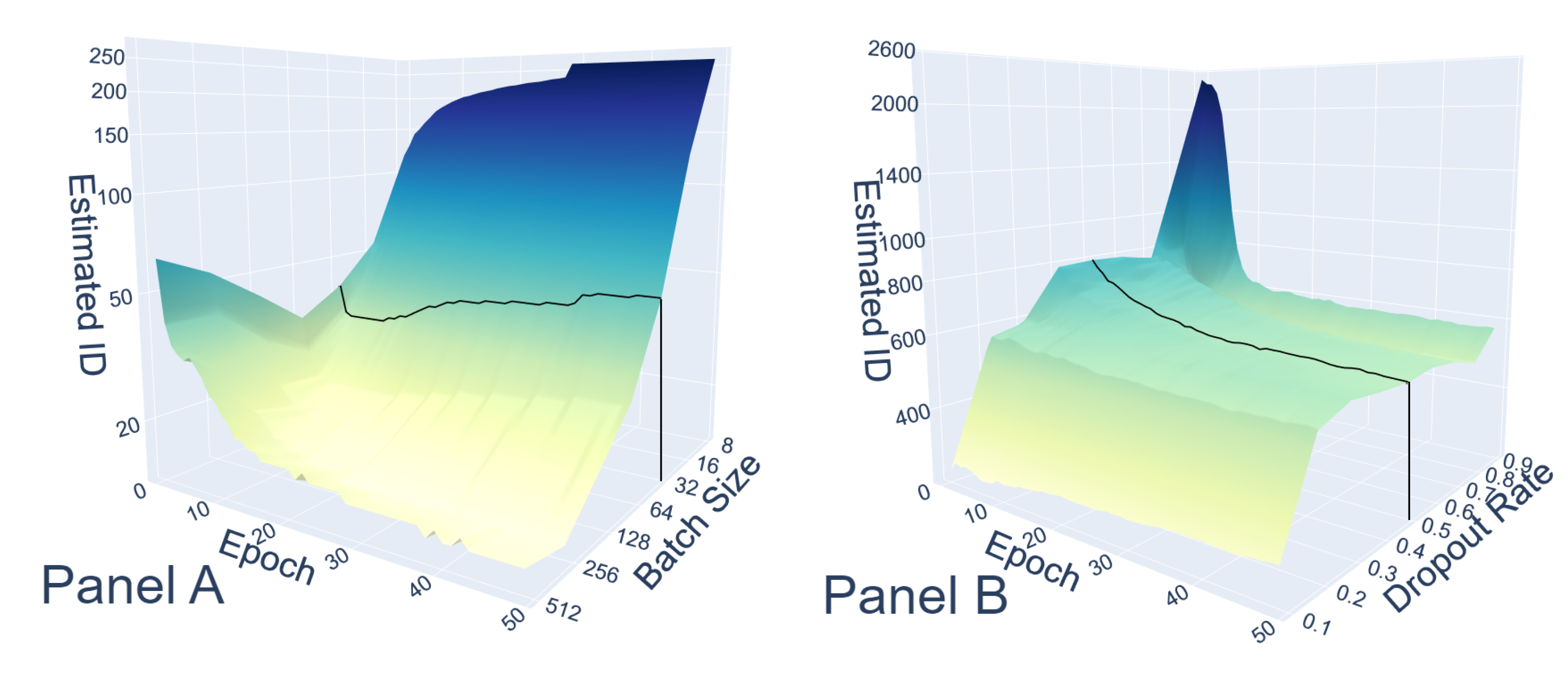
Appendix F. Robustness with Respect to the Number of Neural Networks
References
- Voulodimos, A.; Doulamis, N.; Doulamis, A.; Protopapadakis, E. Deep learning for computer vision: A brief review. Comput. Intell. Neurosci. 2018, 2018, 7068349. [Google Scholar] [CrossRef] [PubMed]
- Khan, S.; Naseer, M.; Hayat, M.; Zamir, S.W.; Khan, F.S.; Shah, M. Transformers in vision: A survey. In ACM Computing Surveys (CSUR); Association for Computing Machinery: New York, NY, USA, 2021. [Google Scholar]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural machine translation by jointly learning to align and translate. arXiv 2014, arXiv:1409.0473. [Google Scholar]
- Stahlberg, F. Neural machine translation: A review. J. Artif. Intell. Res. 2020, 69, 343–418. [Google Scholar] [CrossRef]
- Guidarelli Mattioli, F.; Sciortino, F.; Russo, J. A neural network potential with self-trained atomic fingerprints: A test with the mW water potential. J. Chem. Phys. 2023, 158, 104501. [Google Scholar] [CrossRef] [PubMed]
- Montavon, G.; Samek, W.; Müller, K.R. Methods for interpreting and understanding deep neural networks. Digit. Signal Process. 2018, 73, 1–15. [Google Scholar] [CrossRef]
- Mei, S.; Montanari, A.; Nguyen, P.M. A mean field view of the landscape of two-layer neural networks. Proc. Natl. Acad. Sci. USA 2018, 115, E7665–E7671. [Google Scholar] [CrossRef]
- Fort, S.; Hu, H.; Lakshminarayanan, B. Deep ensembles: A loss landscape perspective. arXiv 2019, arXiv:1912.02757. [Google Scholar]
- Koch, A.d.M.; Koch, E.d.M.; Koch, R.d.M. Why Unsupervised Deep Networks Generalize. arXiv 2020, arXiv:2012.03531. [Google Scholar]
- Poggio, T.; Kawaguchi, K.; Liao, Q.; Miranda, B.; Rosasco, L.; Boix, X.; Hidary, J.; Mhaskar, H. Theory of deep learning III: Explaining the non-overfitting puzzle. arXiv 2017, arXiv:1801.00173. [Google Scholar]
- Allen-Zhu, Z.; Li, Y.; Song, Z. A convergence theory for deep learning via over-parameterization. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 242–252. [Google Scholar]
- Zhou, Z.H. Why over-parameterization of deep neural networks does not overfit? Sci. China Inf. Sci. 2021, 64, 1–3. [Google Scholar] [CrossRef]
- Franklin, J. The elements of statistical learning: Data mining, inference and prediction. Math. Intell. 2005, 27, 83–85. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Huang, Y.; Cheng, Y.; Bapna, A.; Firat, O.; Chen, D.; Chen, M.; Lee, H.; Ngiam, J.; Le, Q.V.; Wu, Y.; et al. Gpipe: Efficient training of giant neural networks using pipeline parallelism. Adv. Neural Inf. Process. Syst. 2019, 32, 103–112. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Radford, A.; Wu, J.; Child, R.; Luan, D.; Amodei, D.; Sutskever, I. Language models are unsupervised multitask learners. OpenAI Blog 2019, 1, 9. [Google Scholar]
- Opper, M. Statistical mechanics of learning: Generalization. In The Handbook of Brain Theory and Neural Networks; Aston University: Birmingham, UK, 1995; pp. 922–925. [Google Scholar]
- Opper, M. Learning to generalize. Front. Life 2001, 3, 763–775. [Google Scholar]
- Advani, M.S.; Saxe, A.M.; Sompolinsky, H. High-dimensional dynamics of generalization error in neural networks. Neural Netw. 2020, 132, 428–446. [Google Scholar] [CrossRef]
- Spigler, S.; Geiger, M.; d’Ascoli, S.; Sagun, L.; Biroli, G.; Wyart, M. A jamming transition from under-to over-parametrization affects loss landscape and generalization. arXiv 2018, arXiv:1810.09665. [Google Scholar]
- Geiger, M.; Spigler, S.; d’Ascoli, S.; Sagun, L.; Baity-Jesi, M.; Biroli, G.; Wyart, M. Jamming transition as a paradigm to understand the loss landscape of deep neural networks. Phys. Rev. E 2019, 100, 012115. [Google Scholar] [CrossRef]
- Liao, Q.; Poggio, T. Theory II: Landscape of the empirical risk in deep learning. arXiv 2017, arXiv:1703.09833. [Google Scholar]
- Li, H.; Xu, Z.; Taylor, G.; Studer, C.; Goldstein, T. Visualizing the loss landscape of neural nets. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2018; Volume 31. [Google Scholar]
- Blundell, C.; Cornebise, J.; Kavukcuoglu, K.; Wierstra, D. Weight uncertainty in neural network. In Proceedings of the International Conference on Machine Learning, PMLR, Lille, France, 6–11 July 2015; pp. 1613–1622. [Google Scholar]
- Gal, Y.; Ghahramani, Z. Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 20–22 June 2016; Volume 48, pp. 1050–1059. [Google Scholar]
- Chollet, F. Deep Learning with Python; Simon and Schuster: New York, NY, USA, 2017. [Google Scholar]
- Fukunaga, K. 15 Intrinsic dimensionality extraction. In Handbook of Statistics; Krishnaiah, P.R., Kanal, L.N., Eds.; Elsevier: Amsterdam, The Netherlands, 1982; Volume 2, pp. 347–360. [Google Scholar] [CrossRef]
- Li, C.; Farkhoor, H.; Liu, R.; Yosinski, J. Measuring the intrinsic dimension of objective landscapes. arXiv 2018, arXiv:1804.08838. [Google Scholar]
- Facco, E.; d’Errico, M.; Rodriguez, A.; Laio, A. Estimating the intrinsic dimension of datasets by a minimal neighborhood information. Sci. Rep. 2017, 7, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Levina, E.; Bickel, P.J. Maximum likelihood estimation of intrinsic dimension. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 5–8 December 2005; pp. 777–784. [Google Scholar]
- Lombardi, G.; Rozza, A.; Ceruti, C.; Casiraghi, E.; Campadelli, P. Minimum neighbor distance estimators of intrinsic dimension. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Athens, Greece, 5–9 September 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 374–389. [Google Scholar]
- Ceruti, C.; Bassis, S.; Rozza, A.; Lombardi, G.; Casiraghi, E.; Campadelli, P. Danco: An intrinsic dimensionality estimator exploiting angle and norm concentration. Pattern Recognit. 2014, 47, 2569–2581. [Google Scholar] [CrossRef]
- Ravichandran, K.; Jain, A.; Rakhlin, A. Using Effective Dimension to Analyze Feature Transformations in Deep Neural Networks. 2019. Available online: https://openreview.net/pdf?id=HJGsj13qTE (accessed on 14 April 2025).
- Ansuini, A.; Laio, A.; Macke, J.H.; Zoccolan, D. Intrinsic dimension of data representations in deep neural networks. In Proceedings of the Advances in Neural Information Processing Systems; Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2019; Volume 32. [Google Scholar]
- Ma, X.; Wang, Y.; Houle, M.E.; Zhou, S.; Erfani, S.; Xia, S.; Wijewickrema, S.; Bailey, J. Dimensionality-driven learning with noisy labels. In Proceedings of the International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 3355–3364. [Google Scholar]
- Baldassi, L.; Malatesta, P.; Zecchina. Unveiling the Structure of Wide Flat Minima in Neural Networks. Phys. Rev. Lett. 2021, 127, 278301. [Google Scholar] [CrossRef]
- Altarabichi, M.G.; Nowaczyk, S.; Pashami, S.; Sheikholharam Mashhadi, P.; Handl, J. Rolling the dice for better deep learning performance: A study of randomness techniques in deep neural networks. Inf. Sci. 2024, 667, 120500. [Google Scholar] [CrossRef]
- Zhuang, D.; Zhang, X.; Song, S.; Hooker, S. Randomness in neural network training: Characterizing the impact of tooling. Proc. Mach. Learn. Syst. 2022, 4, 316–336. [Google Scholar]
- Géron, A. Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems; O’Reilly Media: Sebastopol, CA, USA, 2019. [Google Scholar]
- Ramachandran, P.; Zoph, B.; Le, Q.V. Searching for activation functions. arXiv 2017, arXiv:1710.05941. [Google Scholar]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep sparse rectifier neural networks. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 11–13 April 2011; pp. 315–323. [Google Scholar]
- Masters, D.; Luschi, C. Revisiting small batch training for deep neural networks. arXiv 2018, arXiv:1804.07612. [Google Scholar]
- Campadelli, P.; Casiraghi, E.; Ceruti, C.; Rozza, A. Intrinsic dimension estimation: Relevant techniques and a benchmark framework. Math. Probl. Eng. 2015, 2015, 759567. [Google Scholar] [CrossRef]
- Jolliffe, I. Principal component analysis. Encycl. Stat. Behav. Sci. 2005. [Google Scholar] [CrossRef]
- Cox, M.A.; Cox, T.F. Multidimensional scaling. In Handbook of Data Visualization; Springer: Berlin/Heidelberg, Germany, 2008; pp. 315–347. [Google Scholar]
- Tribello, G.A.; Ceriotti, M.; Parrinello, M. Using sketch-map coordinates to analyze and bias molecular dynamics simulations. Proc. Natl. Acad. Sci. USA 2012, 109, 5196–5201. [Google Scholar] [CrossRef]
- Grassberger, P.; Procaccia, I. Characterization of strange attractors. Phys. Rev. Lett. 1983, 50, 346. [Google Scholar] [CrossRef]
- Fisher, N.I. Statistical Analysis of Circular Data; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Ciregan, D.; Meier, U.; Schmidhuber, J. Multi-column deep neural networks for image classification. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 3642–3649. [Google Scholar]
- Lee, S.; Purushwalkam, S.; Cogswell, M.; Crandall, D.; Batra, D. Why M heads are better than one: Training a diverse ensemble of deep networks. arXiv 2015, arXiv:1511.06314. [Google Scholar]
- Ganaie, M.; Hu, M.; Malik, A.K.; Tanveer, M.; Suganthan, P.N. Ensemble deep learning: A review. arXiv 2021, arXiv:2104.02395. [Google Scholar] [CrossRef]
- Lakshminarayanan, B.; Pritzel, A.; Blundell, C. Simple and scalable predictive uncertainty estimation using deep ensembles. arXiv 2016, arXiv:1612.01474. [Google Scholar]
- Wolpert, D.H. Stacked generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Salehi, M.; Razmara, J.; Lotfi, S. A novel data mining on breast cancer survivability using MLP ensemble learners. Comput. J. 2020, 63, 435–447. [Google Scholar] [CrossRef]
- Garipov, T.; Izmailov, P.; Podoprikhin, D.; Vetrov, D.P.; Wilson, A.G. Loss Surfaces, Mode Connectivity, and Fast Ensembling of DNNs. In Proceedings of the Advances in Neural Information Processing Systems; Bengio, S., Wallach, H., Larochelle, H., Grauman, K., Cesa-Bianchi, N., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2018; Volume 31. [Google Scholar]
- Draxler, F.; Veschgini, K.; Salmhofer, M.; Hamprecht, F. Essentially No Barriers in Neural Network Energy Landscape. In Proceedings of the 35th International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; Volume 80, pp. 1309–1318. [Google Scholar]
- Guerra, F.T. tgfrancesco/NN_intrinsic_dimension: V1.0.0. 2025. Available online: https://zenodo.org/records/15090926 (accessed on 14 April 2025).
- Denti, F.; Doimo, D.; Laio, A.; Mira, A. Distributional results for model-based intrinsic dimension estimators. arXiv 2021, arXiv:2104.13832. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tosti Guerra, F.; Napoletano, A.; Zaccaria, A. The Intrinsic Dimension of Neural Network Ensembles. Entropy 2025, 27, 440. https://doi.org/10.3390/e27040440
Tosti Guerra F, Napoletano A, Zaccaria A. The Intrinsic Dimension of Neural Network Ensembles. Entropy. 2025; 27(4):440. https://doi.org/10.3390/e27040440
Chicago/Turabian StyleTosti Guerra, Francesco, Andrea Napoletano, and Andrea Zaccaria. 2025. "The Intrinsic Dimension of Neural Network Ensembles" Entropy 27, no. 4: 440. https://doi.org/10.3390/e27040440
APA StyleTosti Guerra, F., Napoletano, A., & Zaccaria, A. (2025). The Intrinsic Dimension of Neural Network Ensembles. Entropy, 27(4), 440. https://doi.org/10.3390/e27040440






