Empirical Study on Fluctuation Theorem for Volatility Cascade Processes in Stock Markets
Abstract
1. Introduction
2. Materials and Methods
2.1. Multiplicative Random Cascade Model of Volatility
2.2. Parameter Estimation
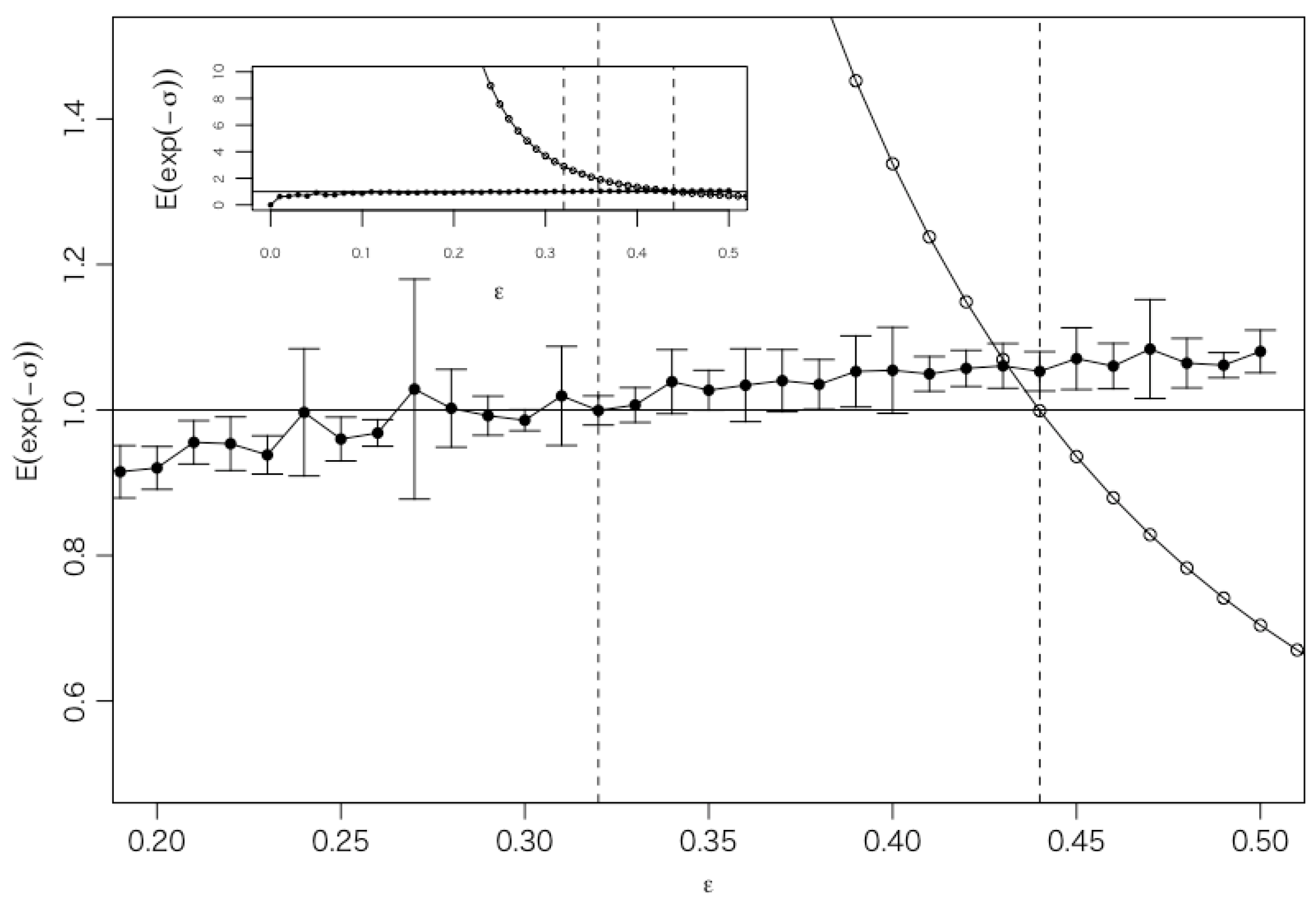
2.3. Integral Fluctuation Theorem
2.4. Empirical Study
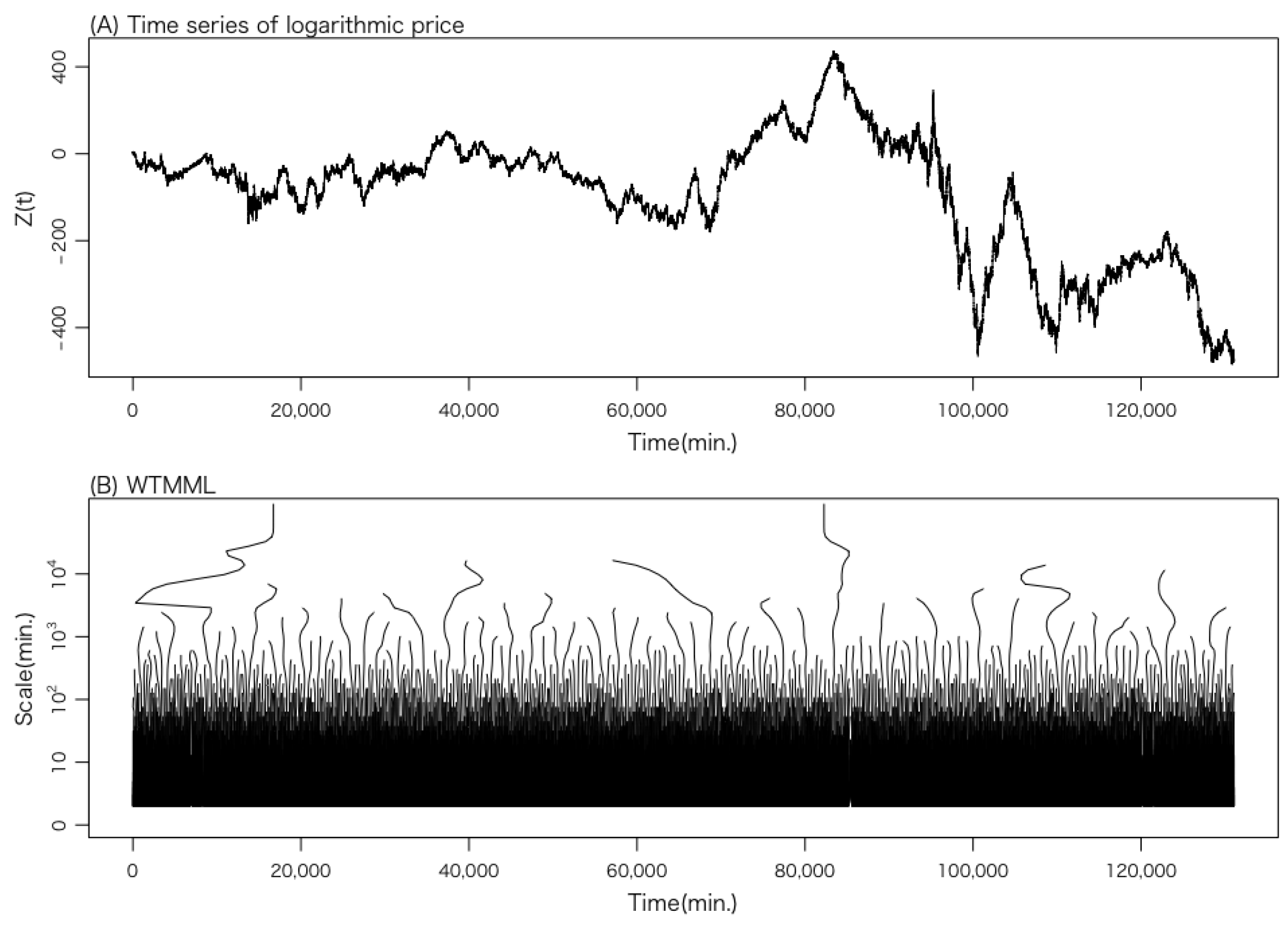
2.4.1. Data
2.4.2. Data Processing
Data Set 1 (LSE Data Set: Normalized Average)
- From the one-minute price data of each stock’s intraday price fluctuations, the logarithmic return was calculated.
- The normalized average of the logarithmic return was computed asTo remove the effect of intraday U-shaped patterns of market activity from the time series, the return was divided by the standard deviation of the corresponding time of day for each issue i.
- We cumulated to obtain the path of the process as follows:
Data Set 2 (TSE Data Set: Normalized Average)
Data Set 3 (TSE Data Set: Individual Stocks)
2.4.3. Wavelet Transform
2.4.4. Wavelet Transform Modulus Maxima Line
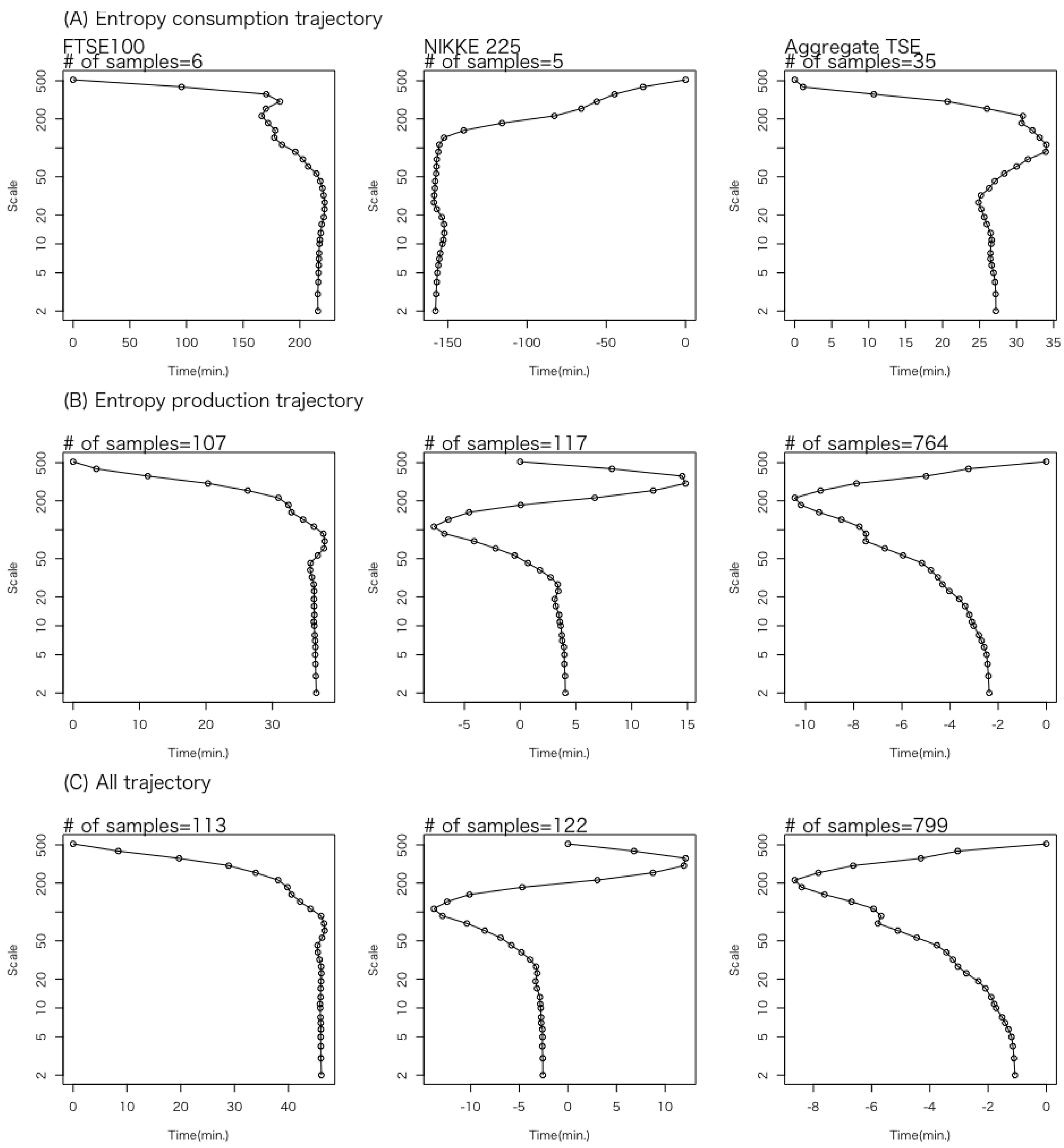
3. Results
3.1. Parameter Estimation Based on Integral Fluctuation Theorem
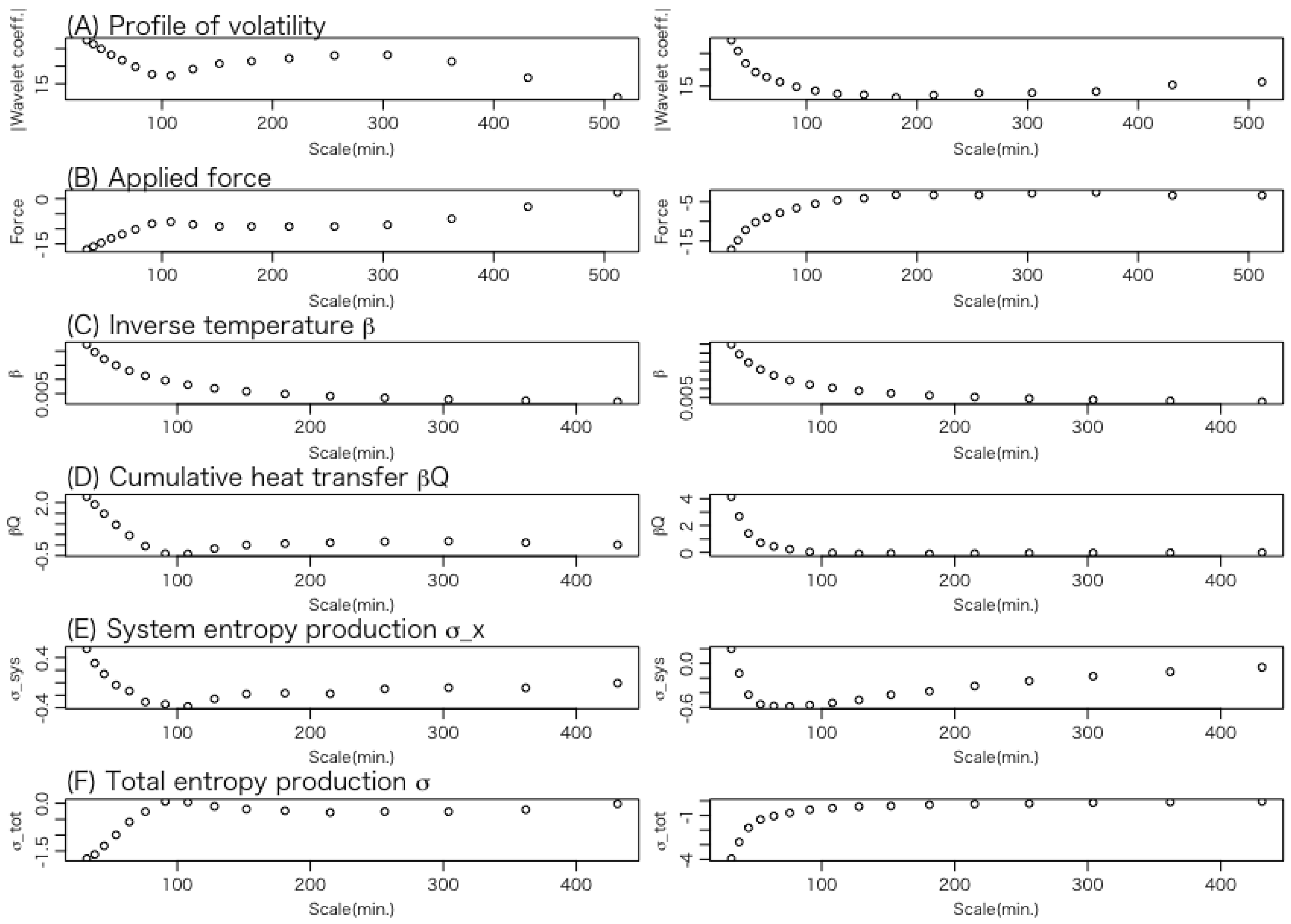
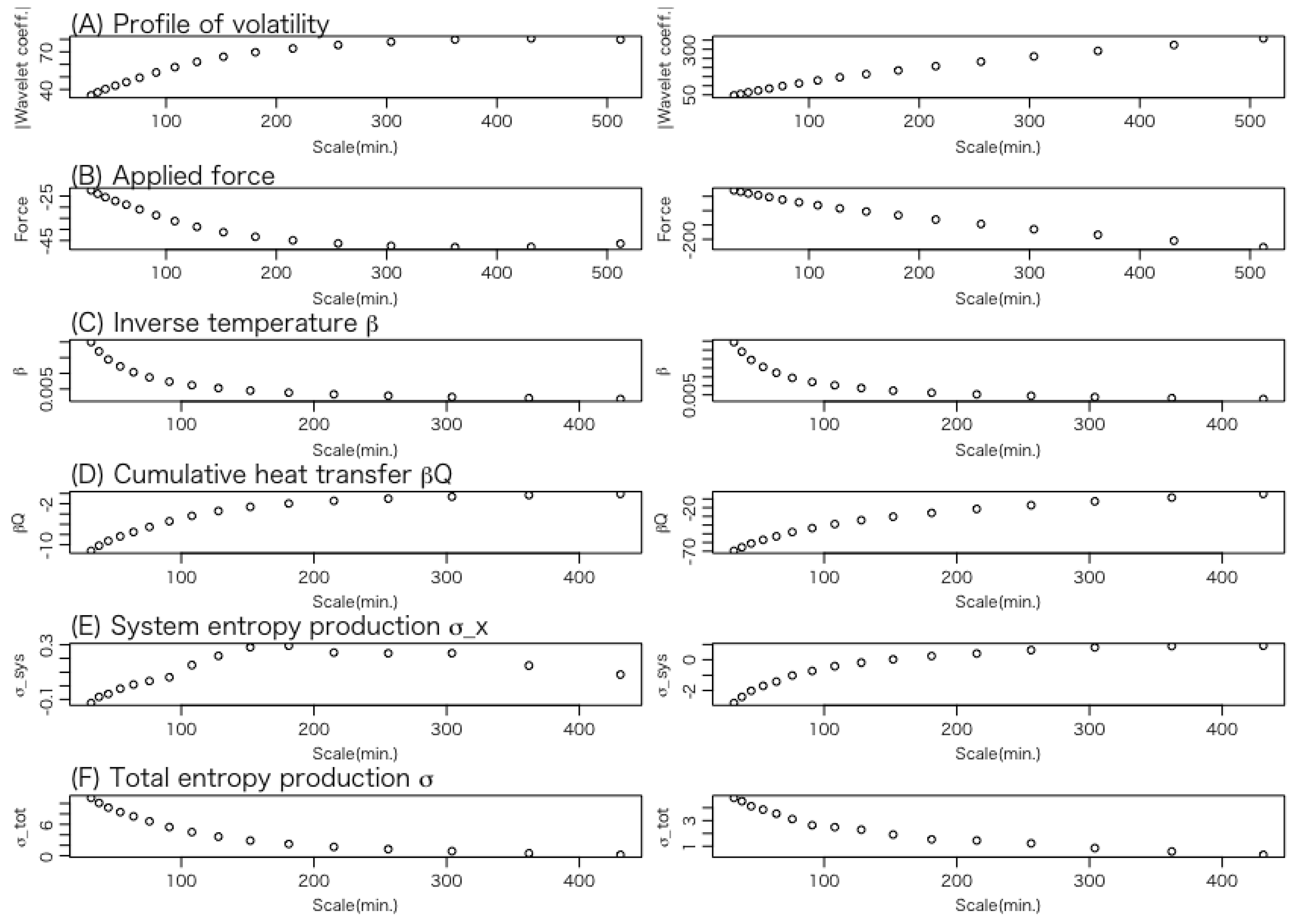
3.2. Details of Trajectories
- (A)
- Volatility: This represents the position of the Brownian particle, which corresponds to the system’s state variable.
- (B)
- Force applied to the system: This indicates the external force acting on the Brownian particle.
- (C)
- Inverse temperature of the heat bath: According to Equations (16) and (26), the temperature represents the trajectory of the variance of volatility.
- (D)
- Heat transfer: This describes the energy transferred from the heat bath to the system, that is, the energy received by the Brownian particle from the heat bath. A negative value indicates a positive amount of heat flowing from the particle back to the heat bath.
- (E)
- Change in the content of the information of the system: As expressed in Equation (32), this quantity can be interpreted as the change in the entropy of the system, a central concept in stochastic thermodynamics.
- (F)
- Change in total entropy: This indicates the change in the total entropy of the system and the heat bath.
4. Discussion
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LSE | London Stock Exchange |
| TSE | Tokyo Stock Exchange |
| SDE | Stochastic differential equation |
| Probability density function | |
| WTMM | Wavelet transform modulus maxima |
| WTMML | Wavelet transform modulus maxima line |
Appendix A. Relations Between Parameters
Appendix B. Wavelet Transformation Modulus Maxima Line
Appendix B.1. Wavelet Transformation Modulus Maxima (WTMM)
- The point is a local maximum or minimum of the wavelet transform coefficient :
- For a point u in the right or left neighborhood of ,and for a point u in the opposite neighborhood,
Appendix B.2. Wavelet Transformation Modulus Maxima Line (WTMML)
- If a point is included in the curve l, then , and the point is a WTMM.
- For any scale , there exists a point on the curve l.
References
- Frisch, U. Turbulence: The Legacy of A. n. Kolmogorov; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Cont, R. Empirical properties of asset returns: Stylized facts and statistical issues. Quant. Financ. 2001, 1, 223–236. [Google Scholar] [CrossRef]
- Bouchaud, J.P.; Potters, M. Theory of Financial Risk and Derivative Pricing: From Statistical Physics to Risk Management, 2nd ed.; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Engle, R.F. Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econometrica 1982, 50, 987–1007. [Google Scholar] [CrossRef]
- Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. J. Econom. 1986, 31, 307–327. [Google Scholar] [CrossRef]
- Baillie, R.T.; Bollerslev, T.; Mikkelsen, H.O. Fractionally integrated generalized autoregressive conditional heteroskedasticity. J. Econom. 1996, 74, 3–30. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Van Ness, J.W. Fractional Brownian motions, fractional noises and applications. SIAM Rev. Soc. Ind. Appl. Math. 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Beran, J. Statistics for Long-Memory Processes; Routledge: London, UK, 2017. [Google Scholar]
- Gatheral, J.; Jaisson, T.; Rosenbaum, M. Volatility is rough. Quant. Financ. 2018, 18, 933–949. [Google Scholar] [CrossRef]
- Fukasawa, M. Volatility has to be rough. Quant. Financ. 2021, 21, 1–8. [Google Scholar] [CrossRef]
- Fukasawa, M.; Takabatake, T.; Westphal, R. Consistent estimation for fractional stochastic volatility model under high-frequency asymptotics. Math. Financ. 2022, 32, 1086–1132. [Google Scholar] [CrossRef]
- Di Nunno, G.; Kubilius, K.; Mishura, Y.; Yurchenko-Tytarenko, A. From constant to rough: A survey of continuous volatility modeling. arXiv 2023, arXiv:2309.01033. [Google Scholar]
- Mandelbrot, B.B. Intermittent turbulence in self-similar cascades: Divergence of high moments and dimension of the carrier. J. Fluid Mech. 1974, 62, 331–358. [Google Scholar] [CrossRef]
- Castaing, B.; Gagne, Y.; Hopfinger, E.J. Velocity probability density functions of high Reynolds number turbulence. Phys. D 1990, 46, 177–200. [Google Scholar] [CrossRef]
- Schmitt, F.; Schertzer, D.; Lovejoy, S. Multifractal analysis of foreign exchange data. Appl. Stoch. Model. Data Anal. 1999, 15, 29–53. [Google Scholar] [CrossRef]
- Calvet, L.E.; Fisher, A.J. Multifractal Volatility; Elsevier Science & Technology: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Lux, T. Turbulence in financial markets: The surprising explanatory power of simple cascade models. Quant. Financ. 2001, 1, 632–640. [Google Scholar] [CrossRef]
- Lux, T. The Markov-switching multifractal model of asset returns. J. Bus. Econ. Stat. 2008, 26, 194–210. [Google Scholar] [CrossRef]
- Sattarhoff, C.; Lux, T. Forecasting the variability of stock index returns with the multifractal random walk model for realized volatilities. Int. J. Forecast. 2023, 39, 1678–1697. [Google Scholar] [CrossRef]
- Richardson, L.F. Weather Prediction by Numerical Process; Cambridge University Press: Cambridge, UK, 1922. [Google Scholar]
- Kolmogorov, A.N. The Local Structure of Turbulence in Incompressible Viscous Fluid for Very Large Reynolds’ Numbers. Proc. Dokl. Akad. Nauk SSSR 1941, 30, 301–305. [Google Scholar]
- Kolmogorov, A.N. A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 1962, 13, 82–85. [Google Scholar] [CrossRef]
- Arneodo, A.; Bacry, E.; Muzy, J. Random cascades on wavelet dyadic trees. J. Math. Phys. 1998, 39, 4142–4164. [Google Scholar] [CrossRef]
- Breymann, W.; Ghashghaie, S.; Talkner, P. A stochastic cascade model for fx dynamics. Int. J. Theor. Appl. Financ. 2000, 3, 357–360. [Google Scholar] [CrossRef]
- Jiménez, J. Intermittency and cascades. J. Fluid Mech. 2000, 409, 99–120. [Google Scholar] [CrossRef]
- Chen, Q.; Chen, S.; Eyink, G.L.; Sreenivasan, K.R. Kolmogorov’s third hypothesis and turbulent sign statistics. Phys. Rev. Lett. 2003, 90, 254501. [Google Scholar] [CrossRef] [PubMed]
- Bacry, E.; Kozhemyak, A.; Muzy, J.F. Continuous cascade models for asset returns. J. Econ. Dyn. Control 2008, 32, 156–199. [Google Scholar] [CrossRef]
- Jiménez, J. Intermittency in turbulence. In Proceedings of the 15th “Aha Huliko” a Winter Workshop, Extreme Events, Honolulu, HI, USA, 23–26 January 2007; pp. 81–90. [Google Scholar]
- Maskawa, J.I.; Kuroda, K.; Murai, J. Multiplicative random cascades with additional stochastic process in financial markets. Evol. Inst. Econ. Rev. 2018, 15, 515–529. [Google Scholar] [CrossRef]
- Friedrich, R.; Peinke, J. Description of a turbulent cascade by a Fokker-Planck equation. Phys. Rev. Lett. 1997, 78, 863–866. [Google Scholar] [CrossRef]
- Renner, C.; Peinke, J.; Friedrich, R. Evidence of Markov properties of high frequency exchange rate data. Phys. A 2001, 298, 499–520. [Google Scholar] [CrossRef]
- Renner, C.; Peinke, J.; Friedrich, R. Experimental indications for Markov properties of small-scale turbulence. J. Fluid Mech. 2001, 433, 383–409. [Google Scholar] [CrossRef]
- Siefert, M.; Peinke, J. Complete multiplier statistics explained by stochastic cascade processes. Phys. Lett. A 2007, 371, 34–38. [Google Scholar] [CrossRef]
- Reinke, N.; Fuchs, A.; Nickelsen, D.; Peinke, J. On universal features of the turbulent cascade in terms of non-equilibrium thermodynamics. J. Fluid Mech. 2018, 848, 117–153. [Google Scholar] [CrossRef]
- Maskawa, J.I.; Kuroda, K. Model of continuous random cascade processes in financial markets. Front. Phys. 2020, 8, 565372. [Google Scholar] [CrossRef]
- Jarzynski, C. Nonequilibrium equality for free energy differences. Phys. Rev. Lett. 1997, 78, 2690–2693. [Google Scholar] [CrossRef]
- Sekimoto, K. Langevin Equation and Thermodynamics. Progr. Theoret. Phys. Suppl. 1998, 130, 17–27. [Google Scholar] [CrossRef]
- Crooks, G.E. Entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 1999, 60, 2721–2726. [Google Scholar] [CrossRef] [PubMed]
- Seifert, U. Entropy production along a stochastic trajectory and an integral fluctuation theorem. Phys. Rev. Lett. 2005, 95, 040602. [Google Scholar] [CrossRef] [PubMed]
- Esposito, M.; Van den Broeck, C. Three detailed fluctuation theorems. Phys. Rev. Lett. 2010, 104, 090601. [Google Scholar] [CrossRef] [PubMed]
- Sekimoto, K. Stochastic Energetics, 2010th ed.; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Seifert, U. Stochastic thermodynamics, fluctuation theorems and molecular machines. Rep. Prog. Phys. 2012, 75, 126001. [Google Scholar] [CrossRef]
- Nickelsen, D.; Engel, A. Probing small-scale intermittency with a fluctuation theorem. Phys. Rev. Lett. 2013, 110, 214501. [Google Scholar] [CrossRef]
- Fuchs, A.; Queirós, S.M.D.; Lind, P.G.; Girard, A.; Bouchet, F.; Wächter, M.; Peinke, J. Small scale structures of turbulence in terms of entropy and fluctuation theorems. Phys. Rev. Fluids 2020, 5, 034602. [Google Scholar] [CrossRef]
- Müller, U.A.; Dacorogna, M.M.; Davé, R.D.; Olsen, R.B.; Pictet, O.V.; von Weizsäcker, J.E. Volatilities of different time resolutions—Analyzing the dynamics of market components. J. Empir. Financ. 1997, 4, 213–239. [Google Scholar] [CrossRef]
- Arnéodo, A.; Muzy, J.F.; Sornette, D. “Direct” causal cascade in the stock market. Eur. Phys. J. B 1998, 2, 277–282. [Google Scholar] [CrossRef]
- Lynch, P.E.; Zumbach, G.O. Market heterogeneities and the causal structure of volatility. Quant. Financ. 2003, 3, 320–331. [Google Scholar] [CrossRef]
- Gardiner, C. Stochastic Methods; Springer: New York, NY, USA, 2009. [Google Scholar]
- Mallat, S. A Wavelet Tour of Signal Processing: The Sparse Way, 3rd ed.; Academic Press: San Diego, CA, USA, 2008. [Google Scholar]
- Addison, P.S. The Illustrated Wavelet Transform Handbook, 2nd ed.; CRC Press: London, UK, 2020. [Google Scholar]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal detrended fluctuation analysis of nonstationary time series. Phys. A 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Gu, G.F.; Zhou, W.X. Detrending moving average algorithm for multifractals. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2010, 82, 011136. [Google Scholar] [CrossRef] [PubMed]
- Mallat, S.; Hwang, W.L. Singularity detection and processing with wavelets. IEEE Trans. Inf. Theory 1992, 38, 617–643. [Google Scholar] [CrossRef]
- Muzy, J.F.; Bacry, E.; Arneodo, A. Multifractal formalism for fractal signals: The structure-function approach versus the wavelet-transform modulus-maxima method. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 1993, 47, 875–884. [Google Scholar] [CrossRef] [PubMed]
- Bacry, E.; Muzy, J.F.; Arneodo, A. Singularity spectrum of fractal signals from wavelet analysis: Exact results. J. Stat. Phys. 1993, 70, 635–674. [Google Scholar] [CrossRef]
- Li, H.; Xiao, Y.; Polukarov, M.; Ventre, C. Thermodynamic analysis of financial markets: Measuring order book dynamics with Temperature and Entropy. Entropy 2023, 26, 24. [Google Scholar] [CrossRef]
- Touzo, L.; Marsili, M.; Zagier, D. Information thermodynamics of financial markets: The Glosten–Milgrom model. J. Stat. Mech. 2021, 2021, 033407. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maskawa, J.-i. Empirical Study on Fluctuation Theorem for Volatility Cascade Processes in Stock Markets. Entropy 2025, 27, 435. https://doi.org/10.3390/e27040435
Maskawa J-i. Empirical Study on Fluctuation Theorem for Volatility Cascade Processes in Stock Markets. Entropy. 2025; 27(4):435. https://doi.org/10.3390/e27040435
Chicago/Turabian StyleMaskawa, Jun-ichi. 2025. "Empirical Study on Fluctuation Theorem for Volatility Cascade Processes in Stock Markets" Entropy 27, no. 4: 435. https://doi.org/10.3390/e27040435
APA StyleMaskawa, J.-i. (2025). Empirical Study on Fluctuation Theorem for Volatility Cascade Processes in Stock Markets. Entropy, 27(4), 435. https://doi.org/10.3390/e27040435







