Statistical Properties of Correlated Semiclassical Bands in Tight-Binding Small-World Networks
Abstract
1. Introduction
2. The Nonlinear Small-World Network Model
2.1. The Dynamical Equation
2.2. Stationary Solutions
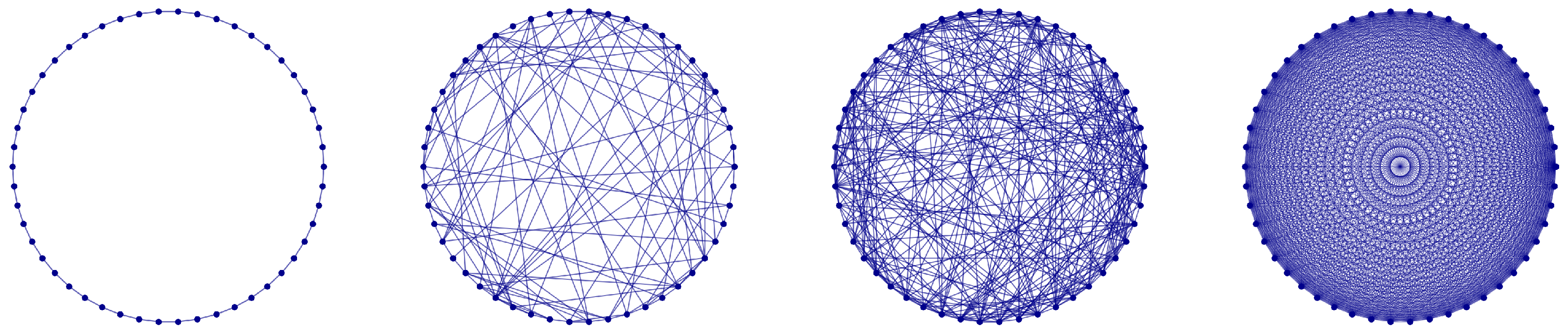
2.3. Small-World Network Geometry
3. Nonlinear Small-World Network Spectra
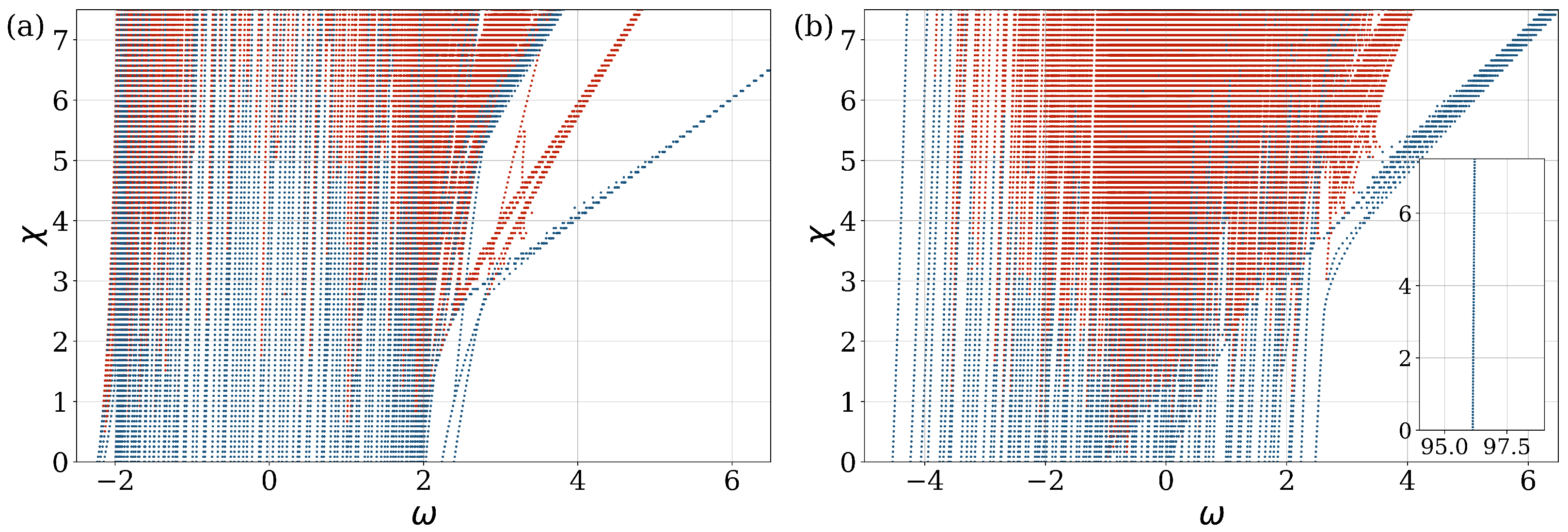
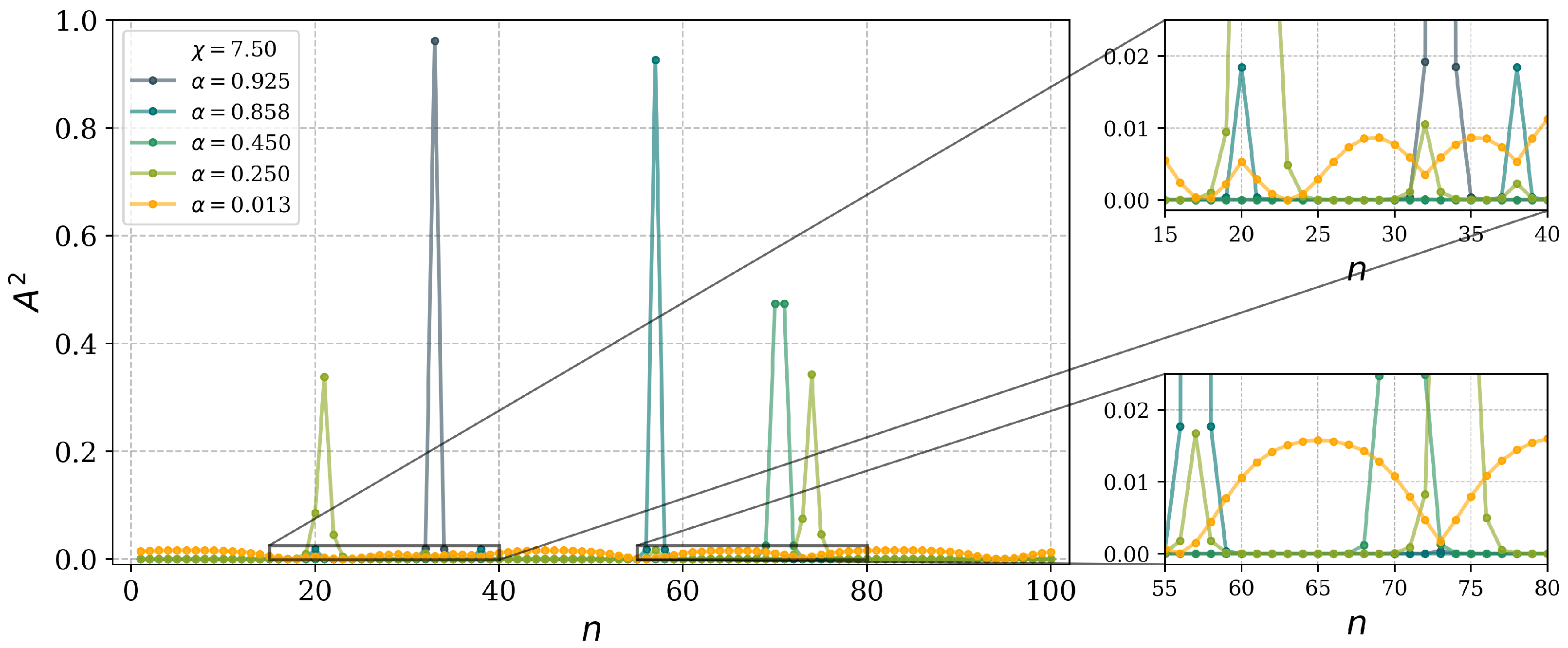
3.1. Frequency Dependence on the Nonlinearity Parameter
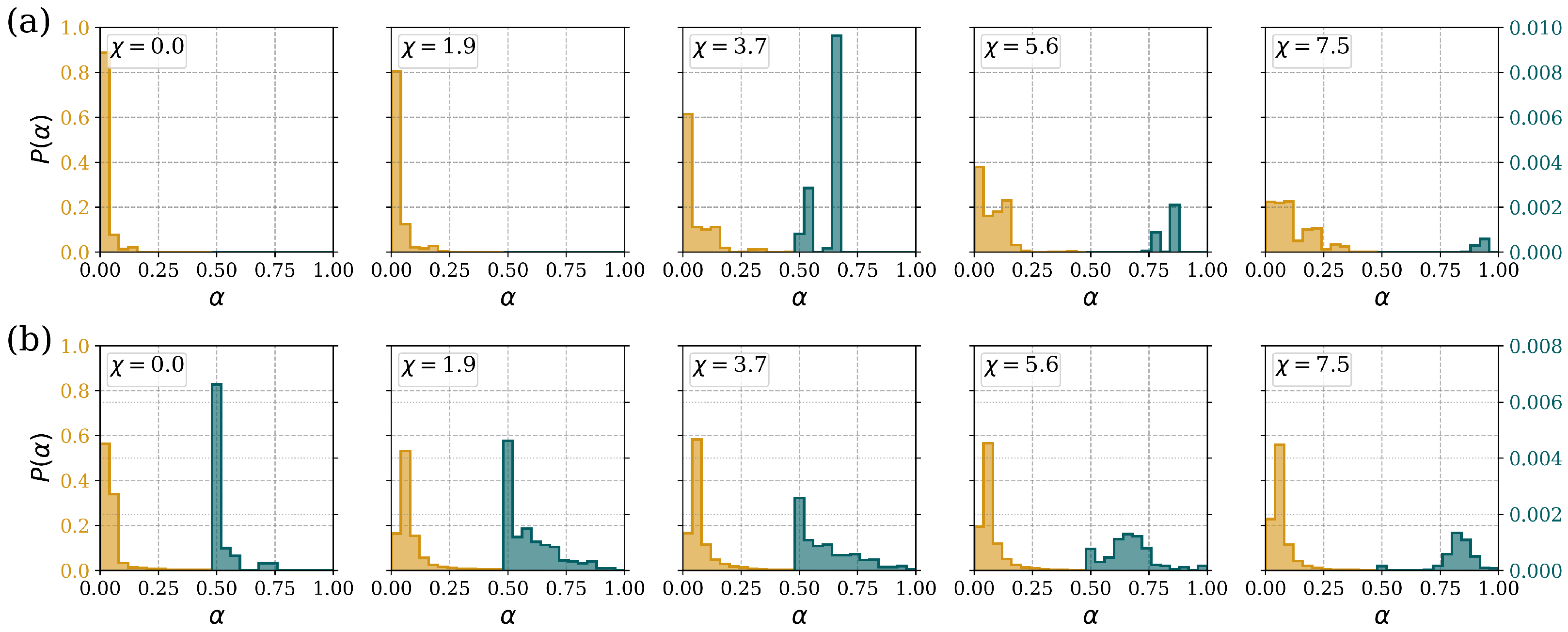
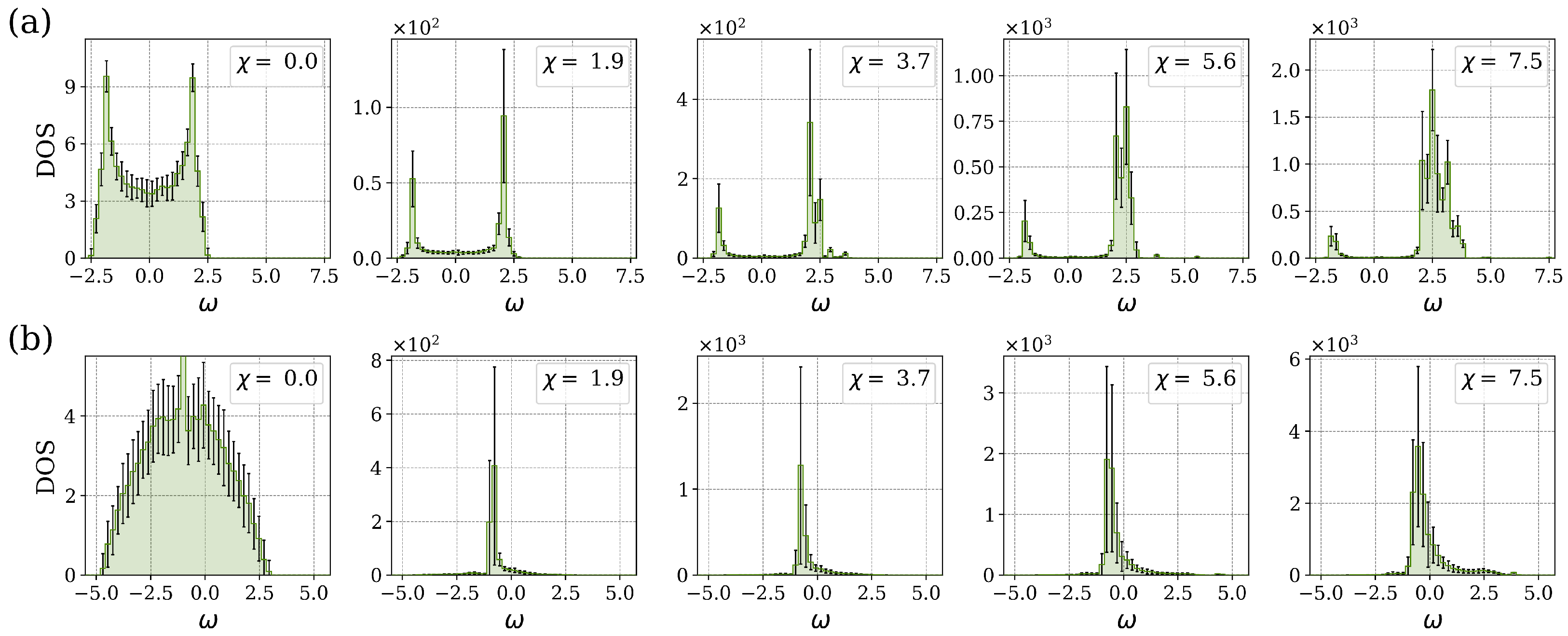
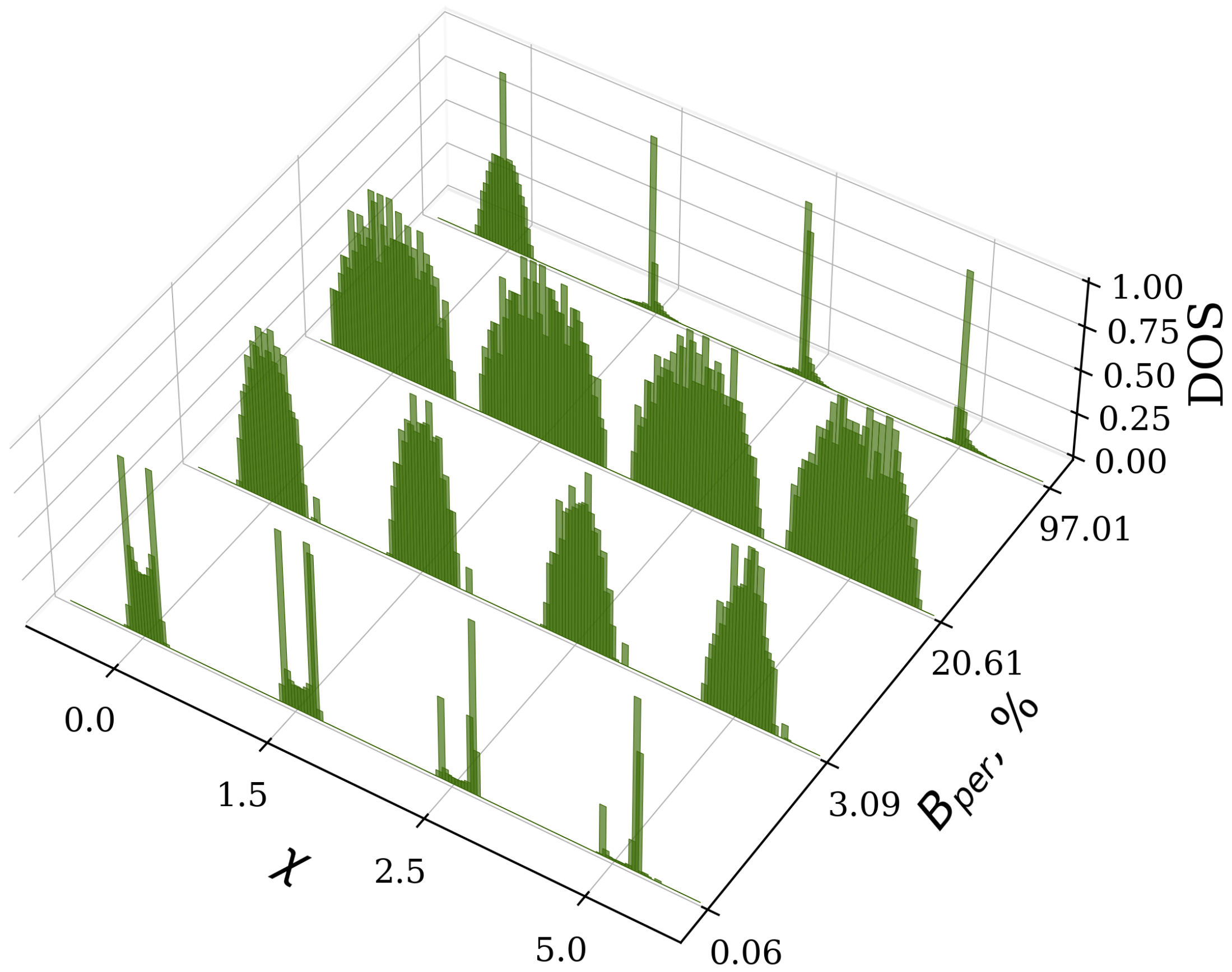
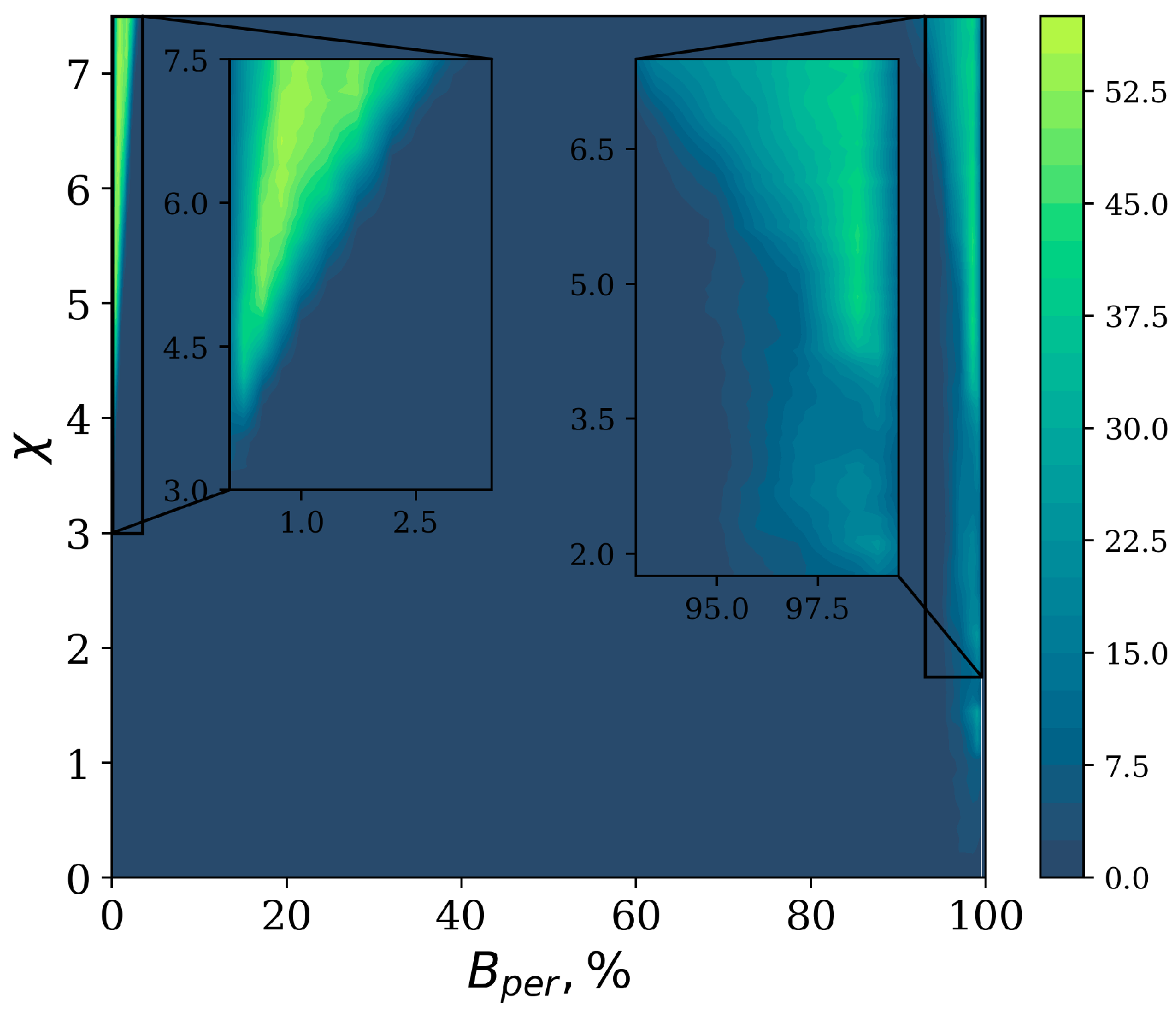
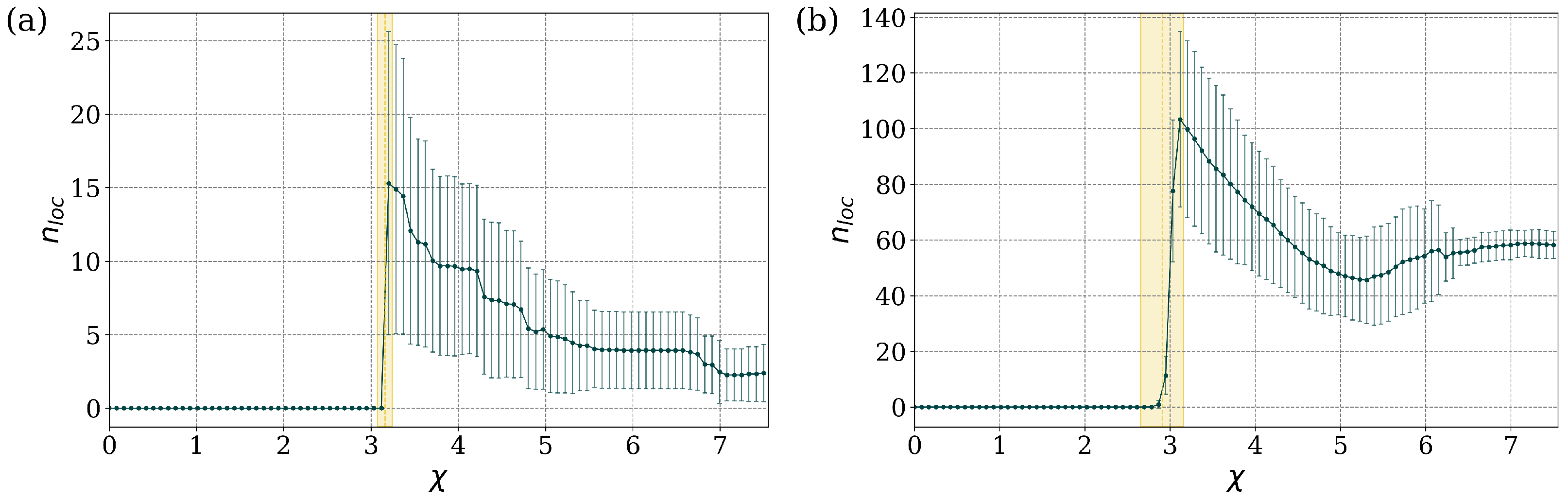
3.2. Random Connections with Equal Strength Bonds
3.3. Random Connections with Unequal Strength Bonds
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| tBLG | twisted bilayer graphene |
| DNLS | Discrete Nonlinear Schrödinger |
| SWN | Small-World Network |
| SW-DNLS | Small-World Discrete Nonlinear Schrödinger system |
| DOS | Density Of States |
| LR | long-range interactions |
| NN | Nearest Neighbor |
| MF | Mean Field |
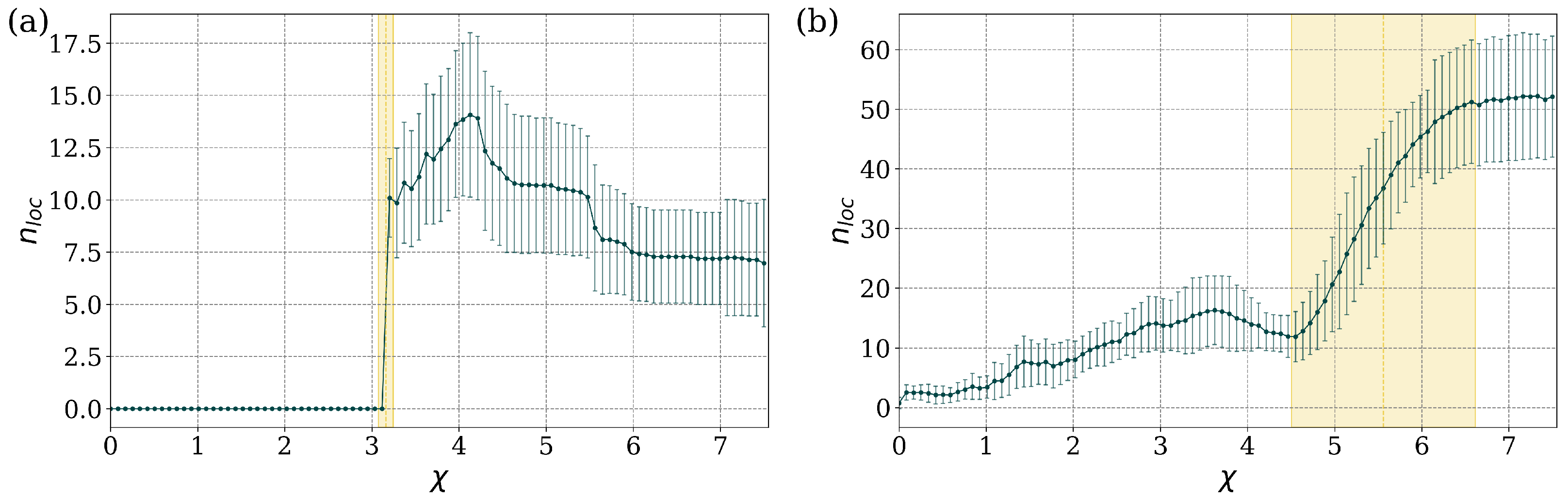
Appendix A. Localization Index

References
- Cao, Y.; Fatemi, V.; Demir, A.; Fang, S.; Tomarken, S.L.; Luo, J.Y.; Sanchez-Yamagishi, J.D.; Watanabe, K.; Taniguchi, T.; Kaxiras, E.; et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 2018, 556, 80–84. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Fatemi, V.; Fang, S.; Watanabe, K.; Taniguchi, T.; Kaxiras, E.; Jarillo-Herrero, P. Unconventional superconductivity in magic-angle graphene superlattices. Nature 2018, 556, 43–50. [Google Scholar] [CrossRef] [PubMed]
- Bistritzer, R.; MacDonald, A.H. Moiré bands in twisted double-layer graphene. Proc. Natl. Acad. Sci. USA 2011, 108, 12233–12237. [Google Scholar] [CrossRef] [PubMed]
- Eilbeck, J.; Lomdahl, P.; Scott, A. The discrete self-trapping equation. Phys. D Nonlinear Phenom. 1985, 16, 318–338. [Google Scholar] [CrossRef]
- Tsironis, G.; Kaxiras, E. Quantum dynamics on tight binding small world networks and flat band spectra. Phys. Lett. A 2024, 497, 129330. [Google Scholar] [CrossRef]
- Perakis, F.; Tsironis, G. Discrete nonlinear Schrödinger equation dynamics in complex networks. Phys. Lett. A 2011, 375, 676–679. [Google Scholar] [CrossRef][Green Version]
- Feddersen, H. Localization of vibrational energy in globular protein. Phys. Lett. A 1991, 154, 391–395. [Google Scholar] [CrossRef]
- Eilbeck, J.; Johansson, M. The discrete nonlinear Schrodinger equation—20 years on. In Proceedings of the Third Conference on Localization and Energy Transfer in Nonlinear Systems, Madrid, Spain, 17–21 June 2002; pp. 44–67. [Google Scholar]
- Carr, J.; Eilbeck, J. Stability of stationary solutions of the discrete self-trapping equation. Phys. Lett. A 1985, 109, 201–204. [Google Scholar] [CrossRef]
- Lederer, F.; Stegeman, G.I.; Christodoulides, D.N.; Assanto, G.; Segev, M.; Silberberg, Y. Discrete solitons in optics. Phys. Rep. 2008, 463, 1–126. [Google Scholar] [CrossRef]
- Kevrekidis, P.G. The Discrete Nonlinear Schrödiner Equation: Mathematical Analysis, Numerical Computations and Physical Perspectives; STMP 232; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Kenkre, V.M. Interplay of Quantum Mechanics with Nonlinearity; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Eilbeck, J. Nonlinear vibrational modes in a hexagonal molecule. Phys. Many-Part. Syst. 1987, 12, 41–51. [Google Scholar]
- Qausar, H.; Ramli, M.; Munzir, S.; Syafwan, M.; Fadhiliani, D. Soliton solution of stationary discrete nonlinear Schrödinger equation with the cubic-quintic nonlinearity. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1087, 012083. [Google Scholar] [CrossRef]
- Hennig, D.; Tsironis, G.P. Wave transmission in nonlinear lattices. Phys. Rep. 1999, 307, 333–432. [Google Scholar] [CrossRef]
- Tsironis, G. Exact dynamics for fully connected nonlinear networks. Phys. Lett. A 2011, 375, 1304–1308. [Google Scholar] [CrossRef][Green Version]
- Molina, M.; Tsironis, G. Dynamics of self-trapping in the discrete nonlinear Schrödinger equation. Phys. D Nonlinear Phenom. 1993, 65, 267–273. [Google Scholar] [CrossRef]
- Decker, D.; Keller, H. Path following near bifurcation. Commun. Pure Appl. Math. 1981, 34, 149–175. [Google Scholar] [CrossRef]
- Rheinboldt, W.C.; Burkardt, J.V. A locally parameterized continuation process. ACM Trans. Math. Softw. 1983, 9, 215–235. [Google Scholar] [CrossRef]
- Simpson, R.B. A Method for the Numerical Determination of Bifurcation States of Nonlinear Systems of Equations. SIAM J. Numer. Anal. 1975, 12, 439–451. [Google Scholar] [CrossRef]
- Eilbeck, J.C.; Lomdahl, P.S.; Scott, A.C. Soliton structure in crystalline acetanilide. Phys. Rev. B 1984, 30, 4703–4712. [Google Scholar] [CrossRef]
- Seydel, R. Tutorial on continuation. Int. J. Bifurc. Chaos 1991, 1, 3–11. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Perakis, F.; Mattheakis, M.; Tsironis, G.P. Small-world networks of optical fiber lattices. J. Opt. 2014, 16, 102003. [Google Scholar] [CrossRef]
- Watts, D.J. Networks, Dynamics, and the Small-World Phenomenon. Am. J. Sociol. 1999, 105, 493–527. [Google Scholar] [CrossRef]
- Aguirre, C.; Huerta, R.; Corbacho, F.; Pascual, P. Analysis of Biologically Inspired Small-World Networks. In Proceedings of the Artificial Neural Networks—ICANN 2002, Madrid, Spain, 28–30 August 2002; Dorronsoro, J.R., Ed.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 27–32. [Google Scholar] [CrossRef]
- Xu, Z.; Sui, D.Z. Small-world characteristics on transportation networks: A perspective from network autocorrelation. J. Geogr. Syst. 2007, 9, 189–205. [Google Scholar] [CrossRef]
- Latora, V.; Marchiori, M. Is the Boston subway a small-world network? Phys. A Stat. Mech. Its Appl. 2002, 314, 109–113. [Google Scholar] [CrossRef]
- Latora, V.; Marchiori, M. Efficient Behavior of Small-World Networks. Phys. Rev. Lett. 2001, 87, 198701. [Google Scholar] [CrossRef]
- Bassett, D.S.; Bullmore, E.T. Small-World Brain Networks Revisited. Neuroscientist 2017, 23, 499–516. [Google Scholar] [CrossRef] [PubMed]
- Silva, T.C.; Zhao, L. Machine Learning in Complex Networks; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Zippo, A.G.; Gelsomino, G.; Duin, P.V.; Nencini, S.; Caramenti, G.C.; Valente, M.; Biella, G.E. Small-world networks in neuronal populations: A computational perspective. Neural Netw. 2013, 44, 143–156. [Google Scholar] [CrossRef]
- Simard, D.; Nadeau, L.; Kröger, H. Fastest learning in small-world neural networks. Phys. Lett. A 2005, 336, 8–15. [Google Scholar] [CrossRef]
- Penati, T.; Sansottera, M.; Paleari, S.; Koukouloyannis, V.; Kevrekidis, P. On the nonexistence of degenerate phase-shift discrete solitons in a dNLS nonlocal lattice. Phys. D Nonlinear Phenom. 2018, 370, 1–13. [Google Scholar] [CrossRef]
- Guckenheimer, J.; Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields; Applied Mathematical Sciences; Springer: New York, NY, USA, 1983. [Google Scholar] [CrossRef]
- Edwards, J.T.; Thouless, D.J. Numerical studies of localization in disordered systems. J. Phys. C Solid State Phys. 1972, 5, 807. [Google Scholar] [CrossRef]
- Tsironis, G.P. Artificial Intelligence and Complex Dynamical Systems; Understanding Complex Systems; Springer: Berlin/Heidelberg, Germany, 2025. [Google Scholar]
- Dijkstra, H.A.; Wubs, F.W. Numerical Bifurcation Analysis. In Bifurcation Analysis of Fluid Flows; Cambridge University Press: Cambridge, UK, 2023; pp. 163–185. [Google Scholar]
- Uecker, H. Continuation and Bifurcation in Nonlinear PDEs—Algorithms, Applications, and Experiments. Jahresber. Der Dtsch. Math.-Ver. 2022, 124, 43–80. [Google Scholar] [CrossRef]
- Farrell, P.E.; Birkisson, A.; Funke, S.W. Deflation Techniques for Finding Distinct Solutions of Nonlinear Partial Differential Equations. SIAM J. Sci. Comput. 2015, 37, A2026–A2045. [Google Scholar] [CrossRef]
- Farrell, P.E.; Beentjes, C.H.L.; Birkisson, Á. The computation of disconnected bifurcation diagrams. arXiv 2016, arXiv:1603.00809. [Google Scholar] [CrossRef]
- Xia, J.; Farrell, P.E.; Castro, S.G. Nonlinear bifurcation analysis of stiffener profiles via deflation techniques. Thin-Walled Struct. 2020, 149, 106662. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almazova, N.; Tsironis, G.P.; Kaxiras, E. Statistical Properties of Correlated Semiclassical Bands in Tight-Binding Small-World Networks. Entropy 2025, 27, 420. https://doi.org/10.3390/e27040420
Almazova N, Tsironis GP, Kaxiras E. Statistical Properties of Correlated Semiclassical Bands in Tight-Binding Small-World Networks. Entropy. 2025; 27(4):420. https://doi.org/10.3390/e27040420
Chicago/Turabian StyleAlmazova, Natalya, Giorgos P. Tsironis, and Efthimios Kaxiras. 2025. "Statistical Properties of Correlated Semiclassical Bands in Tight-Binding Small-World Networks" Entropy 27, no. 4: 420. https://doi.org/10.3390/e27040420
APA StyleAlmazova, N., Tsironis, G. P., & Kaxiras, E. (2025). Statistical Properties of Correlated Semiclassical Bands in Tight-Binding Small-World Networks. Entropy, 27(4), 420. https://doi.org/10.3390/e27040420







