Measurement-Induced Symmetry Restoration and Quantum Mpemba Effect
Abstract
1. Introduction
- Monitored hopping fermion dynamics from the ground state. The system is initially prepared in the ground state of the spin chain and evolves under a -preserving Hamiltonian. While previous studies have established conditions for the quantum Mpemba effect in purely unitary evolution [9] or with weak dissipation [25], our results reveal that monitoring significantly broadens the class of initial states exhibiting this phenomenon (see the left column of the table in Figure 1). This provides a clear demonstration of a genuinely measurement-induced Mpemba effect—one that arises exclusively due to the interplay between unitary dynamics and measurement.
- Quench from an anisotropic Su–Schrieffer–Heeger (SSH) ground state. The system starts from the ground state of an anisotropic SSH model and evolves under the same -preserving Hamiltonian. Under unitary evolution, the symmetry remains broken, preventing the Mpemba effect from emerging. Strikingly, beyond a critical measurement rate, the symmetry is fully restored, triggering the Mpemba effect (see the right column of the table in Figure 1). This constitutes a genuinely measurement-induced symmetry restoration, with no counterpart in purely unitary dynamics.
2. Methods
2.1. Quantum Mpemba Effect
2.2. Lack of Symmetry Restoration
3. Results
3.1. Non-Hermitian Chain
3.1.1. Correlation Functions
3.2. Anisotropic SSH Chain
3.2.1. Correlation Functions
3.2.2. Hermitian Dynamics and Lack of Symmetry Restoration
3.2.3. Non-Hermitian Dynamics and Mpemba Effect
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Time Evolution of the SSH Ground State with Anisotropic Terms
Appendix B. Useful Properties of Toeplitz Matrices
References
- Mpemba, E.B.; Osborne, D.G. Cool? Phys. Educ. 1979, 14, 410–413. [Google Scholar] [CrossRef]
- Lu, Z.; Raz, O. Nonequilibrium thermodynamics of the Markovian Mpemba effect and its inverse. Proc. Natl. Acad. Sci. USA 2017, 114, 5083–5088. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Bechhoefer, J. Exponentially faster cooling in a colloidal system. Nature 2020, 584, 64–68. [Google Scholar] [CrossRef] [PubMed]
- Lasanta, A.; Vega Reyes, F.; Prados, A.; Santos, A. When the Hotter Cools More Quickly: Mpemba Effect in Granular Fluids. Phys. Rev. Lett. 2017, 119, 148001. [Google Scholar] [CrossRef]
- Teza, G.; Bechhoefer, J.; Lasanta, A.; Raz, O.; Vucelja, M. Speedups in nonequilibrium thermal relaxation: Mpemba and related effects. arXiv 2025. [Google Scholar] [CrossRef]
- Ares, F.; Murciano, S.; Calabrese, P. Entanglement asymmetry as a probe of symmetry breaking. Nat. Commun. 2023, 14, 2036. [Google Scholar] [CrossRef]
- Rylands, C.; Klobas, K.; Ares, F.; Calabrese, P.; Murciano, S.; Bertini, B. Microscopic Origin of the Quantum Mpemba Effect in Integrable Systems. Phys. Rev. Lett. 2024, 133, 010401. [Google Scholar] [CrossRef]
- Chalas, K.; Ares, F.; Rylands, C.; Calabrese, P. Multiple crossings during dynamical symmetry restoration and implications for the quantum Mpemba effect. J. Stat. Mech. 2024, 2024, 103101. [Google Scholar] [CrossRef]
- Murciano, S.; Ares, F.; Klich, I.; Calabrese, P. Entanglement asymmetry and quantum Mpemba effect in the XY spin chain. J. Stat. Mech. 2024, 2401, 013103. [Google Scholar] [CrossRef]
- Rylands, C.; Vernier, E.; Calabrese, P. Dynamical symmetry restoration in the Heisenberg spin chain. J. Stat. Mech. 2024, 2024, 123102. [Google Scholar] [CrossRef]
- Yamashika, S.; Calabrese, P.; Ares, F. Quenching from superfluid to free bosons in two dimensions: Entanglement, symmetries, and quantum Mpemba effect. arXiv 2024. [Google Scholar] [CrossRef]
- Yamashika, S.; Ares, F.; Calabrese, P. Entanglement asymmetry and quantum Mpemba effect in two-dimensional free-fermion systems. Phys. Rev. B 2024, 110, 085126. [Google Scholar] [CrossRef]
- Klobas, K. Non-equilibrium dynamics of symmetry-resolved entanglement and entanglement asymmetry: Exact asymptotics in Rule 54. J. Phys. A 2024, 57, 505001. [Google Scholar] [CrossRef]
- Turkeshi, X.; Calabrese, P.; De Luca, A. Quantum Mpemba Effect in Random Circuits. arXiv 2024. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, H.K.; Yin, S.; Zhang, S.X. Symmetry Restoration and Quantum Mpemba Effect in Symmetric Random Circuits. Phys. Rev. Lett. 2024, 133, 140405. [Google Scholar] [CrossRef]
- Foligno, A.; Calabrese, P.; Bertini, B. Nonequilibrium Dynamics of Charged Dual-Unitary Circuits. PRX Quantum 2025, 6, 010324. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, H.K.; Yin, S.; Zhang, S.X.; Yao, H. Quantum Mpemba effects in many-body localization systems. arXiv 2024. [Google Scholar] [CrossRef]
- Joshi, L.K.; Franke, J.; Rath, A.; Ares, F.; Murciano, S.; Kranzl, F.; Blatt, R.; Zoller, P.; Vermersch, B.; Calabrese, P.; et al. Observing the Quantum Mpemba Effect in Quantum Simulations. Phys. Rev. Lett. 2024, 133, 010402. [Google Scholar] [CrossRef]
- Nava, A.; Fabrizio, M. Lindblad dissipative dynamics in the presence of phase coexistence. Phys. Rev. B 2019, 100, 125102. [Google Scholar] [CrossRef]
- Chatterjee, A.K.; Takada, S.; Hayakawa, H. Quantum Mpemba Effect in a Quantum Dot with Reservoirs. Phys. Rev. Lett. 2023, 131, 080402. [Google Scholar] [CrossRef]
- Chatterjee, A.K.; Takada, S.; Hayakawa, H. Multiple quantum Mpemba effect: Exceptional points and oscillations. Phys. Rev. A 2024, 110, 022213. [Google Scholar] [CrossRef]
- Aharony Shapira, S.; Shapira, Y.; Markov, J.; Teza, G.; Akerman, N.; Raz, O.; Ozeri, R. Inverse Mpemba Effect Demonstrated on a Single Trapped Ion Qubit. Phys. Rev. Lett. 2024, 133, 010403. [Google Scholar] [CrossRef] [PubMed]
- Zatsarynna, K.; Nava, A.; Egger, R.; Zazunov, A. Green’s function approach to Josephson dot dynamics and application to quantum Mpemba effects. Phys. Rev. B 2025, 111, 104506. [Google Scholar] [CrossRef]
- Nava, A.; Egger, R. Mpemba Effects in Open Nonequilibrium Quantum Systems. Phys. Rev. Lett. 2024, 133, 136302. [Google Scholar] [CrossRef]
- Ares, F.; Vitale, V.; Murciano, S. Quantum Mpemba effect in free-fermionic mixed states. Phys. Rev. B 2025, 111, 104312. [Google Scholar] [CrossRef]
- Caceffo, F.; Murciano, S.; Alba, V. Entangled multiplets, asymmetry, and quantum Mpemba effect in dissipative systems. J. Stat. Mech. 2024, 2024, 063103. [Google Scholar] [CrossRef]
- Carollo, F.; Lasanta, A.; Lesanovsky, I. Exponentially Accelerated Approach to Stationarity in Markovian Open Quantum Systems through the Mpemba Effect. Phys. Rev. Lett. 2021, 127, 060401. [Google Scholar] [CrossRef]
- Zhang, J.; Xia, G.; Wu, C.W.; Chen, T.; Zhang, Q.; Xie, Y.; Su, W.; Qiu, C.; Chen, P.; Li, W.; et al. Observation of quantum strong Mpemba effect. Nat. Commun. 2025, 16, 301. [Google Scholar] [CrossRef]
- Moroder, M.; Culhane, O.; Zawadzki, K.; Goold, J. Thermodynamics of the Quantum Mpemba Effect. Phys. Rev. Lett. 2024, 133, 140404. [Google Scholar] [CrossRef]
- Ares, F.; Calabrese, P.; Murciano, S. The quantum Mpemba effects. arXiv 2025. [Google Scholar] [CrossRef]
- Fisher, M.P.; Khemani, V.; Nahum, A.; Vijay, S. Random Quantum Circuits. Annu. Rev. Condens. Matter Phys. 2023, 14, 335–379. [Google Scholar] [CrossRef]
- Potter, A.C.; Vasseur, R. Quantum Sciences and Technology; Springer: Cham, Switzerland, 2022; p. 211. [Google Scholar]
- Fazio, R.; Keeling, J.; Mazza, L.; Schirò, M. Many-Body Open Quantum Systems. arXiv 2024. [Google Scholar] [CrossRef]
- Lunt, O.; Richter, J.; Pal, A. Quantum Simulation Using Noisy Unitary Circuits and Measurements. In Entanglement in Spin Chains; Springer International Publishing: Berlin/Heidelberg, Germany, 2022; pp. 251–284. [Google Scholar] [CrossRef]
- Jacobs, K. Quantum Measurement Theory and Its Applications; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Cao, X.; Tilloy, A.; De Luca, A. Entanglement in a fermion chain under continuous monitoring. SciPost Phys. 2019, 7, 024. [Google Scholar] [CrossRef]
- Sierant, P.; Chiriacò, G.; Surace, F.M.; Sharma, S.; Turkeshi, X.; Dalmonte, M.; Fazio, R.; Pagano, G. Dissipative Floquet Dynamics: From Steady State to Measurement Induced Criticality in Trapped-ion Chains. Quantum 2022, 6, 638. [Google Scholar] [CrossRef]
- Gullans, M.J.; Huse, D.A. Scalable Probes of Measurement-Induced Criticality. Phys. Rev. Lett. 2020, 125, 070606. [Google Scholar] [CrossRef]
- Li, Y.; Chen, X.; Fisher, M.P.A. Measurement-driven entanglement transition in hybrid quantum circuits. Phys. Rev. B 2019, 100, 134306. [Google Scholar] [CrossRef]
- Skinner, B.; Ruhman, J.; Nahum, A. Measurement-Induced Phase Transitions in the Dynamics of Entanglement. Phys. Rev. X 2019, 9, 031009. [Google Scholar] [CrossRef]
- Bao, Y.; Choi, S.; Altman, E. Theory of the phase transition in random unitary circuits with measurements. Phys. Rev. B 2020, 101, 104301. [Google Scholar] [CrossRef]
- Gullans, M.J.; Huse, D.A. Dynamical Purification Phase Transition Induced by Quantum Measurements. Phys. Rev. X 2020, 10, 041020. [Google Scholar] [CrossRef]
- Jian, C.M.; You, Y.Z.; Vasseur, R.; Ludwig, A.W.W. Measurement-induced criticality in random quantum circuits. Phys. Rev. B 2020, 101, 104302. [Google Scholar] [CrossRef]
- Zabalo, A.; Gullans, M.J.; Wilson, J.H.; Gopalakrishnan, S.; Huse, D.A.; Pixley, J.H. Critical properties of the measurement-induced transition in random quantum circuits. Phys. Rev. B 2020, 101, 060301. [Google Scholar] [CrossRef]
- Zabalo, A.; Gullans, M.J.; Wilson, J.H.; Vasseur, R.; Ludwig, A.W.W.; Gopalakrishnan, S.; Huse, D.A.; Pixley, J.H. Operator Scaling Dimensions and Multifractality at Measurement-Induced Transitions. Phys. Rev. Lett. 2022, 128, 050602. [Google Scholar] [CrossRef] [PubMed]
- Lira-Solanilla, A.; Turkeshi, X.; Pappalardi, S. Multipartite entanglement structure of monitored quantum circuits. arXiv 2024. [Google Scholar] [CrossRef]
- Sierant, P.; Turkeshi, X. Universal Behavior beyond Multifractality of Wave Functions at Measurement-Induced Phase Transitions. Phys. Rev. Lett. 2022, 128, 130605. [Google Scholar] [CrossRef]
- Sierant, P.; Schirò, M.; Lewenstein, M.; Turkeshi, X. Measurement-induced phase transitions in (d+1)-dimensional stabilizer circuits. Phys. Rev. B 2022, 106, 214316. [Google Scholar] [CrossRef]
- Nahum, A.; Skinner, B. Entanglement and dynamics of diffusion-annihilation processes with Majorana defects. Phys. Rev. Res. 2020, 2, 023288. [Google Scholar] [CrossRef]
- Alberton, O.; Buchhold, M.; Diehl, S. Entanglement Transition in a Monitored Free-Fermion Chain: From Extended Criticality to Area Law. Phys. Rev. Lett. 2021, 126, 170602. [Google Scholar] [CrossRef]
- Turkeshi, X.; Biella, A.; Fazio, R.; Dalmonte, M.; Schiró, M. Measurement-induced entanglement transitions in the quantum Ising chain: From infinite to zero clicks. Phys. Rev. B 2021, 103, 224210. [Google Scholar] [CrossRef]
- Turkeshi, X.; Dalmonte, M.; Fazio, R.; Schirò, M. Entanglement transitions from stochastic resetting of non-Hermitian quasiparticles. Phys. Rev. B 2022, 105, L241114. [Google Scholar] [CrossRef]
- Tirrito, E.; Santini, A.; Fazio, R.; Collura, M. Full counting statistics as probe of measurement-induced transitions in the quantum Ising chain. SciPost Phys. 2023, 15, 096. [Google Scholar] [CrossRef]
- Lumia, L.; Tirrito, E.; Fazio, R.; Collura, M. Measurement-induced transitions beyond Gaussianity: A single particle description. Phys. Rev. Res. 2024, 6, 023176. [Google Scholar] [CrossRef]
- Piccitto, G.; Russomanno, A.; Rossini, D. Entanglement transitions in the quantum Ising chain: A comparison between different unravelings of the same Lindbladian. Phys. Rev. B 2022, 105, 064305. [Google Scholar] [CrossRef]
- Piccitto, G.; Rossini, D.; Russomanno, A. The impact of different unravelings in a monitored system of free fermions. Eur. Phys. J. B 2024, 97, 90. [Google Scholar] [CrossRef]
- Tsitsishvili, M.; Poletti, D.; Dalmonte, M.; Chiriacò, G. Measurement induced transitions in non-Markovian free fermion ladders. SciPost Phys. Core 2024, 7, 011. [Google Scholar] [CrossRef]
- Muzzi, C.; Tsitsishvili, M.; Chiriacò, G. Entanglement enhancement induced by noise in inhomogeneously monitored systems. Phys. Rev. B 2025, 111, 014312. [Google Scholar] [CrossRef]
- Coppola, M.; Tirrito, E.; Karevski, D.; Collura, M. Growth of entanglement entropy under local projective measurements. Phys. Rev. B 2022, 105, 094303. [Google Scholar] [CrossRef]
- Cecile, G.; Lóio, H.; De Nardis, J. Measurement-induced phase transitions by matrix product states scaling. Phys. Rev. Res. 2024, 6, 033220. [Google Scholar] [CrossRef]
- Lóio, H.; De Luca, A.; De Nardis, J.; Turkeshi, X. Purification timescales in monitored fermions. Phys. Rev. B 2023, 108, L020306. [Google Scholar] [CrossRef]
- Kells, G.; Meidan, D.; Romito, A. Topological transitions in weakly monitored free fermions. SciPost Phys. 2023, 14, 031. [Google Scholar] [CrossRef]
- Nehra, R.; Romito, A.; Meidan, D. Controlling measurement induced phase transitions with tunable detector coupling. arXiv 2024. [Google Scholar] [CrossRef]
- Buchhold, M.; Müller, T.; Diehl, S. Revealing measurement-induced phase transitions by pre-selection. arXiv 2022. [Google Scholar] [CrossRef]
- Starchl, E.; Fischer, M.H.; Sieberer, L.M. Generalized Zeno effect and entanglement dynamics induced by fermion counting. arXiv 2025. [Google Scholar] [CrossRef]
- Xing, B.; Turkeshi, X.; Schiró, M.; Fazio, R.; Poletti, D. Interactions and integrability in weakly monitored Hamiltonian systems. Phys. Rev. B 2024, 109, L060302. [Google Scholar] [CrossRef]
- Fresco, G.D.; Gal, Y.L.; Valenti, D.; Schirò, M.; Carollo, A. Entanglement growth in the dark intervals of a locally monitored free-fermion chain. arXiv 2025. [Google Scholar] [CrossRef]
- Lee, T.E.; Chan, C.K. Heralded Magnetism in Non-Hermitian Atomic Systems. Phys. Rev. X 2014, 4, 041001. [Google Scholar] [CrossRef]
- Biella, A.; Schiró, M. Many-Body Quantum Zeno Effect and Measurement-Induced Subradiance Transition. Quantum 2021, 5, 528. [Google Scholar] [CrossRef]
- Turkeshi, X.; Schiró, M. Entanglement and correlation spreading in non-Hermitian spin chains. Phys. Rev. B 2023, 107, L020403. [Google Scholar] [CrossRef]
- Gal, Y.L.; Turkeshi, X.; Schirò, M. Volume-to-area law entanglement transition in a non-Hermitian free fermionic chain. SciPost Phys. 2023, 14, 138. [Google Scholar] [CrossRef]
- Zerba, C.; Silva, A. Measurement phase transitions in the no-click limit as quantum phase transitions of a non-hermitean vacuum. SciPost Phys. Core 2023, 6, 051. [Google Scholar] [CrossRef]
- Paviglianiti, A.; Silva, A. Multipartite entanglement in the measurement-induced phase transition of the quantum Ising chain. Phys. Rev. B 2023, 108, 184302. [Google Scholar] [CrossRef]
- Guerra, E.M.; Gornyi, I.; Gefen, Y. Correlations and Krylov spread for a non-Hermitian Hamiltonian: Ising chain with a complex-valued transverse magnetic field. arXiv 2025. [Google Scholar] [CrossRef]
- Soares, R.D.; Schirò, M. Non-unitary quantum many-body dynamics using the Faber polynomial method. SciPost Phys. 2024, 17, 128. [Google Scholar] [CrossRef]
- Zhang, C.; Granet, E. Antiunitary symmetry breaking and a hierarchy of purification transitions in Floquet non-unitary circuits. arXiv 2023. [Google Scholar] [CrossRef]
- Granet, E.; Zhang, C.; Dreyer, H. Volume-Law to Area-Law Entanglement Transition in a Nonunitary Periodic Gaussian Circuit. Phys. Rev. Lett. 2023, 130, 230401. [Google Scholar] [CrossRef]
- Dóra, B.; Moca, C.P. Quantum Quench in PT-Symmetric Luttinger Liquid. Phys. Rev. Lett. 2020, 124, 136802. [Google Scholar] [CrossRef]
- Dóra, B.; Sticlet, D.; Moca, C.P. Correlations at PT-Symmetric Quantum Critical Point. Phys. Rev. Lett. 2022, 128, 146804. [Google Scholar] [CrossRef]
- Dóra, B.; Moca, C.P. Full counting statistics in the many-body Hatano-Nelson model. Phys. Rev. B 2022, 106, 235125. [Google Scholar] [CrossRef]
- Despres, J.; Mazza, L.; Schirò, M. Breakdown of linear spin-wave theory in a non-Hermitian quantum spin chain. Phys. Rev. B 2024, 110, 094304. [Google Scholar] [CrossRef]
- Dóra, B.; Werner, M.A.; Moca, C.P. Quantum quench dynamics in the Luttinger liquid phase of the Hatano-Nelson model. Phys. Rev. B 2023, 108, 035104. [Google Scholar] [CrossRef]
- Bácsi, A.; Dóra, B. Dynamics of entanglement after exceptional quantum quench. Phys. Rev. B 2021, 103, 085137. [Google Scholar] [CrossRef]
- Dupays, L.; del Campo, A.; Dóra, B. Slow approach to adiabaticity in many-body non-Hermitian systems: The Hatano-Nelson model. Phys. Rev. B 2025, 111, 045130. [Google Scholar] [CrossRef]
- Chakrabarti, N.; Nirbhan, N.; Bhattacharyya, A. Dynamics of monitored SSH Model in Krylov Space: From Complexity to Quantum Fisher Information. arXiv 2025. [Google Scholar] [CrossRef]
- Chitambar, E.; Gour, G. Quantum resource theories. Rev. Mod. Phys. 2019, 91, 025001. [Google Scholar] [CrossRef]
- Calabrese, P.; Cardy, J. Entanglement entropy and conformal field theory. J. Phys. A 2009, 42, 504005. [Google Scholar] [CrossRef]
- Calabrese, P.; Cardy, J. Evolution of entanglement entropy in one-dimensional systems. J. Stat. Mech. Theory Exp. 2005, 2005, P04010. [Google Scholar] [CrossRef]
- Fagotti, M.; Calabrese, P. Evolution of entanglement entropy following a quantum quench: Analytic results for the XY chain in a transverse magnetic field. Phys. Rev. A 2008, 78, 010306. [Google Scholar] [CrossRef]
- Alba, V.; Calabrese, P. Entanglement and thermodynamics after a quantum quench in integrable systems. Proc. Natl. Acad. Sci. USA 2017, 114, 7947–7951. [Google Scholar] [CrossRef]
- Calabrese, P. Entanglement and thermodynamics in non-equilibrium isolated quantum systems. Phys. A Stat. Mech. Its Appl. 2018, 504, 31–44. [Google Scholar] [CrossRef]
- Ares, F.; Murciano, S.; Piroli, L.; Calabrese, P. Entanglement asymmetry study of black hole radiation. Phys. Rev. D 2024, 110, L061901. [Google Scholar] [CrossRef]
- Ares, F.; Murciano, S.; Calabrese, P.; Piroli, L. Entanglement asymmetry dynamics in random quantum circuits. arXiv 2025. [Google Scholar] [CrossRef]
- Yu, H.; Li, Z.X.; Zhang, S.X. Symmetry Breaking Dynamics in Quantum Many-Body Systems. arXiv 2025. [Google Scholar] [CrossRef]
- Ares, F.; Murciano, S.; Vernier, E.; Calabrese, P. Lack of symmetry restoration after a quantum quench: An entanglement asymmetry study. SciPost Phys. 2023, 15, 089. [Google Scholar] [CrossRef]
- Fagotti, M.; Calabrese, P. Entanglement entropy of two disjoint blocks in XY chains. J. Stat. Mech. 2010, 1004, P04016. [Google Scholar] [CrossRef]
- Buchhold, M.; Minoguchi, Y.; Altland, A.; Diehl, S. Effective Theory for the Measurement-Induced Phase Transition of Dirac Fermions. Phys. Rev. X 2021, 11, 041004. [Google Scholar] [CrossRef]
- Fava, M.; Piroli, L.; Bernard, D.; Nahum, A. Monitored fermions with conserved U(1) charge. Phys. Rev. Res. 2024, 6, 043246. [Google Scholar] [CrossRef]
- Fava, M.; Piroli, L.; Swann, T.; Bernard, D.; Nahum, A. Nonlinear Sigma Models for Monitored Dynamics of Free Fermions. Phys. Rev. X 2023, 13, 041045. [Google Scholar] [CrossRef]
- Jian, C.M.; Shapourian, H.; Bauer, B.; Ludwig, A.W.W. Measurement-induced entanglement transitions in quantum circuits of non-interacting fermions: Born-rule versus forced measurements. arXiv 2023. [Google Scholar] [CrossRef]
- Jian, C.M.; Bauer, B.; Keselman, A.; Ludwig, A.W.W. Criticality and entanglement in nonunitary quantum circuits and tensor networks of noninteracting fermions. Phys. Rev. B 2022, 106, 134206. [Google Scholar] [CrossRef]
- Müller, T.M.; Buchhold, M.; Diehl, S. Monitored interacting Dirac fermions. arXiv 2025. [Google Scholar] [CrossRef]
- Poboiko, I.; Pöpperl, P.; Gornyi, I.V.; Mirlin, A.D. Theory of Free Fermions under Random Projective Measurements. Phys. Rev. X 2023, 13, 041046. [Google Scholar] [CrossRef]
- Chahine, K.; Buchhold, M. Entanglement phases, localization and multifractality of monitored free fermions in two dimensions. arXiv 2023. [Google Scholar] [CrossRef]
- Poboiko, I.; Pöpperl, P.; Gornyi, I.V.; Mirlin, A.D. Measurement-induced transitions for interacting fermions. Phys. Rev. B 2025, 111, 024204. [Google Scholar] [CrossRef]
- Leung, C.Y.; Romito, A. Entanglement and operator correlation signatures of many-body quantum Zeno phases in inefficiently monitored noisy systems. Phys. Rev. A 2025, 111, 022427. [Google Scholar] [CrossRef]
- Klocke, K.; Moore, J.E.; Buchhold, M. Power-Law Entanglement and Hilbert Space Fragmentation in Nonreciprocal Quantum Circuits. Phys. Rev. Lett. 2024, 133, 070401. [Google Scholar] [CrossRef]
- Klocke, K.; Buchhold, M. Majorana Loop Models for Measurement-Only Quantum Circuits. Phys. Rev. X 2023, 13, 041028. [Google Scholar] [CrossRef]
- Szyniszewski, M.; Lunt, O.; Pal, A. Disordered monitored free fermions. Phys. Rev. B 2023, 108, 165126. [Google Scholar] [CrossRef]
- Lunt, O.; Pal, A. Measurement-induced entanglement transitions in many-body localized systems. Phys. Rev. Res. 2020, 2, 043072. [Google Scholar] [CrossRef]
- Piccitto, G.; Chiriacò, G.; Rossini, D.; Russomanno, A. Entanglement behavior and localization properties in monitored fermion systems. arXiv 2025. [Google Scholar] [CrossRef]
- De Tomasi, G.; Khaymovich, I.M. Stable many-body localization under random continuous measurements in the no-click limit. Phys. Rev. B 2024, 109, 174205. [Google Scholar] [CrossRef]
- Agrawal, U.; Zabalo, A.; Chen, K.; Wilson, J.H.; Potter, A.C.; Pixley, J.H.; Gopalakrishnan, S.; Vasseur, R. Entanglement and Charge-Sharpening Transitions in U(1) Symmetric Monitored Quantum Circuits. Phys. Rev. X 2022, 12, 041002. [Google Scholar] [CrossRef]
- Russomanno, A.; Piccitto, G.; Rossini, D. Entanglement transitions and quantum bifurcations under continuous long-range monitoring. Phys. Rev. B 2023, 108, 104313. [Google Scholar] [CrossRef]
- Passarelli, G.; Turkeshi, X.; Russomanno, A.; Lucignano, P.; Schirò, M.; Fazio, R. Many-Body Dynamics in Monitored Atomic Gases without Postselection Barrier. Phys. Rev. Lett. 2024, 132, 163401. [Google Scholar] [CrossRef] [PubMed]
- Delmonte, A.; Li, Z.; Passarelli, G.; Song, E.Y.; Barberena, D.; Rey, A.M.; Fazio, R. Measurement-induced phase transitions in monitored infinite-range interacting systems. arXiv 2024. [Google Scholar] [CrossRef]
- Sharma, S.; Turkeshi, X.; Fazio, R.; Dalmonte, M. Measurement-induced criticality in extended and long-range unitary circuits. SciPost Phys. Core 2022, 5, 023. [Google Scholar] [CrossRef]
- Minato, T.; Sugimoto, K.; Kuwahara, T.; Saito, K. Fate of Measurement-Induced Phase Transition in Long-Range Interactions. Phys. Rev. Lett. 2022, 128, 010603. [Google Scholar] [CrossRef]
- Block, M.; Bao, Y.; Choi, S.; Altman, E.; Yao, N.Y. Measurement-Induced Transition in Long-Range Interacting Quantum Circuits. Phys. Rev. Lett. 2022, 128, 010604. [Google Scholar] [CrossRef]
- Müller, T.; Diehl, S.; Buchhold, M. Measurement-Induced Dark State Phase Transitions in Long-Ranged Fermion Systems. Phys. Rev. Lett. 2022, 128, 010605. [Google Scholar] [CrossRef]
- Ladewig, B.; Diehl, S.; Buchhold, M. Monitored open fermion dynamics: Exploring the interplay of measurement, decoherence, and free Hamiltonian evolution. Phys. Rev. Res. 2022, 4, 033001. [Google Scholar] [CrossRef]
- Turkeshi, X.; Piroli, L.; Schiró, M. Enhanced entanglement negativity in boundary-driven monitored fermionic chains. Phys. Rev. B 2022, 106, 024304. [Google Scholar] [CrossRef]
- Turkeshi, X.; Piroli, L.; Schirò, M. Density and current statistics in boundary-driven monitored fermionic chains. Phys. Rev. B 2024, 109, 144306. [Google Scholar] [CrossRef]
- Salatino, G.; Passarelli, G.; Russomanno, A.; Santoro, G.E.; Lucignano, P.; Fazio, R. Exploring Topological Boundary Effects through Quantum Trajectories in Dissipative SSH Models. arXiv 2024. [Google Scholar] [CrossRef]
- Turkeshi, X.; Murciano, S. Data and Code for “Measurement-induced symmetry restoration and quantum Mpemba effect”. Zenodo 2025. [Google Scholar] [CrossRef]

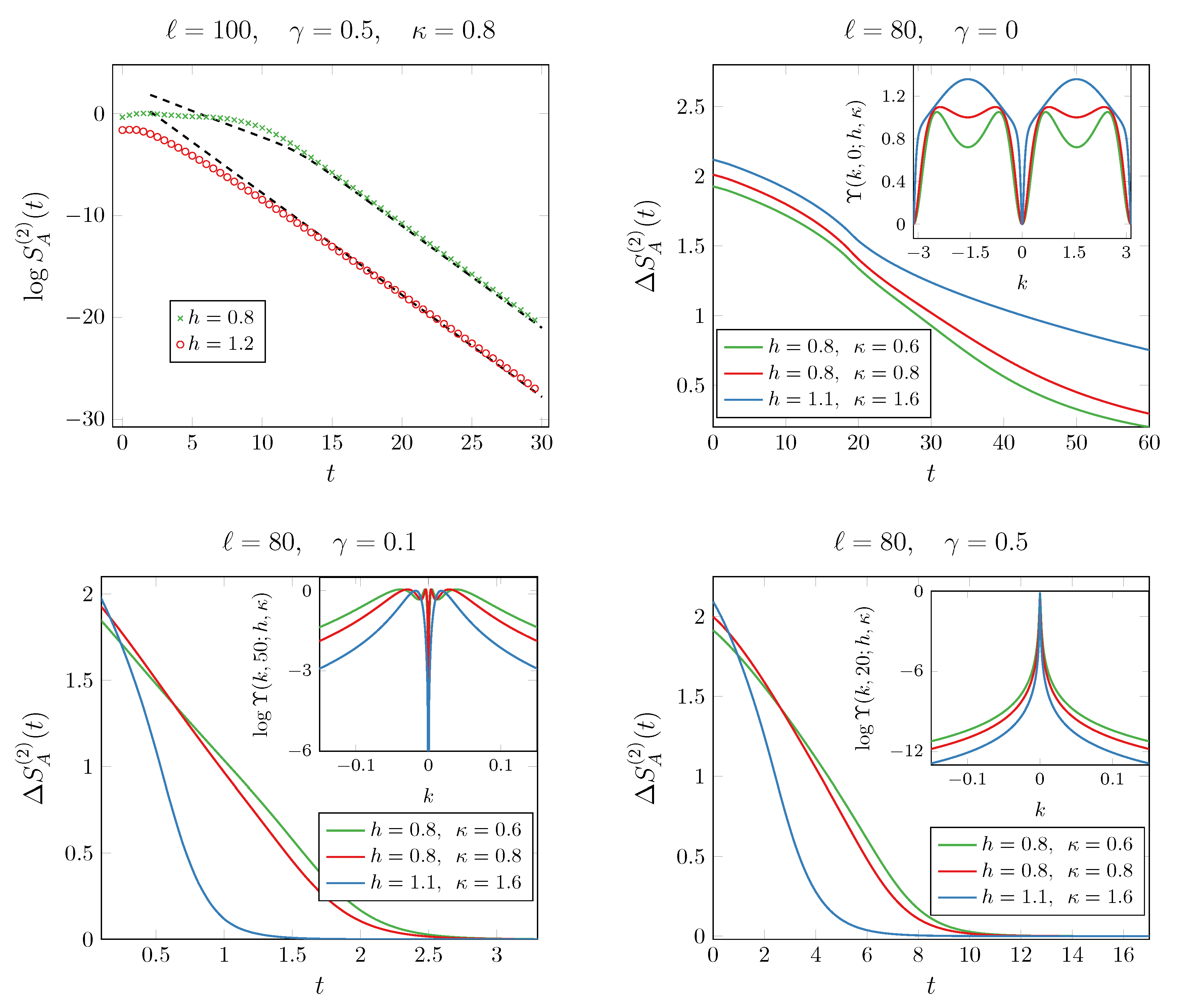
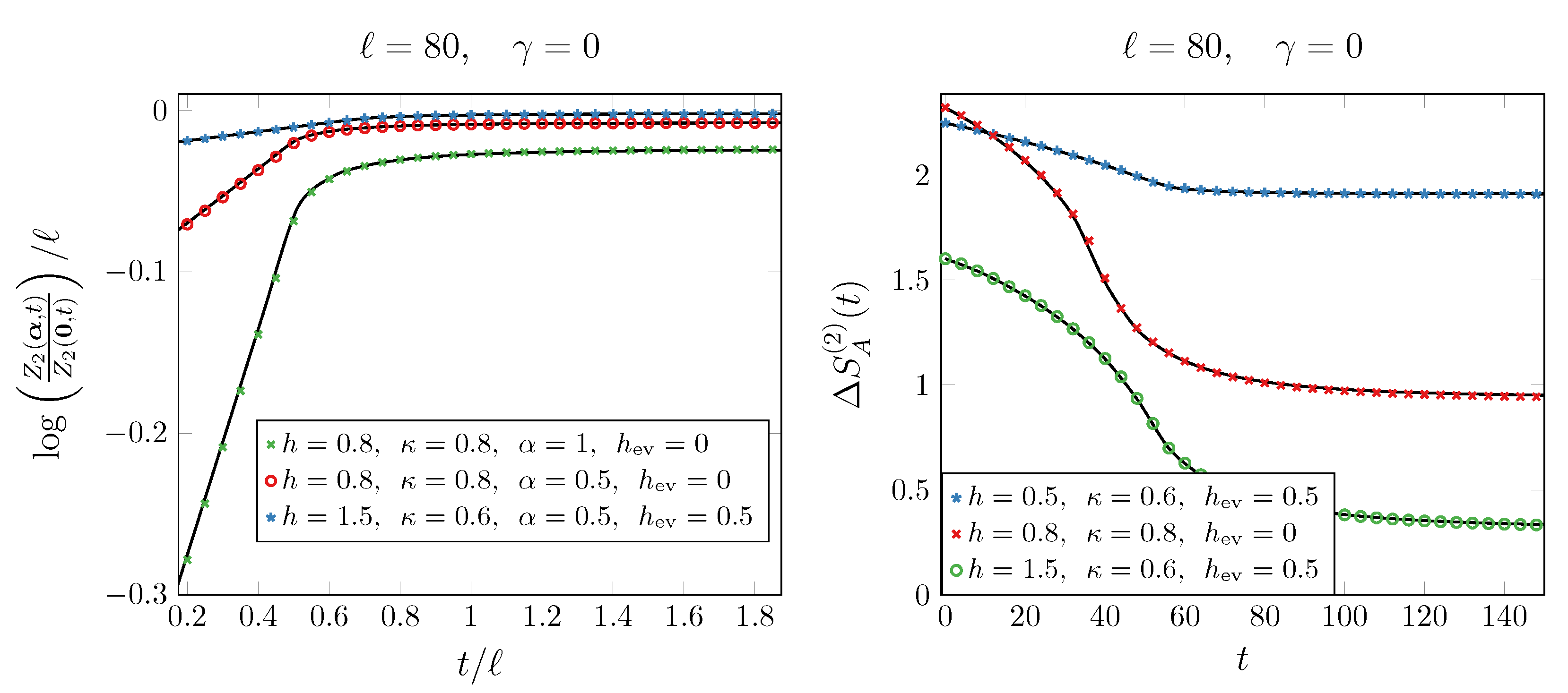
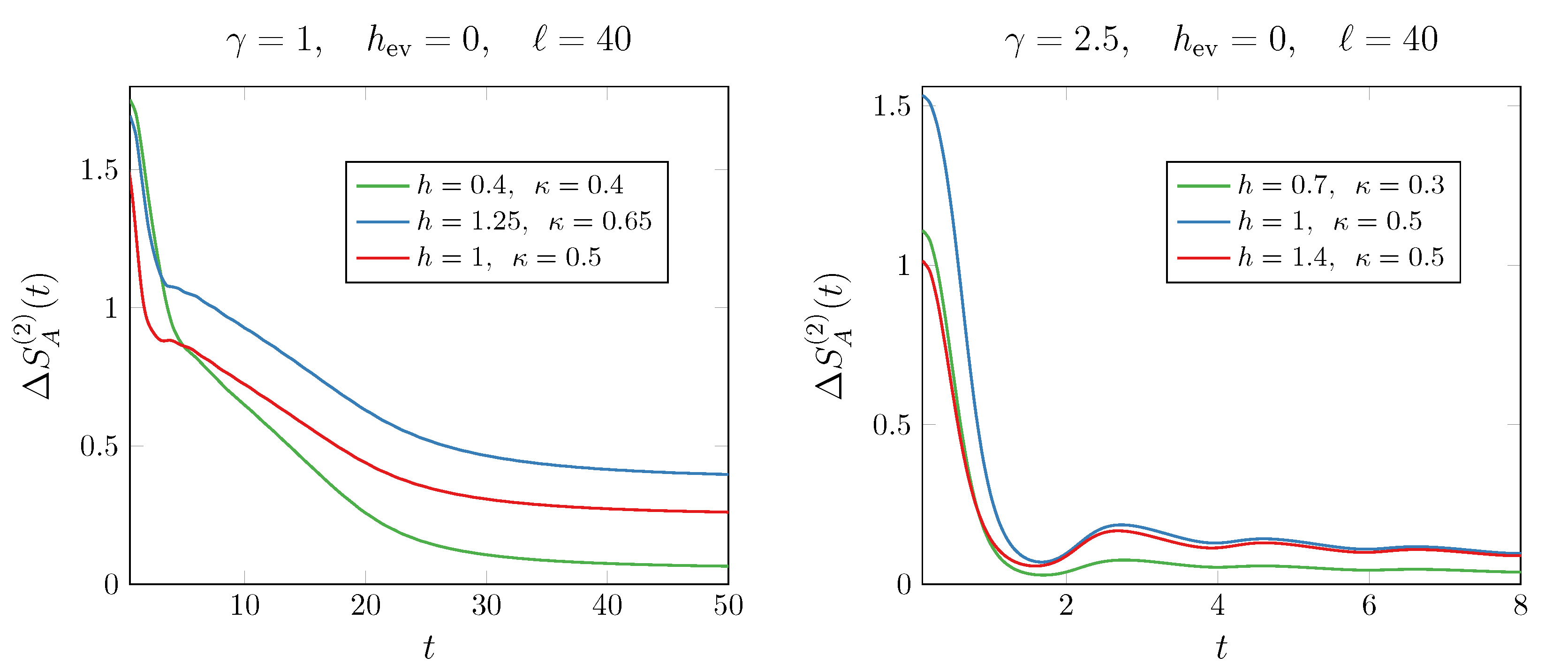
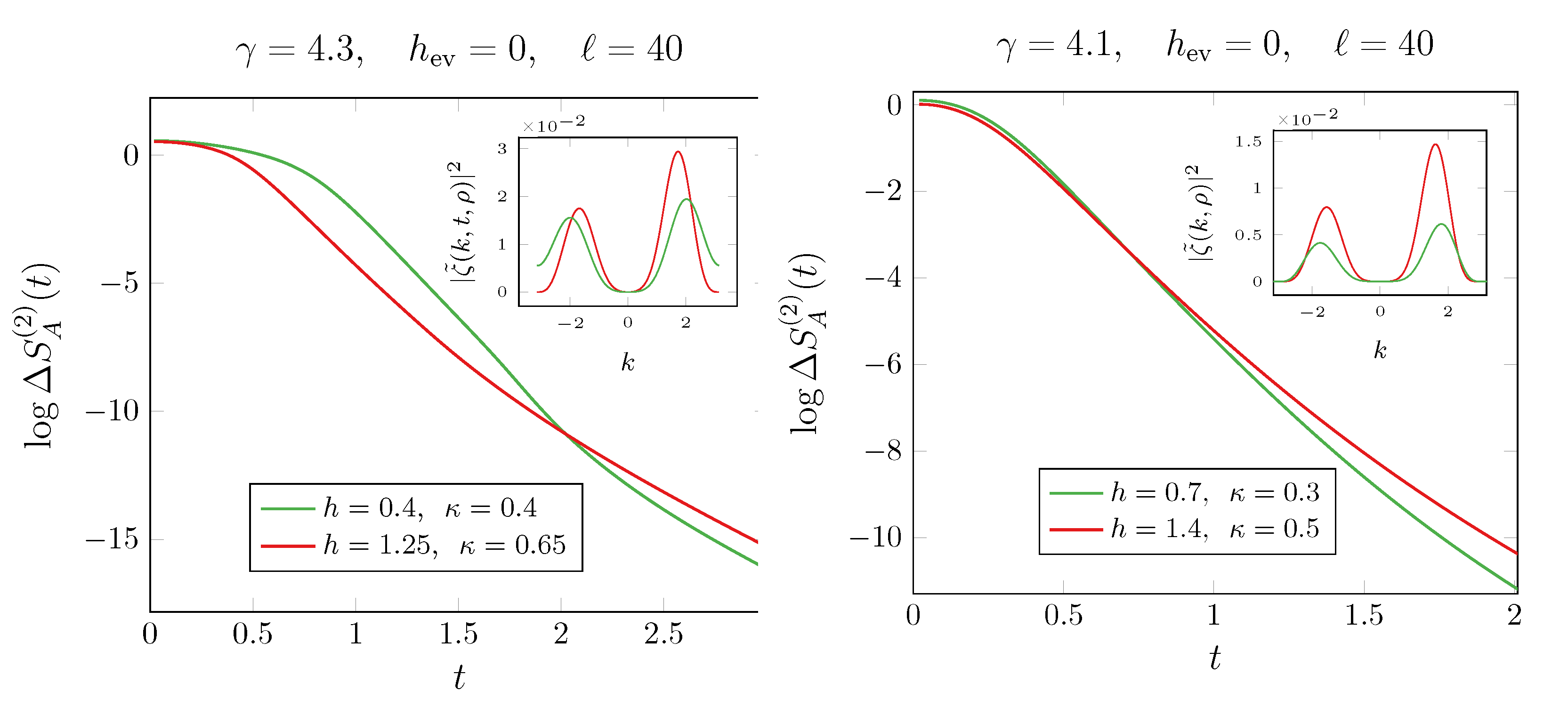
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Giulio, G.; Turkeshi, X.; Murciano, S. Measurement-Induced Symmetry Restoration and Quantum Mpemba Effect. Entropy 2025, 27, 407. https://doi.org/10.3390/e27040407
Di Giulio G, Turkeshi X, Murciano S. Measurement-Induced Symmetry Restoration and Quantum Mpemba Effect. Entropy. 2025; 27(4):407. https://doi.org/10.3390/e27040407
Chicago/Turabian StyleDi Giulio, Giuseppe, Xhek Turkeshi, and Sara Murciano. 2025. "Measurement-Induced Symmetry Restoration and Quantum Mpemba Effect" Entropy 27, no. 4: 407. https://doi.org/10.3390/e27040407
APA StyleDi Giulio, G., Turkeshi, X., & Murciano, S. (2025). Measurement-Induced Symmetry Restoration and Quantum Mpemba Effect. Entropy, 27(4), 407. https://doi.org/10.3390/e27040407





