LOMDP: Maximizing Desired Opinions in Social Networks by Considering User Expression Intentions
Abstract
1. Introduction
- (1)
- We propose the concept of expression capacity, which determines whether a user becomes a silent node at a given moment based on factors such as user personality, event heat, and group effects. To the best of our knowledge, this is the first time that the influence of silent nodes has been introduced into the desired opinion maximization problem, and it is the first time that the decay factor of event heat has been taken into account in the dynamics of opinion propagation.
- (2)
- To address the seed selection limitations in previous algorithms, we propose the Limited Opinion Maximization (LOM) algorithm, which divides networks into communities, evenly places seeds, and activates nodes with maximal expected returns in multiple stages, thereby significantly enhancing propagation effectiveness.
- (3)
- We propose the Limited Opinion Dynamic Propagation Optimization Model (LODP), an improved dynamic opinion model that integrates the classical FJ model with finite confidence opinions and silent node influence, thereby substantially enhancing the accuracy of dynamic opinion modeling.
- (4)
- We evaluate the effectiveness of the proposed method by comparing it with several baseline algorithms using four social network datasets, demonstrating its superior performance.
2. Related Work
2.1. Influence Maximization
- Greedy algorithm
- 2.
- Heuristic algorithm
2.2. Opinion Maximization
2.3. Opinion Dynamics
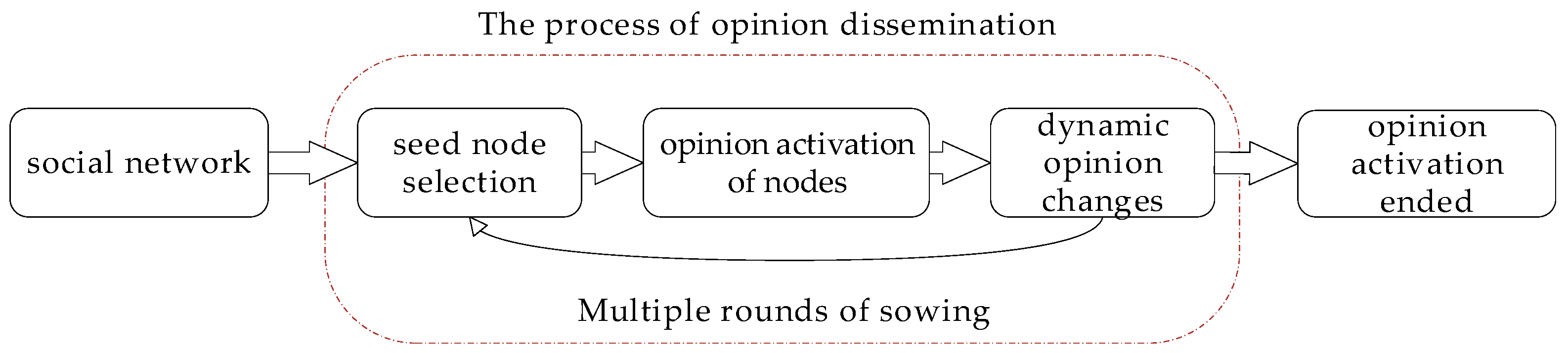
3. Model
3.1. Subsection
3.2. Node Expression Capacity
- (i)
- In real social networks, there are inevitably silent nodes. According to cognitive psychology theories [33], every individual has personality traits that influence their behavior. For example, introverts may be reluctant to express their opinions, which may lead them to become silent nodes. In addition, according to social psychology theories [34], people may choose to remain silent due to social pressure from authority or conformity.
- (ii)
- The propagation of an opinion is not endless; it eventually reaches a termination point. One reason for this is that the “heat” of an event gradually diminishes, leading to decreasing user attention over time.
- (iii)
- Silent nodes can impact the selection of seed nodes and the propagation of information. For example, a highly influential sports blogger may choose to remain silent about events in the gaming domain. If the sports blogger is selected as a seed node for propagation based solely on the influence factor, the final desired outcome may be suboptimal, as their silence could hinder the effective spread of the targeted opinion.
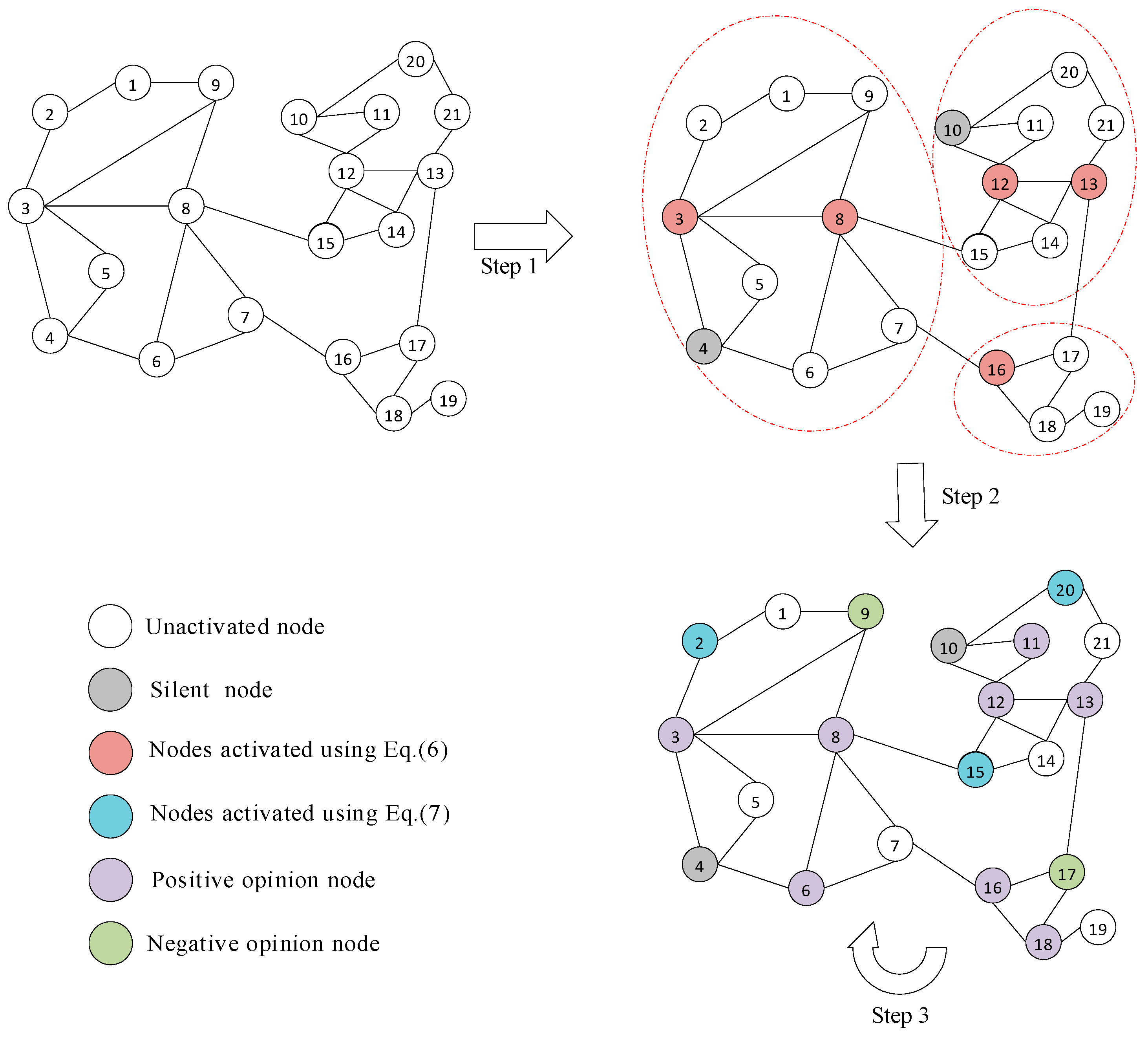
3.3. Seed Node Selection Algorithm
| Algorithm 1 LOM Algorithm |
| Input: Network G = (V, E, W), the number of seed nodes, k, the number of sowing stages, l, and stage time, T Output: list of seed nodes, S BEGIN S←∅ for r = 1:l, do if r == 1, then Divide G into communities: community_dict = {community, nodes_number} for each community, do Seed_counts = k × nodes_number/len(G.nodes) Seeds <- sort community nodes by Equation (6) S <- S∪Seeds[:k/l] end for end if if r > 1, do Seeds <- sort G.nodes by Equation (7) S<- S ∪ Seeds[:k/l] end if end for Obtain the seed node set S. END |
3.4. Dynamic Opinion Change Model
| Algorithm 2 Node Activation and Opinion Changes |
| Input: Network , the number of seed nodes, , the number of sowing stages, , and stage time, Output: list of seed nodes, BEGIN for t = 1:T, do for in G.nodes, do if is not active, do Initialize in-degree node set V <- ∅ if node is active and , do node is activated update by Equation (9) end if end if end for update opinion by Equation (8) end for END |
4. Experiments
4.1. Datasets and Baseline Algorithms
- Degree algorithm: Calculates node influence based on degree centrality.
- PageRank algorithm: Iteratively computes the importance of web pages based on their linking relationships, with more links indicating higher influence.
- Degree Discount algorithm: Assigns higher influence to nodes with higher degrees but discounts the influence of each connection as the node’s degree increases.
- IMRank algorithm: Models node influence as a probability distribution that reflects both the node’s structural position and its role in information dissemination.
- CELF++ algorithm: Enhances the efficiency of influence calculation by employing an optimized greedy approach that focuses on the incremental gain of influence for each node.
- AOMF algorithm: Estimates a node’s potential positive impact, initiating multiple iterations of linear threshold propagation to simulate influence spread.
4.2. Hypotheses and Parameters
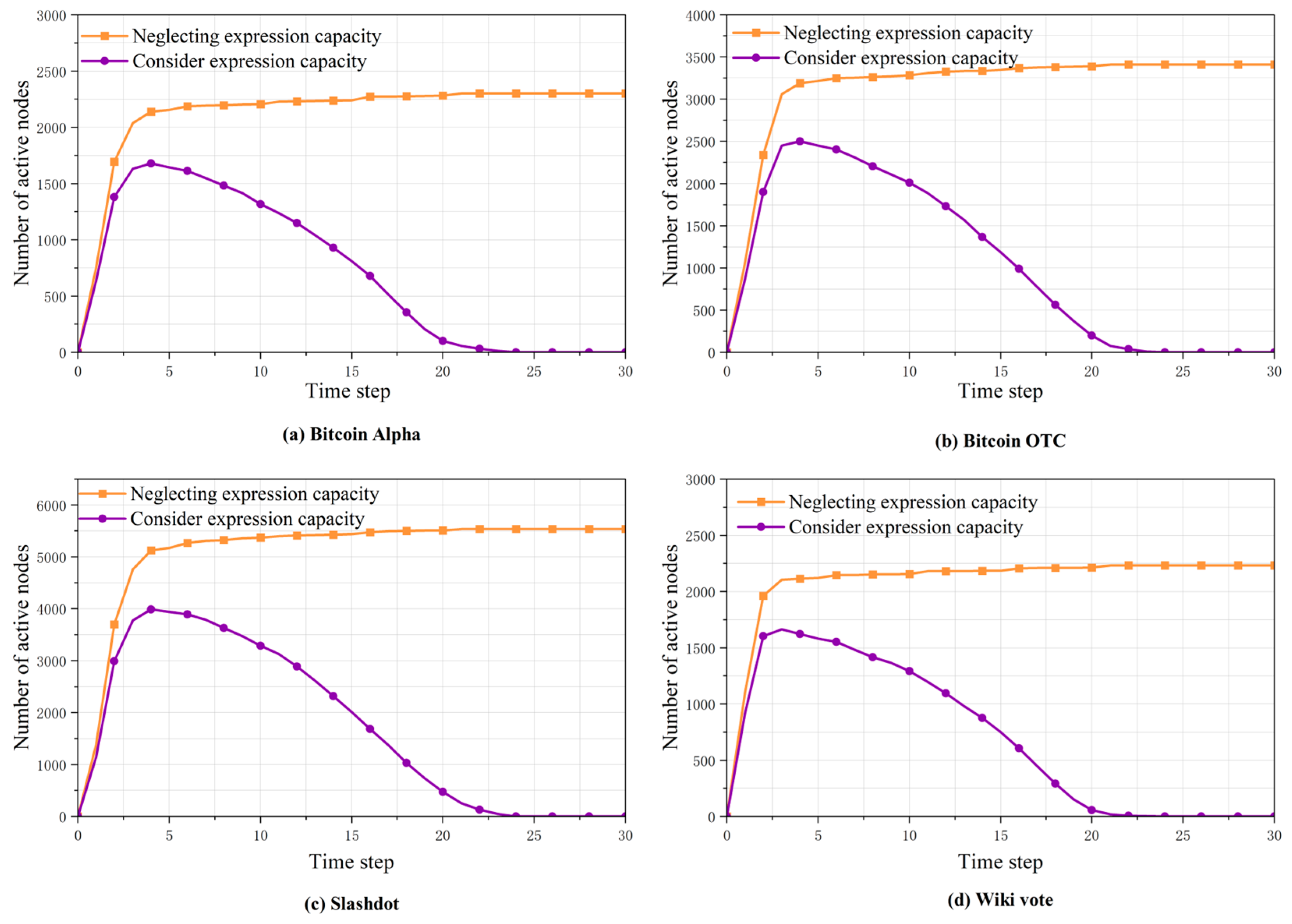
4.3. Comparison of the Number of Active Nodes When Considering Expression Capacity
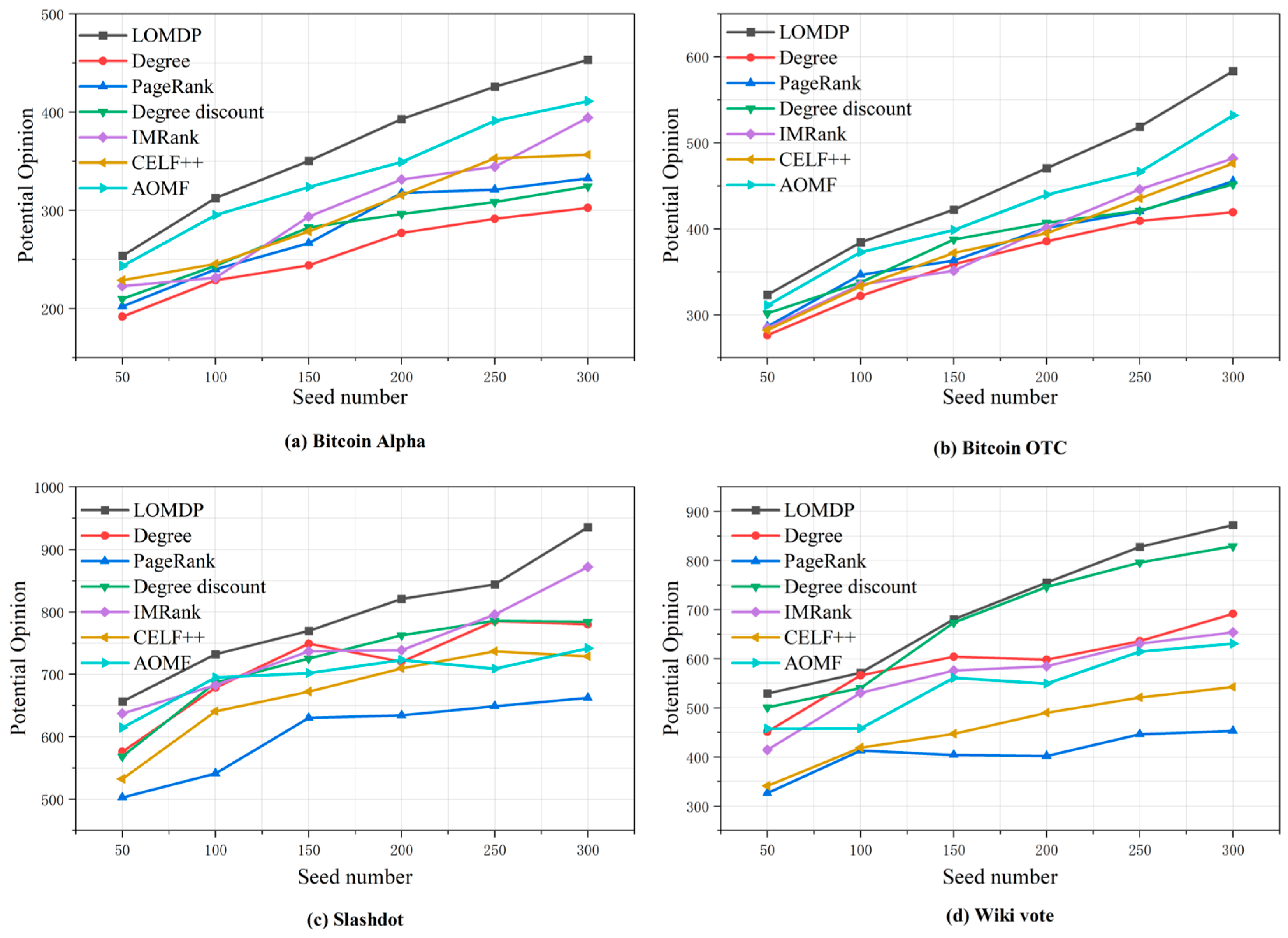
4.4. Analysis of Potential Desired Returns
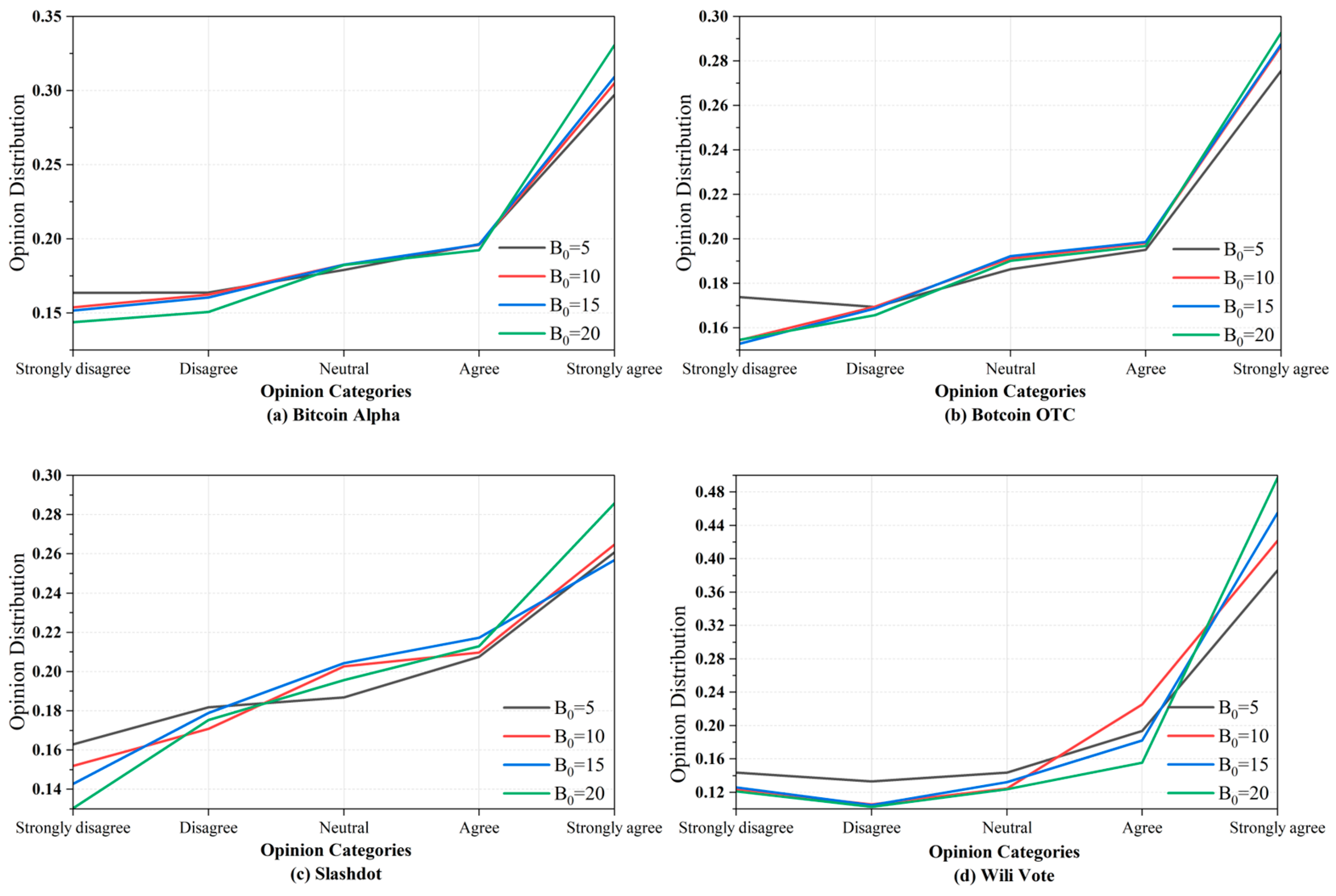
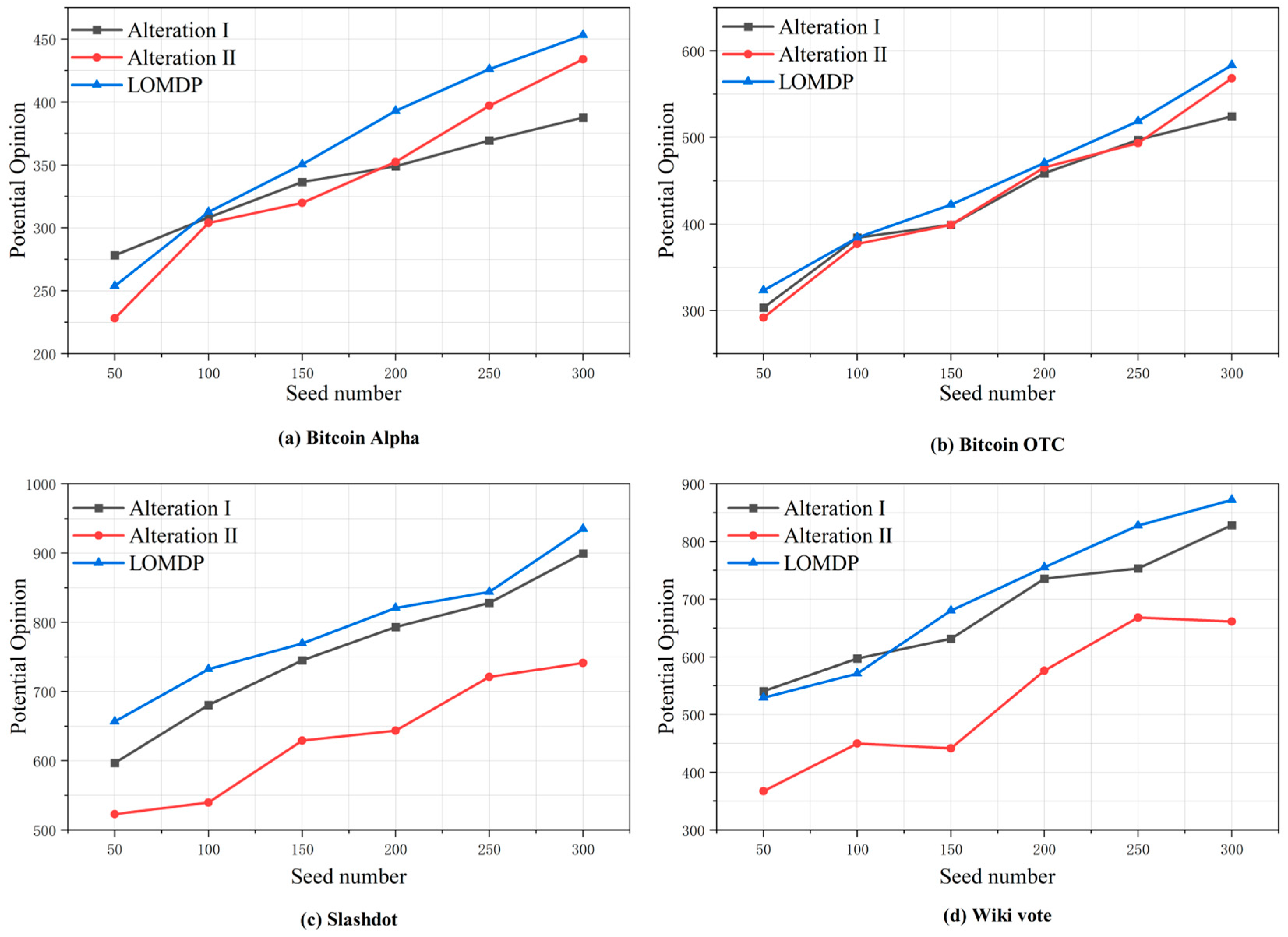
4.5. Comparison of Potential Views
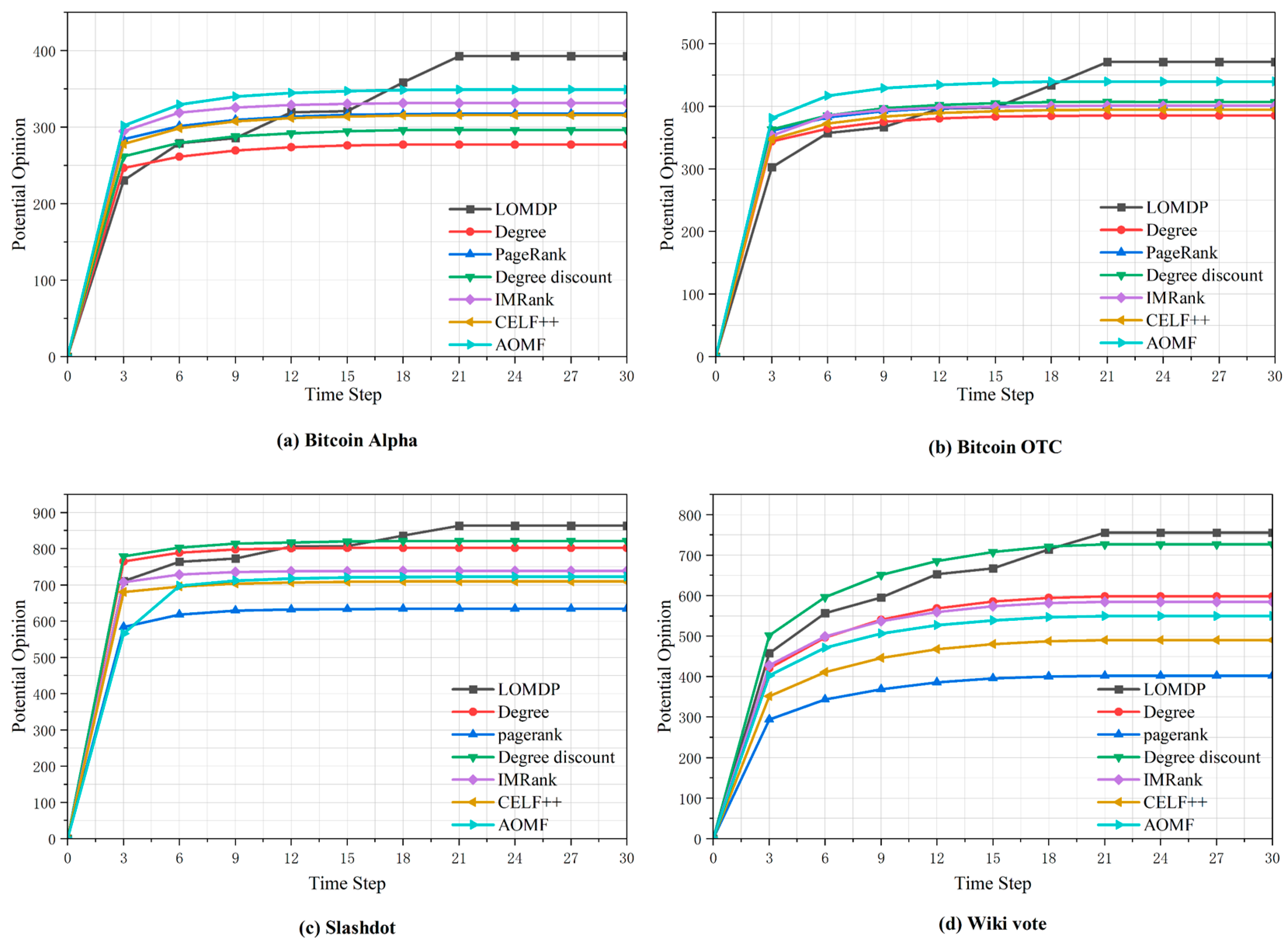
4.6. Analysis of Potential Opinions and Propagation Time
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LOMDP | Limited Opinion Maximization with Dynamic Propagation Optimization |
| POM | Positive Opinion Maximization |
| DOM | Desired Opinion Maximization |
| LOM | Limited Opinion Maximization |
| LODP | Limited Opinion Dynamic Propagation Optimization Model |
| IM | Influence Maximization |
| OM | Opinion Maximization |
| CELF | Cost-Effective Lazy Forward |
| CELF++ | Cost-Effective Lazy Forward Selection ++ |
| SAIM | Social Action-Based Influence Maximization Model |
| MIA | Memetic Influence Algorithm |
| RIS | Randomized Incremental Search |
| IC | Independent Cascade Model |
| LT | Linear Threshold Model |
| IC-N | Independent Cascade-Negative model |
| SRIS | Signed Reverse Influence Sampling |
| AOMF | Activated Opinion Maximization Framework |
| PUEA | Potential User Discovery based on Emotion Aggregation |
| FJ | Friedkin–Johnsen Model |
| DW | Deffuant–Weisbuch Model |
| HK | Hegselmann–Krause Model |
| EPO | Expressed Private Opinion |
| MEPO | Modified Expressed Private Opinion |
| SNHK | Social Network Hegselmann–Krause |
| NE | Node Expression |
References
- Barbieri, N.; Bonchi, F.; Manco, G. Topic-Aware Social Influence Propagation Models. In Proceedings of the 2012 IEEE 12th International Conference on Data Mining, Brussels, Belgium, 10–13 December 2012; pp. 81–90. [Google Scholar]
- Chen, W.; Collins, A.; Cummings, R.; Ke, T.; Liu, Z.; Rincon, D.; Sun, X.; Wang, Y.; Wei, W.; Yuan, Y. Influence Maximization in Social Networks When Negative Opinions May Emerge and Propagate. In Proceedings of the 2011 SIAM International Conference on Data Mining (SDM), Mesa, AZ, USA, 28–30 April 2011; pp. 379–390. [Google Scholar]
- Bustamante-Castañeda, F.; Caputo, J.G.; Cruz-Pacheco, G.; Knippel, A.; Mouatamide, F. Epidemic model on a network: Analysis and applications to COVID-19. Phys. A Stat. Mech. Its Appl. 2021, 564, 125520. [Google Scholar] [CrossRef]
- He, Q.; Sun, L.; Wang, X.; Wang, Z.; Huang, M.; Yi, B.; Wang, Y.; Ma, L. Positive opinion maximization in signed social networks. Inf. Sci. 2021, 558, 34–49. [Google Scholar] [CrossRef]
- Dai, J.; Zhu, J.; Wang, G. Opinion influence maximization problem in online social networks based on group polarization effect. Inf. Sci. 2022, 609, 195–214. [Google Scholar]
- Domingos, P.; Richardson, M. Mining the Network Value of Customers. In Proceedings of the Seventh International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 26–29 August 2001. [Google Scholar]
- Singh, S.S.; Kumar, A.; Singh, K.; Biswas, B. LAPSO-IM: A learning-based influence maximization approach for social networks. Appl. Soft Comput. 2019, 82, 105554. [Google Scholar]
- Kempe, D.; Kleinberg, J.; Tardos, É. Maximizing the spread of influence through a social network. In Proceedings of the Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 24–27 August 2003; Association for Computing Machinery: New York, NY, USA, 2003; pp. 137–146. [Google Scholar]
- Leskovec, J.; Krause, A.; Guestrin, C.; Faloutsos, C.; VanBriesen, J.; Glance, N. Cost-effective outbreak detection in networks. In Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery And Data Mining, San Jose, CA, USA, 12–15 August 2007; Association for Computing Machinery: New York, NY, USA, 2007; pp. 420–429. [Google Scholar]
- Goyal, A.; Lu, W.; Lakshmanan, L.V.S. CELF++: Optimizing the Greedy Algorithm for Influence Maximization in Social Networks. In Proceedings of the 21st International Conference on World Wide Web, Hyderabad, India, 28 March–1 April 2011; pp. 47–48. [Google Scholar]
- Ye, M.; Qin, Y.; Govaert, A.; Anderson, B.D.O.; Cao, M. An influence network model to study discrepancies in expressed and private opinions. Automatica 2019, 107, 371–381. [Google Scholar]
- Azaouzi, M.; Romdhane, L.B. An Efficient Two-Phase Model for Computing Influential Nodes in Social Networks Using Social Actions. J. Comput. Sci. Technol. 2018, 33, 286–304. [Google Scholar] [CrossRef]
- Page, L.; Brin, S.; Motwani, R.; Winograd, T. The PageRank Citation Ranking: Bringing Order to the Web. Available online: https://gwern.net/doc/technology/google/1998-page.pdf (accessed on 6 January 2024).
- Wei, D.; Ya, L.; Zhang, Y.; Deng, Y. Degree centrality based on the weighted network. In Proceedings of the 2012 24th Chinese Control and Decision Conference (CCDC), Taiyuan, China, 23–25 May 2012; pp. 3976–3979. [Google Scholar]
- Kundu, S.; Murthy, C.A.; Pal, S.K. A New Centrality Measure for Influence Maximization in Social Networks. In Pattern Recognition and Machine Intelligence; Kuznetsov, S.O., Mandal, D.P., Kundu, M.K., Pal, S.K., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 242–247. [Google Scholar]
- Chen, W.; Wang, Y.; Yang, S. Efficient influence maximization in social networks. In Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Paris, France, 28 June–1 July 2009. [Google Scholar]
- Chen, W.; Wang, C.; Wang, Y. Scalable Influence Maximization for Prevalent Viral Marketing in Large-Scale Social Networks. In Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 25–28 July 2010; pp. 1029–1038. [Google Scholar]
- Borgs, C.; Brautbar, M.; Chayes, J.T.; Lucier, B.J.A. Influence Maximization in Social Networks: Towards an Optimal Algorithmic Solution. arXiv 2012, arXiv:1212.0884. [Google Scholar]
- Zhu, W.; Huang, Y.; Yang, S.; Miao, Y.; Peng, C. A Positive Influence Maximization Algorithm in Signed Social Networks. Comput. Mater. Contin. 2023, 76, 1977–1994. [Google Scholar] [CrossRef]
- Liu, X.; Kong, X.; Yu, P.S. Active Opinion Maximization in Social Networks. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 1840–1849. [Google Scholar]
- Li, W.; Li, Y.; Liu, W.; Wang, C. An Influence Maximization Method Based on Crowd Emotion Under an Emotion-Based Attribute Social Network. Inf. Process. Manag. 2022, 59, 102818. [Google Scholar]
- Dong, Y.; Zhan, M.; Kou, G.; Ding, Z.; Liang, H. A survey on the fusion process in opinion dynamics. Inf. Fusion 2018, 43, 57–65. [Google Scholar]
- Clifford, P.; Sudbury, A. A Model for Spatial Conflict. Biometrika 1973, 60, 581–588. [Google Scholar]
- Oestereich, A.L.; Pires, M.A.; Queirós, S.M.D.; Crokidakis, N. Phase Transition in the Galam’s Majority-Rule Model with Information-Mediated Independence. Physics 2023, 5, 911–922. [Google Scholar] [CrossRef]
- DeGroot, M.H.; Consensus, R.A. Reaching a consensus. J. Am. Stat. Assoc. 1974, 69, 118–121. [Google Scholar]
- Friedkin, N.E.; Johnsen, E.C. Social Influence and Opinions. J. Math. Sociol. 1990, 15, 193–206. [Google Scholar]
- Deffuant, G.; Neau, D.; Amblard, F.; Weisbuch, G. Mixing Beliefs Among Interacting Agents. Adv. Complex Syst. 2000, 3, 87–98. [Google Scholar]
- Hegselmann, R.; Krause, U. Opinion Dynamics and Bounded Confidence Models, Analysis and Simulation. J. Artif. Soc. Soc. Simul. 2002, 5, 1–2. [Google Scholar]
- Hou, J.; Li, W.; Jiang, M. Opinion dynamics in modified expressed and private model with bounded confidence. Phys. A Stat. Mech. Its Appl. 2021, 574, 125968. [Google Scholar]
- Wu, Z.; Zhou, Q.; Dong, Y.; Xu, J.; Altalhi, A.; Herrera, F. Mixed Opinion Dynamics Based on DeGroot Model and Hegselmann-Krause Model in Social Networks. IEEE Trans. Syst. Man Cybern. Syst. 2022, 53, 296–308. [Google Scholar]
- Jin, X.; Ye, Q. Spiral of Silence: A Powerful Perspective of Understanding the Public Opinion. Master’s Thesis, City University of Hong Kong, Hong Kong, China, 2018. [Google Scholar]
- Noelle-Neumann, E. The Spiral of Silence A Theory of Public Opinion. J. Commun. 2006, 24, 43–51. [Google Scholar]
- Kihlstrom, J.F.; Park, L. Cognitive Psychology: Overview. In Reference Module in Neuroscience and Biobehavioral Psychology; Stein, J., Ed.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 1–14. [Google Scholar]
- Bică, A. Peer pressure: Conformity outweighs reciprocity in social anxiety. Curr. Psychol. 2023, 42, 18142–18149. [Google Scholar]
- Akbarpour, M.; Jackson, M. Diffusion in Networks and the Unexpected Virtue of Burstiness. arXiv 2017, arXiv:1608.07899. [Google Scholar]
- da Silva, S.L.E.F. Newton’s Cooling Law in Generalised Statistical Mechanics. Phys. A Stat. Mech. Its Appl. 2021, 565, 125539. [Google Scholar] [CrossRef]
- Clauset, A.; Newman, M.; Moore, C. Finding community structure in very large networks. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2005, 70, 066111. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Spezzano, F.; Subrahmanian, V.S.; Faloutsos, C. Edge Weight Prediction in Weighted Signed Networks. In Proceedings of the 2016 IEEE 16th International Conference on Data Mining (ICDM), Barcelona, Spain, 12–15 December 2016; pp. 221–230. [Google Scholar]
- Kumar, S.; Hooi, B.; Makhija, D.; Kumar, M.; Faloutsos, C.; Subrahmanian, V.S. REV2: Fraudulent User Prediction in Rating Platforms. Data Min. Knowl. Discov. 2018, 32, 1025–1055. [Google Scholar]
- Leskovec, J.; Huttenlocher, D.; Kleinberg, J. Governance in Social Media: A Case Study of the Wikipedia Promotion Process. arXiv 2010, arXiv:1004.3547. [Google Scholar] [CrossRef]
- Dong, Y.; Tang, J.; Wu, S.; Tian, J.; Chawla, N.; Rao, J.; Cao, H. Link Prediction and Recommendation Across Heterogeneous Social Networks. IEEE Trans. Ind. Electron. 2018, 65, 123–130. [Google Scholar]
- Cheng, S.; Shen, H.; Huang, J.; Chen, W.; Cheng, X. IMRank: Influence Maximization via Finding Self-Consistent Ranking. Data Inf. Retr. 2014, 2014, 475–484. [Google Scholar]

| Dataset | Nodes | Links | Avg. Degree |
|---|---|---|---|
| Bitcoin Alpha | 3783 | 34,186 | 18.07 |
| Bitcoin OTC | 5881 | 35,592 | 12.10 |
| Wiki Vote | 7115 | 103,689 | 29.15 |
| Slashdot | 13,182 | 516,575 | 78.37 |
| Opinion Values | Opinion Categories |
|---|---|
| Strongly disagree | |
| Disagree | |
| Neutral | |
| Agree | |
| Strongly agree |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Wu, B.; Wu, T. LOMDP: Maximizing Desired Opinions in Social Networks by Considering User Expression Intentions. Entropy 2025, 27, 360. https://doi.org/10.3390/e27040360
Wang X, Wu B, Wu T. LOMDP: Maximizing Desired Opinions in Social Networks by Considering User Expression Intentions. Entropy. 2025; 27(4):360. https://doi.org/10.3390/e27040360
Chicago/Turabian StyleWang, Xuan, Bin Wu, and Tong Wu. 2025. "LOMDP: Maximizing Desired Opinions in Social Networks by Considering User Expression Intentions" Entropy 27, no. 4: 360. https://doi.org/10.3390/e27040360
APA StyleWang, X., Wu, B., & Wu, T. (2025). LOMDP: Maximizing Desired Opinions in Social Networks by Considering User Expression Intentions. Entropy, 27(4), 360. https://doi.org/10.3390/e27040360







