Information-Theoretic Measures of Metacognitive Efficiency: Empirical Validation with the Face Matching Task
Abstract
1. Introduction
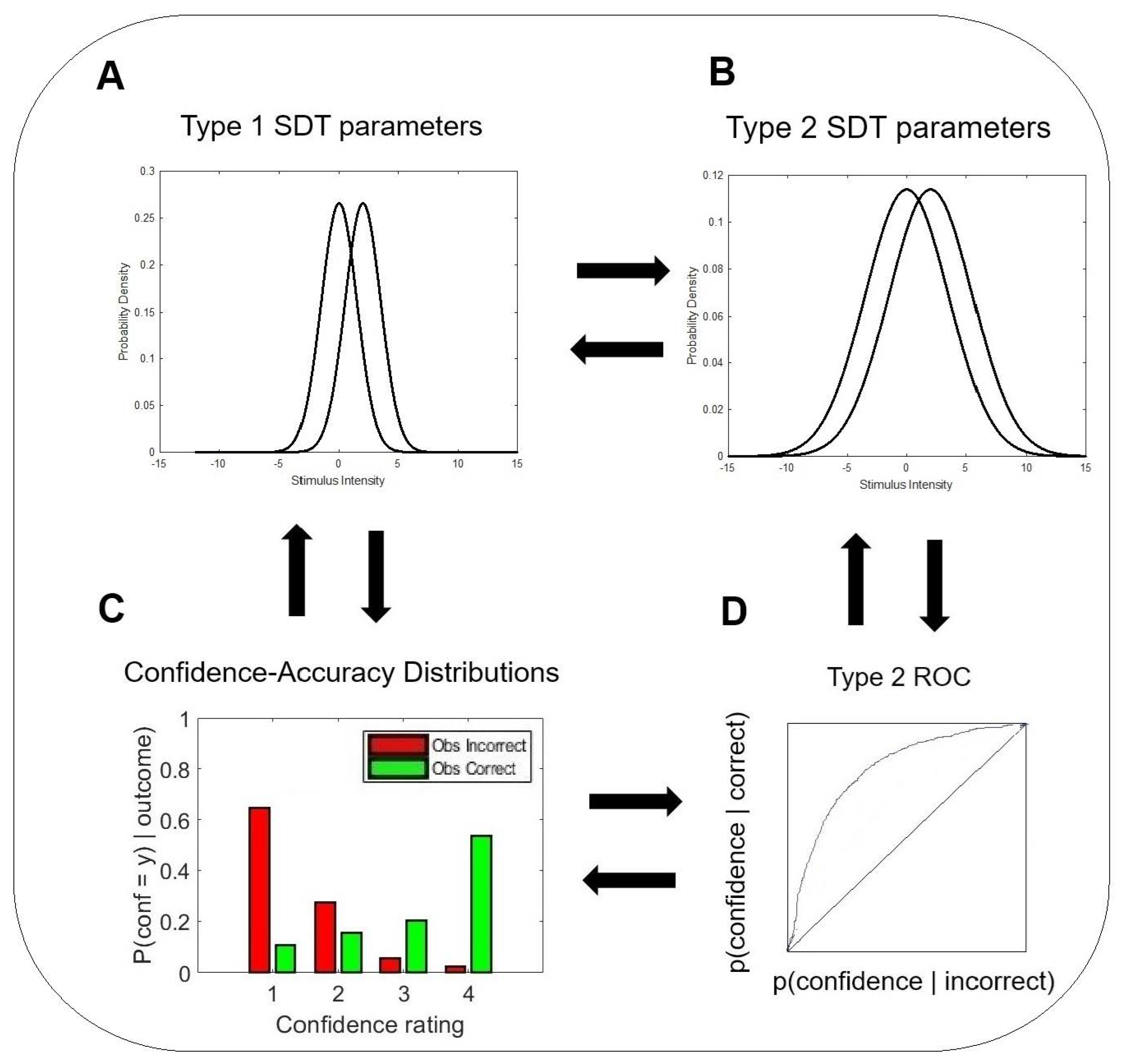
2. An Information-Theoretic Approach to Metacognitive Efficiency
2.1.
2.2. , , and
3. Empirical Validation
3.1. The Face-Matching Task
3.2. Metacognition in the Face-Matching Task
4. Method
4.1. Participants
4.2. Stimuli and Apparatus
4.3. Procedure and Design
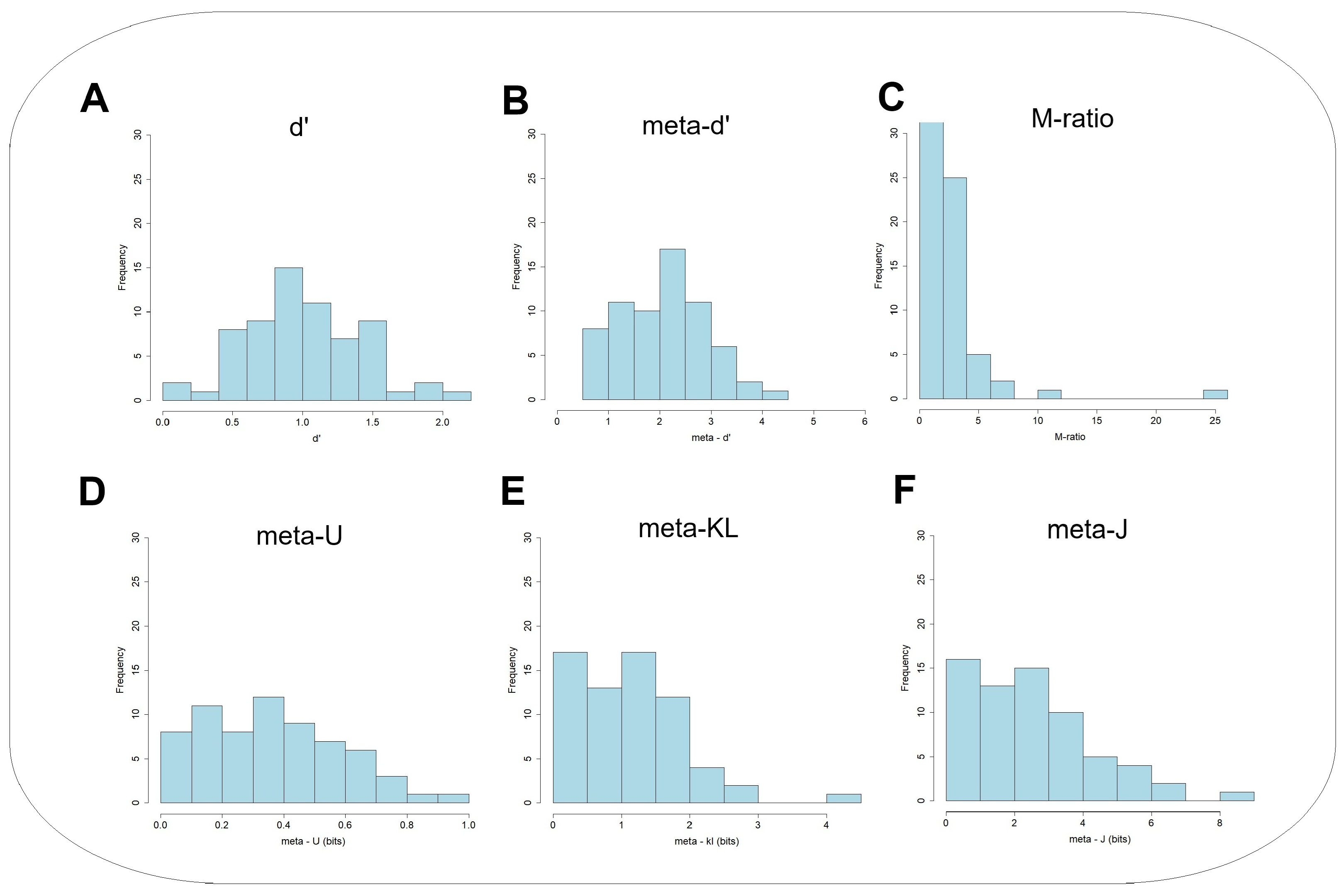
5. Results
5.1. Face Matching
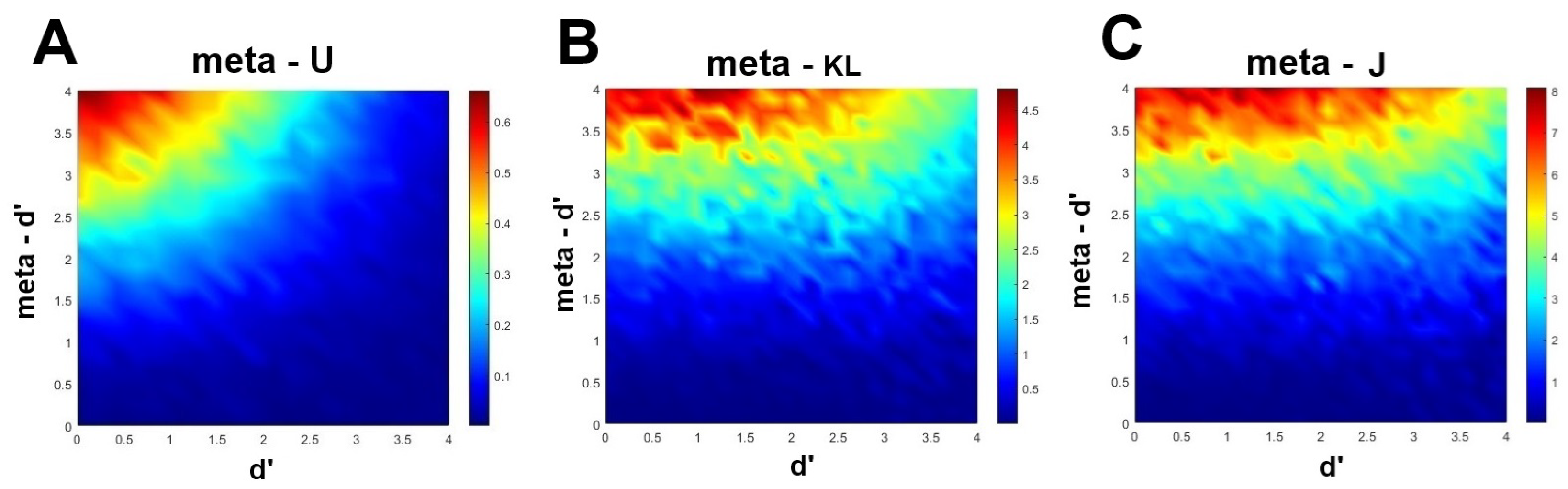
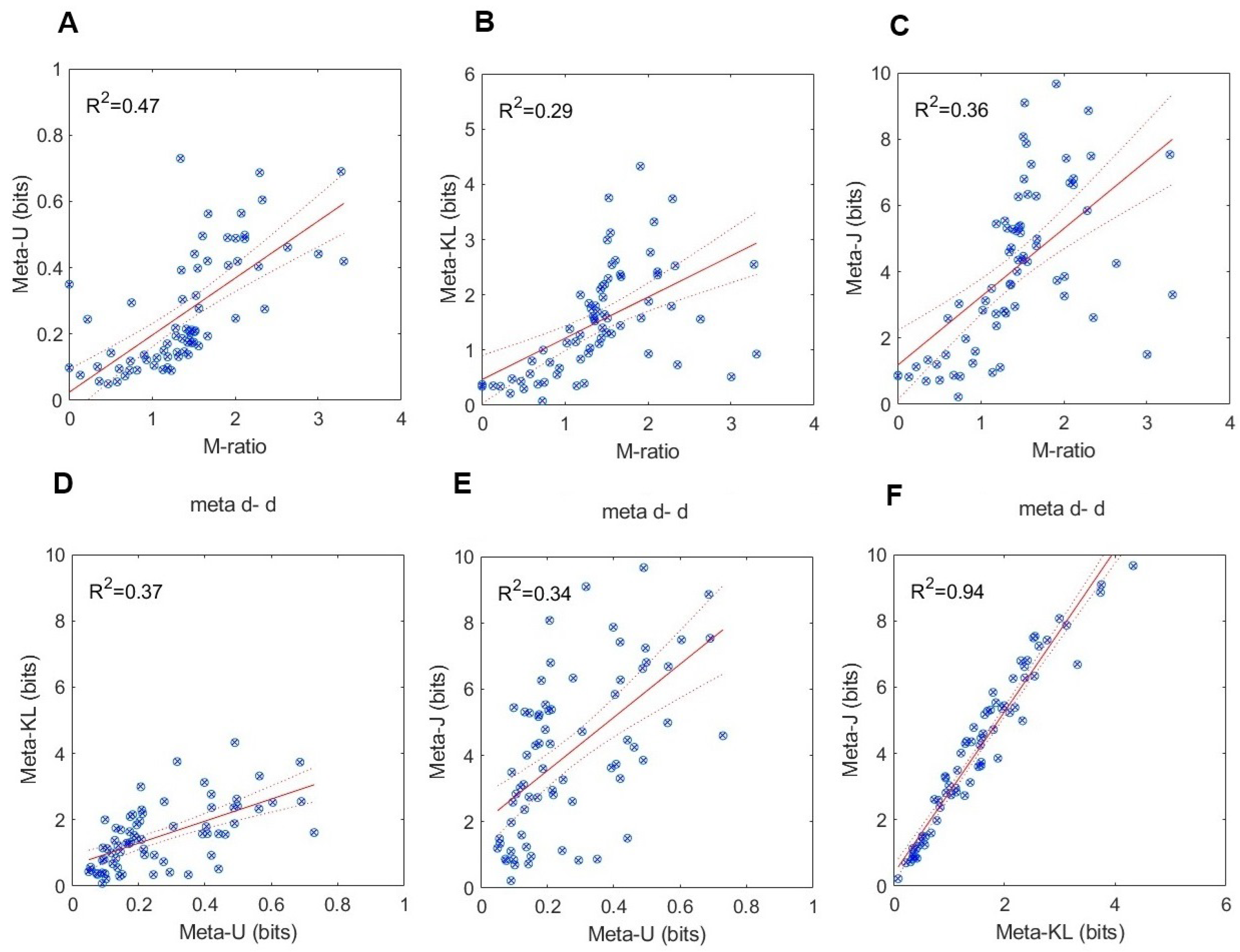
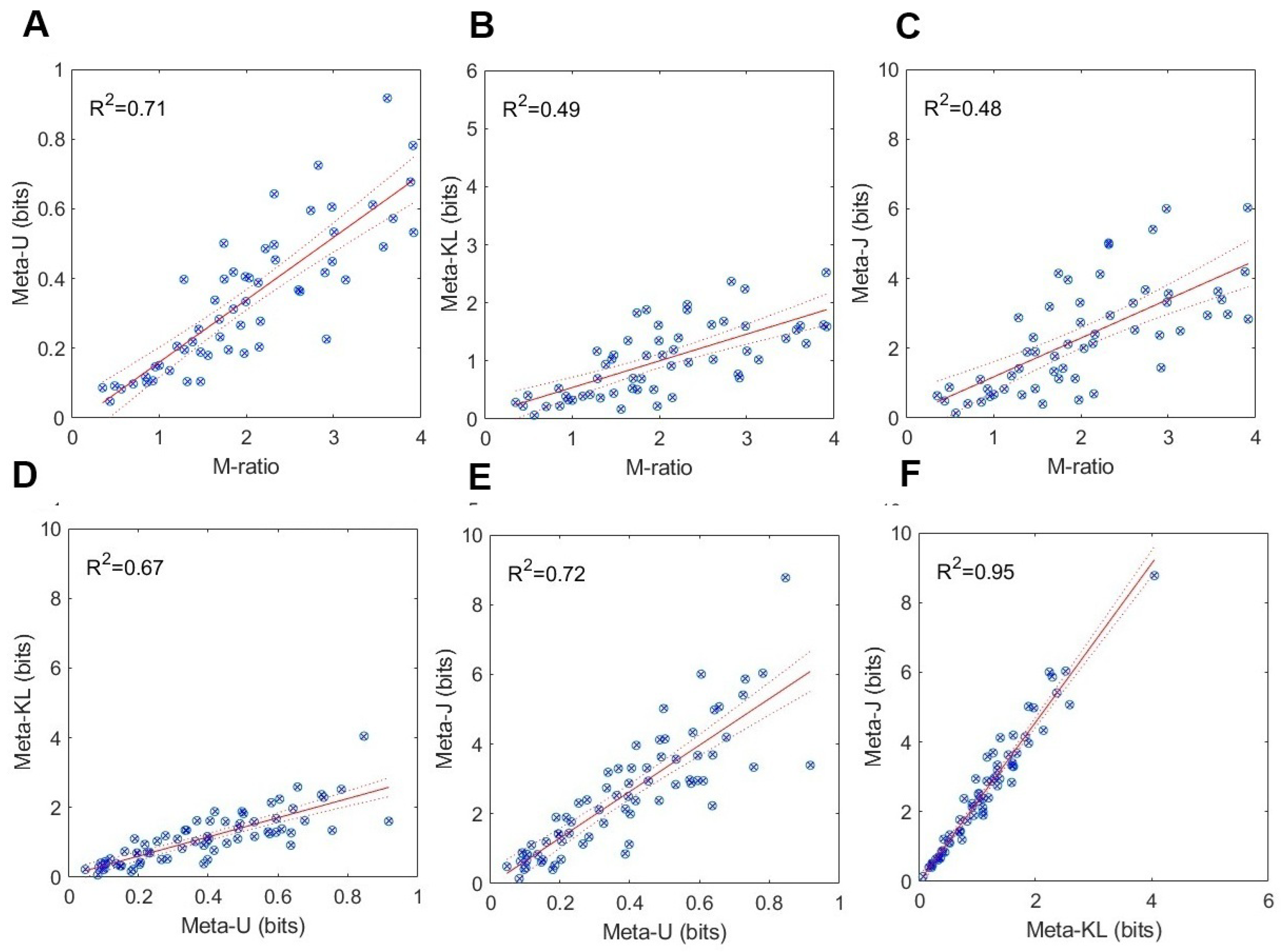
5.2. Testing for Construct Validity
6. General Discussion
6.1. Dependency on Type 1 Performance
6.2. Practical Advice to Practitioners of Information-Based Measures
6.3. Implications for Face Recognition
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Maniscalco, B.; Lau, H. A signal detection theoretic approach for estimating metacognitive sensitivity from confidence ratings. Conscious. Cogn. 2012, 21, 422–430. [Google Scholar] [CrossRef] [PubMed]
- Maniscalco, B.; Lau, H. Signal detection theory analysis of type 1 and type 2 data: Meta-d, response-specific meta-d, and the unequal variance SDT model. In The Cognitive Neuroscience of Metacognition; Springer: Berlin/Heidelberg, Germany, 2014; pp. 25–66. [Google Scholar]
- Dayan, P. Metacognitive information theory. Open Mind 2023, 7, 392–411. [Google Scholar] [PubMed]
- Fitousi, D. Bits of Confidence: Metacognition as Uncertainty Reduction. 2025, Submitted. Available online: https://osf.io/z5swc/.
- Schulz, L.; Rollwage, M.; Dolan, R.J.; Fleming, S.M. Dogmatism manifests in lowered information search under uncertainty. Proc. Natl. Acad. Sci. USA 2020, 117, 31527–31534. [Google Scholar] [CrossRef]
- Schulz, L.; Fleming, S.M.; Dayan, P. Metacognitive computations for information search: Confidence in control. Psychol. Rev. 2023, 130, 604–639. [Google Scholar]
- Peirce, C.S.; Jastrow, J. On small differences in sensation. Mem. Natl. Acad. Sci. 1884, 3–11, 73–83. [Google Scholar]
- Henmon, V.A.C. The relation of the time of a judgment to its accuracy. Psychol. Rev. 1911, 18, 186–201. [Google Scholar] [CrossRef]
- Lau, H. In Consciousness We Trust: The Cognitive Neuroscience of Subjective Experience; Oxford University Press: Oxford, UK, 2022. [Google Scholar]
- Metcalfe, J.; Shimamura, A.P. Metacognition: Knowing About Knowing; MIT Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Fleming, S.M.; Dolan, R.J. The neural basis of metacognitive ability. Philos. Trans. R. Soc. B Biol. Sci. 2012, 367, 1338–1349. [Google Scholar] [CrossRef]
- Fleming, S.M.; Weil, R.S.; Nagy, Z.; Dolan, R.J.; Rees, G. Relating introspective accuracy to individual differences in brain structure. Science 2010, 329, 1541–1543. [Google Scholar] [CrossRef] [PubMed]
- Fleming, S.M. Metacognition and confidence: A review and synthesis. Annu. Rev. Psychol. 2024, 75, 241–268. [Google Scholar] [CrossRef]
- Meyniel, F.; Schlunegger, D.; Dehaene, S. The sense of confidence during probabilistic learning: A normative account. PLoS Comput. Biol. 2015, 11, e1004305. [Google Scholar] [CrossRef]
- Koriat, A.; Goldsmith, M. Monitoring and control processes in the strategic regulation of memory accuracy. Psychol. Rev. 1996, 103, 490–517. [Google Scholar] [PubMed]
- Koriat, A. Monitoring one’s own knowledge during study: A cue-utilization approach to judgments of learning. J. Exp. Psychol. Gen. 1997, 126, 349–370. [Google Scholar] [CrossRef]
- Koriat, A. The feeling of knowing: Some metatheoretical implications for consciousness and control. Conscious. Cogn. 2000, 9, 149–171. [Google Scholar]
- Persaud, N.; McLeod, P.; Cowey, A. Post-decision wagering objectively measures awareness. Nat. Neurosci. 2007, 10, 257–261. [Google Scholar]
- Van den Berg, R.; Zylberberg, A.; Kiani, R.; Shadlen, M.N.; Wolpert, D.M. Confidence is the bridge between multi-stage decisions. Curr. Biol. 2016, 26, 3157–3168. [Google Scholar] [PubMed]
- Hoven, M.; Lebreton, M.; Engelmann, J.B.; Denys, D.; Luigjes, J.; van Holst, R.J. Abnormalities of confidence in psychiatry: An overview and future perspectives. Transl. Psychiatry 2019, 9, 268. [Google Scholar] [CrossRef]
- Bahrami, B.; Olsen, K.; Latham, P.E.; Roepstorff, A.; Rees, G.; Frith, C.D. Optimally interacting minds. Science 2010, 329, 1081–1085. [Google Scholar] [PubMed]
- Vaccaro, A.G.; Fleming, S.M. Thinking about thinking: A coordinate-based meta-analysis of neuroimaging studies of metacognitive judgements. Brain Neurosci. Adv. 2018, 2, 2398212818810591. [Google Scholar]
- Fitousi, D. A Signal-detection based confidence-similarity model of face-matching. Psychol. Rev. 2024, 131, 625–663. [Google Scholar]
- Garner, W.R.; Hake, H.W.; Eriksen, C.W. Operationism and the concept of perception. Psychol. Rev. 1956, 63, 149–159. [Google Scholar]
- Clarke, F.R.; Birdsall, T.G.; Tanner, W.P., Jr. Two types of ROC curves and definitions of parameters. J. Acoust. Soc. Am. 1959, 31, 629–630. [Google Scholar] [CrossRef]
- Galvin, S.J.; Podd, J.V.; Drga, V.; Whitmore, J. Type 2 tasks in the theory of signal detectability: Discrimination between correct and incorrect decisions. Psychon. Bull. Rev. 2003, 10, 843–876. [Google Scholar] [CrossRef]
- Fleming, S.M.; Daw, N.D. Self-evaluation of decision-making: A general Bayesian framework for metacognitive computation. Psychol. Rev. 2017, 124, 91–114. [Google Scholar] [CrossRef]
- Green, D.M.; Swets, J.A. Signal Detection Theory and Psychophysics; Wiley: New York, NY, USA, 1966; Volume 1. [Google Scholar]
- Macmillan, N.A.; Creelman, C.D. Detection Theory: A User’s Guide; Psychology Press: East Sussex, UK, 2004. [Google Scholar]
- Nelson, T.O. A comparison of current measures of the accuracy of feeling-of-knowing predictions. Psychol. Bull. 1984, 95, 109–133. [Google Scholar] [CrossRef] [PubMed]
- Fleming, S.M. HMeta-d: Hierarchical Bayesian estimation of metacognitive efficiency from confidence ratings. Neurosci. Conscious. 2017, 2017, nix007. [Google Scholar] [CrossRef]
- Kunimoto, C.; Miller, J.; Pashler, H. Confidence and accuracy of near-threshold discrimination responses. Conscious. Cogn. 2001, 10, 294–340. [Google Scholar] [CrossRef] [PubMed]
- Maniscalco, B.; Peters, M.A.; Lau, H. Heuristic use of perceptual evidence leads to dissociation between performance and metacognitive sensitivity. Atten. Percept. Psychophys. 2016, 78, 923–937. [Google Scholar] [CrossRef] [PubMed]
- Shekhar, M.; Rahnev, D. Sources of metacognitive inefficiency. Trends Cogn. Sci. 2021, 25, 12–23. [Google Scholar] [CrossRef]
- Luce, R.D. Whatever happened to information theory in psychology? Rev. Gen. Psychol. 2003, 7, 183–188. [Google Scholar]
- Knill, D.C.; Pouget, A. The Bayesian brain: The role of uncertainty in neural coding and computation. Trends Neurosci. 2004, 27, 712–719. [Google Scholar] [CrossRef]
- Feldman, J. Information-theoretic signal detection theory. Psychol. Rev. 2021, 128, 976–987. [Google Scholar] [PubMed]
- Killeen, P.; Taylor, T. Bits of the ROC: Signal detection as information transmission. 2001; unpublished work. [Google Scholar]
- Fitousi, D. Mutual information, perceptual independence, and holistic face perception. Atten. Percept. Psychophys. 2013, 75, 983–1000. [Google Scholar]
- Fitousi, D.; Algom, D. The quest for psychological symmetry through figural goodness, randomness, and complexity: A selective review. i-Perception 2024, 15, 1–24. [Google Scholar]
- Fitousi, D. Quantifying Entropy in Response Times (RT) Distributions Using the Cumulative Residual Entropy (CRE) Function. Entropy 2023, 25, 1239. [Google Scholar] [CrossRef]
- Friston, K. The free-energy principle: A unified brain theory? Nat. Rev. Neurosci. 2010, 11, 127–138. [Google Scholar]
- Norwich, K.H. Information, Sensation, and Perception; Academic Press: San Diego, CA, USA, 1993. [Google Scholar]
- Hirsh, J.B.; Mar, R.A.; Peterson, J.B. Psychological entropy: A framework for understanding uncertainty-related anxiety. Psychol. Rev. 2012, 119, 304–320. [Google Scholar] [PubMed]
- Shannon, C. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar]
- Shannon, C.; Weaver, W. The Mathematical Theory of Communication; First Published in 1949; Urbana University of Illinois Press: Champaign, IL, USA, 1949. [Google Scholar]
- Friston, K. The free-energy principle: A rough guide to the brain? Trends Cogn. Sci. 2009, 13, 293–301. [Google Scholar]
- Pouget, A.; Drugowitsch, J.; Kepecs, A. Confidence and certainty: Distinct probabilistic quantities for different goals. Nat. Neurosci. 2016, 19, 366–374. [Google Scholar]
- Li, H.H.; Ma, W.J. Confidence reports in decision-making with multiple alternatives violate the Bayesian confidence hypothesis. Nat. Commun. 2020, 11, 2004. [Google Scholar]
- Koriat, A. Subjective confidence in one’s answers: The consensuality principle. J. Exp. Psychol. Learn. Mem. Cogn. 2008, 34, 945–959. [Google Scholar] [CrossRef] [PubMed]
- Koriat, A. The self-consistency model of subjective confidence. Psychol. Rev. 2012, 119, 80–113. [Google Scholar] [PubMed]
- Kullback, S. Information Theory and Statistics; Courier Corporation: North Chelmsford, MA, USA, 1959. [Google Scholar]
- Jeffrey, R.C. Probability and the Art of Judgment; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Cover, T.; Thomas, J. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 1991. [Google Scholar]
- Pearl, J. Jeffrey’s rule, passage of experience, and neo-Bayesianism. In Knowledge Representation and Defeasible Reasoning; Springer: Berlin/Heidelberg, Germany, 1990; pp. 245–265. [Google Scholar]
- Burton, A.M.; White, D.; McNeill, A. The Glasgow face matching test. Behav. Res. Methods 2010, 42, 286–291. [Google Scholar] [CrossRef] [PubMed]
- White, D.; Towler, A.; Kemp, R. Understanding professional expertise in unfamiliar face matching. In Forensic Face Matching: Research and Practice; Oxford University Press: Oxford, UK, 2021; pp. 62–88. [Google Scholar]
- Megreya, A.M.; Burton, A.M. Unfamiliar faces are not faces: Evidence from a matching task. Mem. Cogn. 2006, 34, 865–876. [Google Scholar]
- Megreya, A.M.; Burton, A.M. Hits and false positives in face matching: A familiarity-based dissociation. Percept. Psychophys. 2007, 69, 1175–1184. [Google Scholar] [CrossRef]
- Kemp, R.; Towell, N.; Pike, G. When seeing should not be believing: Photographs, credit cards and fraud. Appl. Cogn. Psychol. Off. J. Soc. Appl. Res. Mem. Cogn. 1997, 11, 211–222. [Google Scholar] [CrossRef]
- Fysh, M.C.; Bindemann, M. The Kent face matching test. Br. J. Psychol. 2018, 109, 219–231. [Google Scholar]
- O’Toole, A.J.; An, X.; Dunlop, J.; Natu, V.; Phillips, P.J. Comparing face recognition algorithms to humans on challenging tasks. ACM Trans. Appl. Percept. (TAP) 2012, 9, 1–13. [Google Scholar]
- Bate, S.; Mestry, N.; Portch, E. Individual differences between observers in face matching. In Forensic Face Matching: Research and Practice; Oxford University Press: Oxford, UK, 2021; pp. 117–145. [Google Scholar]
- Towler, A.; White, D.; Kemp, R.I. Evaluating training methods for facial image comparison: The face shape strategy does not work. Perception 2014, 43, 214–218. [Google Scholar] [CrossRef]
- Jenkins, R.; White, D.; Van Montfort, X.; Burton, A.M. Variability in photos of the same face. Cognition 2011, 121, 313–323. [Google Scholar] [CrossRef]
- Bindemann, M.; Attard, J.; Leach, A.; Johnston, R.A. The effect of image pixelation on unfamiliar-face matching. Appl. Cogn. Psychol. 2013, 27, 707–717. [Google Scholar] [CrossRef]
- Megreya, A.M.; Bindemann, M. Feature instructions improve face-matching accuracy. PLoS ONE 2018, 13, e0193455. [Google Scholar]
- Kramer, R.S. Face matching and metacognition: Invetigating individual differences and a training intervention. PeerJ 2023, 11, e14821. [Google Scholar]
- Bobak, A.K.; Hancock, P.J.; Bate, S. Super-recognisers in action: Evidence from face-matching and face memory tasks. Appl. Cogn. Psychol. 2016, 30, 81–91. [Google Scholar] [CrossRef] [PubMed]
- Gray, K.L.; Bird, G.; Cook, R. Robust associations between the 20-item prosopagnosia index and the Cambridge Face Memory Test in the general population. R. Soc. Open Sci. 2017, 4, 160923. [Google Scholar] [CrossRef]
- Livingston, L.A.; Shah, P. People with and without prosopagnosia have insight into their face recognition ability. Q. J. Exp. Psychol. 2018, 71, 1260–1262. [Google Scholar]
- Ventura, P.; Livingston, L.A.; Shah, P. Adults have moderate-to-good insight into their face recognition ability: Further validation of the 20-item Prosopagnosia Index in a Portuguese sample. Q. J. Exp. Psychol. 2018, 71, 2677–2679. [Google Scholar]
- Bruce, V.; Henderson, Z.; Greenwood, K.; Hancock, P.J.; Burton, A.M.; Miller, P. Verification of face identities from images captured on video. J. Exp. Psychol. Appl. 1999, 5, 339–360. [Google Scholar] [CrossRef]
- Hopkins, R.F.; Lyle, K.B. Image-size disparity reduces difference detection in face matching. Appl. Cogn. Psychol. 2020, 34, 39–49. [Google Scholar]
- Rahnev, D.; Fleming, S.M. How experimental procedures influence estimates of metacognitive ability. Neurosci. Conscious. 2019, 2019, niz009. [Google Scholar]
- Guggenmos, M. Measuring metacognitive performance: Type 1 performance dependence and test-retest reliability. Neurosci. Conscious. 2021, 2021, niab040. [Google Scholar] [PubMed]
- Rausch, M.; Hellmann, S.; Zehetleitner, M. Measures of metacognitive efficiency across cognitive models of decision confidence. Psychol. Methods 2023, 1–20. [Google Scholar] [CrossRef]
- Guggenmos, M.; Wilbertz, G.; Hebart, M.N.; Sterzer, P. Mesolimbic confidence signals guide perceptual learning in the absence of external feedback. Elife 2016, 5, e13388. [Google Scholar] [PubMed]
- Shekhar, M.; Rahnev, D. The nature of metacognitive inefficiency in perceptual decision making. Psychol. Rev. 2021, 128, 45–70. [Google Scholar]
- Berger, T. Rate-Distortion Theory; Wiley Encyclopedia of Telecommunications: New York, NY, USA, 2003. [Google Scholar]
- Sims, C.R. Rate–distortion theory and human perception. Cognition 2016, 152, 181–198. [Google Scholar]
- Tishby, N.; Pereira, F.C.; Bialek, W. The information bottleneck method. arXiv 2000, arXiv:physics/0004057. [Google Scholar]
- Fitousi, D. Complexity versus accuracy in metacognitive decision making: An information-bottleneck model. 2025; manuscript in preparation. [Google Scholar]
- Mamassian, P.; de Gardelle, V. Modeling perceptual confidence and the confidence forced-choice paradigm. Psychol. Rev. 2022, 129, 976. [Google Scholar]
- Rahnev, D. Visual metacognition: Measures, models, and neural correlates. Am. Psychol. 2021, 76, 1445–1453. [Google Scholar]
- Tishby, N.; Zaslavsky, N. Deep learning and the information bottleneck principle. In Proceedings of the 2015 IEEE Information Theory Workshop (ITW), Jerusalem, Israel, 26 April–1 May 2015; pp. 1–5. [Google Scholar]
- Samaha, J.; Barrett, J.J.; Sheldon, A.D.; LaRocque, J.J.; Postle, B.R. Dissociating perceptual confidence from discrimination accuracy reveals no influence of metacognitive awareness on working memory. Front. Psychol. 2016, 7, 851. [Google Scholar]
- Peters, M.A.; Thesen, T.; Ko, Y.D.; Maniscalco, B.; Carlson, C.; Davidson, M.; Doyle, W.; Kuzniecky, R.; Devinsky, O.; Halgren, E.; et al. Perceptual confidence neglects decision-incongruent evidence in the brain. Nat. Hum. Behav. 2017, 1, 0139. [Google Scholar]
- Zylberberg, A.; Barttfeld, P.; Sigman, M. The construction of confidence in a perceptual decision. Front. Integr. Neurosci. 2012, 6, 79. [Google Scholar]
- Koizumi, A.; Maniscalco, B.; Lau, H. Does perceptual confidence facilitate cognitive control? Atten. Percept. Psychophys. 2015, 77, 1295–1306. [Google Scholar]
- Thurstone, L.L. Three psychophysical laws. Psychol. Rev. 1927, 34, 424–432. [Google Scholar]
- Garner, W.R. Rating scales, discriminability, and information transmission. Psychol. Rev. 1960, 67, 343–352. [Google Scholar] [PubMed]
- Kramer, R.S.; Jones, A.; Fitousi, D. Face familiarity and similarity: Within- and between-identity representations are altered by learning. J. Exp. Psychol. Hum. Percept. Perform. 2025; in press. [Google Scholar]
- Damasio, A.R.; Damasio, H.; Van Hoesen, G.W. Prosopagnosia: Anatomic basis and behavioral mechanisms. Neurology 1982, 32, 331–341. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fitousi, D. Information-Theoretic Measures of Metacognitive Efficiency: Empirical Validation with the Face Matching Task. Entropy 2025, 27, 353. https://doi.org/10.3390/e27040353
Fitousi D. Information-Theoretic Measures of Metacognitive Efficiency: Empirical Validation with the Face Matching Task. Entropy. 2025; 27(4):353. https://doi.org/10.3390/e27040353
Chicago/Turabian StyleFitousi, Daniel. 2025. "Information-Theoretic Measures of Metacognitive Efficiency: Empirical Validation with the Face Matching Task" Entropy 27, no. 4: 353. https://doi.org/10.3390/e27040353
APA StyleFitousi, D. (2025). Information-Theoretic Measures of Metacognitive Efficiency: Empirical Validation with the Face Matching Task. Entropy, 27(4), 353. https://doi.org/10.3390/e27040353





