Protecting the Entanglement of X-Type Systems via Weak Measurement and Reversal in the Generalized Amplitude Damping Channel
Abstract
1. Introduction
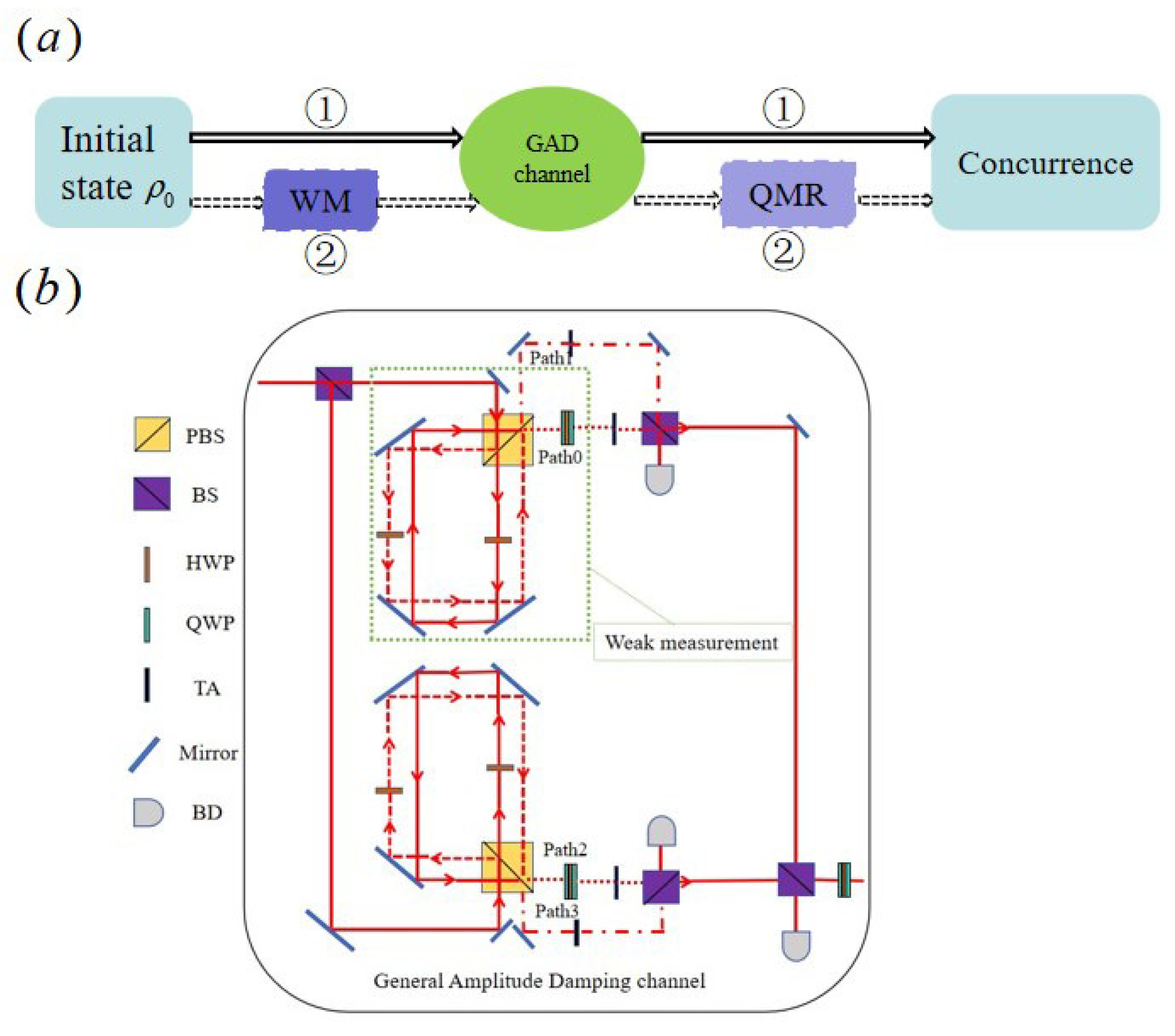
2. Physical Model and Dynamics Process of the System in the GAD Channel
3. The Protection of X-Type System
3.1. Weak Measurement
3.2. Quantum Measurement Reversal
3.3. The Evolution of the System After Pre-WM and Post-QMR Operations
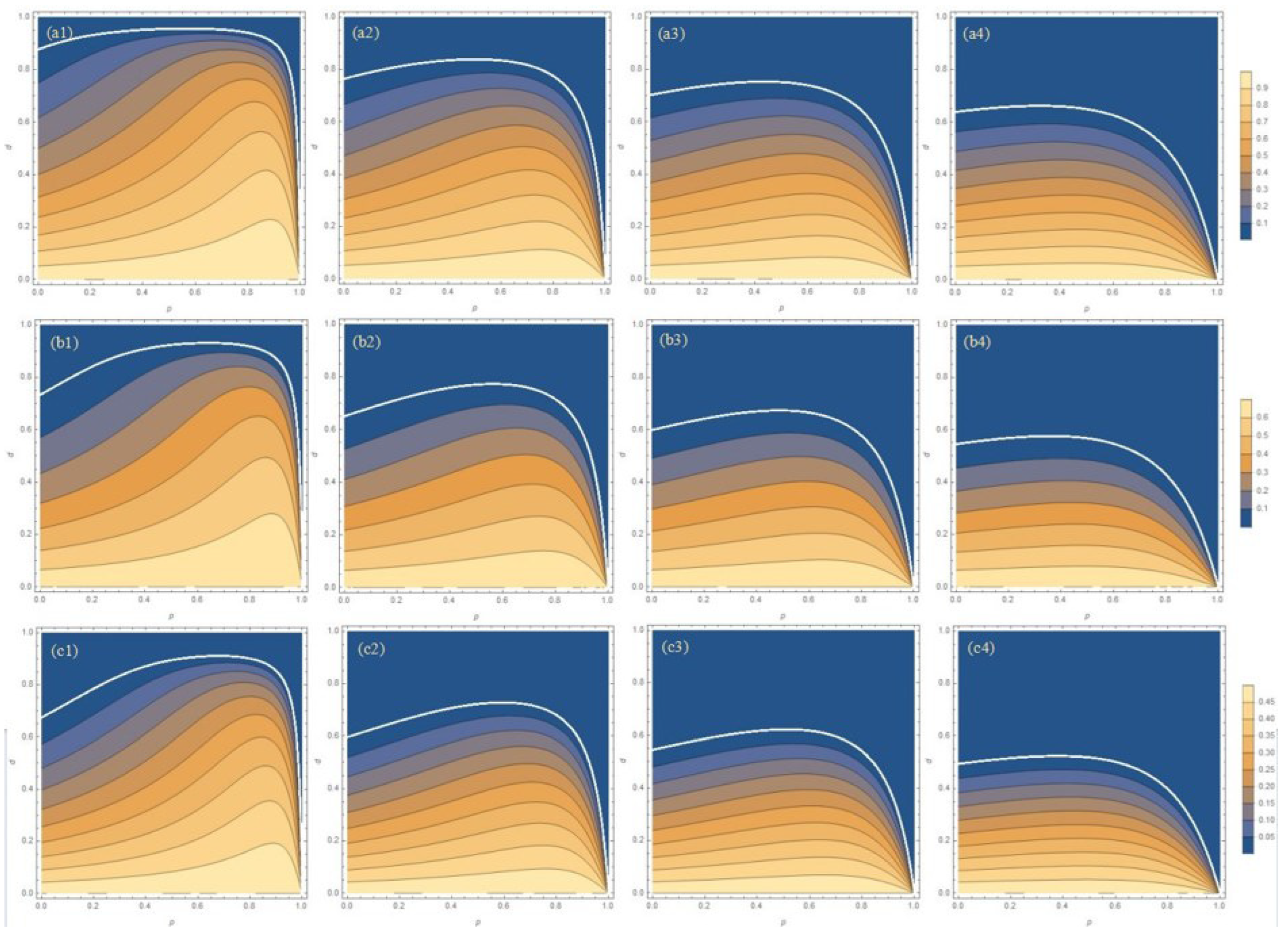
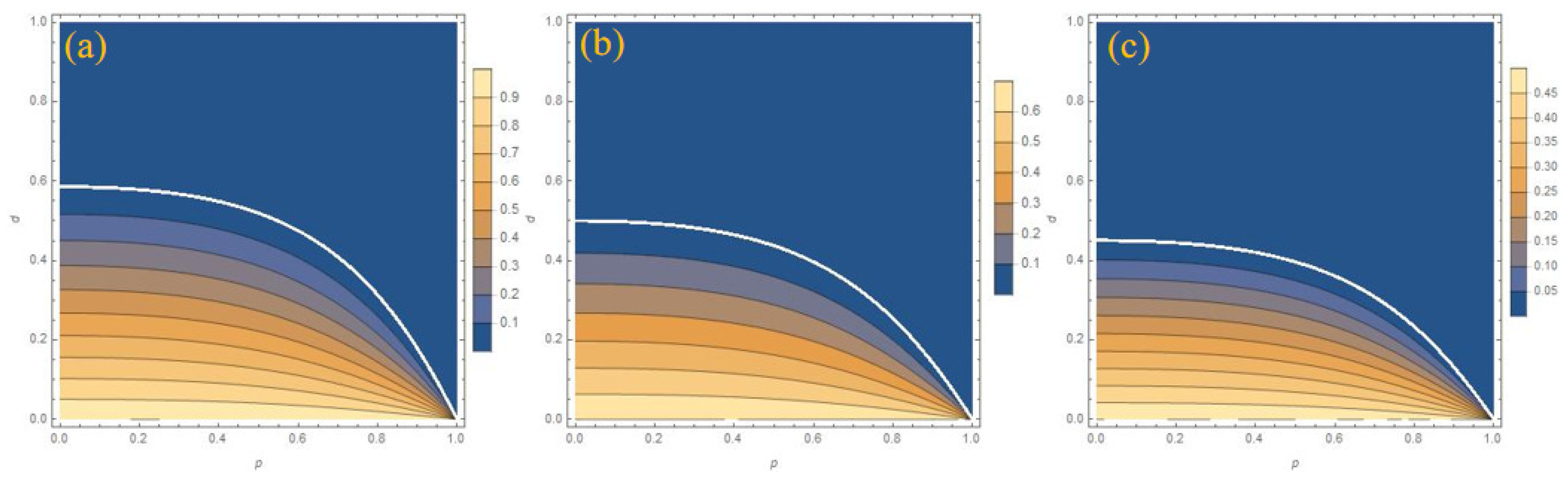
3.4. The Probability of Success for the System with the WMR Operation
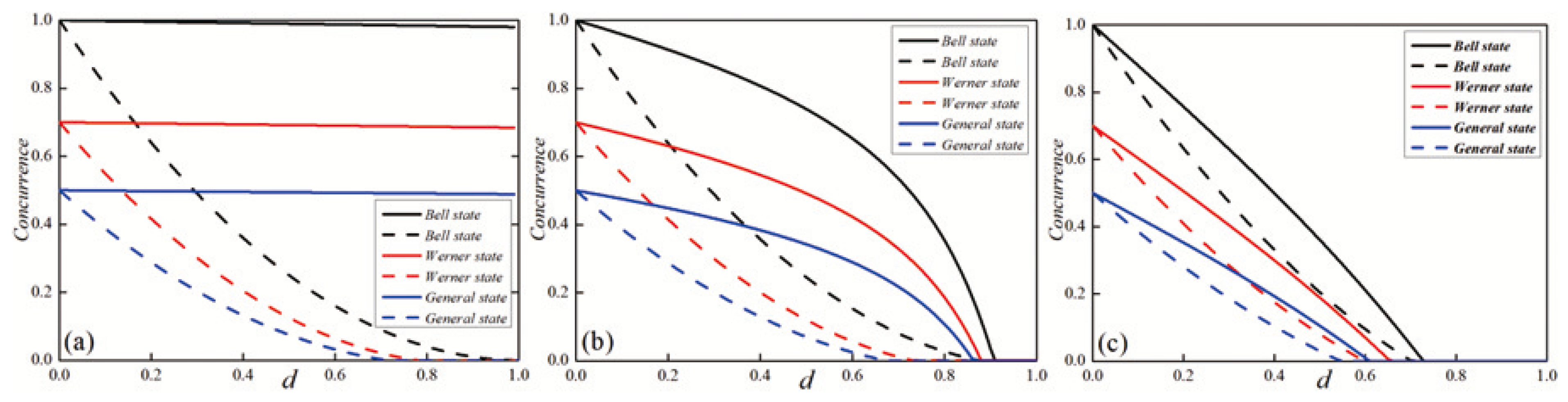
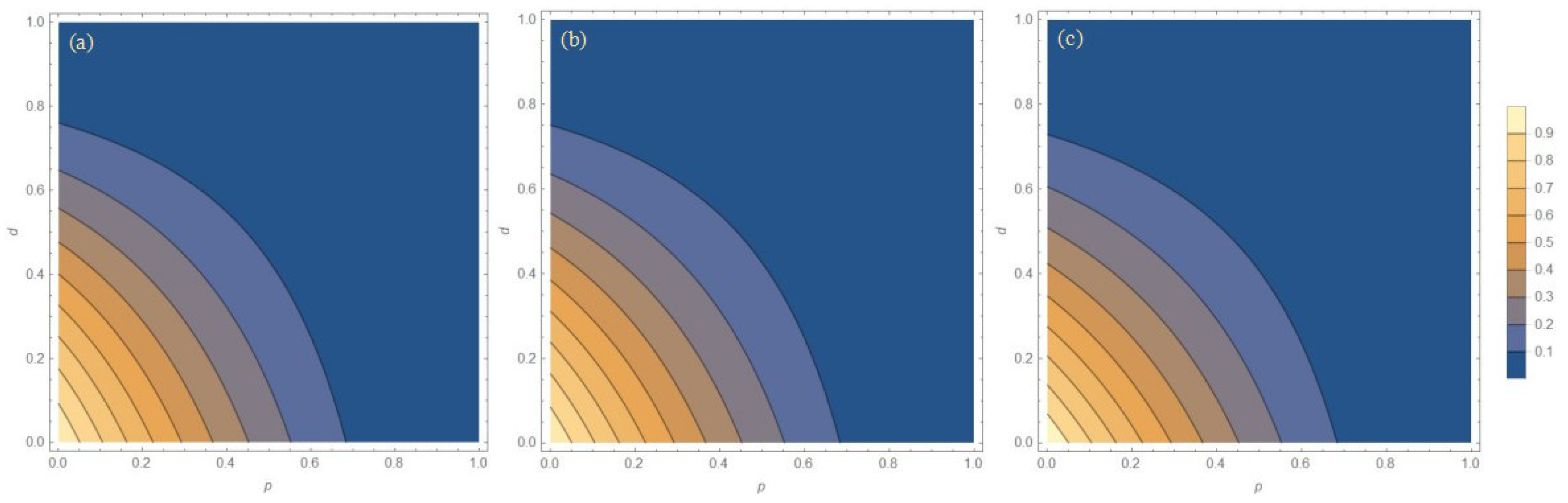
3.5. Protecting Entanglement in Zero Temperature
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Horodedecki, R.; Horodedecki, P.; Horodedecki, M.; Horodedecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865. [Google Scholar]
- Zyczkowski, K.; Horodedecki, P.; Horodedecki, M.; Horodedecki, R. Dynamics of quantum entanglement. Phys. Rev. A 2001, 86, 012101. [Google Scholar]
- Zurek, W.H. Sub-planck structure in phase space and its relevance for quantum decoherence. Nature 2001, 412, 712–717. [Google Scholar]
- Xiao, Y.; Zhou, H.Y.; Gu, M.L.; Ma, X.F. Unified framework for quantumness–coherence, discord, and entanglement. Phys. Rev. A 2018, 97, 012331. [Google Scholar]
- Aharonov, Y.; Albert, D.Z.; Vaidman, L. How the result of a component of the spin of a spin-1/2 particle can turn out to be 100. Phys. Rev. Lett. 1988, 60, 1351. [Google Scholar] [PubMed]
- Aharonov, Y.; Albert, D.Z.; Casher, A.; Vaidman, L. Surprising quantum effects. Phys. Lett. A 1987, 124, 199. [Google Scholar]
- Tian, M.B.; Zhang, G.F. Improving the capacity of quantum dense coding by weak measurement and reversal measurement. Quantum Inf. Comput. 2018, 19, 19. [Google Scholar]
- Li, Y.L.; Xiao, X. Recovering quantum correlations from amplitude damping decoherence by weak measurement reversal. Quantum Inf. Process 2013, 12, 3067–3077. [Google Scholar]
- Zhu, G.Y.; Tantivasadakarn, N.; Vishwanath, A.; Trebst, S.; Ruben Verresen, R. Nishimori’s cat: Stable long-range entanglement from finite-depth unitaries and weak measurements. Phys. Rev. Lett. 2023, 131, 200201. [Google Scholar]
- Siva, K.; Koolstra, G.; Steinmetz, J.; Livingston, W.P.; Das, D.; Chen, L.; Kreikebaum, J.M.; Stevenson, N.; Jünger, C.; Santiago, D.I.; et al. Time-dependent hamiltonian reconstruction using continuous weak measurements. PRX Quantum 2023, 4, 040324. [Google Scholar]
- Tan, Q.Y.; Wang, L.; Li, J.X.; Tang, J.W.; Wang, X.W. Amplitude damping decoherence suppression of two-qubit entangled states by weak measurements. Int. J. Theor. Phys. 2013, 52, 612–619. [Google Scholar] [CrossRef]
- Kim, Y.S.; Cho, Y.W.; Ra, Y.S.; Kim, Y.H. Reversing the weak quantum measurement for a photonic qubit. Opt. Express 2009, 17, 11978–11985. [Google Scholar] [CrossRef] [PubMed]
- Korotkov, A.N.; Keane, K. Decoherence suppression by quantum measurement reversal. Phys. Rev. A 2010, 81, 040103. [Google Scholar] [CrossRef]
- Man, Z.X.; Xia, Y.J. Manipulating entanglement of two qubits in a commom environment by means of weak measurement and quantum measurement reversals. Phys. Rev. A 2012, 86, 012325. [Google Scholar] [CrossRef]
- Man, Z.X.; Xia, Y.J. Enhancing entanglement of two qubits undergoing independent decoherences by local pre- and postmeasurements. Phys. Rev. A 2012, 86, 052322. [Google Scholar] [CrossRef]
- Sun, Q.Q.; Al-Amri, Q.M.; Davidovich, L.; Zubairy, M.S. Reversing entanglement change by weak measurement. Phys. Rev. A 2010, 82, 052323. [Google Scholar] [CrossRef]
- Kim, Y.S.; Lee, J.C.; Kwon, O.; Kim, Y.H. Protecting entanglement from decoherence using weak measurement and quantum measurement reversal. Nat. Phys. 2012, 8, 117–120. [Google Scholar] [CrossRef]
- Xiao, X. Protecting qubit-qutrit entanglement from amplitude damping decoherence via weak measurement and reversal. Phys. Scr. 2014, 89, 065102. [Google Scholar] [CrossRef]
- Xiao, X.; Li, Y.L. Protecting qutrit-qutrit entanglement by weak measurement and reversal. Eur. Phys. J. D 2013, 67, 204. [Google Scholar] [CrossRef]
- Wang, M.J.; Xia, Y.J.; Yang, Y.; Cao, L.Z.; Zhang, Q.W.; Li, Y.D.; Zhao, J.Q. Protecting the entanglement of two-qubit over quantum channels with memory via weak measurement and quantum measurement reversal. Chin. Phys. B 2020, 29, 110307. [Google Scholar] [CrossRef]
- Lin, S.; Hong, J.H.; Chen, Z.H.; Chen, Y.; Zhou, X.X. Optimal weak measurement in the photonic spin Hall effect for arbitrary linear polarization incidence. Opt. Express 2022, 30, 4096–4105. [Google Scholar] [PubMed]
- Qin, Z.R.; Zhang, R.H.; Zhang, L.T.; Ren, L.J.; Zhang, P.; Qi, R.B.; Zhang, Q.F.; Wang, C.L.; Jiang, L.Y. Optimized weak measurement model for in-plane and out-of-plane splitting shifts of Photonic Spin Hall effect. Opt. Commun. 2024, 557, 130283. [Google Scholar]
- Monroe, J.T.; Halpern, N.Y.; Lee, T.; Murch, K.W. Weak measurement of a superconducting qubit reconciles incompatible operators. Phys. Rev. Lett. 2021, 126, 100403. [Google Scholar] [PubMed]
- Sun, Q.Q.; Al-Amri, Q.M.; Zubairy, M.S. Reversing the weak measurement of an arbitrary field with finite photon number. Phys. Rev. A 2009, 80, 033838. [Google Scholar] [CrossRef]
- Zhou, J.M.; Hu, X.L.; Jing, N.H. On super quantum discord for high-dimensional bipartite state. Quantum Inf. Process 2023, 22, 441. [Google Scholar]
- Kwiat, P.G.; Waks, E.; White, A.G.; Appelbaum, I.; EberhardLi, P.H. Ultrabright source of polarization-entangled photons. Phys. Rev. A 1999, 60, R773. [Google Scholar]
- Li, Y.L.; Zu, C.J.; Wei, D.M. Enhance quantum teleportation under correlated amplitude damping deocherence by weak measurement and quantum measurement reversal. Quantum Inf. Process 2019, 18, 2. [Google Scholar]
- Li, Y.L.; Sun, F.X.; Yang, J.; Xiao, X. Enhancing the teleportation of quantum Fisher information by weak measurement and environment-assisted measurement. Quantum Inf. Process 2021, 20, 55. [Google Scholar]
- Wang, C.; Harraz, S.; Zhang, J.Y.; Cong, S. Quantum state protection from finite-temperature thermal noise with application to controlled quantum teleportation. Chin. Phys. B 2023, 32, 050306. [Google Scholar]
- Li, J.K.; Xu, K.; Zhang, G.F. Dense coding capacity in correlated noisy channels with weak measurement. Chin. Phys. B 2021, 30, 110302. [Google Scholar]
- Zou, W.J.; Li, Y.H.; Wang, S.C.; Cao, Y.; Ren, J.G.; Yin, J.; Peng, C.Z.; Wang, X.B.; Pan, J.W. Protecting entanglement from finite-temperature thermal noise via weak measurement and quantum measurement reversal. Phys. Rev. A 2017, 95, 042342. [Google Scholar]
- Wang, S.C.; Yu, Z.W.; Zou, W.J.; Wang, X.B. Protecting quantum states from decoherence of finite temperature using weak measurement. Phys. Rev. A 2014, 89, 022318. [Google Scholar]
- Xue, Q.F.; Zhuang, X.C.; Duan, D.Y.; Zhang, Y.J.; Yan, W.B.; Xia, Y.J.; Franco, R.L.; Man, Z.X. Evidence of genuine quantum effects in nonequilibrium entropy production via quantum photonics. Phys. Rev. A 2024, 110, 042204. [Google Scholar]
- Wootters, W.K. Entanglement of formation of an arbitrary state of two qubits. Phys. Rev. Lett. 1998, 80, 2245. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Liu, H.; Cao, L.; Yang, Y.; Liu, X.; Sun, B.; Zhao, J. Protecting the Entanglement of X-Type Systems via Weak Measurement and Reversal in the Generalized Amplitude Damping Channel. Entropy 2025, 27, 350. https://doi.org/10.3390/e27040350
Wang M, Liu H, Cao L, Yang Y, Liu X, Sun B, Zhao J. Protecting the Entanglement of X-Type Systems via Weak Measurement and Reversal in the Generalized Amplitude Damping Channel. Entropy. 2025; 27(4):350. https://doi.org/10.3390/e27040350
Chicago/Turabian StyleWang, Meijiao, Haojie Liu, Lianzhen Cao, Yang Yang, Xia Liu, Bing Sun, and Jiaqiang Zhao. 2025. "Protecting the Entanglement of X-Type Systems via Weak Measurement and Reversal in the Generalized Amplitude Damping Channel" Entropy 27, no. 4: 350. https://doi.org/10.3390/e27040350
APA StyleWang, M., Liu, H., Cao, L., Yang, Y., Liu, X., Sun, B., & Zhao, J. (2025). Protecting the Entanglement of X-Type Systems via Weak Measurement and Reversal in the Generalized Amplitude Damping Channel. Entropy, 27(4), 350. https://doi.org/10.3390/e27040350





