Kolmogorov–Arnold and Long Short-Term Memory Convolutional Network Models for Supervised Quality Recognition of Photoplethysmogram Signals
Abstract
1. Introduction
2. Related Work
3. Materials and Methods
3.1. Data Preprocessing
3.2. Model Design and Training
- The Convolutional Layer: We first apply 1D convolutional filters to detect spatial patterns such as waveform shapes. We search for the optimal kernel size to evaluate its impact on feature extraction.
- Batch Normalization: We stabilize training by normalizing layer outputs, improving convergence speed and mitigating vanishing or exploding gradients.
- The LSTM Layers: The LSTM layer captures temporal dependencies, such as pulse timing and rhythms.
- Global Average Pooling: The global average pooling aggregates temporal information into a single value per feature map, reducing the sequence length.
- Feed-Forward Layers: Fully connected layers gradually reduce features to a single output, with a sigmoid activation function producing the final binary classification (good vs. poor/fair quality).
- The Convolutional Layer: A 1D CNN expands the number of channels to a small hidden dimension while reducing input sequence length for subsequent layers.
- Max Pooling: Max pooling is applied to further reduce the sequence length. Its output is then averaged across channels before being fed it into the fully connected layers.
- The Feed-Forward Layers: The output is processed through multiple fully connected layers, gradually reducing the sequence to one dimension. A sigmoid activation function is used for the final classification in MLPs, while no a priori activation function is needed by KANs.
4. Results
- Accuracy: Calculates the general percentage of correct forecasts.where is true positives, is true negatives, is false positives, and is false negatives.
- Precision: Computes the ratio of genuine positives in relation to all predicted positives.
- Recall: Measures the percentage of real positives over all true positives.
- F1-Score: The harmonic mean of precision and recall.
- AUC: Evaluates the capability of the model to distinguish between the two classes across different thresholds.where is the true positive rate and is the false positive rate at a given threshold t.
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kyriacou, P.A.; Chatterjee, S. The origin of photoplethysmography. In Photoplethysmography; Academic Press: Cambridge, MA, USA, 2022. [Google Scholar]
- Amini, M.; Zayeri, F.; Salehi, M. Trend analysis of cardiovascular disease mortality, incidence, and mortality-to-incidence ratio: Results from global burden of disease study 2017. BMC Public Health 2021, 21, 401. [Google Scholar]
- Karlen, W.; Ansermino, J.M.; Dumont, G.A. Adaptive pulse segmentation and artifact detection in photoplethysmography for mobile applications. In Proceedings of the 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Diego, CA, USA, 28 August–1 September 2012; pp. 3131–3134. [Google Scholar]
- Li, S.; Liu, L.; Wu, J.; Tang, B.; Li, D. Comparison and Noise Suppression of the Transmitted and Reflected Photoplethysmography Signals. Biomed Res. Int. 2018, 2018, 4523593. [Google Scholar]
- Lindemann, B.; Müller, T.; Vietz, H.; Jazdi, N.; Weyrich, M. A survey on long short-term memory networks for time series prediction. Procedia CIRP 2021, 99, 650–655. [Google Scholar]
- Jeong, D.U.; Lim, K.M. Combined deep CNN–LSTM network-based multitasking learning architecture for noninvasive continuous blood pressure estimation using difference in ECG-PPG features. Sci. Rep. 2021, 11, 13539. [Google Scholar]
- Baker, S.B.; Xiang, W.; Atkinson, I. A hybrid neural network for continuous and non-invasive estimation of blood pressure from raw electrocardiogram and photoplethysmogram waveforms. Comput. Methods Programs Biomed. 2021, 207, 106191. [Google Scholar]
- Shin, H. Deep convolutional neural network-based signal quality assessment for photoplethysmogram. Comput. Biol. Med. 2022, 145, 105430. [Google Scholar]
- Zhang, Y.; Zheng, Y.; Lin, W.H.; Zhang, H.; Zhou, X.L. Challenges and Opportunities in Cardiovascular Health Informatics. IEEE Trans. Biomed. Eng. 2013, 60, 633–642. [Google Scholar]
- Charlton, P.H.; Kyriacou, P.A.; Mant, J.; Marozas, V.; Chowienczyk, P.J.; Alastruey, J. Wearable Photoplethysmography for Cardiovascular Monitoring. Proc. IEEE 2022, 110, 355–381. [Google Scholar]
- Hajj, C.E.; Kyriacou, P.A. A review of machine learning techniques in photoplethysmography for the non-invasive cuff-less measurement of blood pressure. Biomed. Signal Process. Control. 2020, 58, 101870. [Google Scholar]
- Mishra, B.; Nirala, N. A Survey on Denoising Techniques of PPG Signal. In Proceedings of the 2020 IEEE International Conference for Innovation in Technology (INOCON), Bangalore, India, 6–8 November 2020; pp. 1–8. [Google Scholar]
- Sarker, I.H. Deep Learning: A Comprehensive Overview on Techniques, Taxonomy, Applications and Research Directions. SN Comput. Sci. 2021, 2, 420. [Google Scholar]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar]
- Liu, Z.; Wang, Y.; Vaidya, S.; Ruehle, F.; Halverson, J.; Soljacic, M.; Hou, T.Y.; Tegmark, M. KAN: Kolmogorov-Arnold Networks. arXiv 2024, arXiv:2404.19756. [Google Scholar]
- Sarker, I.H. Machine Learning: Algorithms, Real-World Applications and Research Directions. SN Comput. Sci. 2021, 2, 160. [Google Scholar]
- Salton, F.; Kette, S.; Confalonieri, P.; Fonda, S.; Lerda, S.; Hughes, M.; Confalonieri, M.; Ruaro, B. Clinical Evaluation of the ButterfLife Device for Simultaneous Multiparameter Telemonitoring in Hospital and Home Settings. Diagnostics 2022, 12, 3115. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bengio, Y.; Hinton, G.E. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [PubMed]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2012, 60, 84–90. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar]
- Lu, Y.; Lu, J. A universal approximation theorem of deep neural networks for expressing probability distributions. In Proceedings of the 34th International Conference on Neural Information Processing Systems, Red Hook, NY, USA, 6–12 December 2020. [Google Scholar]
- Schmidt-Hieber, J. The Kolmogorov–Arnold representation theorem revisited. Neural Netw. 2021, 137, 119–126. [Google Scholar] [CrossRef]
- Eilers, P.H.C.; Marx, B.D. Flexible smoothing with B-splines and penalties. Stat. Sci. 1996, 11, 89–121. [Google Scholar]
- de Boor, C. On Calculating B-splines. J. Approx. Theory 1972, 6, 50–62. [Google Scholar] [CrossRef]


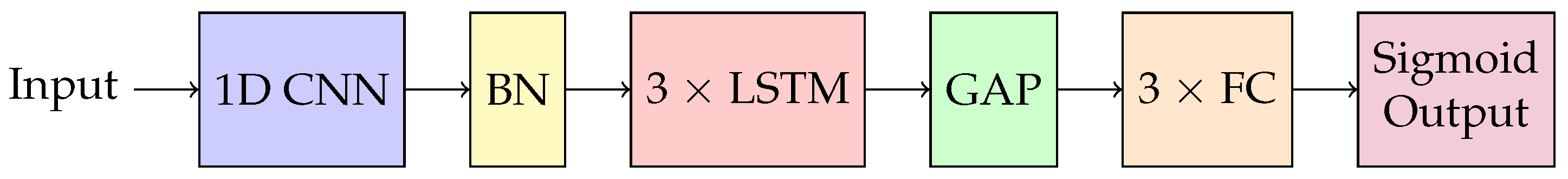


| Metric | CNN-LSTM | MLP | KAN |
|---|---|---|---|
| Accuracy | 95% | 86% | 89% |
| Precision | 96% | 84% | 89% |
| Recall | 94% | 93% | 93% |
| F1-Score | 95% | 89% | 91% |
| AUC | 99% | 90% | 95% |
| Architecture | Trainable Parameters |
|---|---|
| CNN-LSTM | 456,865 |
| MLP | 22,526 |
| KAN | 127,206 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehrab, A.; Lapenna, M.; Zanchetta, F.; Simonetti, A.; Faglioni, G.; Malagoli, A.; Fioresi, R. Kolmogorov–Arnold and Long Short-Term Memory Convolutional Network Models for Supervised Quality Recognition of Photoplethysmogram Signals. Entropy 2025, 27, 326. https://doi.org/10.3390/e27040326
Mehrab A, Lapenna M, Zanchetta F, Simonetti A, Faglioni G, Malagoli A, Fioresi R. Kolmogorov–Arnold and Long Short-Term Memory Convolutional Network Models for Supervised Quality Recognition of Photoplethysmogram Signals. Entropy. 2025; 27(4):326. https://doi.org/10.3390/e27040326
Chicago/Turabian StyleMehrab, Aneeqa, Michela Lapenna, Ferdinando Zanchetta, Angelica Simonetti, Giovanni Faglioni, Andrea Malagoli, and Rita Fioresi. 2025. "Kolmogorov–Arnold and Long Short-Term Memory Convolutional Network Models for Supervised Quality Recognition of Photoplethysmogram Signals" Entropy 27, no. 4: 326. https://doi.org/10.3390/e27040326
APA StyleMehrab, A., Lapenna, M., Zanchetta, F., Simonetti, A., Faglioni, G., Malagoli, A., & Fioresi, R. (2025). Kolmogorov–Arnold and Long Short-Term Memory Convolutional Network Models for Supervised Quality Recognition of Photoplethysmogram Signals. Entropy, 27(4), 326. https://doi.org/10.3390/e27040326







