Abstract
This study examines the thermal conduction resistance in anisotropic bodies using linear extended irreversible thermodynamics. The fulfilment of the Onsager Reciprocal Relations in anisotropic bodies, such as crystals, has been demonstrated. This fulfilment is achieved by incorporating Newton’s heat transfer coefficients into the calculation of the entropy production rate. Furthermore, a basic principle for the transport of heat, similar to the Onsager–Fuoss formalism for the multicomponent diffusion at a constant temperature, was established. This work has the potential to be applied not just in the field of material science, but also to enhance our understanding of heat conduction in crystals. A novel formalism for heat transfer analogous to Onsager–Fuoss model for multicomponent diffusion was developed. It is believed that this work could be applied for educational purposes.
1. Introduction
Over the past few decades, irreversible thermodynamics has emerged as a potent method for the derivation of macroscopic laws of processes with its application both to the Euclidean framework and to relativistic spacetime [1,2,3]. It is worth mentioning that from the inception of irreversible thermodynamics, extensive study has been performed on its axiomatic system, which is founded on axioms that go considerably beyond those of equilibrium thermodynamics.
The Onsager reciprocal relations (ORR) are fundamental principles in irreversible thermodynamics. ORR states that the matrix of phenomenological resistance coefficients (R) in the flux-force relations is symmetric (Rij = Rji) when there are no magnetic fields and when the fluxes J or thermodynamic forces X are linearly independent (Linearity Axiom: X = R.J) [4,5,6]. Miller [7,8] presented experimental evidence of ORR, while Truesdell and colleagues [9,10] expressed significant scepticism regarding the theoretical basis of ORR. Onsager [4,5] employed the concept of microscopic reversibility to derive these reciprocal relations; however, Truessdell and his colleagues [9,10] argued that the concept of microscopic reversibility is not consistent with Poincare’s recurrence theorem.
Today, ORR is widely recognized by most scientists in the area as being well-established, particularly in the context of irreversible thermodynamics that is near equilibrium [11,12,13,14,15,16,17,18,19,20,21,22,23,24]. Linear Extended Irreversible Thermodynamics (LEIT) is a reliable approach used to deduce fundamental principles governing macroscopic processes that occur far from local equilibrium. This method has significant practical uses in various materials. The ORR is regarded as an axiom in this region [14].
Heat conduction in anisotropic bodies, such as crystals, is closely connected to ORR. The creation of ORR near to equilibrium [4,5] was primarily motivated by the research conducted by Voigt and Curie on heat transmission in crystals [16,23]. The application of LEIT in the field of heat transmission is justified by assuming a sinusoidal starting disturbance of temperature at a specific place on an isolated body [14]. In this scenario, the Fourier law incorporates relaxation time factors as anticipated by the Linear Extended Irreversible Thermodynamics (LEIT) to prevent the violation of the second thermodynamic postulate caused by oscillations in the total entropy of the system [14]. The invention of the Cattaneo equation for heat transmission was motivated, in part, by this observation [14]. The development of Linear Extended Thermodynamics aimed to derive the Cattaneo equation by applying concepts of sound non-equilibrium thermodynamics [14].
Heat transfer in crystals is a significant factor in material science applications, including the improvement of heat transfer through the use of nano-material suspensions [25,26], as well as in the field of optoelectronics [27,28,29]. For instance, materials that are extremely thin at the atomic level, known as Van der Waals (vdW) materials, along with their related heterostructures, offer a versatile platform for manipulating heat transmission at the nanoscale and developing innovative thermoelectric materials [27,28,29].
Specifically, the study of heat conduction in crystals has received significant attention in recent years. Olson et al. [30] created models to establish a connection between the variable spatial anisotropy of heat conductivity and anisotropic crystal formations. Chen and Liu [31] designed a nonlocal discrete model to study anisotropic heat conduction phenomena and investigate the connection between bond properties and material thermal conductivity. In their research, Dong et al. [32] utilized modern computational techniques to investigate the heat transport and associated characteristics of a new crystal known as quasi-hexagonal-phase fullerene (QHPF). Their findings demonstrated that the thermal conductivity in QHPF exhibits anisotropy, making it a viable material for 2D electronic devices. Zhao et al. [33] investigated the thermal conductivity of a significant material at elevated pressure, with potential industrial applications such as diamond manufacturing. It has been demonstrated that the diamond displays clear anisotropic characteristics under a pressure of 120 GPa. Other important applications of heat conduction in crystals include the protein crystal growth rate by means of temperature [34] and thermodiffusion in protein aggregations [35]. Other materials exhibiting anisotropic heat transfer include the wood and the composite materials.
In our earlier study, we investigated the fundamental principles of Onsager Reciprocal Relations (ORR) in an isotropic fluid with isothermal multi-component diffusion, as described in the LEIT [36]. In addition, the Onsager–Fuoss formalism, and the Maxwell-Stefan model, which are basic laws governing isothermal multi-component diffusion in the LEIT, were derived [36].
The recent advance in irreversible thermodynamics [37,38,39] imposes a re-examination of fundamental principles of LEIT such as the ORR. The objective of this study was to investigate the validity of the ORR approach for modelling heat conduction in an anisotropic body, specifically in the absence of elasticity, mass transfer, or chemical reactions, at the limit of Linear Extended Irreversible Thermodynamics (LEIT) that is far from the local equilibrium process. Please notice that in this area ORR is regarded as an axiom [14]. Additionally, the aim was to establish a fundamental law for heat transfer, drawing an analogy to the Onsager–Fuoss formalism used for isothermal multi-component diffusion.
2. Theoretical Section
The entropy production rate per unit volume (σ) for heat conduction in an anisotropic body in the absence of mass transfer, elasticity, or chemical reactions is written as [14]:
where xi are the Cartesian coordinates, T is temperature and δi is the unit vector in the ith direction. The following equation holds true by generalizing the Maxwell-Cattaneo equation [14] for heat conduction in an anisotropic body at the limit of LEIT:
The heat conductivity K is a second rank tensor in the case of anisotropic body.
Following Jou et al. [14] the entropy production rate per unit volume (σ) for heat conduction in an anisotropic body at the limit of LEIT might be derived immediately by fusing the Maxwell-Cattaneo law of heat conduction (Equation (2)) into Equation (1):
The process of obtaining Equations (1)–(3) substantially adheres to the methods employed by Jou and colleagues [14].
In order to investigate the foundations of the ORR, the local heat transfer coefficients (hloc) close to the equilibrium (τ = 0) have been introduced [40]:
where T0i is a constant reference temperature located outside the heat transfer area at the ith axis. This procedure results in the replacement of the temperature gradient with the temperature difference. However, this is not a new or original idea; its inception can be attributed to reference [40]. Equation (4) indicates that the notion of heat transfer coefficients can be easily applied to heat transmission in solids. This observation aligns with established technical ideas, such as the film theory in heat transport [15]. In particular, film theory predicts: where Li is the distance between the point where T0i is located, the point having temperature T. The above film theory prediction was recently generalized to heat transfer in microscopic level by Chen and Liu [31].
It is important to understand that thermal conductivity, represented by the tensor K, is a second-order tensor that describes heat transport in anisotropic media. In simpler terms, the temperature gradient in one direction impacts not only the heat flux in that same direction, but also in the other two remaining directions. Thus, it may be inferred that the local heat transfer coefficient tensor (hloc) is a tensor of second order.
A more profound question arises regarding the heat transfer coefficients that consider heat transfer occurring far from local equilibrium: How can one establish heat transfer coefficients for heat transfer far from local equilibrium (τ ≠ 0) in a manner that also encompasses the scenario of heat transfer approaching equilibrium (τ = 0)? In reference [40], the answer to this dilemma is provided by developing the idea of residual heat transfer coefficients (hres). In particular by combining the local heat transfer coefficient close to the equilibrium (hloc) with the residual heat transfer coefficient (hres) the heat flux in an anisotropic body at the LEIT is expressed as:
where hi is the overall heat transfer coefficient. The above law is Newton’s law of cooling or heating written in three-dimensional form [15] and it could be used as an ad hoc definition of both the residual and overall heat transfer coefficients. The concept of heat transfer coefficients is well established in the literature, and it is widely used in the designing of complex engineering applications [15] by using the film theory. This theory predicts: [15]. A typical example is the heat transfer coefficient of a pipe wall participating in a heat transfer process. In engineering applications, we have to also consider in calculations the heat transfer coefficient of pipe wall. In film theory this coefficient is approximated as the ratio of wall thermal conductivity divided by wall thickness.
Let us now assume that the heat fluxes are linearly dependent. This is achieved by multiplying both left- and right-hand side of Equation (5) defining the overall heat transfer coefficients (Equation (5)) by a parameter λ and setting the summation equal to zero. Accordingly, the following relations could be directly derived:
where w = λ·h.
The above equations are analogous to the respecting equations of multi-component diffusion [36,41].
One can directly show by further using Equations (4) and (5) the following relationship between relaxation times (τ) and heat transfer coefficients:
By introducing Equation (5) into Equation (3) one could write the entropy production rate σ in terms of the overall heat transfer coefficients as:
After introduction of the transformation to the above equation, the following equation has been directly derived by assuming that the entropy production rate σ is uniquely defined and independent of the constant temperature T0:
The above transformation implies that the reference temperature T0i is changed by adding a constant temperature T0. A clear physical meaning for this transformation results by considering the heat transfer system on a vehicle moving with a constant and uniform velocity. Obviously, an observer on the ground will observe the particles of the heat transfer system moving with an additional velocity, corresponding to an additional temperature T0. However, our observations in Euclidean geometry indicate that the temperature of the system remains unaffected. X is the thermodynamic force defined as:
The linearity postulate [42] is strongly related to the above transformation. By taking into account the above definition of thermodynamic forces and applying the linearity postulate to Equation (8) the following equation has been derived:
where Rij are the resistance coefficients. One could anticipate based on the similarities between heat and mass transfer that resistance coefficients are functions of intensive variables of the system such as temperature.
By applying the transformation to the above equation and again, by assuming that the driving thermodynamic force is independent of the constant temperature, T0, the following restrictions are directly derived:
The following is the result of applying the linearity principle to Equation (9):
The aforementioned equations are valid because the fluxes are specified in terms of an arbitrary temperature and in the most generic situation . The mathematical part of Equation (13) is due to Tyrrell and Harris [11].
According to Equations (12) and (13) above, the square matrix of R is symmetrical (Rij = Rji), or in other words, the ORR holds true.
It is worth mentioning that the mathematical methodology applied in this work is not a novel idea; The above mathematical methodology was validated in previous work [41,43] for ORR in the case of isothermal multi-component diffusion [41] and simultaneous heat and mass transfer [43] close to equilibrium. Moreover, the mathematical methodology described in previous work [41,43] was recently generalized [37] for multi-component diffusion close to equilibrium. However, this work deals with heat transfer in LEIT framework that is far from local equilibrium process [14].
However, in previous work [36] fundamental equations such as the Onsager–Fuoss model for isothermal multi-component diffusion at the limit of LEIT were derived:
where Xdi is the thermodynamic driving force for diffusion, adi is a thermodynamic parameter, cj stands for molar concentration of the j-th substance, μi is the chemical potential under constant temperature (T) and pressure (P), represents the molar flux of the i-th substance relative to the centre of mass, is the velocity of the i-th substance, Rd,ij is the resistance coefficient for diffusion between the i-th and the j-th substance, respectively.
The above equation could be viewed as an intermediate step to the derivation of Maxwell-Stefan equations that are directly obtained from Equation (14) by using the standard definition of chemical potential [36].
A deeper question arises from the preceding analysis: Does any parallel exist between the laws governing heat transfer and the fundamental laws governing diffusion, such as the Onsager-Fuoss model elucidated in Equation (14)?
Please, note that by applying the linearity postulate and the ORR to the dissipation function, multiplying Equation (12) by (T-T0i), and subtracting it from the linearity postulate Equation (11), one could arrive at the following equation:
Equation (15) can be interpreted as a reliable and broad representation of heat transfer through conduction, based on the Onsager–Fuoss model Equation (14), specifically for isothermal multi-component diffusion. An important benefit of utilizing Equation (15) further is its simplicity, as it does not include second order derivatives. By directly comparing Equation (14) with Equation (15), it becomes evident that the overall heat transfer coefficients (h) in Equation (14) behave similarly to concentration, but the reference velocity (vi) is substituted with the constant reference temperature (T0j). Nevertheless, the relaxation term is not included on the left side of Equation (15) as it is combined with the overall heat transfer coefficient. From a theoretical point of view, Equation (14) allows a detailed stability analysis following previous work for isothermal multi-component diffusion [44,45] and by replacing the chemical potential gradient by the term as well as molar concentrations by overall heat transfer coefficients (hj).
The above Equation (15) could be further applied to derive an alternative framework for heat transfer as shown in the results and discussion section.
3. Results and Discussion
In order to further validate the theory, one has to resort to computation experimentation. In our numerical experiment, heat transfer in an anisotropic cube (see Figure 1), made of wood or a composite material, having edge equal to 1 m. was considered. To introduce the LEIT, we assume an appropriate initial disturbance, such as a sinusoidal starting disturbance of temperature at a point of the cube [14]. In this experiment, the conditions for point A (Figure 1) as summarized in Table 1, were assumed. The reference temperatures were located outside the cube at planes 12, 13 and 23, respectively. Our task is to calculate the resistance coefficients for heat transfer.
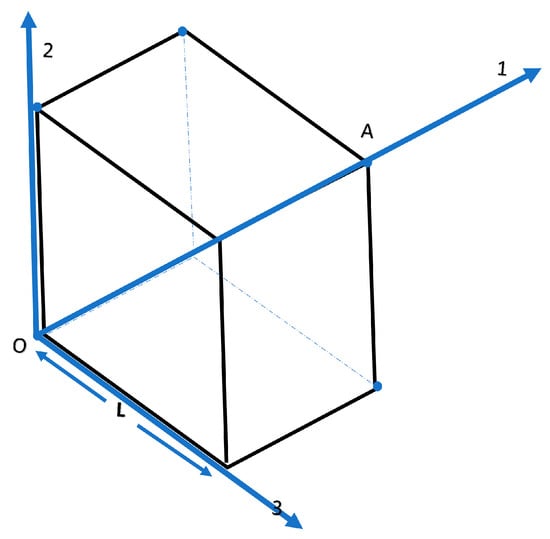
Figure 1.
Schematic representation of heat transfer in a cube.

Table 1.
Input data in numerical experiment.
The resulting value of T03 by using Equation (6) is 293.75 K.
By further using the definition of local heat transfer coefficients Equation (4) as well as the film theory () Equation (15) is rewritten as:
The above equation is rewritten by introducing the modified resistance coefficients () as:
By introducing in Equation (17) the definition of overall heat transfer coefficients Equation (5) the following equation is directly derived:
The data summarized in Table 1 were introduced in Equations (17) and (18) by further using the ORR and the theoretical framework of previous section. The resulting nonlinear algebraic system was solved by utilizing standard methods of numerical analysis [46]. The resulting values for the modified resistance coefficients () are summarized in Table 2.

Table 2.
Output data of the numerical experiment.
Using Equation (12), the rest resistance coefficients could be computed directly from the data reported in Table 2. Regarding stability considerations, one could directly show by using the above calculated resistance coefficients, the heat fluxes illustrated in Table 1 and Equation (1) that σ = 3.66 × 10−2 W.m−3K−1 > 0.
Given the resistance coefficients and the heat transfer coefficients (see Table 2), we could directly calculate i = 1, 2, 3 by further using the Onsager–Fuoss model for heat transmission (Equation (15)). By using these data, one could also directly estimate thermal conductivity and relaxation time tensors from the Maxwell-Cattaneo model Equation (2) by repeating this process at different times. This necessity arises from the fact that we have to calculate the derivative of heat flux with respect to time in order to apply the Maxwell-Cattaneo model Equation (2).
In order to better validate the work’s findings, let us modify the reference temperatures, T0i, by adding a constant temperature T0. It is directly demonstrated that the temperature T is increased by the same temperature T0 by assuming that the resistance coefficients stay nearly constant for slight temperature variations and by accounting for Equation (6): ; .
On the other hand, one could expect that the heat fluxes stay unchanged. The resistance coefficients displayed also in Table 2 are the result of a computing experiment that used the remainder of the data described in Table 1 and assumed a fluctuation of both temperature T and reference temperatures by 10 K. This may be explained by the fact that, in accordance with Equations (17) and (18), temperature and fluxes depend only on the difference in the reference temperature (T0i–T0j).
There is a clear physical meaning to the above computational experiment: If a measurement apparatus located outside the heat transfer framework in Euclidean space is re-calibrated by measuring an additional constant temperature T0, an observer of heat transfer located outside the heat transfer framework will observe a different temperature T + T0 while the fluxes and dissipation function stay unchanged.
However, the above assumptions might hold true only for Euclidean space. In a relativistic framework one could have to take into account the variation in certain quantities such as mass or energy between the observer and the body. Another major assumption in the Euclidean space is that the resistance coefficients do not depend on the framework. Please note that work in the field of heat conduction in a relativistic extended framework has appeared in the literature [47]. The authors aim to generate interest among peers in the field to extend these ideas to the relativistic context, where non-equilibrium thermodynamics plays a crucial role in numerous cosmological models.
4. Conclusions
This study re-evaluates the suitability of the Onsager reciprocal relation (ORR) for describing heat conduction in an anisotropic substance, such as a crystal that is much removed from a state of equilibrium. Research has demonstrated that the Onsager reciprocal relation (ORR) in LEIT has been successfully validated by utilizing heat transfer coefficients. This validation is based on the assumption that the resistance coefficients, entropy production rate, and heat fluxes are uniquely defined and independent of the constant reference temperature. Furthermore, a new equation for heat transmission at the limit of LEIT, similar to the Onsager–Fuoss model used for isothermal multi-component diffusion, was developed. This work could be used for educational purposes and to further understand heat transfer in anisotropic bodies at the limit of LEIT.
Author Contributions
Conceptualization, G.D.V. and R.K.A.; methodology, G.D.V. and D.S.A.; software, D.T.; writing—original draft preparation, D.T.; writing—review and editing, G.D.V., R.K.A. and D.S.A.; supervision, G.D.V. and R.K.A.; project administration, G.D.V. and D.S.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data of this work is available upon request.
Acknowledgments
The authors are thankful to Sarada Paul Roy and Kate Somerscales for their help in editing the manuscript and J. Paulo Davim, Department Mechanical Engineering, University of Aveiro—Campus Santiago, Aveiro, Portugal for stimulating discussions. The anonymous reviewers of this work are also acknowledged for their constructive comments to further improve this work.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| adi | auxiliary parameter of the system |
| ci | molar concentration |
| h | overall heat transfer coefficient |
| hloc | close to equilibrium local heat transfer coefficients |
| hres | residual heat transfer coefficients |
| molar flux of the i-th substance relative to the velocity of the centre of mass | |
| Jq | heat flux |
| K | thermal conductivity coefficient |
| Li | distance between the point where T0j is located and the point having |
| temperature T. | |
| R | resistance coefficients |
| T | absolute temperature |
| T0 | reference absolute temperature |
| t | time |
| vi | velocity of the i-th substance |
| xj | space coordinate |
| X | thermodynamic driving force |
| w | weighting factors |
| Greek Letters | |
| δ | unit vector |
| λi | auxiliary parameter |
| chemical potential of the i-th substance | |
| σ | entropy production rate per unit volume |
| Τ | relaxation time. |
| Subscripts | |
| d | diffusion |
References
- Li, S.-N.; Cao, B.-Y. Generalized variational principles for heat conduction models based on Laplace transform. Int. J. Heat Mass Transf. 2016, 103, 1176–1180. [Google Scholar]
- Li, S.-N.; Cao, B.-Y. On Entropic Framework Based on Standard and Fractional Phonon Boltzmann Transport Equations. Entropy 2019, 21, 204. [Google Scholar] [CrossRef] [PubMed]
- Parker, M.C.; Jeynes, C. A Relativistic Entropic Hamiltonian–Lagrangian Approach to the Entropy Production of Spiral Galaxies in Hyperbolic Spacetime. Universe 2021, 7, 325. [Google Scholar] [CrossRef]
- Onsager, L. Reciprocal Relations in Irreversible Processes I. Phys. Rev. 1931, 37, 405–426. [Google Scholar] [CrossRef]
- Onsager, L. Reciprocal Relations in Irreversible Processes II. Phys. Rev. 1931, 37, 2265–2279. [Google Scholar] [CrossRef]
- Casimir, H.B.G. On Onsager Principle of Microscopic Reversibility. Rev. Mod. Phys. 1945, 17, 343–350. [Google Scholar] [CrossRef]
- Miller, D.G. Ternary Isothermal Diffusion and the Validity of the Onsager Reciprocity Relations. J. Phys. Chem. 1959, 63, 570–578. [Google Scholar] [CrossRef]
- Miller, D.G. Thermodynamics of Irreversible Processes: The Experimental Verification of the Onsager Reciprocal Relations. Chem. Rev. 1960, 60, 15–37. [Google Scholar] [CrossRef]
- Coleman, B.D.; Truesdel, C. On the Reciprocal Relations of Onsager. J. Chem. Phys. 1960, 33, 28–31. [Google Scholar] [CrossRef]
- Truesdell, C.A. Rational Thermodynamics; Springer: New York, NY, USA, 1984. [Google Scholar]
- Tyrrell, H.J.V.; Harris, K.R. Diffusion in Liquids: A Theoretical and Experimental Study; Butterworths: London, UK, 1984. [Google Scholar]
- de Groot, S.R.; Mazur, P. Non-Equilibrium Thermodynamics, 2nd ed.; Dover Publications: New York, NY, USA, 1984; pp. 11–82. [Google Scholar]
- Kuiken, G.D.C. Thermodynamics of Irreversible Processes—Applications to Diffusion and Rheology, 1st ed.; Wiley: New York, NY, USA, 1994; pp. 1–135. [Google Scholar]
- Jou, D.; Lebon, G.; Casas-Vazquez, J. Extended Irreversible Thermodynamics, 3rd ed.; Springer: Berlin, Germany, 2001; pp. 39–70. [Google Scholar]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena, 2nd ed.; Wiley: New York, NY, USA, 2002; pp. 764–798. [Google Scholar]
- Kondepudi, D.; Prigogine, I. Thermodynamics Nonequilibrium. In Encyclopedia of Applied Physics, 2nd ed.; Trigg, G.L., Ed.; Wiley-VCH: Weinheim, Germany, 2003. [Google Scholar]
- Demirel, Y.A.; Sandler, S.I. Nonequilibrium Thermodynamics in Engineering and Science. J. Phys. Chem. B 2004, 108, 31–43. [Google Scholar] [CrossRef]
- Öttinger, H.C. Beyond Equilibrium Thermodynamics, 1st ed.; Wiley: New York, NY, USA, 2005. [Google Scholar]
- Demirel, Y. Nonequilibrium Thermodynamics, Transport and Rate Processes in Physical, Chemical and Biological Systems, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2007; pp. 1–144. [Google Scholar]
- Rastogi, R.P. Introduction to Non-Equilibrium Physical Chemistry, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Müller, I.; Müller, W.H. Fundamentals of Thermodynamics and Applications; Springer: Heidelberg, Germany, 2009. [Google Scholar]
- Michaelides, E.E. Transport Properties of Nanofluids. A Critical Review. J. Non Equil. Thermodyn. 2023, 38, 1–79. [Google Scholar] [CrossRef]
- Kondepudi, D.; Prigogine, I. Modern Thermodynamics: From Heat Engines to Dissipative Structures, 2nd ed.; Wiley: New York, NY, USA, 2015; pp. 333–455. [Google Scholar]
- Arya, R.K.; Verros, G.D. On the validity of Onsager Reciprocal Relations (ORR) for heat transfer in anisotropic solids. Axioms 2022, 11, 104. [Google Scholar] [CrossRef]
- Reinecke, B.N.; Shan, J.W.K.; Suabedissen, K.; Cherkasova, A.S. On the anisotropic thermal conductivity of magnetorheological suspensions. J. Appl. Phys. 2008, 104, 023507. [Google Scholar] [CrossRef]
- Li, M.-G.; Zheng, C.; Zhao, Q.; Chen, X.; Wu, W.-T. Anisotropic heat transfer of ferro-nanofluid in partially heated rectangular enclosures under magnetic field. Case Stud. Therm. Eng. 2021, 26, 101145. [Google Scholar] [CrossRef]
- Kim, S.; Menabde, S.G.; Brar, V.W.; Jang, M.S. Functional Mid-Infrared Polaritonics in van der Waals Crystals. Adv. Optical Mater. 2020, 8, 1901194. [Google Scholar] [CrossRef]
- Gonzalez-Munoz, S.; Agarwal, K.; Castanon, E.G.; Kudrynskyi, Z.R.; Kovalyuk, Z.D.; Spièce, J.; Kazakova, O.; Patanè, A.; Kolosov, O.V. Direct Measurements of Anisotropic Thermal Transport in γ-InSe Nanolayers via Cross-Sectional Scanning Thermal Microscopy. Adv. Mater. Interfaces 2023, 10, 2300081. [Google Scholar] [CrossRef]
- Cai, Y.; Faizan, M.; Mu, H.; Zhang, Y.; Zou, H.; Zhao, H.J.; Fu, Y.; Zhang, L. Anisotropic phonon thermal transport in two-dimensional layered materials. Front. Phys. 2023, 18, 43303. [Google Scholar] [CrossRef]
- Olson, D.H.; Angelici Avincola, V.; Parker, C.G.; Braun, J.L.; Gaskins, J.T.; Tomko, J.A.; Opila, E.J.; Hopkins, P.E. Anisotropic thermal conductivity tensor of β-Y2Si2O7 for orientational control of heat flow on micrometer scales. Acta Mater. 2020, 189, 299–305. [Google Scholar] [CrossRef]
- Chen, H.; Liu, D. Formulation of a nonlocal discrete model for anisotropic heat conduction problems. Int. J. Therm. Sci. 2022, 182, 107816. [Google Scholar] [CrossRef]
- Dong, H.; Cao, C.; Ying, P.; Fan, Z.; Qian, P.; Su, Y. Anisotropic and high thermal conductivity in monolayer quasi-hexagonal fullerene: A comparative study against bulk phase fullerene. Int. J. Heat Mass Transf. 2023, 206, 123943. [Google Scholar] [CrossRef]
- Zhao, Y.; Yan, F.; Liu, X. Thermal transport characteristics of diamond under stress. Diam. Relat. Mater. 2023, 136, 110016. [Google Scholar] [CrossRef]
- Sanamaría-Holek, I.; Gadomski, A.; Rubí, J.M. Controlling protein crystal growth rate by means of temperature. J. Phys. Condens. Matter 2011, 23, 235101. [Google Scholar] [CrossRef]
- Gadomski, A.; Kruszewska, N. Thermodiffusion as a close-to-interface effect that matters in non-isothermal (dis)orderly protein aggregations. Phys. Lett. Sect. A Gen. At. Solid State Phys. 2014, 378, 2881–2887. [Google Scholar] [CrossRef]
- Thapliyal, D.; Arya, R.K.; Verros, G.D. On the multi-component diffusion in the linear region of the extended thermodynamics framework. Eur. Phys. J. Plus 2021, 136, 1138. [Google Scholar] [CrossRef]
- Agren, J. The Onsager Reciprocity Relations Revisited. J. Phase Equilib. Diffus. 2022, 43, 640–647. [Google Scholar] [CrossRef]
- Liu, Z.-K. Theory of cross phenomena and their coefficients beyond Onsager theorem. Mater. Res. Lett. 2022, 10, 393–439. [Google Scholar] [CrossRef]
- Liu, Z.-K. Thermodynamics and its prediction and CALPHAD modeling: Review, state of the art, and perspectives. Calphad 2023, 82, 102580. [Google Scholar] [CrossRef]
- Verros, G.D. Comprehensive Criteria for the Extrema in Entropy Production Rate for Heat Transfer in the Linear Region of Extended Thermodynamics Framework. Axioms 2020, 9, 113. [Google Scholar] [CrossRef]
- Verros, G.D. On the Validity of the Onsager Reciprocal Relations in Multi-component Diffusion. Phys. Lett. A 2007, 365, 34–38. [Google Scholar] [CrossRef]
- Arya, R.K.; Thapliyal, D.; Verros, G.D.; Singh, N.; Singh, D.; Kumar, R.; Srivastava, R.K.; Tiwari, A.K. On the Validity of a Linearity Axiom in Diffusion and Heat Transfer. Coatings 2022, 12, 1582. [Google Scholar] [CrossRef]
- Verros, G.D. On the Validity of the Onsager Reciprocal Relations in Simultaneous Heat and Multi-component Diffusion. Phys. A Stat. Mech. Its Appl. 2007, 385, 487–492. [Google Scholar] [CrossRef]
- Glansdorff, P.; Nicolis, G.; Prigogine, I. The thermodynamic stability theory of non-equilibrium States. Proc. Natl. Acad. Sci. USA 1974, 71, 197–199. [Google Scholar] [CrossRef] [PubMed]
- Vilar, J.M.G.; Rubí, J.M. Thermodynamics “beyond” local equilibrium. Proc. Natl. Acad. Sci. USA 2001, 98, 11081–11084. [Google Scholar] [CrossRef]
- Stewart, W.E.; Caracotsios, M.; Sørensen, J.P. Parameter estimation from multiresponse data. AIChE J. 1992, 38, 641–650. [Google Scholar] [CrossRef]
- Gavassino, L. Relativistic Heat Conduction in the Large-Flux Regime. Entropy 2024, 26, 147. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).