Practical Consequences of the Bias in the Laplace Approximation to Marginal Likelihood for Hierarchical Models
Abstract
1. Introduction
2. Laplace Approximation of the Marginal Likelihood Function for Hierarchical Models
- Maximize with respect to u for a fixed value of . Let us denote this value by or, with a slight abuse of notation, by . Let denote the Hessian matrix, the matrix of second derivatives, at the location of the maximum. Notice that it is implicitly assumed that as a function of u, for every fixed value of , has a unique maximum and is differentiable as a function of u. Hence, it is required that all latent variables are continuous random variables.
- Then is the Laplace approximation to the marginal likelihood ([23] Equation (3)).
- The profile likelihood function for any function of the parameters can be computed by using any constrained optimization routine, namely: .
- Equation (1) will be exactly true provided is a quadratic function of u. For example, if follows a Gaussian distribution for all values of . Notice that for the LMM, this is assumed, and hence, Henderson’s method III works.
- Equation (1) might hold true if the number of random effects is fixed or if they increase at a slower rate than the rate at which the sample size increases. For example, in the multi-stratum studies, if the number of strata is (e.g., [22,29]) where n is the sample size and m is the number of strata. In this case, information about the random effects u in the data y increases to infinity at an appropriate rate. Then, the conditional distribution is likely to converge to a Gaussian distribution as the sample size increases. Hence, at least asymptotically, the Laplace approximation may be good.
- In most other situations, unless explicitly demonstrated, is of order (e.g., [26], Section 4.1). In general, varies with . An immediate consequence is that the score function, the first derivative with respect to based on the LAML even asymptotically, is not a zero unbiased estimating function ([21,30,31]). An immediate consequence of the biased estimating function is that the resultant estimators are inconsistent.
- The fact that varies with also affects the second derivative matrix, and the resultant estimating function is not information unbiased ([21,31]). The lack of information unbiasedness implies that statistical inferences such as the confidence intervals or the likelihood ratio tests based on the Laplace approximated marginal and profile likelihood function are likely to be misleading.
- Equation (1) clearly fails if the conditional distribution is not unimodal. Establishing unimodality of the conditional distribution is difficult in practice. For example, consider models where the dimension of the latent variables U is larger than the dimension of the observations Y. In such a situation, there are possibly several values of U that are compatible with an observed value of . Hence, the conditional distribution is likely to be multimodal and LAML would not be applicable.
3. Counter Examples
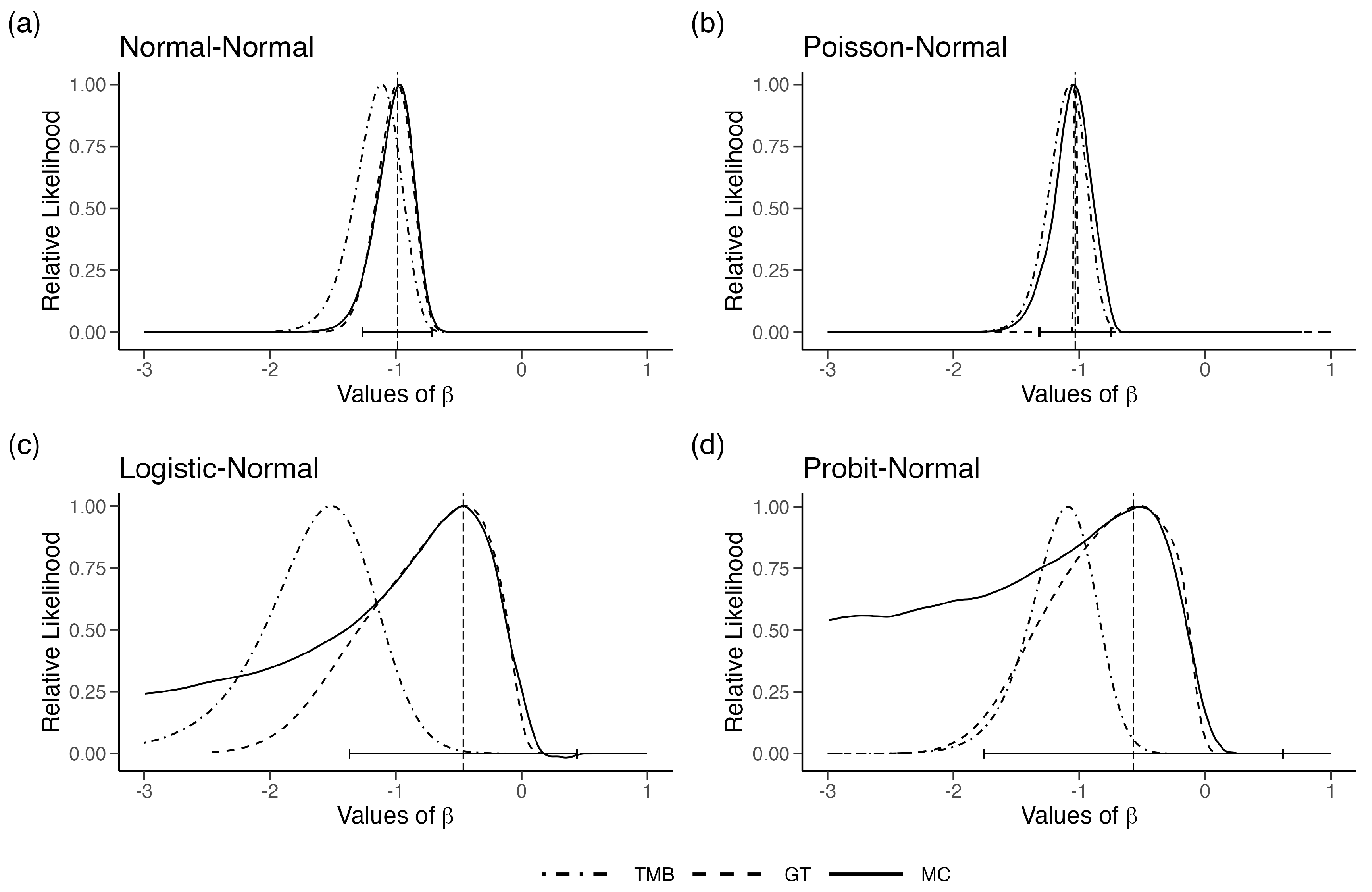
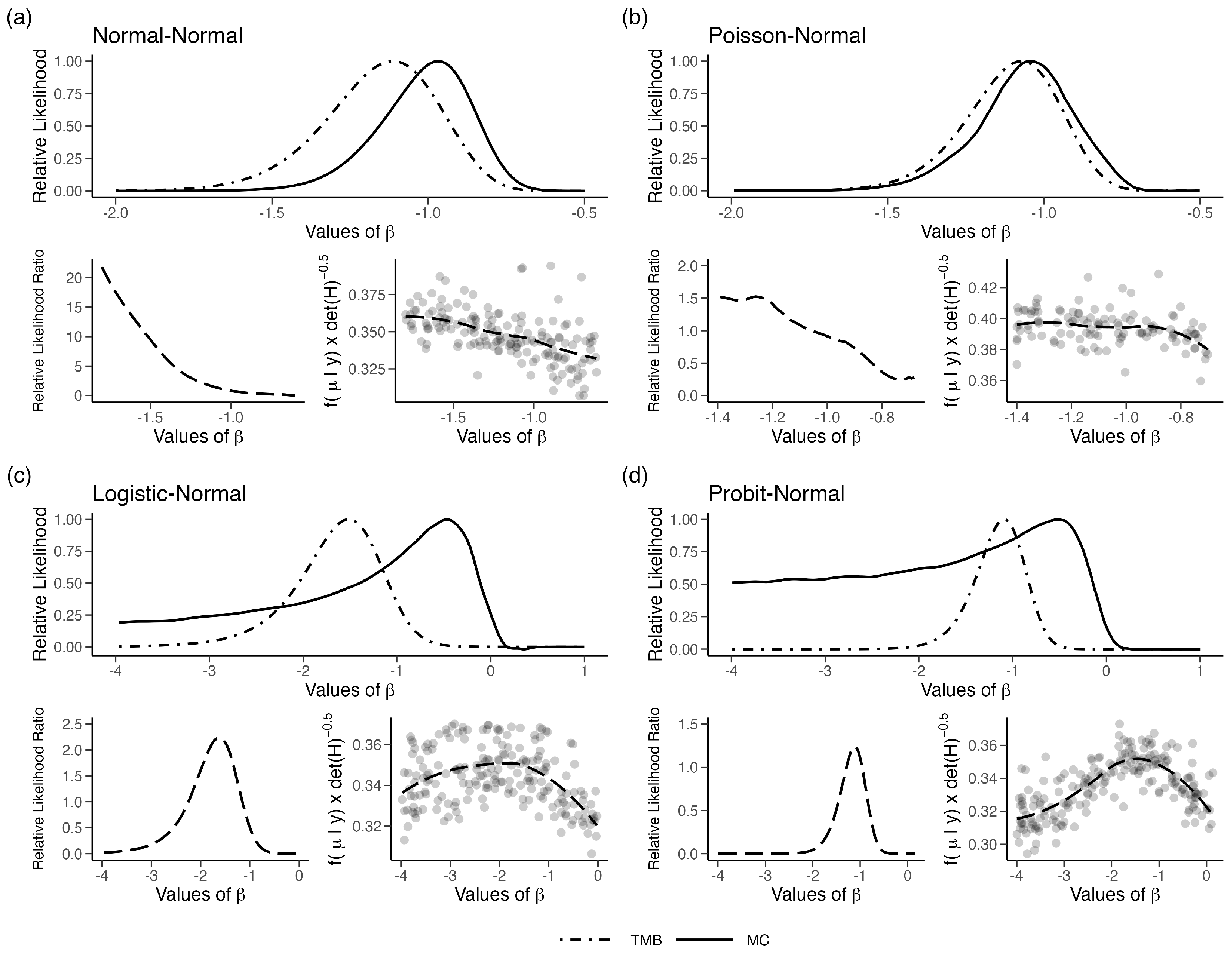
3.1. Single Parameter Models
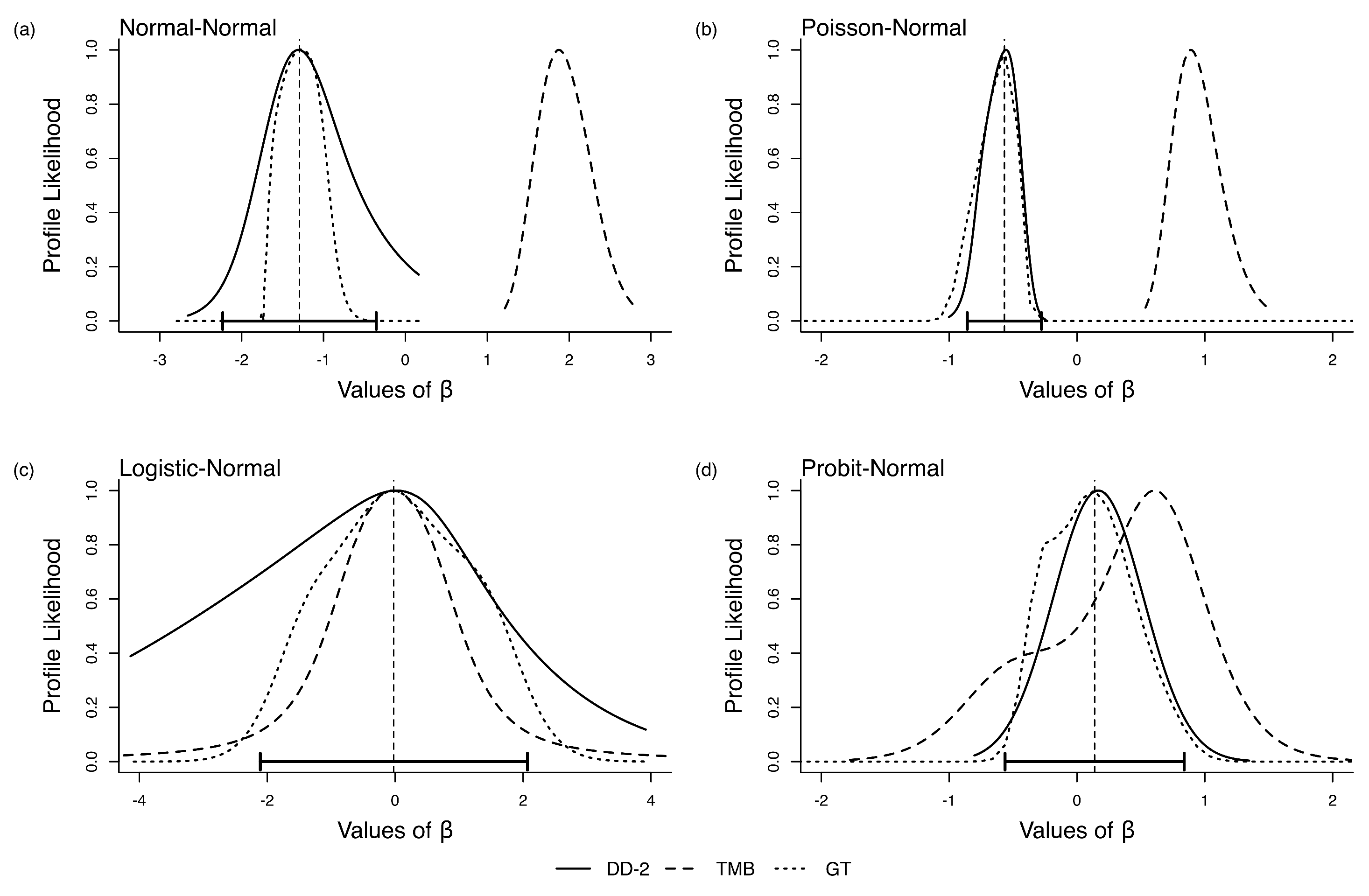
3.2. Profile Likelihood and Multiparameter Models
3.3. Nonidentifiable Models
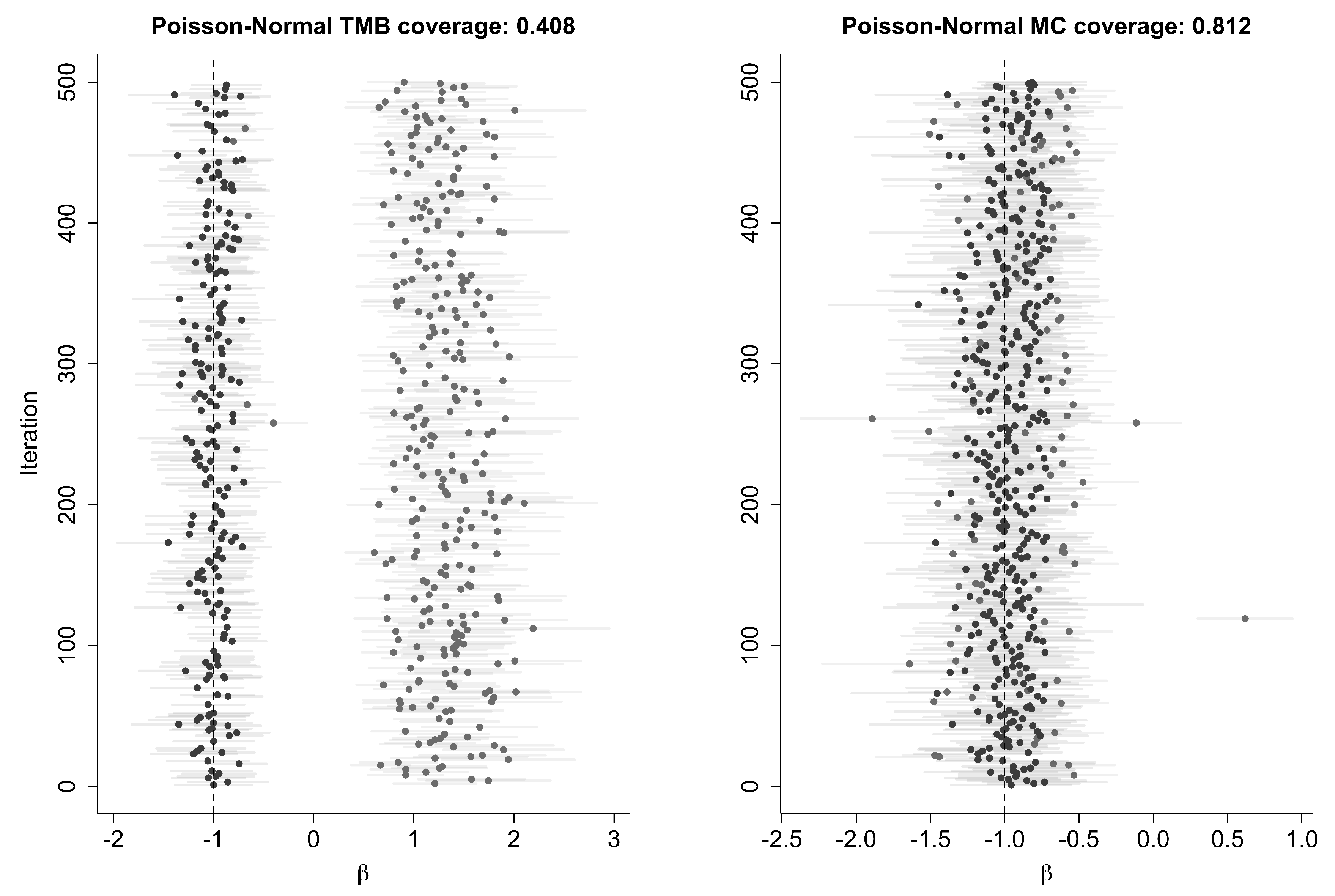
3.4. Coverage Probabilities Using LAML
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gelman, A.; Hill, J. Data Analysis Using Regression and Multilevel/Hierarchical Models; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- McCulloch, C.E.; Searle, S.R. Generalized, Linear, and Mixed Models; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Clark, J.S.; Gelfand, A.E. Hierarchical Modelling for the Environmental Sciences: Statistical Methods and Applications; OUP Oxford: Oxford, UK, 2006. [Google Scholar]
- Searle, S.R.; Casella, G.; McCulloch, C.E. Variance Components; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Robert, C. Monte Carlo Statistical Methods; Springer: New York, NY, USA, 1999. [Google Scholar]
- Plummer, M. Simulation-based Bayesian analysis. Annu. Rev. Stat. Its Appl. 2023, 10, 401–425. [Google Scholar] [CrossRef]
- Tierney, L.; Kadane, J.B. Accurate approximations for posterior moments and marginal densities. J. Am. Stat. Assoc. 1986, 81, 82–86. [Google Scholar] [CrossRef]
- Kass, R.E.; Tierney, L.; Kadane, J.B. Laplace’s method in Bayesian analysis. Contemp. Math. 1991, 115, 89–99. [Google Scholar]
- Pawitan, Y. In All Likelihood: Statistical Modelling and Inference Using Likelihood; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Thompson, E.A. Monte Carlo likelihood in genetic mapping. Stat. Sci. 1994, 9, 355–366. [Google Scholar] [CrossRef]
- Hojbejerre, M. Profile likelihood in directed graphical models from BUGS output. Stat. Comput. 2003, 13, 57–66. [Google Scholar] [CrossRef]
- Ponciano, J.M.; Taper, M.L.; Dennis, B.; Lele, S.R. Hierarchical models in ecology: Confidence intervals, hypothesis testing, and model selection using data cloning. Ecology 2009, 90, 356–362. [Google Scholar] [CrossRef]
- Lele, S.R.; Dennis, B.; Lutscher, F. Data cloning: Easy maximum likelihood estimation for complex ecological models using Bayesian Markov chain Monte Carlo methods. Ecol. Lett. 2007, 10, 551–563. [Google Scholar] [CrossRef]
- Lele, S.R.; Nadeem, K.; Schmuland, B. Estimability and likelihood inference for generalized linear mixed models using data cloning. J. Am. Stat. Assoc. 2010, 105, 1617–1625. [Google Scholar] [CrossRef]
- McCulloch, C.E. Maximum likelihood algorithms for generalized linear mixed models. J. Am. Stat. Assoc. 1997, 92, 162–170. [Google Scholar] [CrossRef]
- Lele, S.R. Profile Likelihood for Hierarchical Models Using Data Doubling. Entropy 2023, 25, 1262. [Google Scholar] [CrossRef]
- Efron, B. Bayes and likelihood calculations from confidence intervals. Biometrika 1993, 80, 3–26. [Google Scholar] [CrossRef]
- Breslow, N.E.; Clayton, D.G. Approximate inference in generalized linear mixed models. J. Am. Stat. Assoc. 1993, 88, 9–25. [Google Scholar] [CrossRef]
- Breslow, N.E.; Lin, X. Bias correction in generalised linear mixed models with a single component of dispersion. Biometrika 1995, 82, 81–91. [Google Scholar] [CrossRef]
- Lee, Y.; Nelder, J.A. Hierarchical generalized linear models. J. R. Stat. Soc. Ser. Stat. Methodol. 1996, 58, 619–656. [Google Scholar] [CrossRef]
- Meng, X.L. Decoding the h-likelihood. Stat. Sci. 2009, 24, 280–293. [Google Scholar] [CrossRef]
- Neyman, J.; Scott, E.L. Consistent estimates based on partially consistent observations. Econom. J. Econom. Soc. 1948, 16, 1–32. [Google Scholar] [CrossRef]
- Skaug, H.J.; Fournier, D.A. Automatic approximation of the marginal likelihood in non-Gaussian hierarchical models. Comput. Stat. Data Anal. 2006, 51, 699–709. [Google Scholar] [CrossRef]
- Kristensen, K.; Nielsen, A.; Berg, C.W.; Skaug, H.; Bell, B. TMB: Automatic differentiation and Laplace approximation. J. Stat. Softw. 2016, 70, 1–21. [Google Scholar] [CrossRef]
- Bolker, B.M.; Gardner, B.; Maunder, M.; Berg, C.W.; Brooks, M.; Comita, L.; Crone, E.; Cubaynes, S.; Davies, T.; de Valpine, P.; et al. Strategies for fitting nonlinear ecological models in R, AD M odel B uilder, and BUGS. Methods Ecol. Evol. 2013, 4, 501–512. [Google Scholar] [CrossRef]
- Rue, H.; Martino, S.; Chopin, N. Approximate Bayesian inference for latent Gaussian models by using integrated nested Laplace approximations. J. R. Stat. Soc. Ser. (Stat. Methodol.) 2009, 71, 319–392. [Google Scholar] [CrossRef]
- Han, J.; Lee, Y. Enhanced laplace approximation. J. Multivar. Anal. 2024, 202, 105321. [Google Scholar] [CrossRef]
- Thorson, J.; Kristensen, K. Spatio-Temporal Models for Ecologists; CRC Press: Boca Raton, FL, USA, 2024. [Google Scholar]
- Andersen, E.B. Asymptotic properties of conditional maximum-likelihood estimators. J. R. Stat. Soc. Ser. Stat. Methodol. 1970, 32, 283–301. [Google Scholar] [CrossRef]
- Godambe, V.P. An optimum property of regular maximum likelihood estimation. Ann. Math. Stat. 1960, 31, 1208–1211. [Google Scholar] [CrossRef]
- Lindsay, B. Conditional score functions: Some optimality results. Biometrika 1982, 69, 503–512. [Google Scholar] [CrossRef]
- Carroll, R.J.; Ruppert, D.; Stefanski, L.A. Measurement Error in Nonlinear Models; CRC Press: Boca Raton, FL, USA, 1995; Volume 105. [Google Scholar]
- Buonaccorsi, J.P. Measurement Error: Models, Methods, and Applications; Chapman and Hall/CRC: Boca Raton, FL, USA, 2010. [Google Scholar]
- Team, R.C. R: A Language and Environment for Statistical Computing [Computer Software]; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Plummer, M. JAGS Version 3.3. 0 User Manual; International Agency for Research on Cancer: Lyon, France, 2012. [Google Scholar]
- Sólymos, P. dclone: Data Cloning in R. R J. 2010, 2, 29–37. [Google Scholar] [CrossRef]
- Stefanski, L.A.; Carroll, R.J. Covariate measurement error in logistic regression. Ann. Stat. 1985, 13, 1335–1351. [Google Scholar] [CrossRef]
- Heydari, J.; Lawless, C.; Lydall, D.A.; Wilkinson, D.J. Bayesian hierarchical modelling for inferring genetic interactions in yeast. J. R. Stat. Soc. Ser. Appl. Stat. 2016, 65, 367–393. [Google Scholar] [CrossRef] [PubMed]
- Wakefield, J.; De Vocht, F.; Hung, R.J. Bayesian mixture modeling of gene-environment and gene-gene interactions. Genet. Epidemiol. Off. Publ. Int. Genet. Epidemiol. Soc. 2010, 34, 16–25. [Google Scholar] [CrossRef]
- Raue, A.; Kreutz, C.; Maiwald, T.; Bachmann, J.; Schilling, M.; Klingmüller, U.; Timmer, J. Structural and practical identifiability analysis of partially observed dynamical models by exploiting the profile likelihood. Bioinformatics 2009, 25, 1923–1929. [Google Scholar] [CrossRef]
- Xie, Y.; Carlin, B.P. Measures of Bayesian learning and identifiability in hierarchical models. J. Stat. Plan. Inference 2006, 136, 3458–3477. [Google Scholar] [CrossRef]
- Lele, S.R. Model complexity and information in the data: Could it be a house built on sand? Ecology 2010, 91, 3493–3496. [Google Scholar] [CrossRef] [PubMed]
- Campbell, D.; Lele, S. An ANOVA test for parameter estimability using data cloning with application to statistical inference for dynamic systems. Comput. Stat. Data Anal. 2014, 70, 257–267. [Google Scholar] [CrossRef]
- Gustafson, P. On model expansion, model contraction, identifiability and prior information: Two illustrative scenarios involving mismeasured variables. Stat. Sci. 2005, 20, 111–140. [Google Scholar] [CrossRef]
- Ponciano, J.M.; Burleigh, J.G.; Braun, E.L.; Taper, M.L. Assessing parameter identifiability in phylogenetic models using data cloning. Syst. Biol. 2012, 61, 955–972. [Google Scholar] [CrossRef]
- Dennis, B.; Ponciano, J.M.; Lele, S.R.; Taper, M.L.; Staples, D.F. Estimating density dependence, process noise, and observation error. Ecol. Monogr. 2006, 76, 323–341. [Google Scholar] [CrossRef]


| Model | Model Parameters | Inference Parameter | MC Coverage | LAML Coverage |
|---|---|---|---|---|
| Normal-Normal | , , , | 0.932 | 0.838 | |
| Normal-Normal | , , , | 0.946 | 0.846 | |
| Logit-Normal | , , | 0.995 | 0.880 | |
| Probit-Normal | , , | 0.900 | 0.908 | |
| Poisson-Normal | , | 0.836 | 0.384 | |
| Poisson-Normal | , | 0.812 | 0.408 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lele, S.R.; Glen, C.G.; Ponciano, J.M. Practical Consequences of the Bias in the Laplace Approximation to Marginal Likelihood for Hierarchical Models. Entropy 2025, 27, 289. https://doi.org/10.3390/e27030289
Lele SR, Glen CG, Ponciano JM. Practical Consequences of the Bias in the Laplace Approximation to Marginal Likelihood for Hierarchical Models. Entropy. 2025; 27(3):289. https://doi.org/10.3390/e27030289
Chicago/Turabian StyleLele, Subhash R., C. George Glen, and José Miguel Ponciano. 2025. "Practical Consequences of the Bias in the Laplace Approximation to Marginal Likelihood for Hierarchical Models" Entropy 27, no. 3: 289. https://doi.org/10.3390/e27030289
APA StyleLele, S. R., Glen, C. G., & Ponciano, J. M. (2025). Practical Consequences of the Bias in the Laplace Approximation to Marginal Likelihood for Hierarchical Models. Entropy, 27(3), 289. https://doi.org/10.3390/e27030289









