Noise and Dynamical Synapses as Optimization Tools for Spiking Neural Networks
Abstract
1. Introduction
2. Materials and Methods
2.1. The Analog XOR Task
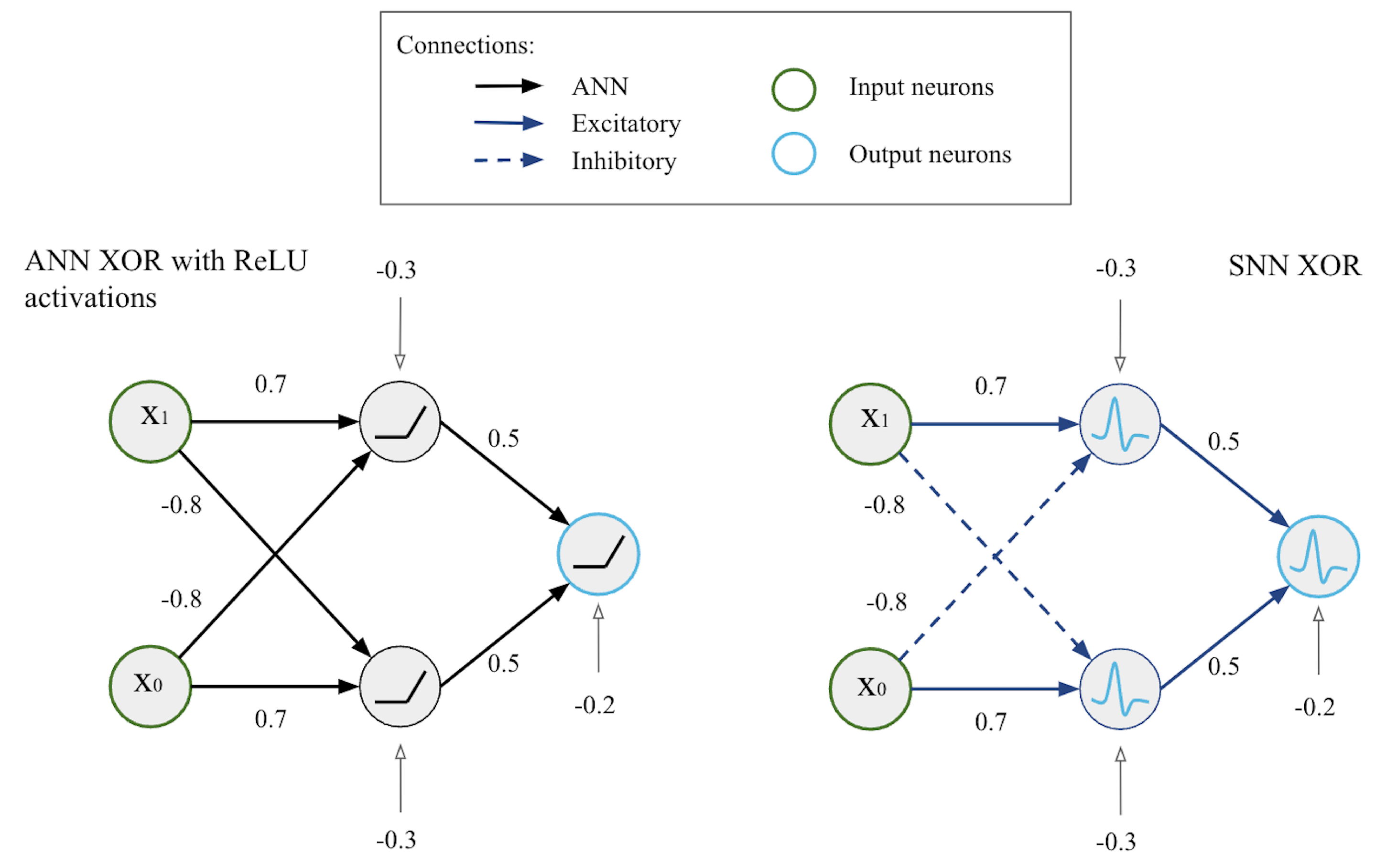
2.2. The Circuits’ Structure
2.3. Implementation of Noisy Spiking Neurons
- is the base current (18 pA) plus the biases set by the network architecture;
- is the postsynaptic input current;
- and is Gaussian white noise generated from the probability density function of normal distribution with 0 mean and standard deviation D:
- is the colored noise implemented with the Orstein–Uhlenbeck process [21]. is defined with Gaussian noise and the damping term a as
3. Results
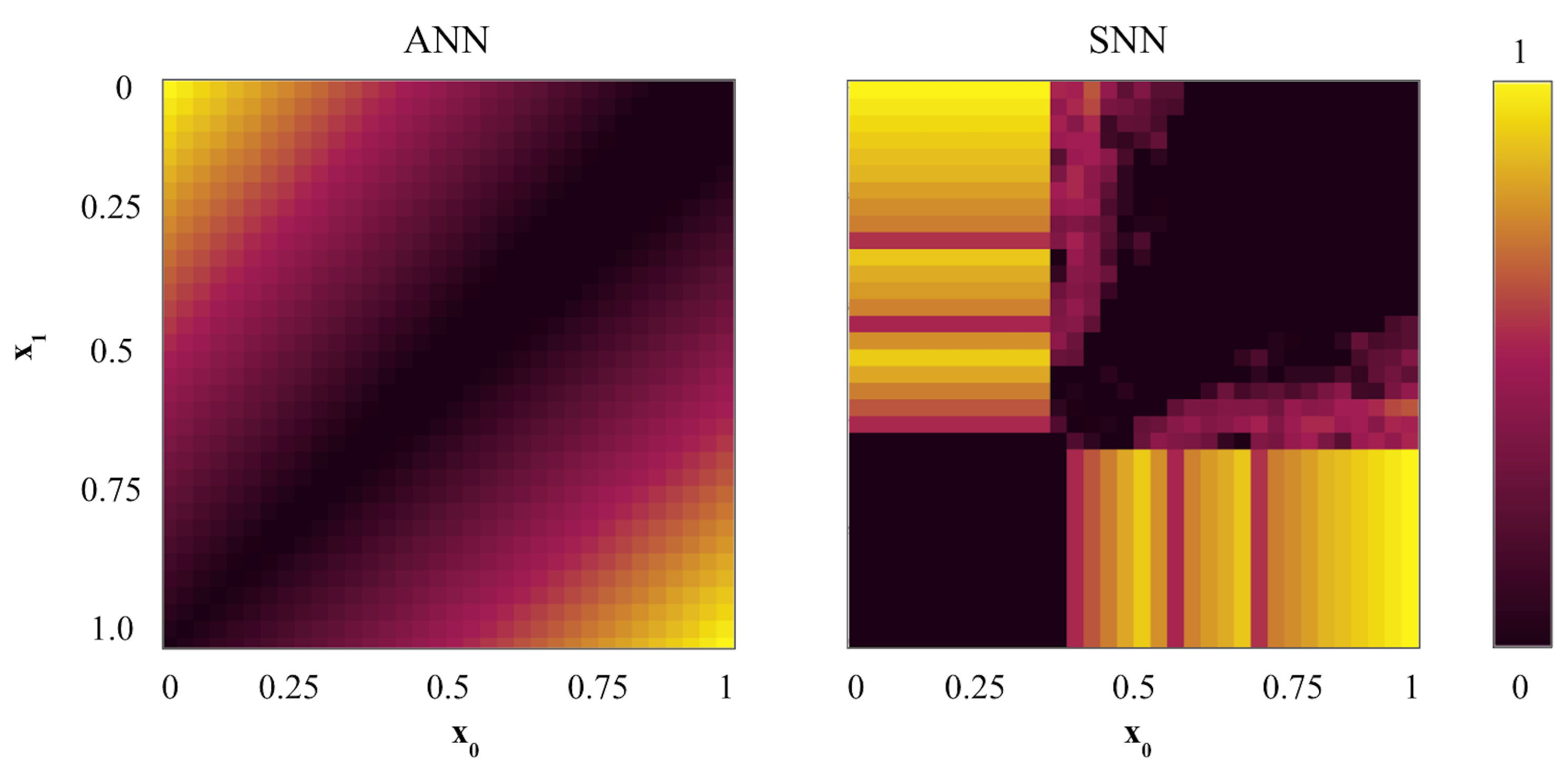
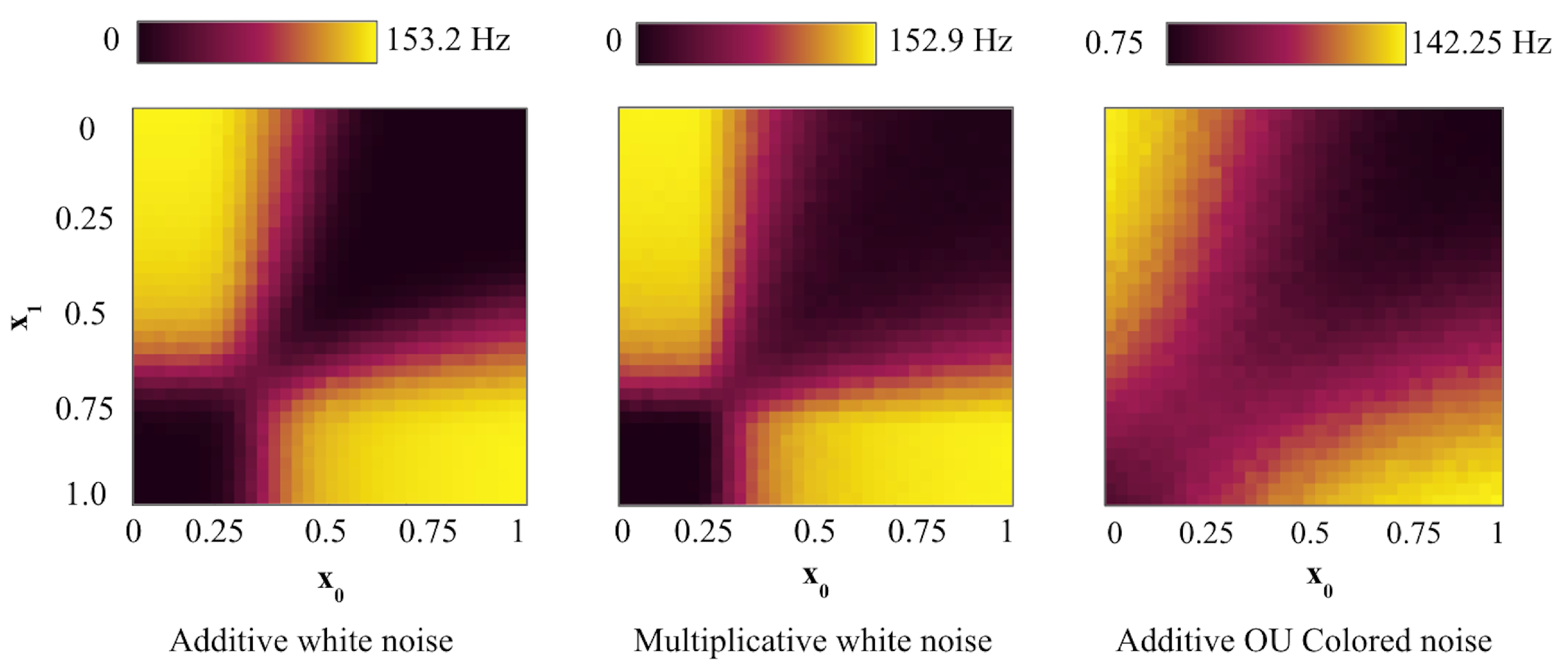
3.1. Networks Output Comparison: Non-Linear Separability with Fewer Neurons
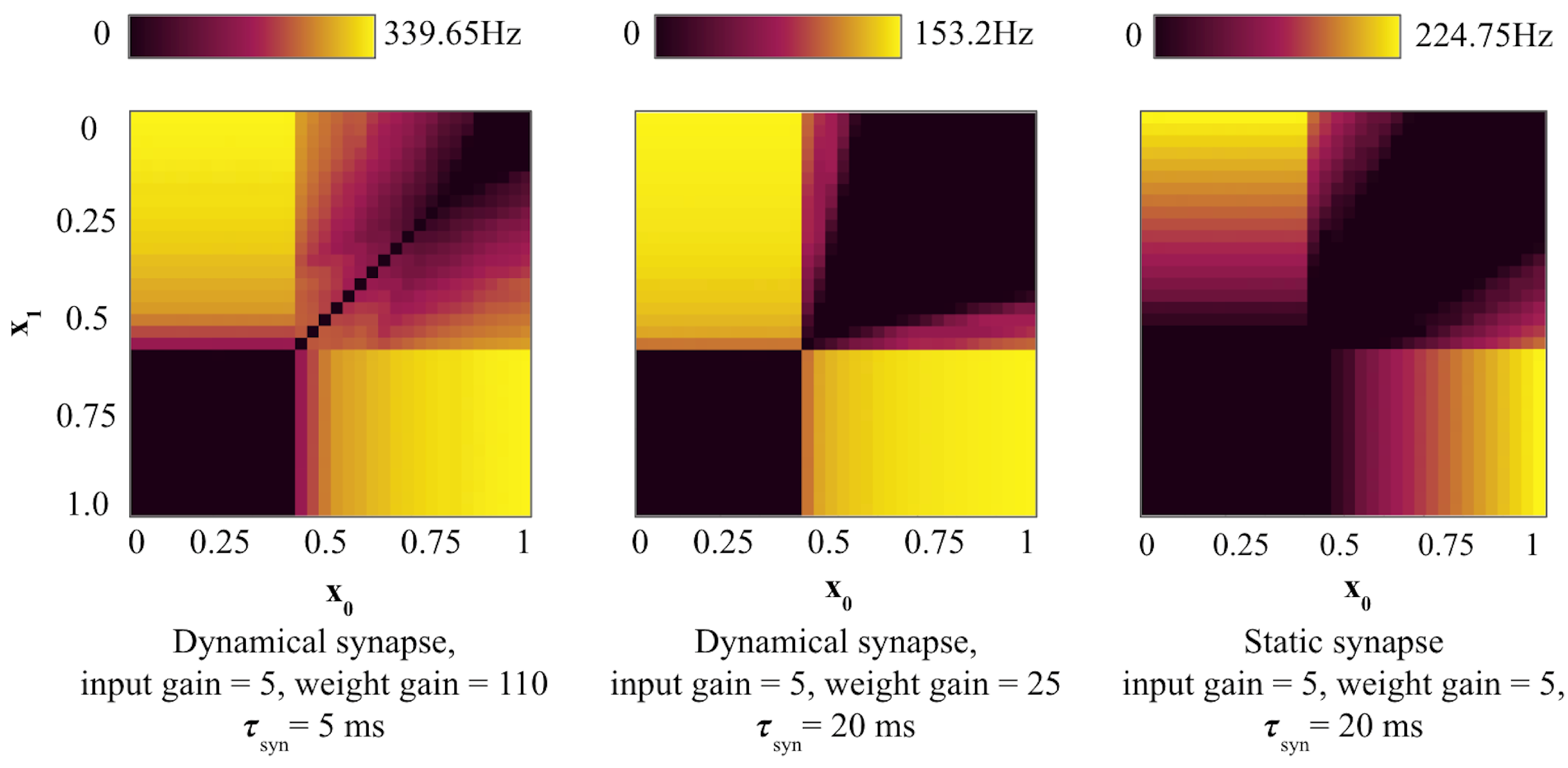
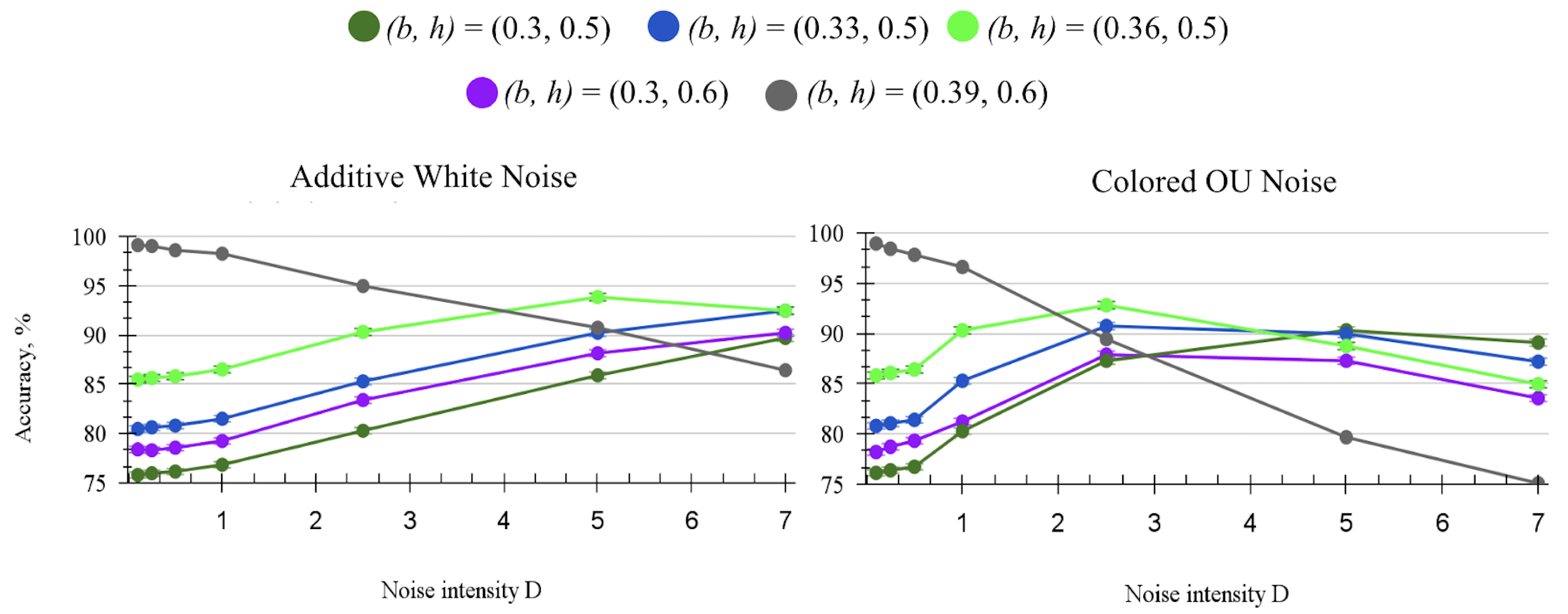
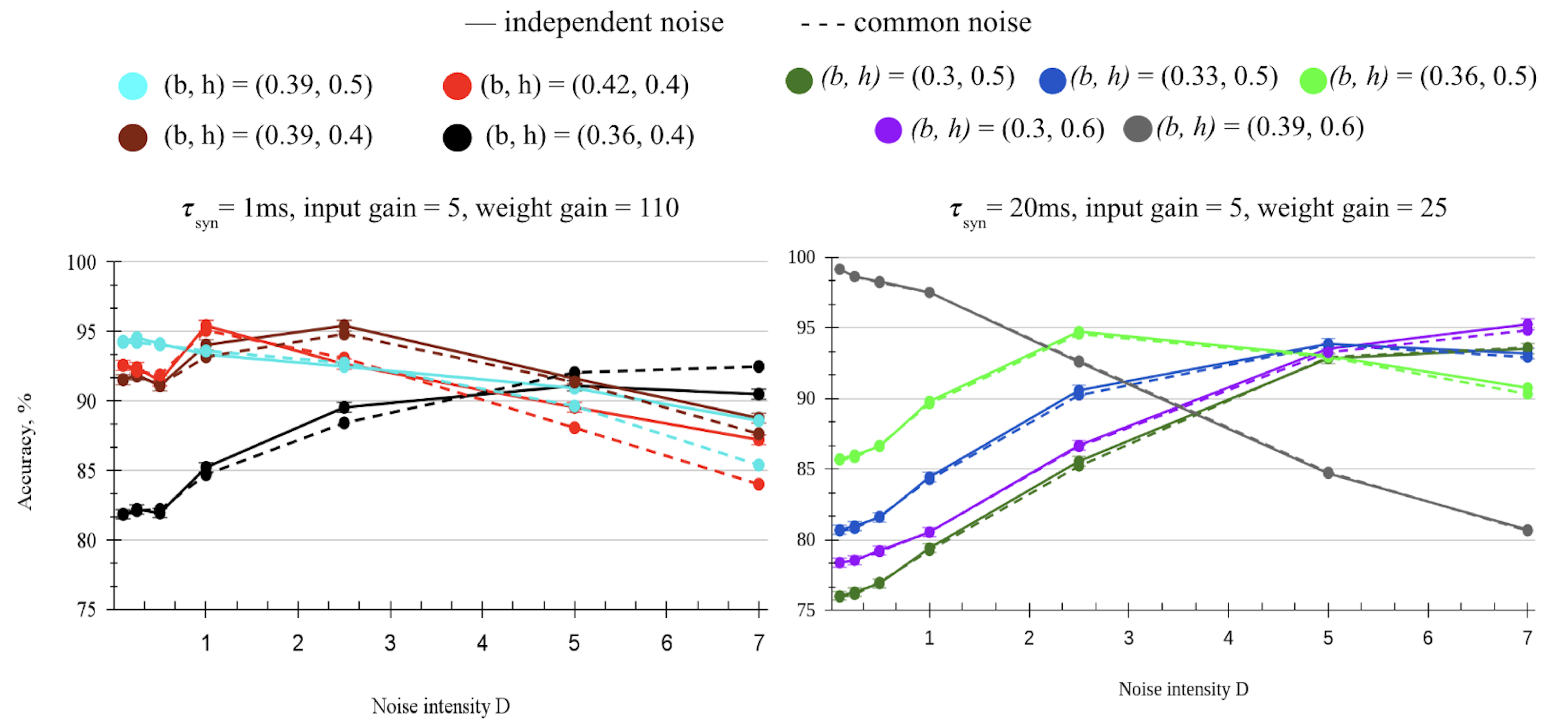
3.2. Dynamical Synapses in Leaky SNN and Their Effect on Stochastic Resonance
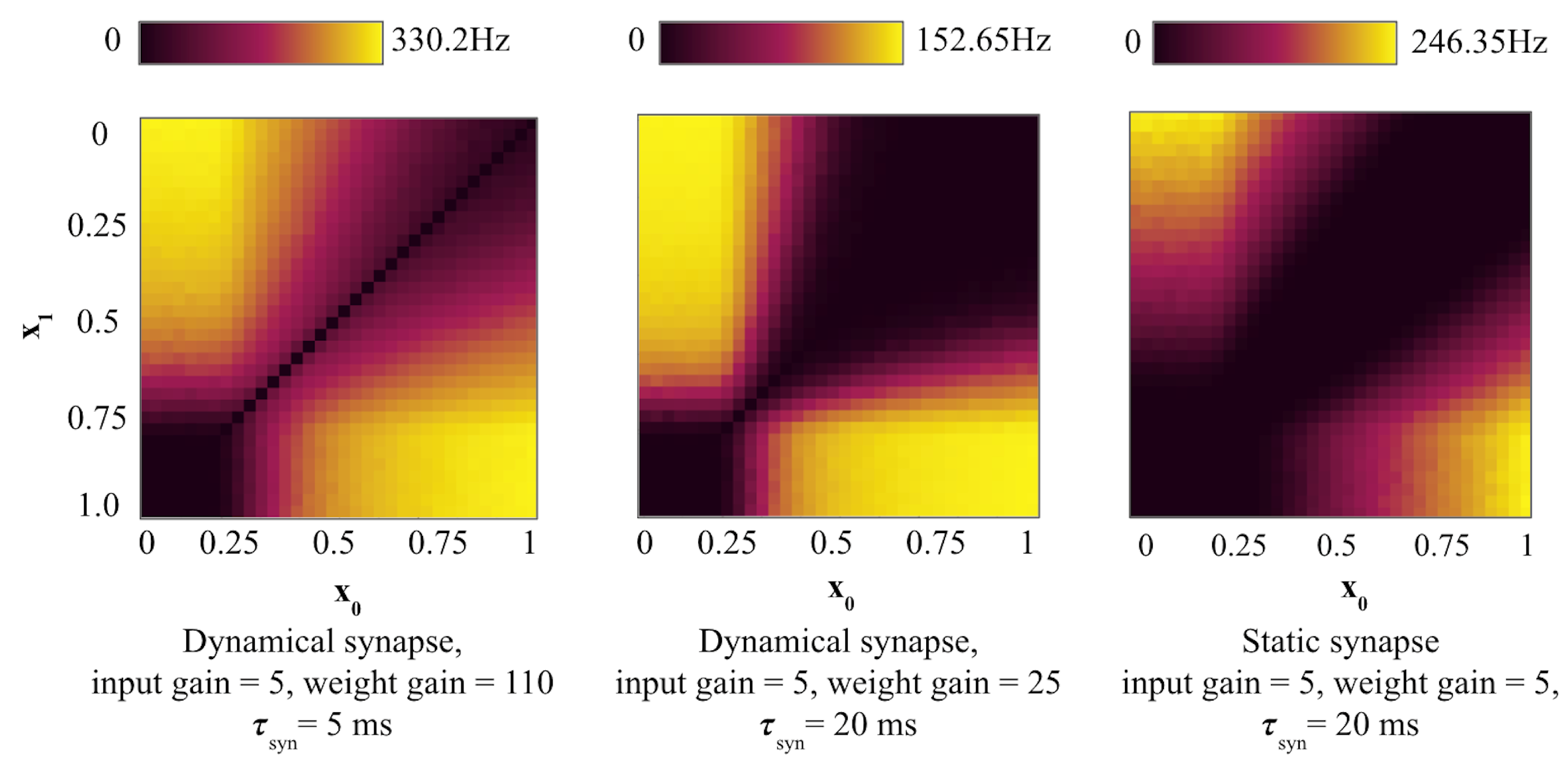
3.3. Improving Accuracy for Sub-Optimal Boundaries in Leaky Dynamic SNN with Noise-Induced Stochastic Resonance
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mead, C. Neuromorphic Engineering: In Memory of Misha Mahowald. Neural Comput. 2023, 35, 343–383. [Google Scholar] [CrossRef] [PubMed]
- Brilliant.org. Available online: https://brilliant.org/wiki/feedforward-neural-networks/ (accessed on 12 December 2024).
- Stöckl, C.; Maass, W. Optimized spiking neurons classify images with high accuracy through temporal coding with two spikes. arXiv 2021, arXiv:2002.00860. [Google Scholar] [CrossRef]
- Cao, Y.; Chen, Y.; Khosla, D. Spiking deep convolutional neural networks for energy-efficient object recognition. Int. J. Comput. Vis. 2015, 113, 54–66. [Google Scholar] [CrossRef]
- Kim, S.; Park, S.; Na, B.; Yoon, S. Spiking-YOLO: Spiking Neural Network for Energy-Efficient Object Detection. Proc. Aaai Conf. Artif. Intell. 2020, 34, 11270–11277. [Google Scholar] [CrossRef]
- Legenstein, R.; Maass, W. Ensembles of spiking neurons with noise support optimal probabilistic inference in a dynamically changing environment. PLoS Comput Biol. 2014, 10, e1003859. [Google Scholar] [CrossRef]
- Favier, K.; Yonekura, S.; Kuniyoshi, Y. Spiking neurons ensemble for movement generation in dynamically changing environments. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vegas, NV, USA, 24–29 October 2020; pp. 3789–3794. [Google Scholar]
- Rueckauer, B.; Lungu, I.A.; Hu, Y.; Pfeiffer, M.; Liu, S.C. Conversion of continuous-valued deep networks to efficient event-driven networks for image classification. Front. Neurosci. 2017, 11, 682. [Google Scholar] [CrossRef]
- Capone, C.; Muratore, P.; Paolucci, P.S. Error-based or target-based? A unified framework for learning in recurrent spiking networks. PLoS Comput. Biol. 2022, 18, e1010221. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.H.; Delbruck, T.; Pfeiffer, M. Training deep spiking neural networks using backpropagation. Front. Neurosci. 2016, 10, 508. [Google Scholar] [CrossRef]
- Lee, C.; Panda, P.; Srinivasan, G.; Roy, K. Training deep spiking convolutional neural networks with stdp-based unsupervised pre-training followed by supervised fine-tuning. Front. Neurosci. 2018, 12, 435. [Google Scholar] [CrossRef] [PubMed]
- Sacramento, J.; Costa, R.P.; Bengio, Y.; Senn, W. Dendritic cortical microcircuits approximate the backpropagation algorithm. In Proceedings of the Thirty-Second Annual Conference on Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 2–8 December 2018. [Google Scholar]
- Meulemans, A.; Carzaniga, F.S.; Suykens, J.A.K.; Sacramento, J.; Grewe, B.F. A Theoretical Framework for Target Propagation. arXiv 2020, arXiv:2006.14331. [Google Scholar]
- Nakajima, M.; Inoue, K.; Tanaka, K.; Kuniyoshi, Y.; Hashimoto, T.; Nakajima, K. Physical deep learning with biologically inspired training method: Gradient-free approach for physical hardware. Nat Commun. 2022, 13, 7847. [Google Scholar] [CrossRef]
- Bertalmío, M.; Gomez-Villa, A.; Martín, A.; Vazquez-Corral, J.; Kane, D.; Malo, J. Evidence for the intrinsically nonlinear nature of receptive fields in vision. Sci. Rep. 2020, 10, 16277. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.H. Binary Outer Product Expansion of Convolutional Kernels. IEEE J.-STSP 2020, 14, 871–883. [Google Scholar]
- Liang, H.; Gong, X.; Chen, M.; Yan, Y.; Li, W.; Gilbert, C.D. Interactions between feedback and lateral connections in the primary visual cortex. Proc Natl. Acad. Sci. USA 2017, 114, 8637–8642. [Google Scholar] [CrossRef] [PubMed]
- Faisal, A.A.; Selen, L.P.; Wolpert, D.M. Noise in the nervous system. Nat Rev. Neurosci. 2008, 9, 292–303. [Google Scholar] [CrossRef] [PubMed]
- Gerstner, W.; Kistler, W.M. Spiking Neuron Models: Single Neurons, Populations, Plasticity; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Fries, P. A mechanism for cognitive dynamics: Neuronal communication through neuronal coherence. TiCS 2005, 9, 474–480. [Google Scholar] [CrossRef] [PubMed]
- Hanggi, P.; Jung, P. Colored noise in dynamical system. Adv. Chem. Phys. 1995, 89, 239–326. [Google Scholar]
- Gewaltig, M.O.; Diesmann, M. NEST (NEural Simulation Tool). Scholarpedia 2007, 2, 1430. [Google Scholar] [CrossRef]
- Tsodyks, M.; Uziel, A.; Markram, H. Synchrony generation in recurrent networks with frequency-dependent synapses. J. Neurosci. 2000, 20, RC50. [Google Scholar] [CrossRef] [PubMed]
- Aviel, Y.; Horn, D.; Abeles, M. Synfire waves in small balanced networks. Neurocomputing 2004, 58–60, 123–127. [Google Scholar] [CrossRef]
- Reichert, D.P.; Serre, T. Neuronal synchrony in complex-valued deep networks. arXiv 2013, arXiv:1312.6115. [Google Scholar]
- Sutherland, C.; Doiron, B.; Longtin, A. Feedback-induced gain control in stochastic spiking networks. Biol. Cybern. 2009, 100, 475–489. [Google Scholar] [CrossRef] [PubMed]
- Tsodyks, M.; Wu, S. Short-term synaptic plasticity. Scholarpedia 2013, 8, 3153. [Google Scholar] [CrossRef]
- Diehl, P.U.; Neil, D.; Binas, J.; Cook, M.; Liu, S.C.; Pfeiffer, M. Fast-classifying, high-accuracy spiking deep networks through weight and threshold balancing. In Proceedings of the 2015 International Joint Conference on Neural Networks (IJCNN), Killarney, Ireland, 12–17 July 2015; pp. 1–8. [Google Scholar]
- Ventura, E.; Benedetti, M. Training neural networks with structured noise improves classification and generalization. arXiv 2023, arXiv:2302.13417. [Google Scholar]
- Abeles, M.; Hayon, G.; Lehmann, D. Modeling compositionality by dynamic binding of synfire chains. J. Comput. Neurosci. 2004, 17, 179–201. [Google Scholar] [CrossRef] [PubMed]


| Normalized | ||
|---|---|---|
| <b | <b | <h (LOW) |
| <b | ≥b | ≥h (HIGH) |
| ≥b | <b | ≥h (HIGH) |
| ≥b | ≥b | <h (LOW) |
| Code Variable | Description, Units | Value |
|---|---|---|
| C_m | Membrane capacitance, pF | 10.0 |
| tau_m | Membrane time constant, ms | 10.0 |
| E_L | Resting membrane potential, mV | 0.0 |
| V_m | Initial membrane potential, mV | 0.0 |
| V_reset | Reset potential of the membrane, mV | 16.0 |
| V_min | Lowest value for the membrane potential | −1.798 |
| refractory_input | Discard input during refractory period | False |
| I_e | Constant input current, pA | 18.0 + bias |
| V_th | Spike threshold, mV | 20.0 |
| tau_fac | Synapse facilitation time constant, ms | 1 |
| tau_rec | Synapse recovery time constant, ms | 10 |
| tau_syn | Synaptic time constant (), ms | 1 |
| t_sim | Simulation resolution, ms | 0.1 |
| T | Simulation time, s | 20.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garipova, Y.; Yonekura, S.; Kuniyoshi, Y. Noise and Dynamical Synapses as Optimization Tools for Spiking Neural Networks. Entropy 2025, 27, 219. https://doi.org/10.3390/e27030219
Garipova Y, Yonekura S, Kuniyoshi Y. Noise and Dynamical Synapses as Optimization Tools for Spiking Neural Networks. Entropy. 2025; 27(3):219. https://doi.org/10.3390/e27030219
Chicago/Turabian StyleGaripova, Yana, Shogo Yonekura, and Yasuo Kuniyoshi. 2025. "Noise and Dynamical Synapses as Optimization Tools for Spiking Neural Networks" Entropy 27, no. 3: 219. https://doi.org/10.3390/e27030219
APA StyleGaripova, Y., Yonekura, S., & Kuniyoshi, Y. (2025). Noise and Dynamical Synapses as Optimization Tools for Spiking Neural Networks. Entropy, 27(3), 219. https://doi.org/10.3390/e27030219







