Earthquake Forecasting Based on b Value and Background Seismicity Rate in Yunnan Province, China
Abstract
1. Introduction
2. Data
3. Methods
3.1. b Value Estimation
3.2. Background Seismicity Rate
3.3. Evaluation of Forecast Efficiency
4. Results
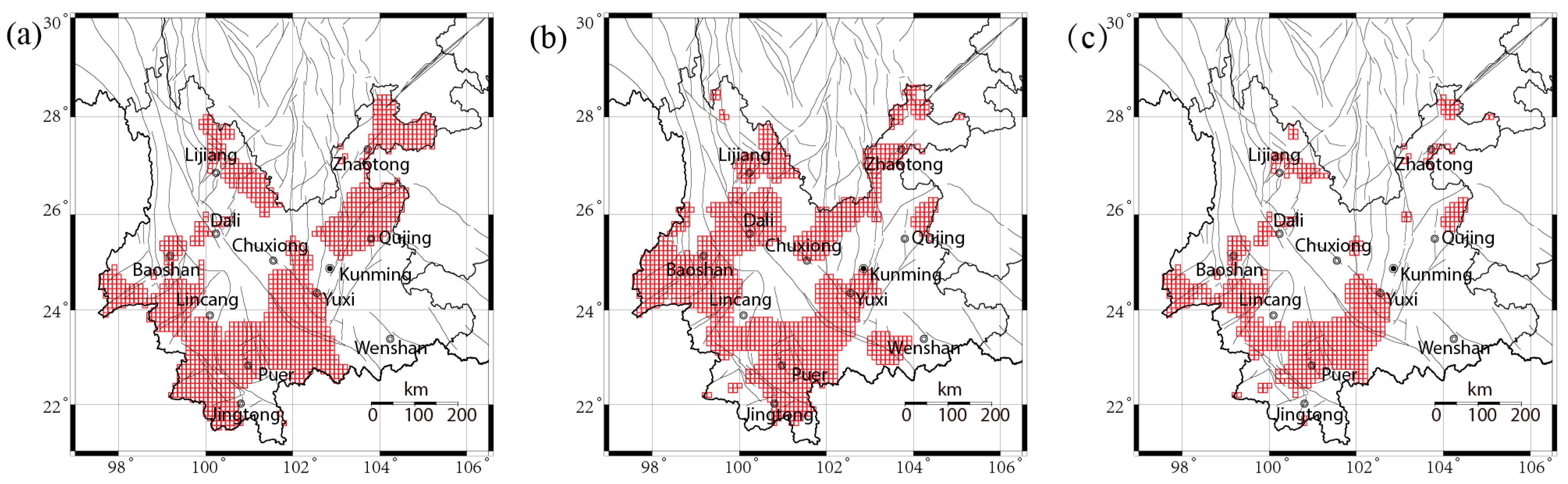
4.1. Revisit of Earthquake Prediction in 2020–2024
4.2. b Value and Background Seismicity Rate in Yunan Province
4.3. Comprehensive Forecast Performance
5. Implication and Application
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gutenberg, B.; Richter, C.F. Frequency of Earthquakes in California. Bull. Seismol. Soc. Am. 1944, 34, 185–188. [Google Scholar] [CrossRef]
- Utsu, T. A Method for Determing the Value of b in a Formula Log N=a-BM Showing the Magnitude-Frequency Relation for Earthquakes. Geophys. Bull. Hokkaido Univ. 1965, 13, 99–103. (In Japanese) [Google Scholar]
- El-Isa, Z.H.; Eaton, D.W. Spatiotemporal Variations in the B-Value of Earthquake Magnitude–Frequency Distributions: Classification and Causes. Tectonophysics 2014, 615–616, 1–11. [Google Scholar] [CrossRef]
- Nanjo, K.Z.; Hirata, N.; Obara, K.; Kasahara, K. Decade-Scale Decrease in b Value Prior to the M9-Class 2011 Tohoku and 2004 Sumatra Quakes. Geophys. Res. Lett. 2012, 39, 20304. [Google Scholar] [CrossRef]
- Shi, H.; Meng, L.; Zhang, X.; Chang, Y.; Yang, Z.; Xie, W.; Hattori, K.; Han, P. Decrease in b Value Prior to the Wenchuan Earthquake (Ms8.0). Chin. J. Geophys. 2018, 61, 1874–1882. [Google Scholar] [CrossRef]
- Kulhánek, O. Seminar on B-Value; Uppsala University: Uppsala, Sweden, 2005. [Google Scholar]
- Nuannin, P. Spatial and Temporal b Value Anomalies Preceding the Devastating off Coast of NW Sumatra Earthquake of December 26, 2004. Geophys. Res. Lett. 2005, 32, L11307. [Google Scholar] [CrossRef]
- Nanjo, K.Z.; Izutsu, J.; Orihara, Y.; Kamogawa, M. Changes in Seismicity Pattern Due to the 2016 Kumamoto Earthquake Sequence and Implications for Improving the Foreshock Traffic-Light System. Tectonophysics 2022, 822, 229175. [Google Scholar] [CrossRef]
- Huang, J.; Turcotte, D.L. Fractal Distributions of Stress and Strength and Variations of B-Value. Earth Planet. Sci. Lett. 1988, 91, 223–230. [Google Scholar] [CrossRef]
- Convertito, V.; Tramelli, A.; Godano, C. B Map Evaluation and On-Fault Stress State for the Antakya 2023 Earthquakes. Sci. Rep. 2024, 14, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Order Parameter Fluctuations in Natural Time and B-Value Variation before Large Earthquakes. Nat. Hazards Earth Syst. Sci. 2012, 12, 3473–3481. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Study of the Temporal Correlations in the Magnitude Time Series before Major Earthquakes in Japan. J. Geophys. Res. Space Phys. 2014, 119, 9192–9206. [Google Scholar] [CrossRef]
- Sarlis, N.V.; Skordas, E.S.; Varotsos, P.A.; Nagao, T.; Kamogawa, M.; Uyeda, S. Spatiotemporal Variations of Seismicity before Major Earthquakes in the Japanese Area and Their Relation with the Epicentral Locations. Proc. Natl. Acad. Sci. USA 2015, 112, 986–989. [Google Scholar] [CrossRef] [PubMed]
- Scholz, C.H. On the Stress Dependence of Earthquake b Value. Geophys. Res. Lett. 2015, 42, 1399–1402. [Google Scholar] [CrossRef]
- Wu, Y.M.; Chen, S.K.; Huang, T.C.; Huang, H.H.; Chao, W.A.; Koulakov, I. Relationship Between Earthquake B-Values and Crustal Stresses in a Young Orogenic Belt. Geophys. Res. Lett. 2018, 45, 1832–1837. [Google Scholar] [CrossRef]
- Spada, M.; Tormann, T.; Wiemer, S.; Enescu, B. Generic Dependence of the Frequency-Size Distribution of Earthquakes on Depth and Its Relation to the Strength Profile of the Crust. Geophys. Res. Lett. 2013, 40, 709–714. [Google Scholar] [CrossRef]
- Schorlemmer, D.; Wiemer, S.; Wyss, M. Variations in Earthquake-Size Distribution across Different Stress Regimes. Nature 2005, 437, 539–542. [Google Scholar] [CrossRef]
- Peng, G.; Lei, X.; Wang, G.; Jiang, F. Precursory Tidal Triggering and b Value Variation before the 2011 Mw 5.1 and 5.0 Tengchong, China Earthquakes. Earth Planet. Sci. Lett. 2021, 574, 117167. [Google Scholar] [CrossRef]
- Ito, R.; Kaneko, Y. Physical Mechanism for a Temporal Decrease of the Gutenberg-Richter b-Value Prior to a Large Earthquake. J. Geophys. Res. Solid. Earth 2023, 128, e2023JB027413. [Google Scholar] [CrossRef]
- Nanjo, K.Z. Were Changes in Stress State Responsible for the 2019 Ridgecrest, California, Earthquakes? Nat. Commun. 2020, 11, 3082. [Google Scholar] [CrossRef] [PubMed]
- Beall, A.; van den Ende, M.; Ampuero, J.P.; Capitanio, F.A.; Fagereng, Å. Linking Earthquake Magnitude-Frequency Statistics and Stress in Visco-Frictional Fault Zone Models. Geophys. Res. Lett. 2022, 49, e2022GL099247. [Google Scholar] [CrossRef]
- Molchan, G. Space—Time Earthquake Prediction: The Error Diagrams. In Seismogenesis and Earthquake Forecasting: The Frank Evison Volume II; Springer: Basel, Switzerland, 2010; pp. 53–63. [Google Scholar]
- Wang, R.; Chang, Y.; Miao, M.; Zeng, Z.; Chen, H.; Shi, H.; Li, D.; Liu, L.; Su, Y.; Han, P. Assessing Earthquake Forecast Performance Based on b Value in Yunnan Province, China. Entropy 2021, 23, 730. [Google Scholar] [CrossRef] [PubMed]
- Hainzl, S.; Kraft, T.; Wassermann, J.; Igel, H.; Schmedes, E. Evidence for Rainfall-Triggered Earthquake Activity. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Hainzl, S.; Ogata, Y. Detecting Fluid Signals in Seismicity Data through Statistical Earthquake Modeling. J. Geophys. Res. Solid. Earth 2005, 110, 1–10. [Google Scholar] [CrossRef]
- Jia, K. Modeling the Spatiotemporal Seismicity Patterns of the Longmen Shan Fault Zone Based on the Coulomb Rate and State Model. Seismol. Res. Lett. 2021, 92, 275–286. [Google Scholar] [CrossRef]
- Heimisson, E.R.; Segall, P. Constitutive Law for Earthquake Production Based on Rate-and-State Friction: Dieterich 1994 Revisited. J. Geophys. Res. Solid Earth 2018, 123, 4141–4156. [Google Scholar] [CrossRef]
- Helmstetter, A.; Shaw, B.E. Afterslip and Aftershocks in the Rate-and-State Friction Law. J. Geophys. Res. Solid. Earth 2009, 114. [Google Scholar] [CrossRef]
- Dieterich, J.H. Earthquake Nucleation on Faults with Rate-and State-Dependent Strength. Tectonophysics 1992, 211, 115–134. [Google Scholar] [CrossRef]
- Nandan, S.; Ouillon, G.; Wiemer, S.; Sornette, D. Objective Estimation of Spatially Variable Parameters of Epidemic Type Aftershock Sequence Model: Application to California. J. Geophys. Res. Solid. Earth 2017, 122, 5118–5143. [Google Scholar] [CrossRef]
- Stevens, V.L.; Avouac, J.P. On the Relationship between Strain Rate and Seismicity in the India–Asia Collision Zone: Implications for Probabilistic Seismic Hazard. Geophys. J. Int. 2021, 226, 220–245. [Google Scholar] [CrossRef]
- Kumazawa, T.; Ogata, Y.; Kimura, K.; Maeda, K.; Kobayashi, A. Background Rates of Swarm Earthquakes That Are Synchronized with Volumetric Strain Changes. Earth Planet. Sci. Lett. 2016, 442, 51–60. [Google Scholar] [CrossRef]
- Bolton, D.C.; Shreedharan, S.; Rivière, J.; Marone, C. Frequency-Magnitude Statistics of Laboratory Foreshocks Vary with Shear Velocity, Fault Slip Rate, and Shear Stress. J. Geophys. Res. Solid. Earth 2021, 126, e2021JB022175. [Google Scholar] [CrossRef] [PubMed]
- Ogata, Y. Prediction and Validation of Short-to-Long-Term Earthquake Probabilities in Inland Japan Using the Hierarchical Space–Time ETAS and Space–Time Poisson Process Models. Earth Planets Space 2022, 74, 1–12. [Google Scholar] [CrossRef]
- Ogata, Y. Statistics of Earthquake Activity: Models and Methods for Earthquake Predictability Studies. Annu. Rev. Earth Planet. Sci. 2017, 45, 497–527. [Google Scholar] [CrossRef]
- Zhuang, J. Long-Term Earthquake Forecasts Based on the Epidemic-Type Aftershock Sequence (ETAS) Model for Short-Term Clustering. Res. Geophys. 2012, 2, 8. [Google Scholar] [CrossRef]
- Xiong, Z.; Zhuang, J.; Zhou, S. Long-Term Earthquake Hazard in North China Estimated from a Modern Catalog. Bull. Seismol. Soc. Am. 2019, 109, 2340–2355. [Google Scholar] [CrossRef]
- Liu, L.; Li, Z.; Jiang, C. Research on Minimum Magnitude of Completeness for Earthquake Catalogue in Yunnan Region. J. Seismol. Res. 2012, 35, 288–293. [Google Scholar] [CrossRef]
- Ogata, Y.; Katsura, K.; Tanemura, M.; Harte, D.; Zhuang, J. Hierarchical Space-Time Point-Process Models (HIST-PPM): Software Documentation. 2020. Available online: https://bemlar.ism.ac.jp/ogata/HIST-PPM-V3/manual.pdf (accessed on 12 January 2025).
- Ogata, Y.; Imoto, M.; Katsura, K. 3-D Spatial Variation of B-Values of Magnitude-Frequency Distribution Beneath the Kanto District, Japan. Geophys. J. Int. 1991, 104, 135–146. [Google Scholar] [CrossRef]
- Ogata, Y.; Katsura, K. Analysis of Temporal and Spatial Heterogeneity of Magnitude Frequency Distribution Inferred from Earthquake Catalogues. Geophys. J. Int. 1993, 113, 727–738. [Google Scholar] [CrossRef]
- Akaike, H. Likelihood and Bayes Procedure. In Bayesian Statistics; Bernardo, J.M., Degroot, M.H., Lindley, D.V., Smith, A.F.M., Eds.; University Press: Valencia, Spain, 1980; Volume 3, pp. 143–166. [Google Scholar]
- Zhuang, J.; Ogata, Y.; Vere-Jones, D. Stochastic Declustering of Space-Time Earthquake Occurrences. J. Am. Stat. Assoc. 2002, 97, 369–380. [Google Scholar] [CrossRef]
- Molchan, G.M. Strategies in Strong Earthquake Prediction. Phys. Earth Planet. Inter. 1990, 61, 84–98. [Google Scholar] [CrossRef]
- Molchan, G.M. Structure of Optimal Strategies in Earthquake Prediction. Tectonophysics 1991, 193, 267–276. [Google Scholar] [CrossRef]
- Chen, H.; Han, P.; Hattori, K. Recent Advances and Challenges in the Seismo-Electromagnetic Study: A Brief Review. Remote Sens. 2022, 14, 5893. [Google Scholar] [CrossRef]
- Han, P.; Hattori, K.; Zhuang, J.; Chen, C.H.; Liu, J.Y.; Yoshida, S. Evaluation of ULF Seismo-Magnetic Phenomena in Kakioka, Japan by Using Molchan’s Error Diagram. Geophys. J. Int. 2017, 208, 482–490. [Google Scholar] [CrossRef]
- Gulia, L.; Wiemer, S. Real-Time Discrimination of Earthquake Foreshocks and Aftershocks. Nature 2019, 574, 193–199. [Google Scholar] [CrossRef]
- Brgmann, R. Reliable Earthquake Precursors? Science 2023, 381, 266–267. [Google Scholar] [CrossRef]
- Pulinets, S.; Herrera, V.M.V. Earthquake Precursors: The Physics, Identification, and Application. Geosciences 2024, 14, 209. [Google Scholar] [CrossRef]
- Wang, R.; Chang, Y.; Han, P.; Miao, M.; Zeng, Z.; Shi, H.; Li, D.; Liu, L.; Su, Y. Optimized Traffic Light System with AIC and Application to the 2021 M6.7 Yangbi Earthquake Sequence. Entropy 2023, 25, 759. [Google Scholar] [CrossRef]
- Han, P.; Zhuang, J.; Hattori, K.; Chen, C.-H.; Febriani, F.; Chen, H.; Yoshino, C.; Yoshida, S. Assessing the Potential Earthquake Precursory Information in ULF Magnetic Data Recorded in Kanto, Japan during 2000–2010: Distance and Magnitude Dependences. Entropy 2020, 22, 859. [Google Scholar] [CrossRef] [PubMed]
- Wessel, P.; Luis, J.F.; Uieda, L.; Scharroo, R.; Wobbe, F.; Smith, W.H.F.; Tian, D. The Generic Mapping Tools Version 6. Geochem. Geophys. Geosyst. 2019, 20, 5556–5564. [Google Scholar] [CrossRef]
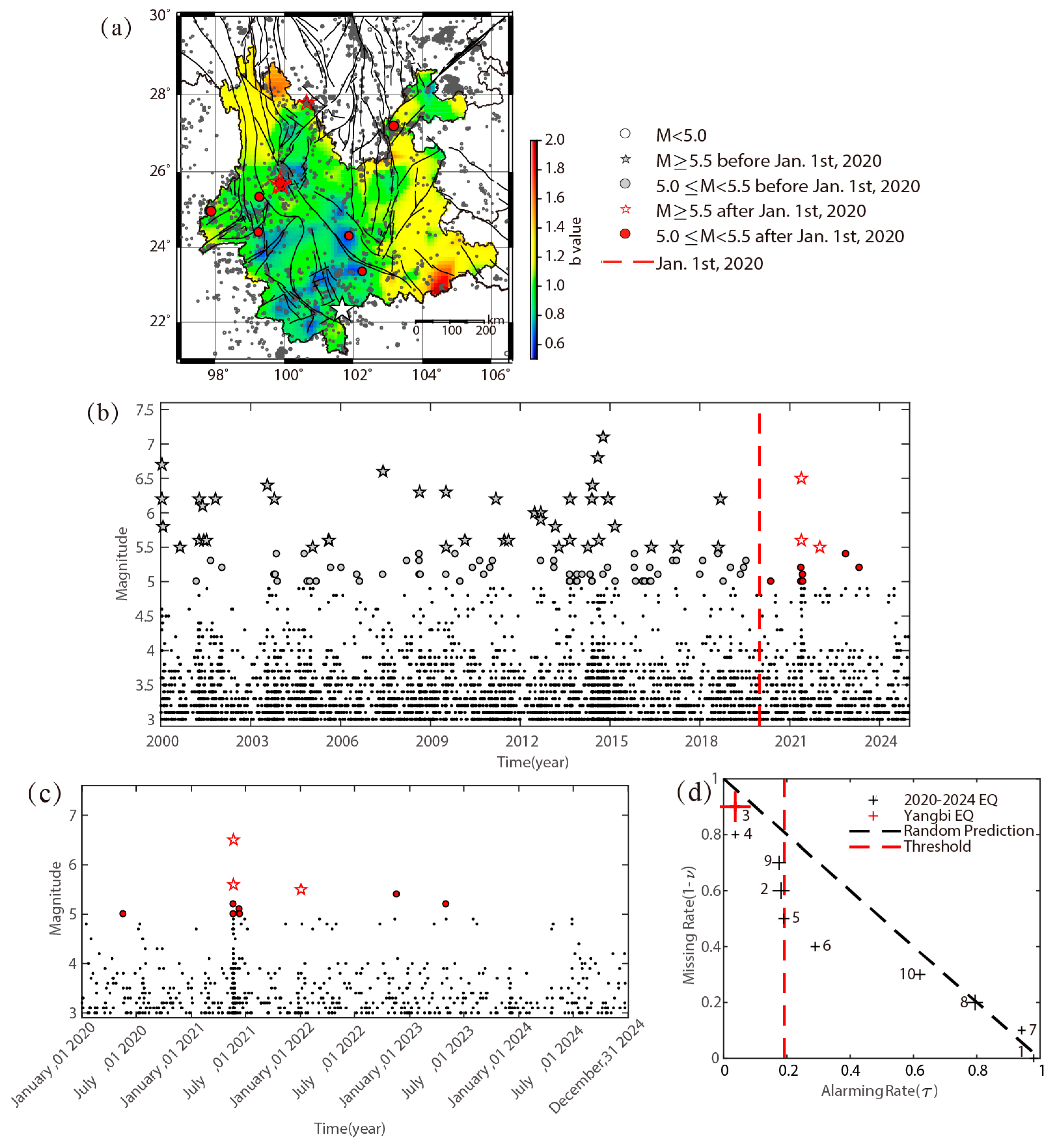
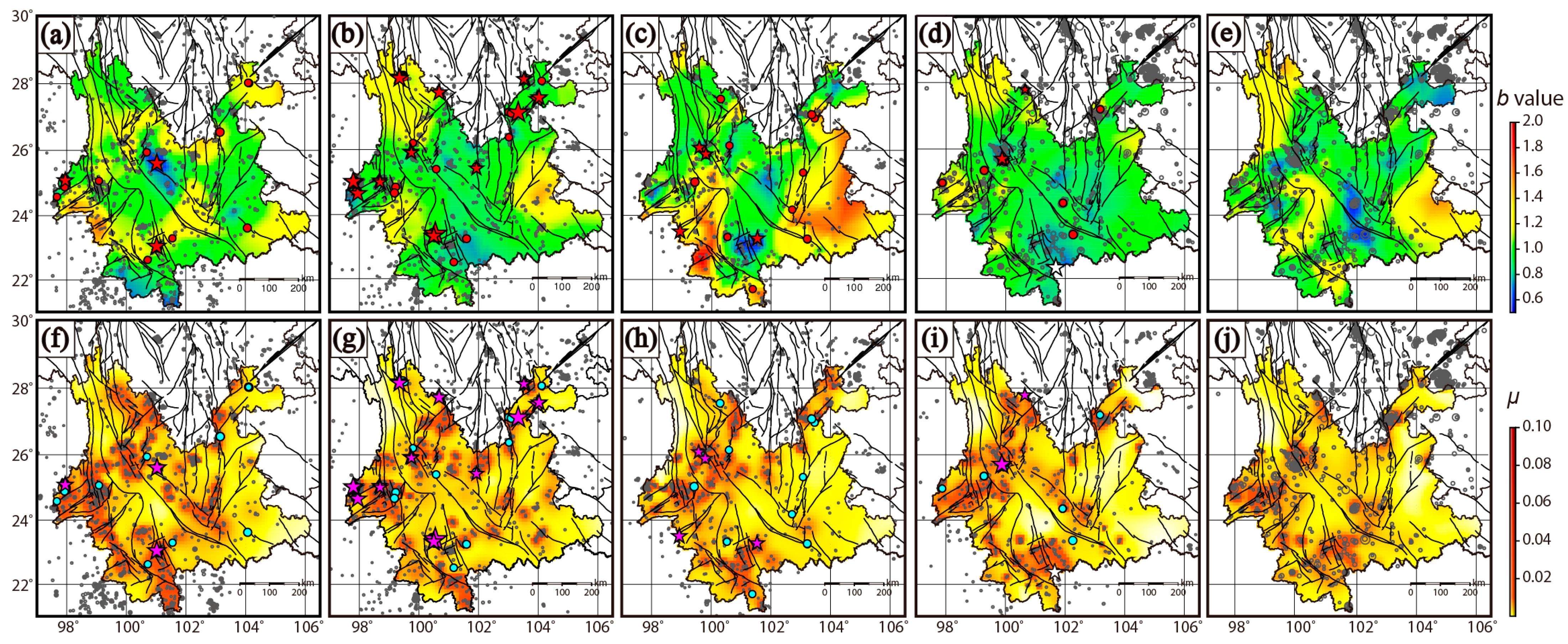
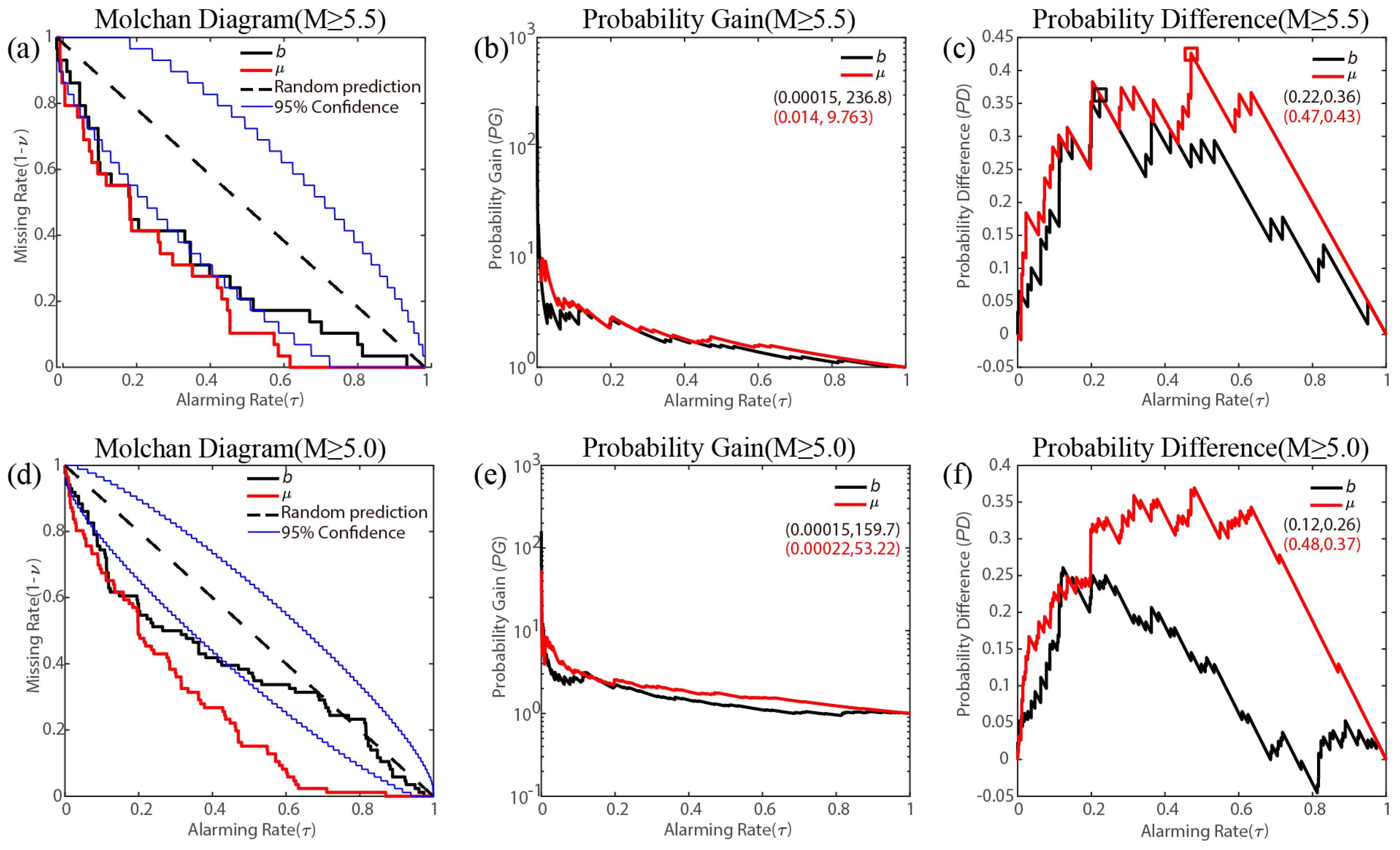
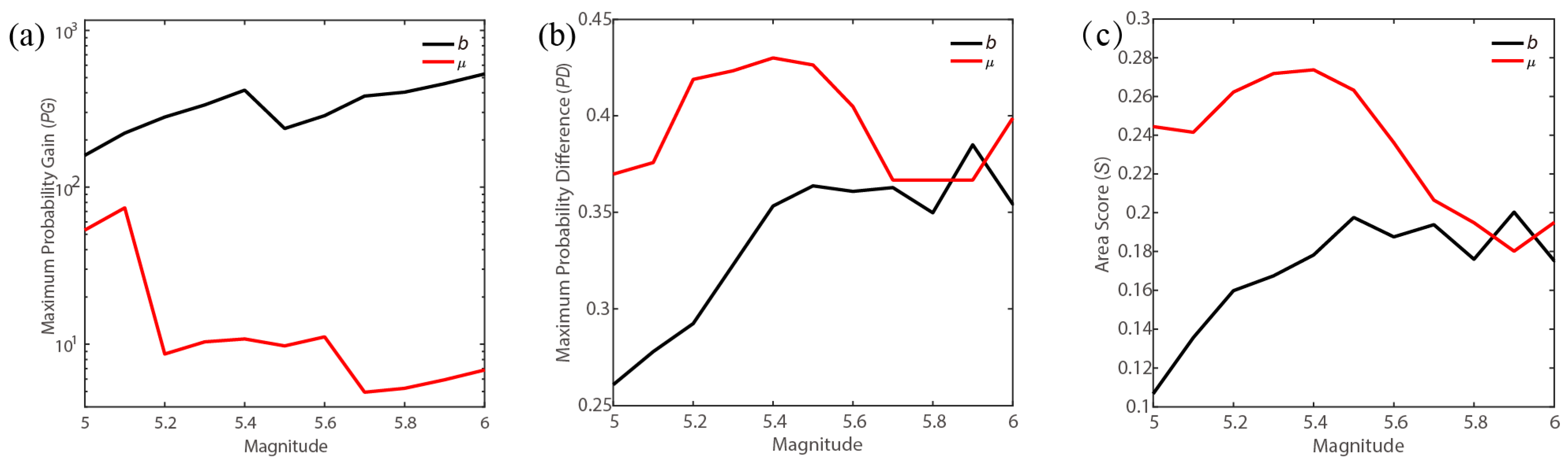
| Serial Number | Time 1 | Location | Magnitude | ||
|---|---|---|---|---|---|
| Longitude | Latitude | Depth (Km) | |||
| 1 | 2020-05-18 21:48:00 | 103.17 | 27.20 | 8 | 5.0 |
| 2 | 2021-05-21 21:21:25 | 99.92 | 25.65 | 10 | 5.6 |
| 3 | 2021-05-21 21:48:35 | 99.88 | 25.70 | 10 | 6.5 |
| 4 | 2021-05-21 21:55:29 | 99.89 | 25.67 | 10 | 5.0 |
| 5 | 2021-05-21 22:31:10 | 99.97 | 25.62 | 8 | 5.2 |
| 6 | 2021-06-10 19:46:07 | 101.92 | 24.35 | 8 | 5.1 |
| 7 | 2021-06-12 18:00:47 | 97.88 | 24.97 | 16 | 5.0 |
| 8 | 2022-01-02 15:02:07 | 100.65 | 27.79 | 10 | 5.5 |
| 9 | 2022-11-19 01:27:34 | 102.26 | 23.37 | 8 | 5.4 |
| 10 | 2023-05-02 23:27:22 | 99.28 | 25.53 | 10 | 5.2 |
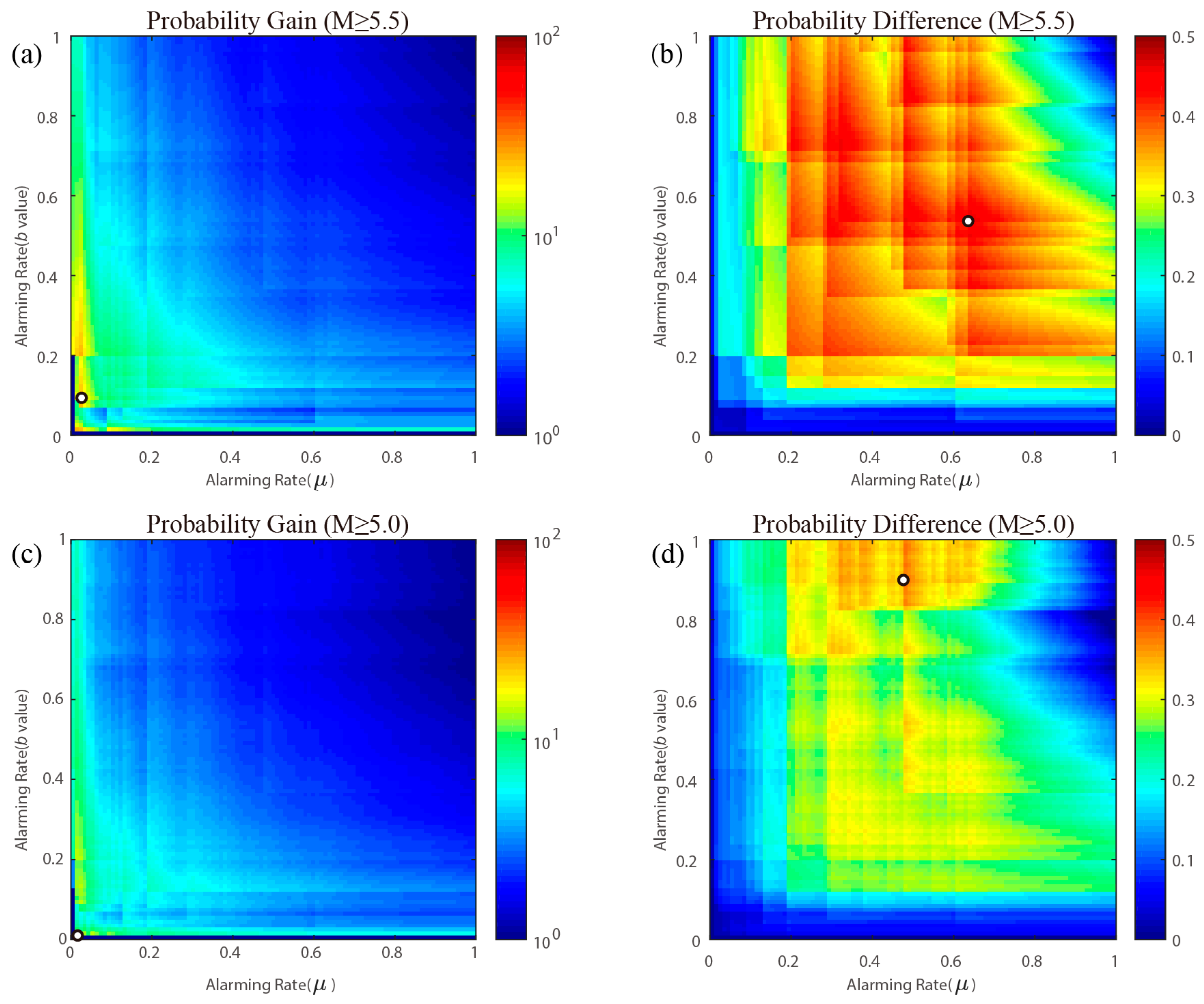
| Magnitude | Type | Maximum Value | Alarming Rate (μ) | Alarming Rate (b) | Comprehensive Alarming Rate | Comprehensive Detecting Rate |
|---|---|---|---|---|---|---|
| PG | 26.68 | 0.03 | 0.09 | 0.0052 | 0.14 | |
| PD | 0.46 | 0.64 | 0.54 | 0.36 | 0.83 | |
| PG | 16.81 | 0.02 | 0.01 | 0.0014 | 0.023 | |
| PD | 0.38 | 0.48 | 0.89 | 0.43 | 0.81 |
| Threshold | Alarming Rate | Detecting Rate | PG | Comprehensive Alarming Rate | Comprehensive Detecting Rate | Comprehensive PG | |
|---|---|---|---|---|---|---|---|
| b | 0.9056 | 0.22 | 0.58 | 2.64 | 0.13 | 0.48 | 3.69 |
| 0.0033 | 0.47 | 0.90 | 1.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Wang, R.; Shi, H.; Miao, M.; Zhuang, J.; Chang, Y.; Jiang, C.; Meng, L.; Li, D.; Liu, L.; et al. Earthquake Forecasting Based on b Value and Background Seismicity Rate in Yunnan Province, China. Entropy 2025, 27, 205. https://doi.org/10.3390/e27020205
Zhang Y, Wang R, Shi H, Miao M, Zhuang J, Chang Y, Jiang C, Meng L, Li D, Liu L, et al. Earthquake Forecasting Based on b Value and Background Seismicity Rate in Yunnan Province, China. Entropy. 2025; 27(2):205. https://doi.org/10.3390/e27020205
Chicago/Turabian StyleZhang, Yuchen, Rui Wang, Haixia Shi, Miao Miao, Jiancang Zhuang, Ying Chang, Changsheng Jiang, Lingyuan Meng, Danning Li, Lifang Liu, and et al. 2025. "Earthquake Forecasting Based on b Value and Background Seismicity Rate in Yunnan Province, China" Entropy 27, no. 2: 205. https://doi.org/10.3390/e27020205
APA StyleZhang, Y., Wang, R., Shi, H., Miao, M., Zhuang, J., Chang, Y., Jiang, C., Meng, L., Li, D., Liu, L., Su, Y., Zhang, Z., & Han, P. (2025). Earthquake Forecasting Based on b Value and Background Seismicity Rate in Yunnan Province, China. Entropy, 27(2), 205. https://doi.org/10.3390/e27020205











