NPA Hierarchy and Extremal Criterion in the Simplest Bell Scenario
Abstract
1. Introduction
2. Plausible Criterion
3. NPA Hierarchy and Simplest Bell Scenario
4. Summary
Funding
Data Availability Statement
Conflicts of Interest
References
- Bell, J. On the Einstein Podolsky Rosen paradox. Physics 1964, 1, 195. [Google Scholar] [CrossRef]
- Cirel’son, B.S. Quantum generalizations of Bell’s inequality. Lett. Math. Phys. 1980, 4, 93. [Google Scholar] [CrossRef]
- Popescu, S.; Rohrlich, D. Quantum nonlocality as an axiom. Found Phys. 1994, 24, 379–385. [Google Scholar] [CrossRef]
- Brunner, N.; Cavalcanti, D.; Pironio, S.; Scarani, V.; Wehner, S. Bell nonlocality. Rev. Mod. Phys. 2014, 86, 419. [Google Scholar] [CrossRef]
- Popescu, S. Bounds on quantum correlations in Bell-inequality experiments. Nat. Phys. 2014, 10, 264. [Google Scholar] [CrossRef]
- Oas, G.; de Barros, J.A. Contextuality from Quantum Physics to Psychology; World Scientific: Singapore, 2016; Chapter 15; pp. 335–366. [Google Scholar]
- Oppenheim, J.; Wehner, S. The Uncertainty Principle Determines the Nonlocality of Quantum Mechanics. Science 2010, 330, 1072. [Google Scholar] [CrossRef]
- Ramanathan, R.; Goyeneche, D.; Muhammad, S.; Mironowicz, P.; Grünfeld, M.; Bourennane, M.; Horodecki, P. Steering is an essential feature of non-locality in quantum theory. Nat. Commun. 2018, 9, 4244. [Google Scholar] [CrossRef] [PubMed]
- Clauser, J.F.; Horne, M.A.; Shimony, A.; Holt, R.A. Proposed Experiment to Test Local Hidden-Variable Theories. Phys. Rev. Lett. 1969, 23, 880. [Google Scholar] [CrossRef]
- Tsirelson, B.S. Quantum analogues of the Bell inequalities. The case of two spatially separated domains. J. Sov. Math. 1987, 36, 557. [Google Scholar] [CrossRef]
- Landau, L.J. Empirical Two-Point Correlation Functions. Found. Phys. 1988, 18, 449. [Google Scholar] [CrossRef]
- Masanes, L. Necessary and sufficient condition for quantum-generated correlations. arXiv 2003, arXiv:quant-ph/0309137. [Google Scholar]
- Le, T.P.; Meroni, C.; Sturmfels, B.; Wernet, R.F.; Ziegler, T. Quantum Correlations in the Minimal Scenario. Quantum 2023, 7, 947. [Google Scholar] [CrossRef]
- Acín, A.; Massar, S.; Pironio, S. Randomness versus Nonlocality and Entanglement. Phys. Rev. Lett. 2012, 108, 100402. [Google Scholar] [CrossRef] [PubMed]
- Rabelo, R.; Zhi, L.Y.; Scarani, V. Device-Independent Bounds for Hardy’s Experiment. Phys. Rev. Lett. 2012, 109, 180401. [Google Scholar] [CrossRef] [PubMed]
- Wolfe, E.; Yelin, S.F. Quantum bounds for inequalities involving marginal expectation values. Phys. Rev. A 2012, 86, 012123. [Google Scholar] [CrossRef]
- Goh, K.T.; Kaniewski, J.m.k.; Wolfe, E.; Vértesi, T.; Wu, X.; Cai, Y.; Liang, Y.C.; Scarani, V. Geometry of the set of quantum correlations. Phys. Rev. A 2018, 97, 022104. [Google Scholar] [CrossRef]
- Ishizaka, S. Necessary and sufficient criterion for extremal quantum correlations in the simplest Bell scenario. Phys. Rev. A 2018, 97, 050102, Erratum in Phys. Rev. A 2024, 109, 059903. [Google Scholar] [CrossRef]
- Mikos-Nuszkiewicz, A.; Kaniewski, J. Extremal points of the quantum set in the Clauser-Horne-Shimony-Holt scenario: Conjectured analytical solution. Phys. Rev. A 2023, 108, 012212. [Google Scholar] [CrossRef]
- Navascués, M.; Pironio, S.; Acín, A. Bounding the Set of Quantum Correlations. Phys. Rev. Lett. 2007, 98, 010401. [Google Scholar] [CrossRef]
- Navascués, M.; Pironio, S.; Acín, A. A convergent hierarchy of semidefinite programs characterizing the set of quantum correlations. New J. Phys. 2008, 10, 073013. [Google Scholar] [CrossRef]
- Navascués, M.; Vétesi, T. Bounding the set of finite dimensional quantum correlations. Phys. Rev. Lett. 2015, 115, 020501. [Google Scholar] [CrossRef] [PubMed]
- Ishizaka, S. Cryptographic quantum bound on nonlocality. Phys. Rev. A 2017, 95, 022108. [Google Scholar] [CrossRef]
- Yamashita, M.; Fujisawa, K.; Nakata, K.; Nakata, M.; Fukuda, M.; Kobayashi, K.; Goto, K. A High-Performance Software Package for Semidefinite Programs: SDPA 7; Research Report No. B-460; Department of Mathematical and Computing Science, Tokyo Institute of Technology: Tokyo, Japan, 2010. [Google Scholar]
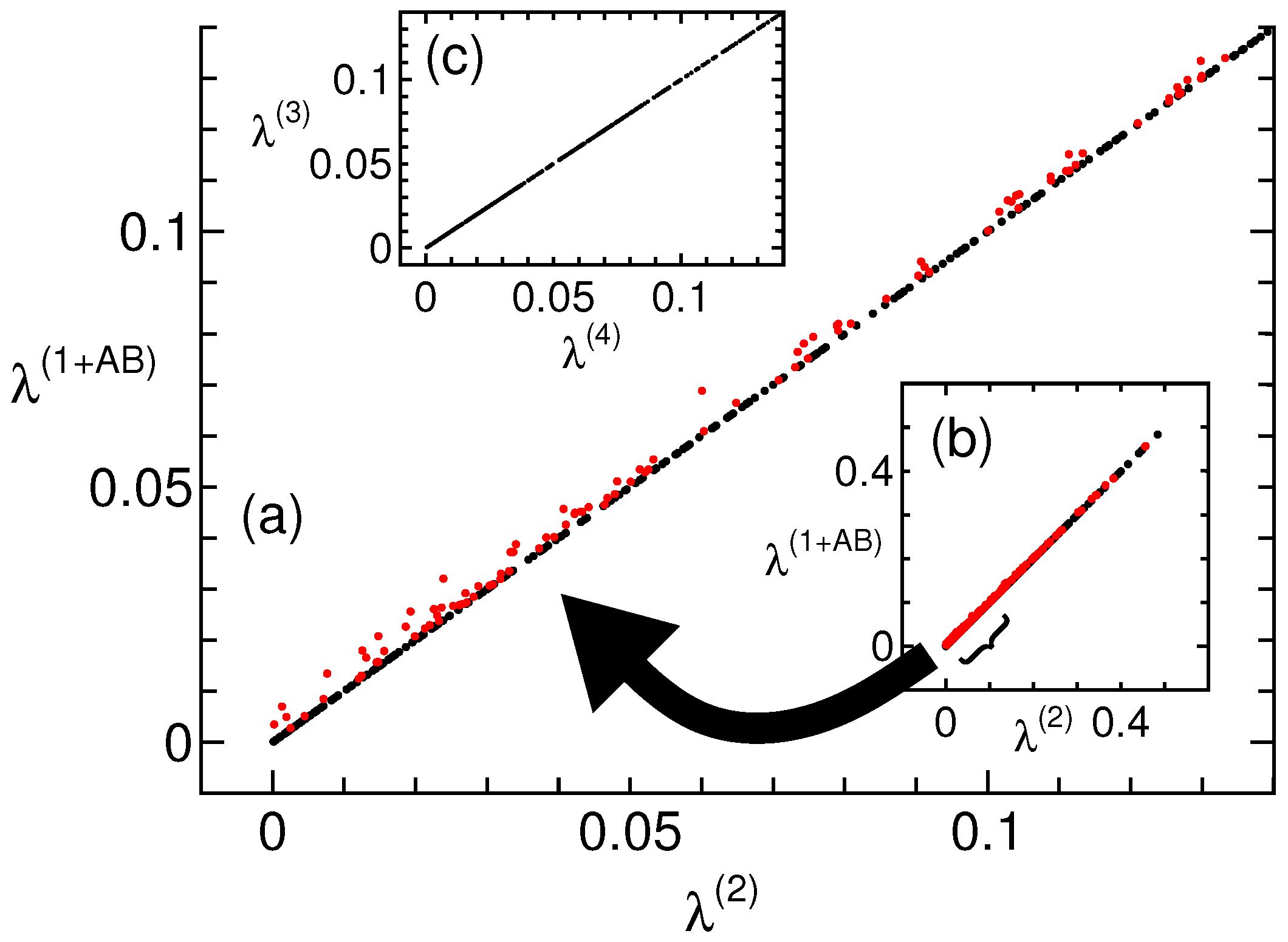
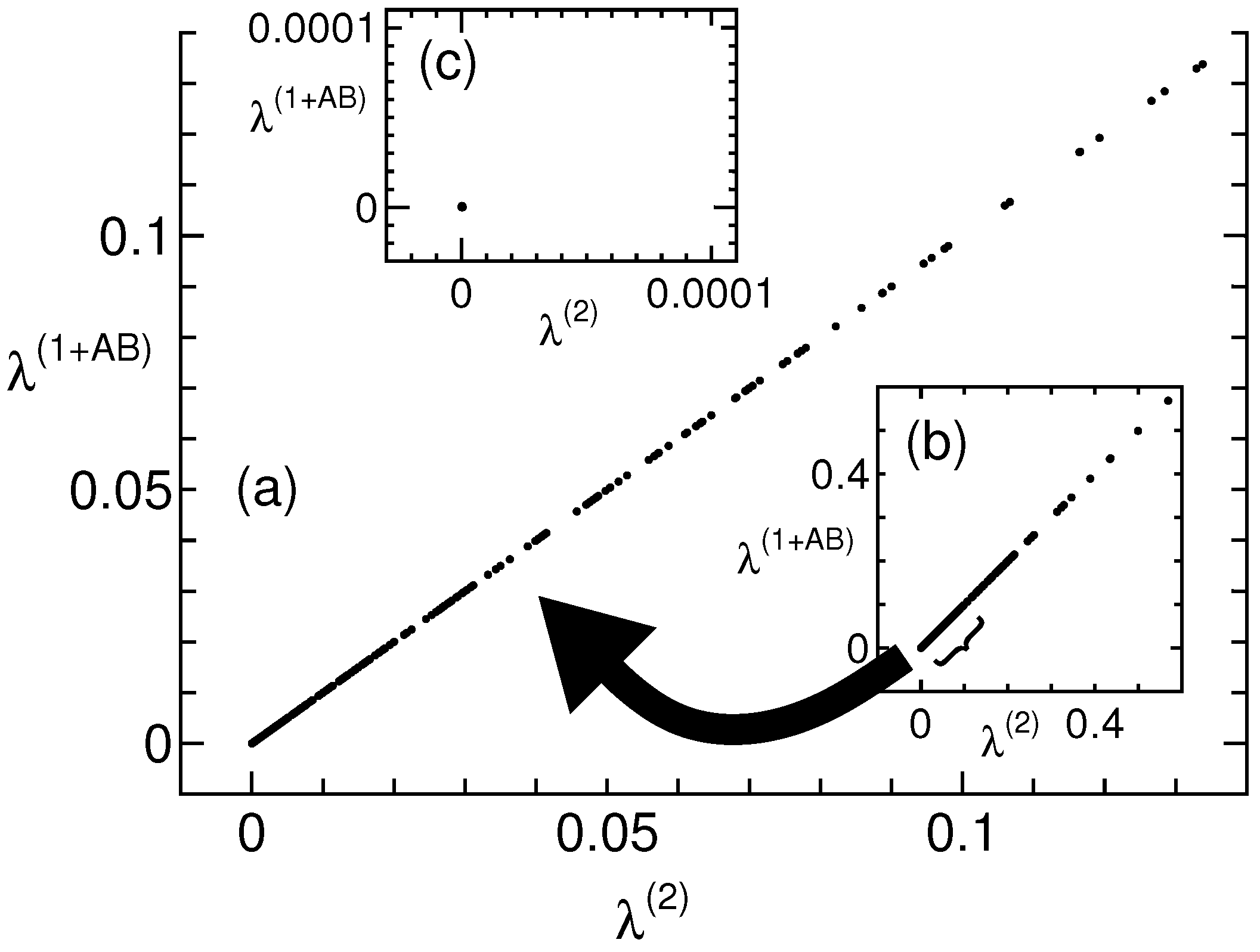
| x | 2nd | ||
|---|---|---|---|
| 0.0 | 2.82842712474619 | 2.82842712474619 | 2.82842712474619 |
| 0.4 | 2.88444102037119 | 2.88444102037119 | 2.88444102037119 |
| 0.8 | 3.04630924234556 | 3.04630924234556 | 3.04630924234556 |
| 1.2 | 3.29848450049413 | 3.29848450049413 | 3.29848450049413 |
| 1.6 | 3.62215405525497 | 3.62215405525497 | 3.62215405525497 |
| 2.0 | 4.00000000000000 | 4.00000000000000 | 4.00000000000000 |
| x | 2nd | ||
| 0.0 | 2.82842712474619 | 2.82842712474619 | 2.82842712474619 |
| 0.2 | 2.83091685885720 | 2.83091685885720 | 2.83091685885720 |
| 0.4 | 2.83923308963559 | 2.83923308963559 | 2.83923308963559 |
| 0.6 | 2.85676984164748 | 2.85676984164748 | 2.85676984164748 |
| 0.8 | 2.89417689813970 | 2.90075597099059 | 2.89417689813970 |
| 1.0 | 3.00000000000000 | 3.01789221335227 | 3.00737232088269 |
| 1.2 | 3.20000000000000 | 3.20000000000000 | 3.20000000000000 |
| 1.4 | 3.40000000000000 | 3.40000000000000 | 3.40000000000000 |
| 1.6 | 3.60000000000000 | 3.60000000000000 | 3.60000000000000 |
| 1.8 | 3.80000000000000 | 3.80000000000000 | 3.80000000000000 |
| 2.0 | 4.00000000000000 | 4.00000000000000 | 4.00000000000000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ishizaka, S. NPA Hierarchy and Extremal Criterion in the Simplest Bell Scenario. Entropy 2025, 27, 182. https://doi.org/10.3390/e27020182
Ishizaka S. NPA Hierarchy and Extremal Criterion in the Simplest Bell Scenario. Entropy. 2025; 27(2):182. https://doi.org/10.3390/e27020182
Chicago/Turabian StyleIshizaka, Satoshi. 2025. "NPA Hierarchy and Extremal Criterion in the Simplest Bell Scenario" Entropy 27, no. 2: 182. https://doi.org/10.3390/e27020182
APA StyleIshizaka, S. (2025). NPA Hierarchy and Extremal Criterion in the Simplest Bell Scenario. Entropy, 27(2), 182. https://doi.org/10.3390/e27020182






