Occupation Times on the Legs of a Diffusion Spider

Abstract

We study the joint moments of occupation times on the legs of a diffusion spider. Specifically, we give a recursive formula for the Laplace transform of the joint moments, which extends earlier results for a one-dimensional diffusion. For a Bessel spider, of which the Brownian spider is a special case, our approach yields an explicit formula for the joint moments of the occupation times.

1. Introduction

When trying to understand and quantify the behavior of a stochastic process, we are often faced with analyzing various functionals of the process. Such functionals include first passage times to subsets of the state space, maximum (minimum) value up to random/fixed times, and occupation times in subsets. The first question is, of course, whether it is possible to find the distribution of the functional. Unfortunately, this is often not possible, or the expression is too complicated to have any practical value. In some cases, the Laplace transform of the distribution is more tractable for further studies than the distribution itself. In addition, the moments of the distribution often determine the distribution uniquely via a series expansion. Hence, being able to calculate the moments is a good contribution in many respects. In this paper, we study the moments of occupation time functionals for a family of stochastic processes that we call diffusion spiders. We proceed now to explain intuitively what lies behind this notion, to give references to earlier works, and to indicate some applications.

The process known as Walsh Brownian motion was introduced by J.B. Walsh in 1978 as an extension of the skew Brownian motion. The Walsh Brownian motion lives in ${\mathbb{R}}^2$, best expressed using polar coordinates. When away from the origin, the angular coordinate stays constant (so the process moves along a line), while the radial distance follows a positive excursion from 0 of a standard Brownian motion. Intuitively and roughly speaking, every time the process reaches the origin, a new angle is randomly selected according to some distribution on $[0,2\pi )$. This process was brilliantly described by Walsh in the following way [1]:

It is a diffusion which, when away from the origin, is a Brownian motion along a ray, but which has what might be called a roundhouse singularity at the origin: when the process enters it, it, like Stephen Leacock’s hero, immediately rides off in all directions at once.

The construction of the Walsh Brownian motion was described in more detail by Barlow, Pitman, and Yor [2]. We also refer to Salisbury [3] and Yano [4].

If the angle is selected according to a discrete distribution, then there are at most countably many rays on which the diffusion lives. The state space of the process then corresponds to a star graph with edges of infinite length, and we call such a graph a spider. Thus, the Walsh Brownian motion can in this case be seen as an early example of a diffusion on a graph, and this process is called a Brownian spider. An example of a spider with five legs is given in Figure 1.

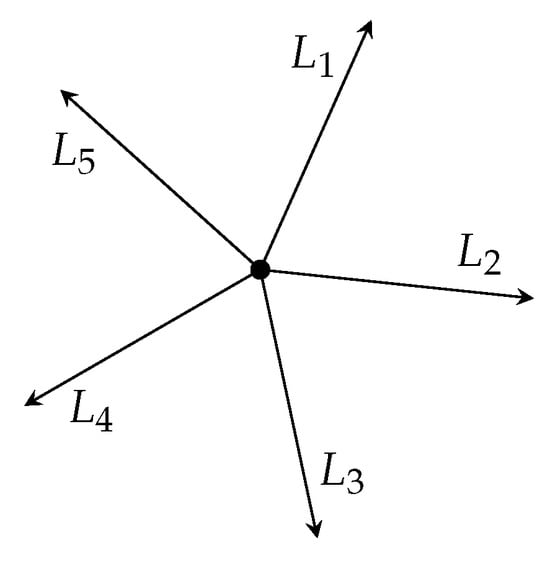
Figure 1. The graph of a diffusion spider with five legs.

To make the diffusion more general, we can relax the requirement that the radial distance follows a Brownian motion and replace it with excursions from 0 of any regular reflected non-negative recurrent one-dimensional diffusion. In this paper, such a process is simply called a diffusion spider, which can also be seen as an abbreviation for “diffusion process on a spider”. The focus of this paper is on the occupation times on the legs of a diffusion spider, that is, the amount of time that the process is located on the different legs up to a given (fixed or random) time. If the underlying diffusion is not recurrent, we could in principle still study occupation times on the legs of the spider, but the problem loses much of its interest if the process at some point is located on a single leg without ever returning to the origin. For this reason, we only consider recurrent diffusions here.

Diffusions on graphs have been subjected to intensive research at least since the pioneering work by Freidlin and Wentzell [5]. We refer to Weber [6] for earlier references, but also for a study in the direction of our paper. In addition to [1,2,7] concerning diffusions on spiders, we recall, in particular, the papers by Papanicolaou, Papageorgiou, and Lepipas [8], Vakeroudis and Yor [9], Fitzsimmons and Kuter [10], Yano [4], Csáki, Csörgő, Földes and Révész [11,12], Ernst [13], Karatzas and Yan [14], Bayraktar and Zhang [15], Lempa, Mordecki and Salminen [16], and Bednarz, Ernst and Osękowski [17].

For results on occupation times and other earlier references, see [4] where the joint law of the occupation times on legs of a diffusion spider (there called a “multiray diffusion”) is analyzed via a double Laplace transform formula generalizing the results in [7] for a spider with excursions following a Bessel process. We also refer to [4] for a formula for the density of the joint law. Refs. [8,9] consider the occupation times for a Brownian spider, and [12] focus on limit theorems for local and occupation times for the Brownian spider. One could consider other stochastic processes on a spider as well, such as random walks [11,12] or continuous-time random walks. We leave the treatment of these interesting topics for eventual future work; however, in this paper, we focus on diffusion spiders, since the methods we apply for finding moment formulas do not lend themselves to a similar treatment of discrete or jump processes. A brief overview of the work by Révész et al. on random walks of spiders and Brownian spiders is given in [18].

As mentioned above, a skew diffusion can be seen as a special case of a diffusion spider. Namely, a one-dimensional diffusion which is skew at 0 corresponds to a spider with two legs (the positive and negative half-lines), which moves like its ordinary counterpart away from zero, but whenever it hits 0, it has a certain (skewed) probability of continuing to the positive side next. Due to this close relation, some applications of diffusion spiders can be anticipated by looking at applications of skew diffusions. The skew Brownian motion, in particular, has been used in models for a large number of phenomena, such as population dynamics over a boundary, ecosystems in rivers, pollutants diffusing in rock layers, shock acceleration of charged particles, and brain imaging; references are given by Lejay [19] and Ramirez et al. [20]. See Appuhamillage et al. [21] for results on the joint distribution of occupation and local times and applications in the dispersion of a solute concentration across an interface. Exact simulations of skew Brownian motion are discussed by Lejay and Pichot [22], statistical aspects by Lejay, Mordecki, and Torres [23], and applications in financial mathematics by Alvarez and Salminen [24], Rosello [25], and Hussain et al. [26]. Furthermore, we refer to Dassios and Zhang [27] for results on hitting times of Brownian spiders and, in particular, applications in the banking business. Finally, for an application of the Brownian spider in queueing theory, see Atar and Cohen [28].

This paper is structured as follows: In the next section, some key results from the theory of linear diffusions are presented, which are crucial in order to introduce and understand the notion of a diffusion spider briefly given in this section. We recall the explicit form of the Green function (resolvent density) derived in [16]. From this expression, we can immediately deduce some regularity properties of the Green function that are important in the subsequent analysis. The basic mathematical tool of the paper is an extension of Kac’s moment formula discussed in Section 3. The first main result, i.e., a recursive formula for the joint moments of the occupation times on the legs of a diffusion spider, is given in Theorem 3, Section 4. This can be seen as an extension of our previous results for one-dimensional diffusions in [29]. In Section 4, we also present a new formula for the joint Laplace transform of the occupation times, see Theorem 4, and connect this to earlier results by Barlow et al. [7] and Yano [4]. In Section 5, some examples are discussed, and we solve (see Theorem 5) the recursive equation for the joint moments for a Bessel spider—of which the Brownian spider is a special case. This is our third main result. At the end of Section 5, we also briefly return to the original Walsh Brownian motion. The proofs of the main results are given in the Appendix A, Appendix B, Appendix C, Appendix D and Appendix E at the end of the paper.

2. Preliminaries

2.1. Linear Diffusions

To make the paper more self-contained, we first recall the basic facts from the theory of linear diffusions needed to introduce the concept of a diffusion spider. Let $X={\left(X_t\right)}_{t\ge 0}$ be a linear diffusion living on ${\mathbb{R}}_{+}=[0,+\infty )$. Let ${\mathbf{P}}_x$ denote the probability measure associated with X when initiated at $x\ge 0$. For $y\ge 0$ introduce the first the hitting time via

$$H_y:=inf\{t\ge 0:X_t=y\}.$$

It is assumed that X is regular and recurrent. Hence, for all $x\ge 0$ and $y\ge 0$ it holds that

$${\mathbf{P}}_x\left(H_y<\infty \right)=1.$$

Moreover, we suppose that 0 is a reflecting boundary and $+\infty$ is a natural boundary (for the boundary classification for linear diffusions, see [30,31]). The ${\mathbf{P}}_x$-distribution of $H_y$ is characterized for $\lambda >0$ via the Laplace transform

$${\mathbf{E}}_x\left({\mathrm{e}}^{-\lambda H_y}\right)=\left\{\begin{array}{cc}{\displaystyle \frac{{\phi }_{\lambda }\left(x\right)}{{\phi }_{\lambda }\left(y\right)}},\hfill & x\ge y,\hfill \\ {\displaystyle \frac{{\psi }_{\lambda }\left(x\right)}{{\psi }_{\lambda }\left(y\right)}},\hfill & x\le y,\hfill \end{array}\right.$$

(1)

where ${\mathbf{E}}_x$ refers to the expectation operator associated with X and ${\phi }_{\lambda }$ (${\psi }_{\lambda }$) is a positive, continuous and decreasing (increasing) solution of the generalized differential equation

$${\displaystyle \mathcal{G}u:=\frac{d}{dm}\frac{d}{dS}u=\lambda u,\lambda >0.}$$

(2)

Here, S and m denote the scale function (strictly increasing and continuous) and the speed measure, respectively, associated with X. Under our assumptions, m is a positive measure. To fix ideas, we also assume that m does not have atoms and that ${\phi }_{\lambda }$ and ${\psi }_{\lambda }$ are differentiable with respect to S. Recall that ${\phi }_{\lambda }$ and ${\psi }_{\lambda }$ are unique solutions—up to multiplicative constants—of Equation (2) with the stated properties and satisfying the associated boundary conditions. Notice also that $\mathcal{G}$, when operating in an appropriate function space, constitutes the infinitesimal generator of X. We also introduce the diffusion $X^{\partial }$ with the same speed and scale as X but for which 0 is a killing boundary. For $X^{\partial }$ there exist functions ${\phi }_{\lambda }^{\partial }$ and ${\psi }_{\lambda }^{\partial }$ describing the distribution of $H_y$ for $X^{\partial }$ similarly as is conducted in (1) for X.

Recall that

$${\psi }^{\partial }\left(0\right)=0,{\displaystyle \frac{d\psi }{dS}}(0+)=0,{\phi }^{\partial }\equiv \phi ,$$

(3)

where the notation is shortened by omitting the subindex $\lambda$. Moreover, we normalize, as in [16],

$$S\left(0\right)=0,\psi \left(0\right)=\phi \left(0\right)={\phi }^{\partial }\left(0\right)=1,\mathrm{and}{\displaystyle \frac{d{\psi }^{\partial }}{dS}}(0+)=1.$$

(4)

As is well known, X has a transition density p with respect to m, i.e., for a Borel subset A of ${\mathbb{R}}_{+}$,

$${\mathbf{P}}_x(X_t\in A)={\int }_{A}p(t;x,y)m\left(dy\right),$$

and the Green function (resolvent density) is given by

$$\begin{array}{cc}\hfill g_{\lambda }(x,y)& :={\int }_0^{\infty }{\mathrm{e}}^{-\lambda t}p(t;x,y)dt\hfill \\ \hfill & =\left\{\begin{array}{cc}{w}_{\lambda }^{-1}\psi \left(y\right)\phi \left(x\right),\hfill & 0\le y\le x,\hfill \\ w_{\lambda }^{-1}\psi \left(x\right)\phi \left(y\right),\hfill & 0\le x\le y,\hfill \end{array}\right.\hfill \end{array}$$

(5)

with the Wronskian

$$w_{\lambda }={\displaystyle \frac{d\psi }{dS}}\left(x\right)\phi \left(x\right)-{\displaystyle \frac{d\phi }{dS}}\left(x\right)\psi \left(x\right)=-{\displaystyle \frac{d\phi }{dS}}(0+).$$

For later use, recall that a diffusion X with starting point $X_0=0$ is called self-similar if for any $a>0$ there exists $b>0$ such that

$${\left(X_{at}\right)}_{t\ge 0}\stackrel{\left(d\right)}{=}{\left(b{X}_t\right)}_{t\ge 0}.$$

Perhaps the most well-known example of a self-similar diffusion is a standard Brownian motion starting in 0, for which the above identity holds with $b=\sqrt{a}$.

2.2. Diffusion Spider

Let $\Gamma \subset {\mathbb{R}}^2$ be a star graph with one vertex at the origin of ${\mathbb{R}}^2$ and R edges of infinite length meeting in the vertex (see Figure 1 for an example). Here, such a graph is called a spider. The edges $L_1,\dots ,L_R$ of the graph are known as the “rays” or—as hereafter called—the “legs” of the spider. The ordered pair $(x,i)$ describes the point on $\Gamma$ located on leg $L_i$ ($i=1,\dots ,R$) at the distance $x\ge 0$ to the origin. We take the origin to be common to all legs, i.e.,

$$(0,1)=(0,2)=\cdots =(0,R),$$

so for simplicity we just write $\mathbf{0}$ for the origin.

Let X be the linear diffusion introduced above. On the graph $\Gamma$ we consider a stochastic process $\mathbf{X}:={\left({\mathbf{X}}_t\right)}_{t\ge 0}$ using the notation

$${\mathbf{X}}_t:=(X_t,{\rho }_t),$$

where ${\rho }_t\in \{1,2,\dots ,R\}$ indicates the leg on which ${\mathbf{X}}_t$ is located at time t and $X_t$ is the distance of ${\mathbf{X}}_t$ to the origin at time t measured along the leg $L_{{\rho }_t}$. On each leg $L_i$, the process $\mathbf{X}$ behaves like the diffusion X until it hits $\mathbf{0}$. The process $\mathbf{X}$ is called a (homogeneous) diffusion spider. We could allow different diffusions on the different legs (the inhomogeneous case), but do not perform so in this paper. As part of the definition of the process, there are positive real numbers ${\beta }_i$, $i=1,\dots ,R$, such that ${\sum }_{i=1}^R{\beta }_i=1$. When $\mathbf{X}$ hits $\mathbf{0}$, it continues, roughly speaking, with probability ${\beta }_i$ onto leg $L_i$. We do not here discuss the rigorous construction of the process, which can be performed, e.g., applying excursion theory; for this and other approaches, see the references given in the introduction. Notations ${\mathbf{P}}_{(x,i)}$ and ${\mathbf{E}}_{(x,i)}$ are used for the probability measure and expectation, respectively, when the diffusion spider starts at point $(x,i)$, that is, on leg number i and at a distance x from the origin. As mentioned above, we write ${\mathbf{P}}_{\mathbf{0}}$ and ${\mathbf{E}}_{\mathbf{0}}$ without specifying a leg when the starting point is the origin.

For the diffusion spider $\mathbf{X}$, we introduce its Green kernel (also called the resolvent kernel) via

$${\mathbf{G}}_{\lambda }u(x,i):={\int }_0^{\infty }{e}^{-\lambda t}{\mathbf{E}}_{(x,i)}\left(u\left({\mathbf{X}}_t\right)\right)dt,$$

where $(x,i)\in \Gamma$, $\lambda >0$ and $u:\Gamma \to \mathbb{R}$ is a bounded measurable function. Moreover, define

$$\begin{array}{cc}\hfill & \mathbf{m}(dx,i):={\beta }_{i}m\left(dx\right),i=1,\dots ,R,\mathbf{m}\left(\left\{\mathbf{0}\right\}\right):=0,\hfill \\ \hfill & \mathbf{S}(dx,i):={\displaystyle \frac{1}{{\beta }_i}}S\left(x\right).\hfill \end{array}$$

(6)

We call $\mathbf{m}$ and $\mathbf{S}$ the speed measure and the scale function, respectively, of $\mathbf{X}$. Clearly, on every leg $L_i$ of the diffusion spider,

$${\displaystyle \frac{d}{d\mathbf{m}}}{\displaystyle \frac{d}{d\mathbf{S}}}={\displaystyle \frac{d}{dm}}{\displaystyle \frac{d}{dS}}.$$

Let $H_{\mathbf{0}}=inf\{t\ge 0:{\mathbf{X}}_t=\mathbf{0}\}$ be the first hitting time of $\mathbf{0}$ for the diffusion spider $\mathbf{X}$. Since on every leg of the diffusion spider we have, loosely speaking, the same one-dimensional diffusion, for every $i=1,2,\dots ,R$ and $x>0$,

$${\mathbf{E}}_{(x,i)}\left({\mathrm{e}}^{-\lambda H_{\mathbf{0}}}\right)={\mathbf{E}}_x\left({\mathrm{e}}^{-\lambda H_0}\right)={\phi }_{\lambda }\left(x\right).$$

(7)

The following theorem, proved in [16], states an explicit expression for the resolvent density of $\mathbf{X}$.

Theorem 1. 

The Green kernel of the diffusion spider $\mathbf{X}$ has a density ${\mathbf{g}}_{\lambda }$ with respect to the speed measure $\mathbf{m}$, which is given for $x\ge 0$ and $y\ge 0$ by

$${\mathbf{g}}_{\lambda }((x,i),(y,j))=\left\{\begin{array}{cc}\phi \left(y\right)\tilde{\psi }(x,i),\hfill & x\le y,i=j,\hfill \\ \phi \left(x\right)\tilde{\psi }(y,i),\hfill & y\le x,i=j,\hfill \\ c_{\lambda }^{-1}\phi \left(y\right)\phi \left(x\right),\hfill & i\ne j,\hfill \end{array}\right.$$

(8)

where

$$\tilde{\psi }(x,i):={\displaystyle \frac{1}{{\beta }_i}}{\psi }^{\partial }\left(x\right)+{\displaystyle \frac{1}{c_{\lambda }}}\phi \left(x\right)$$

(9)

and

$$c_{\lambda }:=-{\displaystyle \frac{d}{dS}}\phi (0+)>0.$$

(10)

From the properties of the functions ${\psi }^{\partial }$ and $\phi$, we immediately have the following result.

Corollary 1. 

The resolvent density (the Green function) ${\mathbf{g}}_{\lambda }$ given in (8) is continuous on Γ, and for every i and j,

$$\underset{(x,i)\to \mathbf{0}}{lim}{\mathbf{g}}_{\lambda }((x,i),(y,j))={\mathbf{g}}_{\lambda }(\mathbf{0},(y,j))={\displaystyle \frac{1}{c_{\lambda }}}\phi \left(y\right)=g_{\lambda }(0,y).$$

(11)

3. Kac’s Moment Formula

The tool that we will use to obtain the recursive expression for the joint moments is an extended variant of the Kac moment formula. Let Y be a regular diffusion taking values on an interval E. In spite of some conflict with our earlier notation, here we also let m, p, and ${\mathbf{E}}_x$ ($x\in E$) denote the speed measure, the transition density and the expectation operator, respectively, associated with Y. Moreover, let $V:E\mapsto \mathbb{R}$ be a measurable and bounded function and define for $t>0$ the additive functional

$$A_t\left(V\right):={\int }_0^{t}V\left(Y_s\right)\mathrm{d}s.$$

The moment formula by M. Kac for integral functionals, see [32], i.e.,

$${\mathbf{E}}_x\left({\left(A_t\left(V\right)\right)}^n\right)=n{\int }_{E}m\left(\mathrm{d}y\right){\int }_0^{t}p(s;x,y)V\left(y\right){\mathbf{E}}_y\left({\left(A_{t-s}\left(V\right)\right)}^{n-1}\right)\mathrm{d}s,$$

is here extended into the following formula for the expected value of a product of powers of different functionals.

Proposition 1. 

Let $V_1,\dots ,V_N$ be measurable and bounded functions on E. For $t>0$, $x\in E$ and $n_1,\dots ,n_N\in \{1,2,\dots \}$,

$${\mathbf{E}}_x\left(\prod _{k=1}^N{\left(A_t\left(V_k\right)\right)}^{n_k}\right)=\sum _{k=1}^N{n}_k{\int }_{E}m\left(\mathrm{d}y\right){\int }_0^{t}p(s;x,y)V_k\left(y\right){\mathbf{E}}_y\left({\displaystyle \frac{{\prod }_{i=1}^N{\left(A_{t-s}\left(V_i\right)\right)}^{n_i}}{A_{t-s}\left(V_k\right)}}\right)\mathrm{d}s.$$

(12)

Proof. 

See Appendix A.

The Formula in (12) is instrumental in the derivation of the results in Theorems 3 and 4 presented in Section 4.2.

4. Main Results

Let ${\left({\mathbf{X}}_t\right)}_{t\ge 0}$ be a diffusion spider with $R\ge 2$ legs meeting in the point $\mathbf{0}$, and let

$$A_t^{\left(i\right)}:={\int }_0^t{\mathbb{1}}_{L_i}\left(X_s\right)\mathrm{d}s$$

be the occupation time on leg number i up to time t. Note that if the underlying diffusion X is self-similar, it follows for any i and any fixed $t\ge 0$ that

$$A_t^{\left(i\right)}\stackrel{\left(\mathrm{d}\right)}{=}t{A}_1^{\left(i\right)},$$

meaning that for any such diffusion spider, we can equally well consider the occupation time up to time 1 instead of a general (fixed) time t.

Figure 2 shows the radial distance from $\mathbf{0}$ as a function of time in a sample path of a Brownian spider with five legs. The excursions from $\mathbf{0}$ are colored to specify which leg the process is located on.

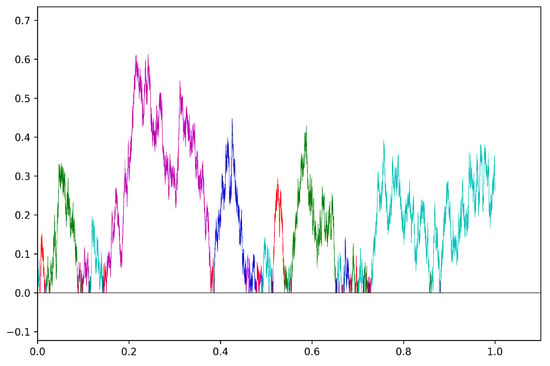
Figure 2. Sample path of the radial distance in a Brownian spider with five legs up to time 1. The five different colors indicate on which leg of the spider the process is located at any given time.

In this section we present formulas for recursively finding the moments of occupation times on the legs of a diffusion spider. In the first and shorter subsection we recapitulate the result for moments of a single occupation time, which is presented in our earlier paper [29]. In the second subsection this result is extended to joint moments of multiple occupation times.

4.1. Moments of the Occupation Time on a Single Leg

As pointed out in Section 6.4 of [29], the occupation time on a single leg $L_i$ of a (homogeneous) diffusion spider has the same law as the occupation time on the positive half-line of a one-dimensional skew diffusion process with the state space $\mathbb{R}$ and with the skewness parameter given by ${\beta }_i$. Namely, the spider is mapped onto $\mathbb{R}$ so that the leg $L_i$ corresponds to the positive half-line $[0,\infty )$, while all other legs are grouped together into a single second leg with parameter ${\sum }_{k\ne i}{\beta }_k=1-{\beta }_i$, which then is taken to be the negative half-line $(-\infty ,0]$. When considering the occupation time on the leg $L_i$; therefore, we can equally well consider the occupation time on $[0,\infty )$ of a one-dimensional diffusion.

The following results are shown in the previous paper [29], although here it is slightly modified to comply with the notation for diffusion spiders introduced in Section 2. In particular, note the differences mentioned in Remark 1.

Theorem 2. 

The Laplace transform of the first moment of $A_t^{\left(i\right)}$ is given by

$${\displaystyle {\mathcal{L}}_t\left\{{\mathbf{E}}_{\mathbf{0}}\left(A_t^{\left(i\right)}\right)\right\}\left(\lambda \right)=\frac{1}{\lambda }{\int }_0^{\infty }{\mathbf{g}}_{\lambda }(\mathbf{0},(y,i)){\beta }_{i}m\left(\mathrm{d}y\right)}$$

(13)

and for the higher moments, $n\ge 2$, recursively by

$$\begin{array}{cc}\hfill {\mathcal{L}}_t\left\{{\mathbf{E}}_{\mathbf{0}}\left({\left(A_t^{\left(i\right)}\right)}^n\right)\right\}\left(\lambda \right)=\sum _{k=1}^n& {\displaystyle \frac{n!D_k^{\left(i\right)}\left(\lambda \right)}{(n-k)!{\lambda }^k}}{\mathcal{L}}_t\left\{{\mathbf{E}}_{\mathbf{0}}\left({\left(A_t^{\left(i\right)}\right)}^{n-k}\right)\right\}\left(\lambda \right)\hfill \\ \hfill & +{\displaystyle \frac{n!}{{\lambda }^{n-1}}}{\mathcal{L}}_t\left\{{\mathbf{E}}_{\mathbf{0}}\left(A_t^{\left(i\right)}\right)\right\}\left(\lambda \right)-{\displaystyle \frac{n!}{{\lambda }^{n+1}}}\sum _{k=1}^n{D}_k^{\left(j\right)}\left(\lambda \right),\hfill \end{array}$$

(14)

where ${\mathcal{L}}_t$ denotes the Laplace transform with respect to t of the function in curly brackets, λ is the Laplace parameter, and

$$D_k^{\left(i\right)}\left(\lambda \right):={\displaystyle \frac{{\lambda }^k}{(k-1)!}}{\int }_0^{\infty }{\mathbf{g}}_{\lambda }(\mathbf{0},(y,i)){\mathbf{E}}_{(y,i)}\left(H_{\mathbf{0}}^{k-1}{\mathrm{e}}^{-\lambda H_{\mathbf{0}}}\right){\beta }_{i}m\left(\mathrm{d}y\right).$$

(15)

Furthermore, if X is self-similar, then for any $\lambda >0$,

$${\mathbf{E}}_{\mathbf{0}}\left({\left(A_1^{\left(i\right)}\right)}^n\right)={\mathbf{E}}_{\mathbf{0}}\left(A_1^{\left(i\right)}\right)-\sum _{k=1}^n{D}_k^{\left(i\right)}\left(\lambda \right)\left(1-{\mathbf{E}}_{\mathbf{0}}\left({\left(A_1^{\left(i\right)}\right)}^{n-k}\right)\right),$$

(16)

and, in particular, $D_k^{\left(i\right)}\left(\lambda \right)$ does not depend on λ for any $i=1,\dots ,R$ and $k=1,2,\dots$.

The proof is given in [29] (Theorem 2) with some minor notational differences.

Remark 1. 

Note the following:

(1)

The one-dimensional diffusion X on $\mathbb{R}$ with speed measure m, in the setting of the other paper [29], here really corresponds to a two-legged diffusion spider $\mathbf{X}$ with speed measure $\mathbf{m}$, which is why $m\left(dx\right)$ has been replaced by ${\beta }_{i}m\left(dx\right)$ in (13) and (15), in accordance with (6).

(2)

There is a sign change in the factor $D_k^{\left(i\right)}\left(\lambda \right)$ as defined in (15) compared to the corresponding expression in [29].

(3)

The variable λ is not at all present on the left hand side of (16), and (using induction) we conclude that the factors $D_k^{\left(i\right)}\left(\lambda \right)$ cannot depend on λ either. Thus, the value $\lambda >0$ can be chosen arbitrarily. As a side note, this is the reason why a factor ${\lambda }^k$ is included in the expression for $D_k^{\left(i\right)}\left(\lambda \right)$ in (15).

4.2. Joint Moments

The result in the previous section (from [29]) is here extended to a recursive formula for the Laplace transforms of the joint moments of the occupation times on multiple legs of a diffusion spider. For self-similar spiders we have a recursive formula directly for the joint moments, as in the case of the occupation time on one leg, cf. (16) in Theorem 2.

Theorem 3. 

For $r\in \{2,\dots ,R\}$ and $n_1,\dots ,n_r\ge 1$,

$${\mathcal{L}}_t\left\{{\mathbf{E}}_{\mathbf{0}}\left(\prod _{i=1}^r{\left(A_t^{\left(i\right)}\right)}^{n_i}\right)\right\}\left(\lambda \right)=\sum _{i=1}^r\sum _{k=1}^{n_i}{\displaystyle \frac{n_i!D_k^{\left(i\right)}\left(\lambda \right)}{(n_i-k)!{\lambda }^k}}{\mathcal{L}}_t\left\{{\mathbf{E}}_{\mathbf{0}}\left({\displaystyle \frac{{\prod }_{j=1}^r{\left(A_t^{\left(j\right)}\right)}^{n_j}}{{\left(A_t^{\left(i\right)}\right)}^k}}\right)\right\}\left(\lambda \right),$$

(17)

where $D_k^{\left(i\right)}$ is defined in (15). If X is self-similar, then for any $\lambda >0$,

$${\mathbf{E}}_{\mathbf{0}}\left(\prod _{i=1}^r{\left(A_1^{\left(i\right)}\right)}^{n_i}\right)=\sum _{i=1}^r\sum _{k=1}^{n_i}{\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{n_i}{k}\right)}{\left(\genfrac{}{}{0pt}{}{n_1+\dots +n_r}{k}\right)}}{D}_k^{\left(i\right)}\left(\lambda \right){\mathbf{E}}_{\mathbf{0}}\left({\displaystyle \frac{{\prod }_{j=1}^r{\left(A_1^{\left(j\right)}\right)}^{n_j}}{{\left(A_1^{\left(i\right)}\right)}^k}}\right).$$

(18)

Proof. 

See Appendix B.

Remark 2. 

Despite the similarity, Theorem 2 does not follow by letting $r=1$ in Theorem 3. On the right-hand sides of equations (14) and (16) are not only the respective parts corresponding to (17) and (18) with $r=1$, but also some additional terms. This difference seems to originate from the fact that up to the first hitting time of $\mathbf{0}$, the occupation time on the starting leg is equal to the elapsed time (and, hence, positive), while the occupation time on any other leg is zero. Therefore, any product of occupation times on more than one leg is also zero up to time $H_{\mathbf{0}}$, as can be seen in (A2), and even though we let the starting point tend to $\mathbf{0}$ when deriving the aforementioned theorems, there remains still a component which is nonzero in the case of a single leg but zero for the joint moments. With this in mind, Theorem 3 should not be seen as a replacement of Theorem 2 but as a complement to it.

The result in Theorem 3 tells us that if we know the Green kernel of the diffusion spider $\mathbf{X}$, we can recursively compute any joint moments of the occupation times on a number of legs. Recall also from (7) that for $y>0$

$${\mathbf{E}}_{(y,i)}\left(H_{\mathbf{0}}^k{\mathrm{e}}^{-\lambda H_{\mathbf{0}}}\right)={\mathbf{E}}_y\left(H_0^k{\mathrm{e}}^{-\lambda H_0}\right)={(-1)}^k{\displaystyle \frac{{\mathrm{d}}^k}{\mathrm{d}{\lambda }^k}}{\phi }_{\lambda }\left(y\right),$$

i.e., we have all the ingredients needed to calculate the factors $D_k^{\left(i\right)}$ using the integral expression in (15).

The generalized version of Kac’s moment formula in Proposition 1 is now used to derive a moment generating function of the occupation times on the legs of a diffusion spider up to an exponential time T.

Theorem 4. 

Let T be exponentially distributed with mean $1/\lambda$, $\lambda >0$, and independent of $\mathbf{X}$. Then, for any $z_1,\dots ,z_R\ge 0$,

$${\mathbf{E}}_{\mathbf{0}}\left(\exp \left(-\sum _{i=1}^R{z}_i{A}_T^{\left(i\right)}\right)\right)={\displaystyle \frac{{\displaystyle 1-\sum _{j=1}^R\frac{\lambda z_j}{\lambda +z_j}{\int }_0^{\infty }{\mathbf{g}}_{\lambda }(\mathbf{0},(y,j))\left(1-{\mathbf{E}}_{(y,j)}\left({\mathrm{e}}^{-(\lambda +z_j)H_{\mathbf{0}}}\right)\right){\beta }_{j}m\left(\mathrm{d}y\right)}}{{\displaystyle 1+\sum _{j=1}^R{z}_j{\int }_0^{\infty }{\mathbf{g}}_{\lambda }(\mathbf{0},(y,j)){\mathbf{E}}_{(y,j)}\left({\mathrm{e}}^{-(\lambda +z_j)H_{\mathbf{0}}}\right){\beta }_{j}m\left(\mathrm{d}y\right)}}}.$$

(19)

Proof. 

See Appendix C.

Formula (21) in the next corollary is due to Yano [4] (Theorem 3.5); see also Theorem 4 in Barlow, Pitman, and Yor [7], where the formula is presented for Bessel spiders (more on them in Section 5.1). We prove here that (20) is equivalent to our formula (19). For a Bessel spider, $c_{\lambda }$ is as given in (22), and notice that this formula shows that the inverse of the local time at 0 of the underlying reflecting Bessel process is a stable subordinator.

Corollary 2. 

For $r\in \{1,2,\dots ,R\}$ and $z_i>0,i=1,2,\dots ,r,$

$${\mathbf{E}}_{\mathbf{0}}\left(\exp \left(-\sum _{i=1}^r{z}_i{A}_T^{\left(i\right)}\right)\right)={\displaystyle \frac{{\displaystyle 1-\sum _{j=1}^r{\beta }_j+\sum _{j=1}^r\frac{\lambda {\beta }_j}{\lambda +z_j}\frac{c_{\lambda +z_j}}{c_{\lambda }}}}{{\displaystyle 1-\sum _{j=1}^r{\beta }_j+\sum _{j=1}^r{\beta }_j\frac{c_{\lambda +z_j}}{c_{\lambda }}}}},$$

(20)

where (cf. (10))

$$c_{\lambda }:=-{\displaystyle \frac{d}{dS}}{\phi }_{\lambda }(0+)>0.$$

In particular, for $z_i>0$, $i=1,2,\dots ,R$,

$${\mathbf{E}}_{\mathbf{0}}\left(\exp \left(-\sum _{i=1}^R{z}_i{A}_T^{\left(i\right)}\right)\right)={\displaystyle \frac{1}{{\displaystyle \sum _{j=1}^R{\beta }_j{c}_{\lambda +z_j}}}{\displaystyle \sum _{j=1}^R\frac{\lambda {\beta }_j{c}_{\lambda +z_j}}{\lambda +z_j}}}.$$

(21)

Proof. 

See Appendix D.

5. Examples

In this section we highlight our results by analyzing a few different diffusion spiders, first and foremost Bessel spiders. For the Brownian spider, which is an important special case of Bessel spiders, it is possible to pursue the formulas further, and this evaluation is presented in a subsection of its own. Finally, we make some comments concerning occupation times for Walsh Brownian motion.

5.1. Bessel Spider

A Bessel process of dimension n and parameter $\nu :=n/2-1$, where n is a positive integer, corresponds to the Euclidean norm of an n-dimensional Brownian motion. The n-dimensional Bessel process has the generator

$${\displaystyle \mathcal{G}f=\frac{1}{2}\frac{d^{2}f}{d{x}^2}+\frac{n-1}{2x}\frac{df}{dx},x>0,}$$

which makes sense not only for integers n but any real values and, hence, any real parameter $\nu$. We define the Bessel spider as a diffusion spider that behaves like a Bessel process with parameter $\nu \in (-1,0)$ (i.e., dimension $2+2\nu$) on each leg and has the corresponding excursion probabilities ${\beta }_i>0$, $i=1,2,\dots R$, such that ${\beta }_1+\dots +{\beta }_R=1$. The restriction on $\nu$ to $(-1,0)$ is so that the process is recurrent and hits 0; see [31] (p. 77). We now let $\mathbf{X}$ be a Bessel spider with $R\ge 2$ legs and apply the result in Theorem 3.

The Bessel spider has the self-similar property, which means that the recurrence equation in (18) applies. Recall that this recurrence hinges on the factors $D_k^{\left(i\right)}$ given in (15). For the purpose of finding ${\mathbf{g}}_{\lambda }(\mathbf{0},(y,i))$, that is, where the point y is on a particular leg $L_i$, we follow the procedure leading to Theorem 1. For the reflected Bessel diffusion on $[0,+\infty )$, we have from [31] (p. 137) that

$$m\left(dx\right)=2x^{2v+1}dx,S\left(x\right)=-{\displaystyle \frac{1}{2\nu }}{x}^{-2\nu },{\phi }_{\lambda }\left(x\right)=x^{-\nu }{K}_{\nu }\left(x\sqrt{2\lambda }\right),$$

where $K_{\nu }$ is a modified Bessel function of the second kind. Then

$$c_{\lambda }:=-{\displaystyle \frac{d}{dS}}\phi (0+)={\left({\displaystyle \frac{2}{\sqrt{2\lambda }}}\right)}^{\nu }\Gamma (\nu +1)=2^{\nu /2}\Gamma (\nu +1){\lambda }^{-\nu /2}$$

(22)

and, hence,

$${\mathbf{g}}_{\lambda }(\mathbf{0},(y,i))={\displaystyle \frac{1}{\Gamma (\nu +1)}}{\left({\displaystyle \frac{\sqrt{2\lambda }}{2}}\right)}^{\nu }{y}^{-\nu }{K}_{\nu }\left(y\sqrt{2\lambda }\right).$$

Note that ${\mathbf{g}}_{\lambda }(\mathbf{0},(y,i))$ is the same for all i. Similarly, the hitting time $H_{\mathbf{0}}$ when starting in $y\in L_i$ corresponds precisely to the hitting time of zero in the reflected Bessel process. The values of $D_k^{\left(i\right)}$ are calculated as in [29] (Proof of Theorem 3), but note that a different normalization is used for m and S in that paper. This way, we get for any $\lambda >0$ that

$$D_k^{\left(i\right)}\left(\lambda \right)=-{\beta }_i\left({\displaystyle \genfrac{}{}{0pt}{}{\nu +k-1}{k}}\right)=-{\displaystyle \frac{{\beta }_i}{k!}}\sum _{j=1}^k\left[{\displaystyle \genfrac{}{}{0.0pt}{}{k}{j}}\right]{\nu }^j,$$

(23)

where $\left[{\displaystyle \genfrac{}{}{0.0pt}{}{n}{k}}\right]$ are unsigned Stirling numbers of the first kind. In the rest of this section, we will drop $\lambda$ and only write $D_k^{\left(i\right)}$, as its value does not depend on $\lambda$.

As explained in Section 4.1, when only considering the occupation time on a single leg $L_i$, we can directly use the earlier obtained results for skew two-sided Bessel processes. Hence, by [29] (Theorem 4), the nth moment of the occupation time on $L_i$ up to time 1 is given by

$${\mathbf{E}}_{\mathbf{0}}\left({\left(A_1^{\left(i\right)}\right)}^n\right)=\sum _{l=1}^n\sum _{k=1}^l{(-1)}^{k-1}{\displaystyle \frac{\Gamma \left(k\right)}{\Gamma \left(n\right)}}\left[{\displaystyle \genfrac{}{}{0.0pt}{}{n}{l}}\right]\left\{{\displaystyle \genfrac{}{}{0.0pt}{}{l}{k}}\right\}{\nu }^{l-1}{\beta }_i^k,$$

(24)

where $\left\{{\displaystyle \genfrac{}{}{0.0pt}{}{n}{k}}\right\}$ are Stirling numbers of the second kind.

Using the recurrence equation in Theorem 3, the result in (24) is here extended to an explicit formula for the joint moments of the occupation times on multiple legs in a Bessel spider with $R\ge 2$ legs. With the numbering of legs being arbitrary, it should be clear that the formula—although written for the first r legs of the spider—holds when considering the occupation times on any number r of the R legs. Contrary to the recursive formula in Theorem 3 (see Remark 2), this formula also holds when $r=1$.

Theorem 5. 

For any $r\in \{1,\dots ,R\}$ and $n_1,\dots ,n_r\ge 1$,

$${\mathbf{E}}_{\mathbf{0}}\left(\prod _{i=1}^r{\left(A_1^{\left(i\right)}\right)}^{n_i}\right)=\sum _{1\le k_1\le l_1\le n_1}\cdots \sum _{1\le k_r\le l_r\le n_r}{(-1)}^{K-1}{\displaystyle \frac{\Gamma \left(K\right)}{\Gamma \left(N\right)}}{\nu }^{L-1}\prod _{j=1}^r\left[{\displaystyle \genfrac{}{}{0.0pt}{}{n_j}{l_j}}\right]\left\{{\displaystyle \genfrac{}{}{0.0pt}{}{l_j}{k_j}}\right\}{\beta }_j^{k_j},$$

(25)

where $N=n_1+\cdots +n_r$, $K=k_1+\cdots +k_r$ and $L=l_1+\dots +l_r$.

A proof of the theorem is given in Appendix E. For a particularly simple instance of the theorem above, consider the joint first moment of the occupation times on r legs in the Bessel spider.

Corollary 3. 

For any $r\in \{1,\dots ,R\}$,

$${\mathbf{E}}_{\mathbf{0}}\left(A_1^{\left(1\right)}{A}_1^{\left(2\right)}\cdots A_1^{\left(r\right)}\right)={(-\nu )}^{r-1}{\beta }_1{\beta }_2\cdots {\beta }_r.$$

(26)

Proof. 

Immediate from (25) with $n_1=\cdots =n_r=1$. □

The first few moments of the occupation times up to time t on one or two legs of a Bessel spider are given in Table 1. Recall that since the Bessel spider is self-similar, the (joint) moments of the occupation times on the legs up to a fixed time t satisfy

$${\displaystyle {\mathbf{E}}_{\mathbf{0}}\left({\left(A_t^{\left(i\right)}\right)}^{n_1}{\left(A_t^{\left(j\right)}\right)}^{n_2}\right)=t^{n_1+n_2}{\mathbf{E}}_{\mathbf{0}}\left({\left(A_1^{\left(i\right)}\right)}^{n_1}{\left(A_1^{\left(j\right)}\right)}^{n_2}\right).}$$

Using this, the moments are found directly from Theorem 5. The variance, covariance, and correlation coefficients are also included in the table. Note, as expected, that the correlation coefficient is always negative and does not depend on the time t or the Bessel parameter $\nu$. If the spider has only two legs, so that ${\beta }_1=1-{\beta }_2$, the process is always located on either of the legs and the correlation coefficient of the occupation times on the legs is then equal to $-1$.

Table 1. Some moments and descriptive statistics for the occupation times on the legs of a Bessel spider.

Moment/Statistic	Value
${\mathbf{E}}_{\mathbf{0}}\left(A_t^{\left(i\right)}\right)$	$t{\beta }_i$
${\mathbf{E}}_{\mathbf{0}}\left({\left(A_t^{\left(i\right)}\right)}^2\right)$	$t^2{\beta }_i(1+\nu -\nu {\beta }_i)$
${\mathbf{E}}_{\mathbf{0}}\left(A_t^{\left(i\right)}{A}_t^{\left(j\right)}\right)$	$-t^2\nu {\beta }_i{\beta }_j$
$\mathrm{Var}\left(A_t^{\left(i\right)}\right)$	$t^2(1+\nu ){\beta }_i(1-{\beta }_i)$
$\mathrm{Cov}\left(A_t^{\left(i\right)},A_t^{\left(j\right)}\right),i\ne j$	$-t^2(1+\nu ){\beta }_i{\beta }_j$
$\mathrm{Corr}\left(A_t^{\left(i\right)},A_t^{\left(j\right)}\right),i\ne j$	$-\sqrt{{\displaystyle \frac{{\beta }_i{\beta }_j}{(1-{\beta }_i)(1-{\beta }_j)}}}$

5.2. Brownian Spider

The special case of a Bessel spider with the parameter $\nu =-{\displaystyle \frac{1}{2}}$ is the Brownian spider mentioned in the introduction, also known as Walsh Brownian motion on a finite number of legs. In this case, the result in Theorem 5 has the following, somewhat simpler expression.

Theorem 6. 

Let $\mathbf{X}$ be a Brownian spider and let $A_1^{\left(i\right)}$ be the occupation time on leg $L_i$ up to time 1. For any $r\in \{1,\dots ,R\}$ and $n_1,\dots ,n_r\ge 1$,

$${\mathbf{E}}_{\mathbf{0}}\left(\prod _{i=1}^r{\left(A_1^{\left(i\right)}\right)}^{n_i}\right)=\sum _{k_1=1}^{n_1}\cdots \sum _{k_r=1}^{n_r}{2}^{-(2N-K-1)}{\displaystyle \frac{\Gamma \left(K\right)}{\Gamma \left(N\right)}}\prod _{j=1}^r{\displaystyle \frac{\Gamma (2n_j-k_j){\beta }_j^{k_j}}{\Gamma \left(k_j\right)\Gamma (n_j-k_j+1)}},$$

(27)

where $N=n_1+\cdots +n_r$ and $K=k_1+\cdots +k_r$.

Proof. 

The result follows from (25) and the identity

$$\sum _{i=k}^n\left[{\displaystyle \genfrac{}{}{0.0pt}{}{n}{i}}\right]\left\{{\displaystyle \genfrac{}{}{0.0pt}{}{i}{k}}\right\}{(-2)}^{n-i}={(-1)}^{n-k}{\displaystyle \frac{(2n-k-1)!}{2^{n-k}(k-1)!(n-k)!}}=:b(n,k),$$

where $b(n,k)$ is a (signed) Bessel number of the first kind. For proofs of this identity and some related ones, see [33,34]. □

5.3. Walsh Brownian Motion

Finally, we briefly return to the Walsh Brownian motion in its original form. As the state space can be the entire ${\mathbb{R}}^2$ and is not restricted to a spider graph with a fixed number of legs, in this section we follow Walsh’s terminology and talk about “rays” rather than “legs”, although it should be clear that the meaning is the same. Here, the diffusion behaves like a Brownian motion on each ray, and when it reaches the origin, the direction $\theta$ of the next ray is selected according to some given distribution on $[0,2\pi )$. As we have already studied the case when this distribution is discrete, i.e., the number of rays is at most countable, we now consider a continuous distribution.

The diffusion will, almost surely, choose a new direction every time it reaches $\mathbf{0}$, so that it visits no ray more than once. Furthermore, the probability of visiting a particular ray (i.e., a ray whose angle is a fixed value) is zero. For this reason, it is not meaningful to consider the occupation times on specific rays in this case. Rather, we can consider the occupation times within sectors of the ${\mathbb{R}}^2$ plane. Let $0={\theta }_0<{\theta }_1<{\theta }_2<\cdots <{\theta }_R=2\pi$ be fixed angles and let $S_i$ consist of all points with angle in $[{\theta }_{i-1},{\theta }_i)$, so that ${\mathbb{R}}^2$ is partitioned into R non-overlapping sectors $S_1,S_2,\dots ,S_R$. If $\Theta \left(X_t\right)$ denotes the angle of the ray on which the diffusion X is located at time t, then

$$A_t^{\left(S_i\right)}={\int }_0^t{\mathbb{1}}_{[{\theta }_{i-1},{\theta }_i)}(\Theta \left(X_s\right))\mathrm{d}s$$

is the occupation time of the diffusion within sector $S_i$ up to time t. This is illustrated in Figure 3, which contains a plot of a simulated Walsh Brownian motion. Each line corresponds to an excursion along a ray from the origin, and the length of each line is proportional to the maximal height of that excursion. The ${\mathbb{R}}^2$ plane has been divided into five separate sectors of equal size, each with its own color, and we may consider the occupation time of the process in these sectors.

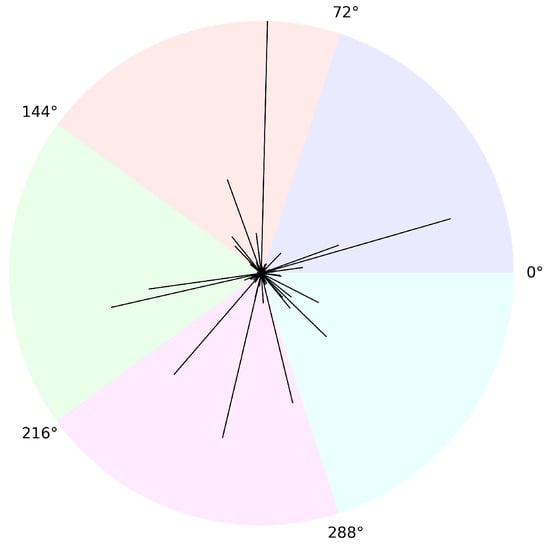
Figure 3. Plot of excursions from the origin of a simulated Walsh Brownian motion.

With respect to the occupation time on a sector, the outcome is the same as if all rays within the sector were combined and mapped onto a single ray. Therefore, the occupation times of a Walsh Brownian motion in the sectors $S_1,\dots ,S_R$ correspond precisely to the occupation times on the R legs of a Brownian spider. Thus, the result in Theorem 6 applies for the occupation times on sectors of a Walsh Brownian motion, with ${\beta }_i$ being equal to the probability of selecting an angle within sector $S_i$ when at the origin. Naturally, if the diffusion behaves like a Bessel process with parameter $\nu \in (-1,0)$ on each ray (this could, perhaps, be called a “Walsh Bessel process”), then Theorem 5 applies instead.