Appendix A. Proofs for Results
The proof for Theorem 2 and results in
Section 2 can be found in [
11], where we also give an alternative expression for Definition 3.
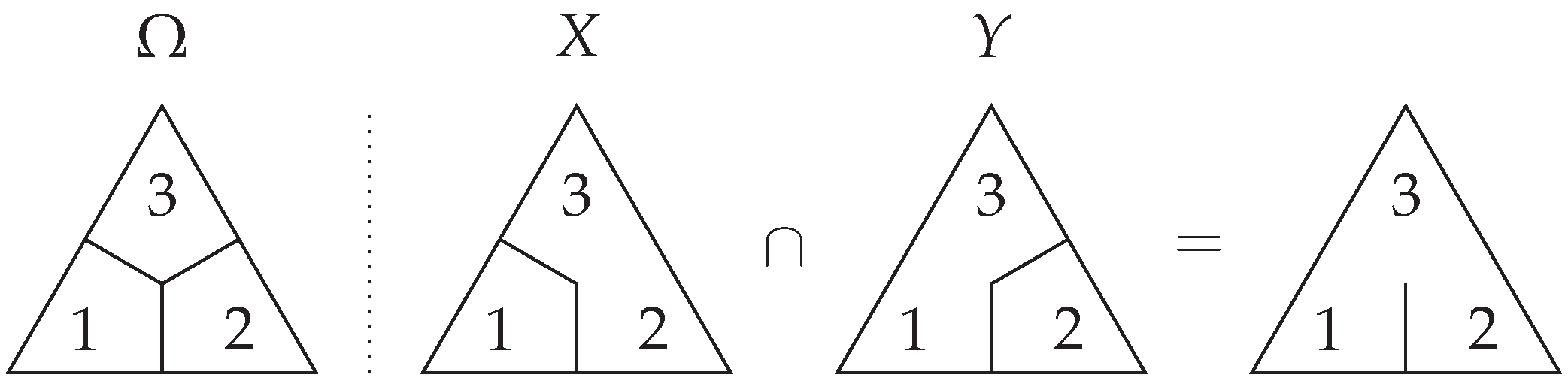
Proof of Proposition 2. Suppose . Then, either or for some or . Hence, as needed. Conversely, if b is contained in , then for some , so b must be contained in either I or J, so .
Suppose that and . Then, there exists and with and . Hence, , so . Conversely, if , then there exists a generator of with . Since , we must have and , so and , so . □
Proof of Lemma 3. By the definition of content, we must have that is an ideal. Moreover, the intersection of ideals is an ideal, so the co-information must also correspond to an ideal. □
Proof of Theorem 3. Firstly, we note that all co-informations correspond to ideals by the previous result in Lemma 3. It suffices to show that all ideals in correspond to some co-information. As such, given an ideal J, we need to find a collection of variables where .
Ideals are unique up to their generators, and we only need to consider sets of generators which are not contained in each other; otherwise, one of them is not needed as a generator. For each generator
, let
. Let
be the set of elements in
. Then, consider the
variables given by the partitions
for every
a non-empty proper subset of
with
. Intuitively, these variables spread the elements in
across two partitions in every combination possible, so that the only guaranteed boundary crosses consistent across the entire collection
are by the
atom and atoms in
. Then
Here, we write
to symbolise that these partitions are taken to obtain atom
. Across the set of generators
, we consider all possible products
where any combination from the
where
can be taken. Note that we write
to mean the coarsest partition which is finer than
A and
B. In practice, every variable corresponds to choosing one of the
for each generator, so every single combination is represented as a variable. Then
exactly, as any other generators will be removed, giving the result. □
Proof of Corollary 2. Given any atom b, we can consider the ideal , and then using conditioning (in the sense of a set difference of information), we may subtract the higher co-information , which is itself an ideal, as the unions of ideals in lattices are ideals. We have that , meaning we may condition it out in order to obtain the expression . That is, b alone populates some region on an I-diagram between all variables .
Taking any collection of atoms hence corresponds to a collection of regions on the maximal I-diagram provided they are not counted with multiplicity. □
Proof of Corollary 3. There are elements in , as the points and the empty set do not contribute to the entropy, leaving atoms, and hence possible entropic expressions without multiplicity, including the zero expression. □
Proof of Theorem 4. Precisely those atoms are all those atoms which cross a boundary in X, that is, they must contain the pair for and where and are different parts in the partition. The atom can be written as the intersection of these two prime ideals.
Since the union of ideals and is the ideal generated by the union of their generators in lattices, we have that must be the union across these parts and hence generated by 2-atoms.
The second expression follows quickly from the first; every atom in must lie in some other part and vice versa. □
Proof of Corollary 4. All other atoms are described by whether or not they are contained in the intersection of the variable ideals , which by the previous result are generated by degree 2 atoms. Hence, the knowledge of how these are distributed will describe the distribution of all other atoms. □
Proof of Theorem 5. We know that and are both degree 2 ideals as they are given by the union of intersections of prime degree 1 ideals, so their intersection can have generators of at most degree 4. Hence, we need to demonstrate that for every degree 3 or degree 4 generator in , there is a degree 2 generator which contains it.
We demonstrate that every degree 4 atom in is contained in a degree 2 ideal. The argument for the degree 3 atoms is very straightforward and uses the same trick. Suppose that we have a degree 4 atom which crosses a boundary in X and in Y. We may restrict to just these four outcomes , on which the partition of X and the partition of Y must now also restrict to a partition.
Since is contained in and , we must have that the local partition of X and the local partition of Y are non-trivial so that crosses a boundary in this partition.
Without loss of generality, the potential local partitions of any random variable
up to reordering of the
are given by
In particular, the total number of possible degree 2 generators in four outcomes is , so taking the intersection of will, by the pigeonhole principle, have a degree 2 atom in their intersection unless both and have at most three degree 2-atoms. Of the four possibilities above, only the first satisfies this possibility, so both X and Y are of this form.
Without loss of generality, we assume is given by . The only possible degree 2 ideal which does not intersect with is given by , so we should expect that . However, this does not correspond to any partition on , as it does not contain a generator containing element 1. Thus, Y cannot have this form, and we must have that must intersect and contain a degree 2 element, so the degree 4 atom is contained in a degree 2 ideal.
For any degree 3 atom, the argument is even simpler; the smallest possible ideal must have either 2 or 0 generators of degree 2 when restricted. If it had 0 generators, then cannot cross a boundary in X, so it would not be present in . Hence, we must have , which has at least two generators of degree 2 with the same being true for Y. As such, they must intersect with each other at a degree 2 atom by the pigeonhole principle, as the total number of possible generators is . □
Proof of Corollary 5. Using a result from [
10], we have that
(the maximally representable subset inside of
). We have now also shown that both
and
are degree 2 ideals. Hence, the generators of the representable subset must be a subset of the generators of the mutual information. □
Proof of Theorem 6. We proceed by induction on M by showing that the theoretical minimum number of generators must still be large enough to force an overlap. We have demonstrated in the previous theorem that the statement is true for . Suppose that the statement is true for , then the ideal corresponding to the co-information for the first variables has generators of degree at most . Multiplying the generators of by the generators for , we hence know that can be generated by atoms of at most degree . Hence, we need to show that any degree atom is actually contained in a degree M ideal.
We will use a similar counting argument to result Theorem 5. In particular, given a finite set of size
k and two subsets of size
and
, the minimum size of their intersection is given by
. Given three subsets, a minimum size for the intersection is then given by
and so on. Hence, given
l subsets, the corresponding expression is
Suppose that is a degree atom contained in the co-information , which we need to demonstrate is contained in a degree M ideal. Restricting to , the minimum number of degree M atoms in for any i is given when corresponds locally to a partition of the form for some single [If this is not immediately clear, consider any partition of —we could choose a coarser sub-partition into two parts which must contain fewer 2-atoms, so minimising the number of 2-atoms overall is equivalent to finding the minimum number of degree 2 atoms in a partition of into 2 parts. This is equivalent to minimising the value of for , which happens at or ].
Hence, there must be a minimum of degree M atoms in (as we have already selected one outcome from the available outcomes—now we must select the other outcomes). The maximum size of the set of all possible degree M atoms in the restriction to is .
Hence, taking the intersection of
M variables, assuming a minimal number of degree
M atoms, and using the expression in Equation (
A6), we need to only to demonstrate that
which always evaluates to unity, proving that there is at least one degree
M ideal containing every degree
atom in the intersection, proving the result. □
Proof of Theorem 4. Let our ideal be . We will proceed by induction on the difference , arguing at each step that the upper set is monotonic in probability of the last element . We note that the sign of the upper set might only change if it contains additional outcomes, so provided we treat this carefully, we can also allow to vary (via restriction) provided that it always contains .
As earlier, we will write to illustrate that we are operating inside some restricting set S. These quasi-ideals are quite justified, as all of the previous results must still hold even if we assume the probabilities inside of S do not sum to 1. These atoms will still have the same measure regardless of the context S in which we find them.
For the first case , we note that consists of the single atom . We will use the shorthand notation for some simplicity. By Theorem 1, which characterises the sign of individual atoms, we have both that for and that varies monotonically in between 0 and . So, the theorem is true for .
Now, suppose that
varies monotonically in
between 0 and
. Then, we first note that
where we use the multiplicative notation to signify that
is added as an outcome to all atoms in
. For example,
Hence, we can view
as a function on
:
We now notice that the second term can be expressed
But now we can see that the difference between and is just d, so this reduces to the case for d. By assumption, we hence have that this ideal varies monotonically on between 0 and .
This means that the entire expression in Equation (
A11) must monotonically vary between 0 and
as a function of
.
Since we can construct each ideal by successively increasing d and this leaves the sign intact (note that no probability tends to infinity), the sign is left unchanged, proving the result. □
Proof of Theorem 7. Let
be an ideal of strong even/positive parity with the result for odd/negative parity following equivalently. By the definition of strong even parity, we must have
Every strong fixed-parity ideal is defined in terms of an a finite sum of ideals with one generator, so we may assume without loss of generality that the has single generators.
By virtue of Lemma 4, we know that . Hence, taking the sum across all the values, we have that all of the terms must be positive. As all terms in the sum positive, so too is . □
Proof of Theorem 8. We will first allow ourselves to consider probabilities not summing to one, demonstrating that the sign has a given parity, and then we shall scale appropriately using the homogeneity property of to obtain meaningful probabilities once more, while the parity shall be fixed.
Suppose
J is a strongly mixed ideal. Then,
J has an even degree generator
g. We first send all atoms in
(as a set) to 0. Then, we have
Summing the probabilities, we let
. Then, we scale
where we now have
. Hence, we have found a given set of probabilities where
.
Repeating the exercise for g of odd degree will similarly show that there are probabilities such that . Hence, can be either positive or negative given a strongly mixed-parity ideal, giving the result. □
Proof of Theorem 9. We begin by briefly demonstrating that
has co-information
given by a strongly odd parity ideal. Given the outcomes
we have that
. In this case, we have
where now we also have
Working backwards, we see that
and
are negative (odd) fixed-parity ideals, so that
in this case is a negative fixed-parity ideal.
To show that there are no other such deterministic functions on three variables, we start by considering the case where
X and
Y are both binary variables. In this case, we know that we can express all events on
Z in terms of
on the four outcomes
In this case, we have
, which is known to have positive measure as it reflects a mutual information. Similarly, any subset
or
will also have a positive measure, so we cannot have an ideal generated by a degree 2 ideal alone. However, the ideal cannot have even and odd generators (as then it would have mixed parity by Theorem 8 and it cannot have generators more than degree 3 by Theorem 6). Hence, the ideal must be exclusively generated by degree 3 atoms and we must nullify these two degree 2 atoms.
Hence, we know that in order to have degree 3 atoms generating , Z must have equal values on the outcome pairs and . Moreover, we cannot have that for all outcomes, as then . Hence, we must have that and ; that is, Z is the XOR gate.
We now extend by induction to give the full result. Let be the number of events in X and the total number of events in Y. In the case where either or is 1, then that variable must be constant and have zero entropy, so the co-information is trivially zero.
We have seen that in the case where
that the only negative fixed-parity system of the form
is the XOR gate. We consider the case
and
to highlight the inductive argument. In this case, again, we know that
Z can be computed deterministically from
X and
Y, allowing us to use the same trick. Labelling outcomes, we have
In this case, we see that
Again, this is a mutual information and hence positive. Thus, we know that for
Z to be purely negative, it must be generated by purely degree 3 atoms, so
Z must remain unchanged on these pairs of outcomes. Assigning a symbol to
, we can use the same trick as before and successively annihilate various pairs of atoms, giving us the following chain:
That is to say, Z does not vary on and the co-information is zero in this case.
We now suppose for the induction that there are no fixed-parity systems with outcomes on X and outcomes on Y. We will demonstrate that we can introduce an additional event to either X or Y and we will still obtain that Z is the trivial variable.
Without loss of generality, we increase by one. This will introduce additional outcomes. As we have (without reference to the probabilities) demonstrated that for , it suffices to show that for every further outcome , there is an atom with .
For each , we shall pick some such that . Using the ordering we have utilised so far and restricting to the bottom of the table, we may assume that as a symbol, and .
Given , we may select the outcome to be the outcome corresponding to and , where in Y we perform arithmetic mod . We must then have that X and Y both change when moving from to . By the definition of content, this means that the atom will be contained in , as needed, so we must have , showing that Z is actually the trivial variable, inductively giving the result. □