Dynamical Systems on Generalised Klein Bottles

Abstract

We propose a high-dimensional generalisation of the standard Klein bottle extending beyond those considered previously. We address the problem of generating continuous scalar fields (distributions) and dynamical systems (flows) on such state spaces, which can provide a rich source of examples for future investigations. We consider a class of high-dimensional dynamical systems that model distributed information processing within the human cortex, which may be capable of exhibiting some Klein bottle symmetries. We deploy topological data analytic methods in order to analyse their resulting dynamical behaviour and suggesting future challenges.

1. Introduction

Data science typically presents observations (in the form of data) from some implied dynamical system of interest and demands that we character the underlying relevant processes and system behaviour. This includes differentiating one source from another, and other related questions regarding their observed state variables’ mutual dependencies and mutual information.

Here, we consider the problem of characterising finite dimensional manifolds that contain such attractors. The most basic problem is to consider a wide range of the possible finite dimensional manifolds which may be present. This leads us naturally to ask what kind of compact closed manifolds exist and whether we may recognise scalar fields (smooth distributions and potentials) or vector fields (flows) flows defined over them, respecting their inherent topologies.

For low-dimensional state spaces, there is a limited set of possible compact closed manifolds. In two dimensions, for example, we have the two-sphere, the two-torus, the Klein bottle and the real projective plane. In higher dimensions, these manifolds may generalise to other objects. Generalising spheres and tori is straightforward.

In this paper, we introduce a generalisation of the Klein bottle, extending beyond those given previously [1]. In k dimensions, this relies on a partition of independent coordinates into $k_1$ periodic coordinates that may be flipped or swapped (as if from moving clockwise to moving anticlockwise, for example) and $k_2$ active periodic components which cause the various flips (such that $k=k_1+k_2$).

By doing so, we access a wide range of compact closed manifolds over which we may define, or there may be discovered, dynamical systems.

We introduce an inverse problem in the form of the observation of a large-scale spiking system, including those carrying out information processing within the cortex of the human brain [2], where the dimension of the attractor may be estimated yet the topological nature of the attractor is elusive. Such problems may become common as high-throughput science enables the complete observation of such large-scale dynamical systems which appear to approach unknown attractors of relatively high dimension that require characterisation. Working from observed time series, such as the spike trains as here, requires an analytical pipeline. The very high state space dimension of such a complex system means that the dimension and topology of the manifold holding the attractor is essential in gaining an understanding of what is occurring and how the system responds to incoming stimuli.

The detailed and rigorous mathematical considerations are deferred to Appendices.

2. Generalised Klein Bottles

For $k_1\ge 1$ and $k_2\ge 0$, we let $B=\left(B_{i,j}\right)$ denote an irreducible binary $k_1\times k_2$ matrix.

We consider ${\mathbb{R}}^{k_1+k_2}$ with independent coordinates, $x={(x_1,x_2\dots ,x_{k_1})}^T$ and $y={(y_1,y_2\dots ,y_{k_2})}^T$, subject to the following set of symmetries:

$$(x+a,y+b)\sim (\phi \left(b\right)x,y)), (a,b)\in {\mathbb{Z}}^{k_1}\times {\mathbb{Z}}^{k_2},$$

(1)

where $\phi \left(b\right):{\mathbb{Z}}^{k_2}\to \mathrm{Aut}\left({\mathbb{Z}}^{k_1}\right)$ is a b-dependent automorphism defined by the Hadamard (elementwise) product

$$\phi \left(b\right)x={(-1)}^{B.b}\odot x=\left({(-1)}^{{(B.b)}_1}{x}_1,\dots ,{(-1)}^{{(B.b)}_{k_1}}{x}_{k_1}\right)$$

and extended to ${\mathbb{R}}^{k_1}$. So, depending on the parity of the ith term of the vector ${(-1)}^{B.b}$, the sign of the ith coordinate, $x_i$, is either flipped (reflected) or else left unchanged.

The symmetries in (1) imply the quotient space is the cube, ${[0,1]}^{k_1+k_2}$, with no boundaries and endowed locally with the Euclidean metric. We refer to the $x_i$ coordinates as toroidal coordinates, since they are 1-periodic. We refer to the $y_j$ coordinates as Klein coordinates since they are one-periodic and when incremented by one they also flip, or reflect, some of the $x_i$ toroidal coordinates (those for which $B_{i,j}=1$). The result is a generalised Klein bottle, which we denote by $\mathbb{K}(k_1,k_2,B)$.

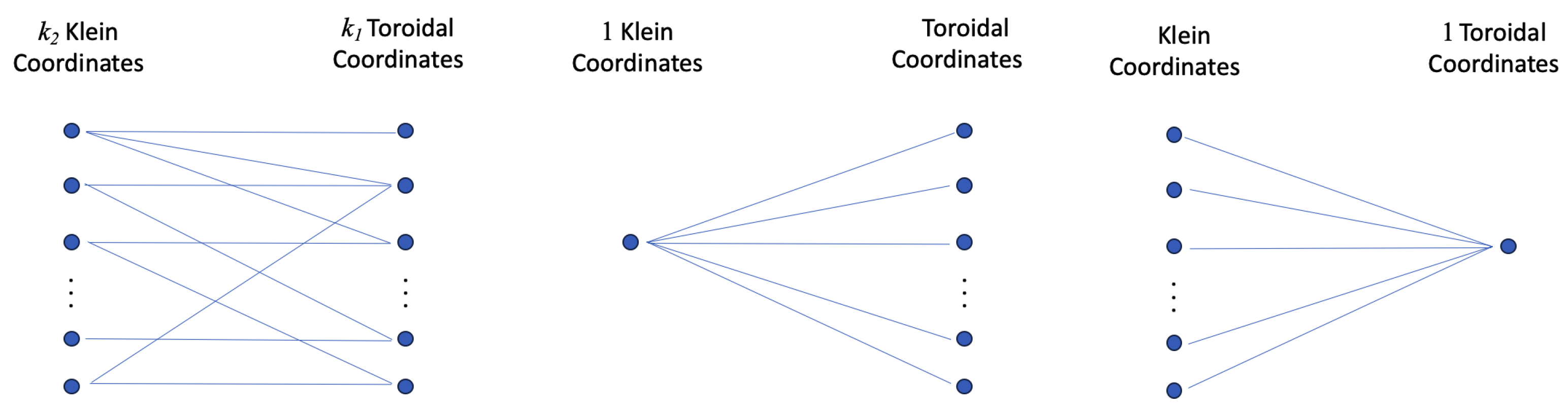
B specifies a bipartite graph indicating which of the toroidal coordinates are flipped by which of the Klein coordinates; see Figure 1. The adjacency matrix, A, for the associated bipartite graph is given in block matrix form by

$$A=\left(\begin{array}{cc}0& B\\ B^T& 0\end{array}\right).$$

Since we have assumed B is irreducible, the corresponding bipartite graph cannot be decomposed into disjoint connected graphs. Necessarily, every Klein coordinate flips at least one toroidal coordinate, and every toroidal coordinate is flipped by at least one Klein coordinate (for if this were not the case, any marooned coordinates could be discarded).

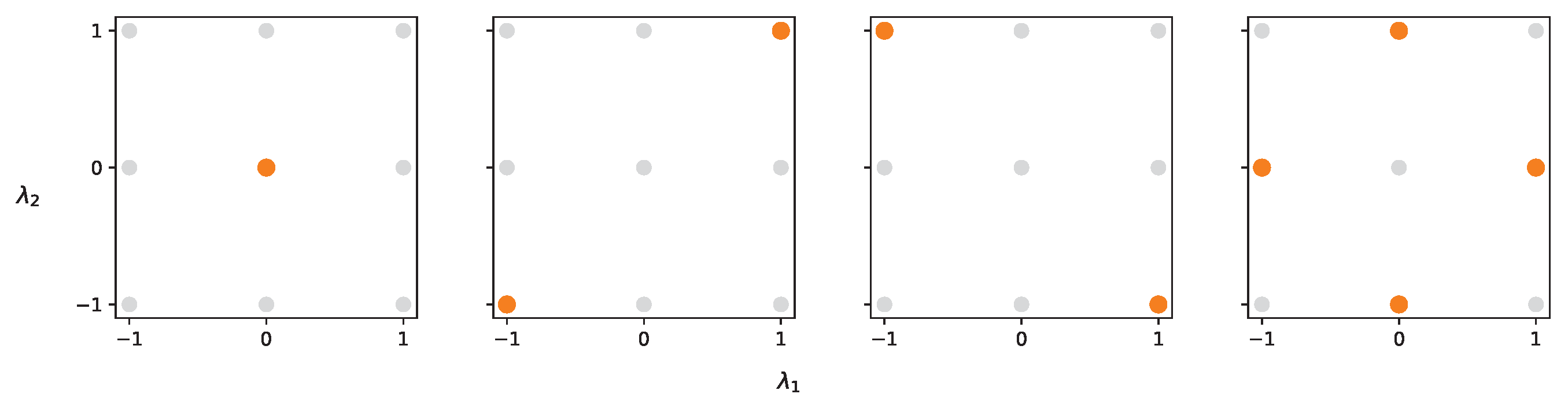
If $k_1=k_2=1$, then we have the standard Klein bottle ($B=\left(1\right)$ in that case), a closed non-orientable two-dimensional surface. If $k_2=0$, then $\mathbb{K}(k_1,0)={\mathbb{T}}^{k_1}$ the $k_1$-dimensional torus. For spaces $\mathbb{K}(1,k_2,B)$, for $k_2\ge 2$, there is but one valid choice of bipartite graph, B. Those spaces are distinct from the Klein bottle generalisations previously considered in [1] (and its descendants), which are $\mathbb{K}(k_1,1,B)$, for some $k_1\ge 2$, where again there is but one valid choice for B; see Figure 1.

When two Klein variables only affect the same toroidal variable, there is a hidden torus. We let $e_i$ denote the unit vectors in the direction of the ith Klein coordinate in ${\mathbb{R}}^{k_2}$. We consider, for example, $\mathbb{K}(1,n,B)$ for $n\ge 1$. For any distinct pair of the n Klein coordinate symmetries, we say those in $y_i$ and $y_j$ (where without loss of generality $i<j$), we deduce

$$\begin{array}{c}(x,\dots y_i+1,\dots ,y_j+1,\dots )\sim (x,\dots y_i,\dots ,y_j,\dots ),\\ (x,\dots y_i-1,\dots ,y_j+1,\dots )\sim (x,\dots y_i,\dots ,y_j,\dots ).\end{array}$$

Hence, there is a two-dimensional torus, ${\mathbb{T}}^2,$ with coordinate directions $(\pm e_i+e_j)/\sqrt{2}$, and periodicities $\sqrt{2}$, within the $(y_i,y_j)$-subspace of $\mathbb{K}(1,n,B)$.

An inference of the this type is true more generally within $\mathbb{K}(k_1,k_2,B)$, provided that the subsets of the toroidal coordinates that are flipped by each of a pair $y_i$ and $y_j$ (and hence the i and jth columns of B) are identical. Such a situation might occur in scenarios where there is some symmetry within the application, meaning that some of that state variables which are represented by Klein coordinates are permutable (exchangeable) and thus may cause similar effects (transformations of finite order) on a common subset of the toroidal coordinates. More generally, this type of hidden symmetry is a consequence of the dimension of the range of B, spanned by its columns, and is strictly less than $k_2$.

3. More Symmetries

For the general case of $\mathbb{K}(k_1,k_2,B)$, we rewrite this to consider $B\in {\mathbb{Z}}^{k_1\times k_2}$ (since only parity of the elements of B matter), and also set $\phi :{\mathbb{Z}}^{k_2}\to \mathrm{Aut}\left({\mathbb{Z}}^{k_1}\right)$, extended to be defined on ${\mathbb{R}}^{k_1}$, via matrix multiplication

$$\phi \left(b\right)x=H\left(b\right).x \mathrm{for} b\in {\mathbb{Z}}^{k_2} \mathrm{and} \mathrm{all} x\in {\mathbb{R}}^{k_1},$$

(2)

where we introduce the diagonal matrix (containing diagonal elements in $\{-1,1\}$) given by

$$H\left(b\right)\equiv \mathrm{Diag}\left\{{(-1)}^{B.b}\right\}$$

(3)

Then, $H\left(b\right).x\equiv {(-1)}^{B.b}\odot x$ (as before).

So far $\phi$ is subordinate to the choice of B. Yet it might be generalised further.

We consider a group automorphism $\phi :{\mathbb{Z}}^{k_2}\to \mathrm{Aut}\left({\mathbb{Z}}^{k_1}\right)$ whose image subgroup in $\mathrm{Aut}\left({\mathbb{Z}}^{k_1}\right)$ is of finite order. The automorphism group $\mathrm{Aut}\left({\mathbb{Z}}^{k_1}\right)$ is the general linear group $\mathrm{GL}(k_1;\mathbb{Z})$; that is, the group of $k_1\times k_1$ matrices with integer entries and determinant $\pm 1$. The image of $\phi$ is an abelian subgroup of $\mathrm{GL}(k_1;\mathbb{Z})$, and the homomorphism can be represented by picking $k_2$ matrices $M_1,\dots ,M_{k_2}\in \mathrm{GL}(k_1,\mathbb{Z})$ that commute with each other:

$$\phi \left(b\right)=H\left(b\right) \mathrm{where} H\left(b\right)=M_1^{b_1}.\cdots M_{k_2}^{b_{k_2}}.$$

(4)

In the diagonal special case for (4), given by (2) and (3) and leading to the space $\mathbb{K}(k_1,k_2,B)$, we have

$$H\left(b\right)=D_1^{b_1}.\cdots .D_{k_2}^{b_{k_2}},$$

(5)

where each $D_i$ is a diagonal matrix with a sequence of $\pm 1$s down the diagonal. Equation (5) represents the natural factorisation of $H\left(b\right)$ as given in (3).

We let $\mathbb{K}(k_1,k_2;\phi )$ denote the space defined by ${\mathbb{R}}^{k_1}\times {\mathbb{R}}^{k_2}$ modulo the following equivalence relation: for any pair of integers $(a,b)\in {\mathbb{Z}}^{k_1}\times {\mathbb{Z}}^{k_2}$,

$$(x+a,y+b)\sim \left(\phi \right(b)x+a,y+b).$$

(6)

This equivalence relation is in fact the quotient of ${\mathbb{R}}^{k_1}\times {\mathbb{R}}^{k_2}$ by action of the semi-direct product $G={\mathbb{Z}}^{k_1}{⋊}_{\phi }{\mathbb{Z}}^{k_2}$, on which multiplication is given by

$$(a^{\prime },b^{\prime })\diamond (a,b)\sim (\phi \left(b^{\prime }\right)a+a^{\prime },b+b^{\prime }).$$

The group ${\mathbb{Z}}^{k_1}{⋊}_{\phi }{\mathbb{Z}}^{k_2}$ acts on ${\mathbb{R}}^{k_1}\times {\mathbb{R}}^{k_2}$ in the following manner:

$$(a,b)·(x,y)=\left(\phi \right(b)x+a,y+b).$$

(7)

One can easily verify this action is compatible with the group multiplication ⋄.

We make some observations about the group action. The action is free: $(a,b)·(x,y)=(x,y)$ if and only if $(a,b)=(0,0)$, the identity element in G. Furthermore, because any non-identity element of G changes in the coordinates of $(x,y)$ by a non-zero, integer amount, the action is a covering space action on ${\mathbb{R}}^{k_1}\times {\mathbb{R}}^{k_2}$, and the covering of ${\mathbb{R}}^{k_1}\times {\mathbb{R}}^{k_2}$ of $\mathbb{K}$ is a regular covering.

Example 1.

We give an example where the image of φ in (4) is not the subgroup of diagonal matrices. For $k_1=2$ and $k_2=1$, we can have the following homomorphism: $\phi :\mathbb{Z}\to \mathrm{GL}(2,\mathbb{Z})$, where

$$\phi \left(b\right)x\equiv H\left(b\right).x \mathrm{where} H\left(b\right)={\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)}^b.$$

(8)

The action of $(a_1,a_2,b)$ on $(x_1,x_2,y)$ is then given by

$$\left(\begin{array}{c}{x}_1\\ x_2\\ y\end{array}\right)\mapsto \left(\begin{array}{c}{\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)}^b\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)\\ y\end{array}\right)+\left(\begin{array}{c}{a}_1\\ a_2\\ b\end{array}\right)$$

(9)

We note that in this case the parity of b controls whether the $x_1$ and $x_2$ coordinates are swapped (i.e., a reflection across the diagonal of the first two components), whereas previously it controlled the reflection of one or more component coordinates.

3.1. Reduction of Symmetries

Since the equivalence relations on ${\mathbb{R}}^{k_1}\times {\mathbb{R}}^{k_2}$ are due to a quotient by a group action, it suffices to write down the equivalence relations generated by the generators of the group, as they imply all of the other equivalence relations. Since the group ${\mathbb{Z}}^{k_1}{⋊}_{\phi }{\mathbb{Z}}^{k_2}$ is generated by the set $\{(e_i,0),(0,e_j)\}$ where $e_i$s and $e_j$s are unit coordinate vectors in ${\mathbb{Z}}^{k_1}$ and ${\mathbb{Z}}^{k_2}$, respectively, we can express the equivalence relations in Equation (6) as follows: for all $(x,y)\in {\mathbb{R}}^{k_1}\times {\mathbb{R}}^{k_2}$,

$$(x,y)\sim (x+e_i,y) \mathrm{and} (x,y)\sim (\phi \left(e_j\right)x,y+e_j).$$

(10)

We can also choose the set of generators to be those that generate the kernel and co-image of $\phi$. We consider in particular the diagonal case Equation (3), where

$$\begin{array}{c}\hfill \phi \left(b\right)=\mathrm{Diag}\left\{{(-1)}^{B.b}\right\}.\end{array}$$

Regardless of the choice of B, if $b\in {\left(2\mathbb{Z}\right)}^{k_2}$, then $\phi \left(b\right)=1$. We now analyse how the choice of B affects the action. Since ${(-1)}^{2(B.b)}=1$ as well, we can trivially write

$$\begin{array}{c}\hfill \phi \left(b\right)=\mathrm{Diag}\left\{{(-1)}^{(B.(b \mathrm{mod} 2\left)\right) \mathrm{mod} 2}\right\}.\end{array}$$

In other words, we regard the binary matrix B as a linear transformation of ${\mathbb{Z}}_2$-vector spaces. The image of $\phi$ are $k_1$-dimensional diagonal matrices with $\pm 1$ entries. The set of such matrices forms a subgroup of $\mathrm{GL}(k_1,\mathbb{Z})$ isomorphic to ${\mathbb{Z}}_2^{k_1}$. The isomorphism is given by

$$\begin{array}{c}\hfill exp:c\in {\mathbb{Z}}_2^{k_1}\mapsto \mathrm{Diag}\left\{{(-1)}^c\right\}.\end{array}$$

(11)

Thus, we can express $\phi$ as the composition that factors through

$$\phi :{\mathbb{Z}}^{k_2}\stackrel{\mathrm{mod} 2}{\to }{\mathbb{Z}}_2^{k_2}\stackrel{B}{\to }{\mathbb{Z}}_2^{k_1}\underset{\cong }{\overset{exp}{\to }}{\mathbb{Z}}_2^{k_1}.$$

(12)

The kernel $ker\phi$ consists of even integers and integers (mod 2) in the kernel of B; the image of $\phi$ is isomorphic to the image of B in ${\mathbb{Z}}_2^{k_1}$. Computationally, the basis vectors of the kernel and image of B can be easily inferred by performing Gaussian elimination on matrices derived from B over the field ${\mathbb{Z}}_2$. We let $r\le k_2$ be the rank of B, and suppose columns $j_1,\dots ,j_r$ of B form a basis for the image of B. We can express the equivalence relations as

$$(x,y)\sim (x+e_i,y)$$

(13)

$$(x,y)\sim (x,y+2e_j)$$

(14)

$$(x,y)\sim (x,y+c) c\in kerB$$

(15)

$$(x,y)\sim ({(-1)}^{B_{j_k}}\odot x,y+e_{j_k}) k=1,\dots ,r.$$

(16)

We note that c is a vector in ${\mathbb{Z}}_2^{k_2}$, realised as a real vector with $\{0,1\}$ entries in ${\mathbb{R}}^{k_2}$. The first two symmetry conditions is a toroidal symmetry on the whole space. The latter two equivalence relations can be expressed as a ${\mathbb{Z}}_2^{k_2}$ action on the torus obtained by imposing the first two equivalence relations on ${\mathbb{R}}^{k_1}\times {\mathbb{R}}^{k_2}$. We expound on this point of view in Appendix A.

Example 2.

We consider the full coupling case, where B is the $k_1\times k_2$ binary matrix with entries all equal to one. The kernel of B is spanned by $(k_2-1)$${\mathbb{Z}}_2$-vectors

$$(1,1,0,\dots ,0),(0,1,1,0,\dots ,0),\dots ,(0,\dots ,1,1),$$

and the image of B is simply vector $(1,\dots ,1)$. Thus, the equivalence relations are generated by

$$\begin{array}{cc}\hfill (x,y)& \sim (x+e_i,y)\hfill \\ \hfill (x,y)& \sim (x,y+2e_j)\hfill \\ \hfill (x,y)& \sim (x,y+e_i+e_{i+1}) i=1,\dots ,k_2-1\hfill \\ \hfill (x,y)& \sim (-x,y+e_1).\hfill \end{array}$$

3.2. Functions on Klein Bottles

We can specify scalar functions on $\mathbb{K}(k_1,k_2,B)$ uniquely with functions $F:{\mathbb{R}}^{k_1+k_2}\to \mathbb{R}$ that satisfy condition

$$F(x,y)=F\left(\right(a,b)·(x,y\left)\right)=F\left(\phi \right(b)x+a,y+b),$$

(17)

for all $(a,b)\in G={\mathbb{Z}}^{k_1}{⋊}_{\phi }{\mathbb{Z}}_{k_2}$. Because $\mathbb{K}(k_1,k_2,B)$ is a quotient of $q:{\mathbb{R}}^{k_1+k_2}\twoheadrightarrow \mathbb{K}(k_1,k_2)$, any function $f:\mathbb{K}\to \mathbb{R}$ admits a lift $F=f\circ q:{\mathbb{R}}^{k_1+k_2}\to \mathbb{R}$ to a function on the covering space. Alternatively, since $\mathbb{K}(k_1,k_2)$ is the orbit space of the group action of ${\mathbb{Z}}^{k_1}⋊{\mathbb{Z}}^{k_2}$ on ${\mathbb{R}}^{k_1+k_2}$, any function F that is constant on the orbits descends to function f on $\mathbb{K}(k_1,k_2)$, such that $F=f\circ q$.

We begin by demonstrating a simple, practical method of construction for a wide range of functions, F, with the desired properties.

We consider $\mathbb{K}(k_1,k_2,B)$, as before. Suppose that we for each $i=1,\dots ,k_1$ have two non-negative smooth functions, $T_{i,1}\left(y\right)$ and $T_{i,2}\left(y\right)$, defined for $y\in {\mathbb{R}}^{k_2}$, such that

$$T_{i,2}\left(0\right)=1 \mathrm{and} T_{i,2}\left(0\right)=0,$$

and if $B_{i,k}=1$, then $T_{i,1}\left(y\right)$ and $T_{i,2}\left(y\right)$ exchange their values each time $y_k$ is incremented by one. Clearly, $T_{i,1}\left(y\right)$ and $T_{i,2}\left(y\right)$ must be two-periodic in all arguments.

Then, for $b\in {\mathbb{Z}}^{k_2}$, we have

$$\begin{array}{c}\hfill (T_{i,1}(y+b),T_{i,2}(y+b))=\left\{\begin{array}{c}(T_{i,1}\left(y\right),T_{i,2}\left(y\right)) \mathrm{if} {(B.b)}_i \mathrm{is} \mathrm{even},\hfill \\ (T_{i,2}\left(y\right),T_{i,1}\left(y\right)) \mathrm{if} {(B.b)}_i \mathrm{is} \mathrm{odd}.\hfill \end{array}\right.\end{array}$$

We consider the following ansatz:

$$F(x,y)=\prod _{i=1}^{k_1}\left(T_{i,1}\left(y\right)f_i\left(x_i\right)+T_{i,2}\left(y\right)f_i(1-x_i)\right)$$

(18)

Here, the $f_i\left(x_i\right)$, for $i=1,\dots ,k_1$, are arbitrary smooth one-periodic functions, and the pair $T_{i,1}\left(y\right)$ and $T_{i,2}\left(y\right)$ switch, or interpolate, the corresponding term in the product between $f_i\left(x_i\right)$ and its flipped form $f_i(1-x_i)$ as the $y_k$s are incremented. Hence, being a constant along orbit, $F(x,y)$ descends to a function defined on $\mathbb{K}(k_1,k_2,B)$. It is separable, and such that, at $y=0$, we have $F(x,0)={\prod }_{j=1}^{k_1}{f}_j\left(x_j\right).$

The switching functions, $T_{i,1}\left(y\right)$, and $T_{i,2}\left(y\right)$, depend on B and may be defined as follows. First, we consider $\mathbb{K}(k_1,k_2,B)$ and define function $S_i\left(y\right)$ depending on the ith row of B:

$$S_i\left(y\right)\equiv \prod _{k=1}^{k_2}{\left({\displaystyle \frac{-(1-cos\pi y_k)}{2}}+{\displaystyle \frac{(1+cos\pi y_k)}{2}}\right)}^{B_{i,k}}, i=1,\dots ,k_1$$

This product of the sum expression for $S_i$ may be expanded out as a sum of product terms, with each term containing a product of exactly $k_2$ factors. Then, we define $T_{i,1}\left(y\right)$ to be the sum of all the positive terms within that sum (those terms having an even number of negative factors each of the form $\{-(1-cos\pi y_k)\}$ for which $B_{i,k}=1$), and $-T_{i,2}\left(y\right)$ to be the sum of all the negative terms within that sum (those terms having an odd number of negative factors each of the form $\{-(1-cos\pi y_k)\}$ for which $B_{i,k}=1$). Then, by definition, $T_{i,1}$, and $T_{i,2}$ are two-periodic in all of their arguments, and we have

$$S_i\left(y\right)=T_{i,1}\left(y\right)-T_{i,2}\left(y\right),$$

expressing $S_i$ as the difference between two non-negative continuous functions, where $S_I\left(0\right)=T_{i,1}\left(0\right)=1$ and $T_{i,2}\left(0\right)=0$.

Note that we may also write

$$S_i\left(y\right)=\prod _{k=1}^{k_2}{(cos\pi y_k)}^{B_{i,k}}.$$

Hence, when each of the $y_k$s for which $B_{i,k}=1$ are independently incremented by one, $S_i$ must change sign, and consequently $T_{i,1}$ and $T_{i,2}$ must exchange their values. The pair thus subsumes the Klein symmetries of $\mathbb{K}(k_1,k_2,B)$.

Defined in this way or otherwise, the pair $T_{i,1}$ and $T_{i,2}$ implies that function F, given by the ansatz in (18), descends to a scalar field on $\mathbb{K}(k_1,k_2,B)$, as required.

In Appendix A, we consider the necessary and sufficient conditions for scalar fields satisfying the symmetry condition $F\left(z\right)=F(g·z)$ and derive a Fourier basis for such scalar fields. The condition is expressed as F being in the kernel of a linear operator $\mathcal{L}$ on scalar fields, which we describe in Equation (A6). This operator can be interpreted as a graph Laplacian; the technical details are briefly summarised in Remark A3.

Using the Fourier transform (which is natural given the periodicities), the symmetry requirements imposed on F imply constraints on the Fourier coefficients of F. These constraints are expressed, once again, linearly: the coefficients are in the kernel of operator ${\mathcal{L}}^{★}$ on the vector space of Fourier coefficients, which is dual to $\mathcal{L}$ (Equation (A7)). By taking the inverse Fourier transform on coefficients in the kernel of ${\mathcal{L}}^{★}$, we can find a Fourier basis for scalar functions that satisfy the symmetry constraints.

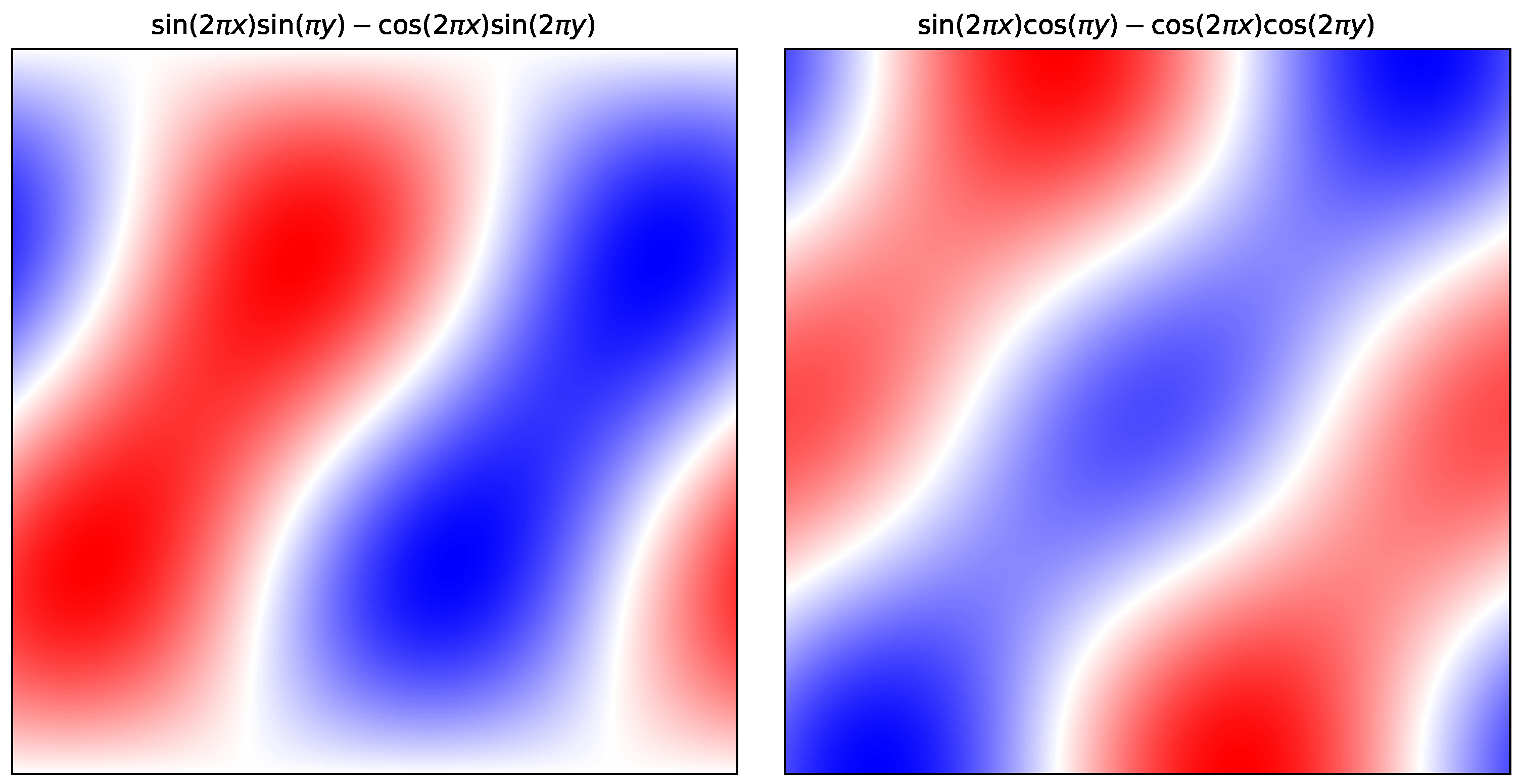
Example 3.

We plot some Fourier modes of scalar fields on the standard Klein bottle in Figure 2 as an illustration. These are formed by linear combinations of Fourier basis functions of the form

$$\begin{array}{cc}\hfill cos\left(2\pi \lambda x\right)cos(\pi \zeta y+\varphi ) & \lambda \in {\mathbb{Z}}_{\ge 0},\zeta even\hfill \\ \hfill sin\left(2\pi \lambda x\right)cos(\pi \zeta y+\varphi ) & \lambda \in {\mathbb{Z}}_{\ge 0},\zeta odd.\hfill \end{array}$$

These are derived in Example A4 in Appendix A. We can verify that these functions satisfy the symmetry conditions: for integers $a,b$, if ζ is even,

$$\begin{array}{cc}\hfill cos\left(2\pi \lambda ({(-1)}^{b}x+a)\right)cos(\pi \zeta (y+b)+\varphi )& =cos\left(2\pi \lambda x\right)cos(\pi \zeta y+\varphi ).\hfill \end{array}$$

On the other hand, if ζ is odd,

$$\begin{array}{cc}\hfill sin\left(2\pi \lambda ({(-1)}^{b}x+a)\right)cos(\pi \zeta (y+b)+\varphi )& ={(-1)}^{b(\zeta +1)}sin\left(2\pi \lambda x\right)cos(\pi \zeta y+\varphi )\hfill \\ \hfill & =sin\left(2\pi \lambda x\right)cos(\pi \zeta y+\varphi ).\hfill \end{array}$$

The calculations in Example A4 show that these functions form a basis for any function admitting a Fourier transform while satisfying the symmetry conditions for the Klein bottle.

3.3. Vector Fields on Klein Bottles

In this section, we offer a parameterisation for continuous vector fields on the Klein bottle, $\mathbb{K}(k_1,k_2,B)$. Unlike Euclidean space, where vector fields can be expressed by any smooth maps ${\mathbb{R}}^d$ to ${\mathbb{R}}^d$, on a Klein bottle we can transport a local coordinate frame around one of the non-contractible loops of $\mathbb{K}(k_1,k_2,B)$ that flips it. In concrete terms, the non-orientability prevents us from expressing vectors at different points on $\mathbb{K}$ with a consistently defined set of global coordinates: we require a flip. In contrast, on the flat torus we can indeed parallel transport a local coordinate frame from one point to any other point and express vectors at different locations with the a coordinate system that is periodic in each toroidal coordinate.

However, we can lift (pull back) vectors on the Klein bottle to its universal covering space ${\mathbb{R}}^{k_1+k_2}$ where we have a global $(x,y)$ coordinate frame. By matching the origin of ${\mathbb{R}}^{k_1+k_2}$ and the coordinate system to the local coordinate system of a point in $\mathbb{K}(k_1,k_2,B)$, the explicit coordinate expression of the vector field lifted in ${\mathbb{R}}^{k_1+k_2}$ should reflect the change in the orientation of the coordinate system in $\mathbb{K}$. We derive the following symmetry condition on lifted vector fields in Appendix B. Writing the lifted vector field V in components $V=(X,Y)$ where $X\in {\mathbb{R}}^{k_1}$ and $Y\in {\mathbb{R}}^{k_2}$, we have, for $(a,b)\in {\mathbb{Z}}^{k_1}⋊{\mathbb{Z}}^{k_2}$,

$${(-1)}^{B.b}\odot X(x,y)=X({(-1)}^{B.b}\odot x+a,y+b)$$

(19)

$$Y(x,y)=Y({(-1)}^{B.b}\odot x+a,y+b).$$

(20)

We begin by demonstrating this possibility via a simplifying ansatz (that subsumes the required Klein symmetries above). We provide a more exhaustive and abstract approach in Appendix B.

First, we consider $\mathbb{K}(k_1,k_2,B)$ and let $T_{i,1}\left(y\right)$ and $T_{i,1}\left(y\right)$ be defined as before, in Section 3.2.

Then, we consider the following ansatz:

$$X_i(x,y)=\left(T_{i,1}\left(y\right)f_{i,i}\left(x_i\right)-T_{i,2}\left(y\right)f_{i,i}(1-x_i)\right)\prod _{j=1 j\ne i}^{k_1}\left(T_{j,1}\left(y\right)f_{i,j}\left(x_j\right)+T_{j,2}\left(y\right)f_{i,j}(1-x_j)\right)$$

(21)

for $i=1,\dots ,k_1;$

$$Y_i(x,y)=\prod _{j=1}^{k_1}\left(T_{j,1}\left(y\right)g_{i,j}\left(x_j\right)+T_{j,2}\left(y\right)g_{i,j}(1-x_j)\right)$$

(22)

for $i=1,\dots ,k_2.$

The form in (21) allows for any of the $x_j$-coordinate dependencies of $X_i$ to be reversed by suitably incrementing the appropriate y-coordinates, and it also induces a change in sign in $X_i$ whenever $x_i$ is reversed. The form in (22) allows for the $x_j$-coordinate dependencies of $Y_i$ to be reversed by suitably incrementing the appropriate y-coordinates.

The vector field given in (21) and (22) respects the appropriate symmetries for $\mathbb{K}(k_1,k_2,B)$, which are inherited from the fact of the swapping of $T_{i,1}$ and $T_{i,2}$ values as appropriate coordinates $y_k$ are incremented by one. Hence, it defines a separable vector field over $\mathbb{K}(k_1,k_2,B)$.

We can, of course, linearly combine similar separable fields to obtain more general flows on $\mathbb{K}(k_1,k_2,B)$. This ansatz establishes existence and provides an accessible way to generate fields.

In Figure 3 and Figure 4, we depict the streamlines for two example flows that were generated in this manner, on $\mathbb{K}(1,1,(1\left)\right)$ and $\mathbb{K}(1,2,(1,1\left)\right)$, respectively.

In Appendix B, we find a Fourier basis for vector fields on $\mathbb{K}(k_1,k_2,B)$. Similar to the approach in Appendix A, we first formulate the symmetry condition as being in the kernel of an operator on the vector space of vector fields. This correspondingly induces a constraint on the Fourier coefficients of the vector fields, expressed as being in the kernel of the dual of the aforementioned operator. We present an example of a vector field on the standard Klein bottle $\mathbb{K}(1,1)$ in Figure 5, constructed on a Fourier basis.

4. A Challenge: Spiking Dynamical Systems Modelling Neural Columns

Here, we discuss an application of dynamical systems with attractors set within compact manifolds having topological structures that need to be determined. This raises a number of challenges.

Human brains have evolved both architectures and dynamics to enable effective information processing with around ${10}^{10}$ neurons. These spiking dynamical systems (SDSs) represent challenges of large-scale state spaces containing many possible cyclic interactions between neurons. Such brains exhibit a directed network-of-networks architecture, with the inner, densely connected, networks of neurons called neural columns (see [3] and the references therein). Near-neighbouring neural columns have relatively sparse directed connections compared to the outer network (between pairs of neurons, one from each).

Following [4] (and subsequent very large-scale simulations [5]), we consider the dynamics of information processing within SDSs representing neural columns, with ${10}^2–{10}^4$ nodes representing the neurons. Each node is both excitable and refractory: if the node is in its ready state when it receives an incoming spike, from an upstream neighbour, then it instantaneously fires and emits an outgoing signal spike along the directed edges to each of its downstream neighbours, which takes a small time to arrive. Once it fires, there must be a short refractory period whilst the node recovers its local chemical equilibrium. During this time, it cannot re-fire and just ignores any further incoming spike signals. Once the refractory period is complete, the node returns to the ready state. The refractory time period prevents arbitrarily fast bursting (rapid repeat firing) phenomena.

We consider sparse directed networks that are irreducible, so that all nodes may be influenced by all others. The whole network should exhibit a relatively small diameter. We set an appropriate set of transit times for each directed edge, independently and identically drawn from a uniform distribution, and a common refractory period time, $\delta$, for all nodes. 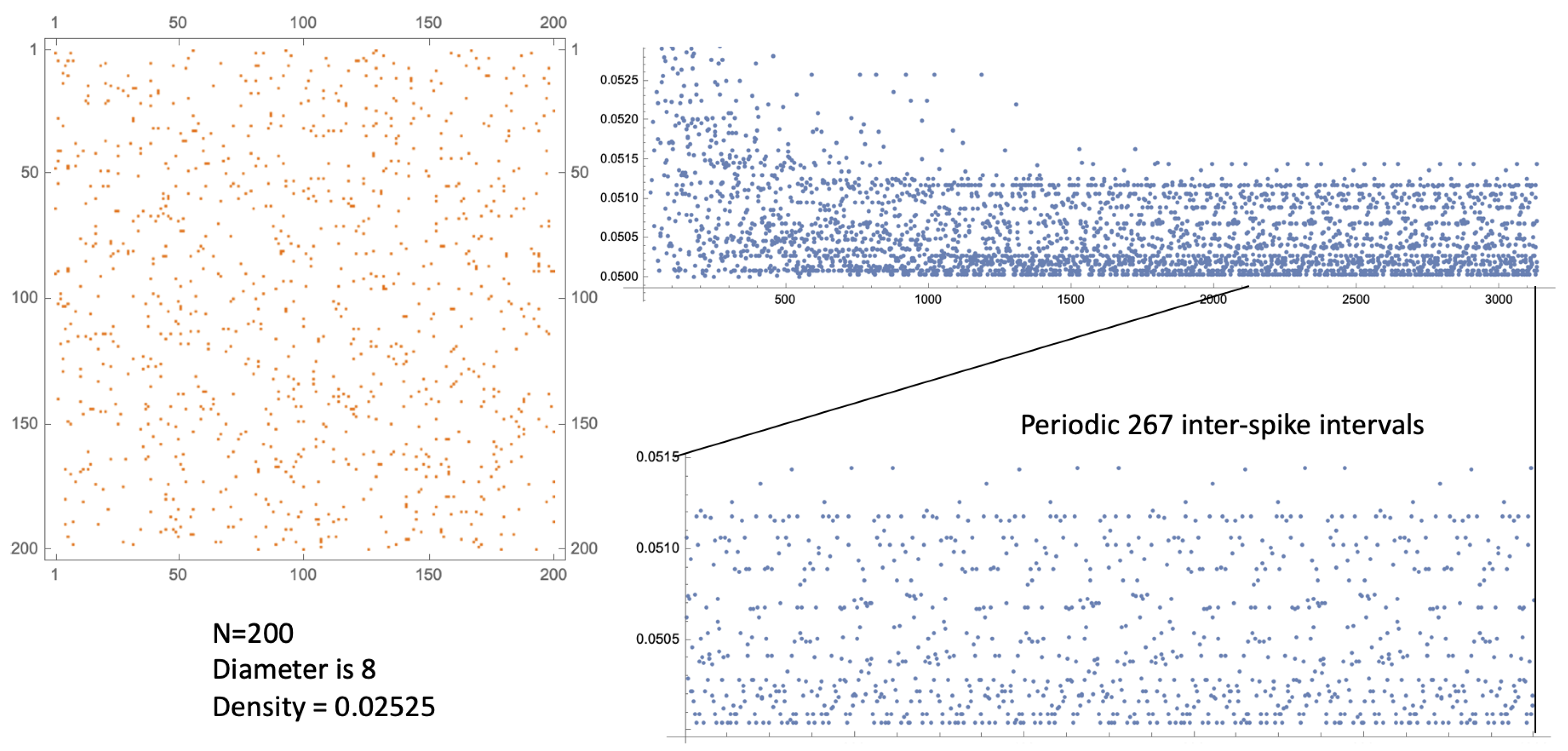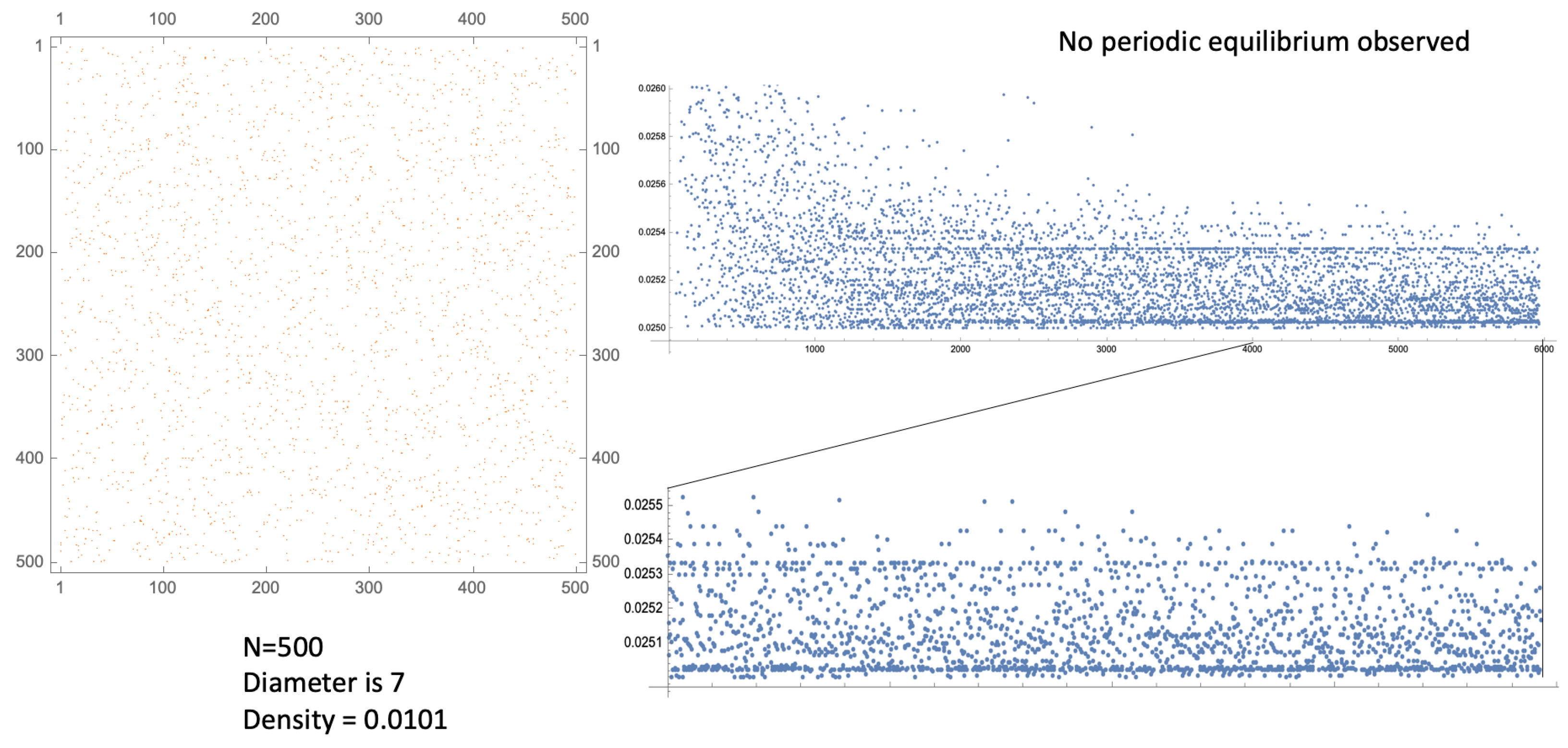Then, the whole SDS may be kick-started with a single spike at $t=0$ at a particular node, while all other nodes begin in their ready resting state. The dynamic results in a firing sequence for each node: a list of firing times at which that node instantaneously spikes. The SDS begins to chatter amongst itself and, after a burn-in period, it settles down to some very long-term pattern (see [6] for an observed instance). It is deterministic and possibly chaotic: see Figure 6 and Figure 7 for typical examples.

Since the network is irreducible, we cannot consider sub-networks of the nodes; and not all independent walks from one specific node to another may be viable: two such walks may result in spike arrival times less that $\delta$ apart, with the latter one ignored. However, the irredicibility does mean that in order to examine the dynamical behaviour of the whole system, it is enough to examine a single node. Furthermore, as the spikes are instantaneous, it is conventional within spike sequence analysis to examine the corresponding sequence of successive inter-spike intervals (ISIs) [6]. By definition, these are real and are bounded below by $\delta$. The SDS model timescale is arbitrary: results depend only on the size of $\delta$ relative to the range of the independent and identically distributed random variable edge transit time.

The SDS examples in Figure 6 and Figure 7 illustrate these features. The ISI sequences suggest dynamics within a bounded attractor, that lies within some manifold, $\mathcal{M}$, say, of unknown dimension and topology. Generalised Klein bottles and tori are candidates for $\mathcal{M}$.

We embed the observed ISI sequence as a point cloud within ${\mathbb{R}}^L$ by discarding the ISI burn-in and moving a window of length L successively along the sequence. Then, we estimate the dimension, $D_{\mathcal{M}}\left(L\right)$, of the curved manifold, $\mathcal{M}\subset {\mathbb{R}}^L$, on which that point cloud lives, from the set of all pairwise distances between points within the cloud via the 2NN (two nearest neighbour) method [7]. For a small L, the point cloud (and $\mathcal{M}$) merely fills up the available dimensions, so $D_{\mathcal{M}}\left(L\right)\sim L$. As L increases further, we have estimates $D_{\mathcal{M}}\left(L\right)<<L$.

Considering a post burn-in ISI sequence of length 1900 from the example given in Figure 7, we need to take $L\ge 40$ to avoid any duplicate points from windows along the sequence (which we know to be non-periodic). For lower values of L, we remove any duplicates from the point cloud (which otherwise interfere with the 2NN algorithm).

We apply this method to the post burn-in ISI sequence, of length 1900, given in Figure 7 in Figure 8 (Left, Green). This suggests dimension, $D_{\mathcal{M}}$, of 5 to 7 at the first obvious plateau, embedded in $L=7$ to 11 dimensions. If L is increased further, then $D_{\mathcal{M}}\left(L\right)$ increases rather slowly as the attractor fills in somewhat. For comparison, we show the result for the 267-periodic case given in Figure 6 (left, red) where, necessarily, we have 267 windowed points. This suggests a dimension, $D_{\mathcal{M}}$, between four and six.

It is clear that this class of SDSs gives rise to highish dimensional compact attractors. What is required is a pipeline that begins from a suitable embedding of the post-burn-in ISIs into some ${\mathbb{R}}^L$ (just as above, which determined the dimension, $D_{\mathcal{M}}\left(L\right)$, of the manifold, $\mathcal{M}$, containing the attractor), followed by a computational method (most likely based on persistent homology) that can determine (a) the main topological features of the manifold containing the point cloud, and subsequently (much more challenging) (b) the topological symmetries that can differentiate between various generalised Klein bottles of given dimensions ($k_1+k_2\approx D_{\mathcal{M}}\left(L\right)$).

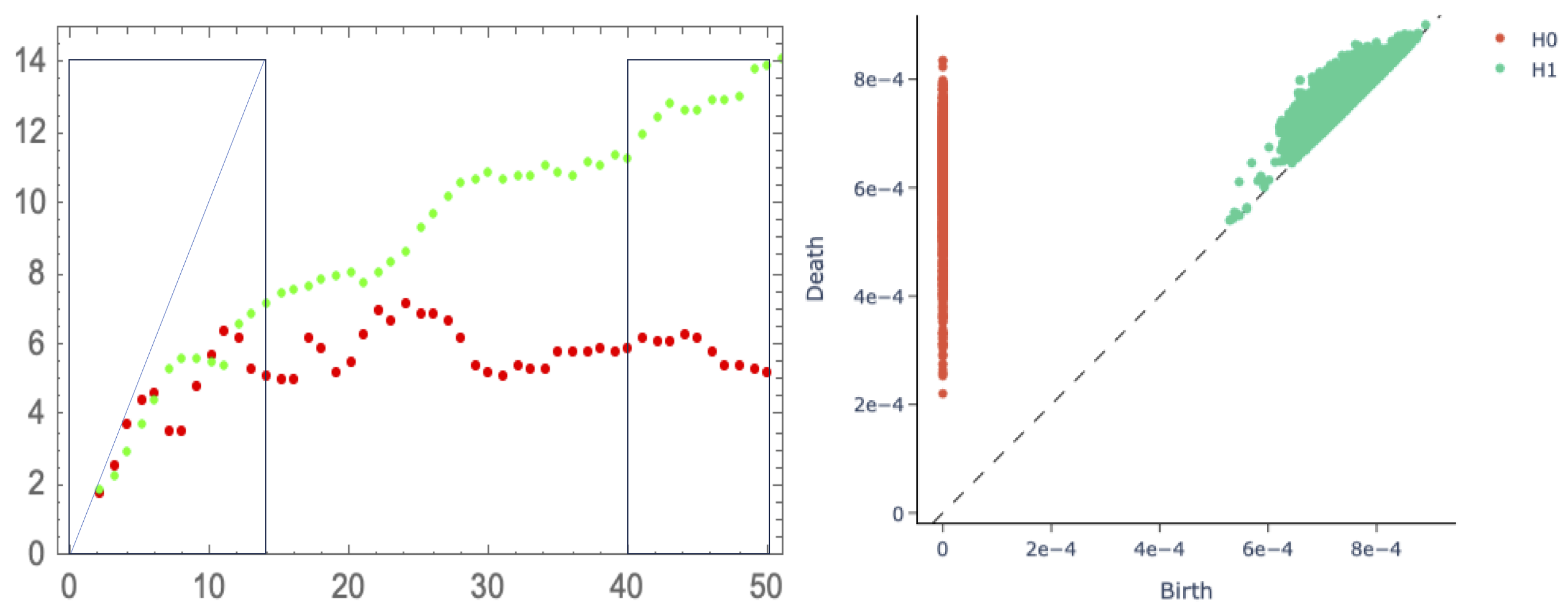
Following Figure 8 (left) and embedding the 267-periodic ISI from Figure 6 into $L=16$ dimensions (whence the estimate $D_{\mathcal{M}}\left(L\right)\approx 5.1$), a persistent homology (PH) analysis is shown in Figure 8 (right). It is somewhat inconclusive, possibly due to the variations in the localised cloud density. This issue is the subject of active research.

It is this characterisation of the SDS’s unknown attracting manifolds that drives the permissive generalisation of Klein bottles presented in this paper. This is the subject of active ongoing research.

5. Discussion

In this paper, we introduced a generalisation of the standard Klein bottle to higher dimensions, beyond those previously considered. We focused on a subclass where the automorphisms are diagonal, inducing flips (reflections) of some independent coordinates.

For all such Klein bottles, we produced both a simple (practical) method and a rigorous argument for the definition of scalar fields (such as smooth probability distributions and potentials) as well as vector fields (flows) that are well defined. These constructions are useful when we wish to consider winding flows over Klein bottles and possibly couple them together.

This class of Klein bottles can be extended to include automorphisms that induce swaps (permutations) between toroidal coordinates (diagonal reflections rather than individual coordinate reflections). In future work, we will extend this approach to consider an even wider class of compact manifolds without boundaries, including real projective geometries, for which there is not a partition of coordinates into Klein variables (controlling the automorphisms), and toroidal variables (acted on by the automorphisms). Since spheres are the universal covering spaces of projective spaces, we would consider lifts of vector fields on the projective plane to its universal covering sphere to parametrise them and express their Fourier basis with spherical harmonics that respect the required symmetries.

Finally, we set out a challenging application where high-dimensional spiking dynamical systems result in attractors over unknown compact manifolds which require characterisation. This is highly problematic when the dimension of such spiking systems is very large and the resulting ISI sequences have to be embedded within a suitable space. The identification of the dimension and the topological properties of resultant attractor manifolds is both a theoretical and a computational challenge.