Towards a Global Scale Quantum Information Network: A Study Applied to Satellite-Enabled Distributed Quantum Computing
Abstract
1. Introduction
2. Generic QIN Network Architectures
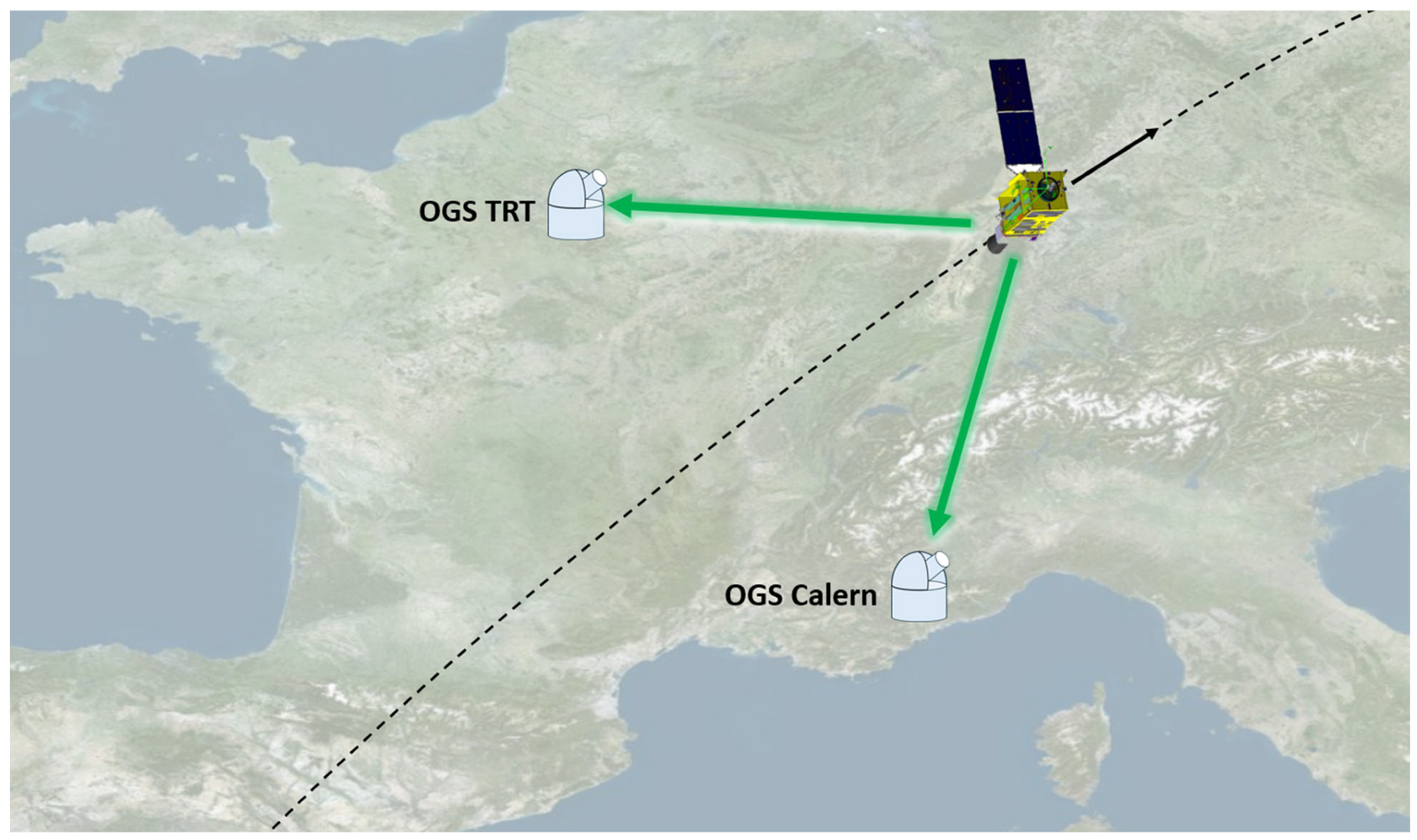
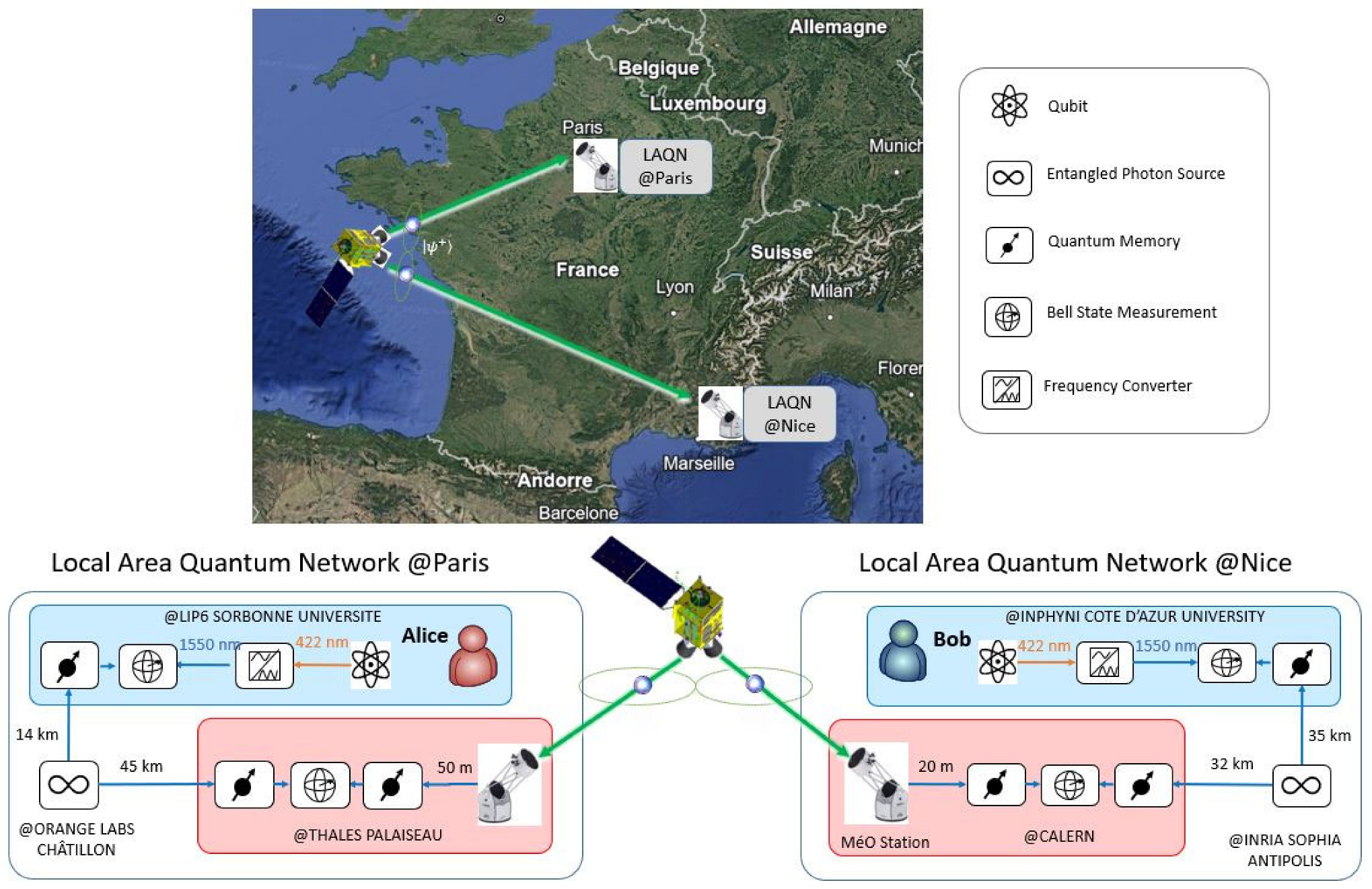
3. Proposal of In-Field Implementation
- Alice, a quantum chip, with one BSM and one quantum memory, located at LIP6 Sorbonne University Laboratory;
- An entangled photon source at ORANGE LAB at Châtillon;
- A BSM device, with two quantum memories and with an optical ground station (i.e., a telescope), at THALES Palaiseau.
- Bob, a quantum chip, with one BSM and one quantum memory, located at INPHYNI Côte d’Azur University Laboratory;
- An entangled photon source at INRIA Sophia Antipolis;
- A BSM device, with two quantum memories and an optical ground station (MéO [32]), at Calern.
3.1. Entanglement Distribution Model
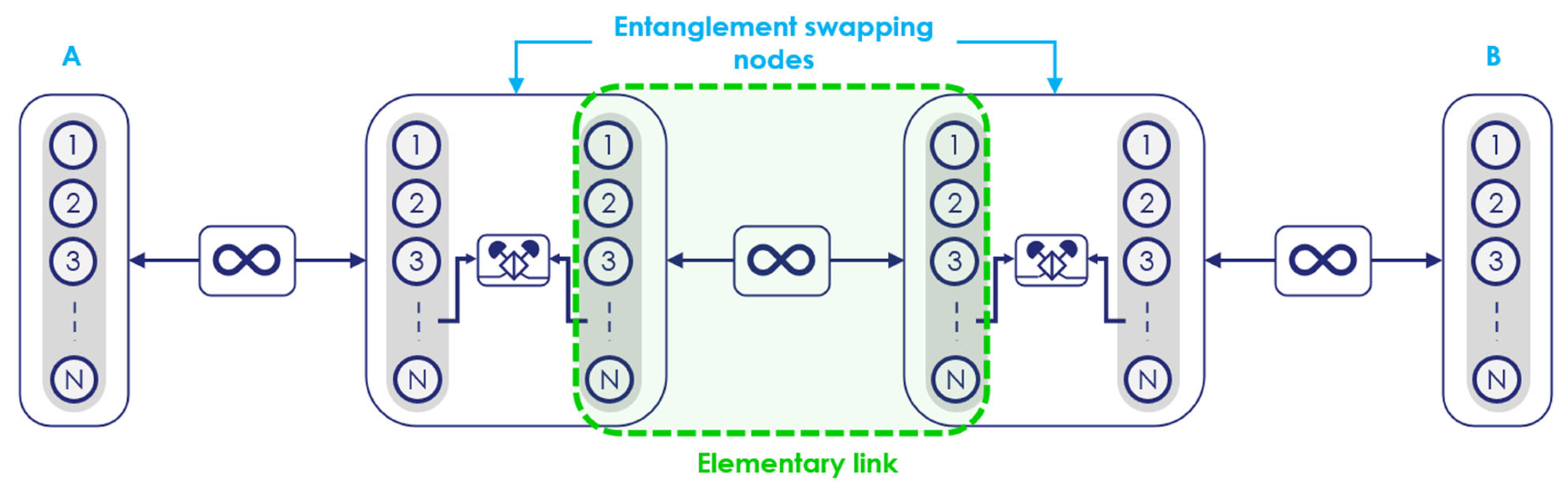
- being the swapping rate, given by the source rate divided by the number of modes of the quantum memories (the swaps are performed after time steps; see the entanglement swapping procedure discussion below);
- , with being the wavelength conversion efficiency from 422 nm to 1550 nm (see use case section) and being the efficiency of quantum memory, given by Equation (A1) in the Appendix A;
- , with being the efficiency of the Bell state measurement device and being the single photon SNSPD detector efficiency;
- and being the efficiency of an elementary ground path, given by Equation (A4) in the Appendix A;
- being the efficiency of the elementary space path, given by Equation (A5) in the Appendix A.
3.2. Entanglement Swapping Procedure
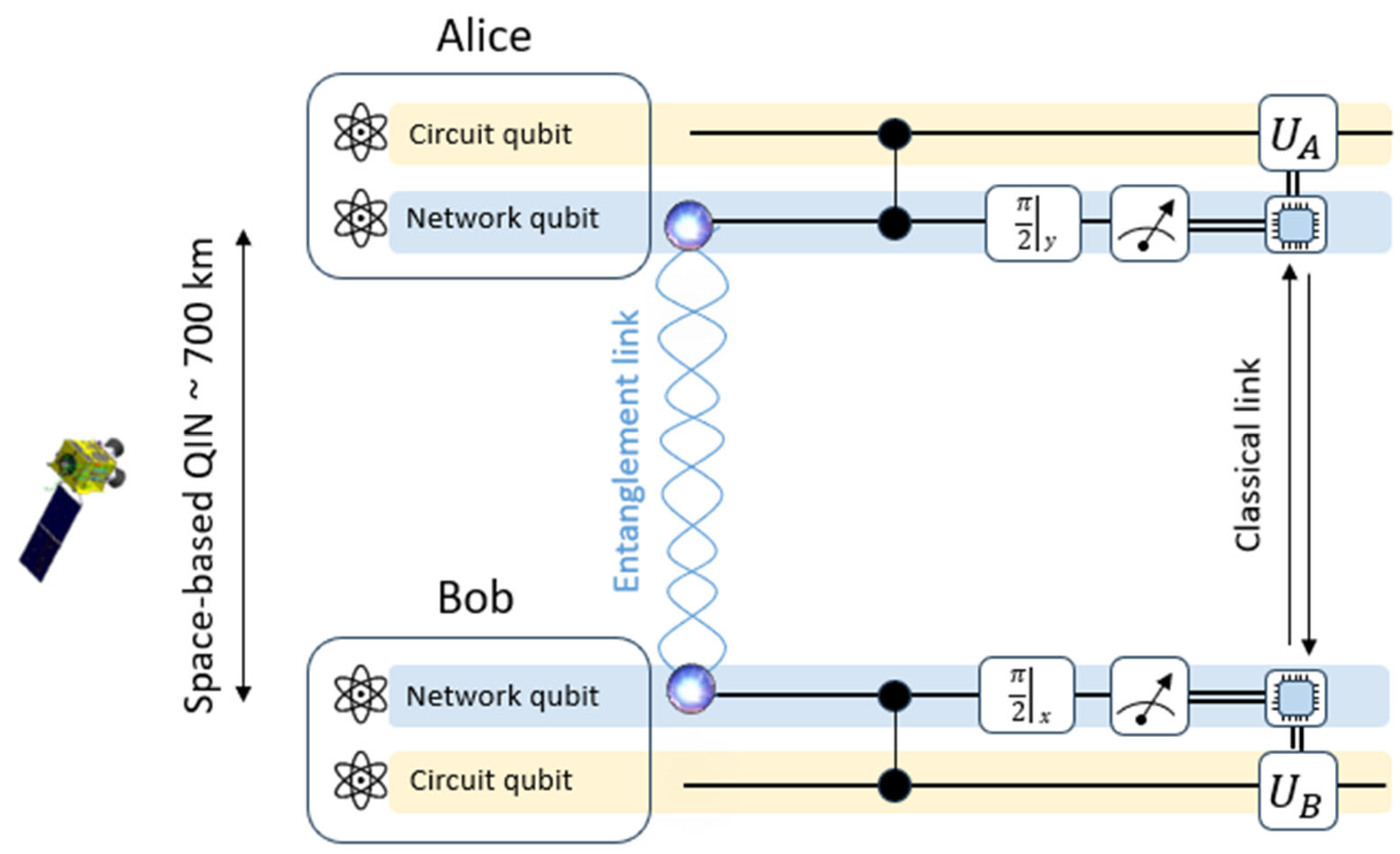
3.3. Quantum Distributed Computing Use Case
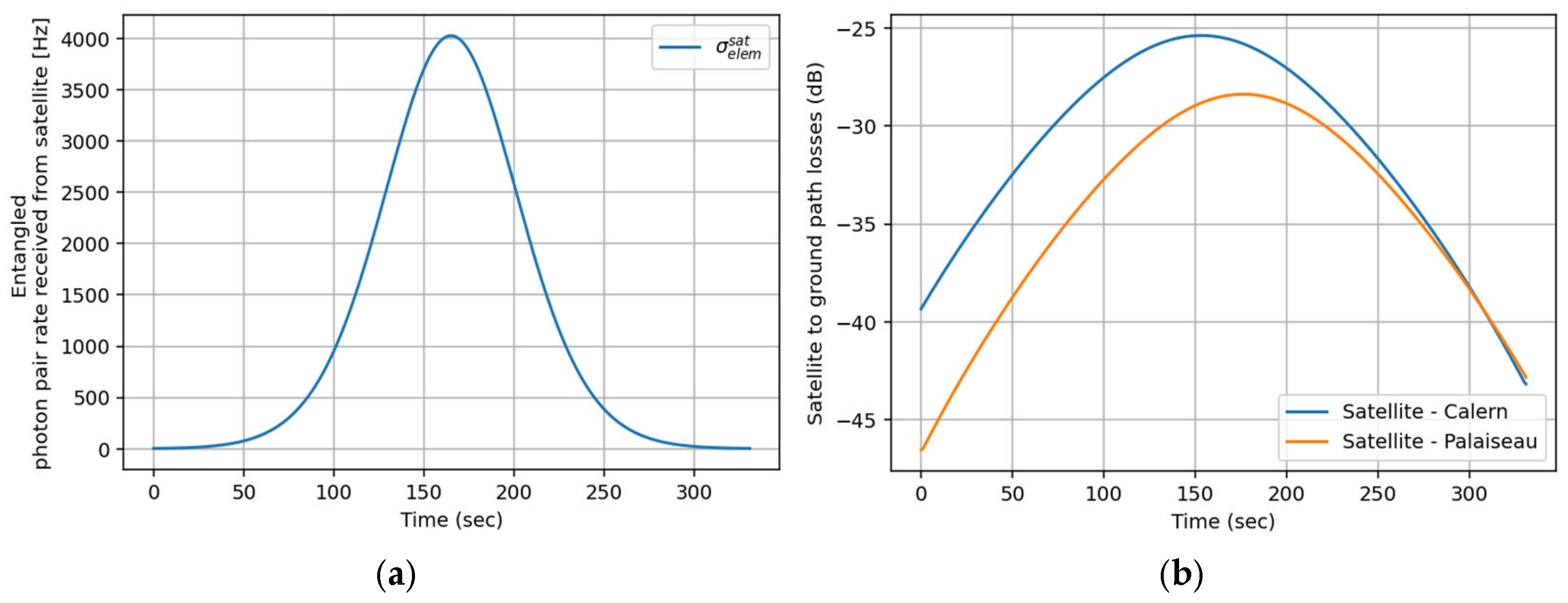
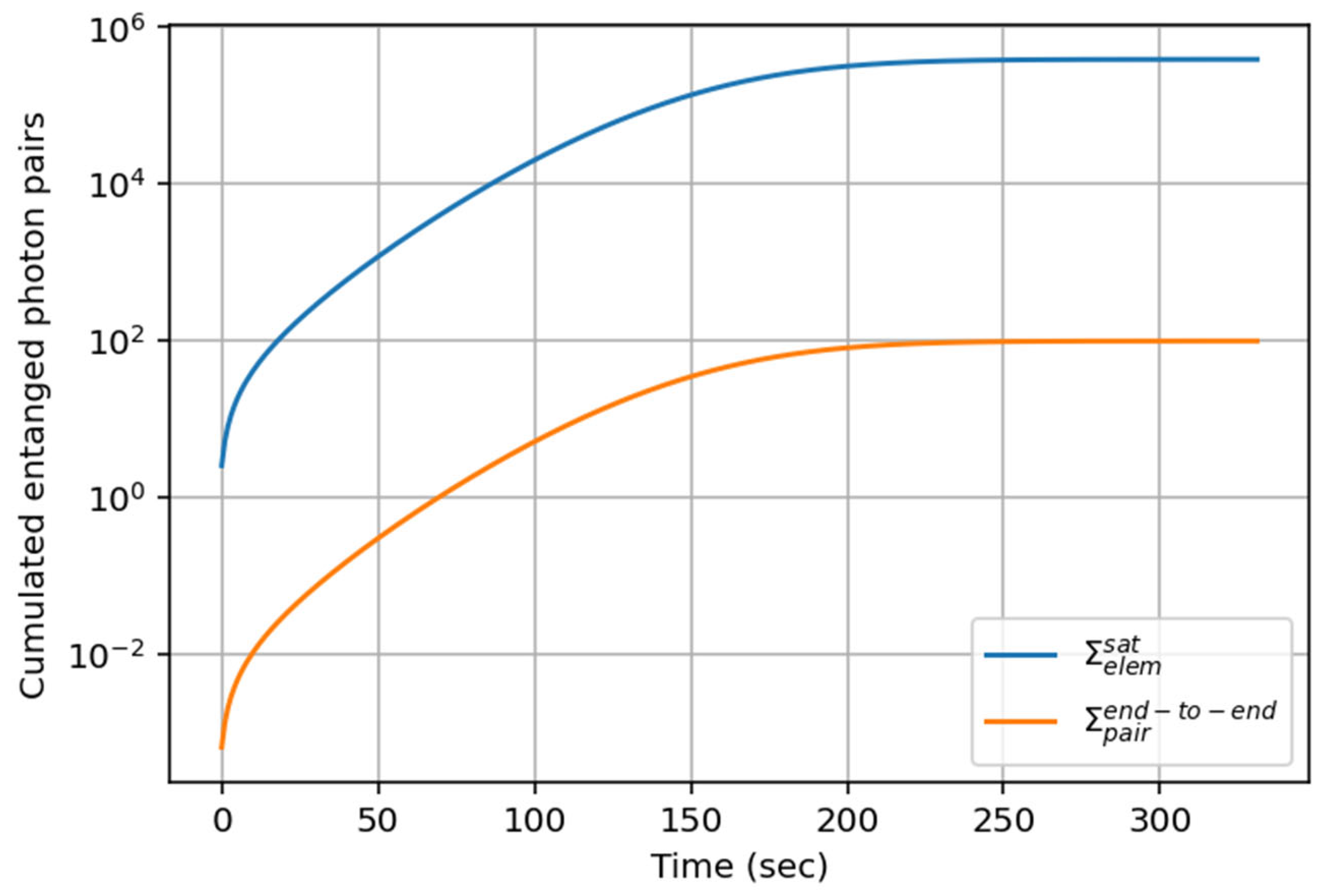
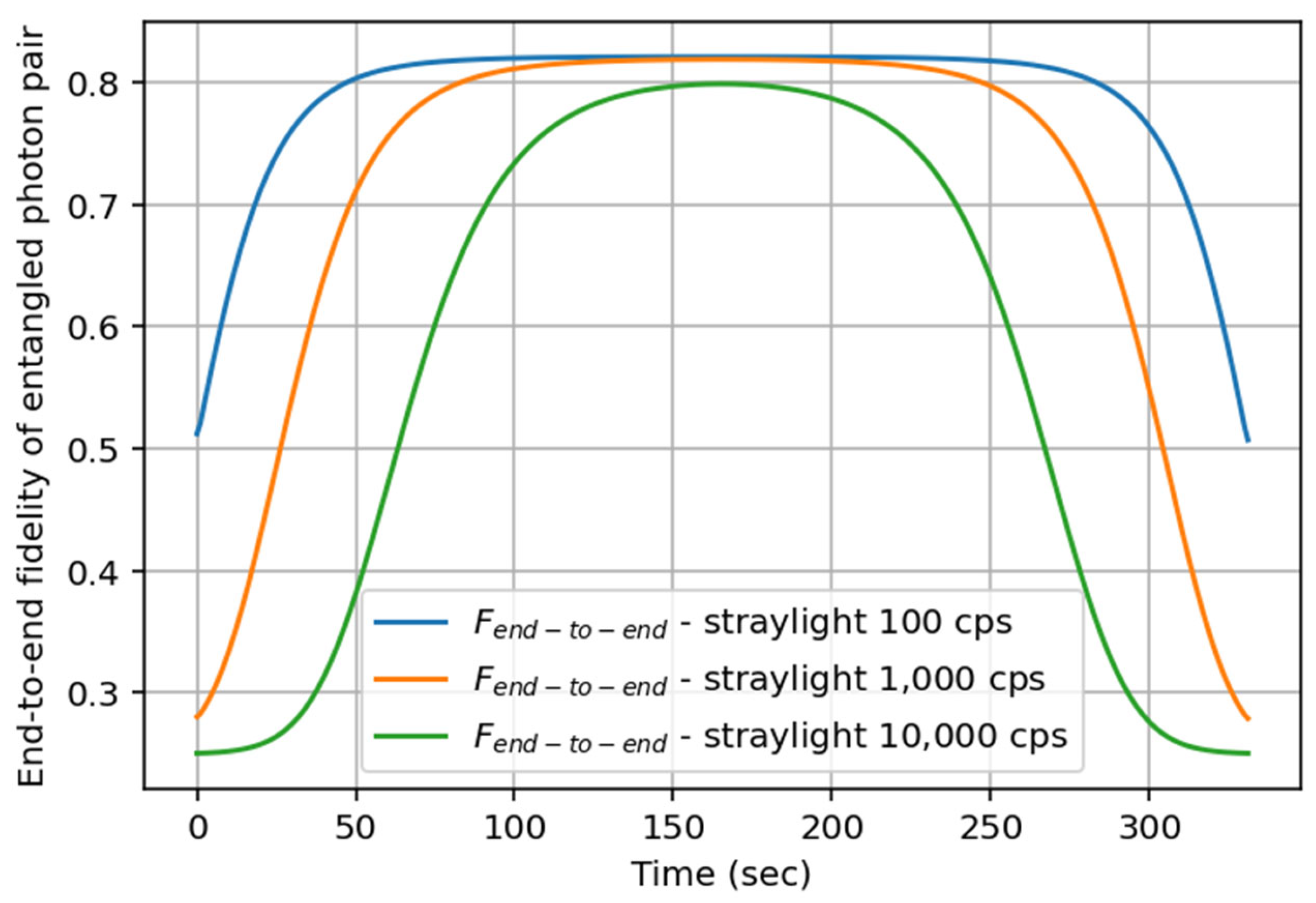
4. Space-Based QIN Performances
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Model for the Efficiency of the Ground Elementary Links

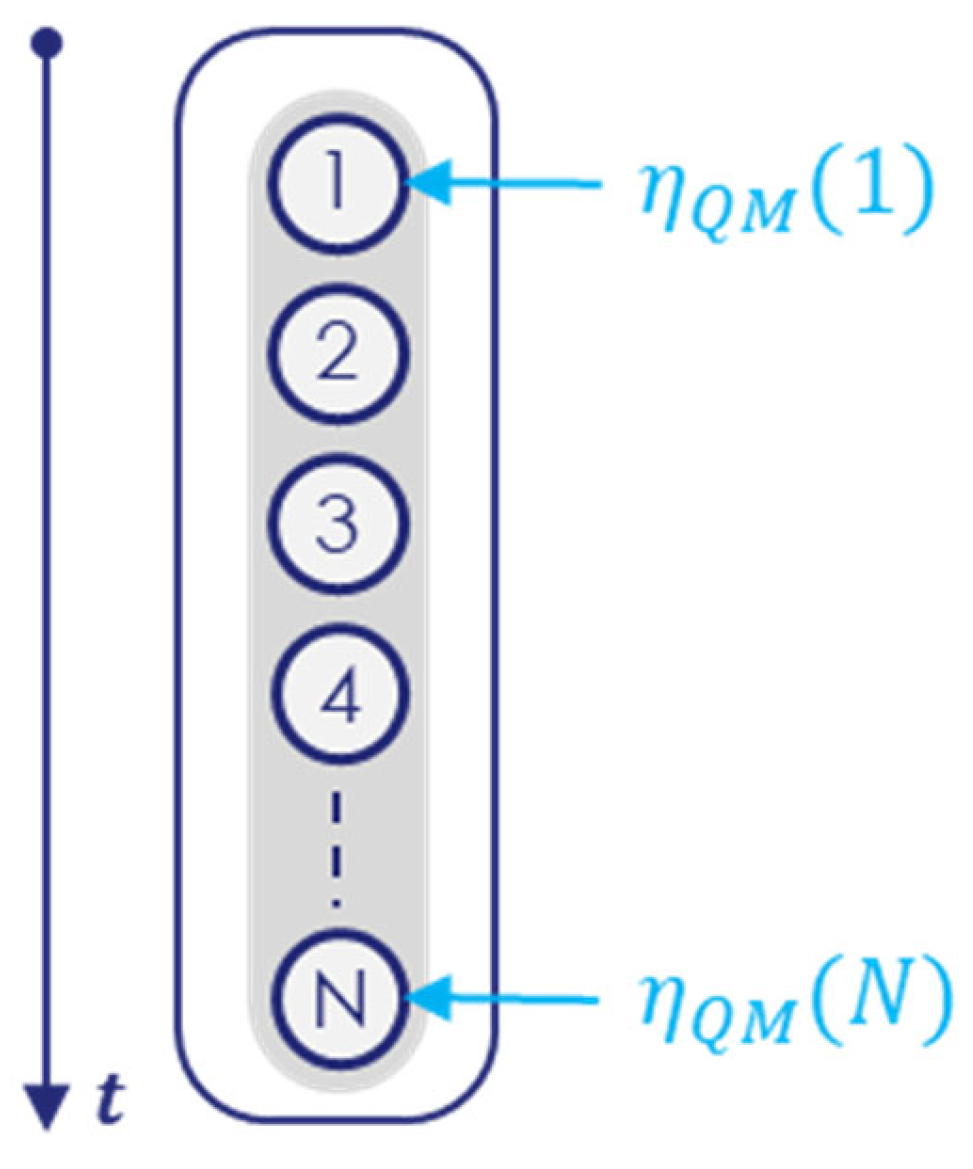
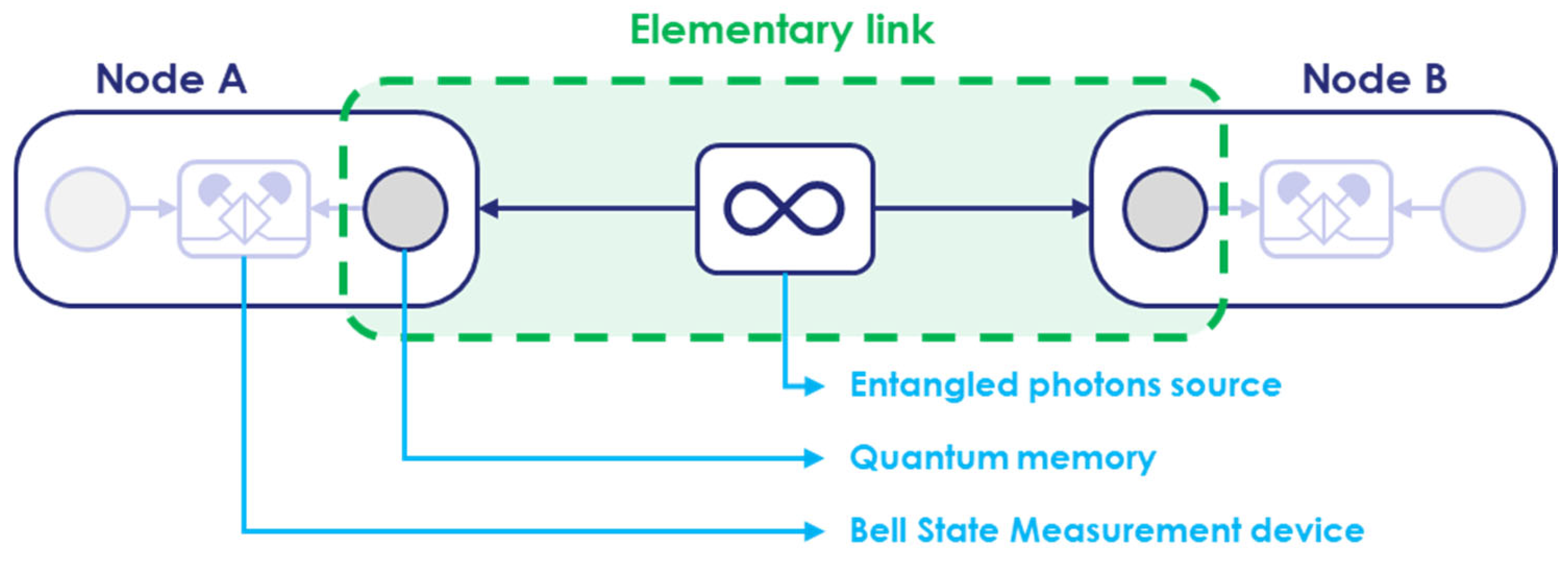
- A source of entangled photon pairs;
- Two propagation channels (on either side of the source);
- Two quantum memories.
- Bell state measurement device (BSM);
- Single photon detectors.
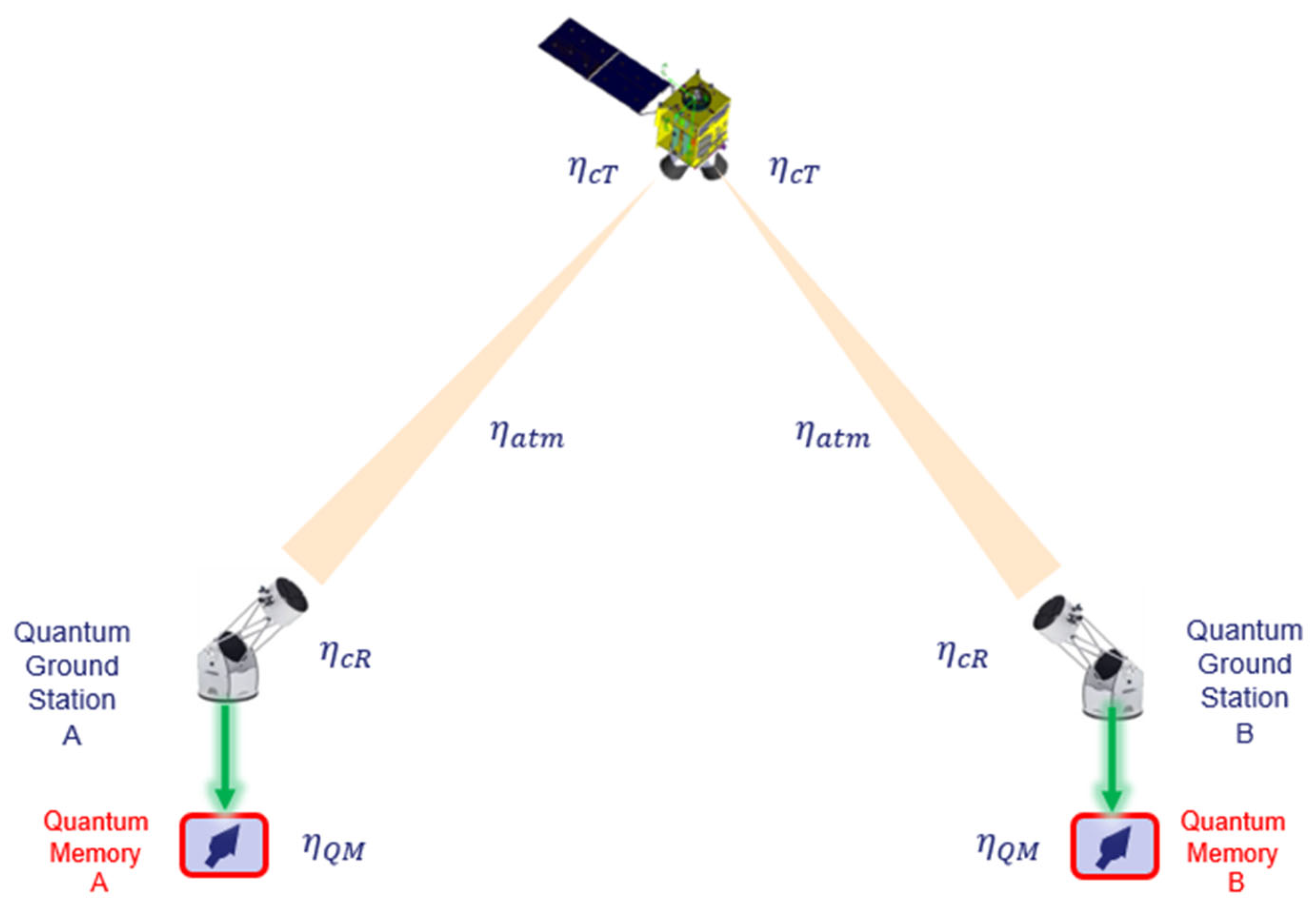
Appendix A.2. Model for the Efficiency of the Space Elementary Link
- being the efficiency of the entangled photons source; see Table A1;
- being the channel efficiency of channel A; see Equation (A7);
- being the channel efficiency of channel B; see Equation (A7);
- being the efficiency of the quantum memory; see Equation (A1).
- being the power of the entangled photon source.
- being the transmitter gain (telescope efficiency). is the internal transmittance of the on-board telescope (including wave front errors and obscuration), is the telescope aperture, and is the beam waist at the output of the telescope.
- being the downlink atmospheric losses (absorption, scattering, cirrus clouds, aerosols)., where is the satellite elevation and is the atmospheric losses when the satellite is at zenith (
- being the receiver gain at the telescope level (telescope efficiency). is the internal losses of the receiver telescope (including wave front errors, obscuration, optical fiber coupling with adaptive optics), is the telescope aperture, and the received beam waist at the ground station side (with ), with being the free space length between the satellite and the receiver’s telescope pupil.
Appendix A.3. Model for the Werner Parameter of the End-to-End Path
- Click rate of detection of a photon coming from the source
- False click rate (due to dark counts, etc., a photon not coming from the source).
Appendix A.4. Satellite Orbit
Appendix A.5. List of Parameters
| Parameter | Symbol | Value |
|---|---|---|
| Satellite altitude | ||
| Satellite inclination | 60 degrees | |
| Right ascension of the ascending node (RAAN) | 72.5 degrees | |
| Start simulation date | 1 January 2025—00:00:00 nighttime | |
| Entangled photon source wavelength | ||
| Entangled photon source efficiency | ||
| Entangled photon source rate | ||
| Wavelength conversion efficiency | 0.8 | |
| Wavelength conversion fidelity | 0.98 | |
| Entangled photon source fidelity | ||
| Quantum memory writing efficiency | 8 | |
| Quantum memory fidelity | ||
| Quantum memory storage modes | ||
| Quantum memory characteristic storage time | ||
| Quantum memory storage window | ||
| SNSPD detector efficiency (for all polarization states) | ||
| SNSPD detector dark count rate for the ground network | ||
| BSM efficiency | ||
| Optical fiber attenuation | ||
| Optical fiber link fidelity | ||
| Tx telescope diameter | ||
| Rx telescope diameter MéO station @Calern | ||
| Rx telescope diameter station @THALES Palaiseau | ||
| Free space link fidelity | ||
| Atmospheric transmittance when the satellite is at zenith | ||
| Internal transmittance of the ground telescope (adaptive optics included for single mode fiber coupling) | ||
| Internal transmittance of the on-board telescope |
References
- Einstein, A.; Podolsky, B.; Rosen, N. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Phys. Rev. 1935, 47, 777–780. [Google Scholar] [CrossRef]
- Steane, A. Quantum computing. Rept. Prog. Phys. 1998, 61, 117–173. [Google Scholar] [CrossRef]
- Nielsen, M.; Chuang, I. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Jiang, L.; Taylor, J.M.; Sorensen, A.S.; Lukin, M.D. Distributed quantum computation based on small quantum registers. Satellite-to-ground quantum key distribution. Phys. Rev. A 2007, 76, 062323. [Google Scholar] [CrossRef]
- Rad, H.A.; Ainsworth, T.; Alexander, R.N.; Altieri, B.; Askarani, M.F.; Baby, R.; Banchi, L.; Baragiola, B.Q.; Bourassa, J.E.; Chadwick, R.S.; et al. Scaling and networking a modular photonic quantum computer. Nature 2025, 638, 912–919. [Google Scholar] [CrossRef] [PubMed]
- Available online: https://www.ibm.com/roadmaps/quantum/2025/ (accessed on 1 November 2025).
- Available online: https://spectrum.ieee.org/quantum-computers (accessed on 27 February 2025).
- Main, D.; Drmota, P.; Nadlinger, D.P.; Ainley, E.M.; Agrawal, A.; Nichol, B.C.; Srinivas, R.; Araneda, G.; Lucas, D.M. Distributed quantum computing across an optical network link. Nature 2025, 638, 383–388. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.L.; Luo, X.Y.; Yu, Y.; Wang, C.Y.; Wang, B.; Hu, Y.; Li, J.; Zheng, M.Y.; Yao, B.; Pan, J.W.; et al. A multinode quantum network over a metropolitan area. Nature 2024, 629, 579–585. [Google Scholar] [CrossRef] [PubMed]
- van Leent, T.; Bock, M.; Garthoff, R.; Redeker, K.; Zhang, W.; Bauer, T.; Rosenfeld, W.; Becher, C.; Weinfurter, H. Long-distance distribution of atom-photon entanglement at telecom wavelength. Phys. Rev. Lett. 2020, 124, 010510. [Google Scholar] [CrossRef]
- Quantum Internet Alliance, Technologies Quantiques|Thales Group, Thales Alenia Space and Partners Sign Contract with ESA for TeQuantS Quantum Satellite Communications Project|Thales Alenia Space, Consortium–LaiQa Project, Quantum Internet-QuTech, TNO Launches Qu-STAR to Pioneer Quantum Internet via Space, Science and Technology-Q-NEXT. Available online: https://www.thalesaleniaspace.com/en/press-releases/thales-alenia-space-and-partners-sign-contract-european-space-agency-tequants (accessed on 2 November 2025).
- de Forges de Parny, L.; Alibart, O.; Debaud, J.; Gressani, S.; Lagarrigue, A.; Martin, A.; Metrat, A.; Schiavon, M.; Troisi, T.; Van Den Bossche, M.; et al. Satellite-based quantum information networks: Use cases, architecture, and roadmap. Commun. Phys. 2023, 6, 12. [Google Scholar] [CrossRef]
- Du, D.; Castillo-Veneros, L.; Cottrill, D.; Cui, G.D.; Stankus, P.; Katramatos, D.; Martínez-Rincón, J.; Figueroa, E. A long-distance quantum-capable internet testbed. arXiv 2024, arXiv:2101.12742. [Google Scholar]
- Available online: https://www.stonybrook.edu/commcms/CDQP-Inaugural-Workshop/About_the_Center/Testbed.php (accessed on 1 November 2025).
- Craddock, A.N.; Lazenby, A.; Portmann, G.B.; Sekelsky, R.; Flament, M.; Namazi, M. Automated distribution of high-rate, high-fidelity polarization entangled photons using deployed metropolitan fibers. arXiv 2024, arXiv:2404.08626. [Google Scholar]
- Knaut, C.M.; Suleymanzade, A.; Wei, Y.C.; Assumpcao, D.R.; Stas, P.J.; Huan, Y.Q.; Machielse, B.; Knall, E.N.; Sutula, M.; Lukin, M.D.; et al. Entanglement of nanophotonic quantum memory nodes in a telecom network. Nature 2024, 629, 573–578. [Google Scholar] [CrossRef] [PubMed]
- Lago-Rivera, D.; Grandi, S.; Rakonjac, J.V.; Seri, A.; de Riedmatten, H. Telecom-heralded entanglement between multimode solid-state quantum memories. Nature 2021, 594, 37–40. [Google Scholar] [CrossRef] [PubMed]
- Rakonjac, J.V.; Grandi, S.; Wengerowsky, S.; Lago-Rivera, D.; Appas, F.; de Riedmatten, H. Transmission of light–matter entanglement over a metropolitan network. Opt. Quantum 2023, 1, 94–102. [Google Scholar] [CrossRef]
- Liu, J.L.; Luo, X.Y.; Yu, Y.; Wang, C.Y.; Wang, B.; Hu, Y.; Li, J.; Zheng, M.Y.; Yao, B.; Pan, J.W.; et al. Creation of memory–memory entanglement in a metropolitan quantum network. Nature 2024, 629, 579–585. [Google Scholar] [CrossRef]
- Pelet, Y.; Sauder, G.; Cohen, M.; Labonté, L.; Alibart, O.; Martin, A.; Tanzilli, S. Operational entanglement-based quantum key distribution over 50 km of real-field optical fibres. arXiv 2023, arXiv:2207.14707. [Google Scholar]
- Available online: https://www.welinq.fr/ (accessed on 1 November 2025).
- Yin, J.; Cao, Y.; Li, Y.-H.; Liao, S.-K.; Zhang, L.; Ren, J.-G.; Cai, W.-Q.; Liu, W.-Y.; Li, B.; Dai, H.; et al. Satellite-based entanglement distribution over 1200 kilometers. Science 2017, 356, 1140–1144. [Google Scholar] [CrossRef]
- Azuma, K.; Economou, S.E.; Elkouss, D.; Hilaire, P.; Jiang, L.; Lo, H.K.; Tzitrin, I. Quantum repeaters: From quantum networks to the quantum internet. Rev. Mod. Phys. 2023, 95, 045006. [Google Scholar] [CrossRef]
- Simon, C. Towards a global quantum network. Nat. Photon 2017, 11, 678–680. [Google Scholar] [CrossRef]
- Pant, M.; Krovi, H.; Towsley, D.; Tassiulas, L.; Jiang, L.; Basu, P.; Englund, D.; Guha, S. Routing entanglement in the quantum internet. Npj Quantum Inf. 2019, 5, 25. [Google Scholar] [CrossRef]
- Floyd, J.C.; Kwiat, P. Toward entanglement swapping between moving platforms. In Proceedings of the Quantum Computing, Communication, and Simulation V, San Francisco, CA, USA, 25–31 January 2025; Volume 13391. [Google Scholar]
- Bakker, D.L.; Jong, Y.; Dirks, B.P.; Amaral, G.C. A Best-Path Approach to the Design of a Hybrid Space-Ground Quantum Network with Dynamic Constraints. Photonics 2024, 11, 268. [Google Scholar] [CrossRef]
- Bouwmeester, D.; Pan, J.W.; Mattle, K.; Eibl, M.; Weinfurter, H.; Zeilinger, A. Experimental quantum teleportation. Nature 1997, 390, 575–579. [Google Scholar] [CrossRef]
- Yehia, R.; Neves, S.; Diamanti, E.; Kerenidis, I. Quantum City: Simulation of a practical near-term metropolitan quantum network. arXiv 2022, arXiv:2211.01190. [Google Scholar] [CrossRef]
- Available online: https://en.institutparisregion.fr/fileadmin/NewEtudes/000pack2/Etude_2682/NR__49_web.pdf (accessed on 1 September 2021).
- Pelet, Y.; Sauder, G.; Tanzilli, S.; Alibart, O.; Martin, A. Entanglement-based clock syntonization for quantum key distribution networks. Demonstration over a 50 km-long link. arXiv 2025, arXiv:2501.16796. [Google Scholar] [CrossRef]
- Coupole du Télescope MéO, sur le Plateau de Calern|CNRS Images. Available online: https://www.oca.eu/fr/instruments-et-stations/station-de-metrologie-optique-meo (accessed on 9 June 2016).
- Werner, R.F. Quantum states with Einstein-Podolsky-Rosen correlations admitting a hidden-variable model. Phys. Rev. A 1989, 40, 4277–4281. [Google Scholar] [CrossRef]
- Brand, S.; Coopmans, T.; Elkouss, D. Efficient Computation of the Waiting Time and Fidelity in Quantum Repeater Chains; OSA Quantum 2.0 Conference QTh7A.11; Optica Publishing Group: Washington, DC, USA, 2020. [Google Scholar]
- Fitzsimons, J.F. Private quantum computation: An introduction to blind quantum computing and related protocols. npj Quantum Inf. 2017, 3, 23. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Forges de Parny, L.; Paccard, L.; Bertrand, M.; Lazzarini, L.; Leloup, V.; Aymeric, R.; Blaise, A.; Molin, S.; Besancenot, P.; Laborde, C.; et al. Towards a Global Scale Quantum Information Network: A Study Applied to Satellite-Enabled Distributed Quantum Computing. Entropy 2025, 27, 1166. https://doi.org/10.3390/e27111166
de Forges de Parny L, Paccard L, Bertrand M, Lazzarini L, Leloup V, Aymeric R, Blaise A, Molin S, Besancenot P, Laborde C, et al. Towards a Global Scale Quantum Information Network: A Study Applied to Satellite-Enabled Distributed Quantum Computing. Entropy. 2025; 27(11):1166. https://doi.org/10.3390/e27111166
Chicago/Turabian Stylede Forges de Parny, Laurent, Luca Paccard, Mathieu Bertrand, Luca Lazzarini, Valentin Leloup, Raphael Aymeric, Agathe Blaise, Stéphanie Molin, Pierre Besancenot, Cyrille Laborde, and et al. 2025. "Towards a Global Scale Quantum Information Network: A Study Applied to Satellite-Enabled Distributed Quantum Computing" Entropy 27, no. 11: 1166. https://doi.org/10.3390/e27111166
APA Stylede Forges de Parny, L., Paccard, L., Bertrand, M., Lazzarini, L., Leloup, V., Aymeric, R., Blaise, A., Molin, S., Besancenot, P., Laborde, C., & van den Bossche, M. (2025). Towards a Global Scale Quantum Information Network: A Study Applied to Satellite-Enabled Distributed Quantum Computing. Entropy, 27(11), 1166. https://doi.org/10.3390/e27111166





