On the Stochastic Dynamics for the Regularized Kappa-Distributed Plasmas
Abstract
1. Introduction
2. The Regularized Kappa Distribution as a Stationary State Under the Generalized Fluctuation–Dissipation Relation
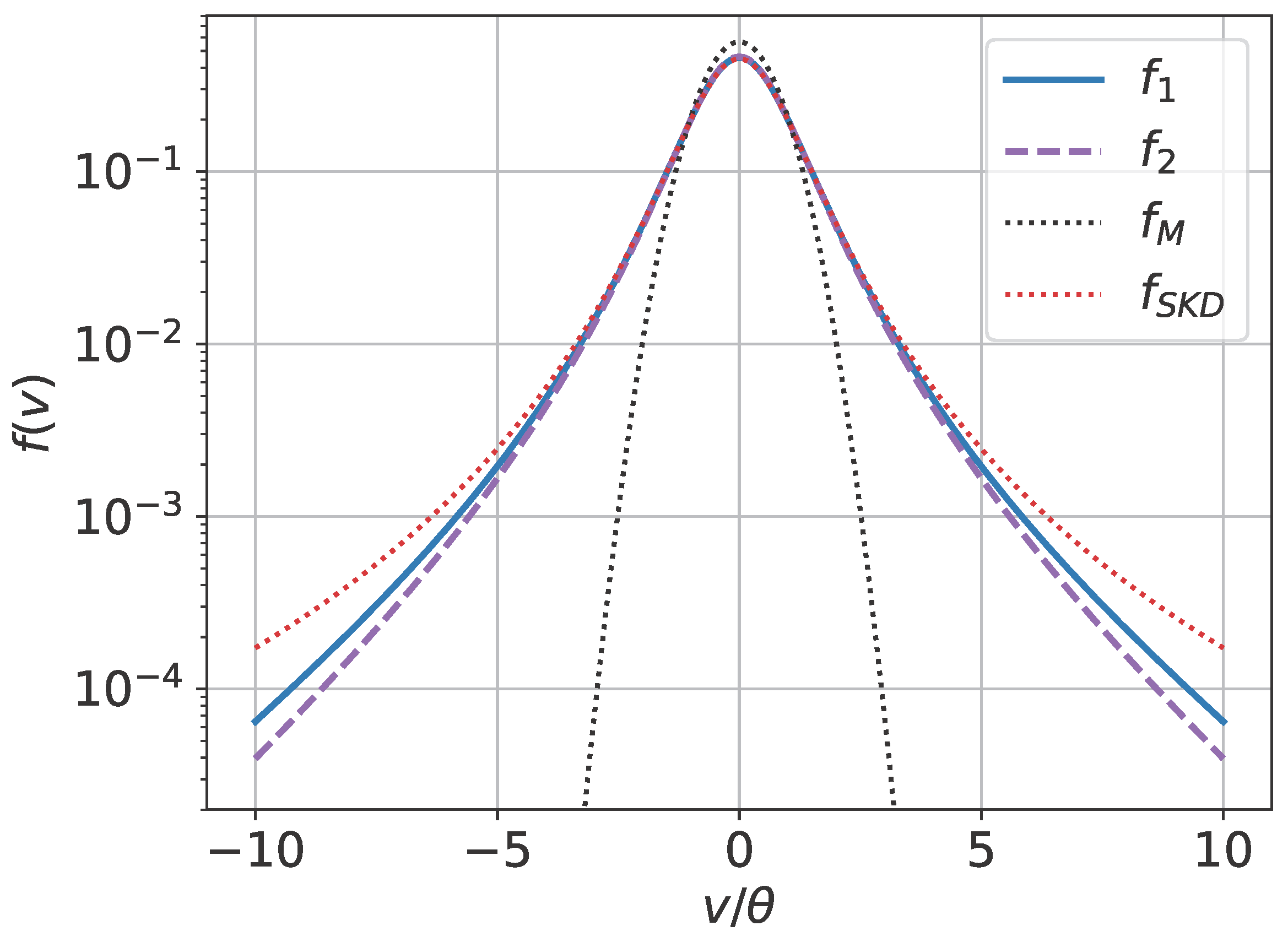
3. The Detailed Balance
4. Conclusions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SKD | Standard Kappa distribution |
| RKD | Regularized Kappa distirbution |
| SFDR | Standard fluctuation–dissipation relation |
| GFDR | Generalized fluctuation–dissipation relation |
| FP | Fokker–Planck |
Appendix A
References
- Olbert, S. Summary of Experimental Results from M.I.T. Detector on IMP-1. In Physics of the Magnetosphere; Springer: Cham, Switzerland, 1968; pp. 641–659. [Google Scholar] [CrossRef]
- Vasyliunas, V.M. A survey of low-energy electrons in the evening sector of the magnetosphere with OGO 1 and OGO 3. J. Geophys. Res. 1968, 73, 2839–2884. [Google Scholar] [CrossRef]
- Maksimovic, M.; Pierrard, V.; Lemaire, J.F. A kinetic model of the solar wind with Kappa distribution functions in the corona. Astron. Astrophys. 1997, 324, 725–734. [Google Scholar]
- Lazar, M.; Yoon, P.H.; Eliasson, B. Electromagnetic cyclotron instabilities in bi-Kappa distributed plasmas: A quasilinear approach. Phys. Plasmas 2017, 24, 042110. [Google Scholar] [CrossRef]
- Wilson, L.B., III; Chen, L.J.; Wang, S.; Schwartz, S.J.; Turner, D.L.; Stevens, M.L.; Kasper, J.C.; Osmane, A.; Caprioli, D.; Bale, S.D.; et al. Electron Energy Partition across Interplanetary Shocks. I. Methodology and Data Product. Astrophys. J. Suppl. Ser. 2019, 243, 8. [Google Scholar] [CrossRef]
- Hapgood, M.; Perry, C.; Davies, J.; Denton, M. The role of suprathermal particle measurements in CrossScale studies of collisionless plasma processes. Planet. Space Sci. 2011, 59, 618–629. [Google Scholar] [CrossRef]
- Eyelade, A.V.; Stepanova, M.; Espinoza, C.M.; Moya, P.S. On the Relation between Kappa Distribution Functions and the Plasma Beta Parameter in the Earth’s Magnetosphere: THEMIS Observations. Astrophys. J. Suppl. Ser. 2021, 253, 34. [Google Scholar] [CrossRef]
- Oka, M.; Phan, T.D.; Øieroset, M.; Turner, D.L.; Drake, J.F.; Li, X.; Fuselier, S.A.; Gershman, D.J.; Giles, B.L.; Ergun, R.E.; et al. Electron energization and thermal to non-thermal energy partition during earth’s magnetotail reconnection. Phys. Plasmas 2022, 29, 052904. [Google Scholar] [CrossRef]
- Livadiotis, G. Collision frequency and mean free path for plasmas described by kappa distributions. AIP Adv. 2019, 9, 105307. [Google Scholar] [CrossRef]
- Wang, H.; Du, J.; Huo, R. The collision frequency of electron-neutral-particle in weakly ionized plasmas with non-Maxwellian velocity distributions. Commun. Theor. Phys. 2021, 73, 095501. [Google Scholar] [CrossRef]
- Wang, Y.; Du, J. The viscosity of charged particles in the weakly ionized plasma with power-law distributions. Phys. Plasmas 2018, 25, 062309. [Google Scholar] [CrossRef]
- Guo, R.; Du, J. Transport coefficients of the fully ionized plasma with kappa-distribution and in strong magnetic field. Phys. A 2019, 523, 156–171. [Google Scholar] [CrossRef]
- Husidic, E.; Lazar, M.; Fichtner, H.; Scherer, K.; Poedts, S. Transport coefficients enhanced by suprathermal particles in nonequilibrium heliospheric plasmas. Astron. Astrophys. 2021, 654, A99. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J.; Shrestha, B.L. Thermodynamics of Pickup Ions in the Heliosphere. Astrophys. J. 2024, 968, 66. [Google Scholar] [CrossRef]
- Cuesta, M.E.; Cummings, A.T.; Livadiotis, G.; McComas, D.J.; Cohen, C.M.S.; Khoo, L.Y.; Sharma, T.; Shen, M.M.; Bandyopadhyay, R.; Rankin, J.S.; et al. Observations of Kappa Distributions in Solar Energetic Protons and Derived Thermodynamic Properties. Astrophys. J. 2024, 973, 76. [Google Scholar] [CrossRef]
- Lazar, M.; Poedts, S.; Schlickeiser, R. Instability of the parallel electromagnetic modes in Kappa distributed plasmas—I. Electron whistler-cyclotron modes. Mon. Not. R. Astron. Soc. 2011, 410, 663–670. [Google Scholar] [CrossRef]
- Lazar, M.; Poedts, S. Instability of the parallel electromagnetic modes in Kappa distributed plasmas—II. Electromagnetic ion–cyclotron modes. Mon. Not. R. Astron. Soc. 2013, 437, 641–648. [Google Scholar] [CrossRef]
- Guo, R. The electron acoustic waves in plasmas with two kappa-distributed electrons at the same temperatures and immobile ions. Phys. Plasmas 2021, 28, 082105. [Google Scholar] [CrossRef]
- Liu, Z. Effects of Nonextensive Electrons on Dust–Ion Acoustic Waves in a Collisional Dusty Plasma with Negative Ions. Entropy 2023, 25, 1363. [Google Scholar] [CrossRef]
- Lazar, M.; López, R.A.; Poedts, S.; Shaaban, S.M. Instability of Langmuir-beam waves: Kappa-distributed electrons. Phys. Plasmas 2023, 30, 082106. [Google Scholar] [CrossRef]
- Guo, R. Different effects of suprathermal electrons and ions on drift instabilities in non-uniform plasmas. Phys. Plasmas 2023, 30, 122113. [Google Scholar] [CrossRef]
- Yoon, P.H.; López, R.A.; Zaheer, S. Bi-Kappa Proton Mirror and Cyclotron Instabilities in the Solar Wind. Astrophys. J. 2023, 950, 131. [Google Scholar] [CrossRef]
- Guo, R. Drift instabilities driven by slab ion temperature gradient in suprathermal plasmas. Plasma Phys. Control. Fusion 2024, 66, 105012. [Google Scholar] [CrossRef]
- Scherer, K.; Fichtner, H.; Lazar, M. Regularized κ -distributions with non-diverging moments. Europhys. Lett. 2017, 120, 50002. [Google Scholar] [CrossRef]
- Scherer, K.; Lazar, M.; Husidic, E.; Fichtner, H. Moments of the Anisotropic Regularized κ-distributions. Astrophys. J. 2019, 880, 118. [Google Scholar] [CrossRef]
- Fichtner, H.; Scherer, K.; Lazar, M.; Fahr, H.J.; Vörös, Z. Entropy of plasmas described with regularized distributions. Phys. Rev. E 2018, 98, 053205. [Google Scholar] [CrossRef]
- Husidic, E.; Lazar, M.; Fichtner, H.; Scherer, K.; Astfalk, P. Linear dispersion theory of parallel electromagnetic modes for regularized Kappa-distributions. Phys. Plasmas 2020, 27, 042110. [Google Scholar] [CrossRef]
- Huo, R.; Du, J. Dispersion and Damping Rate of Ion-Acoustic Waves in Regularized Kappa Distributed Plasma. IEEE Trans. Plasma Sci. 2023, 51, 2383–2387. [Google Scholar] [CrossRef]
- Hau, L.N.; Jao, C.S.; Chang, C.K. The characteristics of ion acoustic solitons in nonthermal regularized kappa distributed plasmas. Phys. Plasmas 2024, 31, 032113. [Google Scholar] [CrossRef]
- Gaelzer, R.; Ziebell, L.F. Collisional charging of dust particles by suprathermal plasmas. II—Regularized kappa distributions. Phys. Plasmas 2025, 32, 033706. [Google Scholar] [CrossRef]
- Schröder, D.L.; Fichtner, H.; Lazar, M.; Verscharen, D.; Klein, K.G. Temperature anisotropy instabilities of solar wind electrons with regularized kappa-halos resolved with ALPS. Phys. Plasmas 2025, 32, 032109. [Google Scholar] [CrossRef]
- Pierrard, V.; Péters de Bonhome, M.; Halekas, J.; Audoor, C.; Whittlesey, P.; Livi, R. Exospheric Solar Wind Model Based on Regularized Kappa Distributions for the Electrons Constrained by Parker Solar Probe Observations. Plasma 2023, 6, 518–540. [Google Scholar] [CrossRef]
- Hasegawa, A.; Mima, K.; Duong-van, M. Plasma Distribution Function in a Superthermal Radiation Field. Phys. Rev. Lett. 1985, 54, 2608–2610. [Google Scholar] [CrossRef]
- Ma, C.; Summers, D. Formation of power-law energy spectra in space plasmas by stochastic acceleration due to whistler-mode waves. Geophys. Res. Lett. 1998, 25, 4099–4102. [Google Scholar] [CrossRef]
- Leubner, M.P. A nonextensive entropy approach to kappa-distributions. Astrophys. Space Sci. 2002, 282, 573–579. [Google Scholar] [CrossRef]
- Vocks, C.; Mann, G. Generation of Suprathermal Electrons by Resonant Wave-Particle Interaction in the Solar Corona and Wind. Astrophys. J. 2003, 593, 1134–1145. [Google Scholar] [CrossRef]
- Shizgal, B.D. Suprathermal particle distributions in space physics: Kappa distributions and entropy. Astrophys. Space Sci. 2007, 312, 227–237. [Google Scholar] [CrossRef]
- Bian, N.H.; Emslie, A.G.; Stackhouse, D.J.; Kontar, E.P. The formation of kappa-distribution accelerated electron populations in solar flares. Astrophys. J. 2014, 796, 142. [Google Scholar] [CrossRef]
- Yoon, P.H. Electron kappa distribution and quasi-thermal noise. J. Geophys. Res. Space Phys. 2014, 119, 7074–7087. [Google Scholar] [CrossRef]
- Kiefer, T.; Schlegel, T. Implications for the electron distribution from the stationary hydrodynamic model of a one-dimensional plasma expansion into vacuum. Phys. Plasmas 2012, 19, 102101. [Google Scholar] [CrossRef]
- Du, J.L. Power-law distributions and fluctuation-dissipation relation in the stochastic dynamics of two-variable Langevin equations. J. Stat. Mech. Theory Exp. 2012, 2012, P02006. [Google Scholar] [CrossRef]
- Guo, R.; Du, J. Power-law behaviors from the two-variable Langevin equation: Ito’s and Stratonovich’s Fokker–Planck equations. J. Stat. Mech. Theory Exp. 2013, 2013, P02015. [Google Scholar] [CrossRef]
- Shizgal, B.D. Kappa and other nonequilibrium distributions from the Fokker-Planck equation and the relationship to Tsallis entropy. Phys. Rev. E 2018, 97, 052144. [Google Scholar] [CrossRef] [PubMed]
- Livadiotis, G. On the Origin of Polytropic Behavior in Space and Astrophysical Plasmas. Astrophys. J. 2019, 874, 10. [Google Scholar] [CrossRef]
- Guo, R. Stationary states of polytropic plasmas. Phys. Plasmas 2020, 27, 122104. [Google Scholar] [CrossRef]
- Biró, T.S.; Jakovác, A. Power-law tails from multiplicative noise. Phys. Rev. Lett. 2005, 94, 132302. [Google Scholar] [CrossRef]
- Oylukan, A.D.; Shizgal, B. Nonequilibrium distributions from the Fokker-Planck equation: Kappa distributions and Tsallis entropy. Phys. Rev. E 2023, 108, 014111. [Google Scholar] [CrossRef]
- Zwanzig, R. Nonequilibrium Statistical Mechanics; Oxford University Press: New York, NY, USA, 2001. [Google Scholar] [CrossRef]
- Trigger, S.A. Fokker-Planck equation for Boltzmann-type and active particles: Transfer probability approach. Phys. Rev. E 2003, 67, 046403. [Google Scholar] [CrossRef]
- Trigger, S.; van Heijst, G.; Schram, P. Velocity-dependent friction and diffusion for grains in neutral gases, dusty plasmas and active systems. Phys. A 2005, 347, 77–98. [Google Scholar] [CrossRef]
- Wittkowski, R.; Schelin, A.B.; Spatschek, K.H. Mean Motion in Stochastic Plasmas With a Space-Dependent Diffusion Coefficient. Contrib. Plasm. Phys. 2009, 49, 55–69. [Google Scholar] [CrossRef]
- Dunkel, J.; Hänggi, P. Relativistic Brownian motion. Phys. Rep. 2009, 471, 1–73. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Invariant Kappa Distribution in Space Plasmas out of Equilibrium. Astrophys. J. 2011, 741, 88. [Google Scholar] [CrossRef]
- Haas, F.; Fichtner, H.; Scherer, K. Electron holes in a regularized kappa background. Nonlinear Proc. Geoph. 2023, 30, 277–287. [Google Scholar] [CrossRef]
- Pearson, K.X. Contributions to the mathematical theory of evolution.—II. Skew variation in homogeneous material. Philos. Trans. R. Soc. Lond. A 1895, 186, 343–414. [Google Scholar] [CrossRef]
- Haken, H. Cooperative phenomena in systems far from thermal equilibrium and in nonphysical systems. Rev. Mod. Phys. 1975, 47, 67–121. [Google Scholar] [CrossRef]
- Haken, H. Exact stationary solution of the master equation for systems far from thermal equilibrium in detailed balance. Phys. Lett. A 1974, 46, 443–444. [Google Scholar] [CrossRef]
- Guo, R.; Du, J. Are power-law distributions an equilibrium distribution or a stationary nonequilibrium distribution? Phys. A 2014, 406, 281–286. [Google Scholar] [CrossRef]
- Olver, F.W.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. NIST Handbook of Mathematical Functions; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, R. On the Stochastic Dynamics for the Regularized Kappa-Distributed Plasmas. Entropy 2025, 27, 1138. https://doi.org/10.3390/e27111138
Guo R. On the Stochastic Dynamics for the Regularized Kappa-Distributed Plasmas. Entropy. 2025; 27(11):1138. https://doi.org/10.3390/e27111138
Chicago/Turabian StyleGuo, Ran. 2025. "On the Stochastic Dynamics for the Regularized Kappa-Distributed Plasmas" Entropy 27, no. 11: 1138. https://doi.org/10.3390/e27111138
APA StyleGuo, R. (2025). On the Stochastic Dynamics for the Regularized Kappa-Distributed Plasmas. Entropy, 27(11), 1138. https://doi.org/10.3390/e27111138