Implementing Quantum Secret Sharing on Current Hardware
Abstract
1. Introduction
2. Preliminaries
- (i)
- Each is called unauthorized and satisfywhere denotes the set complement of S and is some fixed state for systems S that is independent of , i.e., no statistical information about the relative values of and can be obtained.
- (ii)
- Each is called authorized, and there exists a decoder such that
2.1. General Encoding
2.2. General Decoding
2.3. Initializing a Secret
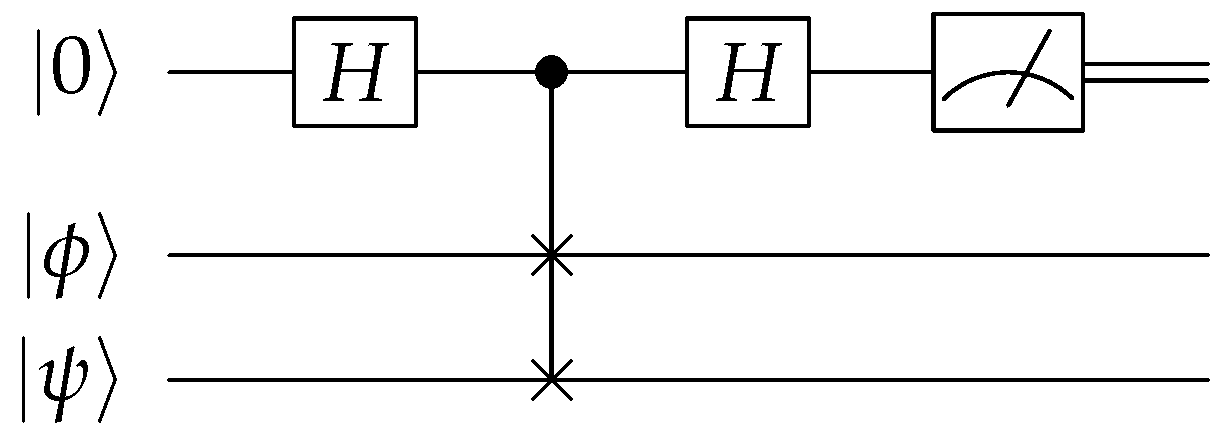
2.4. Measures of Performance
2.5. Error Mitigation
3. Specific Examples
3.1. ((3,5)) QSS Using the Five-Qubit Code
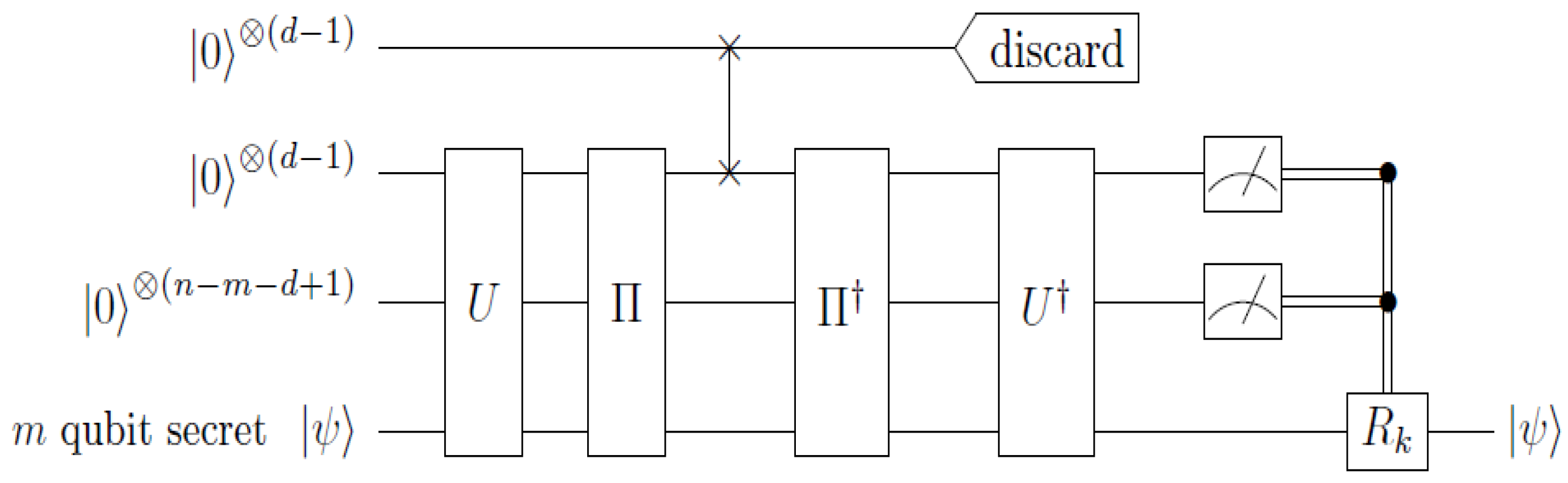
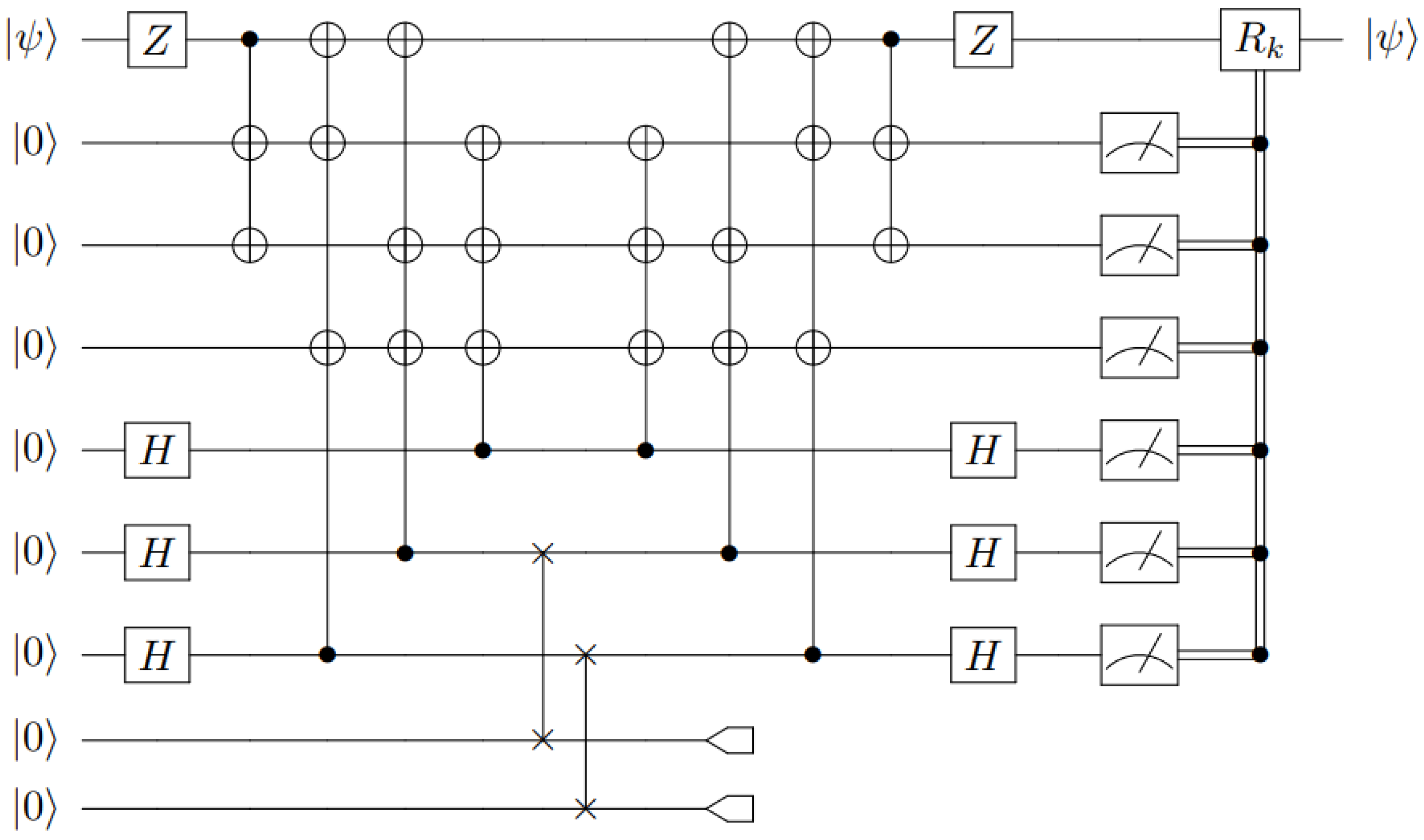
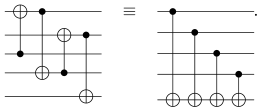 Performing Equation (6) in reverse defines the encoding unitary U, as depicted in Figure 5. Here, we have chosen the permutation among the unauthorized set to be trivial for convenience.
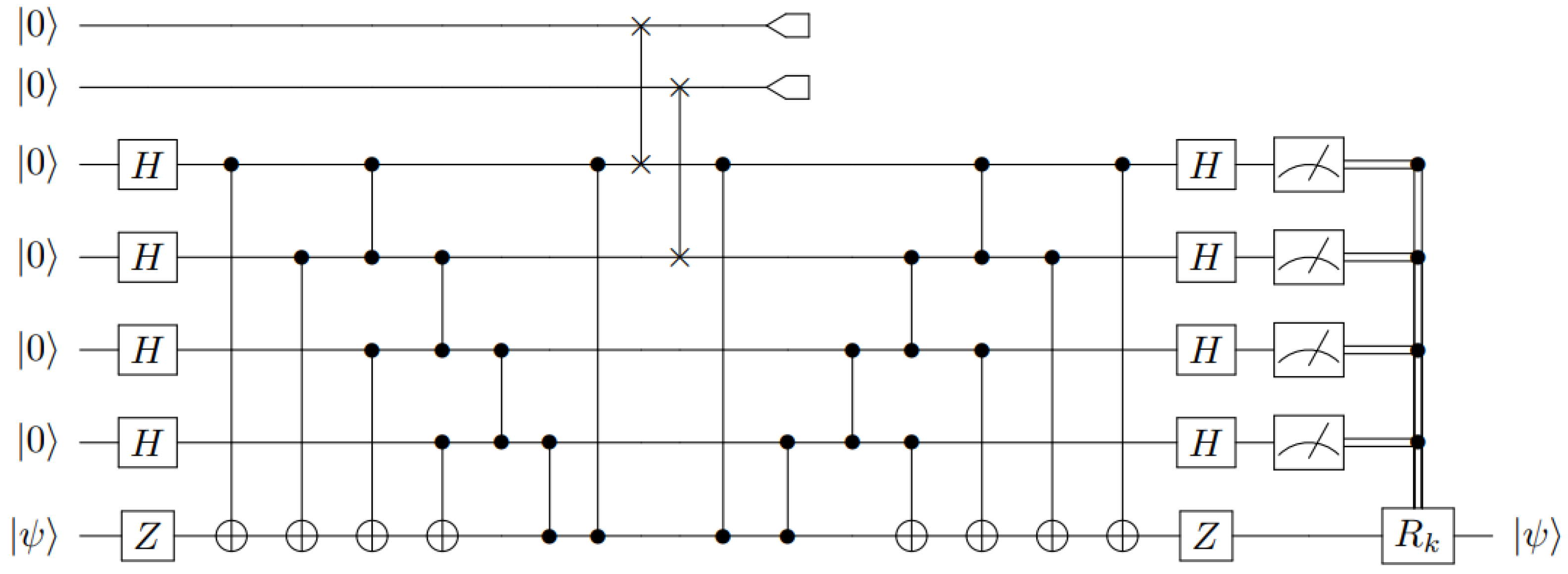
Performing Equation (6) in reverse defines the encoding unitary U, as depicted in Figure 5. Here, we have chosen the permutation among the unauthorized set to be trivial for convenience.3.2. ((5,7)) QSS Using the Steane Code
3.3. More Authorized Sets Using the Steane Code
3.4. ((2,3)) QSS Qutrit Code
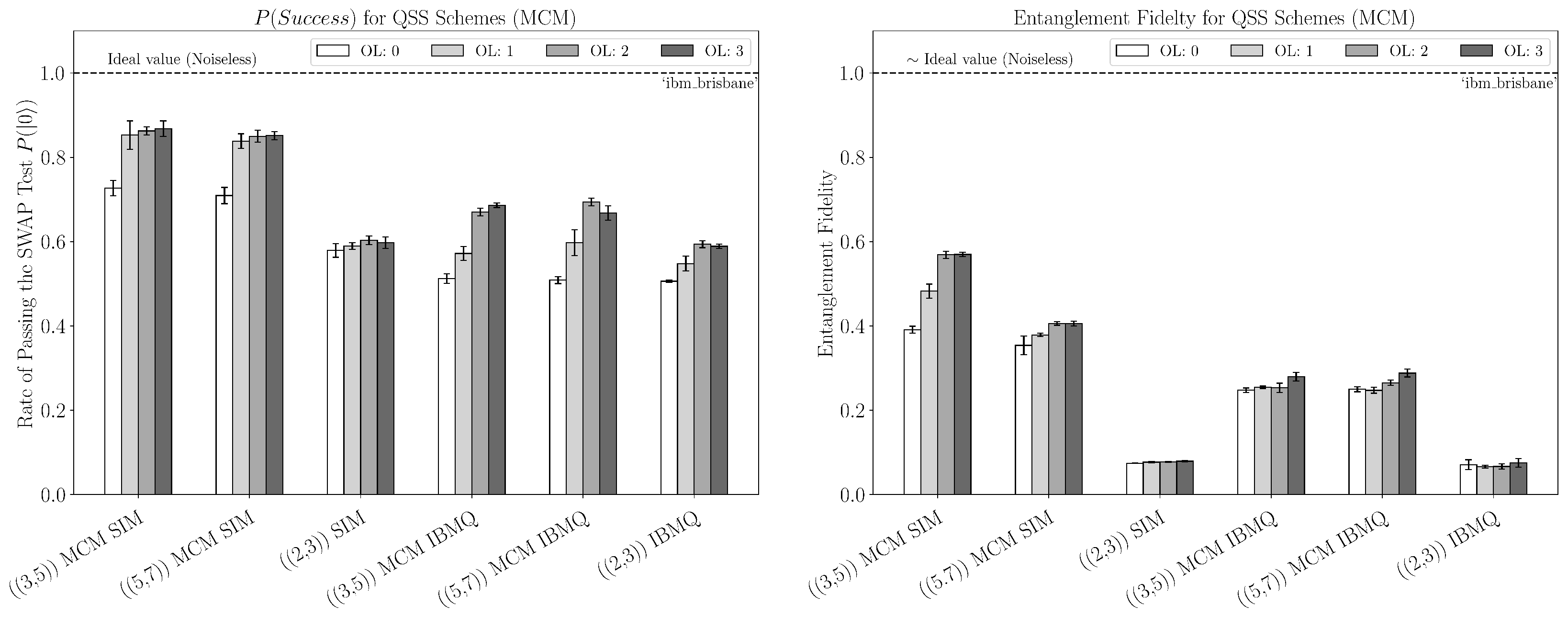
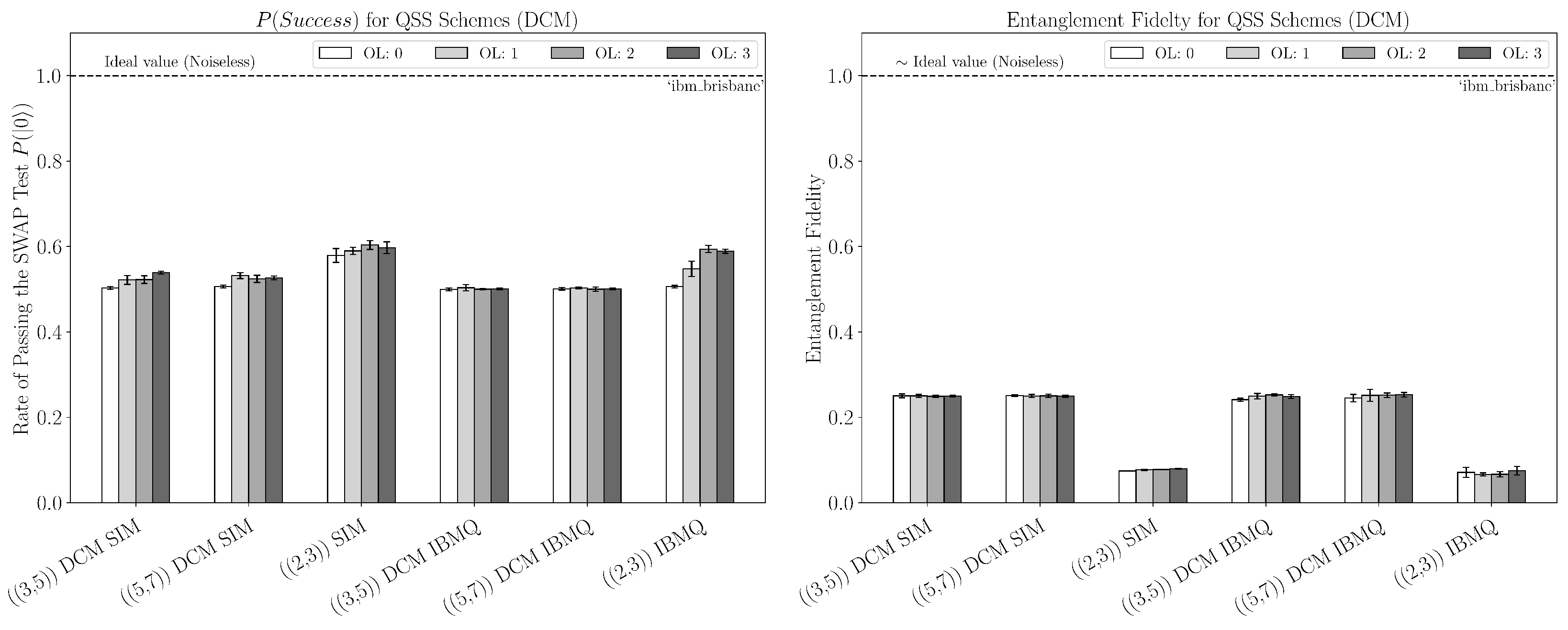
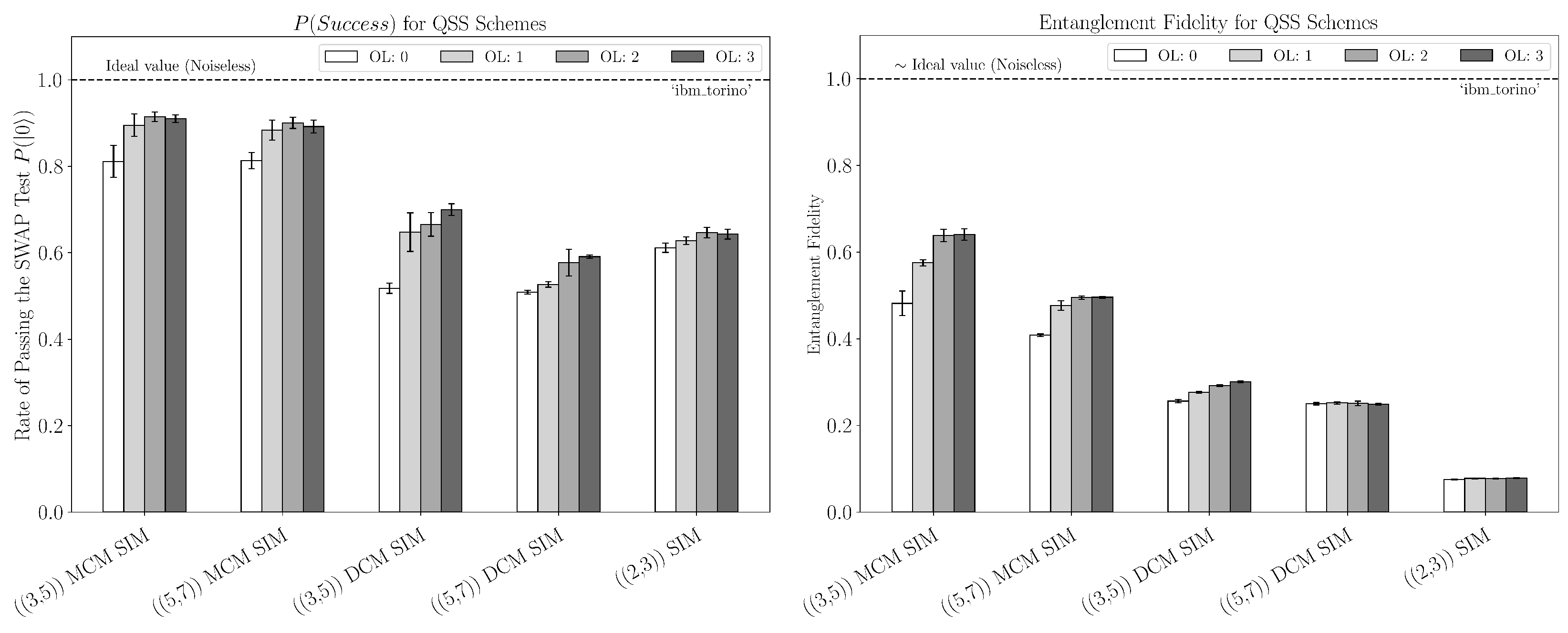
4. Results
5. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Syndrome Tables and Corrections
| syndrome = (0,0,0,0) | syndrome = (1,0,1,0) | syndrome = (1,1,1,0) | syndrome = (0,1,0,0) | |
| correction | correction | correction | correction | |
| syndrome = (1,0,1,1) | syndrome = (0,0,0,1) | syndrome = (0,1,0,1) | syndrome = (1,1,1,1) | |
| correction | correction | correction | correction | |
| syndrome = (0,0,1,1) | syndrome = (1,0,0,1) | syndrome = (1,1,0,1) | syndrome = (0,1,1,1) | |
| correction | correction | correction | correction | |
| syndrome = (1,0,0,0) | syndrome = (0,0,1,0) | syndrome = (0,1,1,0) | syndrome = (1,1,0,0) | |
| correction | correction | correction | correction |
| syndrome = (0,0,0,0,0,0) | syndrome = (0,1,1,0,0,0) | syndrome = (0,1,1,0,0,1) | syndrome = (0,0,0,0,0,1) | |
| correction | correction | correction | correction | |
| syndrome = (1,0,1,0,0,0) | syndrome = (1,1,0,0,0,0) | syndrome = (1,1,0,0,0,1) | syndrome = (1,0,1,0,0,1) | |
| correction | correction | correction | correction | |
| syndrome = (1,0,1,0,1,0) | syndrome = (1,1,0,0,1,0) | syndrome = (1,1,0,0,1,1) | syndrome = (1,0,1,0,1,1) | |
| correction | correction | correction | correction | |
| syndrome = (0,0,0,0,1,0) | syndrome = (0,1,1,0,1,0) | syndrome = (0,1,1,0,1,1) | syndrome = (0,0,0,0,1,1) | |
| correction | correction | correction | correction |
Appendix B. The Steane Code and Three-Qubit Erasures
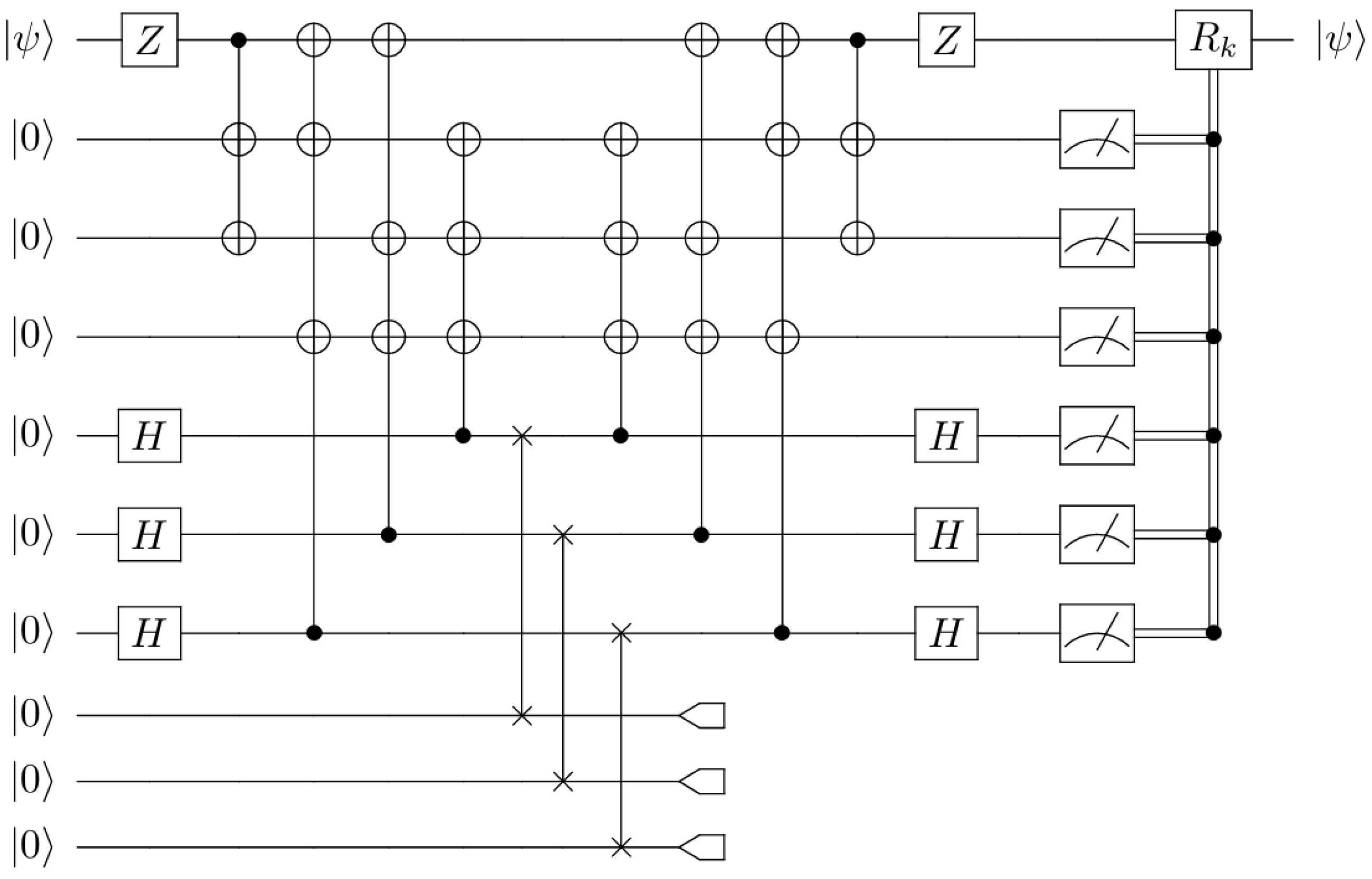
| Error | Syndrome | Correction | Error | Syndrome | Correction |
|---|---|---|---|---|---|
Appendix C. Depth and Multi-Qubit Operations for the QSS Schemes

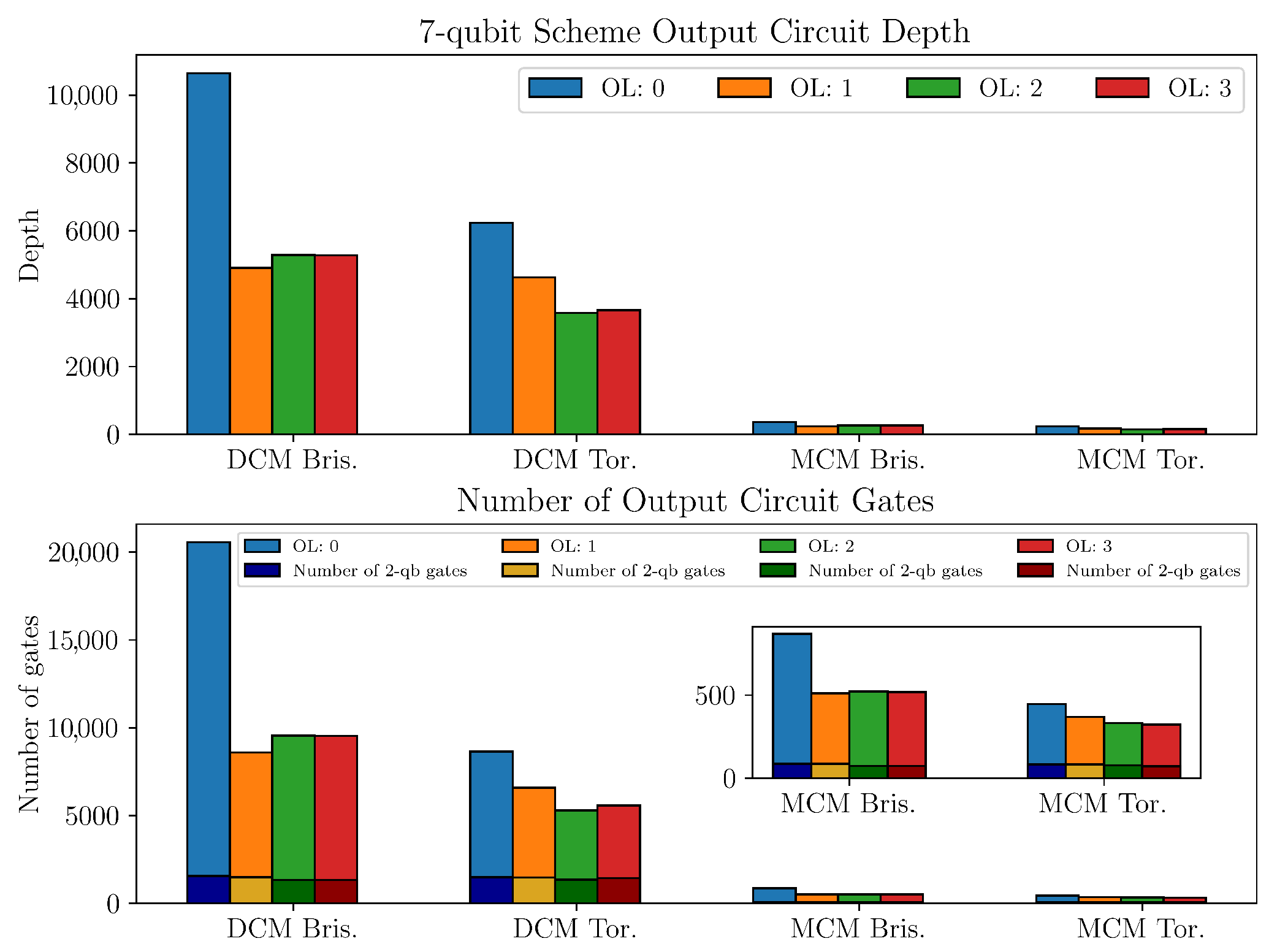
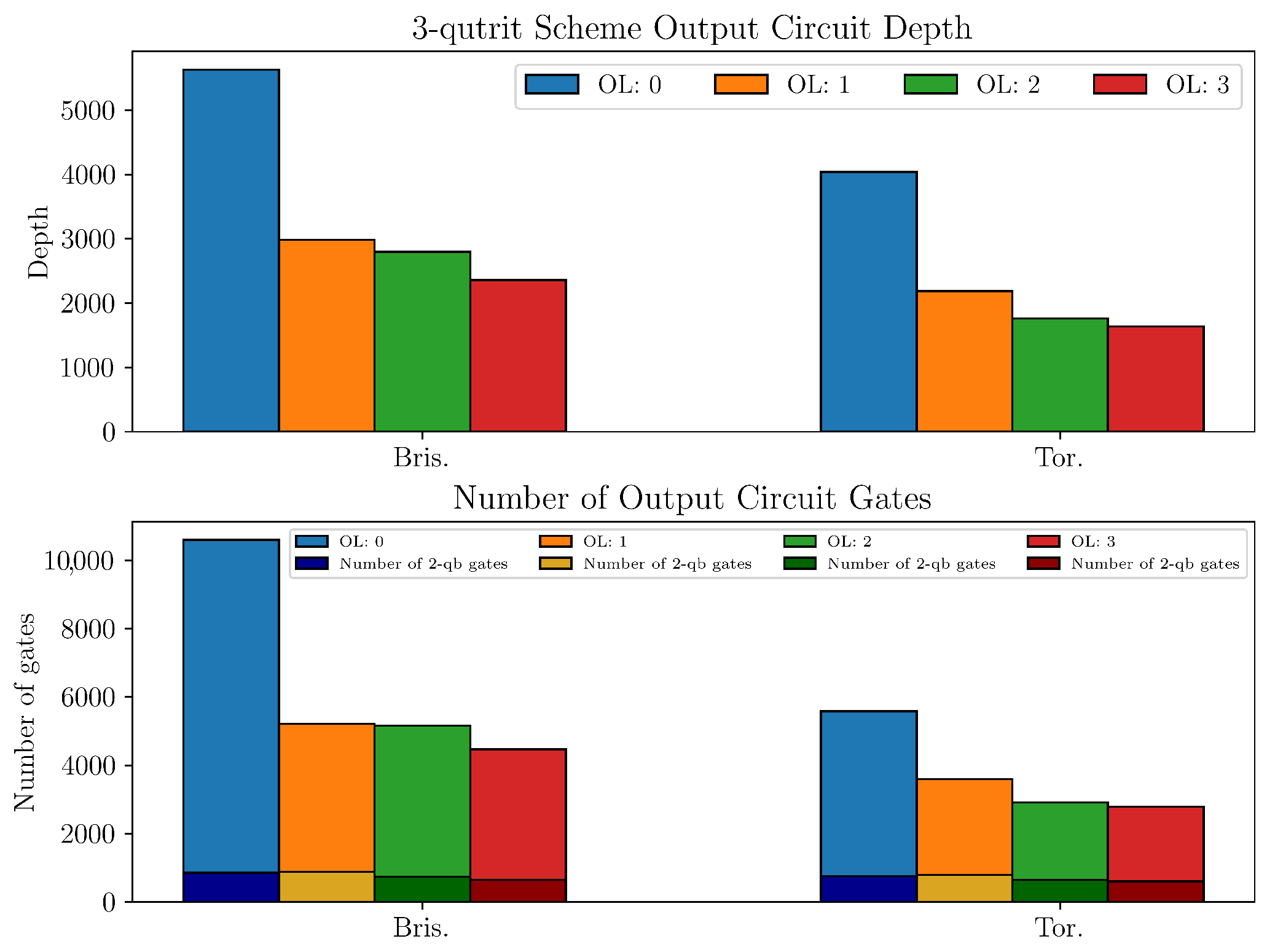
References
- Cleve, R.; Gottesman, D.; Lo, H.K. How to Share a Quantum Secret. Phys. Rev. Lett. 1999, 83, 648–651. [Google Scholar] [CrossRef]
- Blakley, G.R. Safeguarding cryptographic keys. In Proceedings of the 1979 International Workshop on Managing Requirements Knowledge (MARK), New York, NY, USA, 4–7 June 1979; pp. 313–318. [Google Scholar] [CrossRef]
- Shamir, A. How to Share a Secret. Commun. ACM 1979, 22, 612–613. [Google Scholar] [CrossRef]
- Hillery, M.; Bužek, V.; Berthiaume, A. Quantum secret sharing. Phys. Rev. A 1999, 59, 1829–1834. [Google Scholar] [CrossRef]
- Gottesman, D. Theory of quantum secret sharing. Phys. Rev. A 2000, 61, 042311. [Google Scholar] [CrossRef]
- Smith, A.D. Quantum secret sharing for general access structures. arXiv 2000, arXiv:quant-ph/0001087. [Google Scholar]
- Nascimento, A.C.A.; Mueller-Quade, J.; Imai, H. Improving quantum secret-sharing schemes. Phys. Rev. A 2001, 64, 042311. [Google Scholar] [CrossRef][Green Version]
- Imai, H.; Mueller-Quade, J.; Nascimento, A.; Tuyls, P.; Winter, A. A Quantum Information Theoretical Model for Quantum Secret Sharing Schemes. Quantum Inf. Comput. 2003, 5, 69–80. [Google Scholar] [CrossRef]
- Markham, D.; Sanders, B.C. Graph states for quantum secret sharing. Phys. Rev. A 2008, 78, 042309. [Google Scholar] [CrossRef]
- Sarvepalli, P. Bounds on the information rate of quantum-secret-sharing schemes. Phys. Rev. A 2011, 83, 042324. [Google Scholar] [CrossRef]
- Gheorghiu, V. Generalized semiquantum secret-sharing schemes. Phys. Rev. A 2012, 85, 052309. [Google Scholar] [CrossRef]
- Fortescue, B.; Gour, G. Reducing the Quantum Communication Cost of Quantum Secret Sharing. IEEE Trans. Inf. Theory 2012, 58, 6659–6666. [Google Scholar] [CrossRef][Green Version]
- Yang, W.; Huang, L.; Shi, R.; He, L. Secret sharing based on quantum Fourier transform. Quantum Inf. Process. 2013, 12, 2465–2474. [Google Scholar] [CrossRef]
- Gheorghiu, V.; Sanders, B.C. Accessing quantum secrets via local operations and classical communication. Phys. Rev. A 2013, 88, 022340. [Google Scholar] [CrossRef]
- Marin, A.; Markham, D. Equivalence between sharing quantum and classical secrets and error correction. Phys. Rev. A 2013, 88, 042332. [Google Scholar] [CrossRef]
- Li, L.; Qiu, D.; Mateus, P. Quantum secret sharing with classical Bobs. J. Phys. A Math. Theor. 2013, 46, 045304. [Google Scholar] [CrossRef]
- Ouyang, Y.; Tan, S.H.; Zhao, L.; Fitzsimons, J.F. Computing on quantum shared secrets. Phys. Rev. A 2017, 96, 052333. [Google Scholar] [CrossRef]
- Lipinska, V.; Murta, G.; Ribeiro, J.; Wehner, S. Verifiable hybrid secret sharing with few qubits. Phys. Rev. A 2020, 101, 032332. [Google Scholar] [CrossRef]
- Senthoor, K.; Sarvepalli, P.K. Theory of Communication Efficient Quantum Secret Sharing. IEEE Trans. Inf. Theory 2022, 68, 3164–3186. [Google Scholar] [CrossRef]
- Ouyang, Y.; Goswami, K.; Romero, J.; Sanders, B.C.; Hsieh, M.H.; Tomamichel, M. Approximate reconstructability of quantum states and noisy quantum secret sharing schemes. Phys. Rev. A 2023, 108, 012425. [Google Scholar] [CrossRef]
- Tittel, W.; Zbinden, H.; Gisin, N. Experimental demonstration of quantum secret sharing. Phys. Rev. A 2001, 63, 042301. [Google Scholar] [CrossRef]
- Gaertner, S.; Kurtsiefer, C.; Bourennane, M.; Weinfurter, H. Experimental Demonstration of Four-Party Quantum Secret Sharing. Phys. Rev. Lett. 2007, 98, 020503. [Google Scholar] [CrossRef] [PubMed]
- Hao, L.; Wang, C.; Long, G.L. Quantum secret sharing protocol with four state Grover algorithm and its proof-of-principle experimental demonstration. Opt. Commun. 2011, 284, 3639–3642. [Google Scholar] [CrossRef]
- Wei, K.J.; Ma, H.Q.; Yang, J.H. Experimental circular quantum secret sharing over telecom fiber network. Opt. Express 2013, 21, 16663. [Google Scholar] [CrossRef]
- Bell, B.A.; Markham, D.; Herrera-Martí, D.A.; Marin, A.; Wadsworth, W.J.; Rarity, J.G.; Tame, M.S. Experimental demonstration of graph-state quantum secret sharing. Nat. Commun. 2014, 5, 5480. [Google Scholar] [CrossRef]
- Lu, H.; Zhang, Z.; Chen, L.K.; Li, Z.D.; Liu, C.; Li, L.; Liu, N.L.; Ma, X.; Chen, Y.A.; Pan, J.W. Secret Sharing of a Quantum State. Phys. Rev. Lett. 2016, 117, 030501. [Google Scholar] [CrossRef]
- Williams, B.P.; Lukens, J.M.; Peters, N.A.; Qi, B.; Grice, W.P. Quantum secret sharing with polarization-entangled photon pairs. Phys. Rev. A 2019, 99, 062311. [Google Scholar] [CrossRef]
- Lee, S.M.; Lee, S.W.; Jeong, H.; Park, H.S. Quantum Teleportation of Shared Quantum Secret. Phys. Rev. Lett. 2020, 124, 060501. [Google Scholar] [CrossRef]
- de Oliveira, M.; Nape, I.; Pinnell, J.; TabeBordbar, N.; Forbes, A. Experimental high-dimensional quantum secret sharing with spin-orbit-structured photons. Phys. Rev. A 2020, 101, 042303. [Google Scholar] [CrossRef]
- Suter, D.; Álvarez, G.A. Colloquium: Protecting quantum information against environmental noise. Rev. Mod. Phys. 2016, 88, 041001. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information: 10th Anniversary Edition; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Laflamme, R.; Miquel, C.; Paz, J.P.; Zurek, W.H. Perfect Quantum Error Correcting Code. Phys. Rev. Lett. 1996, 77, 198–201. [Google Scholar] [CrossRef]
- Calderbank, A.R.; Shor, P.W. Good quantum error-correcting codes exist. Phys. Rev. A 1996, 54, 1098–1105. [Google Scholar] [CrossRef]
- Steane, A. Multiple-particle interference and quantum error correction. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1996, 452, 2551–2577. [Google Scholar] [CrossRef]
- Majumdar, R.; Sur-Kolay, S. Optimal Error Correcting Code For Ternary Quantum Systems. arXiv 2020, arXiv:1906.11137. [Google Scholar]
- Grassl, M.; Beth, T.; Pellizzari, T. Codes for the quantum erasure channel. Phys. Rev. A 1997, 56, 33–38. [Google Scholar] [CrossRef]
- Nation, P.D.; Kang, H.; Sundaresan, N.; Gambetta, J.M. Scalable Mitigation of Measurement Errors on Quantum Computers. PRX Quantum 2021, 2, 040326. [Google Scholar] [CrossRef]
- Sarvepalli, P. Nonthreshold quantum secret-sharing schemes in the graph-state formalism. Phys. Rev. A 2012, 86, 042303. [Google Scholar] [CrossRef]
- Sarvepalli, P.K.; Klappenecker, A. Sharing classical secrets with Calderbank-Shor-Steane codes. Phys. Rev. A 2009, 80, 022321. [Google Scholar] [CrossRef]
- Bäumer, E.; Tripathi, V.; Seif, A.; Lidar, D.; Wang, D.S. Quantum Fourier Transform using Dynamic Circuits. arXiv 2024, arXiv:2403.09514. [Google Scholar]
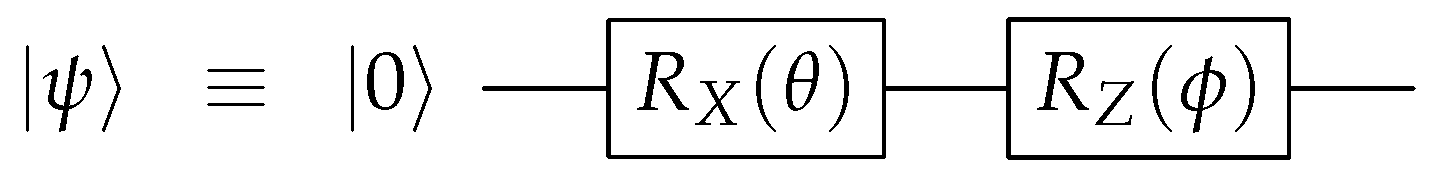



| Element | Operator | Element | Operator |
|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Graves, J.; Nelson, M.; Chitambar, E. Implementing Quantum Secret Sharing on Current Hardware. Entropy 2025, 27, 993. https://doi.org/10.3390/e27100993
Graves J, Nelson M, Chitambar E. Implementing Quantum Secret Sharing on Current Hardware. Entropy. 2025; 27(10):993. https://doi.org/10.3390/e27100993
Chicago/Turabian StyleGraves, Jay, Mike Nelson, and Eric Chitambar. 2025. "Implementing Quantum Secret Sharing on Current Hardware" Entropy 27, no. 10: 993. https://doi.org/10.3390/e27100993
APA StyleGraves, J., Nelson, M., & Chitambar, E. (2025). Implementing Quantum Secret Sharing on Current Hardware. Entropy, 27(10), 993. https://doi.org/10.3390/e27100993







