A Dissipative Phenomenon: The Mechanical Model of the Cosmological Axion Influence
Abstract
1. Introducion
Mathematical Preminilaries: Two Kind of Klein-Gordon Equations
2. Three Types of Transversal Wave Propagation—Related Propagation Equations
2.1. Wave Equation of Free Motion
2.2. Wave Equation with a Repulsive Interaction
2.3. Wave Equation with an Attractive Interaction
3. Axion Effect on the Frequency: Red Shift Process
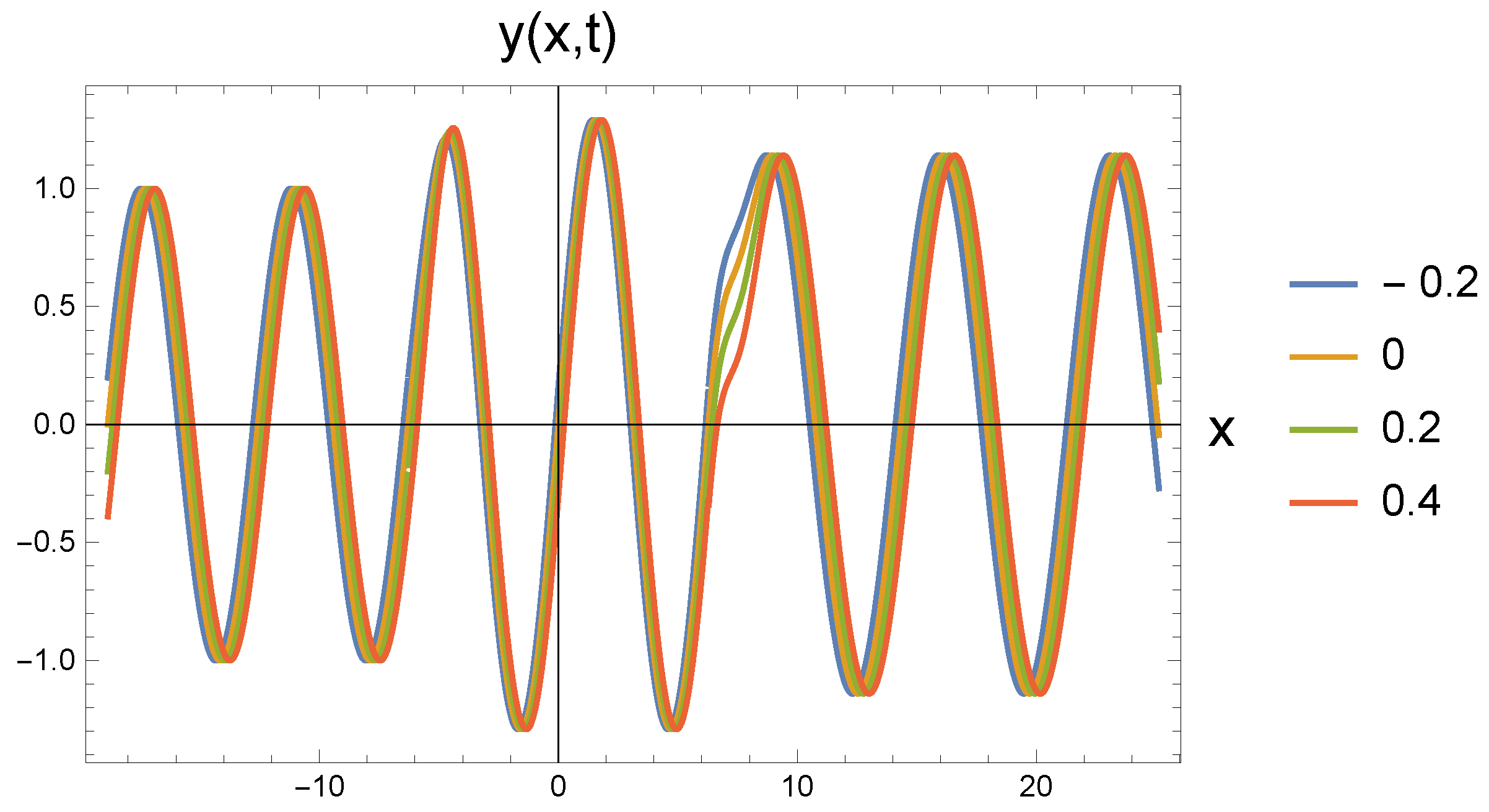
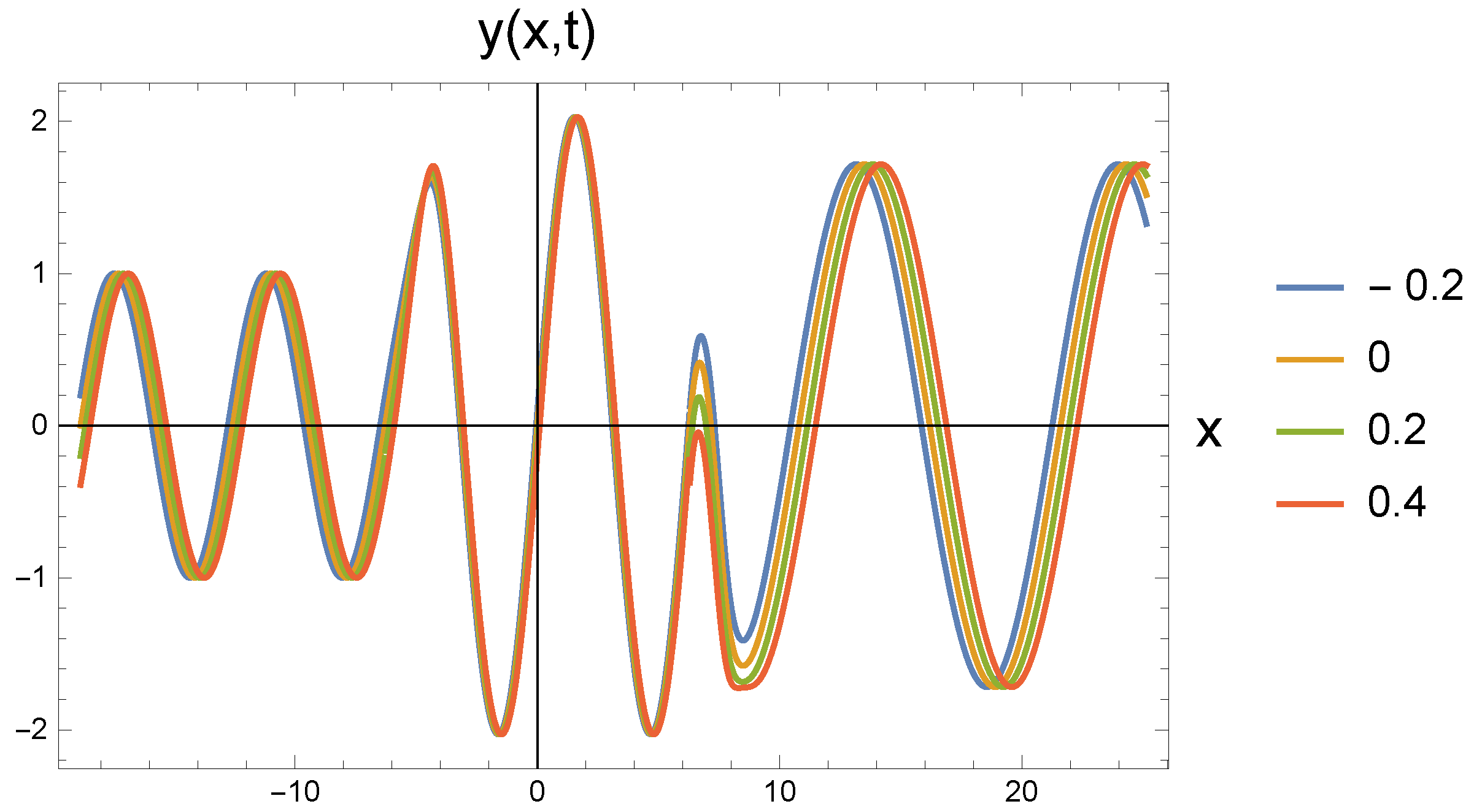
4. Graphical Discussion
5. Entropy Production of the Red Shift in the Cosmological Microwave Background Radiation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Morse, M.; Feshbach, H. Methods of Theoretical Physics; McGraw-Hill: New York, NY, USA, 1953. [Google Scholar]
- Weinberg, S. The Quantum Theory of Fields; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Wess, J.; Zumino, B. Supergage Transformations in Four Dimensions. Nucl. Phys. B 1974, 70, 39. [Google Scholar] [CrossRef]
- Wess, J.; Zumino, B. Supergage Invariant Extension of Quantum Electrodynamics. Nucl. Phys. B 1974, 78, 1. [Google Scholar] [CrossRef]
- Recami, E. Classical Tachyons and Possible Applications. Riv. Nuovo C. 1986, 9, 1. [Google Scholar] [CrossRef]
- Bollini, C.G.; Giambiagi, J.J. Generalized Klein-Gordon equations in d dimensions from supersymmetry. Phys. Rev. D 1985, 32, 3316. [Google Scholar] [CrossRef]
- Agudin, J.L.; Platzeck, A.M. Tachyons and the Radiation of an Accelerated Charge. Phys. Rev. D 1982, 26, 1923. [Google Scholar] [CrossRef]
- Barci, D.G.; Bollini, C.G.; Rocca, M. The Tachyon Propagator. Il Nuovo C. A 1993, 106, 603. [Google Scholar] [CrossRef][Green Version]
- Barci, D.G.; Bollini, C.G.; Oxman, L.E.; Rocca, M. Higher Order Equations and Constituent Fields. Int. J. Mod. Phys. A 1994, 23, 4169. [Google Scholar] [CrossRef]
- Márkus, F.; Gambár, K. Symmetry Breaking and Dynamic Transition in the Negative Mass Term Klein–Gordon Equations. Symmetry 2024, 16, 144. [Google Scholar] [CrossRef]
- Sikivie, P.; Sullivan, N.; Tanner, D.B. Proposal for Axion Dark Matter Detection Using an Circuit. Phys. Rev. Lett. 2014, 112, 131301. [Google Scholar] [CrossRef]
- Sikivie, P. Invisible axion search methods. Rev. Mod. Phys. 2021, 93, 015004. [Google Scholar] [CrossRef]
- Brevik, I. Axion Electrodynamics and the Axionic Casimir Effect. Universe 2021, 7, 133. [Google Scholar] [CrossRef]
- Patkós, A. Radiation Backreaction in Axion Electrodynamics. Symmetry 2022, 14, 1113. [Google Scholar] [CrossRef]
- Chadha-Day, F. Axion-like Particle Oscillations. J. Cosmol. Astropart. Phys. 2022, 13. [Google Scholar] [CrossRef]
- Nenno, D.M.; Gacia, C.A.C.; Gooh, J.; Felser, C.; Narang, P. Axion Physics in Condesnsed-Matter Systems. Nat. Rev. Phys. 2020, 2, 682. [Google Scholar]
- Du, N.; Force, N.; Khatiwada, R.; Lentz, E.; Ottens, R.; Rosenberg, L.J.; Rybka, G.; Carosi, G.; Woollett, N.; Bowring, D.; et al. Search for Invisible Axion Dark Matter with the Axion Dark Matter Experiment. Phys. Rev. Lett. 2018, 120, 151301. [Google Scholar] [CrossRef]
- Chigusa, S.; Hazumi, M.; Herbschleb, E.D.; Matsuzaki, Y.; Mizuochi, N.; Nakayama, K. Nuclear spin metrology with nitrogen vacancy center in diamond for axion dark matter detection. Phys. Rev. D 2025, 111, 075028. [Google Scholar] [CrossRef]
- Wu, D.; Liang, H.; Jiao, M.; Cai, Y.-F.; Duan, C.-K.; Wang, Y.; Rong, X.; Du, J. Improved Limits on an Exotic Spin- and Velocity-Dependent Interaction at the Micrometer Scale with an Ensemble-NV-Diamond Magnetometer. Phys. Rev. Lett. 2023, 131, 071801. [Google Scholar] [CrossRef]
- Kollarics, S.; Simon, F.; Bojtor, A.; Koltai, K.; Klujber, G.; Szieberth, M.; Márkus, B.G.; Beke, D.; Kamarás, K.; Gali, A.; et al. Ultrahigh Nitrogen-Vacancy Center Concentration in Diamond. Carbon 2022, 188, 393. [Google Scholar] [CrossRef]
- Kollarics, S.; Márkus, B.; Kucsera, R.; Thiering, G.; Gali, Á.; Németh, G.; Kamarás, K.; Forró, L.; Simon, F. Terahertz Emission from Diamond Nitrogen-Vacancy Centers. Sci. Adv. 2024, 10, 1. [Google Scholar] [CrossRef]
- Hohenberg, P.C.; Halperin, B.I. Theory of dynamic critical phenomena. Rev. Mod. Phys. 1977, 49, 435. [Google Scholar] [CrossRef]
- Scheffer, M.; Carpenter, S.R.; Lenton, T.M.; Bascompte, J.; Brock, W.; Dakos, V.; van de Koppel, J.; van de Leemput, I.A.; Levin, S.A.; van Nes, E.H.; et al. Anticipating Critical Transitions. Science 2012, 338, 344. [Google Scholar] [CrossRef]
- Preskill, J.; Wise, M.B.; Wilczek, F. Cosmology of Invisible Axion. Phys. Lett. 1983, 120B, 127. [Google Scholar] [CrossRef]
- Tatum, E.T.; Seshavatharam, U.V.S. How the Flat Space Cosmology Model Correlates the Recombination CMB Temperature of 3000 K with a Redshift of 1100. J. Mod. Phys. 2024, 15, 174. [Google Scholar] [CrossRef]
- Turner, M.S. Cosmic and Local Mass Density of “Invisible” Axions. Phys. Rev. D 1996, 33, 889. [Google Scholar] [CrossRef] [PubMed]

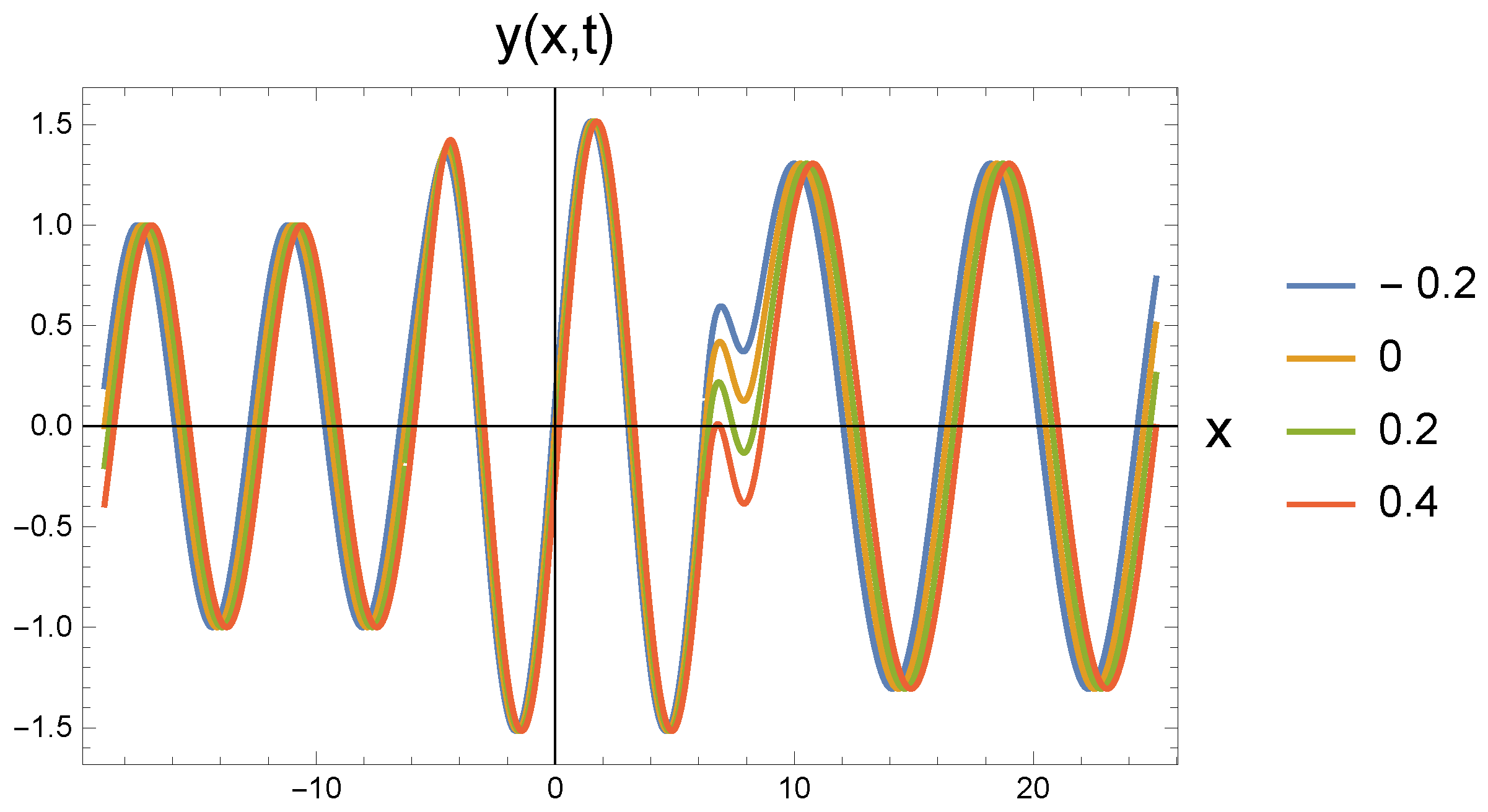
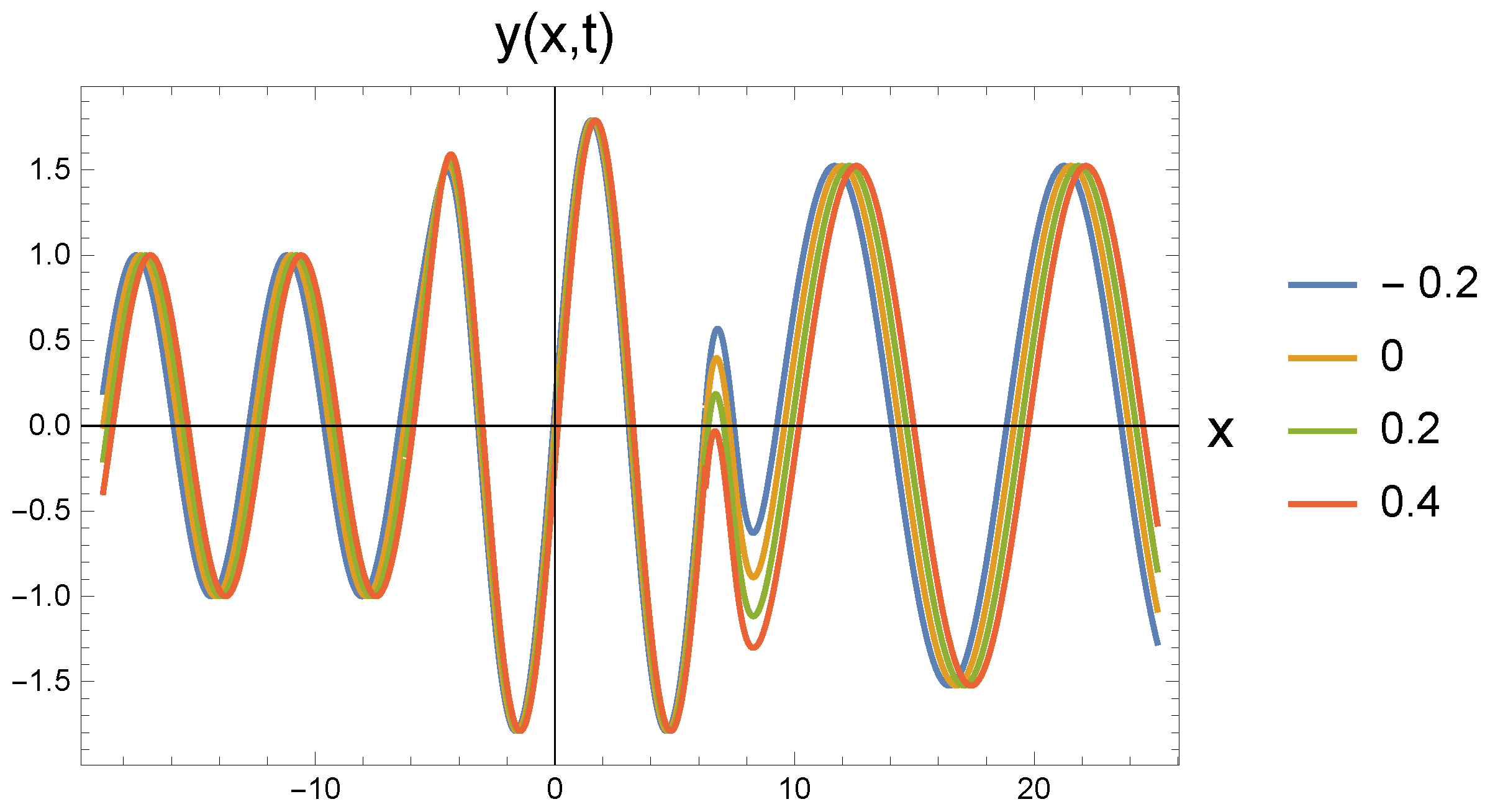
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Márkus, F.; Gambár, K. A Dissipative Phenomenon: The Mechanical Model of the Cosmological Axion Influence. Entropy 2025, 27, 1036. https://doi.org/10.3390/e27101036
Márkus F, Gambár K. A Dissipative Phenomenon: The Mechanical Model of the Cosmological Axion Influence. Entropy. 2025; 27(10):1036. https://doi.org/10.3390/e27101036
Chicago/Turabian StyleMárkus, Ferenc, and Katalin Gambár. 2025. "A Dissipative Phenomenon: The Mechanical Model of the Cosmological Axion Influence" Entropy 27, no. 10: 1036. https://doi.org/10.3390/e27101036
APA StyleMárkus, F., & Gambár, K. (2025). A Dissipative Phenomenon: The Mechanical Model of the Cosmological Axion Influence. Entropy, 27(10), 1036. https://doi.org/10.3390/e27101036





