Enhance the Performance of Expectation Propagation Detection in Spatially Correlated Massive MIMO Channels via DFT Precoding
Abstract
1. Introduction
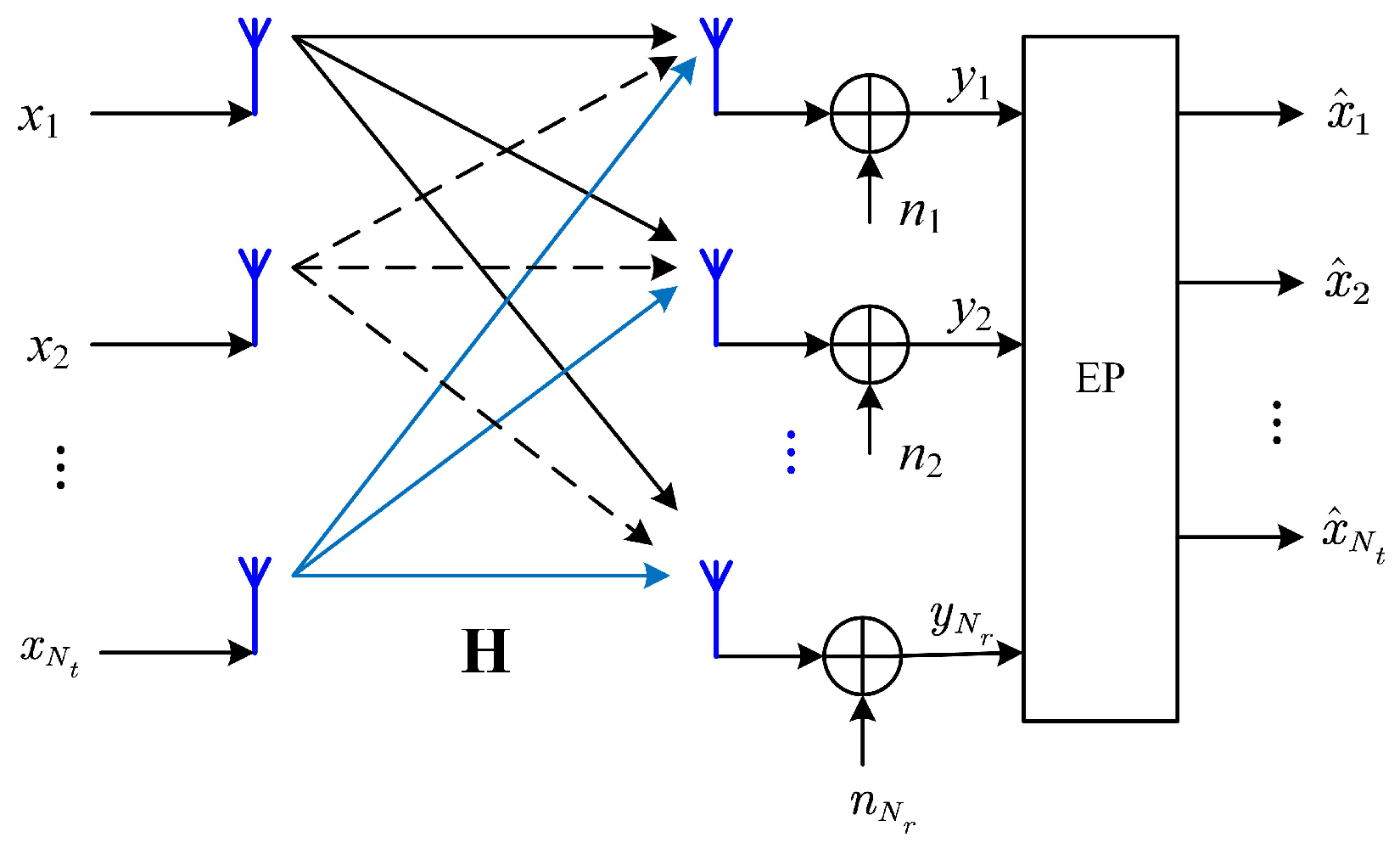
2. System Model
3. Expectation Propagation
3.1. Expectation Propagation Algorithm
- (1)
- Initialization: Set and for all . Form vectors and .
- (2)
- Posterior update: At iteration l, compute
- (3)
- Cavity distribution: For each symbol , compute the parameters of cavity distribution as
- (4)
- Moment matching and parameters update: Define the distribution , compute its mean and variance:
- (5)
- Iteration: Repeat steps 2–4 until convergence or the maximum number of iterations L is reached.
- (6)
- Decision: The final detection output is taken as
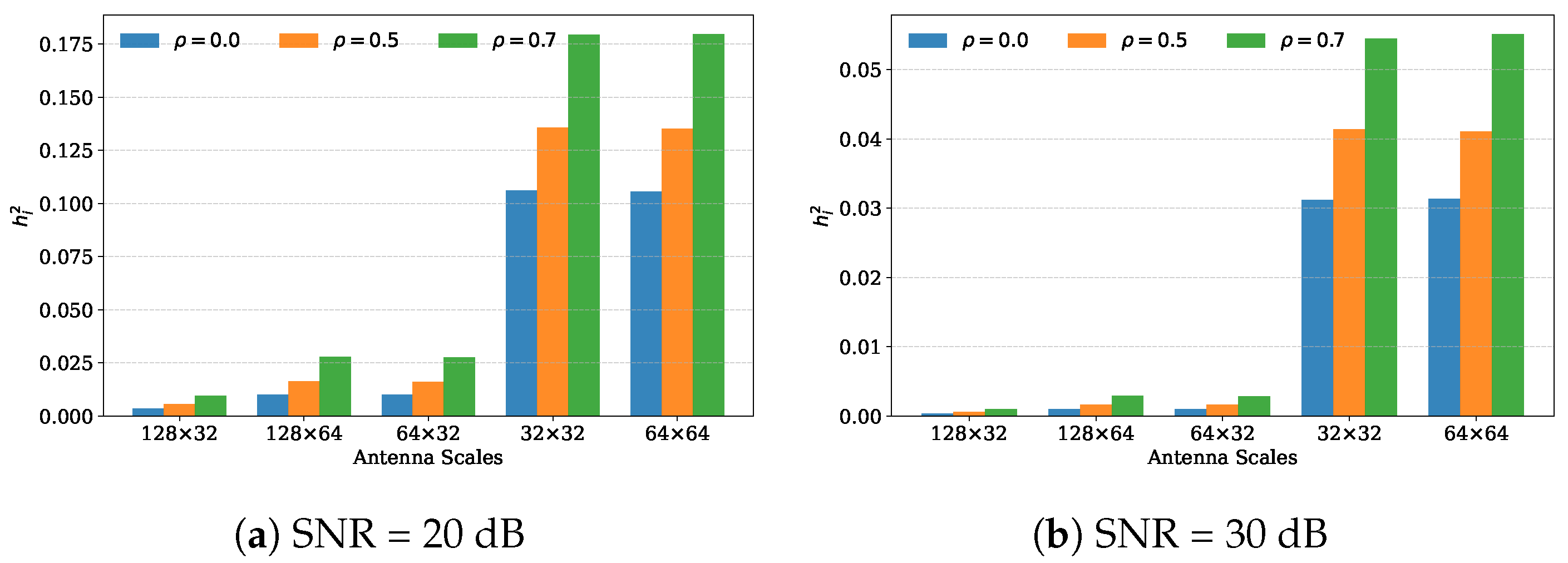
3.2. Transmit Antenna Correlation Degrades the Performance of EP
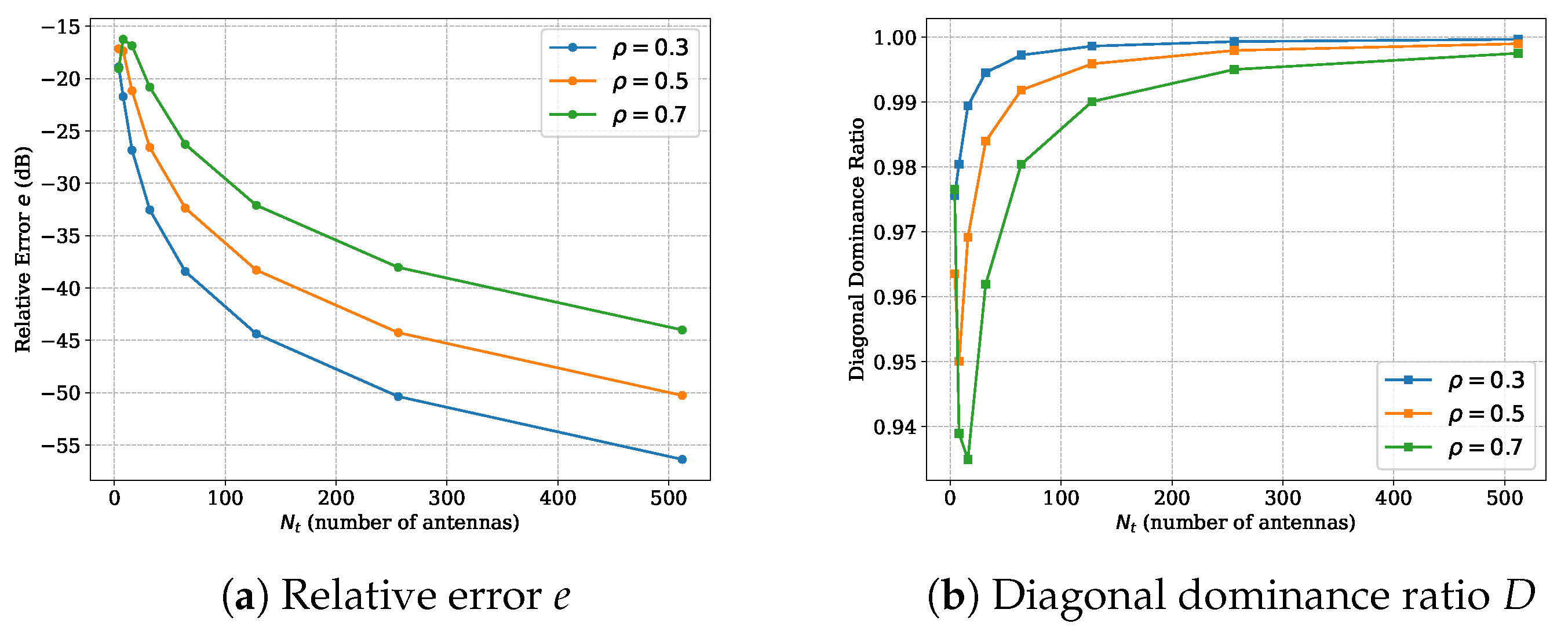
4. Eliminating Antenna Correlation Using DFT Precoding
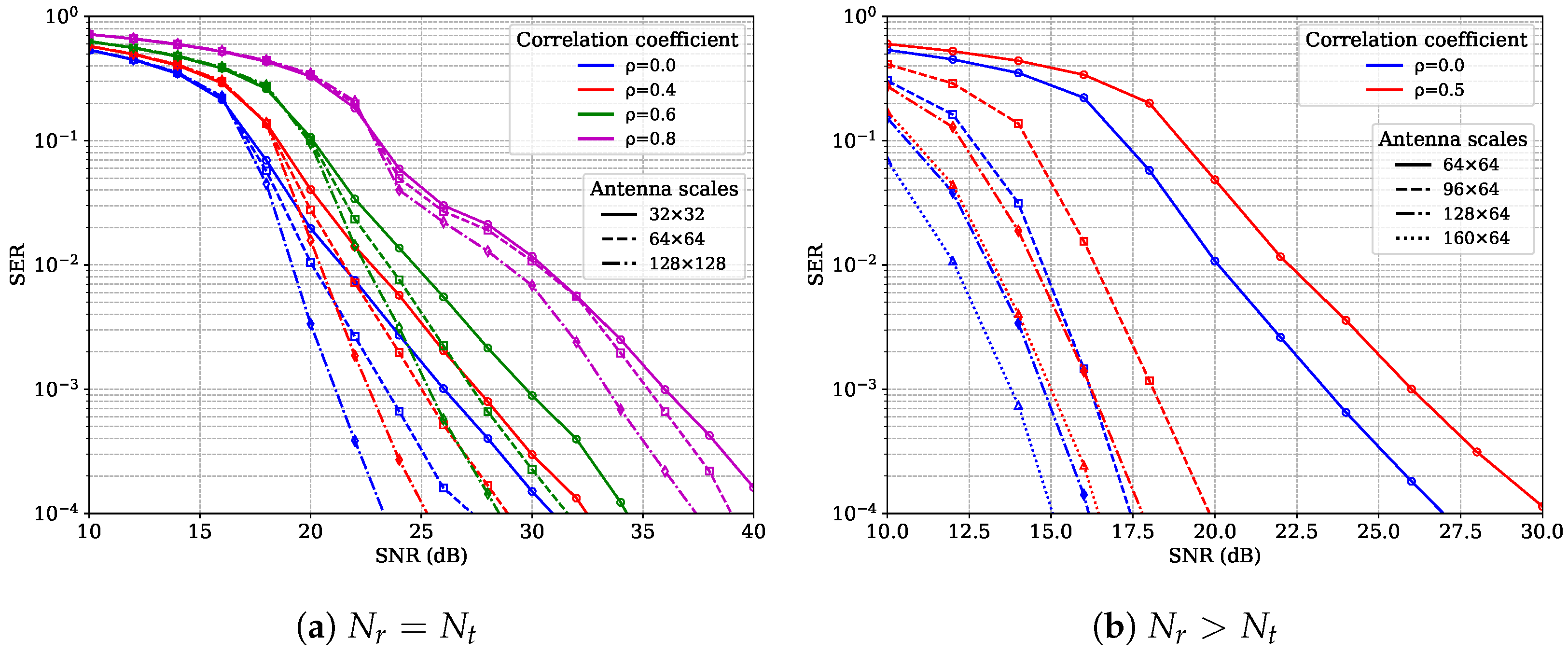
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Björnson, E.; Kara, F.; Kolomvakis, N.; Kosasih, A.; Ramezani, P.; Salman, M.B. Enabling 6G Performance in the Upper Mid-Band by Transitioning From Massive to Gigantic MIMO. IEEE Open J. Commun. Soc. 2025, 6, 5450–5463. [Google Scholar] [CrossRef]
- Ngo, H.Q.; Interdonato, G.; Larsson, E.G.; Caire, G.; Andrews, J.G. Ultradense Cell-Free Massive MIMO for 6G: Technical Overview and Open Questions. Proc. IEEE 2024, 112, 805–831. [Google Scholar] [CrossRef]
- Huo, Y.; Lin, X.; Di, B.; Zhang, H.; Hernando, F.J.L.; Tan, A.S.; Mumtaz, S.; Demir, Ö.T.; Chen-Hu, K. Technology Trends for Massive MIMO towards 6G. Sensors 2023, 23, 6062. [Google Scholar] [CrossRef]
- Albreem, M.A.; Juntti, M.; Shahabuddin, S. Massive MIMO Detection Techniques: A Survey. IEEE Commun. Surv. Tutor. 2019, 21, 3109–3132. [Google Scholar] [CrossRef]
- He, H.; Kosasih, A.; Yu, X.; Zhang, J.; Letaief, K.B. GNN-Enhanced Approximate Message Passing for Massive/Ultra-Massive MIMO Detection. In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), Glasgow, UK, 26–29 March 2023; pp. 1–6. [Google Scholar]
- He, H.; Yu, X.; Zhang, J.; Letaief, K.B. Message Passing Meets Graph Neural Networks: A New Paradigm for Massive MIMO Systems. IEEE Trans. Wirel. Commun. 2024, 23, 4709–4723. [Google Scholar] [CrossRef]
- Minka, T.P. Expectation propagation for approximate Bayesian inference. arXiv 2013, arXiv:1301.2294. [Google Scholar] [CrossRef]
- Céspedes, J.; Olmos, P.M.; Sánchez-Fernández, M.; Perez-Cruz, F. Expectation Propagation Detection for High-Order High-Dimensional MIMO Systems. IEEE Trans. Commun. 2014, 62, 2840–2849. [Google Scholar] [CrossRef]
- Dong, Y.; Li, H.; Zhang, Z.; Wang, X.; Dai, X. Efficient EP Detectors Based on Channel Sparsification for Massive MIMO Systems. IEEE Commun. Lett. 2020, 24, 539–542. [Google Scholar] [CrossRef]
- Yao, G.; Chen, H.; Hu, J. An improved expectation propagation based detection scheme for MIMO systems. IEEE Trans. Commun. 2021, 69, 2163–2175. [Google Scholar] [CrossRef]
- Tan, X.; Ueng, Y.-L.; Zhang, Z.; You, X.; Zhang, C. A low-complexity massive MIMO detection based on approximate expectation propagation. IEEE Trans. Veh. Technol. 2019, 68, 7260–7272. [Google Scholar] [CrossRef]
- Tan, X.; Ding, M.; Ji, Z.; Zhang, Z.; You, X.; Zhang, C. An improved power expectation propagation detector for massive MIMO systems. IEEE Trans. Veh. Technol. 2023, 73, 1353–1357. [Google Scholar] [CrossRef]
- Schmid, L.; Sulz, D.; Schmalen, L. Fast and Robust Expectation Propagation MIMO Detection via Preconditioned Conjugated Gradient. In Proceedings of the 2024 58th Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 27–30 October 2024; pp. 1603–1608. [Google Scholar]
- Ou, Z.; Yang, H. Adaptive Expectation Propagation for MIMO Signal Detection. In Proceedings of the 2024 IEEE 24th International Conference on Communication Technology (ICCT), Chengdu, China, 18–20 October 2024; pp. 510–515. [Google Scholar]
- Liu, Z.; He, D.; Wu, N.; Yan, Q.; Li, Y. Model-Driven IEP-GNN Framework for MIMO Detection With Bayesian Optimization. IEEE Wirel. Commun. Lett. 2024, 13, 387–391. [Google Scholar] [CrossRef]
- Lu, Q.; Luan, S.; Chang, X.-W. GCEPNet: Graph Convolution-Enhanced Expectation Propagation for Massive MIMO Detection. In Proceedings of the 2024 IEEE Global Communications Conference (GLOBECOM), Cape Town, South Africa, 8–12 December 2024; pp. 444–449. [Google Scholar]
- Xin, P.; Wang, H.; Liu, Y.; Chen, J.; Song, T.; Wang, D. An Artificial Intelligence-Assisted Expectation Propagation Detection for MIMO Systems. Electronics 2023, 12, 388. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, J.; Wen, C.-K.; Jin, S.; Han, S. Graph Neural Network-Enhanced Expectation Propagation Algorithm for MIMO Turbo Receivers. IEEE Trans. Signal Process. 2023, 71, 3458–3473. [Google Scholar] [CrossRef]
- Chen, H.; Yao, G.; Hu, J. Algorithm parameters selection method with deep learning for EP MIMO detector. IEEE Trans. Veh. Technol. 2021, 70, 10146–10156. [Google Scholar] [CrossRef]
- Ge, Y.; Tan, X.; Ji, Z.; Zhang, Z.; You, X.; Zhang, C. Improving approximate expectation propagation massive MIMO detector with deep learning. IEEE Wirel. Commun. Lett. 2021, 10, 2145–2149. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, J.; Zhang, J.; Liu, G.; Zhang, Y.; Yao, Y. A theoretical analysis of favorable propagation on massive MIMO channels with generalized angle distributions. Electronics 2022, 11, 2150. [Google Scholar] [CrossRef]
- Sanguinetti, L.; Björnson, E.; Hoydis, J. Toward Massive MIMO 2.0: Understanding Spatial Correlation, Interference Suppression, and Pilot Contamination. IEEE Trans. Commun. 2020, 68, 232–257. [Google Scholar] [CrossRef]
- Demir, Ö.T.; Björnson, E.; Sanguinetti, L. Channel Modeling and Channel Estimation for Holographic Massive MIMO With Planar Arrays. IEEE Wirel. Commun. Lett. 2022, 11, 997–1001. [Google Scholar] [CrossRef]
- Li, Y.-N.R.; Xiao, H.; Li, J.; Wu, H. Wireless backhaul of dense small cell networks with high dimension MIMO. In Proceedings of the 2014 IEEE Globecom Workshops (GC Wkshps), Austin, TX, USA, 8–12 December 2014; pp. 1254–1259. [Google Scholar]
- Neil, C.T.; Garcia-Rodriguez, A.; Smith, P.J.; Dmochowski, P.A.; Masouros, C.; Shafi, M. On the Performance of Spatially Correlated Large Antenna Arrays for Millimeter-Wave Frequencies. IEEE Trans. Antennas Propag. 2018, 66, 132–148. [Google Scholar] [CrossRef]
- He, S.; Du, J.; Liao, Y. Multi-User Scheduling for 6G V2X Ultra-Massive MIMO System. Sensors 2021, 21, 6742. [Google Scholar] [CrossRef]
- Bai, L.; Huang, Z.; Cheng, X. A Non-Stationary Model With Time-Space Consistency for 6G Massive MIMO mmWave UAV Channels. IEEE Trans. Wirel. Commun. 2023, 22, 2048–2064. [Google Scholar] [CrossRef]
- Li, G.-H.; Yue, D.-W.; Jin, S.-N. Spatially Correlated Rayleigh Fading Characteristics of RIS-Aided mmWave MIMO Communications. IEEE Commun. Lett. 2023, 27, 2222–2226. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, H.; Song, S.; Wang, Z. Correlated Channel-Oriented Expectation Propagation-Based Detector for Massive MIMO Systems. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 71, 1429–1442. [Google Scholar] [CrossRef]
- Busari, S.A.; Huq, K.M.S.; Mumtaz, S.; Rodriguez, J.; Haas, H. Millimeter-Wave Massive MIMO Communication for Future Wireless Systems: A Survey. IEEE Commun. Surv. Tutor. 2018, 20, 836–869. [Google Scholar] [CrossRef]
- Karabulut, U.; Awada, A.; Viering, I.; Simsek, M.; Fettweis, G.P. Spatial and Temporal Channel Characteristics of 5G 3D Channel Model with Beamforming for User Mobility Investigations. IEEE Commun. Mag. 2018, 56, 38–45. [Google Scholar] [CrossRef]
- Gray, R.M. Toeplitz and circulant matrices: A review. Found. Trends Commun. Inf. Theory 2006, 2, 155–239. [Google Scholar] [CrossRef]
- Giannakis, G.B.; Liu, Z.; Ma, X.; Zhou, S. Space-Time Coding for Broadband Wireless Communications; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Li, N.; Wei, Z.; Yang, H.; Zhang, X.; Yang, D. Hybrid Precoding for mmWave Massive MIMO Systems With Partially Connected Structure. IEEE Access 2017, 5, 15142–15151. [Google Scholar] [CrossRef]
- Cheng, Z.; Wei, Z.; Yang, H. Low-Complexity Joint User and Beam Selection for Beamspace mmWave MIMO Systems. IEEE Commun. Lett. 2020, 24, 2065–2069. [Google Scholar] [CrossRef]
- Longoria-Gandara, O.; Parra-Michel, R. Estimation of Correlated MIMO Channels using Partial Channel State Information and DPSS. IEEE Trans. Wirel. Commun. 2011, 10, 3711–3719. [Google Scholar] [CrossRef]
- Shiu, D.S.; Foschini, G.J.; Gans, M.J.; Kahn, J.M. Fading Correlation and Its Effect on the Capacity of Multielement Antenna Systems. IEEE Trans. Commun. 2000, 48, 502–513. [Google Scholar] [CrossRef]
- Aalo, V.A. Performance of maximal-ratio diversity systems in a correlated Nakagami-fading environment. IEEE Trans. Commun. 1995, 43, 2360–2369. [Google Scholar] [CrossRef]
- Wang, H.; Cheng, B.; Tan, X.; You, X.; Zhang, C. An efficient approximate expectation propagation detector with block-diagonal neumann-series. IEEE Trans. Circuits Syst. I Regul. Pap. 2023, 70, 1403–1416. [Google Scholar] [CrossRef]
- Berra, S.; Benchabane, A.; Chakraborty, S.; Maruta, K.; Dinis, R.; Beko, M. A Low Complexity Linear Precoding Method for Extremely Large-Scale MIMO Systems. IEEE Open J. Veh. Technol. 2025, 6, 240–255. [Google Scholar] [CrossRef]
- Björnson, E. What Is the Difference Between Beamforming and Precoding? 2017. Available online: https://ma-mimo.ellintech.se/2017/10/03/what-is-the-difference-between-beamforming-and-precoding/ (accessed on 28 September 2025).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, H.; Tang, J.; Ou, Z.; Liu, Y.; Yang, H. Enhance the Performance of Expectation Propagation Detection in Spatially Correlated Massive MIMO Channels via DFT Precoding. Entropy 2025, 27, 1030. https://doi.org/10.3390/e27101030
Luo H, Tang J, Ou Z, Liu Y, Yang H. Enhance the Performance of Expectation Propagation Detection in Spatially Correlated Massive MIMO Channels via DFT Precoding. Entropy. 2025; 27(10):1030. https://doi.org/10.3390/e27101030
Chicago/Turabian StyleLuo, Huaicheng, Jia Tang, Zeliang Ou, Yitong Liu, and Hongwen Yang. 2025. "Enhance the Performance of Expectation Propagation Detection in Spatially Correlated Massive MIMO Channels via DFT Precoding" Entropy 27, no. 10: 1030. https://doi.org/10.3390/e27101030
APA StyleLuo, H., Tang, J., Ou, Z., Liu, Y., & Yang, H. (2025). Enhance the Performance of Expectation Propagation Detection in Spatially Correlated Massive MIMO Channels via DFT Precoding. Entropy, 27(10), 1030. https://doi.org/10.3390/e27101030





