Two-Dimensional Image Lempel–Ziv Complexity Calculation Method and Its Application in Defect Detection
Abstract
1. Introduction
2. Background Knowledge of Lempel–Ziv Complexity
3. The Proposed Two-Dimensional Lempel–Ziv Complexity
4. Results and Discussion
4.1. Case Study 1: The Simulation Signal
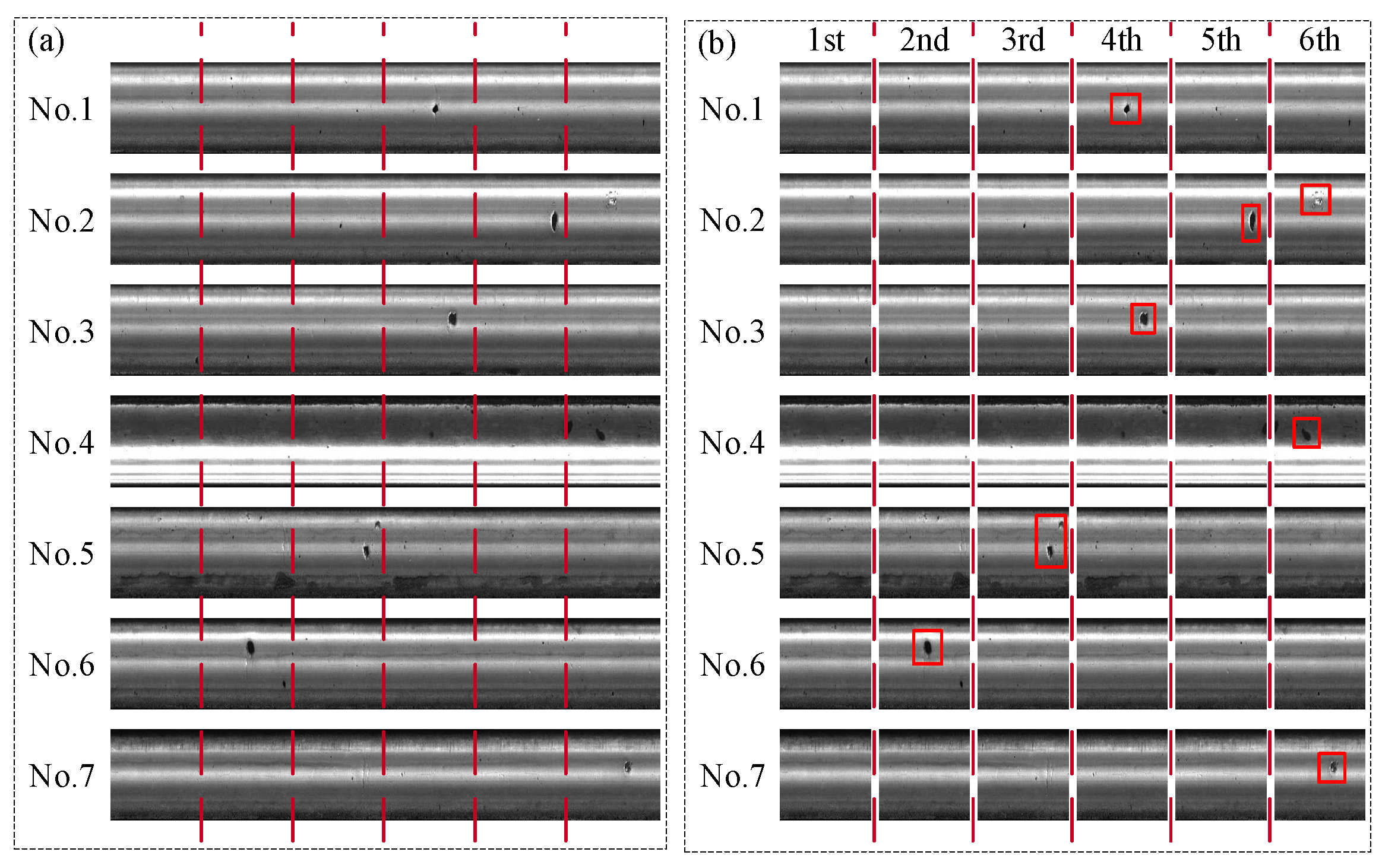
4.2. Case Study 2: Type-I RSDDs Dataset
4.3. Case Study 3: AITEX Dataset
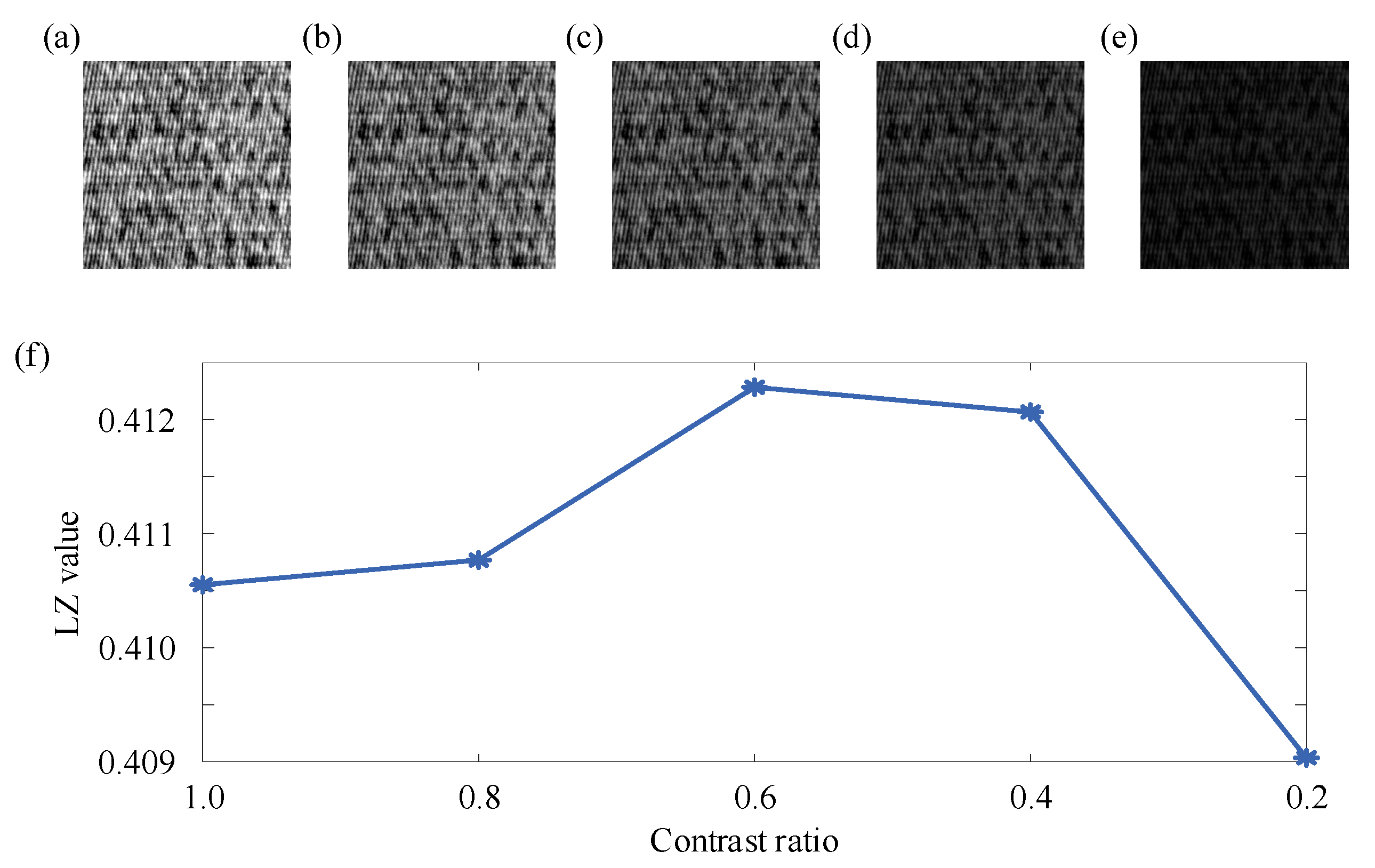
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, S.; Li, Y.B.; Noman, K.; Li, Z.X.; Feng, K.; Liu, Z.; Deng, Z.C. Multivariate multiscale dispersion Lempel-Ziv complexity for fault diagnosis of machinery with multiple channels. Inf. Fusion 2024, 104, 102152. [Google Scholar] [CrossRef]
- Muchnik, A.A.; Positselsky, S.Y. Kolmogorov entropy in the context of computability theory. Theor. Comput. Sci. 2002, 271, 15–35. [Google Scholar] [CrossRef]
- Bauwens, B.; Gács, P.; Romashchenko, A.; Shen, A. Inequalities for space-bounded Kolmogorov complexity. Computability 2022, 11, 165–185. [Google Scholar] [CrossRef]
- Zamora, J.; Sublime, J. An Ensemble and Multi-View Clustering Method Based on Kolmogorov Complexity. Entropy 2023, 25, 371. [Google Scholar] [CrossRef] [PubMed]
- Lempel, A.; Ziv, J. On the Complexity of Finite Sequences. IEEE Trans. Inf. Theory 1976, 22, 75–81. [Google Scholar] [CrossRef]
- Rantalainen, T.; Koivunen, K.; Portegijs, E.; Rantanen, T.; Palmberg, L.; Karavirta, L.; Chastin, S. Is Complexity of Daily Activity Associated with Physical Function and Life-Space Mobility among Older Adults? Med. Sci. Sports Exerc. 2022, 54, 1210–1217. [Google Scholar] [CrossRef]
- Barile, C.; Casavola, C.; Pappalettera, G.; Kannan, V.P. Interpreting the Lempel-Ziv complexity of acoustic emission signals for identifying damage modes in composite materials. Struct. Health Monit. 2022, 22, 1708–1720. [Google Scholar] [CrossRef]
- Zhu, L.J.; Wang, D.M.; Yue, J.K.; Lu, J.Y.; Li, G.F. Leakage detection method of natural gas pipeline combining improved variational mode decomposition and Lempel-Ziv complexity analysis. Trans. Inst. Meas. Control 2022, 44, 2865–2876. [Google Scholar] [CrossRef]
- Zhang, M.Y.; Zhang, D.; Fu, S.S.; Kujala, P.; Hirdaris, S. A predictive analytics method for maritime traffic flow complexity estimation in inland waterways. Reliab. Eng. Syst. Safe 2022, 220, 108317. [Google Scholar] [CrossRef]
- Ren, Z.; Yue, M.Y.; Han, X.; Zhao, Z.Y.; Wang, B.; Hong, Y.; Zhao, T.; Wang, N.; Zhao, P.; Hong, Y.X.; et al. The potential of the Lempel-Ziv complexity of the EEG in diagnosing cognitive impairment in patients with temporal lobe epilepsy. Eplileptic Disord. 2023, 25, 331–342. [Google Scholar] [CrossRef]
- Biggs, D.; Boncompte, G.; Pedemonte, J.C.; Fuentes, C.; Cortinez, L.I. The effect of age on electroencephalogram measures of anesthesia hypnosis: A comparison of BIS, Alpha Power, Lempel-Ziv complexity and permutation entropy during propofol induction. Front. Aging Neurosci. 2022, 14, 910886. [Google Scholar] [CrossRef]
- Aamodt, A.; Nilsen, A.S.; Markhus, R.; Kusztor, A.; HasanzadehMoghadam, F.; Kauppi, N.; Thürer, B.; Storm, J.F.; Juel, B.E. EEG Lempel-Ziv complexity varies with sleep stage, but does not seem to track dream experience. Front. Hum. Neurosci. 2023, 16, 987714. [Google Scholar] [CrossRef]
- Yin, J.C.; Zhuang, X.Y.; Sui, W.T.; Sheng, Y.L. Manifold learning and Lempel-Ziv complexity-based fault severity recognition method for bearing. Measurement 2023, 213, 112714. [Google Scholar] [CrossRef]
- Li, Y.J.; Tan, L.; Xiao, M.; Xiong, Q. Hierarchical dispersion Lempel-Ziv complexity for fault diagnosis of rolling bearing. Meas. Sci. Technol. 2023, 34, 035015. [Google Scholar] [CrossRef]
- Zhang, Y.T.; Wei, S.S.; Liu, H.; Zhao, L.N.; Liu, C.Y. A novel encoding Lempel-Ziv complexity algorithm for quantifying the irregularity of physiological time series. Comput. Methods Programs Biomed. 2016, 133, 7–15. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.T.; Ma, Z.G.; Dong, W.T. Nonlinear Quality Indices Based on a Novel Lempel-Ziv Complexity for Assessing Quality of Multi-Lead ECGs Collected in Real Time. J. Inf. Process. Syst. 2020, 16, 508–521. [Google Scholar] [CrossRef]
- Yin, J.; Xu, M.; Zheng, H. Fault diagnosis of bearing based on Symbolic Aggregate approXimation and Lempel-Ziv. Measurement 2019, 138, 206–216. [Google Scholar] [CrossRef]
- Bai, Y.; Liang, Z.H.; Li, X.L. A permutation Lempel-Ziv complexity measure for EEG analysis. Biomed. Signal Process. 2015, 19, 102–114. [Google Scholar] [CrossRef]
- Bai, Y.; Liang, Z.H.; Li, X.L.; Voss, L.J.; Sleigh, J.W. Permutation Lempel-Ziv complexity measure of electroencephalogram in GABAergic anaesthetics. Physiol. Meas. 2015, 36, 2483–2501. [Google Scholar] [CrossRef]
- Shumbayawonda, E.; Tosun, P.D.; Fernández, A.; Hughes, M.P.; Abásolo, D. Complexity Changes in Brain Activity in Healthy Ageing: A Permutation Lempel-Ziv Complexity Study of Magnetoencephalograms. Entropy 2018, 20, 506. [Google Scholar] [CrossRef]
- Li, Y.X.; Geng, B.; Jiao, S.B. Dispersion entropy-based Lempel-Ziv complexity: A new metric for signal analysis. Chaos Solitons Fract. 2022, 161, 112400. [Google Scholar] [CrossRef]
- Jiao, S.; Geng, B.; Li, Y.; Zhang, Q.; Wang, Q.; Li, Y.; Wang, W. Comparative study of feature extraction and classification based on dispersion Lempel-Ziv complexity. Int. J. Numer. Model. 2022, 35, e2949. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis: A new measure of complexity loss in heart failure. J. Electrocardiol. 2003, 36, 39–40. [Google Scholar] [CrossRef]
- Jiang, Y.; Peng, C.K.; Xu, Y. Hierarchical entropy analysis for biological signals. J. Comput. Appl. Math. 2011, 236, 728–742. [Google Scholar] [CrossRef]
- Li, Y.B.; Liu, F.L.; Wang, S.; Yin, J.C. Multiscale Symbolic Lempel-Ziv: An Effective Feature Extraction Approach for Fault Diagnosis of Railway Vehicle Systems. IEEE Trans. Ind. Inf. 2021, 17, 199–208. [Google Scholar] [CrossRef]
- Yi, Y.M.; Li, Y.X.; Wu, J.X. Multi-scale permutation Lempel-Ziv complexity and its application in feature extraction for Ship-radiated noise. Front. Mar. Sci. 2022, 9, 1047332. [Google Scholar] [CrossRef]
- Borowska, M. Multiscale Permutation Lempel-Ziv Complexity Measure for Biomedical Signal Analysis: Interpretation and Application to Focal EEG Signals. Entropy 2021, 23, 832. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.X.; Jiang, X.R.; Tang, B.Z.; Ning, F.Y.; Lou, Y.L. Feature extraction methods of ship-radiated noise: From single feature of multi-scale dispersion Lempel-Ziv complexity to mixed double features. Appl. Acoust. 2022, 199, 109032. [Google Scholar] [CrossRef]
- Mao, X.G.; Shang, P.J.; Xu, M.; Peng, C.K. Measuring time series based on multiscale dispersion Lempel-Ziv complexity and dispersion entropy plane. Chaos Solitons Fract. 2020, 137, 109868. [Google Scholar] [CrossRef]
- Xiao, L.L. A New Feature Extraction Method of Marine Ambient Noise Based on Multiscale Dispersion Entropy. Math. Probl. Eng. 2022, 2022, 7618380. [Google Scholar] [CrossRef]
- Han, B.; Wang, S.; Zhu, Q.Q.; Yang, X.H.; Li, Y.B. Intelligent Fault Diagnosis of Rotating Machinery Using Hierarchical Lempel-Ziv Complexity. Appl. Sci. 2020, 10, 4221. [Google Scholar] [CrossRef]
- Li, Y.B.; Wang, S.; Deng, Z.C. Intelligent fault identification of rotary machinery using refined composite multi-scale Lempel-Ziv complexity. J. Manuf. Syst. 2021, 61, 725–735. [Google Scholar] [CrossRef]
- Li, Y.; Jiao, S.; Geng, B. Refined composite multiscale fluctuation-based dispersion Lempel-Ziv complexity for signal analysis. ISA Trans. 2022, 133, 273–284. [Google Scholar] [CrossRef]
- Li, Y.X.; Yi, Y.M.; Wu, J.X.; Gu, Y.P. A novel feature extraction method for ship-radiated noise based on hierarchical refined composite multi-scale dispersion entropy-based Lempel-Ziv complexity. Deep Sea Res. Part I Oceanogr. Res. Pap. 2023, 199, 104111. [Google Scholar] [CrossRef]
- Li, Y.X.; Wu, J.X.; Yi, Y.M.; Gu, Y.P. Unequal-step multiscale integrated mapping dispersion Lempel-Ziv complexity: A novel complexity metric for signal analysis. Chaos Solitons Fract. 2023, 175, 113945. [Google Scholar] [CrossRef]
- Li, Y.J.; Tan, L.; Li, P.; Xiong, Q. Refined time-shift multiscale dispersion Lempel-Ziv complexity to diagnose rolling bearing faults. J. Mech. Sci. Technol. 2023, 9, 4557–4566. [Google Scholar] [CrossRef]
- Hong, H.; Liang, M. Fault severity assessment for rolling element bearings using the Lempel–Ziv complexity and continuous wavelet transform. J. Sound Vib. 2009, 320, 452–468. [Google Scholar] [CrossRef]
- Cui, L.; Gong, X.; Zhang, J.; Wang, H. Double-dictionary matching pursuit for fault extent evaluation of rolling bearing based on the Lempel-Ziv complexity. J. Sound Vib. 2016, 385, 372–388. [Google Scholar] [CrossRef]
- Cui, L.; Li, B.; Ma, J.; Jin, Z. Quantitative trend fault diagnosis of a rolling bearing based on Sparsogram and Lempel-Ziv. Measurement 2018, 128, 410–418. [Google Scholar] [CrossRef]
- Du, J.; Cui, L.; Zhang, J.; Li, J.; Huang, J.; Adam, G.; Glowacz, A. The Method of Quantitative Trend Diagnosis of Rolling Bearing Fault Based on Protrugram and Lempel–Ziv. Shock Vib. 2018, 2018, 4303109. [Google Scholar] [CrossRef]
- Dang, P.F.; Yang, Z.X.; Wen, B.G.; Wang, M.G.; Han, Q.K. Fault severity assessment of rolling bearing based on optimized multi-dictionaries matching pursuit and Lempel-Ziv complexity. ISA Trans. 2021, 116, 191–202. [Google Scholar] [CrossRef]
- Yin, J.; Lei, M.; Zheng, H.; Yang, Y.; Li, Y.; Xu, M. The Average Coding Length of Huffman Coding Based Signal Processing and Its Application in Fault Severity Recognition. Appl. Sci. 2019, 9, 5051. [Google Scholar] [CrossRef]
- Noman, K.; Li, Y.B.; Si, S.B.; Wang, S.; Mao, G. Oscillatory Lempel-Ziv Complexity Calculation as a Nonlinear Measure for Continuous Monitoring of Bearing Health. IEEE Trans. Reliab. 2022, 72, 151–165. [Google Scholar] [CrossRef]
- Wang, H.; Yang, T.; Han, Q.; Luo, Z. Approach to the Quantitative Diagnosis of Rolling Bearings Based on Optimized VMD and Lempel–Ziv Complexity under Varying Conditions. Sensors 2023, 23, 4044. [Google Scholar] [CrossRef] [PubMed]
- Altintop, C.G.; Latifoglu, F.; Akin, A.K.; Bayram, A.; Ciftci, M. Classification of Depth of Coma Using Complexity Measures and Nonlinear Features of Electroencephalogram Signals. Int. J. Neural Syst. 2022, 32, 2250018. [Google Scholar] [CrossRef] [PubMed]
- Golesorkhi, M.; Gomez-Pilar, J.; Catal, Y.; Tumati, S.; Yagoub, M.; Stamatakis, E.A.; Northoff, G. From temporal to spatial topography: Hierarchy of neural dynamics in higher- and lower-order networks shapes their complexity. Cereb. Cortex. 2022, 32, 5637–5653. [Google Scholar] [CrossRef] [PubMed]
- Barile, C.; Casavola, C.; Pappalettera, G.; Kannan, V.P.; Renna, G. Investigation of Interlaminar Shear Properties of CFRP Composites at Elevated Temperatures Using the Lempel-Ziv Complexity of Acoustic Emission Signals. Materials 2022, 15, 4252. [Google Scholar] [CrossRef]
- Luo, L.; Wang, X.F.; Lu, J.S.; Chen, G.P.; Luan, G.M.; Li, W.; Wang, Q.; Fang, F. Local field potentials, spiking activity, and receptive fields in human visual cortex. Sci. China Life Sci. 2023, 67, 614–617. [Google Scholar] [CrossRef]
- Turcsany, D.; Bargiela, A.; Maul, T. Local receptive field constrained deep networks. Inf. Sci. 2016, 349, 229–247. [Google Scholar] [CrossRef]
- Gan, J.R.; Li, Q.T.; Wang, J.Z.; Yu, H.M. A Hierarchical Extractor-Based Visual Rail Surface Inspection System. IEEE Sens. J. 2017, 17, 7935–7944. [Google Scholar] [CrossRef]
- Al-Kadi, O.; Watson, D. Texture analysis of aggressive and nonaggressive lung tumor CE CT images. IEEE Trans. Bio-Med. Eng. 2008, 55, 1822–1830. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, R.C.; Woods, R.E.; Eddins, S.L. Digital Image Processing Using MATLAB, 2nd ed.; Gatesmark Publishing: Knoxville, TN, USA, 2007. [Google Scholar]
- Machado, P.; Romero, J.; Nadal, M.; Santos, A.; Correia, J.; Carballal, A. Computerized measures of visual complexity. Acta Psychol. 2015, 160, 43–57. [Google Scholar] [CrossRef] [PubMed]
- Forsythe, A.; Nadal, M.; Sheehy, N.; Cela-Conde, C.J.; Sawey, M. Predicting beauty: Fractal dimension and visual complexity in art. Brit. J. Psychol. 2011, 102, 49–70. [Google Scholar] [CrossRef] [PubMed]
- Mengiste, E.; Mannem, K.R.; Prieto, S.A.; de Soto, B.G. Transfer-Learning and Texture Features for Recognition of the Conditions of Construction Materials with Small Data Sets. J. Comput. Civ. Eng. 2024, 38, 04023036. [Google Scholar] [CrossRef]
- Silvestre-Blanes, J.; Albero-Albero, T.; Miralles, I.; Pérez-Llorens, R.; Moreno, J. A Public Fabric Database for Defect Detection Methods and Results. Autex Res. J. 2019, 19, 363–374. [Google Scholar] [CrossRef]
- Yang, C.C. Finest image sharpening by use of the modified mask filter dealing with highest spatial frequencies. Optik 2014, 125, 1942–1944. [Google Scholar] [CrossRef]
- Wei, Y.Z.; Xu, M. Detection of lane line based on Robert operator. J. Meas. Eng. 2021, 9, 156–166. [Google Scholar] [CrossRef]
- Chang, Q.; Li, X.; Li, Y.; Miyazaki, J. Multi-directional Sobel operator kernel on GPUs. J. Parallel Distrib. Comput. 2023, 177, 160–170. [Google Scholar] [CrossRef]
- Lee, H.G.; Ham, S.; Kim, J. Isotropic Finite Difference Discretization of Laplacian Operator. Appl. Comput. Math. 2023, 22, 259–274. [Google Scholar] [CrossRef]
- Zhou, B.; Qin, L.; Gong, W. Stereo-Matching Algorithm Using Weighted Guided Image Filtering Based on Laplacian of Gaussian Operator. Laser Optoelectron. Prog. 2019, 56, 101502. [Google Scholar] [CrossRef]









| Serial Number of 2D Signal | Description |
|---|---|
| I1 | zeros (128, 128) |
| I2 | ones (128, 128) |
| I3 | zeros (128, 128) and the 10th row is 1 |
| I4 | zeros (128, 128) and the 10th column is 1 |
| I5 | zeros (128, 128) and the 10th, 11th, 12th, 13th, 14th, and 15th rows are 1 |
| I6 | zeros (128, 128) and the 10th and 20th row are 1 |
| I7 | zeros (128, 128) and the 10th and 21st rows are 1 |
| I8 | zeros (128, 128) and the 10th, 21st, and 43rd rows are 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, J.; Sui, W.; Zhuang, X.; Sheng, Y.; Li, Y. Two-Dimensional Image Lempel–Ziv Complexity Calculation Method and Its Application in Defect Detection. Entropy 2025, 27, 1014. https://doi.org/10.3390/e27101014
Yin J, Sui W, Zhuang X, Sheng Y, Li Y. Two-Dimensional Image Lempel–Ziv Complexity Calculation Method and Its Application in Defect Detection. Entropy. 2025; 27(10):1014. https://doi.org/10.3390/e27101014
Chicago/Turabian StyleYin, Jiancheng, Wentao Sui, Xuye Zhuang, Yunlong Sheng, and Yongbo Li. 2025. "Two-Dimensional Image Lempel–Ziv Complexity Calculation Method and Its Application in Defect Detection" Entropy 27, no. 10: 1014. https://doi.org/10.3390/e27101014
APA StyleYin, J., Sui, W., Zhuang, X., Sheng, Y., & Li, Y. (2025). Two-Dimensional Image Lempel–Ziv Complexity Calculation Method and Its Application in Defect Detection. Entropy, 27(10), 1014. https://doi.org/10.3390/e27101014






