A Secure and Efficient White-Box Implementation of SM4
Abstract
:1. Introduction
1.1. Related Work
1.2. Our Contribution
1.3. Organization
2. Preliminaries
2.1. SM4 Algorithm
2.2. Xiao–Lai Scheme
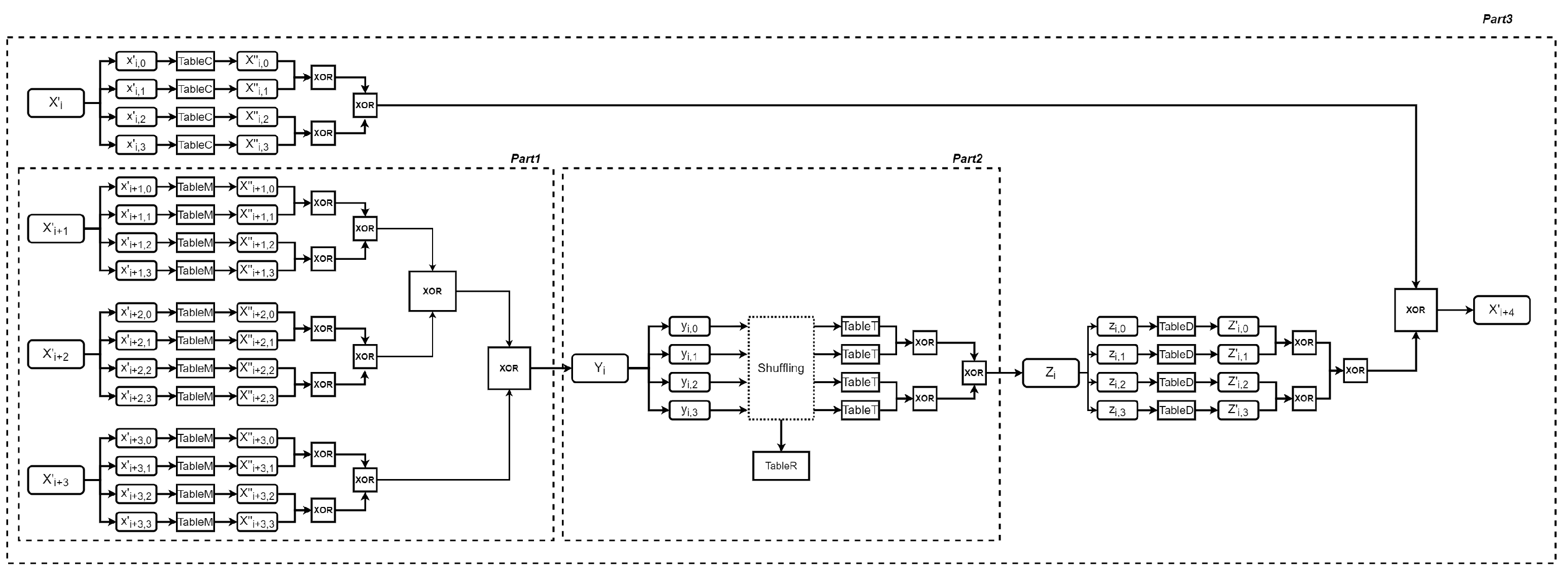
3. Improved SM4 White-Box Scheme
3.1. Design Ideas
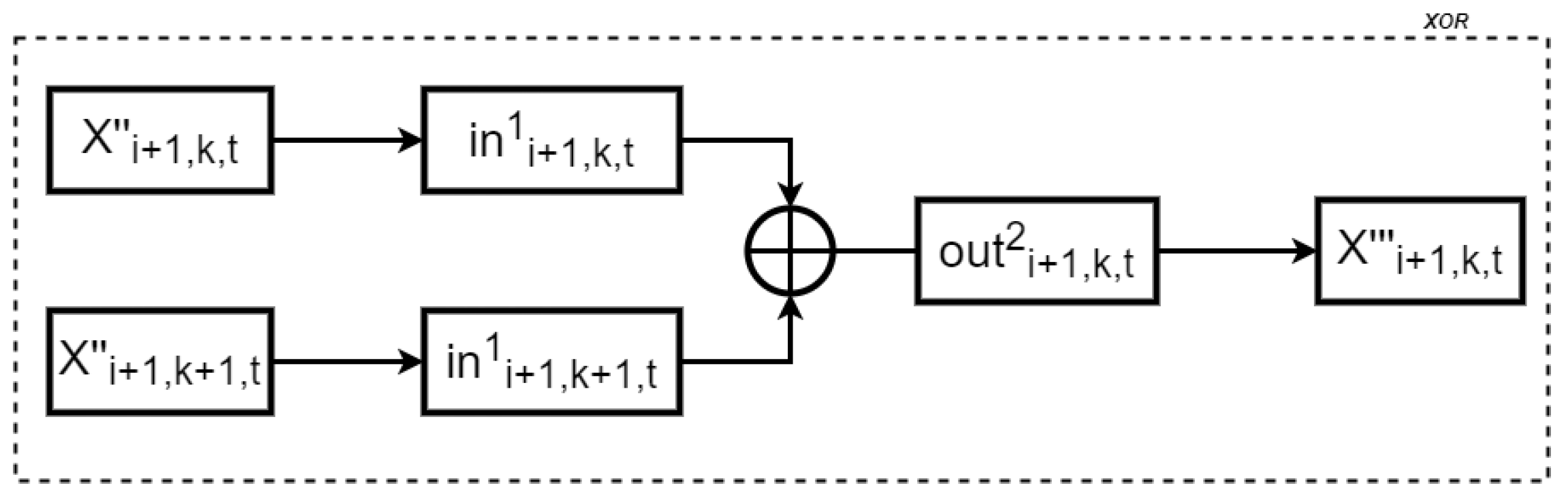
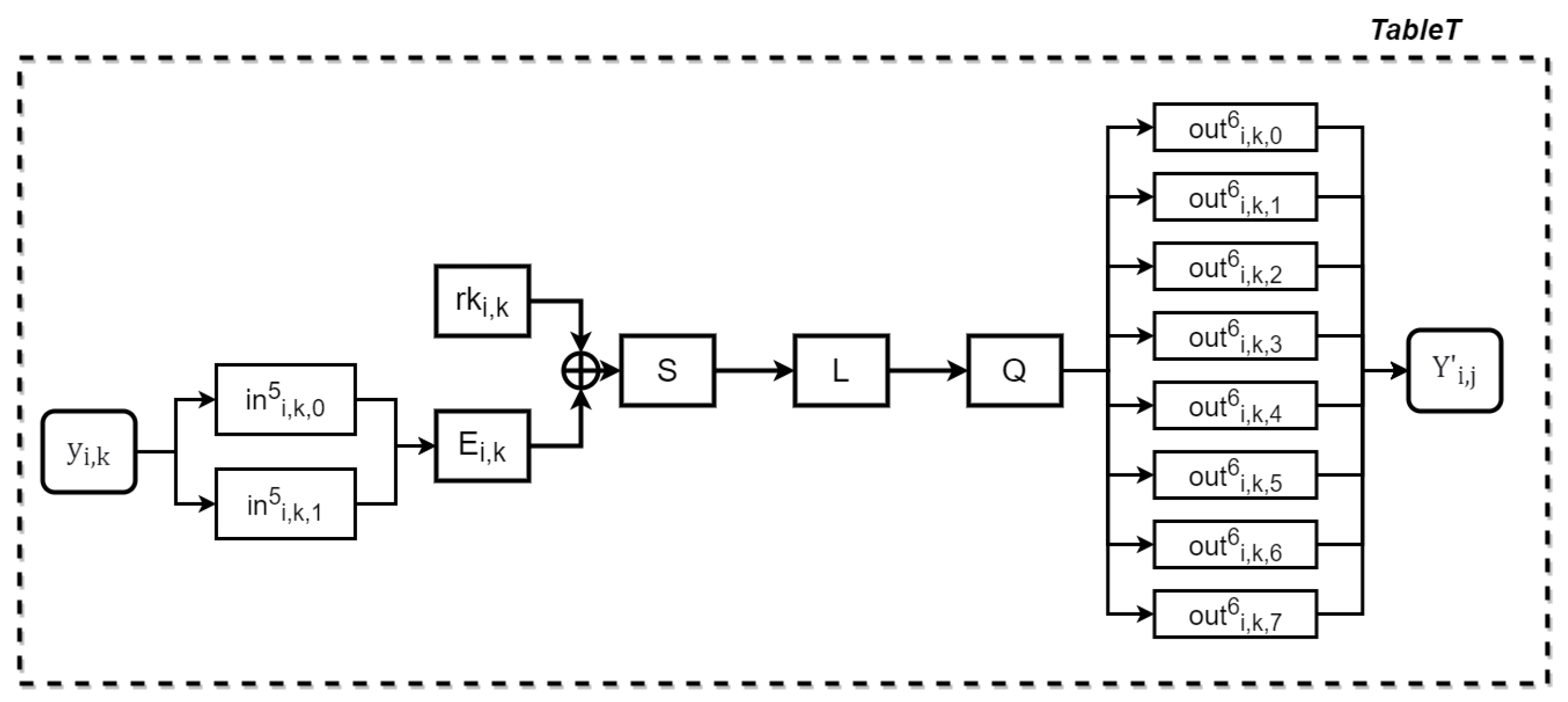
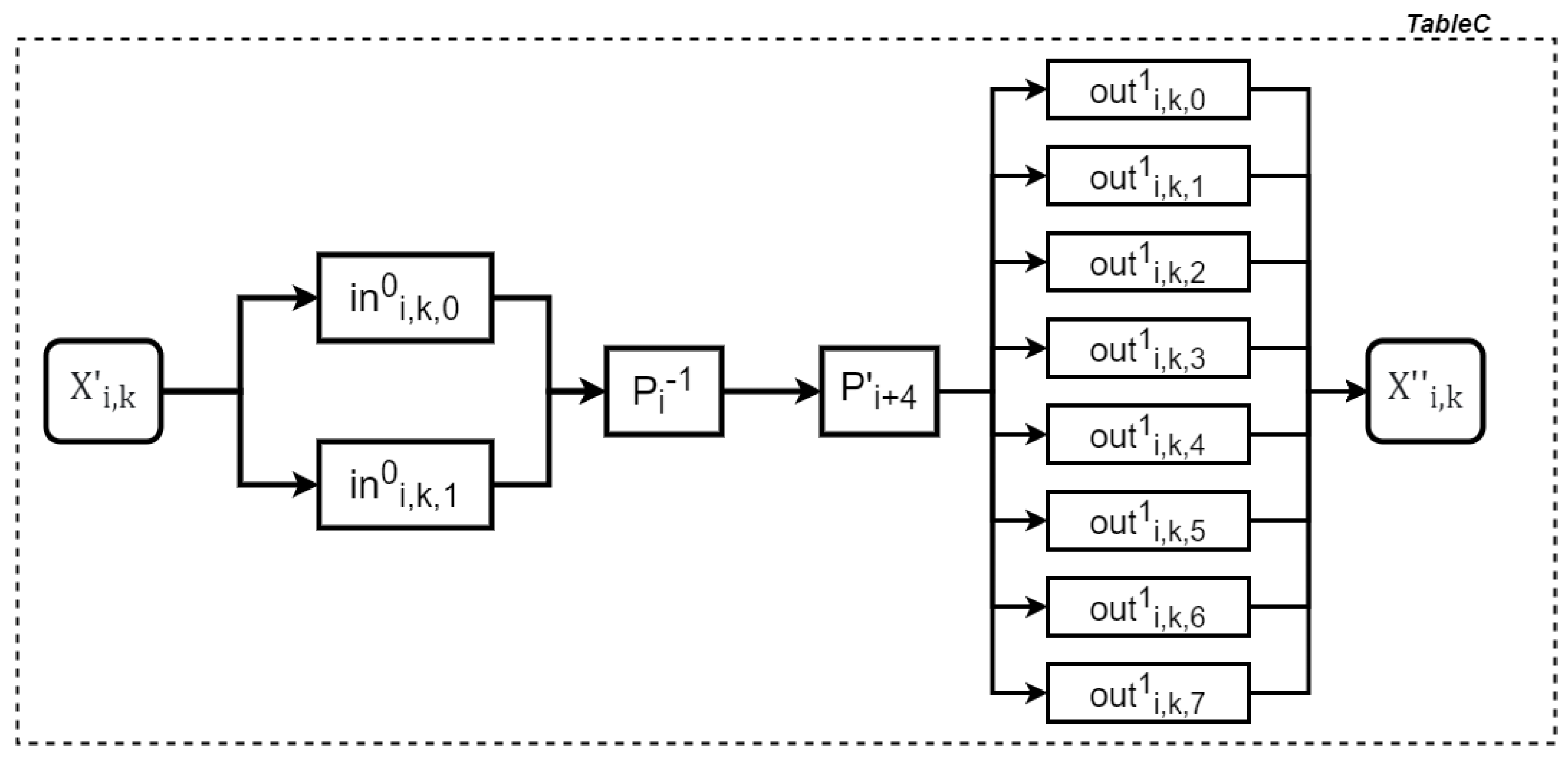
3.2. Construction of Our Scheme
4. Performance
5. Security Analysis: White-Box Obfuscation
5.1. Algebraic Attacks
5.1.1. BGE Attack
5.1.2. Lin–Lai Analysis
5.1.3. Pan et al.’s Analysis
5.2. DCA Experiments
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Chow, S.; Eisen, P.; Johnson, H.; Van Oorschot, P.C. A white-box DES implementation for DRM applications. In Proceedings of the ACM Workshop on Digital Rights Management, Washington, DC, USA, 18 November 2002; pp. 1–15. [Google Scholar]
- Chow, S.; Eisen, P.; Johnson, H.; Van Oorschot, P.C. White-box cryptography and an AES implementation. Sel. Areas Cryptogr. 2003, 9, 250–270. [Google Scholar]
- Billet, O.; Gilbert, H.; Ech-Chatbi, C. Cryptanalysis of a White Box AES Implementation. In Proceedings of the International Workshop on Selected Areas in Cryptography, Waterloo, ON, Canada, 9–10 August 2004. [Google Scholar]
- Alpirez Bock, E.; Bos, J.W.; Brzuska, C.; Hubain, C.; Michiels, W.; Mune, C.; Sanfelix Gonzalez, E.; Teuwen, P.; Treff, A. White-box cryptography: Don’t forget about grey-box attacks. J. Cryptol. 2019, 32, 1095–1143. [Google Scholar] [CrossRef]
- Alpirez Bock, E.; Brzuska, C.; Michiels, W.; Treff, A. On the Ineffectiveness of Internal Encodings—Revisiting the DCA Attack on White-Box Cryptography. In Proceedings of the International Conference on Applied Cryptography and Network Security, Leuven, Belgium, 2–4 July 2018. [Google Scholar]
- Lee, S.; Kim, T.; Kang, Y. A masked white-box cryptographic implementation for protecting against Differential Computation Analysis. IEEE Trans. Inf. Forensics Secur. 2018, 13, 2602–2615. [Google Scholar] [CrossRef]
- Lee, S.; Kim, M. Improvement on a masked white-box cryptographic implementation. IEEE Access 2020, 8, 90992–91004. [Google Scholar] [CrossRef]
- Biryukov, A.; Udovenko, A. Attacks and Countermeasures for White-box Designs. In Proceedings of the 24th International Conference on the Theory and Application of Cryptology and Information Security, Brisbane, Australia, 2–6 December 2018. [Google Scholar]
- Xiao, Y.Y.; Lai, X.J. White-Box cryptography and implementations of SMS4. In Proceedings of the 2009 CACR Annual Meeting, Denver, CO, USA, 18–22 April 2009. [Google Scholar]
- Lin, T.T.; Lai, X.J. Efficient Attack to White-Box SMS4 Implementation. J. Softw. 2013, 24, 2238–2249. [Google Scholar] [CrossRef]
- Bai, K.; Wu, C. A secure white-box SM4 implementation. Secur. Commun. Netw. 2015, 9, 996–1006. [Google Scholar] [CrossRef]
- Pan, W.L.; Qin, T.H.; Jia, Y.; Zhang, L.T. Cryptanalysis of two white-box SM4 implementations. J. Cryptologic Res. 2018, 5, 651–670. [Google Scholar]
- Shi, Y.; Wei, W.; He, Z. A Lightweight White-Box Symmetric Encryption Algorithm against Node Capture for WSNs. Sensors 2015, 15, 11928–11952. [Google Scholar] [CrossRef] [PubMed]
- Yao, S.; Chen, J. A new method for white-box implementation of SM4 algorithm. J. Cryptologic Res. 2020, 7, 358–374. [Google Scholar]
- Zhang, Y.Y.; Xu, D.; Chen, J. Analysis and Improvement of White-box SM4 Implementation. J. Electron. Inf. Technol. 2022, 44, 2903–2913. [Google Scholar]
- Yuan, Z.Q.; Chen, J. Differential Computation Analysis of White-box SM4 Scheme. J. Softw. 2022, 34, 3891–3904. [Google Scholar]
- Yuan, Z.Q.; Chen, J. A white-box SM4 scheme against Differential Computation Analysis. J. Cryptologic Res. 2023, 10, 386–396. [Google Scholar]
- Zhao, D.Y.; Wang, Y.B.; Li, Y.; Hu, X.B.; Yu, Y.Y.; Chen, S.; Zheng, S.H. An Efficient Masked White-Box Implementation of SM4. Electronics 2024, 13, 2326. [Google Scholar] [CrossRef]
- SideChannelMarvels/Deadpool. Available online: https://github.com/SideChannelMarvels (accessed on 1 October 2024).






| Scheme | BGE Analysis | Lin–Lai Analysis | Pan Analysis | DCA | Memory |
|---|---|---|---|---|---|
| Xiao–Lai scheme [9] | Yes | No | No | No | 148.625 KB |
| Bai–Wu scheme [11] | Yes | Yes | No | No | 32.5 MB |
| Yuan’s scheme [17] | Yes | Yes | Yes | Yes | 34.5 MB |
| Zhang’s scheme [15] | Yes | Yes | Yes | Yes | 24.3 MB |
| Zhao’s scheme [18] | Yes | Yes | Yes | Yes | 7.8 MB |
| Our Scheme | Yes | Yes | Yes | Yes | 1.44 MB |
| Symbol | Description |
|---|---|
| i | The index of the current round of iteration, . |
| j | The index of a 32-bit word within a 128-bit state input to the round function, . |
| k | The index of a byte within a state word, . |
| t | The index of a nibble within a state word, . |
| The word input into the round of iteration. | |
| protected by encodings. | |
| The byte of the word . | |
| The byte of the round key. | |
| The output word of the round of iteration. | |
| The output word of Part 1 during the round of iteration. | |
| The byte of the word . | |
| The output word of Part 2 during the round of iteration. | |
| The byte of the word . | |
| A 32-dimensional invertible affine transformation to protect word . | |
| The linear component of the affine transformation . | |
| The constant component of the affine transformation . | |
| The inverse of the affine transformation . | |
| A 32-dimensional affine transformation generated by . | |
| An 8-dimensional reversible affine transformation. | |
| The compound affine transformation combining and . | |
| A 32-dimensional invertible affine transformation. | |
| m | The index of non-linear encoding, . |
| The 4-order nonlinear encoding to protect the output word of the current table lookup operation. | |
| The 4-order nonlinear decoding to offset the protection of the previous table lookup operation. |
| Table | Memory | Number of | Memory |
|---|---|---|---|
| (Single) | Tables | (Total) | |
| TableSE | 1 KB | 16 KB | |
| TableFE | 1 KB | 16 KB | |
| TableM | 1 KB | 384 KB | |
| TableT | 1 KB | 128 KB | |
| TableC | 1 KB | 128 KB | |
| TableD | 1 KB | 128 KB | |
| XOR | 0.125 KB | 672 KB | |
| TableR | 0.375 KB | 1 | 0.375 KB |
| Total | N/A | N/A | 1472 KB |
| Scheme | Memory | Generation Time | Total Tables | Total XORs | Affine Transformation | Encryption Time |
|---|---|---|---|---|---|---|
| (One WB Instance) | (s) | (8-to-32-bit) | (32-bit) | (ms) | ||
| Xiao–Lai Scheme [9] | 148.625 KB | 0.021 | 128 | 192 | 160 | 0.06 [18] |
| Bai–Wu Scheme [11] | 32.5 MB | 3.97 | 640 | 640 | 0 | 0.001 [18] |
| Yao’s Scheme [14] | 276.625 KB | 0.092 | 128 | 96 + 96 (64-bit) | 160 | 0.06 [18] |
| Zhang’s Scheme [15] | 24.3 MB | — | 640 | 192 | 128 | — |
| Yuan’s Scheme [17] | 34.5 MB | — | 672 | 536 | 0 | — |
| Zhao’s Scheme [18] | 7.8 MB | 2.66 | 192 | 208 | 216 | 0.08 [18] |
| Our Scheme | 1.44 MB | 0.044 | 800 | 672 | 0 | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, X.; Yu, Y.; Tu, Y.; Wang, J.; Chen, S.; Bao, Y.; Zhang, T.; Xing, Y.; Zheng, S. A Secure and Efficient White-Box Implementation of SM4. Entropy 2025, 27, 1. https://doi.org/10.3390/e27010001
Hu X, Yu Y, Tu Y, Wang J, Chen S, Bao Y, Zhang T, Xing Y, Zheng S. A Secure and Efficient White-Box Implementation of SM4. Entropy. 2025; 27(1):1. https://doi.org/10.3390/e27010001
Chicago/Turabian StyleHu, Xiaobo, Yanyan Yu, Yinzi Tu, Jing Wang, Shi Chen, Yuqi Bao, Tengyuan Zhang, Yaowen Xing, and Shihui Zheng. 2025. "A Secure and Efficient White-Box Implementation of SM4" Entropy 27, no. 1: 1. https://doi.org/10.3390/e27010001
APA StyleHu, X., Yu, Y., Tu, Y., Wang, J., Chen, S., Bao, Y., Zhang, T., Xing, Y., & Zheng, S. (2025). A Secure and Efficient White-Box Implementation of SM4. Entropy, 27(1), 1. https://doi.org/10.3390/e27010001





