Abstract
This study explores the role of information entropy in understanding nuclear density distributions, including both stable configurations and non-traditional structures such as neutron halos and -clustering. By quantifying the uncertainty and disorder inherent in nucleon distributions in nuclear many-body systems, information entropy provides a macroscopic measure of the physical properties of the system. A more dispersed and disordered density distribution results in a higher value of information entropy. This intrinsic relationship between information entropy and system complexity allows us to quantify uncertainty and disorder in nuclear structures by analyzing various geometric parameters such as nuclear radius, diffuseness, neutron skin, and cluster structural features.
1. Introduction
Information entropy, a concept introduced by Claude Shannon to measure uncertainty in communication theory [1], has extensive applications in many scientific disciplines. In nuclear physics, a pioneering study on information entropy was performed in Ref. [2], where the multiplicity information was proposed and applied to search for nuclear liquid gas phase transition [3,4]. Applications of entropy or information entropy have been extended in different physics fields, e.g., Refs. [5,6,7,8,9,10,11,12,13,14,15,16,17]. It has become a valuable tool for the study of complex systems, providing a way to quantify uncertainty and disorder in nuclear systems. Its applications range from the study of nuclear structure to the analysis of the dynamics of particle production in high-energy collisions [18,19,20,21]. As the field advances, the integration of information entropy with theoretical models and experimental data could lead to deeper insights into the fundamental properties of nuclear matter.
Research on weakly bound nuclei has revealed unique quantum phenomena such as halo and skin formation [22,23,24,25,26,27,28,29,30,31,32,33,34,35], molecular orbitals, and cluster structures [36,37,38,39,40,41,42,43,44,45,46]. These discoveries have reshaped our understanding of nucleon distributions in atomic nuclei, which often deviate from idealized spherical or geometric models. The resulting patterns are complex and irregular, driven by factors such as nucleon interactions, energy levels, and clustering dynamics.
These non-uniform nucleon distributions result in regions of varying density, from densely packed areas to sparser edges. This irregularity directly affects the strength and range of nuclear forces, which, in turn, affects how nuclei interact and behave during reactions [47,48]. This complexity challenges traditional models of nuclear structure and underscores the need for more nuanced investigations.
Understanding these dynamics is critical to accurately modeling nuclear structures and predicting their behavior in various situations. By studying these patterns, researchers can gain deeper insights into the coexistence of mean-field and cluster dynamics, shedding light on fundamental nuclear properties and processes. This knowledge is central to the advancement of nuclear physics and can guide future studies of nuclear interactions and reactions.
In analogy to the information entropy for discrete values, the differential entropy for a continuous random variable X with probability density function is defined [49] as
with the normalization condition . This approach supports the broader application of information entropy in nuclear physics, allowing the analysis of continuous distributions.
The purpose of this study is to explore how information entropy is used in nuclear physics to understand nuclear density distributions, including both stable configurations and unconventional arrangements such as the halo structure and the clustering structure. The total information entropy of a system can serve as a comprehensive measure of physical information, providing a view of the nucleon distribution in a nuclear many-body system that reflects the disordered information of spatial configurations.
2. Information Entropy of Diverse Nuclear Structures
2.1. Information Entropy of the Density Distribution with Woods–Saxon Type
The nuclear Woods–Saxon distribution is a widely used model in nuclear physics to describe the spatial distribution of nucleons in an atomic nucleus [50,51,52,53]. It is essential for the study of heavier nuclei with diffuse surfaces and provides a smooth transition from the high-density core to the low-density edge, accurately reflecting the structure of many nuclei. Its flexibility allows it to fit experimental data, making it a valuable tool in nuclear physics for analyzing structures and processes such as reactions, scattering, and decay.
The nuclei 16O, 40Ca, 116Sn, and 208Pb with Woods–Saxon type density distribution [52]
are considered as examples to examine the information entropy. The normalization coefficient , the diffuseness parameter a, and the radius satisfy the normalization condition
where W can be the number of protons Z, neutrons N, or nucleons . The parameters and a describe the spatial distribution of protons and neutrons in a nucleus. The parameter for proton and neutron distributions is denoted as and , respectively [52]. They are given by and . The a parameter for the proton and neutron distributions is defined as and , respectively. The diffuseness parameters and of the nuclei 16O, 40Ca, 116Sn, and 208Pb are scaled by the same parameter to serve as a variable. The diffuseness parameters are modified by the scaling factor , which serves as a variable to adjust the diffuseness parameters and, consequently, alter the density distribution. By using Equation (4), we can calculate the entropy as a function of and analyze the correlation between entropy and the diffuseness parameter.
The information entropy in the nuclear system with radial density distribution of the Woods–Saxon type is defined as
where is the Boltzmann constant, introduced to maintain the consistency of units in information entropy, rather than to highlight its thermodynamic significance. As shown in Figure 1, the information entropy tends to increase linearly with an increasing diffusion parameter, indicating an increase in the uncertainty of the radial distribution of nucleons. Heavier nuclei exhibit larger information entropy values, suggesting that a greater number of nucleons enhances the complexity of the nuclear distribution and increases the uncertainty in the nuclear radial distribution. However, the rate of increase in information entropy for heavier nuclei is less pronounced, indicating a potential saturation effect as the system reaches a certain level of complexity.
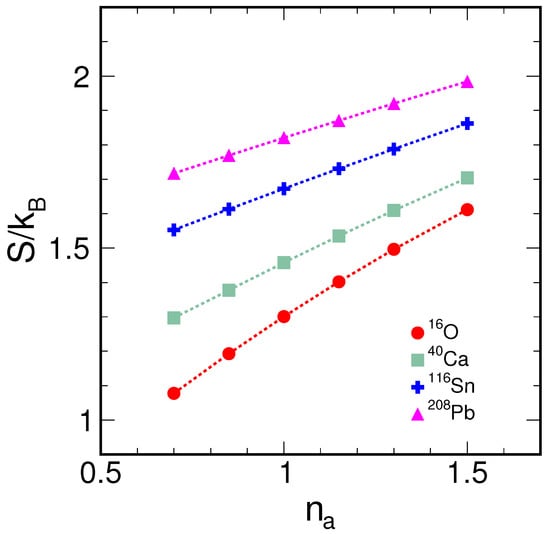
Figure 1.
(color online) Information entropy varying as the diffuseness scaling parameter for nuclei 16O, 40Ca, 116Sn, and 208Pb with Woods–Saxon type density distribution for nucleons.
The information entropy is observed to be a function of the neutron skin thickness in neutron-rich nuclei. This thickness is defined as the difference between the square root radii of neutrons and protons, expressed as , where and are the square root radii for neutrons and protons, respectively. By fixing the parameters , , and and varying , we can examine the variable . With varying, the density distribution changes accordingly, allowing us to calculate the entropy corresponding to each value of . Consequently, the information entropy can be examined as a function of neutron skin thickness in neutron-rich nuclei. As shown in Figure 2, the relationship between information entropy and neutron skin thickness is linearly positive; as the neutron skin becomes thicker, the information entropy increases in a linear mode. Among the neutron-rich nuclei studied, such as 48Ca, 132Sn, 208Pb, and 218Pb, the heavier nuclei, such as 218Pb and 208Pb, have higher information entropy compared to 132Sn, followed by 48Ca. Furthermore, all these nuclei show almost the same trend in the increase in the information entropy with respect to the neutron skin thickness. The neutron skin thickness parameter is crucial for gaining insight into the nuclear symmetry energy and the equation of state, which are fundamental aspects of nuclear physics. Information entropy provides new insights into the study of these phenomena.
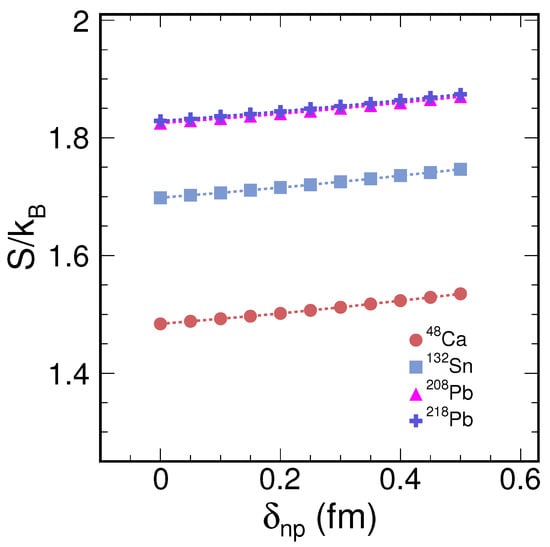
Figure 2.
(color online) Information entropy varying as neutron skin thickness for nuclei 48Ca, 132Sn, 208Pb, and 218Pb with Woods–Saxon type density distribution for nucleons.
2.2. Information Entropy of the He/Li Isotope with Neutron-Rich Tail
In loosely bound nuclei, the neutron density distribution extends into an unusually long tail, known as the neutron halo phenomenon. Despite the low density that characterizes the halo, its presence significantly influences the nuclear reaction cross section and imparts special properties to these nuclei [54,55].
The analysis of proton elastic scattering cross sections for the helium isotopes 4He, 6He, and 8He involves the use of four different phenomenological density distribution models [56]. These models—SF (Symmetrized Fermi), GH (Gaussian–Halo), GG (Gaussian–Gaussian), and GO (Gaussian–Oscillator)—are defined on the basis of the point-nucleon density, and each includes two free parameters. These parameters were obtained in Refs. [56,57,58] to reproduce an extended matter density characteristic of helium and lithium isotopes. The SF and GH parameterizations are used to model nucleon distributions in a nucleus without distinguishing between neutrons and protons. These models do not take into account the complex internal structure of many-body nuclear systems. In contrast, the GG and GO parametrizations assume a nuclear composition that includes a core and a halo, where the halo is composed entirely of neutrons, and each component has distinct spatial distributions. This approach provides a more nuanced representation of the nucleus, recognizing the spatial segregation between core nucleons and halo neutrons.
Figure 3 shows the information entropy for helium and lithium isotopes as determined by four different phenomenological density distribution models. The nucleon distribution in 4He is optimally captured by the SF and GH parameterizations, which treat neutrons and protons equivalently and yield the lowest information entropy. Conversely, the halo nucleus 11Li, which is characterized by its core-halo structure, is best described by the GH, GG, and GO models and has the highest information entropy. For 6Li, the information entropy values are consistent across all four distribution models. Notably, the neutron-rich helium isotope has a significantly higher information entropy compared to 4He. Models GH, GG, and GO are applied to 6He, 8He, 8Li, and 9Li. Comparing the information entropy between the neutron-rich nuclei 6He, 8He, 6Li, 8Li, and 9Li, the values are relatively close.
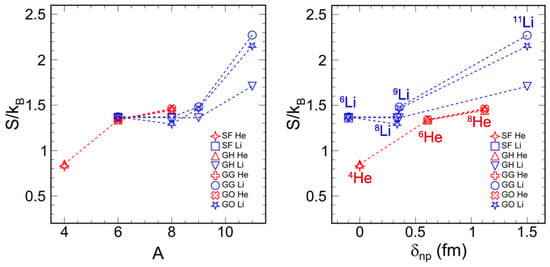
Figure 3.
(color online) The information entropy for He isotope and Li isotope (left). Correlation of information entropy with neutron skin thickness for He isotope and Li isotope (right).
According to the right side of Figure 3, the information entropy is strongly correlated with the neutron skin thickness. For both lithium and helium isotopes, the information entropy increases as the neutron skin becomes thicker. Although 6He and 8He have larger neutron skin thicknesses, they do not exhibit significantly larger information entropies compared to 6Li, 8Li, and 9Li due to their similar nucleon numbers.
Information entropy is a measure of uncertainty and disorder in nuclear density distributions. By evaluating the probability distribution over different points in the nucleus and their associated entropy values, we gain insight into the internal complexity of nuclear structures. Halo nuclei, such as 11Li, typically have higher entropy because their nuclear density is more radially dispersed.
2.3. Application of Information Entropy in Nuclear Cluster Formation
It has been suggested that atomic nuclei with tetrahedral symmetry could be found throughout the nuclear table [59]. In particular, the tetrahedral structure formed by four particles in 16O has been proposed in several studies [39,45,60,61,62]. The rotation–vibration spectrum of a 4 configuration with tetrahedral symmetry (denoted ) has been studied, and evidence for its occurrence in the lower energy levels of 16O has been found through experimental excitation spectra. This symmetry-based structure has implications for several areas of physics, suggesting that atomic nuclei with tetrahedral symmetry may be of significant interest.
It was shown that the conditions for cluster formation can be traced back in part to the depth of the confining nuclear potential using the theoretical framework of energy density functionals [63,64]. The depth of the nuclear potential for a harmonic oscillator is given by
where R is the radius of the system, m is the mass of the nucleon, ℏ is the reduced Planck constant, and b is the nucleon dispersion in the cluster distribution. As the dimensionless ratio (of b to the typical interfermion distance , quantifying nuclear clustering) increases, the nuclear system transitions from a crystalline to a clustered and then to a quantum liquid phase. The trend curves shown on the left of Figure 4 are the depth curves of the nuclear potential versus b for three geometric situations characterized by , the distance of the center of the -cluster relative to the center of 16O.
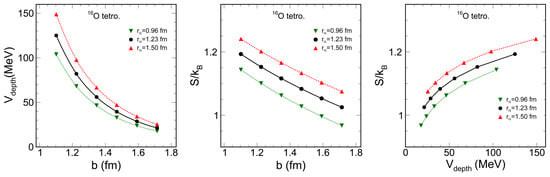
Figure 4.
(color online) The nuclear potential depth curves for a harmonic oscillator in 16O with tetrahedral cluster structure (left). The correlation of the information entropy with the cluster dispersion (center). The correlation of the information entropy with the depth of the nuclear potential for a harmonic oscillator (right).
To study the role of information entropy in 16O with tetrahedral cluster structure, where the distribution of nucleons within an alpha particle based on the alpha particle model is Gaussian type [65],
where is the mass of the cluster; is the nucleon distribution deviation for parameterizing the dispersion of the cluster; is the vector of the cluster relative to the center of mass of 16O. The centers of each cluster are defined as ; ; and ; , where , and is the edge length (the center distance of any two clusters). for the tetrahedral structure of 16O.
The correlation curves of the information entropy with the cluster dispersion are shown in the middle of Figure 4 for three geometric configurations characterized by the parameter . The information entropy tends to decrease monotonically as the dispersion parameter b increases. A larger leads to a larger system radius, which results in a higher information entropy. The right panel of Figure 4 shows some correlation curves between information entropy and potential depth. As the potential depth gradually decreases, the information entropy also decreases.
Studies [63,64] have concluded that the formation of nuclear clusters can be partially attributed to the depth of the confining nuclear potential, and it has been observed that as the parameter b increases, the nuclear system undergoes a phase transition from a crystalline state to a clustered state and finally to a quantum liquid state. The present investigations show a significant correlation between the information entropy and the parameter b. Consequently, it could be reasonable to say that variations in the information entropy are indicative of the nuclear phase transitions.
When fitting the correlation points for a given value of (i.e., a given size of the system) through a simple relation
where and are fitting parameters, we can obtain a good prediction curve of as a function of with least squares fitting accuracy of order . Equation (7) establishes a relationship between nuclear depth and information entropy, linking the microstate to randomness. A higher entropy indicates a higher degree of disorder. The depth of the nuclear potential determines the degree of confinement and energy level structure of the nucleons in the nucleus, which affects the quality, size, and shape of the nucleus, as well as nuclear reactions. The analysis of Figure 4 suggests that for 16O, which is characterized by a tetrahedral cluster structure, an increase in the depth of the nuclear potential corresponds to a greater localization of nucleons within the clusters, while higher entropy indicates increased disorder. This suggests an inherent correlation between nuclear potential depth and information entropy.
As the dispersion parameter a increases, the central density of the Woods–Saxon type 16O relatively decreases, leading to a larger spread of density at a larger radius and, consequently, to an increase in information entropy (Figure 1). For 16O with an alpha cluster structure, for a given alpha spacing, increasing the cluster dispersion parameter b causes the central density of the 16O distribution to increase, making it more like a liquid phase. As a result, the information entropy decreases with increasing b (Figure 4), which corresponds to the situation of a lower dispersion parameter a for the Woods–Saxon type. In general, this illustrates that the more centrally distributed the nucleons are, the lower the information entropy of the system will be, and vice versa.
Information entropy is proposed as an available tool for the analysis of nuclear clustering mechanisms. By calculating the information entropy, the degree of disorder in the nuclei with cluster structures can be revealed, and their formation mechanisms can be further understood. Nuclear clustering is an important aspect of nuclear structure, and this clustering behavior is mainly observed in light nuclei, leading to unique nuclear properties that deviate from traditional mean-field models. In this case, a higher entropy value indicates a more dispersed and disordered cluster structure, while a lower entropy value implies a more centralized arrangement, like a quantum liquid phase.
3. Summary
This study investigates the role of information entropy in nuclear physics, focusing on nuclear density distributions, including halo structures and alpha clustering. Information entropy measures uncertainty and disorder, providing insight into the internal complexity of nuclear structures. There is a linear relationship between information entropy and diffusion parameters, indicating increasing uncertainty in the radial nucleon distribution with increasing diffusion. Heavier nuclei typically have higher information entropy, suggesting greater complexity in larger systems.
In addition, there is a strong correlation between information entropy and neutron skin thickness, which is an important parameter for understanding nuclear symmetry energy. The analysis of helium and lithium isotopes shows different levels of information entropy, with the halo nucleus 11Li showing the highest entropy due to its widely dispersed core-halo structure. On the other hand, the most tightly bound nucleus, 4He, has the lowest level of information entropy.
For 16O, which is characterized by a tetrahedral cluster structure, the information entropy decreases as the potential depth gradually decreases. By studying the difference in information entropy in a nucleus, we can gain insight into the stability and dynamics of nuclear clusters. It underscores the value of information entropy as a key tool for revealing and exploring the diversity of nuclear structures.
Current models of nuclear density distribution, while phenomenological rather than based on microscopic quantum mechanics, effectively capture the approximate features of nucleon distribution in atomic nuclei. Information entropy offers a novel perspective by quantifying the diversity of nuclear structures, thereby improving our understanding of nuclear systems. However, these models are limited in that they do not fully capture the subtleties of quantum effects at the microscopic level. In future studies, we aim to further validate the current concepts and results by incorporating microscopic density distributions of atomic nuclei.
Author Contributions
Conceptualization, Y.-G.M. and W.-H.M.; methodology, Y.-G.M. and W.-H.M.; software, W.-H.M.; validation, Y.-G.M. and W.-H.M.; formal analysis, Y.-G.M. and W.-H.M.; investigation, Y.-G.M. and W.-H.M.; resources, Y.-G.M. and W.-H.M.; data curation, W.-H.M.; writing—original draft preparation, W.-H.M.; writing—review and editing, Y.-G.M.; visualization, W.-H.M.; supervision, Y.-G.M.; project administration, Y.-G.M.; funding acquisition, Y.-G.M. and W.-H.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Natural Science Foundation of Shanghai with Grants No. 23JC1400200, the National Natural Science Foundation of China with Grants No. 11905036, 12147101 and 11890710, the National Key R&D Program from the Ministry of Science and Technology of China (2022YFA1604900), and the STCSM under Grant No. 23590780100.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Ma, Y.G. Application of information theory in nuclear liquid gas phase transition. Phys. Rev. Lett. 1999, 83, 3617. [Google Scholar] [CrossRef]
- Ma, Y.G.; Natowitz, J.B.; Wada, R.; Hagel, K.; Wang, J.; Keutgen, T.; Majka, Z.; Murray, M.; Qin, L.; Smith, P.; et al. Critical behavior in light nuclear systems: Experimental aspects. Phys. Rev. C 2005, 71, 054606. [Google Scholar] [CrossRef]
- Ma, Y.G.; Pang, L.G.; Wang, R.; Zhou, K. Phase transition study meets machine learning. Chin. Phys. Lett. 2023, 40, 122101. [Google Scholar] [CrossRef]
- Denbigh, K.G.; Denbigh, J.S. Entropy in Relation to Uncomplete Knowledge; Cambridge University: Cambridge, UK, 1995. [Google Scholar]
- Longair, M.S. Chapter 10: Kinetic theory and the origin of statistical mechanics. In Theoretical Concepts in Physics; Cambridge University Press: Oxford, UK, 1984; ISBN 0521821266. [Google Scholar]
- Moustakidis, C.C.; Massen, S.E.; Panos, C.P.; Grypeos, M.E.; Antonov, A.N. Evaluation of cluster expansions and correlated one-body properties of nuclei. Phys. Rev. C 2001, 64, 014314. [Google Scholar] [CrossRef]
- Massen, S.E. Application of information entropy to nuclei. Phys. Rev. C 2003, 67, 014314. [Google Scholar] [CrossRef]
- Csernai, L.; Kapusta, J.I. Entropy and cluster production in nuclear collisions. Phys. Rep. 1986, 131, 223. [Google Scholar] [CrossRef]
- Ma, C.W.; Ma, Y.G. Shannon information entropy in heavy-ion collisions. Prog. Part. Nucl. Phys. 2018, 99, 120. [Google Scholar] [CrossRef]
- Cao, Z.; Hwa, R.C. Chaotic behavior of particle production in branching processes. Phys. Rev. D 1996, 53, 6608. [Google Scholar] [CrossRef]
- Ma, C.W.; Wei, H.L.; Wang, S.S.; Ma, Y.G.; Wada, R.; Zhang, Y.L. Isobaric yield ratio difference and Shannon information entropy. Phys. Lett. B 2015, 742, 19. [Google Scholar] [CrossRef]
- Xu, J.; Ko, C.M. Chemical freeze-out in relativistic heavy-ion collisions. Phys. Lett. B 2017, 772, 290. [Google Scholar] [CrossRef]
- Csernai, L.; Spinnangr, S.; Velle, S. Quantitative assessment of increasing complexity. Phys. A Stat. Mech. Appl. 2017, 473, 363. [Google Scholar] [CrossRef]
- Lichtenberg, D.B.; Namgung, W.; Predazzi, E.; Wills, J.G. Baryon Masses in a Relativistic Quark-Diquark Model. Phys. Rev. Lett. 1982, 48, 1653. [Google Scholar] [CrossRef]
- Ma, C.W.; Liu, Y.P.; Wei, H.L.; Pu, J.; Cheng, K.X.; Wang, Y.T. Determination of neutron-skin thickness using configurational information entropy. Nucl. Sci. Tech. 2022, 33, 6. [Google Scholar] [CrossRef]
- Wei, H.L.; Zhu, X.; Yuan, C. Configurational information entropy analysis of fragment mass cross distributions to determine the neutron skin thickness of projectile nuclei. Nucl. Sci. Tech. 2022, 33, 111. [Google Scholar] [CrossRef]
- Biales, A.; Peshanshi, R. Moments of rapidity distributions as a measure of short-range fluctuations in high-energy collisions. Nucl. Phys. B 1986, 273, 703–718. [Google Scholar] [CrossRef]
- Li, F.; Chen, G. The evolution of information entropy components in relativistic heavy-ion collisions. Eur. Phys. J. A 2020, 56, 167. [Google Scholar] [CrossRef]
- Pu, J.; Yu, Y.B.; Cheng, K.X.; Wang, Y.T.; Guo, Y.F.; Ma, C.W. Exploring critical fluctuation phenomenon according to net-proton multiplicity information entropy in AMPT model. Phys. Lett. B 2023, 841, 137909. [Google Scholar] [CrossRef]
- Deng, X.G.; Ma, Y.G. Information entropy for central 197Au+197Au collisions in the UrQMD model. arXiv 2024, arXiv:2404.03424. [Google Scholar] [CrossRef]
- Tanihata, I.; Hamagaki, H.; Hashimoto, O.; Shida, Y.; Yoshikawa, N.; Sugimoto, K.; Yamakawa, O.; Kobayashi, T.; Takahashi, N. Measurements of Interaction Cross Sections and Nuclear Radii in the Light p-Shell Region. Phys. Rev. Lett. 1985, 55, 2676. [Google Scholar] [CrossRef]
- Xu, S.Z.; Zhang, S.S.; Jiang, X.Q.; Scott, S.M. The complex momentum representation approach and its application to low-lying resonances in 17O and 29,31F. Nucl. Sci. Tech. 2023, 34, 5. [Google Scholar] [CrossRef]
- Bagchi, S.; Kanungo, R.; Tanaka, Y.K.; Geissel, H.; Doornenbal, P.; Horiuchi, W.; Hagen, G.; Suzuki, T.; Tsunoda, N.; Ahn, D.S.; et al. Two-Neutron Halo is Unveiled in 29F. Phys. Rev. Lett. 2020, 124, 222504. [Google Scholar] [CrossRef] [PubMed]
- Fang, D.Q. Neutron skin thickness and its effects in nuclear reactions. Nucl. Tech. 2023, 46, 080016. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, Y.F.; Xu, F.R. First-principles Gamow shell model study of nuclei in the drip line region. Nucl. Tech. 2023, 46, 080012. [Google Scholar] [CrossRef]
- Ma, Y.G.; Zhang, S. Influence of Nuclear Structure in Relativistic Heavy-Ion Collisions. In Handbook of Nuclear Physics; Springer: Singapore, 2023. [Google Scholar] [CrossRef]
- Chen, J.; Dong, X.; Ma, Y.G.; Xu, Z. Measurements of the lightest hypernucleus (3KH): Progress and perspective. Sci. Bull. 2023, 68, 3252–3260. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Fang, D.Q.; Wang, S.M.; Hua, H. Structure and 2p decay mechanism of 18Mg. Nucl. Sci. Tech. 2024, 35, 107. [Google Scholar] [CrossRef]
- Su, Y.; Li, Z.Y.; Liu, L.L.; Dong, G.X.; Wang, X.B.; Chen, Y.J. Sensitivity impacts owing to the variations in the type of zero-range pairing forces on the fission properties using the density functional theory. Nucl. Sci. Tech. 2024, 35, 62. [Google Scholar] [CrossRef]
- Yan, T.Z.; Li, S. Isotopic dependence of the yield ratios of light fragments from different projectiles and their unified neutron skin thicknesses. Nucl. Sci. Tech. 2024, 35, 65. [Google Scholar] [CrossRef]
- Zheng, Z.Y.; Chen, S.W.; Liu, Q. The breaking of spin symmetry in the single-particle resonances in deformed nuclei. Nucl. Sci. Tech. 2024, 35, 66. [Google Scholar] [CrossRef]
- Geng, K.P.; Du, P.X.; Li, J.; Fang, D.L. Calculation of microscopic nuclear level densities based on covariant density functional theory. Nucl. Sci. Tech. 2023, 34, 141. [Google Scholar] [CrossRef]
- An, R.; Sun, S.; Cao, L.G.; Zhang, F.S. Constraining nuclear symmetry energy with the charge radii of mirror-pair nuclei. Nucl. Sci. Tech. 2023, 34, 119. [Google Scholar] [CrossRef]
- Huo, E.B.; Li, K.R.; Qu, X.Y.; Zhang, Y.; Sun, T.T. Continuum Skyrme Hartree-Fock-Bogoliubov theory with Green’s function method for neutron-rich Ca, Ni, Zr, and Sn isotopes. Nucl. Sci. Tech. 2023, 34, 105. [Google Scholar] [CrossRef]
- von Oertzen, W.; Freer, M.; Kanada-En’yo, Y. Nuclear clusters and nuclear molecules. Phys. Rep. 2006, 432, 43. [Google Scholar] [CrossRef]
- Ma, W.H.; Patel, D.; Yang, Y.Y.; Wang, J.S.; Kanada-En’yo, Y.; Chen, R.F.; Lubian, J.; Ye, Y.L.; Yang, Z.H.; Ren, Z.Z.; et al. Observation of 6He + t cluster states in 9Li. Phys. Rev. C 2021, 103, L061302. [Google Scholar] [CrossRef]
- Horiuchi, H. Outlook and future perspectives. J. Phys. Conf. Ser. 2008, 111, 012054. [Google Scholar] [CrossRef]
- He, W.B.; Ma, Y.G.; Cao, X.G.; Cai, X.Z.; Zhang, G.Q. Giant Dipole Resonance as a Fingerprint of α Clustering Configurations in 12C and 16O. Phys. Rev. Lett. 2014, 113, 032506. [Google Scholar] [CrossRef]
- Zhou, B.; Funaki, Y.; Horiuchi, H.; Ma, Y.G.; Röpke, G.; Schuck, P.; Tohsaki, A.; Yamada, T. The 5α condensate state in 20Ne. Nat. Commun. 2023, 14, 8206. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Zhang, S.; Ma, Y.G. System dependence of away-side broadening and α-clustering light nuclei structure effect in dihadron azimuthal correlations. Phys. Lett. B 2022, 831, 137198. [Google Scholar] [CrossRef]
- Wang, S.S.; Ma, Y.G.; He, W.B.; Fang, D.Q.; Cao, X.G. Influences of α-clustering configurations on the giant dipole resonance in hot compound systems. Phys. Rev. C 2023, 108, 014609. [Google Scholar] [CrossRef]
- Cao, Y.T.; Deng, X.G.; Ma, Y.G. Effect of initial-state geometric configurations on the nuclear liquid-gas phase transition. Phys. Rev. C 2023, 108, 024610. [Google Scholar] [CrossRef]
- Cao, R.X.; Zhang, S.; Ma, Y.G. Effects of the α-cluster structure and the intrinsic momentum component of nuclei on the longitudinal asymmetry in relativistic heavy-ion collisions. Phys. Rev. C 2023, 108, 064906. [Google Scholar] [CrossRef]
- Ma, Y.G. Effects of α-clustering structure on nuclear reaction and relativistic heavy-ion collisions. Nucl. Tech. 2023, 46, 080001. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Zhang, S.; Ma, Y.G. Signatures of an α + core structure in 44Ti + 44Ti collisions at TeV by a multiphase transport model. Eur. Phys. J. A 2024, 60, 73. [Google Scholar] [CrossRef]
- Ozawa, A. Matter Radii and Density Distributions. In Handbook of Nuclear Physics; Springer: Singapore, 2023. [Google Scholar] [CrossRef]
- Ding, M.Q.; Fang, D.Q.; Ma, Y.G. Effects of neutron-skin thickness on light-particle production. Phys. Rev. C 2024, 109, 024616. [Google Scholar] [CrossRef]
- Thomas, M.T.C.A.J.; Joy, A.T. Elements of Information Theory, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
- Woods, R.D.; Saxon, D.S. Diffuse Surface Optical Model for Nucleon-Nuclei Scattering. Phys. Rev. 1954, 95, 577. [Google Scholar] [CrossRef]
- Vries, H.D.; Jager, C.W.D.; Vries, C.D. Nuclear charge-density-distribution parameters from elastic electron scattering. At. Data Nucl. Data Tables 1987, 36, 495–536. [Google Scholar] [CrossRef]
- Chamon, L.C.; Carlson, B.V.; Gasques, L.R.; Pereira, D.; De Conti, C.; Alvarez, M.A.G.; Hussein, M.S.; Ribeiro, M.C.; Rossi, E.S., Jr.; Silva, C.P. Toward a global description of the nucleus-nucleus interaction. Phys. Rev. C 2002, 66, 014610. [Google Scholar] [CrossRef]
- Shou, Q.Y.; Ma, Y.G.; Sorensen, P.; Tang, A.H.; Videbæk, F.; Wang, H. Parameterization of deformed nuclei for Glauber modeling inrelativistic heavy ion collisions. Phys. Lett. B 2015, 749, 215. [Google Scholar] [CrossRef]
- Tanihata, I. Neutron halo nuclei. J. Phys. G Nucl. Part. Phys. 1996, 22, 157. [Google Scholar] [CrossRef]
- Parker, M.C.; Jeynes, C.; Catford, W.N. Halo properties in helium nuclei from the perspective of geometrical thermodynamics. Ann. Phys. 2022, 534, 2100278. [Google Scholar] [CrossRef]
- Alkhazov, G.D.; Dobrovolsky, A.V.; Egelhof, P.; Geissel, H.; Irnich, H.; Khanzadeev, A.V.; Korolev, G.A.; Lobodenko, A.A.; Münzenberg, G.; Mutterer, M.; et al. Nuclear matter distributions in the 6He and 8He nuclei from differential cross sections for small-angle proton elastic scattering at intermediate energy. Nucl. Phys. A 2002, 712, 269–299. [Google Scholar] [CrossRef]
- Dobrovolsky, A.V.; Alkhazov, G.D.; Andronenko, M.N.; Bauchet, A.; Egelhof, P.; Fritz, S.; Geissel, H.; Gross, C.; Khanzadeev, A.V.; Korolev, G.A.; et al. Study of the nuclear matter distribution in neutron-rich Li isotopes. Nucl. Phys. A 2006, 766, 1–24. [Google Scholar] [CrossRef]
- Moriguchi, T.; Ozawa, A.; Ishimoto, S.; Abe, Y.; Fukuda, M.; Hachiuma, I.; Ishibashi, Y.; Ito, Y.; Kuboki, T.; Lantz, M.; et al. Density distributions of 11Li deduced from reaction cross-section measurements. Phys. Rev. C 2013, 88, 024610. [Google Scholar] [CrossRef]
- Dudek, J.; Gozdz, A.; Schunck, N.; Miskiewicz, M. Nuclear tetrahedral symmetry: Possibly present throughout the periodic table. Phys. Rev. Lett. 2002, 88, 252502. [Google Scholar] [CrossRef]
- Bijker, R.; Iachello, F. Evidence for Tetrahedral Symmetry in 16O. Phys. Rev. Lett. 2014, 112, 152501. [Google Scholar] [CrossRef] [PubMed]
- Ding, C.; Pang, L.G.; Zhang, S.; Ma, Y.G. Signals of α clusters in 16O+16O collisions at the LHC from relativistic hydrodynamic simulations. Chin. Phys. C 2023, 47, 024105. [Google Scholar] [CrossRef]
- Ma, Y.G.; Zhang, S. α-clustering effects in relativistic heavy-ion collisions. Sci. Sin. Phys. Mech. Astron. 2024, 54, 292004. (In Chinese) [Google Scholar] [CrossRef]
- Ebran, J.P.; Khan, E.; Nikšić, T.; Vretenar, D. How atomic nuclei cluster. Nature 2012, 487, 341–344. [Google Scholar] [CrossRef]
- Ebran, J.P.; Khan, E.; Nikšić, T.; Vretenar, D. Localization and clustering in atomic nuclei. J. Phys. G Nucl. Part. Phys. 2017, 44, 103001. [Google Scholar] [CrossRef]
- Bijker, R. The algebraic cluster model: Three-body clusters. Ann. Phys. 2002, 298, 334–360. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).