The Evaluation of Climate Change Competitiveness via DEA Models and Shannon Entropy: EU Regions
Abstract
1. Introduction
2. Theoretical Background
2.1. Regional Climate Change Competitiveness Index
2.2. DEA Model
- —the indices of the decision-making units;
- —the indices of outputs;
- —the indices of inputs;
- —value of output r for unit j;
- —value of input i for unit j;
- —weight assigned to output r;
- —weight assigned to input i.
2.3. Proposed Model with Shannon Entropy
- Evaluating efficiency using different DEA models;
- Assessing the importance of each DEA model through Shannon entropy;
- Aggregating the efficiency scores from the various DEA models.
- 1.
- Calculation of non-zero optimal weights. In this step, we use the DEA model to calculate the non-zero optimal weights, according to Formulas (3) and (4).
- 2.
- Compute the values of and (weight normalization). The normalization of the non-zero optimal weights is prepared for the calculation of Shannon entropy.Remark: Directly comparing inputs with outputs is inappropriate because these variables are complementary rather than substitutable in DEA models. Therefore, in this step, we separately normalized the non-zero input weights and output weights.
- 3.
- Compute entropy el as:where and are the entropy constants and defined as and , respectively. We assume there is always more than one input or output, meaning m > 1 or s > 1. Especially, the entropy of a single input or single output is assumed to be equal to 0.
- 4.
- Calculate the importance degree of optimal weights. Although inputs and outputs may have different practical implications, when translated into Shannon entropies, they both reflect a measure of disorder. As a result, the Shannon entropies of inputs and outputs can be analyzed collectively. The importance degree of a DMU, (= 1, 2, …, n), is defined as follows:Remark: The degree of importance aligns with maximizing the Shannon entropy. Specifically, the importance degree derived from the Shannon entropy is based on the variance between input weights and output weights.
- 5.
- Compute the common weight. and represent the aggregation of the optimal weights from each DMU with the importance degree as:where t = 1, 2, …, m and r = 1, 2, …, s.
3. Results
3.1. DEA Approaches to the RCCCI
3.1.1. Model and Research Sample
3.1.2. DEA Approach
- Preparation of standardized data.
- Preparation of models and optimization using the DEA method.
- Model optimization using the entropy method.
- Model preparation and DEA-like optimization.
Ad. 1. Preparation of Standardized Data
- —inputs.
- —decision-making units.
- —values before normalization.
- —values after normalization.
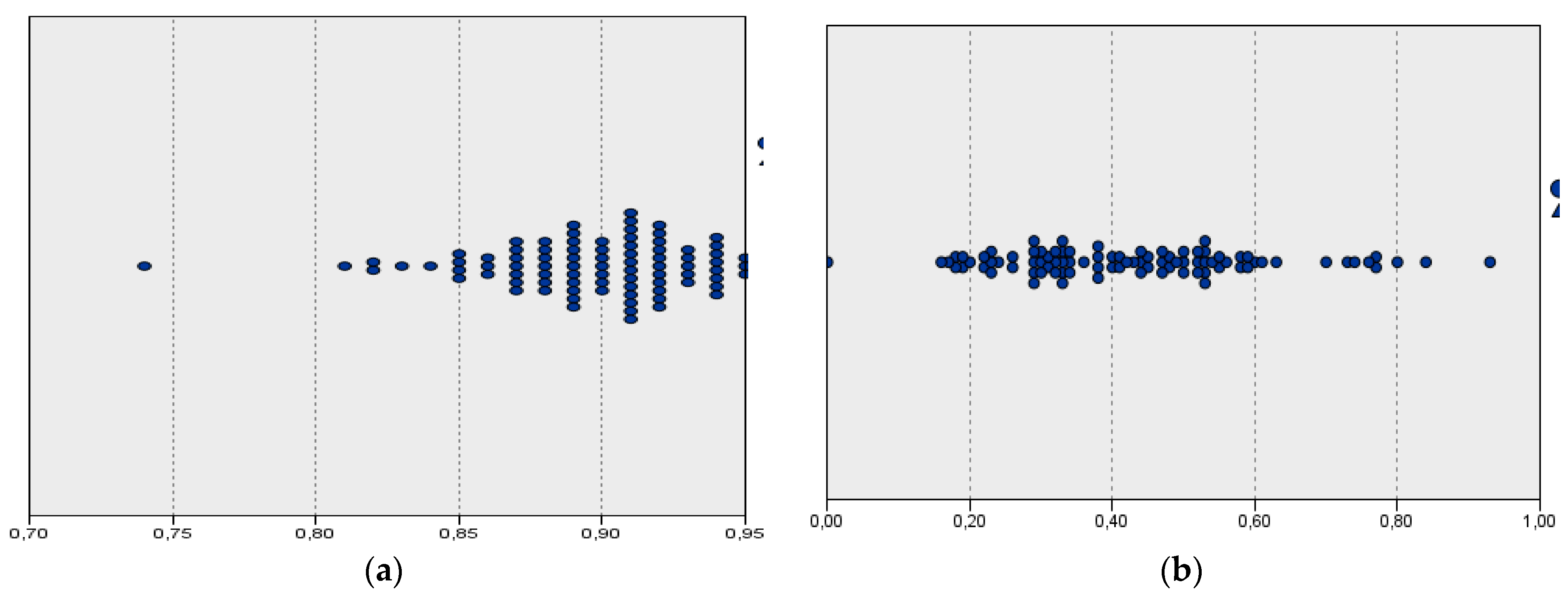
Ad. 2. DEA Models and Optimization
Ad. 3. Model Optimization Using the Entropy Method
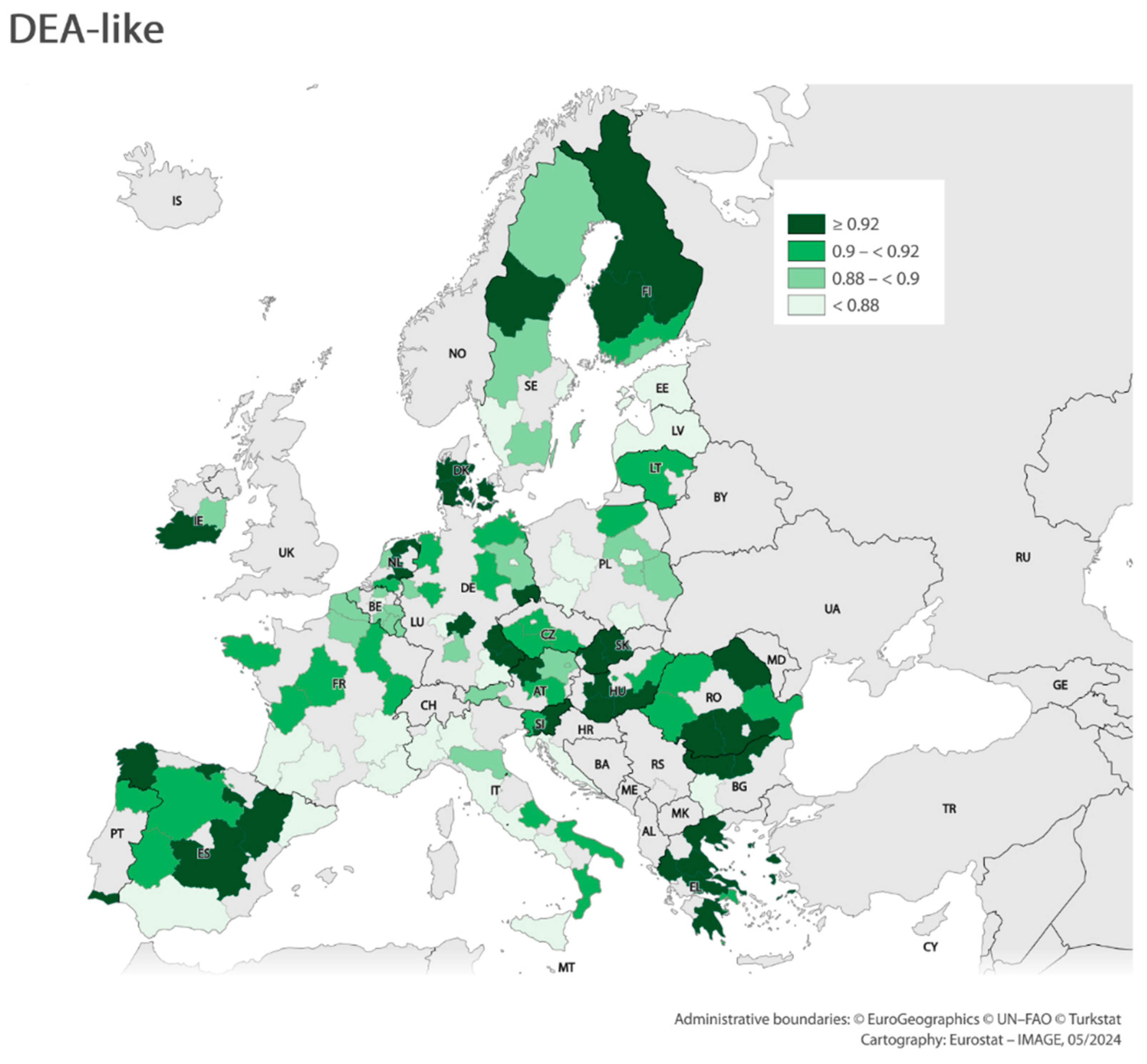
Ad. 4. DEA-like Models and Optimization
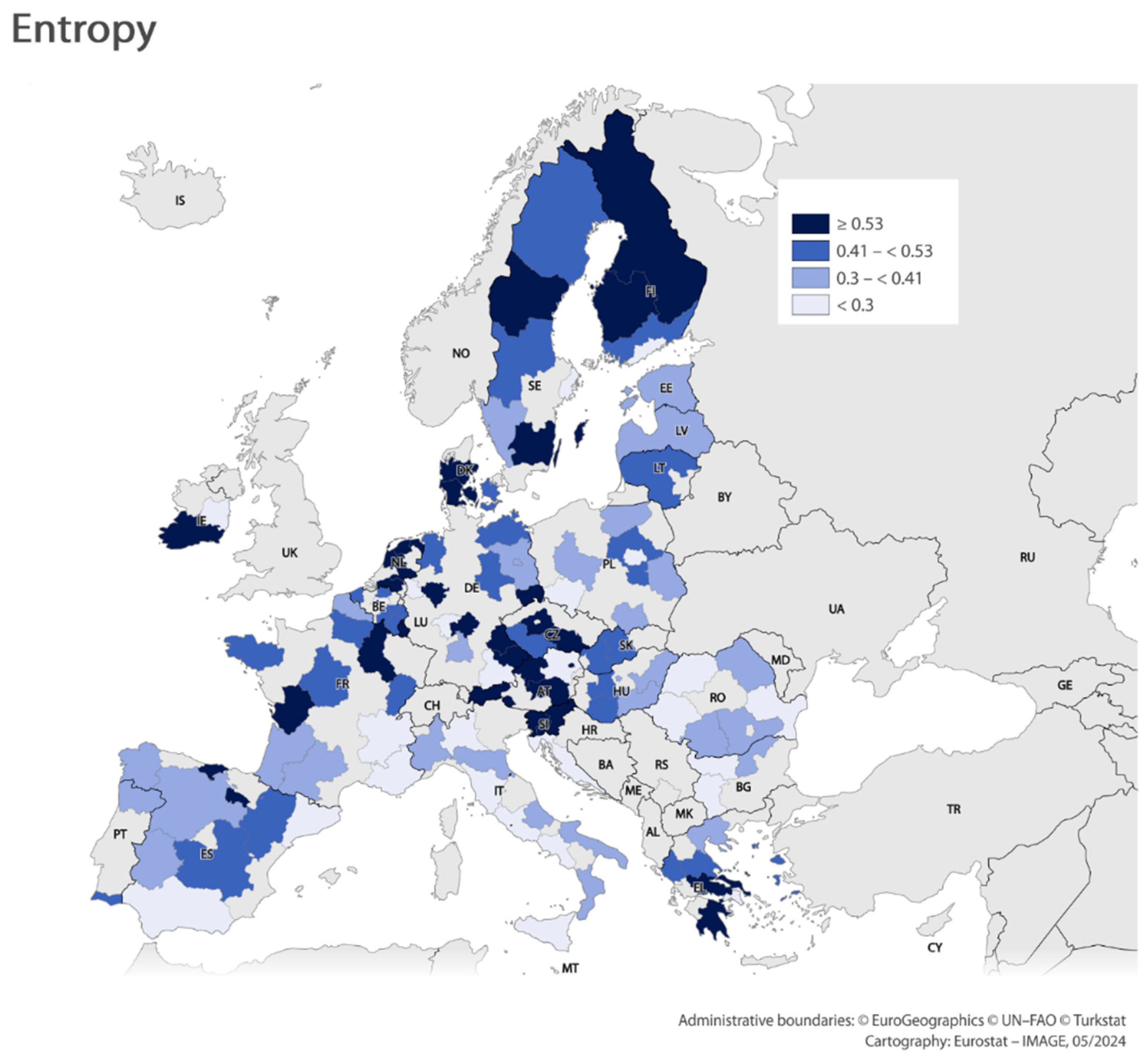
3.2. Entropy Approach to the RCCCI
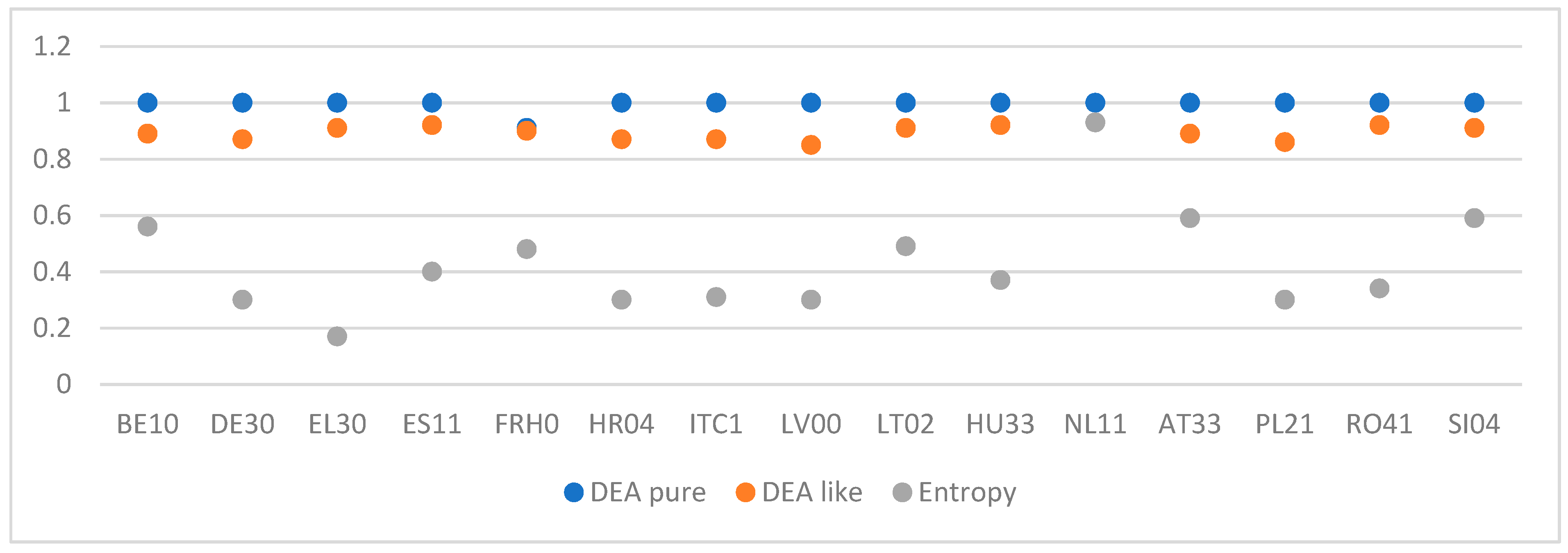
3.3. Efficiency Scores
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Porter, M. The Competitive Advantage of Nations; The Free Press: New York, NY, USA, 1990. [Google Scholar]
- Falciola, J.; Jansen, M.; Rollo, V. Defining firm competitiveness: A multidimensional framework. World Dev. 2020, 129, 104857. [Google Scholar] [CrossRef]
- Bruneckienė, J.; Zykienė, I.; Mičiulienė, I. Rethinking National Competitiveness for Europe 2050: The Case of EU Countries. Sustainability 2023, 15, 10697. [Google Scholar] [CrossRef]
- Huggins, R. Creating a UK competitiveness index: Regional and local benchmarking. Reg. Stud. 2003, 37, 89–96. [Google Scholar] [CrossRef]
- Karman, A.; Miszczuk, A.; Bronisz, U. Discovering the factors driving regional competitiveness in the face of climate change. Misc. Geogr.—Reg. Stud. Dev. 2023, 27, 17. [Google Scholar] [CrossRef]
- Cherchye, L.; Moesen, W.; Rogge, N.; Van Puyenbroeck, T.; Saisana, M.; Saltelli, A.; Liska, R.; Tarantola, S. Creating composite indicators with DEA and robustness analysis: The case of the technology achievement index. J. Oper. Res. Soc. 2008, 59, 239–251. [Google Scholar] [CrossRef]
- Marttunen, M.; Lienert, J.; Belton, V. Structuring problems for Multi-Criteria Decision Analysis in practice: A literature review of method combinations. Eur. J. Oper. Res. 2017, 263, 1–17. [Google Scholar] [CrossRef]
- Zhou, P.; Ang, B.W. Indicators for assessing sustainability performance. In Handbook of Performability Engineering; Misra, K.B., Ed.; Springer: London, UK, 2008; pp. 905–918. [Google Scholar]
- Booysen, F. An overview and evaluation of composite indices of development. Soc. Indic. Res. 2002, 59, 115–151. [Google Scholar] [CrossRef]
- Hatefi, S.M.; Torabi, S.A. A common weight MCDA–DEA approach to construct composite indicators. Ecol. Econ. 2010, 70, 114–120. [Google Scholar] [CrossRef]
- Macmillan, W.D. The estimation and application of multi-regional economic planning models using data envelopment analysis. Pap. Reg. Sci. 1986, 60, 41–57. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Li, S. Using data envelopment analysis to evaluate efficiency in the economic performance of Chinese cities. Socio-Econ. Plan. Sci. 1989, 23, 325–344. [Google Scholar] [CrossRef]
- Hashimoto, A.; Ishikawa, H. Using DEA to evaluate the state of society as measured by multiple social indicators. Socio-Econ. Plan. Sci. 1993, 27, 257–268. [Google Scholar] [CrossRef]
- Suzuki, S.; Nijkamp, P. Significance of DEA for Regional Performance Measurement. In Regional Performance Measurement and Improvement; New Frontiers in Regional Science: Asian Perspectives; Springer: Singapore, 2017; Volume 9. [Google Scholar]
- Martić, M.; Savić, G. An application of DEA for comparative analysis and ranking of regions in Serbia with regards to social-economic development. Eur. J. Oper. Res. 2001, 132, 343–356. [Google Scholar] [CrossRef]
- Yang, J.; Wu, J.; Li, X.; Zhu, Q. Sustainability performance analysis of environment innovation systems using a two-stage network DEA model with shared resources. Front. Eng. Manag. 2022, 9, 425–438. [Google Scholar] [CrossRef]
- Zhang, L. An additive super-efficiency DEA approach to measuring regional environmental performance in China. INFOR Inf. Syst. Oper. Res. 2017, 55, 211–226. [Google Scholar] [CrossRef]
- Martín, J.C.; Mendoza, C.; Román García, C. Regional Spanish tourism competitiveness: A DEA-MONITUR approach. Region 2017, 4, 153–173. [Google Scholar] [CrossRef]
- Charles, V.; Díaz, G. A Non-radial DEA Index for Peruvian Regional Competitiveness. Soc. Indic. Res. 2017, 134, 747–770. [Google Scholar] [CrossRef]
- Charles, V.; Zegarra, L.F. Measuring regional competitiveness through data envelopment analysis: A peruvian case. Expert Syst. Appl. 2014, 41, 5371–5381. [Google Scholar] [CrossRef]
- Karman, A.; Miszczuk, A.; Bronisz, U. Regional climate change competitiveness— modelling approach. Energies 2021, 14, 3704. [Google Scholar] [CrossRef]
- Malovics, G. The role of natural capital in regional development. In 2nd Central European Conference in Regional Science—CERS; Technical University of Košice: Košice, Slovakia, 2007. [Google Scholar]
- Kasztelan, A. The green competitiveness of Polish regions. Res. Pap. Wroc. Univ. Econ. Bus. 2020, 64, 32–41. [Google Scholar] [CrossRef]
- Rivers, N. Impacts of climate policy on the competitiveness of Canadian industry: How big and how to mitigate? Energy Econ. 2010, 32, 1092–1104. [Google Scholar] [CrossRef]
- Naqvi, A. Decoupling trends of emissions across EU regions and the role of environmental policies. J. Clean. Prod. 2021, 323, 1–24. [Google Scholar] [CrossRef]
- Dijkstra, L.; Papadimitriou, E.; Cabeza Martinez, B.; de Dominicis, L.; Kovacic, M. EU Regional Competitiveness Index 2.0. European Commission. 2023. Available online: https://ec.europa.eu/regional_policy/sources/work/rci_2022/eu-rci2_0-2022_en.pdf (accessed on 30 July 2024).
- Baldwin, J.R.; Dixon, J. Infrastructure Capital: What is it? Where is it? How much of it is there? Can. Product. Rev. 2008, 16. [Google Scholar] [CrossRef]
- Nijkamp, P. Infrastructure and Regional development: A multidimensional policy analysis. Empir. Econ. 1986, 11, 1–21. [Google Scholar] [CrossRef]
- Opitz, I.; Zoll, F.; Zasada, I.; Doernberg, A.; Siebert, R.; Piorr, A. Consumer-producer interactions in community-supported agriculture and their relevance for economic stability of the farm—An empirical study using an analytic hierarchy process. J. Rural. Stud. 2019, 68, 22–32. [Google Scholar] [CrossRef]
- Benner, C. Labour Flexibility and Regional Development: The Role of Labour Market Intermediaries. Reg. Stud. 2003, 37, 621–633. [Google Scholar] [CrossRef]
- Wang, H.; Ang, B.W.; Su, B. A Multi-region Structural Decomposition Analysis of Global CO2 Emission Intensity. Ecol. Econ. 2017, 142, 163–176. [Google Scholar] [CrossRef]
- Tian, K.; Dietzenbacher, E.; Yan, B.; Duan, Y. Upgrading or downgrading: China’s regional carbon emission intensity evolution and its determinants. Energy Econ. 2020, 91, 104891. [Google Scholar] [CrossRef]
- Del-Aguila-Arcentales, S.; Alvarez-Risco, A.; Yáñez, J.A. Innovation and its effects on compliance with Sustainable Development Goals and competitiveness in European Union countries. J. Open Innov. Technol. Mark. Complex. 2023, 9, 100127. [Google Scholar] [CrossRef]
- Geels, F.W. From sectoral systems of innovation to socio-technical systems: Insights about dynamics and change from sociology and institutional theory. Res. Policy 2004, 33, 897–920. [Google Scholar] [CrossRef]
- Cortinovis, N.; Xiao, J.; Boschma, R.; van Oort, F.G. Quality of government and social capital as drivers of regional diversification in Europe. J. Econ. Geogr. 2017, 17, 1179–1208. [Google Scholar] [CrossRef]
- Muringani, J.; Fitjar, R.D.; Rodríguez-Pose, A. Social capital and economic growth in the regions of Europe. Environ. Plan. A Econ. Space 2021, 53, 1412–1434. [Google Scholar] [CrossRef]
- Bahmanpour Khalesi, H.; Noorian, F. Identification regional competitiveness sectors in Fars province. J. Fine Arts Archit. Urban Plan. 2017, 22, 33–44. [Google Scholar]
- Deniz, Z.Ç. Regional Economic Development and Competitiveness: A Study of Leading and Competitive Sectors of Diyarbakir-Sanliurfa Region, Turkey. In Proceedings of the European Regional Science Association: “Regional Development & Globalisation: Best Practices”, St. Petersburg, Russia, 26–29 August 2014. [Google Scholar]
- Stanculescu, O. Industries as Vectors of Regional Competitiveness Case Study-The North-West Region of Romania. Ann. Univ. Apulensis Ser. Oeconomica 2015, 17, 141–150. [Google Scholar] [CrossRef]
- Farrell, M.J. The measurement of efficiency of production. J. R. Stat. Soc. (Ser. A) 1957, 120, 251–281. [Google Scholar]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision-making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Basso, A.; Funari, S. Measuring the performance of ethical mutual funds: A DEA approach. J. Oper. Res. Soc. 2003, 54, 521–531. [Google Scholar] [CrossRef]
- Kao, C.; Hung, H.T. Data envelopment analysis with common weights: The compromise solution approach. J. Oper. Res. Soc. 2005, 56, 1196–1203. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 623–656. [Google Scholar] [CrossRef]
- Soleimani-Damaneh, M.; Zarepisheh, M. Shannon’s entropy for combining the efficiency results of different DEA models: Method and application. Expert Syst. Appl. 2009, 36, 5146–5150. [Google Scholar] [CrossRef]
- Qi, X.-G.; Guo, B. Determining Common Weights in Data Envelopment Analysis with Shannon’s Entropy. Entropy 2014, 16, 6394–6414. [Google Scholar] [CrossRef]
- Wang, Y.M.; Luo, Y.; Liang, L. Ranking decision making units by imposing a minimum weight restriction in the data envelopment analysis. J. Comput. Appl. Math. 2009, 223, 469–484. [Google Scholar] [CrossRef]
- Sexton, T.R.; Silkman, R.H.; Hogan, A.J. Measuring efficiency: An assessment of data envelopment analysis. In Data Envelopment Analysis: Critique and Extensions; Silkman, R.H., Ed.; Jossey-Bass: San Francisco, CA, USA, 1986; Volume 32, pp. 73–105. [Google Scholar]
- Mahlberg, B.; Obersteiner, M. Remeasuring the HDI by Data Envelopement Analysis. 2001. Available online: https://ssrn.com/abstract=1999372 (accessed on 30 July 2024).
- Tone, K. (Ed.) Advances in DEA Theory and Applications; Wiley: Chichester, UK, 2017. [Google Scholar]
- Dyson, R.G.; Thanassoulis, E. Reducing weight flexibility in data envelopment analysis. J. Oper. Res. Soc. 1988, 39, 563–576. [Google Scholar] [CrossRef]
- Lao, Y.; Liu, L. Performance evaluation of bus lines with data envelopment analysis and geographic information systems. Comput. Environ. Urban Syst. 2009, 33, 247–255. [Google Scholar] [CrossRef]
- Zhou, P.; Ang, B.W.; Poh, K.L. A mathematical programming approach to constructing composite indicators. Ecol. Econ. 2007, 62, 291–297. [Google Scholar] [CrossRef]




| Inputs | |
|---|---|
| Institutions | Basic_Ins |
| Macroeconomic stability | Basic_MS |
| Infrastructure | Basic_Inf |
| Education | Basic_Edu |
| Institutions related to climate change | Basic_IRtCC |
| Concentration of economic entities | Basic_CoEE |
| Water quality | Natural_WQ |
| Air quality | Natural_AQ |
| Biodiversity | Natural_Bio |
| Effectiveness in achieving climate goals | Natural_EiACG |
| Social development | Social_SD |
| Awareness | Social_Aw |
| Attitude | Social_At |
| Perceived quality of life | Social_PQoF |
| Health | Social_H |
| NGO power | Social_NGOP |
| Technological readiness | Innovation_TR |
| Innovativeness | Innovation_Inn |
| Labour market efficiency | Efficiency_LME |
| Market size | Efficiency_MS |
| Economic emission intensity | Efficiency_EEI |
| Resource efficiency | Efficiency_RE |
| Agriculture | Sector_Agr |
| Tourism | Sector_Tou |
| Energy | Sector_Ene |
| Transport | Sector_Tra |
| Industry | Sector_Ind |
| Buildings | Sector_Bui |
| Output | |
| Regional climate change competitiveness | RCCCI |
| Geo_Code | Geo_Label | Basic_Ins | Basic_MS | Basic_Inf | Basic_Edu | Basic_IRtCC | Basic_CoEE | Natural_AQ | Natural_Bio | Natural_EiACG | Social_SD | Social_Aw | Social_At | Social_PQoL | Social_H | Social_NGOP | Innovation_TR | Innovation_Inn | Efficiency_LME | Efficiency_MS | Efficiency_RE | Sector_Agr | Sector_Tou | Sector_Ene | Sector_Tra | Sector_Ind | Sector_Bui | RCCCI_Weight |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BE10 | Région de Bruxelles—Capitale | 0.03 | 0.00 | 2.76 | 0.58 | 0.00 | 0.00 | 0.00 | 2.16 | 0.00 | 0.00 | 0.66 | 0.00 | 0.00 | 3.68 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.31 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.16 | 0.12 |
| DE30 | Berlin | 0.09 | 0.10 | 0.16 | 0.00 | 0.00 | 0.00 | 0.00 | 4.48 | 1.54 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3983.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.22 | 0.11 |
| EL30 | Attiki | 0.57 | 0.00 | 4.67 | 0.00 | 0.00 | 0.00 | 0.00 | 1.23 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 2.29 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.58 | 0.16 |
| ES11 | Galicia | 0.02 | 0.00 | 0.00 | 2.13 | 0.00 | 0.00 | 0.00 | 0.00 | 1.61 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 114.60 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.13 |
| FRH0 | Bretagne | 0.00 | 0.00 | 0.00 | 0.23 | 0.00 | 0.12 | 0.00 | 2.61 | 1.40 | 0.00 | 0.00 | 0.00 | 0.15 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3504.09 | 0.00 | 0.00 | 1.06 | 0.00 | 0.00 | 0.11 |
| HR04 | Kontinentalna Hrvatska | 0.18 | 0.00 | 0.32 | 0.00 | 0.00 | 0.80 | 0.11 | 9.06 | 0.00 | 0.00 | 0.39 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.20 | 0.00 | 0.00 | 0.00 | 8.15 | 0.00 | 0.00 | 0.18 |
| ITC1 | Piemonte | 0.01 | 0.00 | 0.00 | 0.34 | 0.00 | 0.00 | 0.00 | 0.00 | 0.27 | 0.10 | 0.48 | 0.00 | 0.00 | 0.00 | 0.49 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 148,080.26 | 0.00 | 0.00 | 2.10 | 0.00 | 0.00 | 0.12 |
| LV00 | Latvija | 0.05 | 0.00 | 0.58 | 0.02 | 0.00 | 0.08 | 0.00 | 0.00 | 0.00 | 0.34 | 0.71 | 0.00 | 0.00 | 11.92 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.21 | 0.00 | 0.12 | 0.00 | 2.69 | 0.00 | 0.23 | 0.17 |
| LT02 | Vidurio ir vakaru | 0.00 | 0.00 | 0.88 | 0.00 | 0.00 | 0.00 | 0.00 | 0.13 | 0.58 | 0.21 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.34 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 14.77 | 0.00 | 1.46 | 0.18 |
| HU33 | Dél-Alföld | 0.00 | 0.00 | 0.40 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.25 | 1.84 | 0.00 | 0.54 | 0.00 | 18.99 | 0.00 | 117.43 | 0.00 | 1.29 | 0.17 |
| NL11 | Groningen | 0.00 | 0.00 | 0.26 | 0.00 | 0.00 | 0.00 | 0.00 | 5.10 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.10 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 22.88 | 0.00 | 2.65 | 0.11 |
| AT33 | Tirol | 0.00 | 0.00 | 2.17 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.74 | 0.00 | 0.22 | 0.00 | 0.00 | 0.78 | 0.00 | 0.00 | 0.45 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.67 | 0.00 | 1.03 | 0.13 |
| PL21 | Malopolskie | 0.00 | 0.00 | 0.00 | 0.11 | 0.00 | 0.00 | 0.05 | 0.00 | 0.68 | 0.00 | 0.97 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.34 | 1163.63 | 0.00 | 17.95 | 0.00 | 0.00 | 0.84 | 0.19 |
| RO41 | Sud-Vest Oltenia | 0.00 | 0.43 | 1.76 | 0.14 | 0.00 | 0.00 | 0.00 | 0.13 | 0.00 | 0.00 | 0.18 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.41 | 0.00 | 0.00 | 0.00 | 18.50 | 0.00 | 1.21 | 0.22 |
| SI04 | Zahodna Slovenija | 0.22 | 0.00 | 0.21 | 0.00 | 0.00 | 0.14 | 0.00 | 0.57 | 0.00 | 0.27 | 0.50 | 0.00 | 0.00 | 18.80 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.23 | 0.00 | 0.00 | 0.00 | 2.25 | 0.00 | 0.18 | 0.14 |
| Geo_Code | Geo_Label | Basic_Ins | Basic_MS | Basic_Inf | Basic_Edu | Basic_IRtCC | Basic_CoEE | Natural_AQ | Natural_Bio | Natural_EiACG | Social_SD | Social_Aw | Social_At | Social_PQoL | Social_H | Social_NGOP | Innovation_TR | Innovation_Inn | Efficiency_LME | Efficiency_MS | Efficiency_RE | Sector_Agr | Sector_Tou | Sector_Ene | Sector_Tra | Sector_Ind | Sector_Bui | RCCCI_Weight |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BE10 | Région de Bruxelles—Capitale | 0.28 | 0.19 | 0.47 | 0.36 | 0.50 | 0.22 | 0.19 | 0.48 | 0.33 | 0.30 | 0.31 | 0.27 | 0.24 | 0.50 | 0.27 | 0.38 | 0.45 | 0.49 | 0.49 | 0.27 | 0.50 | 0.46 | 0.50 | 0.49 | 0.50 | 0.24 | 0.29 |
| DE30 | Berlin | 0.25 | 0.28 | 0.42 | 0.36 | 0.50 | 0.33 | 0.25 | 0.49 | 0.30 | 0.23 | 0.25 | 0.24 | 0.24 | 0.47 | 0.25 | 0.31 | 0.33 | 0.37 | 0.49 | 0.37 | 0.50 | 0.41 | 0.50 | 0.40 | 0.50 | 0.33 | 0.28 |
| EL30 | Attiki | 0.40 | 0.21 | 0.45 | 0.42 | 0.50 | 0.48 | 0.25 | 0.49 | 0.20 | 0.30 | 0.20 | 0.31 | 0.50 | 0.47 | 0.35 | 0.38 | 0.37 | 0.50 | 0.50 | 0.48 | 0.50 | 0.50 | 0.50 | 0.32 | 0.50 | 0.44 | 0.40 |
| ES11 | Galicia | 0.32 | 0.29 | 0.36 | 0.50 | 0.50 | 0.36 | 0.25 | 0.31 | 0.26 | 0.19 | 0.20 | 0.21 | 0.26 | 0.49 | 0.38 | 0.39 | 0.41 | 0.47 | 0.50 | 0.39 | 0.50 | 0.48 | 0.50 | 0.48 | 0.50 | 0.45 | 0.32 |
| FRH0 | Bretagne | 0.25 | 0.28 | 0.36 | 0.37 | 0.50 | 0.38 | 0.25 | 0.48 | 0.30 | 0.23 | 0.24 | 0.26 | 0.25 | 0.48 | 0.28 | 0.40 | 0.40 | 0.44 | 0.49 | 0.30 | 0.50 | 0.47 | 0.50 | 0.48 | 0.50 | 0.31 | 0.10 |
| HR04 | Kontinentalna Hrvatska | 0.39 | 0.34 | 0.29 | 0.30 | 0.50 | 0.46 | 0.50 | 0.48 | 0.23 | 0.23 | 0.32 | 0.32 | 0.34 | 0.47 | 0.39 | 0.39 | 0.43 | 0.38 | 0.50 | 0.48 | 0.50 | 0.48 | 0.50 | 0.48 | 0.50 | 0.36 | 0.44 |
| ITC1 | Piemonte | 0.36 | 0.23 | 0.26 | 0.40 | 0.50 | 0.33 | 0.25 | 0.32 | 0.23 | 0.25 | 0.23 | 0.32 | 0.30 | 0.47 | 0.37 | 0.38 | 0.41 | 0.42 | 0.49 | 0.31 | 0.50 | 0.46 | 0.50 | 0.48 | 0.50 | 0.34 | 0.31 |
| LV00 | Latvija | 0.32 | 0.39 | 0.34 | 0.37 | 0.50 | 0.28 | 0.19 | 0.47 | 0.23 | 0.42 | 0.50 | 0.38 | 0.34 | 0.49 | 0.42 | 0.41 | 0.34 | 0.44 | 0.50 | 0.34 | 0.50 | 0.48 | 0.50 | 0.46 | 0.50 | 0.34 | 0.41 |
| LT02 | Vidurio ir vakaru | 0.30 | 0.39 | 0.41 | 0.38 | 0.50 | 0.35 | 0.19 | 0.48 | 0.34 | 0.34 | 0.32 | 0.31 | 0.32 | 0.49 | 0.37 | 0.41 | 0.43 | 0.46 | 0.50 | 0.40 | 0.50 | 0.49 | 0.50 | 0.49 | 0.50 | 0.39 | 0.45 |
| HU33 | Dél-Alföld | 0.36 | 0.36 | 0.36 | 0.40 | 0.50 | 0.41 | 0.25 | 0.38 | 0.30 | 0.27 | 0.22 | 0.26 | 0.32 | 0.49 | 0.44 | 0.42 | 0.48 | 0.50 | 0.50 | 0.44 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 0.29 | 0.41 |
| NL11 | Groningen | 0.22 | 0.30 | 0.43 | 0.36 | 0.50 | 0.40 | 0.19 | 0.49 | 0.25 | 0.19 | 0.30 | 0.26 | 0.21 | 0.50 | 0.19 | 0.37 | 0.48 | 0.49 | 0.49 | 0.24 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 0.37 | 0.28 |
| AT33 | Tirol | 0.23 | 0.25 | 0.45 | 0.38 | 0.50 | 0.41 | 0.25 | 0.42 | 0.32 | 0.23 | 0.33 | 0.25 | 0.20 | 0.49 | 0.26 | 0.39 | 0.45 | 0.46 | 0.49 | 0.37 | 0.50 | 0.31 | 0.50 | 0.49 | 0.50 | 0.36 | 0.32 |
| PL21 | Malopolskie | 0.32 | 0.38 | 0.38 | 0.35 | 0.50 | 0.35 | 0.50 | 0.47 | 0.32 | 0.25 | 0.34 | 0.41 | 0.25 | 0.47 | 0.38 | 0.39 | 0.41 | 0.44 | 0.50 | 0.42 | 0.50 | 0.47 | 0.50 | 0.47 | 0.50 | 0.33 | 0.47 |
| RO41 | Sud-Vest Oltenia | 0.44 | 0.42 | 0.39 | 0.46 | 0.50 | 0.37 | 0.25 | 0.40 | 0.22 | 0.24 | 0.40 | 0.50 | 0.32 | 0.48 | 0.50 | 0.43 | 0.47 | 0.47 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 0.36 | 0.55 |
| SI04 | Zahodna Slovenija | 0.31 | 0.30 | 0.40 | 0.36 | 0.50 | 0.41 | 0.25 | 0.45 | 0.24 | 0.29 | 0.28 | 0.21 | 0.27 | 0.49 | 0.24 | 0.39 | 0.46 | 0.46 | 0.50 | 0.34 | 0.50 | 0.45 | 0.50 | 0.49 | 0.50 | 0.40 | 0.34 |
| Geo_Code | Geo_Label | Basic_Ins | Basic_MS | Basic_Inf | Basic_Edu | Basic_IRtCC | Basic_CoEE | Natural_AQ | Natural_Bio | Natural_EiACG | Social_SD | Social_Aw | Social_At | Social_PQoL | Social_H | Social_NGOP | Innovation_TR | Innovation_Inn | Efficiency_LME | Efficiency_MS | Efficiency_RE | Sector_Agr | Sector_Tou | Sector_Ene | Sector_Tra | Sector_Ind | Sector_Bui | Output_Entr | Imp_Degree |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BE10 | Région de Bruxelles—Capitale | −0.02 | 0.00 | −0.35 | −0.16 | 0.00 | 0.00 | 0.00 | −0.33 | 0.00 | 0.00 | −0.18 | 0.00 | 0.00 | −0.37 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −0.11 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −0.06 | 0.00 | 0.02 |
| DE30 | Berlin | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| EL30 | Attiki | −0.14 | 0.00 | −0.37 | 0.00 | 0.00 | 0.00 | 0.00 | −0.23 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −0.31 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −0.36 | 0.00 | 0.02 |
| ES11 | Galicia | 0.00 | 0.00 | 0.00 | −0.07 | 0.00 | 0.00 | 0.00 | 0.00 | −0.06 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −0.03 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| FRH0 | Bretagne | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| HR04 | Kontinentalna Hrvatska | −0.04 | 0.00 | −0.07 | 0.00 | 0.00 | −0.13 | −0.03 | −0.35 | 0.00 | 0.00 | −0.08 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −0.05 | 0.00 | 0.00 | 0.00 | −0.36 | 0.00 | 0.00 | 0.00 | 0.01 |
| ITC1 | Piemonte | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| LV00 | Latvija | −0.02 | 0.00 | −0.12 | −0.01 | 0.00 | −0.03 | 0.00 | 0.00 | 0.00 | −0.08 | −0.13 | 0.00 | 0.00 | −0.25 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −0.05 | 0.00 | −0.04 | 0.00 | −0.29 | 0.00 | −0.06 | 0.00 | 0.01 |
| LT02 | Vidurio ir vakaru | 0.00 | 0.00 | −0.15 | 0.00 | 0.00 | 0.00 | 0.00 | −0.04 | −0.11 | −0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −0.07 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −0.18 | 0.00 | −0.20 | 0.00 | 0.01 |
| HU33 | Dél-Alföld | 0.00 | 0.00 | −0.02 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −0.04 | −0.06 | 0.00 | −0.02 | 0.00 | −0.27 | 0.00 | −0.16 | 0.00 | −0.04 | 0.00 | 0.01 |
| NL11 | Groningen | 0.00 | 0.00 | −0.04 | 0.00 | 0.00 | 0.00 | 0.00 | −0.27 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −0.30 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −0.30 | 0.00 | −0.19 | 0.00 | 0.01 |
| AT33 | Tirol | 0.00 | 0.00 | −0.34 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −0.20 | 0.00 | −0.09 | 0.00 | 0.00 | −0.21 | 0.00 | 0.00 | −0.15 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −0.37 | 0.00 | −0.25 | 0.00 | 0.02 |
| PL21 | Malopolskie | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −0.02 | 0.00 | −0.06 | 0.00 | 0.00 | −0.01 | 0.00 | 0.00 |
| RO41 | Sud-Vest Oltenia | 0.00 | −0.08 | −0.20 | −0.03 | 0.00 | 0.00 | 0.00 | −0.03 | 0.00 | 0.00 | −0.04 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −0.07 | 0.00 | 0.00 | 0.00 | −0.17 | 0.00 | −0.16 | 0.00 | 0.01 |
| SI04 | Zahodna Slovenija | −0.04 | 0.00 | −0.04 | 0.00 | 0.00 | −0.03 | 0.00 | −0.09 | 0.00 | −0.05 | −0.08 | 0.00 | 0.00 | −0.18 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −0.04 | 0.00 | 0.00 | 0.00 | −0.23 | 0.00 | −0.04 | 0.00 | 0.01 |
| Parameter | Weight | Parameter | Weight |
|---|---|---|---|
| Basic_Ins | 0.06 | Social_NGOP | 0.00 |
| Basic_MS | 0.03 | Innovation_TR | 0.03 |
| Basic_Inf | 1.50 | Innovation_Inn | 0.20 |
| Basic_Edu | 0.17 | Efficiency_LME | 1.78 |
| Basic_IRtCC | 778.25 | Efficiency_MS | 0.21 |
| Basic_CoEE | 0.15 | Efficiency_RE | 0.15 |
| Natural_AQ | 0.01 | Sector_Agr | 2971.51 |
| Natural_Bio | 2.19 | Sector_Tou | 0.48 |
| Natural_EiACG | 0.25 | Sector_Ene | 0.43 |
| Social_SD | 0.03 | Sector_Tra | 10.07 |
| Social_Aw | 0.22 | Sector_Ind | 1.58 |
| Social_At | 0.01 | Sector_Bui | 1.74 |
| Social_PQoF | 0.02 | RCCCI_y | 0.15 |
| Social_H | 3.95 |
| Geo_Code | Geo_Label | DEA Pure | DEA-Like | Entropy |
|---|---|---|---|---|
| BE10 | Région de Bruxelles—Capitale | 1.00 | 0.89 | 0.56 |
| DE30 | Berlin | 1.00 | 0.87 | 0.30 |
| EL30 | Attiki | 1.00 | 0.91 | 0.17 |
| ES11 | Galicia | 1.00 | 0.92 | 0.40 |
| FRH0 | Bretagne | 0.91 | 0.9 | 0.48 |
| HR04 | Kontinentalna Hrvatska | 1.00 | 0.87 | 0.30 |
| ITC1 | Piemonte | 1.00 | 0.87 | 0.31 |
| LV00 | Latvija | 1.00 | 0.85 | 0.30 |
| LT02 | Vidurio ir vakaru Lietuvos | 1.00 | 0.91 | 0.49 |
| HU33 | Dél-Alföld | 1.00 | 0.92 | 0.37 |
| NL11 | Groningen | 1.00 | 0.93 | 0.93 |
| AT33 | Tirol | 1.00 | 0.89 | 0.59 |
| PL21 | Malopolskie | 1.00 | 0.86 | 0.30 |
| RO41 | Sud-Vest Oltenia | 1.00 | 0.92 | 0.34 |
| SI04 | Zahodna Slovenija | 1.00 | 0.91 | 0.59 |
| Grade | Grade Centres | Number of Regions | Examples |
|---|---|---|---|
| 1 | 0.77 | 16 | DE22, NL32, AT33 |
| 2 | 0.49 | 53 | BE10, BE35, CZ06, DE80, IE05, ES24, FRH0 |
| 3 | 0.27 | 51 | BG31, DE21, ITG1, PL21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karman, A.; Banaś, J. The Evaluation of Climate Change Competitiveness via DEA Models and Shannon Entropy: EU Regions. Entropy 2024, 26, 732. https://doi.org/10.3390/e26090732
Karman A, Banaś J. The Evaluation of Climate Change Competitiveness via DEA Models and Shannon Entropy: EU Regions. Entropy. 2024; 26(9):732. https://doi.org/10.3390/e26090732
Chicago/Turabian StyleKarman, Agnieszka, and Jarosław Banaś. 2024. "The Evaluation of Climate Change Competitiveness via DEA Models and Shannon Entropy: EU Regions" Entropy 26, no. 9: 732. https://doi.org/10.3390/e26090732
APA StyleKarman, A., & Banaś, J. (2024). The Evaluation of Climate Change Competitiveness via DEA Models and Shannon Entropy: EU Regions. Entropy, 26(9), 732. https://doi.org/10.3390/e26090732






