Impact of Quantum Non-Locality and Electronic Non-Ideality on the Shannon Entropy for Atomic States in Dense Plasma
Abstract
1. Introduction
2. Effective Potential of Electron–Ion Interaction
3. Methodology
4. Results and Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- He, Y.Y.; Zhou, Z.L.; Jiao, L.G.; Liu, A.; Montgomery, H.E.; Ho, Y.K. Hyperpolarizabilities of Hydrogenlike Atoms in Debye and Dense Quantum Plasmas. Phys. Rev. E 2023, 107, 045201. [Google Scholar] [CrossRef] [PubMed]
- Li, X.N.; Zhang, Y.Z.; Jiao, L.G.; Wang, Y.C.; Montgomery, H.E.; Ho, Y.K.; Fritzsche, S. Geometric Properties of the Ground State of H- and He in Dense Quantum Plasmas. Eur. Phys. J. D 2023, 77, 59. [Google Scholar] [CrossRef]
- Hu, H.; Li, L.; Chen, Z.; Chen, W.; Liu, X.; Li, P. Shielding Effect of Quantum Plasma. Phys. Plasmas 2019, 26, 032123. [Google Scholar] [CrossRef]
- Verma, N.; Joshi, R. Shannon Entropy for Hydrogen Atom in Debye and Quantum Plasma Environment. Phys. Plasmas 2023, 30, 063905. [Google Scholar] [CrossRef]
- Colonna, G.; Laricchiuta, A. Thermodynamic and Transport Properties of Equilibrium Debye Plasmas. Entropy 2020, 22, 237. [Google Scholar] [CrossRef] [PubMed]
- Karmakar, A.; Ghoshal, A. Scattering in Non-Ideal Classical Plasmas: Scattering Length and Zero-Energy Resonances. Phys. Plasmas 2019, 26, 102114. [Google Scholar] [CrossRef]
- Lumb Talwar, S.; Lumb, S.; Sen, K.D.; Prasad, V. Non-Ideal Classical Plasma: Laser Pulse Effects and Dynamic Dipole Polarizabilities. J. Phys. B At. Mol. Opt. Phys. 2023, 56, 145001. [Google Scholar] [CrossRef]
- Das, B.; Ghoshal, A. Scattering of Slow Electron from Hydrogen Atom in Non-Ideal Classical Plasmas: Zero-Energy Resonances. Phys. Plasmas 2021, 28, 042106. [Google Scholar] [CrossRef]
- Chen, C.; Zhao, G.P.; Qi, Y.Y.; Liu, L.; Chen, Z.B.; Wang, J.G. Total, State-Selective, and Angular-Differential Cross Sections for Electron Capture in He2++H Collisions in Warm Dense Plasmas. Phys. Plasmas 2022, 29, 062110. [Google Scholar] [CrossRef]
- Shalenov, E.O.; Dzhumagulova, K.N.; Ramazanov, T.S.; Reinholz, H.; Ropke, G. Influence of Dynamic Screening on the Conductivity of Hydrogen Plasma Including Electron–Electron Collisions. Contrib. Plasma Phys. 2019, 59, e201900024. [Google Scholar] [CrossRef]
- Shalenov, E.O.; Dzhumagulova, K.N.; Ramazanov, T.S.; Ropke, G.; Reinholz, H. Dynamical Conductivity of the Dense Semiclassical Plasmas on the Basis of the Effective Potential. Phys. Plasmas 2018, 25, 082706. [Google Scholar] [CrossRef]
- Shalenov, E.O.; Rosmej, S.; Reinholz, H.; Ropke, G.; Dzhumagulova, K.N.; Ramazanov, T.S. Optical Reflectivity Based on the Effective Interaction Potentials of Xenon Plasma. Contrib. Plasma Phys. 2017, 57, 486. [Google Scholar] [CrossRef]
- Dzhumagulova, K.N.; Shalenov, E.O.; Ramazanov, T.S. Elastic Scattering of Low Energy Electrons in Partially Ionized Dense Semiclassical Plasma. Phys. Plasmas 2015, 22, 082120. [Google Scholar] [CrossRef]
- Jumagulov, M.N.; Seisembayeva, M.M.; Shalenov, E.O.; Kossymkyzy, Z.; Ramazanov, T.S.; Dzhumagulova, K.N. Electron Runaway in a Dense Semiclassical Plasma. High Energy Density Phys. 2020, 36, 100832. [Google Scholar] [CrossRef]
- Shalenov, E.O.; Seisembayeva, M.M.; Dzhumagulova, K.N.; Ramazanov, T.S. Effect of Dynamic Screening on the Electron Capture Process in Nonideal Plasma. J. Phys. Conf. Ser. 2019, 1385, 012031. [Google Scholar] [CrossRef]
- Shalenov, E.O.; Seisembayeva, M.M.; Dzhumagulova, K.N.; Ramazanov, T.S. Kinetic Ionization and Recombination Coefficients in the Dense Semiclassical Plasmas on the Basis of the Effective Interaction Potential. J. Phys. Conf. Ser. 2019, 1400, 077035. [Google Scholar] [CrossRef]
- Ma, K.; Chen, C.; Chu, Y.; Jiao, Z.; Chen, Z.B. Theoretical Calculations on the Relativistic Corrections and Photoionization Cross Sections for Hydrogenlike Ions in Finite Temperature Dense Plasmas. Few-Body Syst. 2022, 63, 6. [Google Scholar] [CrossRef]
- Chen, Z.B.; Zhao, G.P.; Qi, Y.Y. Theoretical Studies of the Spectral Characteristics and Electron Impact Dynamics of Ti XXI Placed in the Hot Dense Regimes. J. Electron Spectrosc. Relat. Phenom. 2023, 262, 147283. [Google Scholar] [CrossRef]
- Roozehdar Mogaddam, R.; Sepehri Javan, N.; Javidan, K.; Mohammadzadeh, H. Entanglement Fidelity Ratio for Elastic Collisions in Non-Ideal Two-Temperature Dense Plasma. Phys. Scr. 2020, 95, 115601. [Google Scholar] [CrossRef]
- Mahdavi, M.; Akbarian, H. Calculation of Effective Potential of Hulthen Interaction for a Nonideal Dense Plasma Using Dielectric Response Method. Chin. J. Phys. 2022, 77, 1237. [Google Scholar] [CrossRef]
- Parpia, F.A.; Fischer, C.F. Generalized Coulomb Screening in Dense Plasmas: A Numerical Approach. Phys. Rev. A 2023, 107, 012702. [Google Scholar] [CrossRef]
- Sharma, A.; Agrawal, M.; Vyas, M.; Sen, K.D.; Montgomery, H.E.; Ho, Y.K. Thermodynamic Properties and Information-Theoretic Measures for Hydrogenic Atoms in Quantum Plasmas. Phys. Rev. A 2022, 106, 022802. [Google Scholar] [CrossRef]
- Yadav, A.; Mishra, S.P. Positional and Momentum Shannon Entropies of Hydrogenic Atoms in Weakly Coupled Debye Plasmas. Entropy 2023, 25, 260. [Google Scholar] [CrossRef]
- Dzhumagulova, K.N.; Shalenov, E.O.; Tashkenbayev, Y.A.; Ramazanov, T.S. Study of the Electron-Atom Collisions in Dense Semiclassical Plasma of Noble Gases. J. Plasma Phys. 2022, 88, 905880001. [Google Scholar] [CrossRef]
- Dzhumagulova, K.N.; Shalenov, E.O.; Tashkenbayev, Y.A.; Ramazanov, T.S. Electron-Atom Interactions in Dense Semiclassical Helium Plasma. Phys. Plasmas 2022, 29, 102705. [Google Scholar] [CrossRef]
- Shalenov, E.O.; Nuraly, A.T.; Dzhumagulova, K.N. Bound States of the Hydrogen Atom in High-Density Plasmas. Contrib. Plasma Phys. 2022, 62, e202200017. [Google Scholar] [CrossRef]
- Zeng, J.; Jiang, X.; Cheng, G.; Wu, J.; Yuan, J. Electron Localization Induced Increase in the Electron Impact Excitation Cross Sections and Rate Coefficients of Ions Embedded in a Dense Plasma. Results Phys. 2024, 58, 107522. [Google Scholar] [CrossRef]
- Zhdankin, V. Generalized Entropy Production in Collisionless Plasma Flows and Turbulence. Physical Review. X 2022, 12, 031011. [Google Scholar] [CrossRef]
- Souza, L.C.; Sales, M.R.; Mugnaine, M.; Szezech, J.D.; Caldas, I.L.; Viana, R.L. Chaotic Escape of Impurities and Sticky Orbits in Toroidal Plasmas. Phys. Rev. E 2024, 109, 015202. [Google Scholar] [CrossRef]
- Krommes, J.A. Fundamental Statistical Descriptions of Plasma Turbulence in Magnetic Fields. Phys. Rep. 2002, 360, 1–352. [Google Scholar] [CrossRef]
- Livadiotis, G. Derivation of the Entropic Formula for the Statistical Mechanics of Space Plasmas. Nonlinear Process. Geophys. 2018, 25, 77–88. [Google Scholar] [CrossRef]
- Rastovic, D. Applications of Artificial Intelligence and Multi-Variable Control of Chaos on Tokamak Equilibriums. In Glow Discharges and Tokamaks; Murphy, S.A., Ed.; Nova Science Publishers: New York, NY, USA, 2011; Chapter 10; pp. 407–418. ISBN 978-1-61668-352-8. [Google Scholar]
- Lee, M.-J.; Jung, Y.-D. Characteristics of Shannon’s Information Entropy of Atomic States in Strongly Coupled Plasma. Entropy 2020, 22, 881. [Google Scholar] [CrossRef] [PubMed]
- Jung, Y.-D.; Lee, M.-J. Atomic Shannon entropy in astrophysical nonthermal plasmas. Presented at the XXIX International Conference on Neutrino Physics and Astrophysics, Online conference, June 2020. Available online: https://indico.fnal.gov/event/19348/contributions/186622/ (accessed on 22 June 2020).
- Lee, M.; Jung, Y. Astronomical Data of Atomic Shannon Entropies in Astrophysical Lorentzian Plasmas. Astrophys. J. 2019, 871, 111. [Google Scholar] [CrossRef]
- Groth, S.; Dornheim, T.; Sjostrom, T.; Malone, F.D.; Foulkes, W.M.C.; Bonitz, M. Ab Initio Exchange-Correlation Free Energy of the Uniform Electron Gas at Warm Dense Matter Conditions. Phys. Rev. Lett. 2017, 119, 135001. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.-B.; Qi, Y.-Y.; Sun, H.-Y.; Zhao, G.-P.; Liu, P.-F. Systematic Investigations of Level Delocalization and Spectroscopy of Hydrogen Atom Subjected to a Plasma Environment Using Various Statically Screened Potentials. Phys. Plasmas 2020, 27, 072105. [Google Scholar] [CrossRef]
- Stanton, L.G.; Murillo, M.S. Unified Description of Linear Screening in Dense Plasmas. Phys. Rev. E 2015, 91, 033104. [Google Scholar] [CrossRef]
- Jiao, L.G.; Zan, L.R.; Zhang, Y.Z.; Ho, Y.K. Benchmark Values of Shannon Entropy for Spherically Confined Hydrogen Atom. Int. J. Quantum Chem. 2017, 117, 13. [Google Scholar] [CrossRef]
- Lin, C.-H.; Ho, Y. Quantum Entanglement and Shannon Information Entropy for the Doubly Excited Resonance State in Positronium Negative Ion. Atoms 2015, 3, 422–432. [Google Scholar] [CrossRef]
- Zan, L.R.; Jiao, L.G.; Ma, J.; Ho, Y.K. Information-Theoretic Measures of Hydrogen-Like Ions in Weakly Coupled Debye Plasmas. Phys. Plasmas 2017, 24, 122101. [Google Scholar] [CrossRef]
- Yanez, R.J.; Van Assche, W.; Dehesa, J.S. Position and Momentum Information Entropies of the D-Dimensional Harmonic Oscillator and Hydrogen Atom. Phys. Rev. A 1994, 50, 3065–3079. [Google Scholar] [CrossRef]
- Mishima, K.; Hayashi, M.; Lin, S. Entanglement in Scattering Processes. Phys. Lett. A 2004, 333, 371. [Google Scholar] [CrossRef]


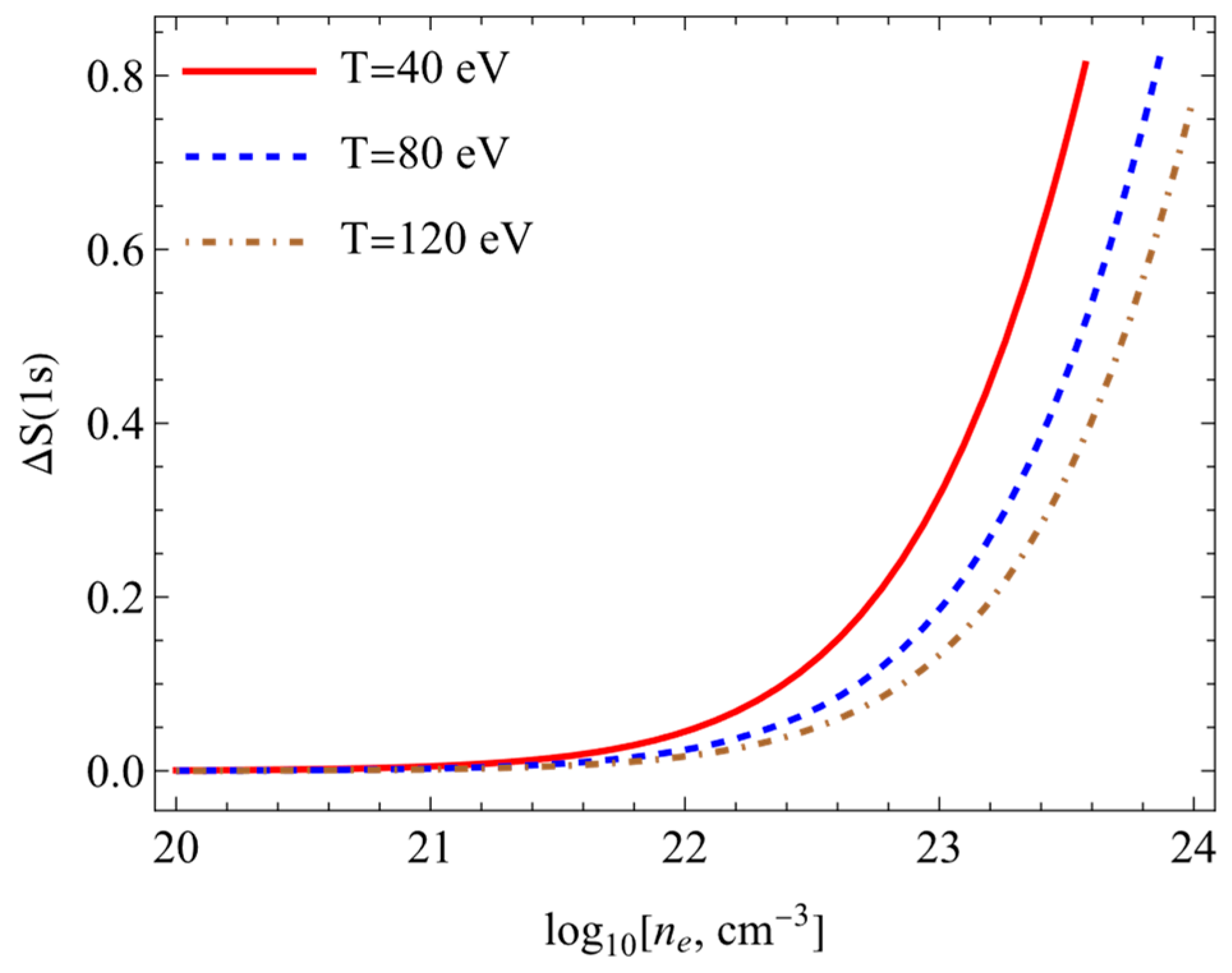
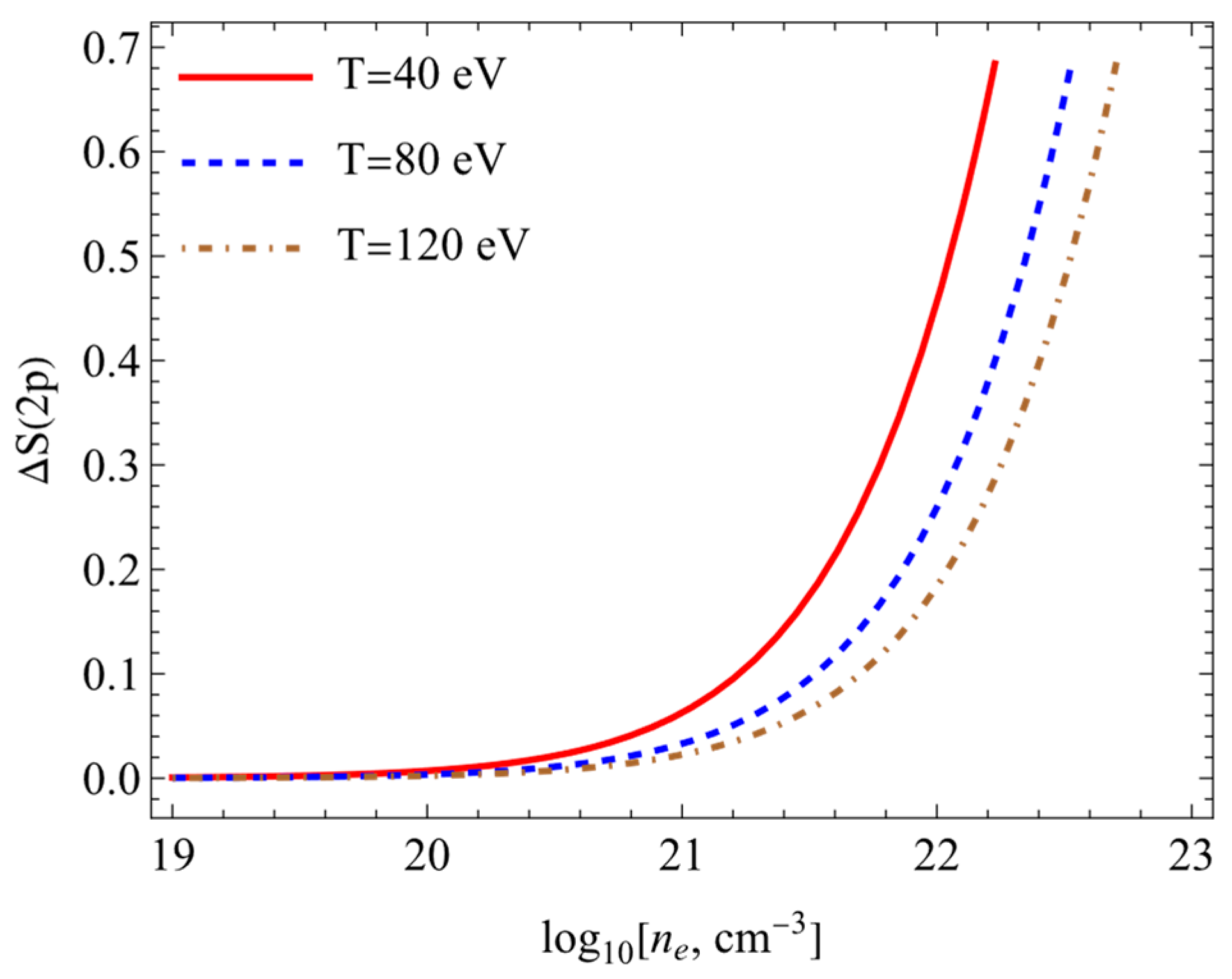
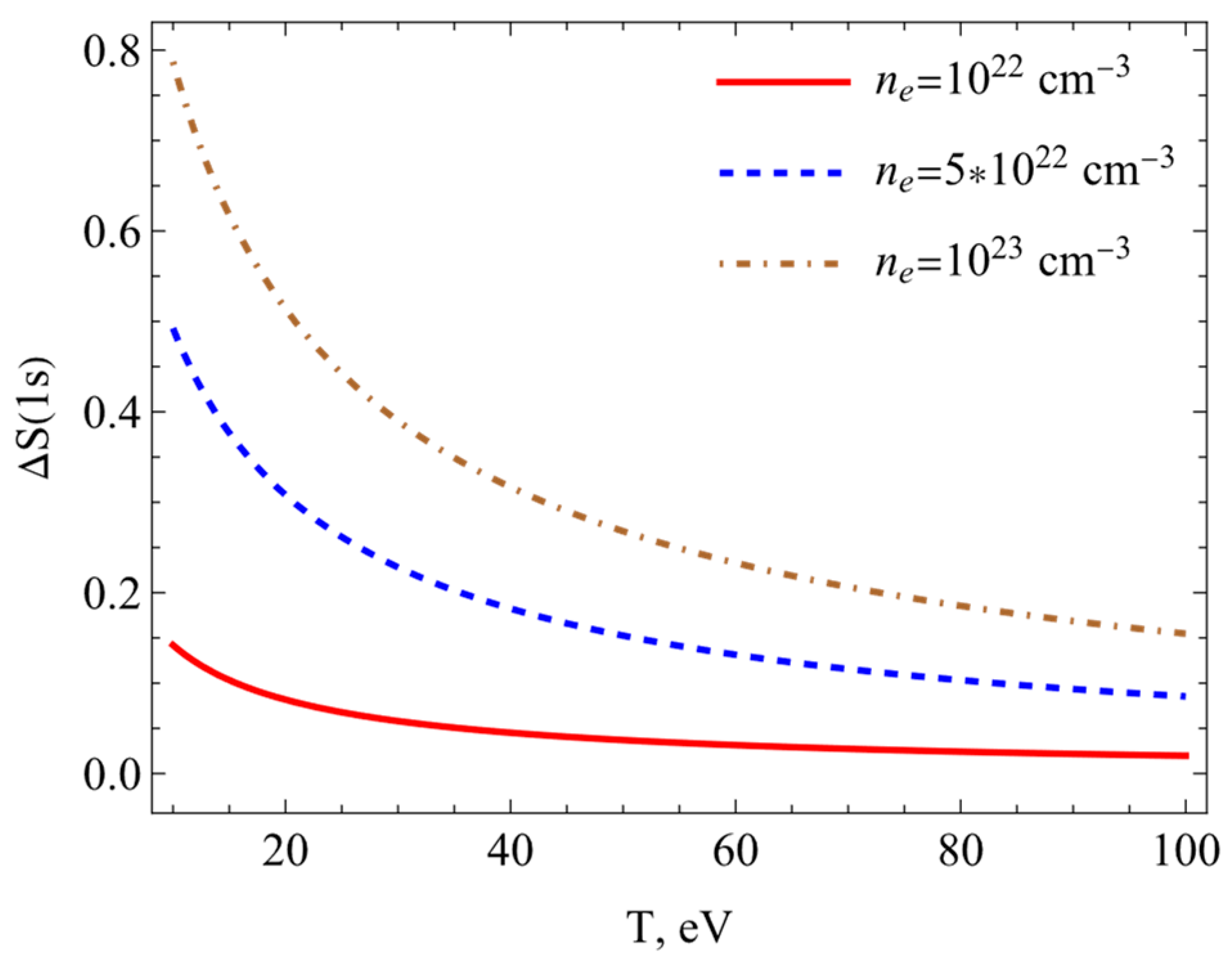
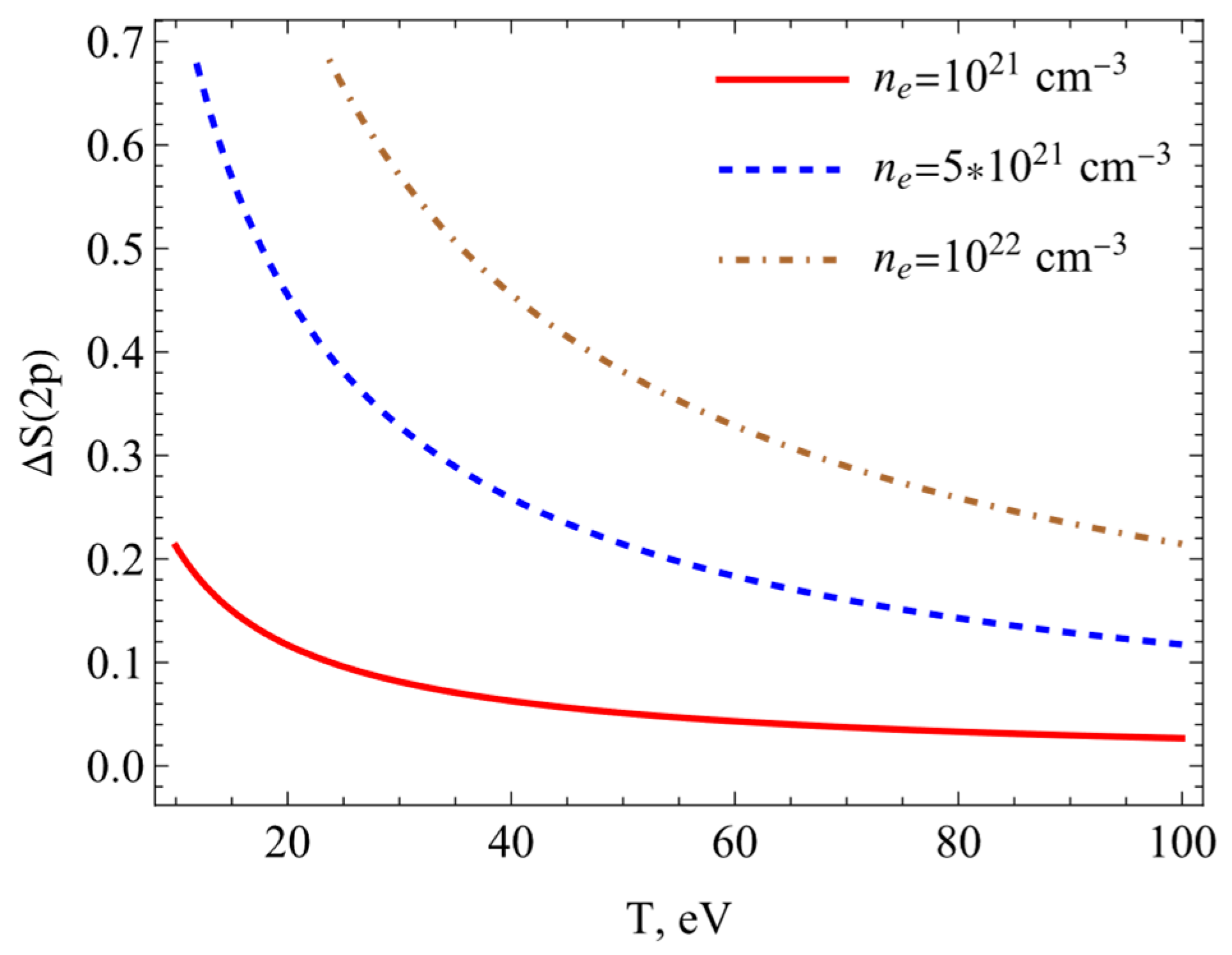


| Model | |||||
|---|---|---|---|---|---|
| 21 | 22 | 23 | 24 | ||
| 50.5 | DHP | 0.002156 | 0.019815 0.019826 a | 0.155426 | 0.830312 |
| SNDP-A | 0.002051 | 0.018773 | 0.145797 | 0.773562 | |
| SNDP-B | 0.004134 | 0.036685 | 0.265969 | - | |
| 202 | DHP | 0.000550 | 0.005263 0.005272 b | 0.046196 | 0.325082 |
| SNDP-A | 0.000542 | 0.005186 | 0.045446 | 0.318487 | |
| SNDP-B | 0.001083 | 0.010180 | 0.085225 | 0.545540 | |
| 454.5 | DHP | 0.000246 | 0.002389 0.002393 c | 0.021843 | 0.170048 |
| SNDP-A | 0.000244 | 0.002373 | 0.021687 | 0.168575 | |
| SNDP-B | 0.000488 | 0.004679 | 0.041358 | 0.297958 | |
| 808 | DHP | 0.000139 | 0.001358 0.001361 d | 0.012687 | 0.104340 |
| SNDP-A | 0.000138 | 0.001353 | 0.012636 | 0.103853 | |
| SNDP-B | 0.000276 | 0.002675 | 0.024341 | 0.187644 | |
| Model | |||||
|---|---|---|---|---|---|
| 20 | 21 | 22 | 23 | ||
| 50.5 | DHP | 0.002879 | 0.026589 | 0.213152 0.213257 a | - |
| SNDP-A | 0.002866 | 0.026457 | 0.211904 | - | |
| SNDP-B | 0.005655 | 0.050643 | 0.378147 | - | |
| 202 | DHP | 0.000733 | 0.007040 | 0.062325 0.062422 b | 0.453349 |
| SNDP-A | 0.000732 | 0.007032 | 0.062243 | 0.452619 | |
| SNDP-B | 0.001455 | 0.013732 | 0.116375 | - | |
| 454.5 | DHP | 0.000328 | 0.003192 | 0.029345 0.029395 c | 0.232816 |
| SNDP-A | 0.000328 | 0.003190 | 0.029328 | 0.232663 | |
| SNDP-B | 0.000652 | 0.006277 | 0.055917 | 0.412632 | |
| 808 | DHP | 0.000185 | 0.001814 | 0.017010 0.017040 d | 0.141772 |
| SNDP-A | 0.000185 | 0.001813 | 0.017004 | 0.141723 | |
| SNDP-B | 0.000368 | 0.003582 | 0.032771 | 0.257123 | |
| Plasma Type | 1s | 2s | 3s | 2p | 3p | |
|---|---|---|---|---|---|---|
| PFJ | - | 1.61371 | 5.57991 | 7.89546 | 5.16582 | 7.70677 |
| PFPW | - | 1.61371 | 5.57999 | 7.89596 | 5.16589 | 7.70723 |
| eV | 19 | 1.61381 | 5.58165 | 7.90401 | 5.16728 | 7.71472 |
| 20 | 1.61475 | 5.59627 | 7.96978 | 5.17961 | 7.77645 | |
| 21 | 1.62353 | 5.71449 | 8.40644 | 5.28263 | 8.19733 | |
| eV | 19 | 1.61391 | 5.58335 | 7.91208 | 5.16869 | 7.72225 |
| 20 | 1.61571 | 5.61123 | 8.03277 | 5.19235 | 7.83611 | |
| 21 | 1.63199 | 5.82120 | 8.73711 | 5.37814 | 8.52553 | |
| eV | 19 | 1.61410 | 5.58662 | 7.92741 | 5.17142 | 7.73658 |
| 20 | 1.61746 | 5.63889 | 8.14261 | 5.21599 | 7.94099 | |
| 21 | 1.64678 | 5.99741 | - | 5.53953 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nuraly, A.T.; Seisembayeva, M.M.; Dzhumagulova, K.N.; Shalenov, E.O. Impact of Quantum Non-Locality and Electronic Non-Ideality on the Shannon Entropy for Atomic States in Dense Plasma. Entropy 2024, 26, 602. https://doi.org/10.3390/e26070602
Nuraly AT, Seisembayeva MM, Dzhumagulova KN, Shalenov EO. Impact of Quantum Non-Locality and Electronic Non-Ideality on the Shannon Entropy for Atomic States in Dense Plasma. Entropy. 2024; 26(7):602. https://doi.org/10.3390/e26070602
Chicago/Turabian StyleNuraly, Askhat T., Madina M. Seisembayeva, Karlygash N. Dzhumagulova, and Erik O. Shalenov. 2024. "Impact of Quantum Non-Locality and Electronic Non-Ideality on the Shannon Entropy for Atomic States in Dense Plasma" Entropy 26, no. 7: 602. https://doi.org/10.3390/e26070602
APA StyleNuraly, A. T., Seisembayeva, M. M., Dzhumagulova, K. N., & Shalenov, E. O. (2024). Impact of Quantum Non-Locality and Electronic Non-Ideality on the Shannon Entropy for Atomic States in Dense Plasma. Entropy, 26(7), 602. https://doi.org/10.3390/e26070602






