Quantum Tunneling and Complex Dynamics in the Suris’s Integrable Map
Abstract
1. Introduction
2. Model
3. Discrepancy between the Wave Function and
4. Toward Semiclassical Understanding for Plateau with Oscillatory Pattern
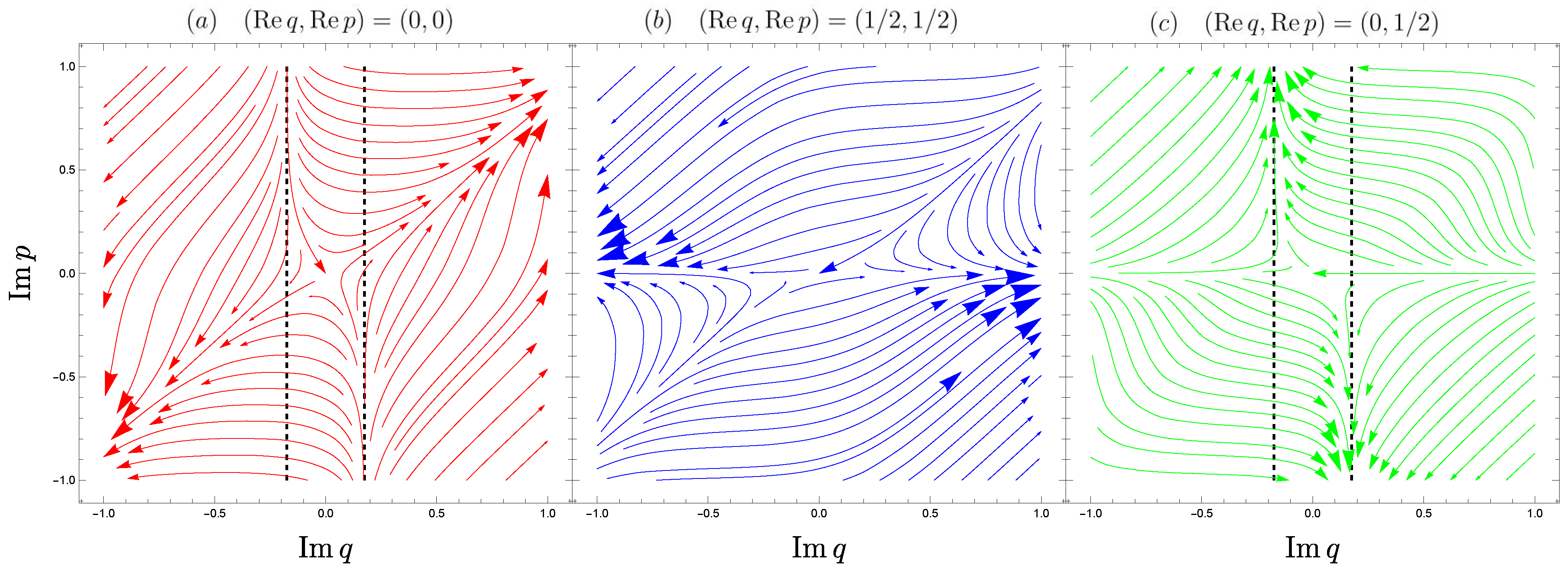
4.1. Complex Dynamics of and
4.2. One-Step Propagation
5. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Voros, A. The return of the quartic oscillator. The complex WKB method. Ann. De L’I.H.P. Phys. Théorique 1983, 39, 211–338. [Google Scholar]
- Dingle, R. Asymptotic Expansions: Their Derivation and Interpretation; Academic Press: London, UK, 1973; Volume 521. [Google Scholar]
- Écalle, J. Les fonctions Résurgentes: (en Trois Parties); Département de Mathématique, Université de Paris-Sud: Bât, France, 1981; Volume 1, p. 425. [Google Scholar]
- Delabaere, E.; Dillinger, H.; Pham, F. Exact semiclassical expansions for one-dimensional quantum oscillators. J. Math. Phys. 1997, 38, 6126–6184. [Google Scholar] [CrossRef]
- Kawai, T.; Takei, Y. Algebraic Analysis of Singular Perturbation Theory; American Mathematical Society: Providence, RI, USA, 2005; Volume 227. [Google Scholar]
- Callan, C.G., Jr.; Coleman, S. Fate of the false vacuum. II. First quantum corrections. Phys. Rev. D 1977, 16, 1762. [Google Scholar] [CrossRef]
- Coleman, S. Fate of the false vacuum: Semiclassical theory. Phys. Rev. D 1977, 15, 2929. [Google Scholar] [CrossRef]
- Coleman, S. Aspects of Symmetry: Selected Erice Lectures; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- McLaughlin, D.W. Complex Time, Contour Independent Path Integrals, and Barrier Penetration. J. Math. Phys. 1972, 13, 1099–1108. [Google Scholar] [CrossRef]
- Freed, K.F. Path Integrals and Semiclassical Tunneling, Wavefunctions, and Energies. J. Chem. Phys. 1972, 56, 692–697. [Google Scholar] [CrossRef]
- George, T.F.; Miller, W.H. Complex-Valued Classical Trajectories for Linear Reactive Collisions of H + H2 below the Classical Threshold. J. Chem. Phys. 1972, 56, 5722–5723. [Google Scholar] [CrossRef]
- Miller, W.H. Quantum mechanical transition state theory and a new semiclassical model for reaction rate constants. J. Chem. Phys. 1974, 61, 1823–1834. [Google Scholar] [CrossRef]
- Ilgenfritz, E.M.; Perlt, H. Complex time path for the tunnelling at intermediate energy. J. Phys. A Math. Gen. 1992, 25, 5729. [Google Scholar] [CrossRef]
- Harrell, E.M. On the rate of asymptotic eigenvalue degeneracy. Commun. Math. Phys. 1978, 60, 73–95. [Google Scholar] [CrossRef]
- Weiss, U.; Haeffner, W. Complex-time path integrals beyond the stationary-phase approximation: Decay of metastable states and quantum statistical metastability. Phys. Rev. D 1983, 27, 2916–2927. [Google Scholar] [CrossRef]
- Simon, B. Instantons, double wells and large deviations. Bull. Am. Math. Soc. 1983, 8, 323–326. [Google Scholar] [CrossRef][Green Version]
- Simon, B. Semiclassical Analysis of Low Lying Eigenvalues, II. Tunneling. Ann. Math. 1984, 120, 89–118. [Google Scholar] [CrossRef]
- Creagh, S.C.; Whelan, N.D. A Matrix Element for Chaotic Tunnelling Rates and Scarring Intensities. Ann. Phys. 1999, 272, 196–242. [Google Scholar] [CrossRef]
- Creagh, S.C.; Lee, S.Y.; Whelan, N.D. Scarring and the Statistics of Tunnelling. Ann. Phys. 2002, 295, 194–215. [Google Scholar] [CrossRef][Green Version]
- Harada, H.; Mouchet, A.; Shudo, A. Riemann surfaces of complex classical trajectories and tunnelling splitting in one-dimensional systems. J. Phys. A Math. Theor. 2017, 50, 435204. [Google Scholar] [CrossRef]
- Shudo, A.; Ikeda, K.S. Complex classical trajectories and chaotic tunneling. Phys. Rev. Lett. 1995, 74, 682. [Google Scholar] [CrossRef] [PubMed]
- Shudo, A.; Ikeda, K.S. Complex Semiclassical Approach to Chaotic Tunneling. In Dynamical Tunneling: Theory and Experiment; CRC Press: Boca Raton, FL, USA, 2011; p. 139. [Google Scholar]
- Koda, R.; Hanada, Y.; Shudo, A. Ergodicity of complex dynamics and quantum tunneling in nonintegrable systems. Phys. Rev. E 2023, 108, 054219. [Google Scholar] [CrossRef] [PubMed]
- Davis, M.J.; Heller, E.J. Quantum dynamical tunneling in bound states. J. Chem. Phys. 1981, 75, 246–254. [Google Scholar] [CrossRef]
- Creagh, S.C. Tunneling in two dimensions. In Tunneling in Complex Systems; Tomsovic, S., Ed.; World Scientific: Singapore, 1998; p. 35. [Google Scholar]
- Keshavamurthy, S.; Schlagheck, P. Dynamical Tunneling: Theory and Experiment; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Milnor, J. Dynamics in One Complex Variable; Princeton University Press: Princeton, NJ, USA, 2011; Volume 160. [Google Scholar]
- Beardon, A.F. Iteration of Rational Functions: Complex Analytic Dynamical Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2000; Volume 132. [Google Scholar]
- Morosawa, S.; Nishimura, Y.; Taniguchi, M.; Ueda, T. Holomorphic Dynamics; Cambridge University Press: Cambridge, UK, 2000; Volume 66. [Google Scholar]
- Takahashi, K. Semiclassical Analysis of Multidimensional Barrier Tunneling. In Dynamical Tunneling: Theory and Experiment; CRC Press: Boca Raton, FL, USA, 2011; p. 95. [Google Scholar]
- Takahashi, K. Effects of resonance states in barrier region on non-exponential decay of wave-packets scattered by rounded-rectangular potentials. J. Phys. A Math. Theor. 2021, 54, 475701. [Google Scholar] [CrossRef]
- Takahashi, K.; Ikeda, K.S. Sawtooth structure in tunneling probability for a periodically perturbed rounded-rectangular potential. Phys. Rev. E 2024, 109, 044203. [Google Scholar] [CrossRef]
- Hanada, Y.; Shudo, A.; Ikeda, K.S. Origin of the enhancement of tunneling probability in the nearly integrable system. Phys. Rev. E 2015, 91, 042913. [Google Scholar] [CrossRef] [PubMed]
- Hanada, Y.; Ikeda, K.S.; Shudo, A. Dynamical tunneling across the separatrix. Phys. Rev. E 2023, 108, 064210. [Google Scholar] [CrossRef] [PubMed]
- Suris, Y.B. Integrable mappings of the standard type. Funct. Anal. Its Appl. 1989, 23, 74–76. [Google Scholar] [CrossRef]
- Yuri, S.B. The Problem of Integrable Discretization: Hamilton Approach; Springer Basel AG: Basel, Switzerland, 2003; Volume 219. [Google Scholar] [CrossRef]
- Iijima, R.; Koda, R.; Hanada, Y.; Shudo, A. Quantum tunneling in ultra-near-integrable systems. Phys. Rev. E 2022, 106, 064205. [Google Scholar] [CrossRef] [PubMed]
- Meiss, J.D. Symplectic maps, variational principles, and transport. Rev. Mod. Phys. 1992, 64, 795–848. [Google Scholar] [CrossRef]
- Takahasi, H.; Mori, M. Double Exponential Formulas for Numerical Integration. Publ. Res. Inst. Math. Sci. 1973, 9, 721–741. [Google Scholar] [CrossRef]
- Berry, M.V.; Balazs, N.L.; Tabor, M.; Voros, A. Quantum maps. Ann. Phys. 1979, 122, 26–63. [Google Scholar] [CrossRef]
- Casati, G.; Chirikov, B.V.; Izraelev, F.M.; Ford, J. Stochastic behavior of a quantum pendulum under a periodic perturbation. In Stochastic Behavior in Classical and Quantum Hamiltonian Systems; Casati, G., Ford, J., Eds.; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 1979; pp. 334–352. [Google Scholar] [CrossRef]
- Advanpix LLC. Multiprecision Computing Toolbox for MATLAB, 5.2.5.15470; Advanpix LLC: Yokohama, Japan, 2015.
- Berry, M.V.; Mount, K.E. Semiclassical approximations in wave mechanics. Rep. Prog. Phys. 1972, 35, 315. [Google Scholar] [CrossRef]
- Shudo, A.; Ishii, Y.; Ikeda, K.S. Julia sets and chaotic tunneling: I. J. Phys. A 2009, 42, 265101. [Google Scholar] [CrossRef]
- Shudo, A.; Ishii, Y.; Ikeda, K.S. Julia sets and chaotic tunneling: II. J. Phys. A 2009, 42, 265102. [Google Scholar] [CrossRef]
- Shudo, A.; Ikeda, K.S. Stokes geometry for the quantum Hénon map. Nonlinearity 2008, 21, 1831. [Google Scholar] [CrossRef]
- Shudo, A.; Ikeda, K.S. Toward pruning theory of the Stokes geometry for the quantum Hénon map. Nonlinearity 2016, 29, 375. [Google Scholar] [CrossRef]
- Bullett, S.; Lomonaco, L.; Siqueira, C. Correspondences in complex dynamics. In New Trends in One-Dimensional Dynamics: In Honour of Welington de Melo on the Occasion of His 70th Birthday IMPA 2016, Rio de Janeiro, Brazil, 14–17 November 2019; Springer: Cham, Switzerland, 2019; pp. 51–75. [Google Scholar] [CrossRef]
- Ishikawa, A.; Tanaka, A.; Ikeda, K.S.; Shudo, A. Diffraction and tunneling in systems with mixed phase space. Phys. Rev. E 2012, 86, 036208. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Ramani, A.; Segur, H. A connection between nonlinear evolution equations and ordinary differential equations of P-type. II. J. Math. Phys. 1980, 21, 1006–1015. [Google Scholar] [CrossRef]
- Haake, F. Quantum Signatures of Chaos; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Greene, J.M.; Percival, I.C. Hamiltonian maps in the complex plane. Phys. D 1981, 3, 530–548. [Google Scholar] [CrossRef][Green Version]
- Percival, I.C. Chaotic boundary of a Hamiltonial map. Phys. D 1982, 6, 67–77. [Google Scholar] [CrossRef]
- Berretti, A.; Chierchia, L. On the complex analytic structure of the golden invariant curve for the standard map. Nonlinearity 1990, 3, 39. [Google Scholar] [CrossRef]
- Berretti, A.; Marmi, S. Standard map at complex rotation numbers: Creation of natural boundaries. Phys. Rev. Lett. 1992, 68, 1443. [Google Scholar] [CrossRef]
- Tomsovic, S.; Ullmo, D. Chaos-assisted tunneling. Phys. Rev. E 1994, 50, 145. [Google Scholar] [CrossRef]
- Brodier, O.; Schlagheck, P.; Ullmo, D. Resonance-assisted tunneling. Ann. Phys. 2002, 300, 88–136. [Google Scholar] [CrossRef]
- Balazs, N.; Voros, A. Wigner’s function and tunneling. Ann. Phys. 1990, 199, 123–140. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hanada, Y.; Shudo, A. Quantum Tunneling and Complex Dynamics in the Suris’s Integrable Map. Entropy 2024, 26, 414. https://doi.org/10.3390/e26050414
Hanada Y, Shudo A. Quantum Tunneling and Complex Dynamics in the Suris’s Integrable Map. Entropy. 2024; 26(5):414. https://doi.org/10.3390/e26050414
Chicago/Turabian StyleHanada, Yasutaka, and Akira Shudo. 2024. "Quantum Tunneling and Complex Dynamics in the Suris’s Integrable Map" Entropy 26, no. 5: 414. https://doi.org/10.3390/e26050414
APA StyleHanada, Y., & Shudo, A. (2024). Quantum Tunneling and Complex Dynamics in the Suris’s Integrable Map. Entropy, 26(5), 414. https://doi.org/10.3390/e26050414





