Importance of Characteristic Features and Their Form for Data Exploration
Abstract
1. Introduction
- Illustration of a research framework dedicated to a gradual discretisation procedure directed by selected rankings of features;
- Exploitation of multiple discretisation algorithms, with supervised and unsupervised interval construction;
- Comparison between domain transformations following rankings in ascending and descending directions;
- Analysis of trends in performance of state-of-the-art classifiers with varied operational backgrounds from the point of view of data representation and interpretation;
- Observation of the impact of considering information on the relevance of attributes during their discretisation on the performance of the selected classifiers;
- Application of the proposed methodology in the stylometric domain for authorship attribution tasks.
2. Background
2.1. Nature of Input Space
2.2. Data Transformations
- N—the number of training instances,
- —the number of training instances from the class ,
- —the number of instances with the x-th value of the given attribute,
- —the number of instances from class with the y-th value of the given attribute,
- —the number of possible cut-points.
2.3. Importance of Attributes
| Algorithm 1 Pseudo-code for Relief |
| Input: set of learning instances X, set A of all N attributes, set of classes Cl, probabilities of classes P(Cl), number of iterations m, number k of considered nearest instances from each class; Output: vector of weights w for all attributes; begin for i = 1 to N do w(i) = 0 end for for i = 1 to m do choose randomly an instance x ∈ X find k nearest hits Hj for each class Cl ≠ class(x) do find k nearest misses Mj(Cl) end for for l = 1 to N do end for end for end {algorithm} |
| Algorithm 2 Pseudo-code for OneR classifier |
| Input: set A of all attributes, set of learning instances X; Output: 1-rule 1-rB; begin CandidateRules←Ø for each attribute a ∈ A do for each value va of attribute a do count how often each class appears find the most frequent class ClF construct a rule IF a = va THEN ClF end for calculate classification accuracy for all rules choose the best rule rB CandidateRules←rB end for choose as 1-rB the best one from CandidateRules end {algorithm} |
2.4. Exploration of Input Space
3. Framework for Discretisation Controlled by Attribute Importance
3.1. Input Data and Attributes
3.2. Rankings
3.3. Discretisation Approaches
3.4. Inducers
3.5. Starting and Stopping Point
3.6. Intermediate Steps and Directions of Processing
| Algorithm 3 Pseudo-code for ranking driven discretisation |
| Input: ranking of attributes RankingA, dataset in the continuous domain Data-R, direction Direction to pursue ranking RankingA, number of attributes N; begin TMP-Data←Data-R mine knowledge from TMP-Data evaluate performance for TMP-Data if Direction = Descending then k = 1 else k = N while (k > 0) AND (k < N + 1) do select attribute from the ranking attr = RankingA[k] discretise attr in TMP-Data mine knowledge from TMP-Data evaluate performance for TMP-Data if Direction = Descending then k = k + 1 else k = k − 1 end while end {algorithm} |
4. Experiments
4.1. Data Preparation
4.2. Rankings Employed
4.3. Discretisation Algorithms
4.4. Performance Evaluation for Classifiers
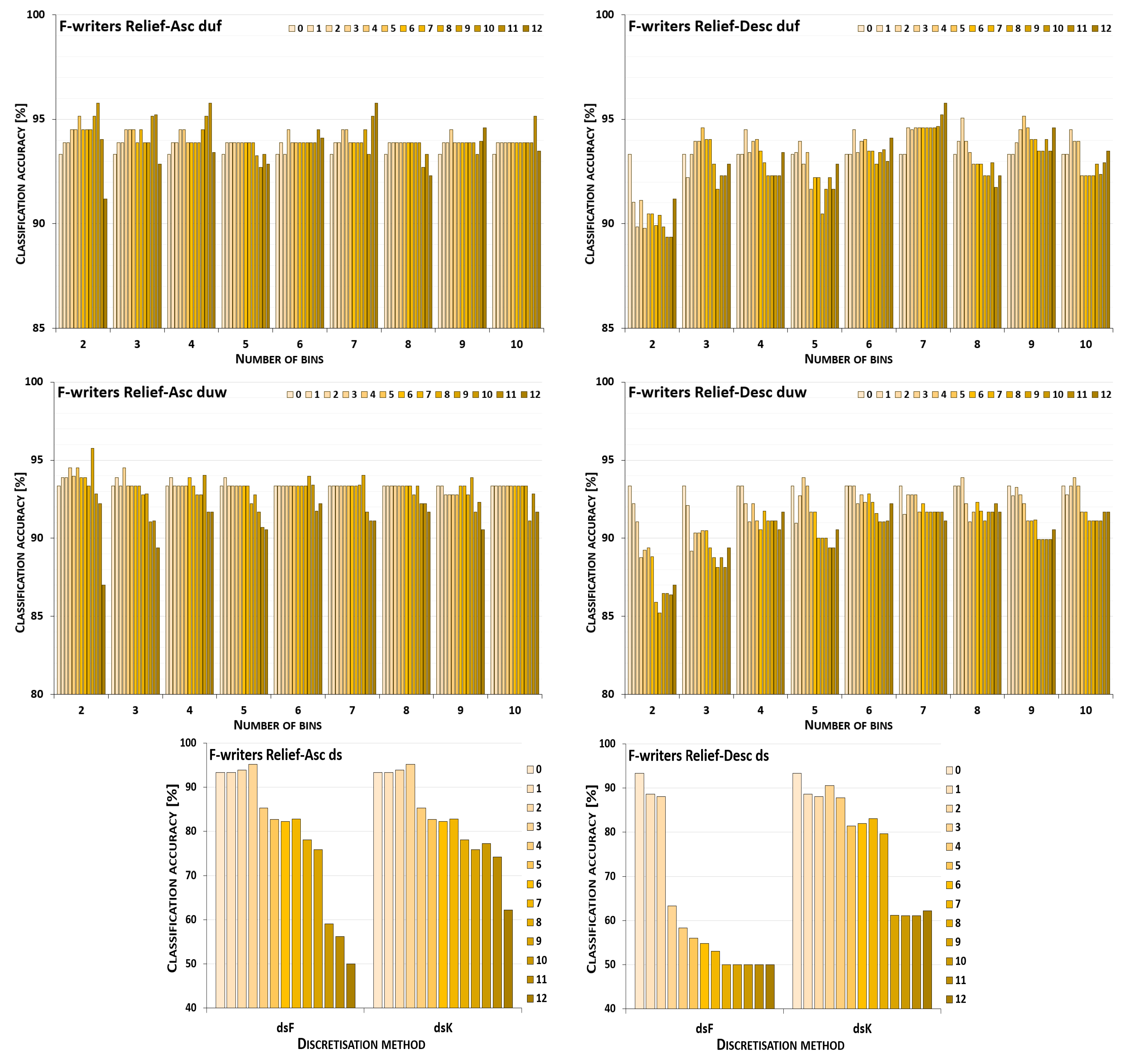
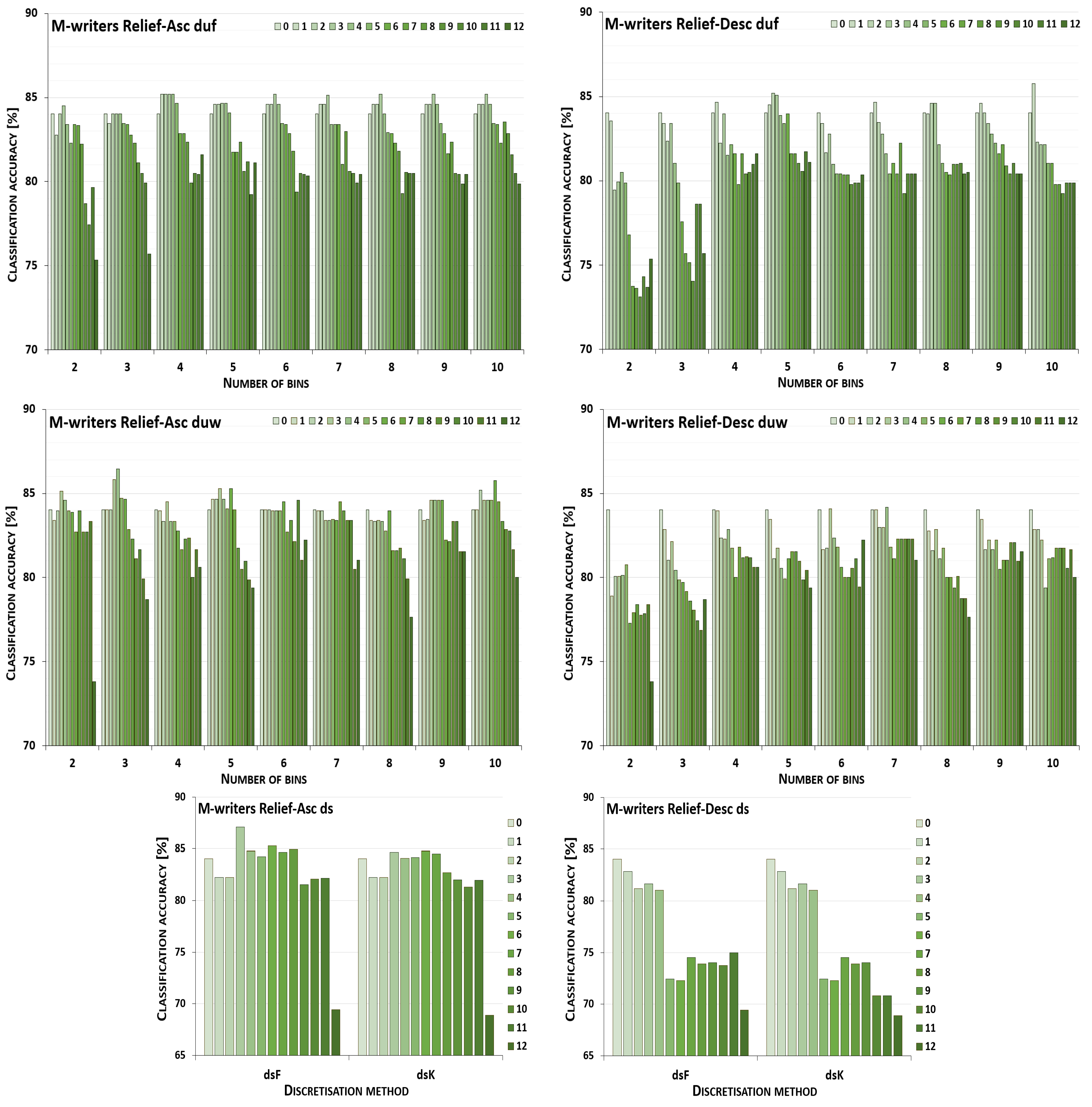
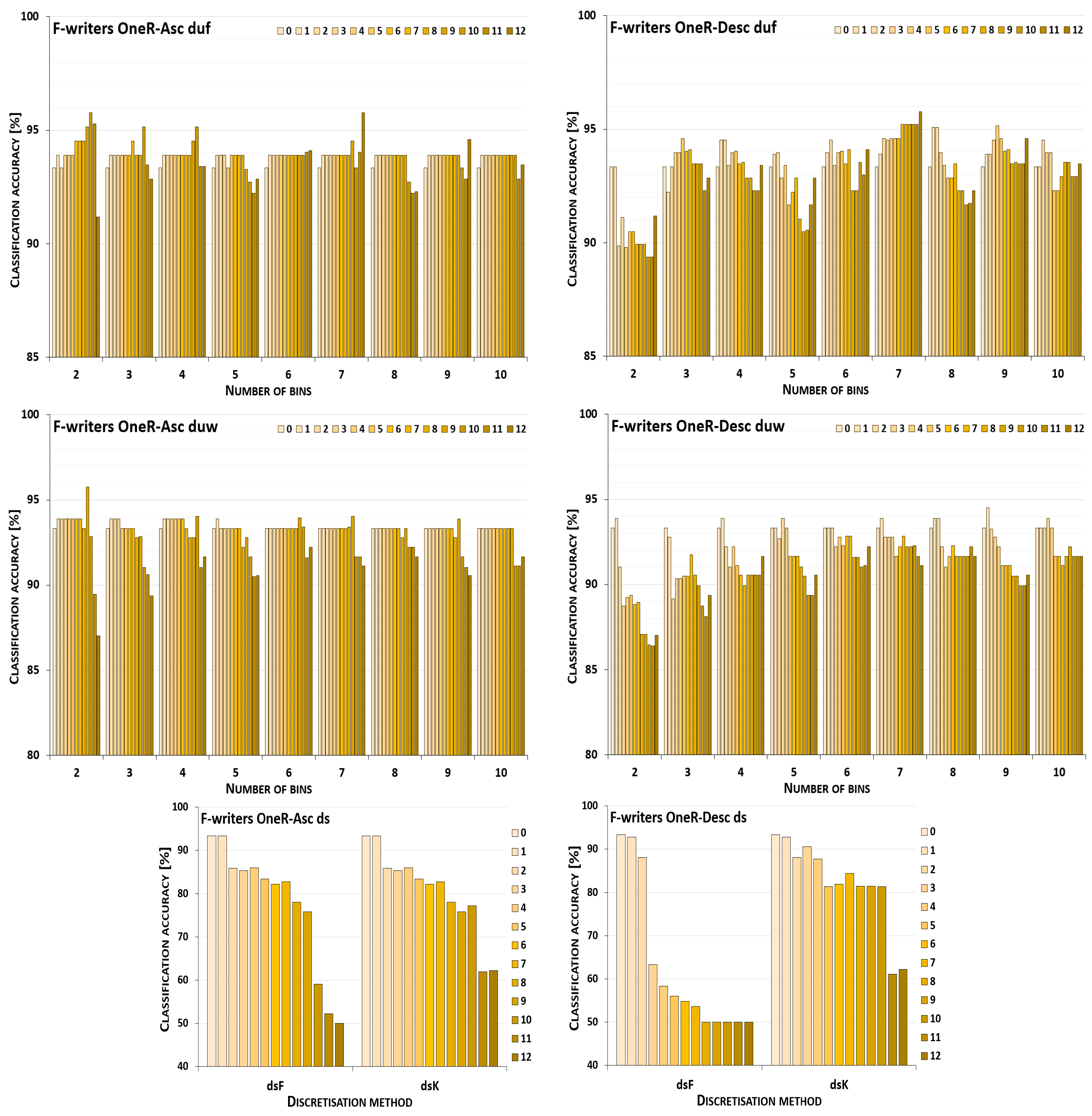
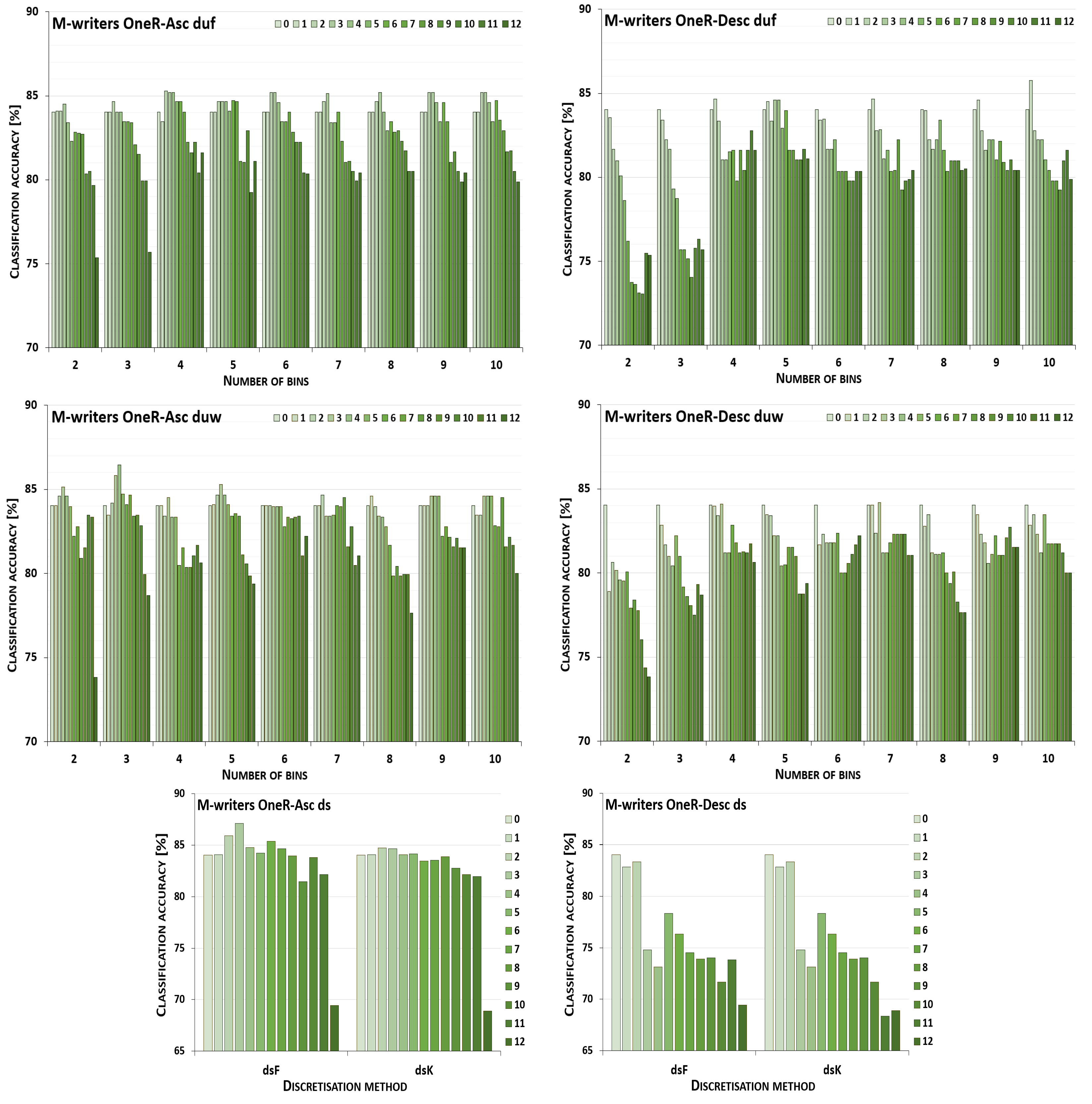
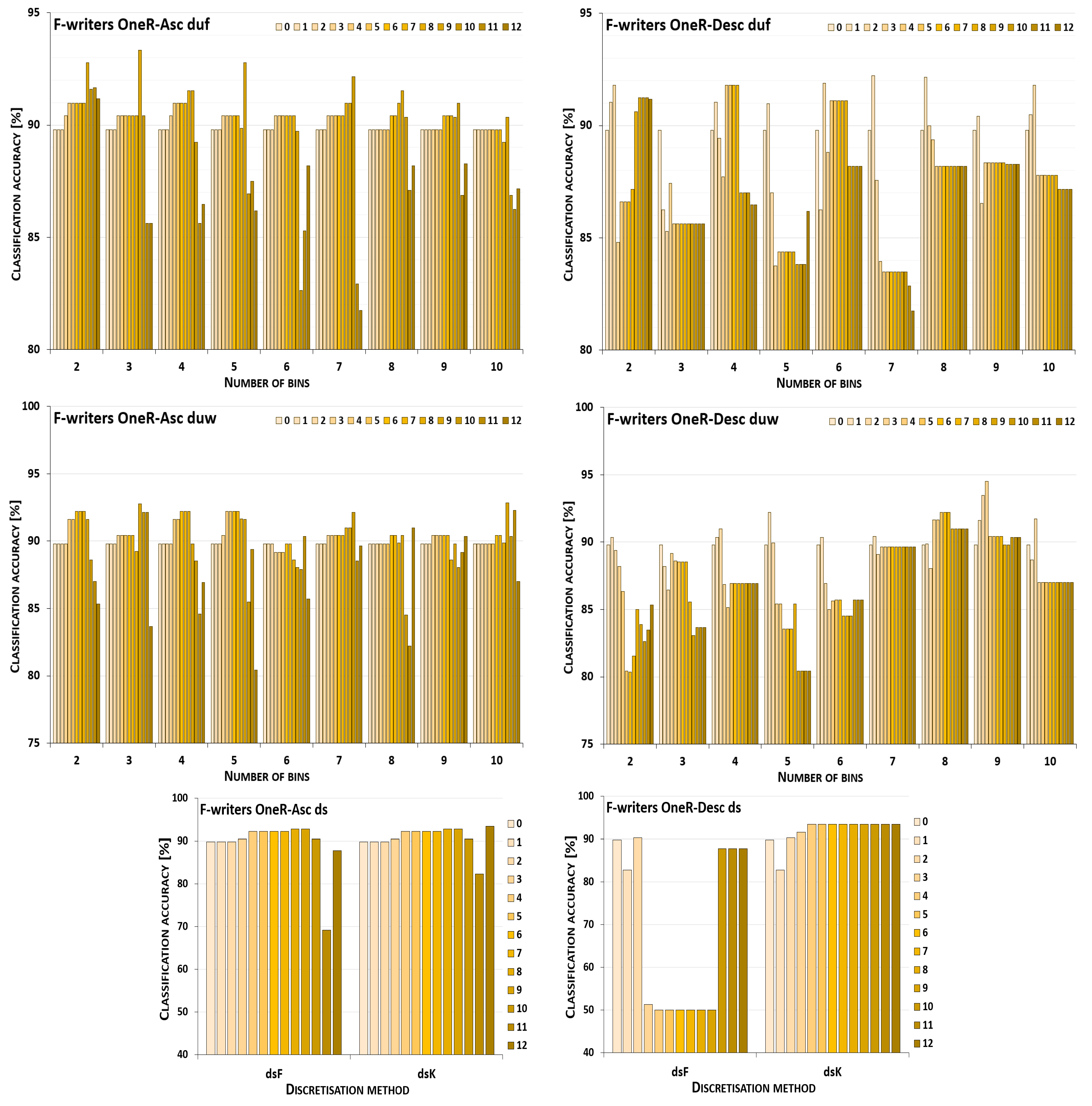
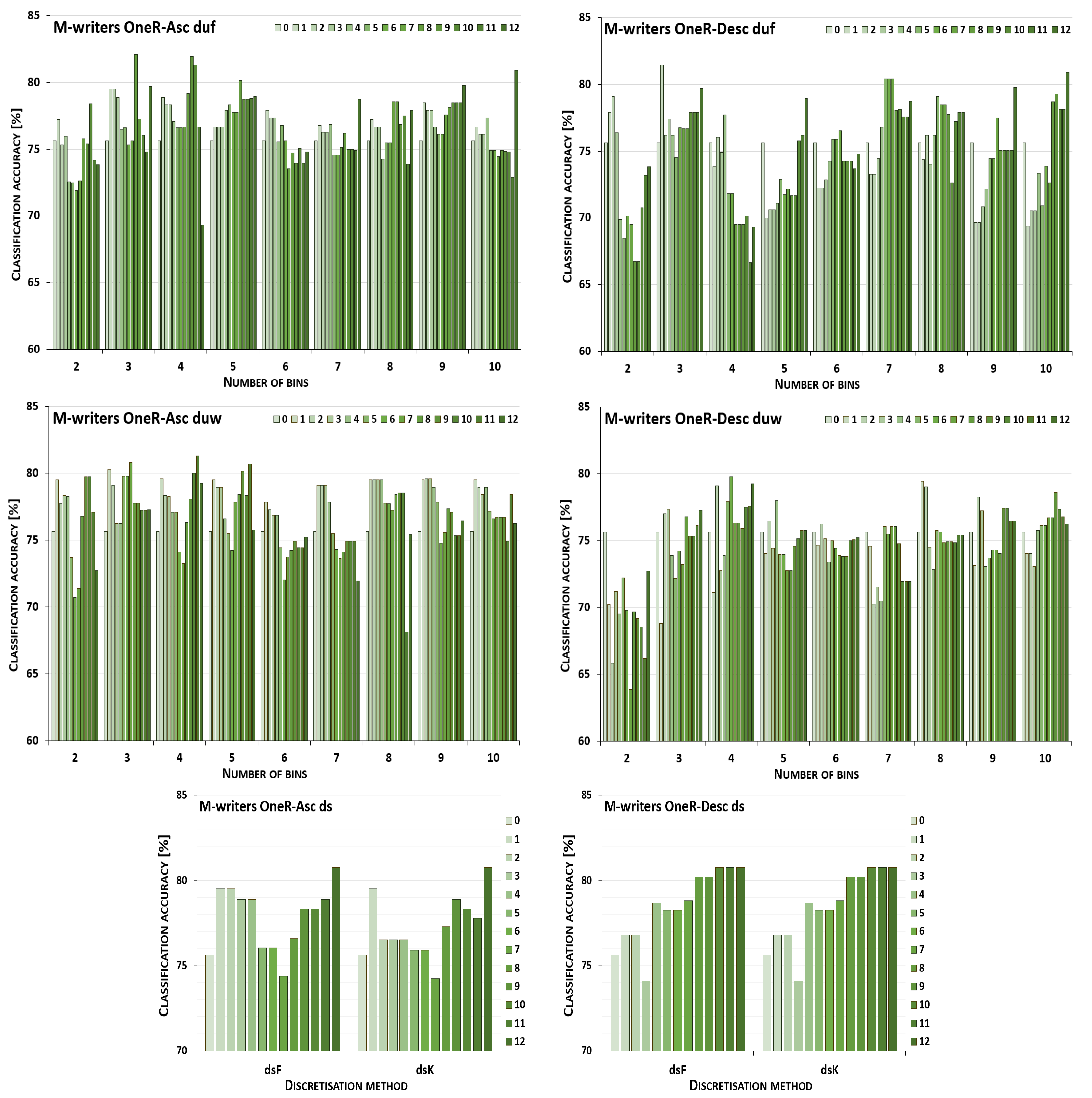
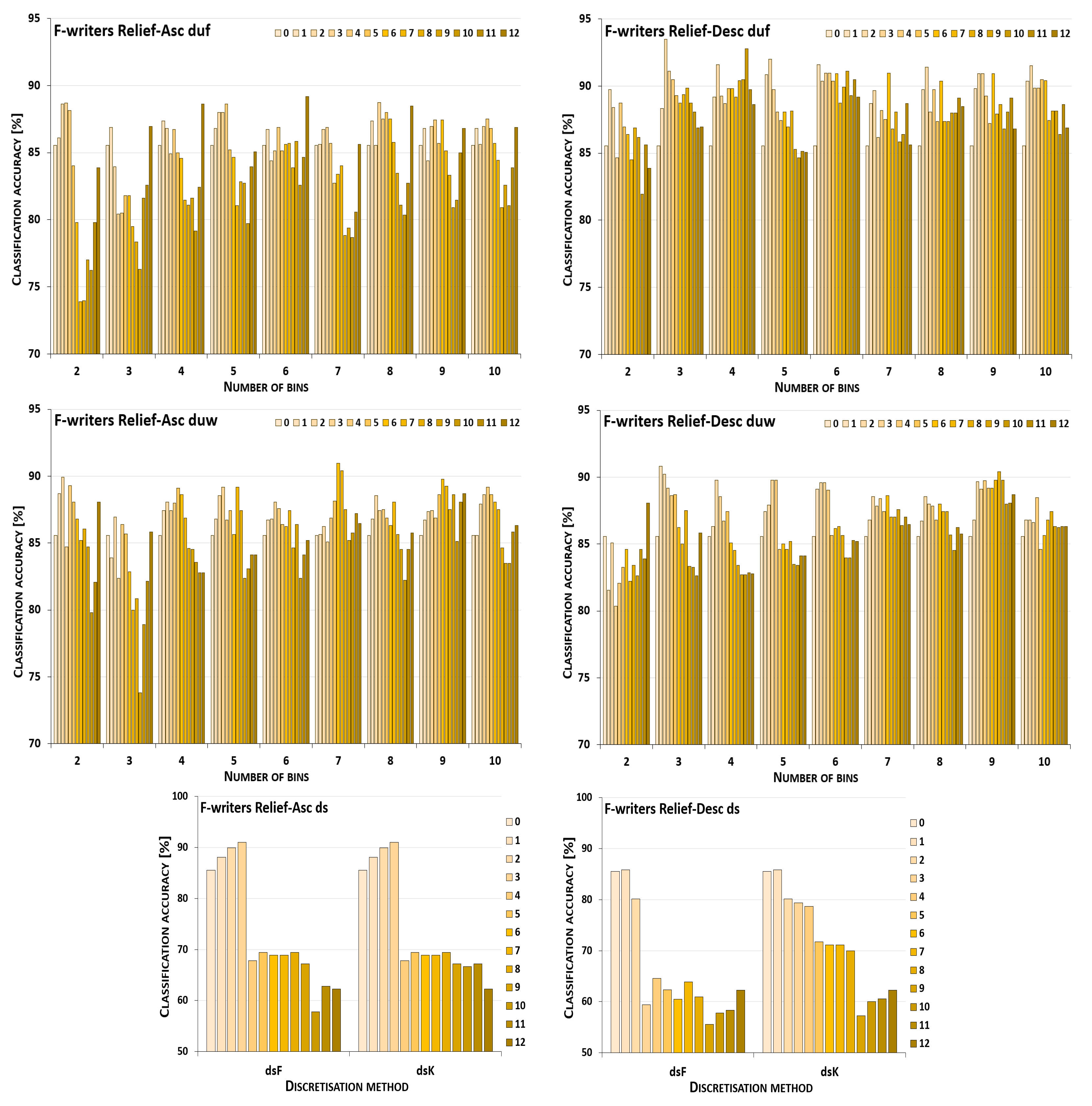
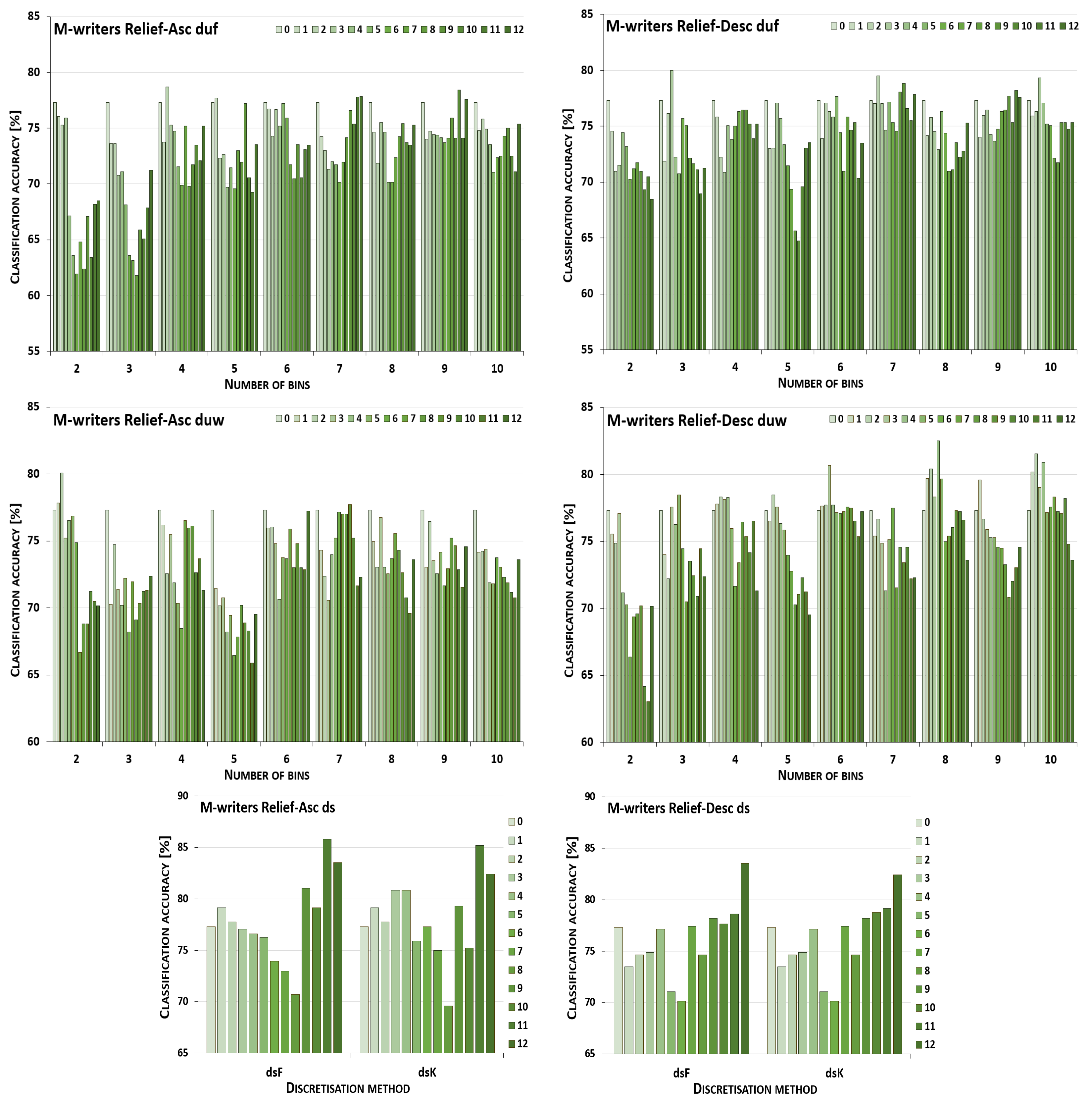
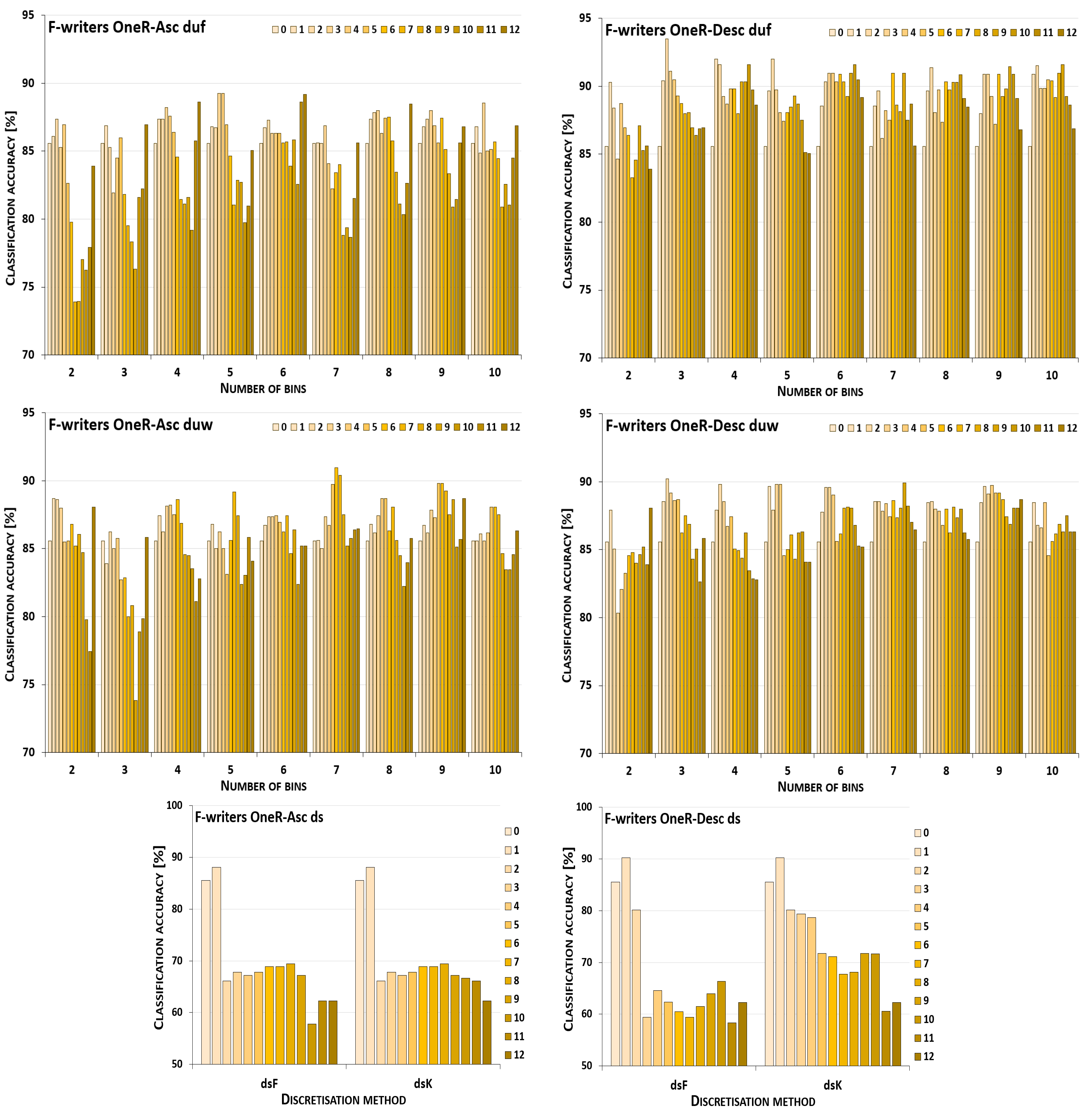
5. Results and Their Discussion
5.1. Reference Points
5.2. Performance Trends
5.3. Summary of Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Han, J.; Kamber, M.; Pei, J. Data Mining: Concepts and Techniques; Morgan Kaufmann: San Francisco, CA, USA, 2011. [Google Scholar]
- Cios, K.J.; Pedrycz, W.; Świniarski, R.W.; Kurgan, L. Data Mining. A Knowledge Discovery Approach; Springer: New York, NY, USA, 2007. [Google Scholar]
- Witten, I.; Frank, E.; Hall, M. Data Mining. Practical Machine Learning Tools and Techniques, 3rd ed.; Morgan Kaufmann: San Francisco, CA, USA, 2011. [Google Scholar]
- Guyon, I.; Elisseeff, A. An Introduction to Variable and Feature Selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Guyon, I.; Gunn, S.; Nikravesh, M.; Zadeh, L. (Eds.) Feature Extraction: Foundations and Applications; Studies in Fuzziness and Soft Computing; Physica-Verlag, Springer: Heidelberg, Germany, 2006; Volume 207. [Google Scholar]
- Liu, H.; Motoda, H. Computational Methods of Feature Selection; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Stańczyk, U. Pruning Decision Rules by Reduct-Based Weighting and Ranking of Features. Entropy 2022, 24, 1602. [Google Scholar] [CrossRef] [PubMed]
- Fernández, A.; García, S.; Galar, M.; Prati, R.C.; Krawczyk, B.; Herrera, F. Data Level Preprocessing Methods. In Learning from Imbalanced Data Sets; Springer International Publishing: Cham, Switzerland, 2018; pp. 79–121. [Google Scholar]
- Kotsiantis, S.; Kanellopoulos, D. Discretization Techniques: A recent survey. Int. Trans. Comput. Sci. Eng. 2006, 1, 47–58. [Google Scholar]
- Kliegr, T.; Izquierdo, E. QCBA: Improving rule classifiers learned from quantitative data by recovering information lost by discretisation. Appl. Intell. 2023, 53, 20797–20827. [Google Scholar] [CrossRef]
- Yang, Y.; Webb, G.I.; Wu, X. Discretization Methods. In Data Mining and Knowledge Discovery Handbook; Maimon, O., Rokach, L., Eds.; Springer: Boston, MA, USA, 2005; pp. 113–130. [Google Scholar]
- Dougherty, J.; Kohavi, R.; Sahami, M. Supervised and Unsupervised Discretization of Continuous Features. In Proceedings of the Machine Learning: Proceedings of the 12th International Conference; Morgan Kaufmann: San Francisco, CA, USA, 1995; pp. 194–202. [Google Scholar]
- Dash, R.; Paramguru, R.L.; Dash, R. Comparative analysis of supervised and unsupervised discretization techniques. Int. J. Adv. Sci. Technol. 2011, 2, 29–37. [Google Scholar]
- Blum, A.L.; Langley, P. Selection of relevant features and examples in machine learning. Artif. Intell. 1997, 97, 245–271. [Google Scholar] [CrossRef]
- Koppel, M.; Schler, J.; Argamon, S. Computational Methods in Authorship Attribution. J. Am. Soc. Inf. Sci. Technol. 2009, 60, 9–26. [Google Scholar] [CrossRef]
- Zhao, Y.; Zobel, J. Searching with Style: Authorship Attribution in Classic Literature. In Proceedings of the Thirtieth Australasian Conference on Computer Science—Volume 62, ACSC ’07, Darlinghurst, Australia, 30 January 2007; pp. 59–68. [Google Scholar]
- Stańczyk, U.; Zielosko, B. Data irregularities in discretisation of test sets used for evaluation of classification systems: A case study on authorship attribution. Bull. Pol. Acad. Sci. Tech. Sci. 2021, 69, 1–12. [Google Scholar] [CrossRef]
- Das, S.; Datta, S.; Chaudhuri, B.B. Handling data irregularities in classification: Foundations, trends, and future challenges. Pattern Recognit. 2018, 81, 674–693. [Google Scholar] [CrossRef]
- Baron, G.; Stańczyk, U. Standard vs. non-standard cross-validation: Evaluation of performance in a space with structured distribution of datapoints. In Knowledge-Based and Intelligent Information & Engineering Systems, Proceedings of the 25th International Conference KES-2021, Szczecin, Poland, 8–10 September 2021; Procedia Computer Science; Wątróbski, J., Salabun, W., Toro, C., Zanni-Merk, C., Howlett, R.J., Jain, L.C., Eds.; Elsevier: Amsterdam, The Netherlands, 2021; Volume 192, pp. 1245–1254. [Google Scholar]
- Toulabinejad, E.; Mirsafaei, M.; Basiri, A. Supervised discretization of continuous-valued attributes for classification using RACER algorithm. Expert Syst. Appl. 2024, 244, 121203. [Google Scholar] [CrossRef]
- Huan, L.; Farhad, H.; Lim, T.; Manoranjan, D. Discretization: An Enabling Technique. Data Min. Knowl. Discov. 2002, 6, 393–423. [Google Scholar]
- Peng, L.; Qing, W.; Gu, Y. Study on Comparison of Discretization Methods. In Proceedings of the 2009 International Conference on Artificial Intelligence and Computational Intelligence, Shanghai, China, 7–8 November 2009; Volume 4, pp. 380–384. [Google Scholar]
- Islam, M.A.; Uddin, M.A.; Aryal, S.; Stea, G. An ensemble learning approach for anomaly detection in credit card data with imbalanced and overlapped classes. J. Inf. Secur. Appl. 2023, 78, 103618. [Google Scholar] [CrossRef]
- García, S.; Luengo, J.; Sáez, J.A.; López, V.; Herrera, F. A Survey of Discretization Techniques: Taxonomy and Empirical Analysis in Supervised Learning. IEEE Trans. Knowl. Data Eng. 2013, 25, 734–750. [Google Scholar] [CrossRef]
- de Sá, C.R.; Soares, C.; Knobbe, A. Entropy-based discretization methods for ranking data. Inf. Sci. 2016, 329, 921–936. [Google Scholar] [CrossRef]
- Stańczyk, U.; Zielosko, B.; Baron, G. Discretisation of conditions in decision rules induced for continuous data. PLoS ONE 2020, 15, e0231788. [Google Scholar] [CrossRef] [PubMed]
- Fayyad, U.M.; Irani, K.B. Multi-interval discretization of continuousvalued attributes for classification learning. In Proceedings of the 13th International Joint Conference on Articial Intelligence, Chambéry, France, 28 August–3 September 1993; Morgan Kaufmann Publishers: San Francisco, CA, USA, 1993; Volume 2, pp. 1022–1027. [Google Scholar]
- Kononenko, I.; Kukar, M. Data Preprocessing. In Machine Learning and Data Mining; Kononenko, I., Kukar, M., Eds.; Woodhead Publishing: Cambridge, UK, 2007; Chapter 7; pp. 181–211. [Google Scholar]
- Grzymala-Busse, J.W. Discretization Based on Entropy and Multiple Scanning. Entropy 2013, 15, 1486–1502. [Google Scholar] [CrossRef]
- Rissanen, J. Modeling by shortest data description. Automatica 1978, 14, 465–471. [Google Scholar] [CrossRef]
- Ross Quinlan, J.; Rivest, R.L. Inferring decision trees using the minimum description length principle. Inf. Comput. 1989, 80, 227–248. [Google Scholar] [CrossRef]
- Hall, M.A. Correlation-Based Feature Subset Selection for Machine Learning. Ph.D. Thesis, Department of Computer Science, University of Waikato, Hamilton, New Zealand, 1998. [Google Scholar]
- Kohavi, R.; John, G.H. Wrappers for feature subset selection. Artif. Intell. 1997, 97, 273–324. [Google Scholar] [CrossRef]
- Mansoori, E. Using statistical measures for feature ranking. Int. J. Pattern Recognit. Artif. Intell. 2013, 27, 1350003. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Saha, P.; Patikar, S.; Neogy, S. A Correlation–Sequential Forward Selection Based Feature Selection Method for Healthcare Data Analysis. In Proceedings of the 2020 IEEE International Conference on Computing, Power and Communication Technologies (GUCON), Greater Noida, India, 2–4 October 2020; pp. 69–72. [Google Scholar]
- Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I. The WEKA Data Mining Software: An Update. SIGKDD Explor. 2009, 11, 10–18. [Google Scholar] [CrossRef]
- Kononenko, I. Estimating attributes:Analysis and extensions of RELIEF. In Proceedings of the Machine Learning: ECML-94; LNCS; Bergadano, F., De Raedt, L., Eds.; Springer Verlag: Berlin, Germany, 1994; Volume 784, pp. 171–182. [Google Scholar]
- Sun, Y.; Wu, D. A RELIEF Based Feature Extraction Algorithm. In Proceedings of the SIAM International Conference on Data Mining, Atlanta, GA, USA, 24–26 April 2008; pp. 188–195. [Google Scholar]
- Holte, R. Very simple classification rules perform well on most commonly used datasets. Mach. Learn. 1993, 11, 63–91. [Google Scholar] [CrossRef]
- Ali, S.; Smith, K.A. On learning algorithm selection for classification. Appl. Soft Comput. 2006, 6, 119–138. [Google Scholar] [CrossRef]
- Friedman, N.; Geiger, D.; Goldszmidt, M. Bayesian Network Classifiers. Mach. Learn. 1997, 29, 131–163. [Google Scholar] [CrossRef]
- Domingos, P.; Pazzani, M. On the Optimality of the Simple Bayesian Classifier under Zero-One Loss. Mach. Learn. 1997, 29, 103–130. [Google Scholar] [CrossRef]
- Quinlan, J.R. C4.5: Programs for Machine Learning; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1993. [Google Scholar]
- Moshkov, M.; Zielosko, B.; Tetteh, E.T. Selected Data Mining Tools for Data Analysis in Distributed Environment. Entropy 2022, 24, 1401. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Xiao, H.; Gao, R.; Zhang, H.; Wang, Y. K-nearest neighbors rule combining prototype selection and local feature weighting for classification. Knowl.-Based Syst. 2022, 243, 108451. [Google Scholar] [CrossRef]
- Zhao, Y.; Zobel, J. Effective and Scalable Authorship Attribution Using Function Words. In Proceedings of the Information Retrieval Technology; Lee, G.G., Yamada, A., Meng, H., Myaeng, S.H., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 174–189. [Google Scholar]
- Rybicki, J.; Eder, M.; Hoover, D. Computational stylistics and text analysis. In Doing Digital Humanities: Practice, Training, Research, 1st ed.; Crompton, C., Lane, R., Siemens, R., Eds.; Routledge: London, UK, 2016; pp. 123–144. [Google Scholar]
- Stamatatos, E. A Survey of Modern Authorship Attribution Methods. J. Am. Soc. Inf. Sci. Technol. 2009, 60, 538–556. [Google Scholar] [CrossRef]
- Škorić, M.; Stanković, R.; Ikonić Nešić, M.; Byszuk, J.; Eder, M. Parallel Stylometric Document Embeddings with Deep Learning Based Language Models in Literary Authorship Attribution. Mathematics 2022, 10, 838. [Google Scholar] [CrossRef]
- Eder, M.; Górski, R.L. Stylistic Fingerprints, POS-tags, and Inflected Languages: A Case Study in Polish. J. Quant. Linguist. 2022, 30, 86–103. [Google Scholar] [CrossRef]
- Rybicki, J. Vive la différence: Tracing the (authorial) gender signal by multivariate analysis of word frequencies. Digit. Scholarsh. Humanit. 2016, 31, 746–761. [Google Scholar] [CrossRef]
- Baron, G.; Harężlak, K. On Approaches to Discretization of Datasets Used for Evaluation of Decision Systems. In Intelligent Decision Technologies 2016: Proceedings of the 8th KES International Conference on Intelligent Decision Technologies (KES-IDT 2016)—Part II; Czarnowski, I., Caballero, M.A., Howlett, J.R., Jain, C.L., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 149–159. [Google Scholar]



| Rank | F-Writers | M-Writers | |||
|---|---|---|---|---|---|
| Relief | OneR | Relief | OneR | ||
| 1 | on | to | by | by | |
| 2 | to | on | if | or | |
| 3 | of | of | so | in | |
| 4 | as | as | or | if | |
| 5 | by | by | in | at | |
| 6 | if | if | as | so | |
| 7 | or | in | at | as | |
| 8 | up | up | on | on | |
| 9 | at | so | no | no | |
| 10 | in | or | of | to | |
| 11 | so | at | up | of | |
| 12 | no | no | to | up | |
| Domain | F-Writers | M-Writers | Domain | F-Writers | M-Writers | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NB | J48 | k-NN | NB | J48 | k-NN | NB | J48 | k-NN | NB | J48 | k-NN | ||||
| Cont. | 93.33 | 89.79 | 85.56 | 84.03 | 75.63 | 77.29 | |||||||||
| dsF | 50.00 | 87.78 | 62.22 | 69.44 | 80.76 | 83.54 | dsK | 62.22 | 93.40 | 62.22 | 68.89 | 80.76 | 82.43 | ||
| duf02 | 91.18 | 91.18 | 83.89 | 75.35 | 73.82 | 68.47 | duw02 | 87.01 | 85.35 | 88.06 | 73.82 | 72.71 | 70.14 | ||
| duf03 | 92.85 | 85.63 | 86.94 | 75.69 | 79.72 | 71.25 | duw03 | 89.38 | 83.68 | 85.83 | 78.68 | 77.29 | 72.36 | ||
| duf04 | 93.40 | 86.46 | 88.61 | 81.60 | 69.31 | 75.21 | duw04 | 91.67 | 86.94 | 82.78 | 80.63 | 79.24 | 71.32 | ||
| duf05 | 92.85 | 86.18 | 85.07 | 81.11 | 78.96 | 73.54 | duw05 | 90.56 | 80.42 | 84.10 | 79.38 | 75.76 | 69.51 | ||
| duf06 | 94.10 | 88.19 | 89.17 | 80.35 | 74.79 | 73.47 | duw06 | 92.22 | 85.69 | 85.21 | 82.22 | 75.21 | 77.22 | ||
| duf07 | 95.76 | 81.74 | 85.63 | 80.42 | 78.75 | 77.85 | duw07 | 91.11 | 89.65 | 86.46 | 81.04 | 71.94 | 72.29 | ||
| duf08 | 92.29 | 88.19 | 88.47 | 80.49 | 77.92 | 75.28 | duw08 | 91.67 | 90.97 | 85.76 | 77.64 | 75.42 | 73.61 | ||
| duf09 | 94.58 | 88.26 | 86.81 | 80.42 | 79.79 | 77.57 | duw09 | 90.56 | 90.35 | 88.68 | 81.53 | 76.46 | 74.58 | ||
| duf10 | 93.47 | 87.15 | 86.88 | 79.86 | 80.90 | 75.35 | duw10 | 91.67 | 87.01 | 86.32 | 80.00 | 76.25 | 73.61 | ||
| F-Writers | M-Writers | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ascending | Descending | Ascending | Descending | |||||||||
| Avg. ± St.dev. | Min | Max | Avg. ± St.dev. | Min | Max | Avg. ± St.dev. | Min | Max | Avg. ± St.dev. | Min | Max | |
| Domain | Relief ranking | |||||||||||
| dsF | 80.38 ± 12.94 | 56.18 | 95.14 | 60.18 ± 14.52 | 50.00 | 88.61 | 83.74 ± 1.79 | 81.53 | 87.08 | 76.60 ± 4.13 | 72.29 | 82.85 |
| dsK | 83.67 ± 07.50 | 74.17 | 95.14 | 78.57 ± 11.70 | 61.11 | 90.56 | 83.15 ± 1.29 | 81.32 | 84.79 | 75.96 ± 4.71 | 70.83 | 82.85 |
| duf | 94.07 ± 00.19 | 92.71 | 95.76 | 93.00 ± 00.49 | 89.38 | 95.21 | 82.73 ± 1.80 | 77.43 | 85.21 | 80.95 ± 1.84 | 73.13 | 85.76 |
| duf02 | 94.58 ± 00.58 | 93.89 | 95.76 | 90.16 ± 00.60 | 89.38 | 91.11 | 81.98 ± 2.33 | 77.43 | 84.51 | 77.14 ± 3.64 | 73.13 | 83.54 |
| duf03 | 94.35 ± 00.50 | 93.89 | 95.21 | 93.20 ± 00.98 | 91.67 | 94.58 | 82.64 ± 1.49 | 79.93 | 84.03 | 79.07 ± 3.28 | 74.03 | 83.40 |
| duf04 | 94.34 ± 00.63 | 93.89 | 95.76 | 93.16 ± 00.81 | 92.29 | 94.51 | 83.13 ± 2.12 | 79.93 | 85.21 | 81.76 ± 1.47 | 79.79 | 84.65 |
| duf05 | 93.67 ± 00.40 | 92.71 | 93.89 | 92.34 ± 01.00 | 90.49 | 93.96 | 82.68 ± 1.93 | 79.24 | 84.65 | 82.96 ± 1.69 | 80.56 | 85.21 |
| duf06 | 93.95 ± 00.32 | 93.33 | 94.51 | 93.54 ± 00.47 | 92.85 | 94.51 | 82.80 ± 2.00 | 79.38 | 85.21 | 80.90 ± 1.22 | 79.79 | 83.40 |
| duf07 | 94.12 ± 00.49 | 93.33 | 95.14 | 94.53 ± 00.44 | 93.33 | 95.21 | 82.69 ± 1.85 | 79.93 | 85.14 | 81.52 ± 1.61 | 79.24 | 84.65 |
| duf08 | 93.73 ± 00.38 | 92.71 | 93.89 | 93.11 ± 00.94 | 91.74 | 95.07 | 82.60 ± 1.93 | 79.31 | 85.21 | 81.87 ± 1.69 | 80.35 | 84.58 |
| duf09 | 93.90 ± 00.27 | 93.33 | 94.51 | 94.00 ± 00.57 | 93.33 | 95.14 | 82.73 ± 1.92 | 79.86 | 85.21 | 82.14 ± 1.43 | 80.42 | 84.58 |
| duf10 | 94.00 ± 00.38 | 93.89 | 95.14 | 93.01 ± 00.82 | 92.29 | 94.51 | 83.33 ± 1.44 | 80.49 | 85.21 | 81.18 ± 1.88 | 79.24 | 85.76 |
| duw | 93.15 ± 00.61 | 90.69 | 95.76 | 91.12 ± 00.97 | 85.21 | 93.89 | 83.30 ± 1.11 | 79.86 | 86.46 | 81.01 ± 0.92 | 76.88 | 84.17 |
| duw02 | 93.88 ± 00.92 | 92.22 | 95.76 | 88.17 ± 02.26 | 85.21 | 92.22 | 83.67 ± 0.79 | 82.71 | 85.14 | 78.87 ± 1.19 | 77.29 | 80.76 |
| duw03 | 92.99 ± 01.05 | 91.04 | 94.51 | 89.64 ± 01.22 | 88.13 | 92.08 | 83.42 ± 2.03 | 79.93 | 86.46 | 79.65 ± 1.89 | 76.88 | 82.85 |
| duw04 | 93.24 ± 00.66 | 91.67 | 94.03 | 91.46 ± 00.84 | 90.56 | 93.33 | 82.66 ± 1.26 | 80.00 | 84.51 | 81.75 ± 1.09 | 80.00 | 83.96 |
| duw05 | 92.84 ± 00.94 | 90.69 | 93.89 | 91.18 ± 01.60 | 89.38 | 93.89 | 83.24 ± 2.05 | 79.86 | 85.28 | 81.11 ± 1.00 | 79.86 | 83.47 |
| duw06 | 93.25 ± 00.54 | 91.74 | 93.96 | 92.17 ± 00.87 | 91.04 | 93.33 | 83.48 ± 1.09 | 81.04 | 84.58 | 81.22 ± 1.32 | 79.44 | 84.10 |
| duw07 | 93.05 ± 00.86 | 91.11 | 94.03 | 92.01 ± 00.52 | 91.53 | 92.78 | 83.40 ± 1.03 | 80.49 | 84.51 | 82.59 ± 0.90 | 81.11 | 84.17 |
| duw08 | 93.08 ± 00.46 | 92.22 | 93.33 | 92.08 ± 00.87 | 91.04 | 93.89 | 82.38 ± 1.26 | 79.93 | 83.96 | 80.64 ± 1.47 | 78.75 | 82.85 |
| duw09 | 92.89 ± 00.59 | 91.67 | 93.89 | 91.28 ± 01.28 | 89.93 | 93.26 | 83.43 ± 1.10 | 81.53 | 84.58 | 81.72 ± 0.83 | 80.49 | 83.47 |
| duw10 | 93.09 ± 00.67 | 91.11 | 93.33 | 92.07 ± 01.06 | 91.11 | 93.89 | 83.99 ± 1.21 | 81.67 | 85.76 | 81.55 ± 1.00 | 79.38 | 82.85 |
| OneR ranking | ||||||||||||
| dsF | 78.54 ± 12.29 | 52.22 | 93.33 | 60.61 ± 15.34 | 50.00 | 92.78 | 84.32 ± 1.58 | 81.46 | 87.08 | 76.06 ± 3.87 | 71.67 | 83.33 |
| dsK | 81.07 ± 08.04 | 61.88 | 93.33 | 82.92 ± 08.32 | 61.11 | 92.78 | 83.59 ± 0.94 | 81.94 | 84.72 | 75.56 ± 4.49 | 68.33 | 83.33 |
| duf | 93.88 ± 00.19 | 92.22 | 95.76 | 93.14 ± 00.51 | 89.38 | 95.21 | 83.09 ± 1.60 | 79.24 | 85.28 | 80.81 ± 1.73 | 73.06 | 85.76 |
| duf02 | 94.42 ± 00.73 | 93.33 | 95.76 | 90.33 ± 01.12 | 89.38 | 93.33 | 82.47 ± 1.64 | 79.65 | 84.51 | 77.28 ± 3.84 | 73.06 | 83.54 |
| duf03 | 94.02 ± 00.44 | 93.47 | 95.14 | 93.54 ± 00.73 | 92.22 | 94.58 | 82.78 ± 1.67 | 79.93 | 84.65 | 78.00 ± 3.24 | 74.03 | 83.40 |
| duf04 | 94.02 ± 00.45 | 93.40 | 95.14 | 93.43 ± 00.79 | 92.29 | 94.51 | 83.54 ± 1.68 | 80.42 | 85.28 | 81.76 ± 1.37 | 79.79 | 84.65 |
| duf05 | 93.52 ± 00.58 | 92.22 | 93.89 | 92.23 ± 01.26 | 90.49 | 93.96 | 83.25 ± 1.92 | 79.24 | 84.72 | 82.80 ± 1.46 | 81.04 | 84.58 |
| duf06 | 93.90 ± 00.04 | 93.89 | 94.03 | 93.50 ± 00.73 | 92.29 | 94.51 | 83.43 ± 1.44 | 80.42 | 85.21 | 81.22 ± 1.36 | 79.79 | 83.47 |
| duf07 | 93.91 ± 00.27 | 93.33 | 94.51 | 94.80 ± 00.44 | 93.89 | 95.21 | 82.68 ± 1.80 | 79.93 | 85.14 | 81.35 ± 1.64 | 79.24 | 84.65 |
| duf08 | 93.63 ± 00.59 | 92.22 | 93.89 | 93.15 ± 01.19 | 91.67 | 95.07 | 83.14 ± 1.35 | 80.49 | 85.21 | 81.70 ± 1.17 | 80.35 | 83.96 |
| duf09 | 93.74 ± 00.34 | 92.85 | 93.89 | 94.01 ± 00.55 | 93.47 | 95.14 | 83.06 ± 1.95 | 79.86 | 85.21 | 81.76 ± 1.22 | 80.42 | 84.58 |
| duf10 | 93.79 ± 00.31 | 92.85 | 93.89 | 93.29 ± 00.70 | 92.29 | 94.51 | 83.42 ± 1.57 | 80.49 | 85.21 | 81.44 ± 1.83 | 79.24 | 85.76 |
| duw | 93.11 ± 00.81 | 89.44 | 95.76 | 91.42 ± 01.04 | 86.39 | 94.51 | 83.05 ± 1.19 | 79.86 | 86.46 | 81.11 ± 1.03 | 74.38 | 84.17 |
| duw02 | 93.51 ± 01.52 | 89.44 | 95.76 | 88.83 ± 02.21 | 86.39 | 93.89 | 83.32 ± 1.34 | 80.90 | 85.14 | 78.48 ± 1.90 | 74.38 | 80.63 |
| duw03 | 92.94 ± 01.11 | 90.63 | 93.89 | 90.25 ± 01.30 | 88.13 | 92.78 | 83.91 ± 1.71 | 79.93 | 86.46 | 80.16 ± 1.75 | 77.50 | 82.85 |
| duw04 | 93.39 ± 00.90 | 91.04 | 94.03 | 91.20 ± 01.14 | 89.93 | 93.89 | 82.18 ± 1.57 | 80.35 | 84.51 | 82.17 ± 1.18 | 81.18 | 84.10 |
| duw05 | 92.82 ± 00.99 | 90.49 | 93.89 | 91.69 ± 01.54 | 89.38 | 93.89 | 83.15 ± 1.81 | 79.86 | 85.28 | 81.25 ± 1.60 | 78.75 | 83.47 |
| duw06 | 93.24 ± 00.58 | 91.60 | 93.96 | 92.27 ± 00.83 | 91.04 | 93.33 | 83.37 ± 0.88 | 81.04 | 84.03 | 81.37 ± 0.84 | 80.00 | 82.36 |
| duw07 | 93.10 ± 00.74 | 91.67 | 94.03 | 92.49 ± 00.63 | 91.67 | 93.89 | 83.30 ± 1.26 | 80.49 | 84.65 | 82.27 ± 1.04 | 81.04 | 84.17 |
| duw08 | 93.08 ± 00.46 | 92.22 | 93.33 | 92.17 ± 00.92 | 91.04 | 93.89 | 81.79 ± 1.86 | 79.86 | 84.58 | 80.56 ± 1.75 | 77.64 | 83.47 |
| duw09 | 92.97 ± 00.85 | 91.04 | 93.89 | 91.54 ± 01.48 | 89.93 | 94.51 | 83.11 ± 1.26 | 81.53 | 84.58 | 81.81 ± 0.86 | 80.56 | 83.47 |
| duw10 | 92.93 ± 00.90 | 91.11 | 93.33 | 92.32 ± 00.96 | 91.11 | 93.89 | 83.30 ± 1.18 | 81.60 | 84.58 | 81.94 ± 1.04 | 80.00 | 83.47 |
| F-Writers | M-Writers | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ascending | Descending | Ascending | Descending | |||||||||
| Avg. ± St.dev. | Min | Max | Avg. ± St.dev. | Min | Max | Avg. ± St.dev. | Min | Max | Avg. ± St.dev. | Min | Max | |
| Domain | Relief ranking | |||||||||||
| dsF | 91.45 ± 1.57 | 89.79 | 94.65 | 74.36 ± 19.08 | 50.00 | 90.28 | 77.53 ± 2.36 | 72.01 | 79.51 | 78.59 ± 1.64 | 76.32 | 80.76 |
| dsK | 91.16 ± 1.17 | 89.79 | 92.78 | 92.41 ± 01.93 | 87.50 | 93.40 | 76.76 ± 2.69 | 71.88 | 80.14 | 78.59 ± 1.64 | 76.32 | 80.76 |
| duf | 89.95 ± 0.92 | 82.64 | 93.33 | 87.54 ± 00.73 | 82.85 | 92.22 | 76.37 ± 0.71 | 70.83 | 80.90 | 74.77 ± 0.81 | 66.67 | 82.08 |
| duf02 | 90.55 ± 1.77 | 85.69 | 92.78 | 88.43 ± 02.42 | 84.79 | 91.81 | 73.64 ± 1.84 | 72.01 | 77.85 | 71.87 ± 3.92 | 66.74 | 77.92 |
| duf03 | 90.24 ± 1.48 | 86.81 | 93.33 | 85.73 ± 00.58 | 85.28 | 87.43 | 76.52 ± 1.31 | 74.44 | 78.89 | 77.54 ± 2.48 | 72.15 | 81.46 |
| duf04 | 90.38 ± 0.82 | 89.24 | 91.53 | 89.36 ± 02.56 | 86.46 | 92.22 | 77.07 ± 1.29 | 75.63 | 79.58 | 72.97 ± 4.56 | 66.67 | 79.51 |
| duf05 | 89.35 ± 2.36 | 83.47 | 92.78 | 84.68 ± 01.01 | 83.75 | 87.01 | 78.43 ± 1.54 | 75.63 | 80.14 | 71.27 ± 0.82 | 69.86 | 72.64 |
| duf06 | 88.77 ± 2.75 | 82.64 | 90.42 | 90.75 ± 01.15 | 88.19 | 91.88 | 75.13 ± 1.99 | 70.83 | 77.92 | 75.00 ± 1.57 | 72.22 | 77.43 |
| duf07 | 90.34 ± 0.76 | 89.79 | 92.15 | 84.36 ± 02.42 | 82.85 | 90.49 | 75.64 ± 0.74 | 74.58 | 76.88 | 78.05 ± 2.14 | 73.26 | 80.42 |
| duf08 | 90.32 ± 0.60 | 89.79 | 91.53 | 88.42 ± 00.67 | 87.64 | 90.00 | 77.54 ± 2.57 | 73.89 | 80.90 | 76.84 ± 1.90 | 72.64 | 78.47 |
| duf09 | 90.13 ± 0.41 | 89.79 | 90.97 | 88.09 ± 00.57 | 86.53 | 88.33 | 77.51 ± 1.01 | 75.63 | 78.75 | 74.43 ± 2.79 | 69.65 | 79.79 |
| duf10 | 89.48 ± 0.91 | 86.88 | 90.35 | 88.04 ± 01.27 | 87.15 | 91.81 | 75.81 ± 1.13 | 72.92 | 77.36 | 74.94 ± 4.14 | 69.38 | 82.08 |
| duw | 89.83 ± 1.22 | 83.68 | 92.85 | 87.63 ± 00.83 | 80.35 | 94.51 | 76.73 ± 1.13 | 68.13 | 81.32 | 74.42 ± 0.98 | 63.19 | 79.86 |
| duw02 | 90.73 ± 1.19 | 88.61 | 92.22 | 84.22 ± 03.09 | 80.35 | 89.38 | 76.67 ± 1.57 | 73.68 | 78.96 | 69.15 ± 3.70 | 63.19 | 74.51 |
| duw03 | 89.79 ± 2.30 | 83.68 | 92.78 | 87.51 ± 01.89 | 83.68 | 89.93 | 76.87 ± 2.02 | 72.43 | 80.14 | 73.81 ± 2.81 | 68.82 | 77.29 |
| duw04 | 90.61 ± 1.20 | 88.54 | 92.22 | 86.81 ± 01.81 | 83.26 | 90.97 | 77.90 ± 2.09 | 74.10 | 81.32 | 76.50 ± 2.45 | 71.11 | 79.86 |
| duw05 | 89.83 ± 2.27 | 85.49 | 92.22 | 85.07 ± 02.45 | 80.42 | 89.93 | 76.84 ± 2.00 | 74.79 | 80.69 | 74.96 ± 1.37 | 72.78 | 77.43 |
| duw06 | 89.03 ± 1.19 | 86.25 | 89.79 | 86.12 ± 01.34 | 85.00 | 89.93 | 74.68 ± 1.75 | 72.50 | 76.88 | 74.05 ± 1.71 | 71.60 | 76.39 |
| duw07 | 89.98 ± 1.55 | 85.90 | 92.15 | 89.46 ± 00.49 | 88.06 | 89.65 | 76.87 ± 1.65 | 74.58 | 79.10 | 74.44 ± 1.67 | 70.00 | 76.04 |
| duw08 | 89.44 ± 1.86 | 84.51 | 90.42 | 90.81 ± 01.73 | 86.94 | 92.22 | 76.69 ± 3.66 | 68.13 | 79.51 | 75.43 ± 1.64 | 72.50 | 79.44 |
| duw09 | 89.20 ± 1.56 | 85.00 | 90.42 | 91.16 ± 01.45 | 90.35 | 94.51 | 77.15 ± 1.56 | 75.35 | 79.58 | 74.48 ± 2.18 | 71.18 | 77.43 |
| duw10 | 89.82 ± 1.79 | 85.14 | 92.85 | 87.56 ± 01.44 | 87.01 | 91.74 | 76.86 ± 1.63 | 74.93 | 78.96 | 76.98 ± 1.26 | 74.03 | 78.61 |
| OneR ranking | ||||||||||||
| dsF | 89.46 ± 6.83 | 69.17 | 92.78 | 63.62 ± 18.74 | 50.00 | 90.28 | 77.77 ± 1.71 | 74.38 | 79.51 | 78.52 ± 2.04 | 74.10 | 80.76 |
| dsK | 90.65 ± 3.01 | 82.29 | 92.78 | 91.98 ± 03.22 | 82.78 | 93.40 | 77.04 ± 1.52 | 74.24 | 79.51 | 78.52 ± 2.04 | 74.10 | 80.76 |
| duf | 89.91 ± 1.27 | 82.64 | 93.33 | 87.66 ± 01.01 | 82.85 | 92.22 | 76.57 ± 0.91 | 71.88 | 82.08 | 74.32 ± 0.60 | 66.67 | 81.46 |
| duf02 | 90.99 ± 0.85 | 89.79 | 92.78 | 89.00 ± 02.61 | 84.79 | 91.81 | 74.72 ± 2.14 | 71.88 | 78.40 | 71.71 ± 4.34 | 66.74 | 79.10 |
| duf03 | 90.13 ± 1.77 | 85.63 | 93.33 | 85.81 ± 00.58 | 85.28 | 87.43 | 77.47 ± 2.25 | 74.79 | 82.08 | 77.23 ± 1.73 | 74.51 | 81.46 |
| duf04 | 90.16 ± 1.68 | 85.63 | 91.53 | 89.36 ± 02.33 | 86.46 | 91.81 | 78.33 ± 1.90 | 76.60 | 81.94 | 71.95 ± 3.34 | 66.67 | 77.71 |
| duf05 | 89.89 ± 1.55 | 86.94 | 92.78 | 85.01 ± 02.18 | 83.75 | 90.97 | 78.02 ± 1.09 | 76.67 | 80.14 | 72.22 ± 2.02 | 70.00 | 76.18 |
| duf06 | 89.07 ± 2.61 | 82.64 | 90.42 | 89.73 ± 01.85 | 86.25 | 91.88 | 75.62 ± 1.54 | 73.54 | 77.92 | 74.20 ± 1.45 | 72.22 | 76.53 |
| duf07 | 89.88 ± 2.40 | 82.92 | 92.15 | 84.63 ± 02.82 | 82.85 | 92.22 | 75.60 ± 0.88 | 74.58 | 76.88 | 77.30 ± 2.67 | 73.26 | 80.42 |
| duf08 | 89.97 ± 1.12 | 87.08 | 91.53 | 88.83 ± 01.26 | 88.19 | 92.15 | 76.46 ± 1.55 | 73.89 | 78.54 | 76.58 ± 2.11 | 72.64 | 79.10 |
| duf09 | 89.85 ± 1.06 | 86.88 | 90.97 | 88.34 ± 00.87 | 86.53 | 90.42 | 77.66 ± 0.94 | 76.11 | 78.47 | 73.54 ± 2.57 | 69.65 | 77.50 |
| duf10 | 89.20 ± 1.34 | 86.25 | 90.35 | 88.22 ± 01.50 | 87.15 | 91.81 | 75.28 ± 1.21 | 72.92 | 77.36 | 74.14 ± 3.75 | 69.38 | 79.31 |
| duw | 90.09 ± 0.88 | 82.22 | 92.85 | 87.63 ± 01.31 | 80.35 | 94.51 | 77.18 ± 1.35 | 68.13 | 81.32 | 74.37 ± 0.65 | 63.89 | 79.79 |
| duw02 | 90.59 ± 1.72 | 87.01 | 92.22 | 84.68 ± 03.50 | 80.35 | 90.35 | 76.63 ± 3.25 | 70.69 | 79.72 | 68.74 ± 2.48 | 63.89 | 72.22 |
| duw03 | 90.73 ± 1.13 | 89.24 | 92.78 | 86.73 ± 02.35 | 83.06 | 89.17 | 78.39 ± 1.63 | 76.25 | 80.83 | 74.57 ± 2.52 | 68.82 | 77.36 |
| duw04 | 90.20 ± 2.26 | 84.58 | 92.22 | 87.45 ± 01.68 | 85.14 | 90.97 | 77.58 ± 2.41 | 73.26 | 81.32 | 76.20 ± 2.66 | 71.11 | 79.79 |
| duw05 | 90.64 ± 2.04 | 85.49 | 92.22 | 84.57 ± 03.80 | 80.42 | 92.22 | 78.11 ± 1.96 | 74.24 | 80.69 | 74.72 ± 1.56 | 72.78 | 77.99 |
| duw06 | 89.24 ± 0.78 | 87.92 | 90.35 | 85.84 ± 01.66 | 84.51 | 90.35 | 75.20 ± 1.79 | 72.01 | 77.85 | 74.59 ± 0.82 | 73.40 | 76.25 |
| duw07 | 90.39 ± 0.89 | 88.54 | 92.15 | 89.67 ± 00.30 | 89.10 | 90.42 | 76.13 ± 2.19 | 73.61 | 79.10 | 73.56 ± 2.33 | 70.28 | 76.04 |
| duw08 | 88.80 ± 2.75 | 82.22 | 90.42 | 91.07 ± 01.24 | 88.06 | 92.22 | 77.67 ± 3.27 | 68.13 | 79.51 | 75.66 ± 1.93 | 72.85 | 79.44 |
| duw09 | 89.75 ± 0.82 | 88.06 | 90.42 | 91.05 ± 01.55 | 89.79 | 94.51 | 77.36 ± 1.88 | 74.79 | 79.58 | 75.39 ± 1.97 | 73.06 | 78.26 |
| duw10 | 90.47 ± 1.08 | 89.79 | 92.85 | 87.59 ± 01.46 | 87.01 | 91.74 | 77.56 ± 1.39 | 74.93 | 79.51 | 75.94 ± 1.64 | 73.06 | 78.61 |
| F-Writers | M-Writers | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ascending | Descending | Ascending | Descending | |||||||||
| Avg. ± St.dev. | Min | Max | Avg. ± St.dev. | Min | Max | Avg. ± St.dev. | Min | Max | Avg. ± St.dev. | Min | Max | |
| Domain | Relief ranking | |||||||||||
| dsF | 72.85 ± 11.39 | 57.78 | 91.04 | 64.47 ± 09.61 | 55.56 | 85.83 | 77.32 ± 4.10 | 70.69 | 85.76 | 75.26 ± 2.86 | 70.14 | 78.61 |
| dsK | 74.06 ± 10.11 | 66.67 | 91.04 | 71.43 ± 09.23 | 57.22 | 85.83 | 77.83 ± 4.04 | 69.58 | 85.21 | 75.41 ± 3.04 | 70.14 | 79.17 |
| duf | 83.80 ± 02.53 | 73.89 | 88.75 | 88.79 ± 01.11 | 81.94 | 93.47 | 72.24 ± 1.74 | 61.81 | 78.68 | 74.12 ± 0.94 | 64.72 | 80.00 |
| duf02 | 81.48 ± 05.85 | 73.89 | 88.68 | 86.36 ± 02.20 | 81.94 | 89.72 | 67.80 ± 5.48 | 61.94 | 76.04 | 71.70 ± 1.69 | 69.31 | 74.58 |
| duf03 | 81.24 ± 02.80 | 76.32 | 86.88 | 89.49 ± 01.76 | 86.88 | 93.47 | 67.69 ± 4.17 | 61.81 | 73.61 | 73.24 ± 3.14 | 68.96 | 80.00 |
| duf04 | 83.74 ± 02.73 | 79.17 | 87.36 | 90.08 ± 01.20 | 88.68 | 92.78 | 73.28 ± 2.64 | 69.79 | 78.68 | 74.65 ± 1.80 | 70.90 | 76.46 |
| duf05 | 84.68 ± 02.96 | 79.72 | 88.61 | 87.84 ± 02.35 | 84.65 | 92.01 | 72.30 ± 2.85 | 69.24 | 77.71 | 71.45 ± 3.84 | 64.72 | 77.08 |
| duf06 | 85.14 ± 01.25 | 82.57 | 86.88 | 90.43 ± 00.84 | 88.75 | 91.60 | 74.13 ± 2.46 | 70.49 | 77.22 | 74.76 ± 2.31 | 70.35 | 77.64 |
| duf07 | 82.95 ± 03.16 | 78.68 | 86.88 | 87.90 ± 01.57 | 85.83 | 90.97 | 73.48 ± 2.37 | 70.14 | 77.78 | 76.75 ± 1.63 | 74.58 | 79.51 |
| duf08 | 85.28 ± 02.92 | 80.35 | 88.75 | 88.76 ± 01.38 | 87.36 | 91.39 | 73.28 ± 1.92 | 70.14 | 75.49 | 73.52 ± 1.73 | 70.97 | 76.32 |
| duf09 | 84.96 ± 02.28 | 80.90 | 87.43 | 89.04 ± 01.47 | 86.81 | 90.90 | 74.73 ± 1.35 | 73.68 | 78.40 | 75.74 ± 1.48 | 73.68 | 78.19 |
| duf10 | 84.75 ± 02.38 | 80.90 | 87.50 | 89.20 ± 01.56 | 86.39 | 91.53 | 73.45 ± 1.65 | 71.04 | 75.83 | 75.29 ± 2.09 | 71.74 | 79.31 |
| duw | 86.09 ± 01.75 | 73.82 | 90.97 | 86.47 ± 01.20 | 80.35 | 90.83 | 72.80 ± 1.06 | 65.90 | 80.07 | 75.25 ± 1.81 | 63.06 | 82.50 |
| duw02 | 85.94 ± 03.10 | 79.79 | 89.93 | 83.06 ± 01.45 | 80.35 | 85.07 | 73.40 ± 4.38 | 66.67 | 80.07 | 70.16 ± 4.49 | 63.06 | 77.08 |
| duw03 | 82.17 ± 03.79 | 73.82 | 86.94 | 86.86 ± 02.93 | 82.64 | 90.83 | 71.00 ± 1.72 | 68.19 | 74.72 | 74.07 ± 2.57 | 70.49 | 78.47 |
| duw04 | 86.45 ± 02.19 | 82.78 | 89.10 | 85.46 ± 02.49 | 82.71 | 89.79 | 73.62 ± 2.69 | 68.47 | 76.53 | 76.00 ± 2.19 | 71.67 | 78.33 |
| duw05 | 86.40 ± 02.36 | 82.36 | 89.17 | 85.93 ± 02.38 | 83.40 | 89.79 | 68.87 ± 1.75 | 65.90 | 71.46 | 74.21 ± 2.86 | 70.28 | 78.47 |
| duw06 | 86.07 ± 01.70 | 82.36 | 88.06 | 86.75 ± 02.18 | 83.96 | 89.58 | 74.03 ± 1.67 | 70.63 | 76.04 | 77.47 ± 1.27 | 75.35 | 80.69 |
| duw07 | 87.18 ± 01.99 | 85.07 | 90.97 | 87.51 ± 00.75 | 86.39 | 88.61 | 74.74 ± 2.43 | 70.56 | 77.71 | 74.29 ± 2.00 | 71.32 | 77.50 |
| duw08 | 86.22 ± 01.87 | 82.22 | 88.54 | 87.02 ± 01.18 | 84.51 | 88.54 | 73.35 ± 2.05 | 69.58 | 76.74 | 78.02 ± 2.33 | 75.00 | 82.50 |
| duw09 | 87.76 ± 01.30 | 85.14 | 89.79 | 89.06 ± 01.05 | 86.81 | 90.42 | 73.51 ± 1.50 | 71.53 | 76.46 | 74.63 ± 2.38 | 70.83 | 79.58 |
| duw10 | 86.62 ± 02.11 | 83.47 | 89.17 | 86.55 ± 00.98 | 84.58 | 88.47 | 72.67 ± 1.30 | 70.76 | 74.38 | 78.36 ± 1.95 | 74.79 | 81.53 |
| OneR ranking | ||||||||||||
| dsF | 68.31 ± 07.42 | 57.78 | 88.13 | 66.05 ± 10.03 | 58.33 | 90.28 | 76.89 ± 3.17 | 74.03 | 85.76 | 75.76 ± 3.74 | 67.01 | 81.25 |
| dsK | 69.48 ± 06.28 | 66.11 | 88.13 | 73.74 ± 07.95 | 60.56 | 90.28 | 77.92 ± 3.68 | 73.47 | 85.21 | 75.86 ± 3.80 | 67.01 | 81.25 |
| duf | 83.98 ± 02.64 | 73.89 | 89.24 | 89.22 ± 00.83 | 83.26 | 93.47 | 72.57 ± 1.70 | 61.04 | 79.38 | 73.65 ± 0.90 | 64.72 | 78.82 |
| duf02 | 80.65 ± 05.21 | 73.89 | 87.36 | 86.48 ± 02.08 | 83.26 | 90.28 | 68.53 ± 6.00 | 61.04 | 78.96 | 72.75 ± 3.46 | 66.18 | 77.50 |
| duf03 | 82.22 ± 03.29 | 76.32 | 86.88 | 89.07 ± 02.15 | 86.39 | 93.47 | 68.63 ± 2.72 | 63.47 | 72.15 | 70.54 ± 2.52 | 65.56 | 75.07 |
| duf04 | 84.60 ± 03.20 | 79.17 | 88.19 | 90.10 ± 01.26 | 87.99 | 92.01 | 73.51 ± 2.21 | 70.28 | 77.64 | 75.73 ± 1.24 | 72.78 | 77.01 |
| duf05 | 84.63 ± 03.38 | 79.72 | 89.24 | 88.55 ± 01.72 | 85.14 | 92.01 | 71.45 ± 1.48 | 69.24 | 74.44 | 71.43 ± 3.50 | 64.72 | 75.90 |
| duf06 | 85.93 ± 01.61 | 82.57 | 88.61 | 90.43 ± 00.87 | 88.54 | 91.60 | 74.37 ± 2.23 | 71.39 | 77.22 | 73.91 ± 2.00 | 70.97 | 77.15 |
| duf07 | 82.75 ± 02.87 | 78.68 | 86.88 | 88.63 ± 01.45 | 86.18 | 90.97 | 74.27 ± 2.57 | 71.32 | 79.38 | 75.96 ± 2.22 | 71.18 | 78.82 |
| duf08 | 85.25 ± 02.85 | 80.35 | 87.99 | 89.70 ± 01.17 | 87.36 | 91.39 | 73.74 ± 2.04 | 70.14 | 75.97 | 73.14 ± 1.65 | 70.69 | 75.76 |
| duf09 | 85.32 ± 02.43 | 80.90 | 87.99 | 89.79 ± 01.37 | 87.22 | 91.46 | 75.13 ± 1.70 | 73.13 | 77.78 | 74.76 ± 2.30 | 70.56 | 77.71 |
| duf10 | 84.50 ± 02.29 | 80.90 | 88.54 | 90.24 ± 00.98 | 88.61 | 91.60 | 73.50 ± 1.91 | 71.04 | 77.15 | 74.65 ± 2.07 | 71.74 | 78.19 |
| duw | 85.73 ± 01.68 | 73.82 | 90.97 | 86.98 ± 01.00 | 80.35 | 90.21 | 72.53 ± 1.56 | 64.65 | 77.29 | 74.61 ± 1.92 | 66.74 | 80.35 |
| duw02 | 85.12 ± 03.53 | 77.43 | 88.68 | 84.17 ± 01.91 | 80.35 | 87.92 | 72.60 ± 4.13 | 64.65 | 77.01 | 72.76 ± 3.76 | 67.71 | 77.22 |
| duw03 | 81.81 ± 03.64 | 73.82 | 86.25 | 87.08 ± 02.31 | 82.64 | 90.21 | 72.52 ± 1.60 | 70.21 | 75.14 | 72.96 ± 2.51 | 67.78 | 76.88 |
| duw04 | 86.07 ± 02.35 | 81.11 | 88.61 | 86.12 ± 02.19 | 82.85 | 89.79 | 73.04 ± 1.65 | 70.35 | 75.56 | 73.98 ± 2.52 | 69.17 | 77.78 |
| duw05 | 85.42 ± 02.04 | 82.36 | 89.17 | 86.71 ± 02.23 | 84.10 | 89.79 | 69.29 ± 2.09 | 65.90 | 74.17 | 72.58 ± 3.12 | 66.74 | 77.92 |
| duw06 | 86.19 ± 01.57 | 82.36 | 87.43 | 87.65 ± 01.50 | 85.28 | 89.58 | 74.10 ± 1.99 | 70.63 | 77.29 | 75.80 ± 2.56 | 69.51 | 77.64 |
| duw07 | 87.34 ± 02.12 | 85.00 | 90.97 | 88.18 ± 00.79 | 87.01 | 89.93 | 73.36 ± 1.81 | 70.56 | 75.83 | 74.19 ± 2.17 | 71.04 | 78.33 |
| duw08 | 86.22 ± 02.04 | 82.22 | 88.68 | 87.60 ± 00.82 | 86.25 | 88.54 | 72.92 ± 2.87 | 69.58 | 77.22 | 77.05 ± 1.74 | 74.38 | 79.72 |
| duw09 | 87.62 ± 01.61 | 85.14 | 89.79 | 88.58 ± 00.91 | 86.88 | 89.72 | 72.78 ± 1.73 | 71.11 | 75.90 | 74.53 ± 3.14 | 68.61 | 79.58 |
| duw10 | 85.74 ± 01.64 | 83.47 | 88.06 | 86.70 ± 01.15 | 84.58 | 88.47 | 72.16 ± 1.40 | 70.00 | 74.38 | 77.62 ± 1.98 | 73.54 | 80.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stańczyk, U.; Zielosko, B.; Baron, G. Importance of Characteristic Features and Their Form for Data Exploration. Entropy 2024, 26, 404. https://doi.org/10.3390/e26050404
Stańczyk U, Zielosko B, Baron G. Importance of Characteristic Features and Their Form for Data Exploration. Entropy. 2024; 26(5):404. https://doi.org/10.3390/e26050404
Chicago/Turabian StyleStańczyk, Urszula, Beata Zielosko, and Grzegorz Baron. 2024. "Importance of Characteristic Features and Their Form for Data Exploration" Entropy 26, no. 5: 404. https://doi.org/10.3390/e26050404
APA StyleStańczyk, U., Zielosko, B., & Baron, G. (2024). Importance of Characteristic Features and Their Form for Data Exploration. Entropy, 26(5), 404. https://doi.org/10.3390/e26050404







