Efficient Implementation of Discrete-Time Quantum Walks on Quantum Computers
Abstract
1. Introduction
2. The Model: DTQW on the N-Cycle
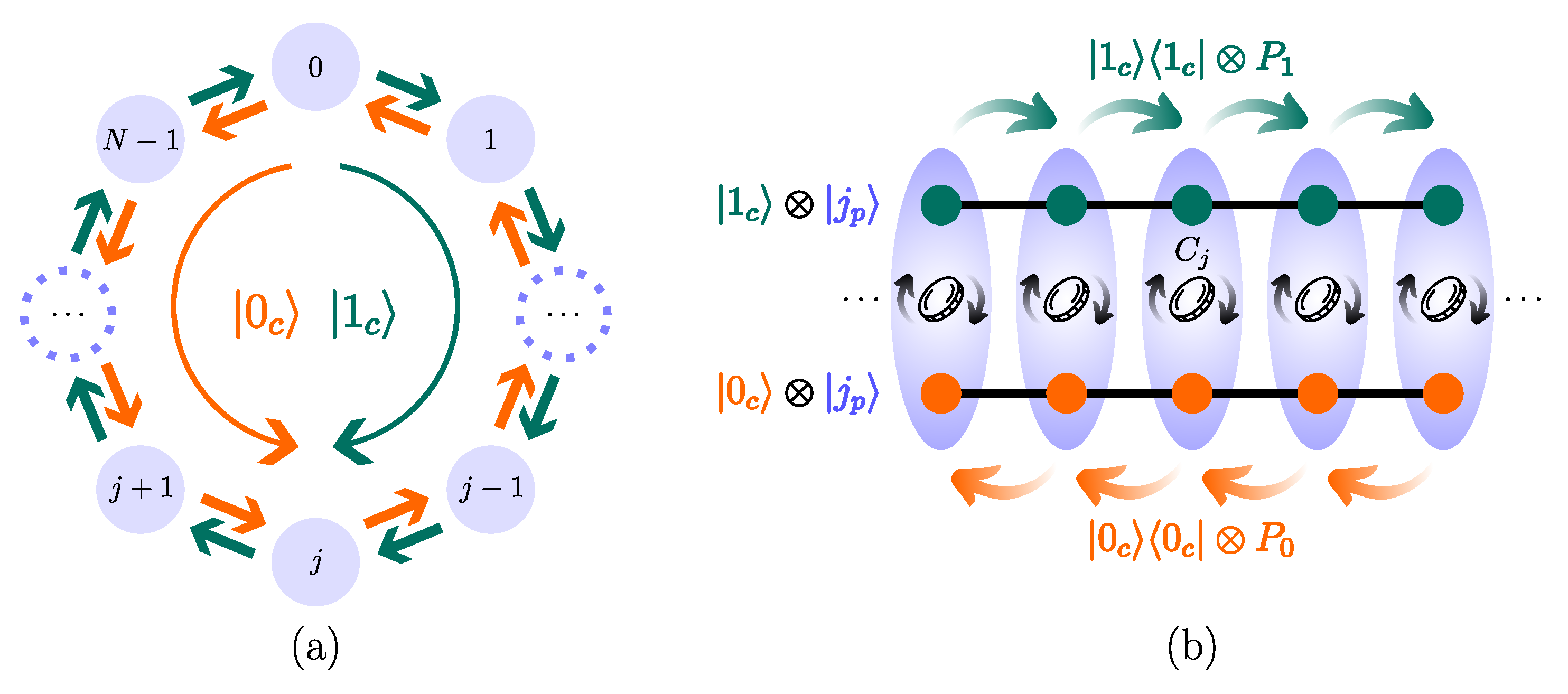
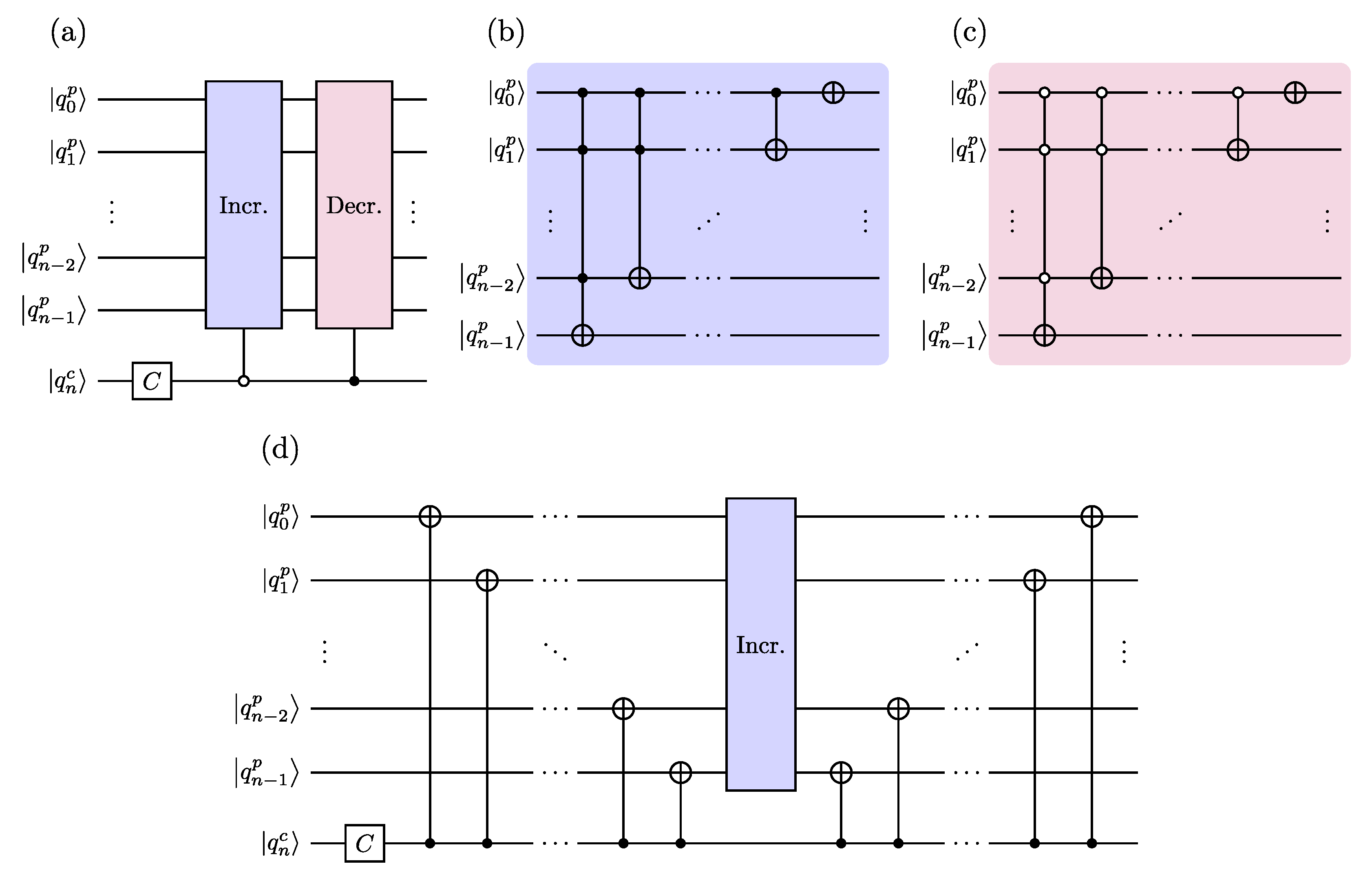
3. Quantum Circuit Implementing the DTQW on the -Cycle
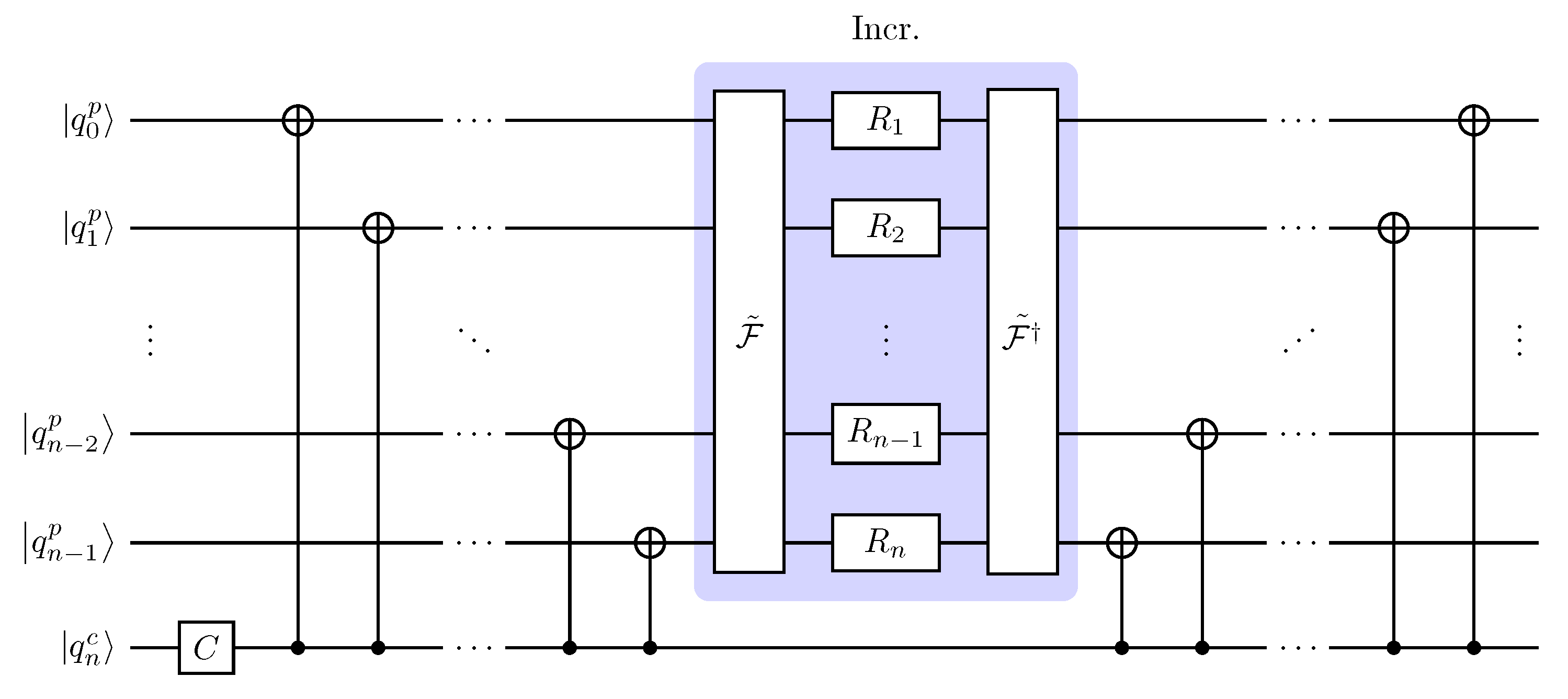
3.1. Quantum Circuit Design
3.2. Comparison with Other Existing Schemes
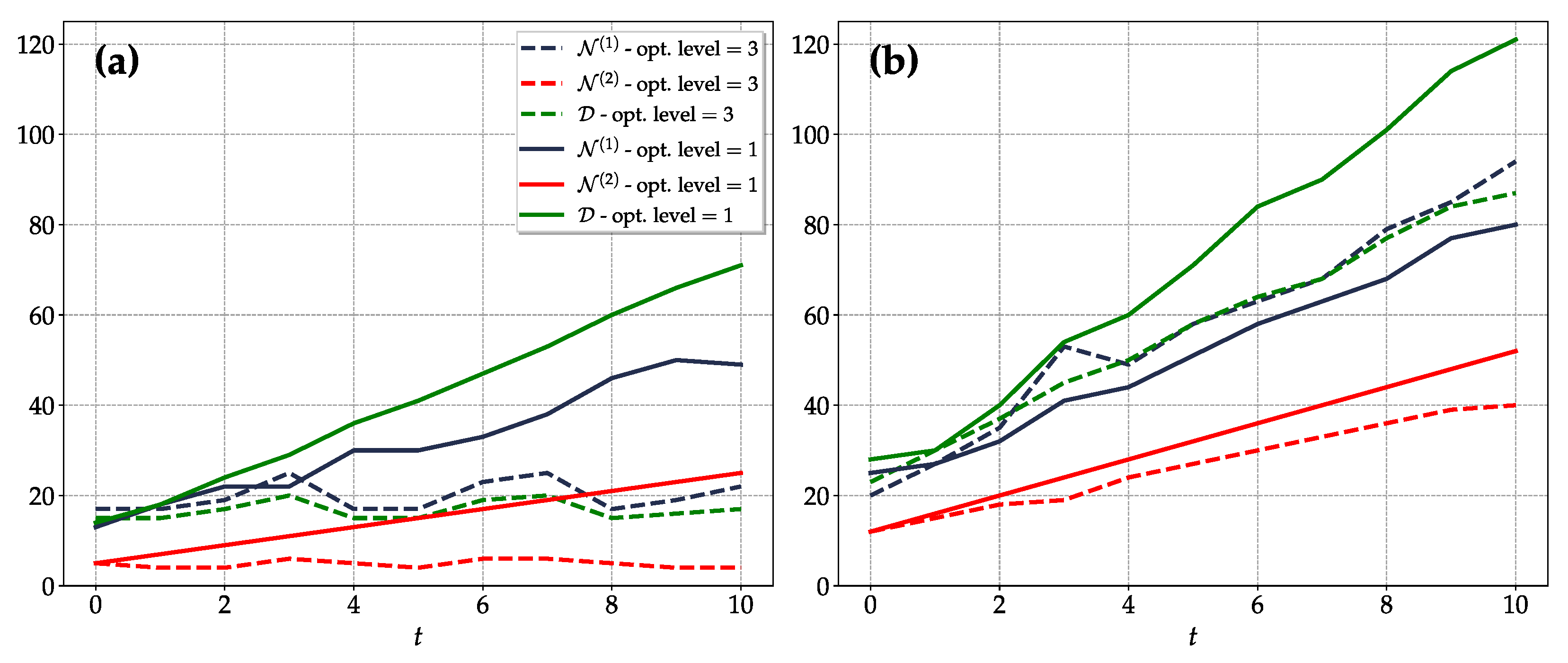
4. Results and Discussion
4.1. Hadamard DTQW
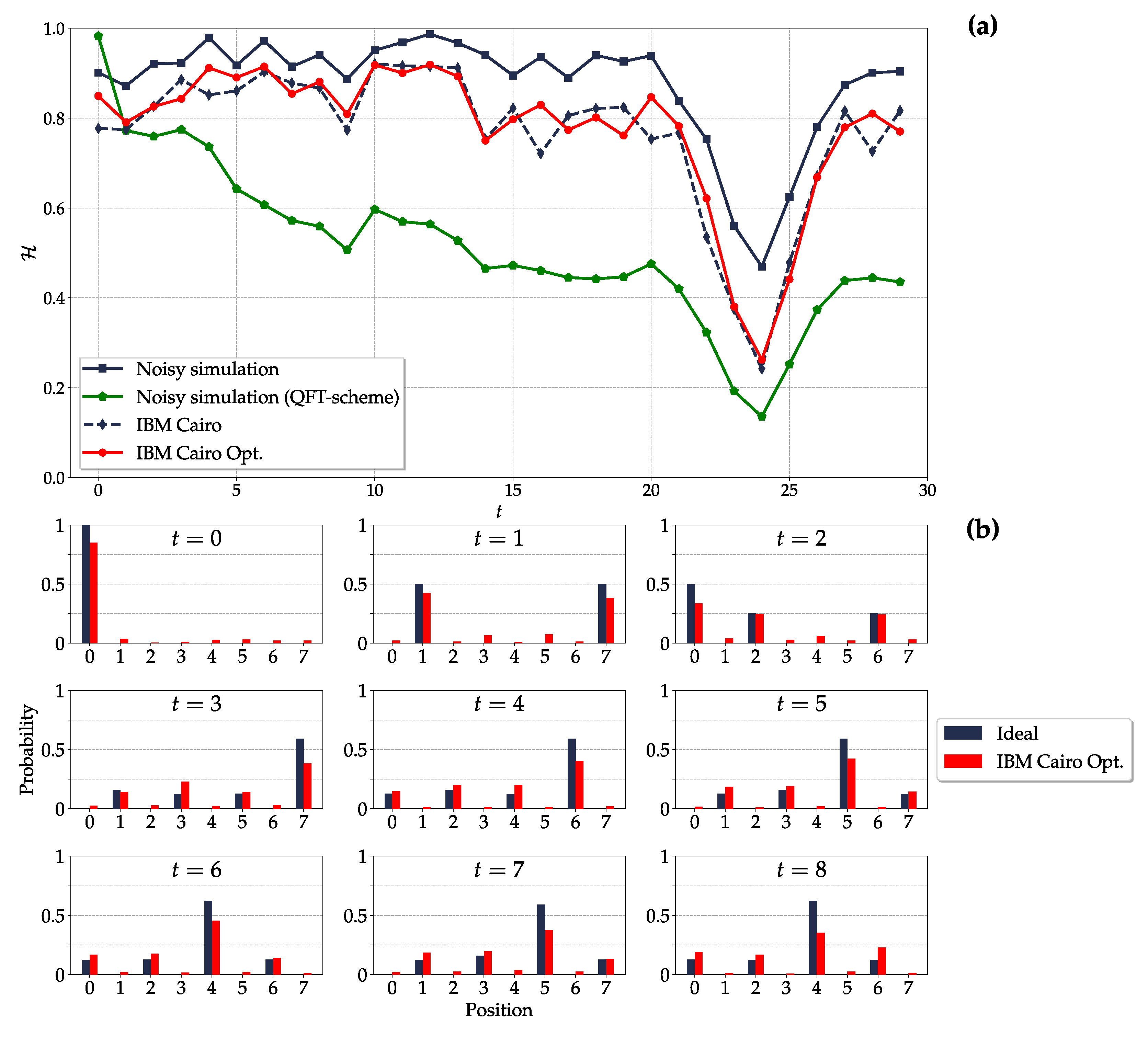
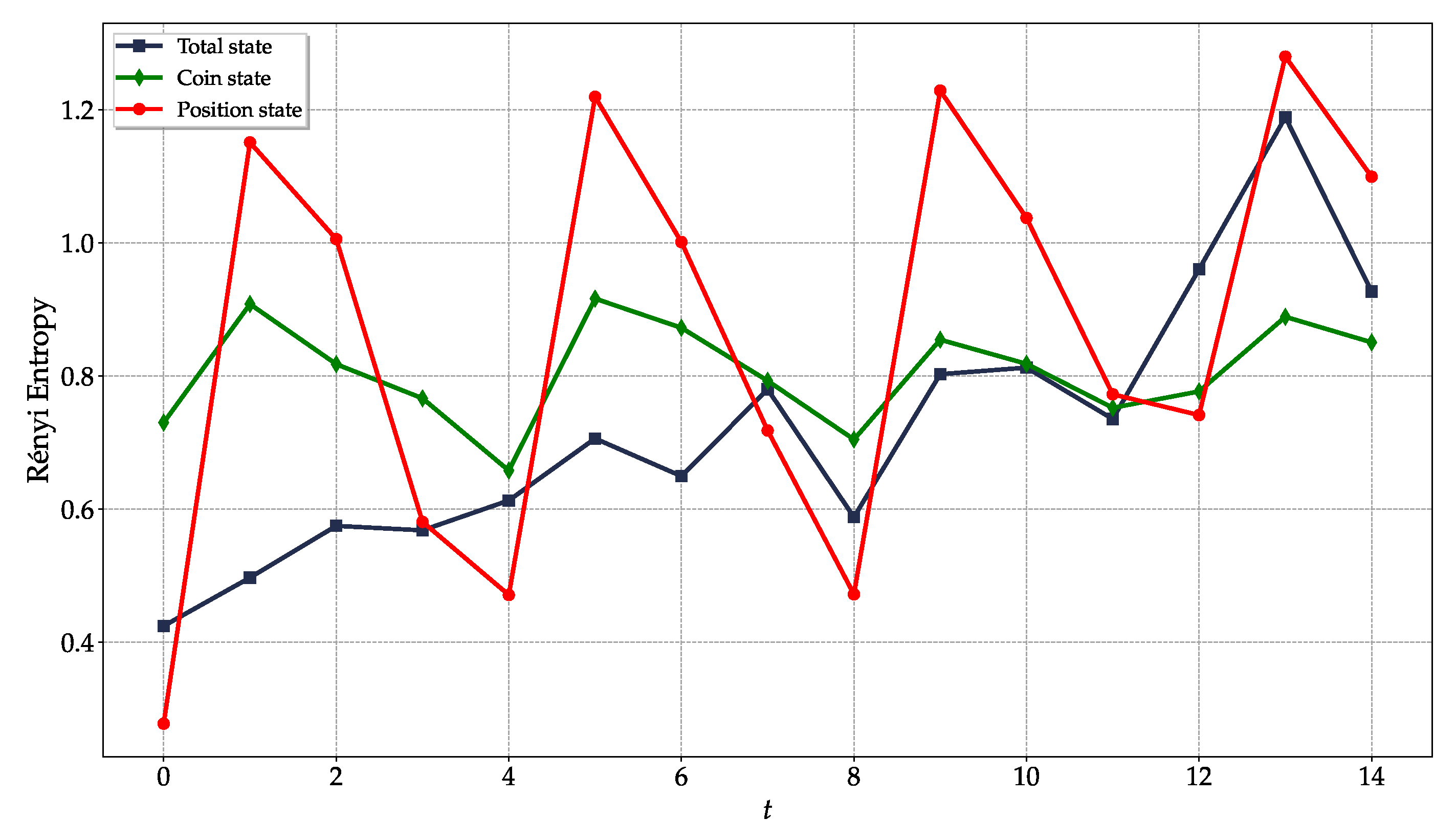
4.2. Figures of Merit
4.3. Circuit Optimization
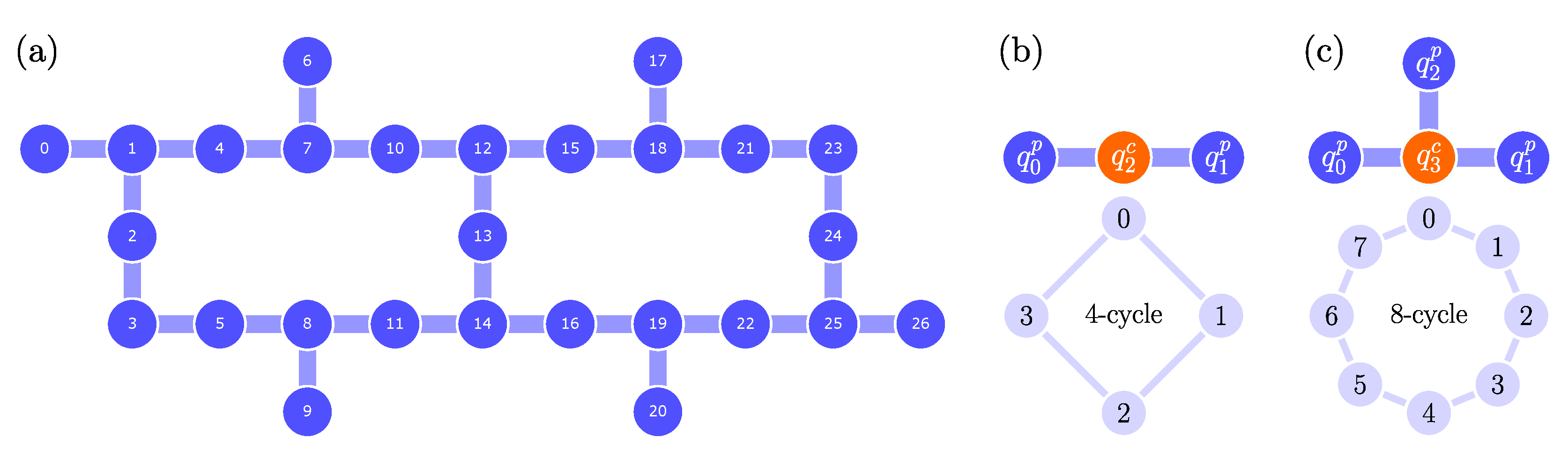
4.4. Analysis of the DTQW on the 4- and 8-Cycles
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CTQW | Continuous-time quantum walk |
| DTQW | Discrete-time quantum walk |
| (I)QFT | (Inverse) quantum Fourier transform |
Appendix A. Eigenvalues and Eigenvectors of Circulant Matrices
Appendix B. Optimization of the Circuit for an Initially Localized Walker
Appendix C. Analysis of the Size of DTQW Quantum Circuits in Different Schemes
- (i)
- The ID scheme here considered and the QFT scheme are based on the same circuit design (Figure 2d), in which the coin gate (one-qubit gate) cannot be executed in parallel to the CNOT gates, because it acts on their control qubit. Hence, the coin gate has unit depth and prevents the simplification of CNOT gates when iteratively concatenating the single time-step quantum circuit to obtain the successive steps. Therefore, in Appendix C.1 and Appendix C.2, the analysis focuses on a single time step, because the size of a circuit implementing t time steps is t times the size of that implementing a single time step.
- (ii)
- Controlled gates having different target qubits but the same control qubit (here, it is the coin) are executed in sequence (not in parallel) in actual quantum computers. This affects the depth of circuits and regards the CNOT gates in the ID and QFT schemes (Appendix C.1 and Appendix C.2, respectively) and the controlled- gates in our scheme (Appendix C.3).
- (iii)
- The (I)QFT on an n-qubit register (no SWAP) requires n one-qubit gates (Hadamard) and two-qubit gates (controlled-) and has depth [86]. This regards the analysis of the QFT scheme (Appendix C.2) and our scheme (Appendix C.3).
Appendix C.1. ID Scheme
Appendix C.2. QFT Scheme
Appendix C.3. Present Scheme
Appendix D. Transpilation of the Proposed Quantum Circuit for the Hadamard DTQW on the 4- and 8-Cycles
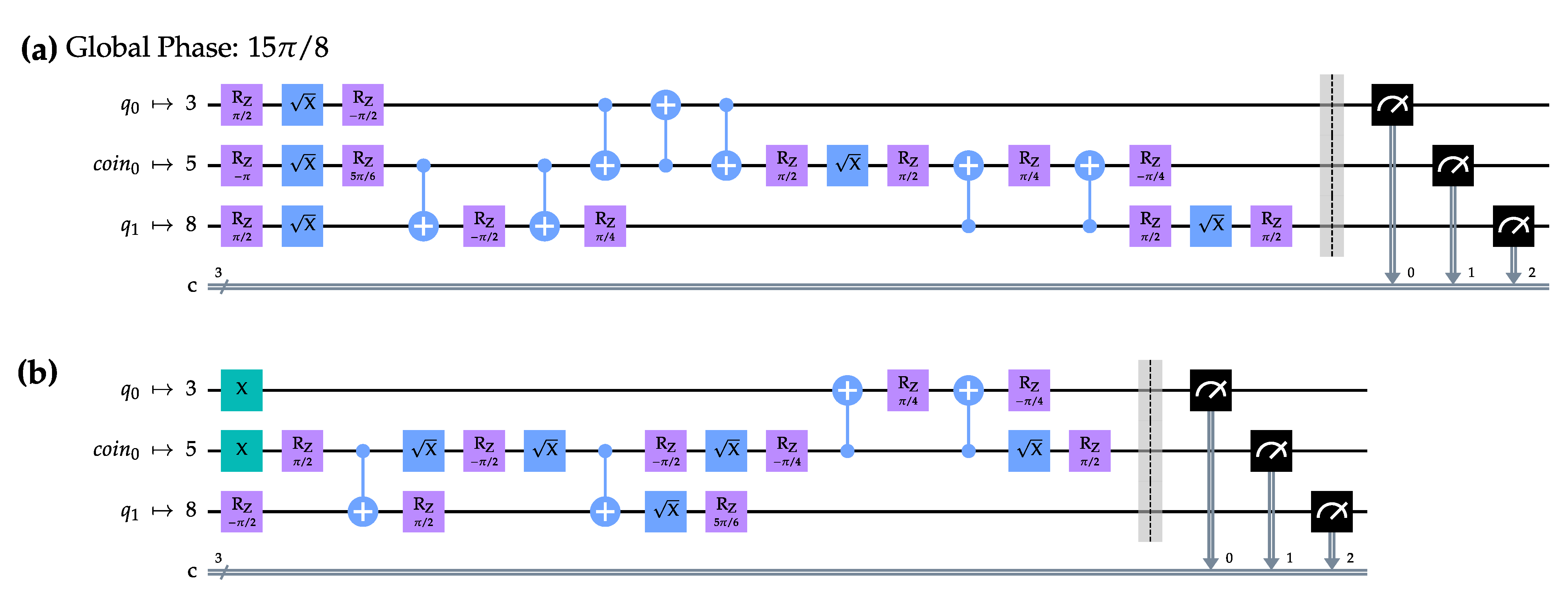
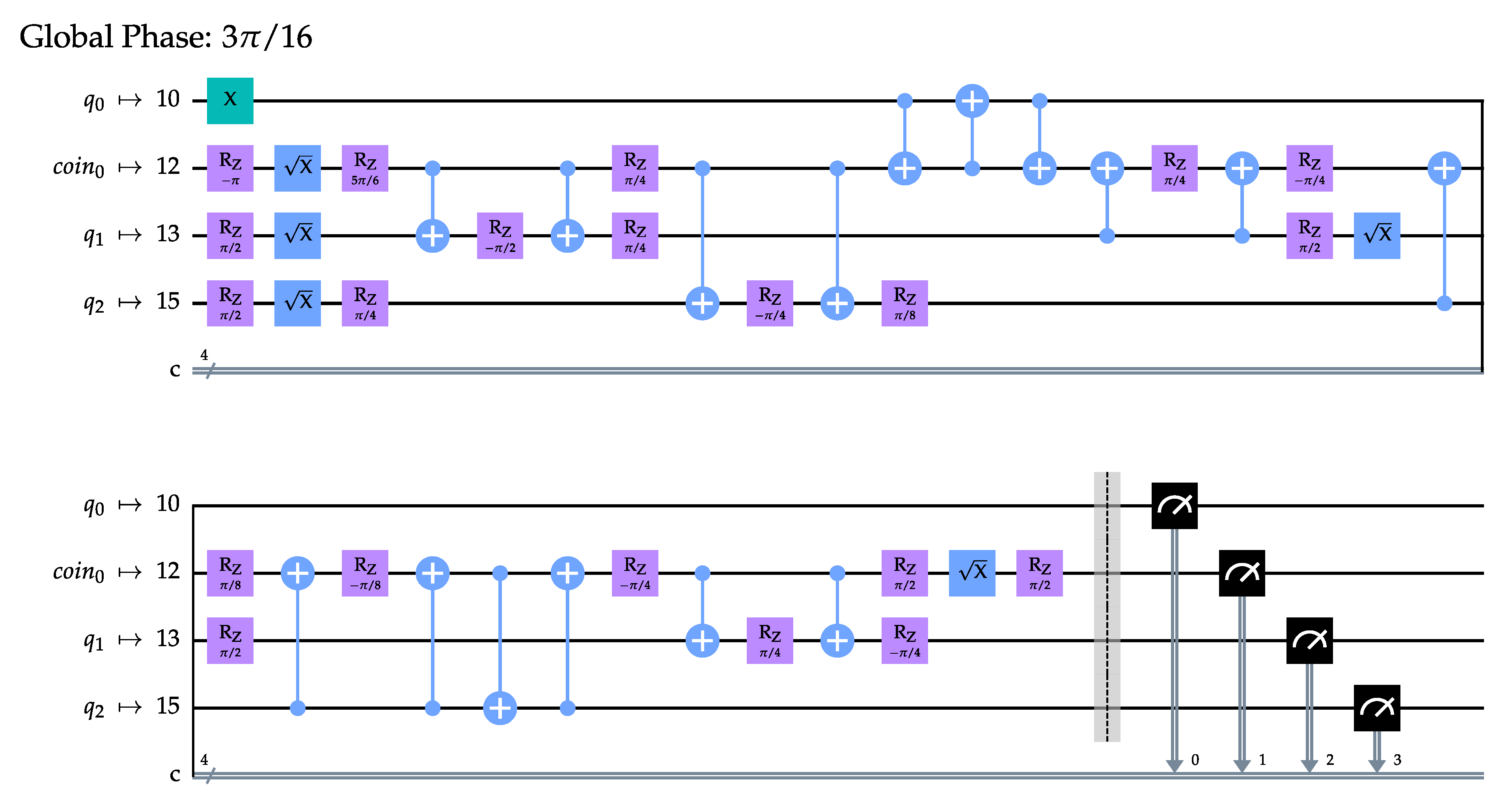
References
- Aharonov, Y.; Davidovich, L.; Zagury, N. Quantum random walks. Phys. Rev. A 1993, 48, 1687–1690. [Google Scholar] [CrossRef]
- Farhi, E.; Gutmann, S. Quantum computation and decision trees. Phys. Rev. A 1998, 58, 915–928. [Google Scholar] [CrossRef]
- Feynman, R.P.; Hibbs, A.R. Quantum Mechanics and Path Integrals; International Series in Pure and Applied Physics; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Ambainis, A. Quantum walks and their algorithmic applications. Int. J. Quantum Inf. 2003, 1, 507–518. [Google Scholar] [CrossRef]
- Childs, A.M.; Cleve, R.; Deotto, E.; Farhi, E.; Gutmann, S.; Spielman, D.A. Exponential Algorithmic Speedup by a Quantum Walk. In Proceedings of the Thirty-Fifth Annual ACM Symposium on Theory of Computing, STOC ’03, New York, NY, USA, 9–11 June 2003; pp. 59–68. [Google Scholar] [CrossRef]
- Kendon, V.M. A random walk approach to quantum algorithms. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2006, 364, 3407–3422. [Google Scholar] [CrossRef]
- Lovett, N.B.; Cooper, S.; Everitt, M.; Trevers, M.; Kendon, V. Universal quantum computation using the discrete-time quantum walk. Phys. Rev. A 2010, 81, 042330. [Google Scholar] [CrossRef]
- Singh, S.; Chawla, P.; Sarkar, A.; Chandrashekar, C.M. Universal quantum computing using single-particle discrete-time quantum walk. Sci. Rep. 2021, 11, 11551. [Google Scholar] [CrossRef]
- Chawla, P.; Singh, S.; Agarwal, A.; Srinivasan, S.; Chandrashekar, C.M. Multi-qubit quantum computing using discrete-time quantum walks on closed graphs. Sci. Rep. 2023, 13, 12078. [Google Scholar] [CrossRef]
- Childs, A.M. Universal Computation by Quantum Walk. Phys. Rev. Lett. 2009, 102, 180501. [Google Scholar] [CrossRef]
- Lahini, Y.; Steinbrecher, G.R.; Bookatz, A.D.; Englund, D. Quantum logic using correlated one-dimensional quantum walks. Npj Quantum Inf. 2018, 4, 2. [Google Scholar] [CrossRef]
- Shenvi, N.; Kempe, J.; Whaley, K.B. Quantum random-walk search algorithm. Phys. Rev. A 2003, 67, 052307. [Google Scholar] [CrossRef]
- Childs, A.M.; Goldstone, J. Spatial search by quantum walk. Phys. Rev. A 2004, 70, 022314. [Google Scholar] [CrossRef]
- Roget, M.; Guillet, S.; Arrighi, P.; Di Molfetta, G. Grover Search as a Naturally Occurring Phenomenon. Phys. Rev. Lett. 2020, 124, 180501. [Google Scholar] [CrossRef]
- Apers, S.; Chakraborty, S.; Novo, L.; Roland, J. Quadratic Speedup for Spatial Search by Continuous-Time Quantum Walk. Phys. Rev. Lett. 2022, 129, 160502. [Google Scholar] [CrossRef]
- Campos, E.; Venegas-Andraca, S.E.; Lanzagorta, M. Quantum tunneling and quantum walks as algorithmic resources to solve hard K-SAT instances. Sci. Rep. 2021, 11, 16845. [Google Scholar] [CrossRef]
- Douglas, B.L.; Wang, J.B. A classical approach to the graph isomorphism problem using quantum walks. J. Phys. A Math. Theor. 2008, 41, 075303. [Google Scholar] [CrossRef]
- Tamascelli, D.; Zanetti, L. A quantum-walk-inspired adiabatic algorithm for solving graph isomorphism problems. J. Phys. A Math. Theor. 2014, 47, 325302. [Google Scholar] [CrossRef]
- Schofield, C.; Wang, J.B.; Li, Y. Quantum walk inspired algorithm for graph similarity and isomorphism. Quantum Inf. Process. 2020, 19, 281. [Google Scholar] [CrossRef]
- Loke, T.; Tang, J.W.; Rodriguez, J.; Small, M.; Wang, J.B. Comparing classical and quantum PageRanks. Quantum Inf. Process. 2016, 16, 25. [Google Scholar] [CrossRef]
- Chawla, P.; Mangal, R.; Chandrashekar, C.M. Discrete-time quantum walk algorithm for ranking nodes on a network. Quantum Inf. Process. 2020, 19, 158. [Google Scholar] [CrossRef]
- Moutinho, J.a.P.; Melo, A.; Coutinho, B.; Kovács, I.A.; Omar, Y. Quantum link prediction in complex networks. Phys. Rev. A 2023, 107, 032605. [Google Scholar] [CrossRef]
- Goldsmith, M.; Saarinen, H.; García-Pérez, G.; Malmi, J.; Rossi, M.A.C.; Maniscalco, S. Link Prediction with Continuous-Time Classical and Quantum Walks. Entropy 2023, 25, 730. [Google Scholar] [CrossRef] [PubMed]
- Faccin, M.; Migdał, P.; Johnson, T.H.; Bergholm, V.; Biamonte, J.D. Community Detection in Quantum Complex Networks. Phys. Rev. X 2014, 4, 041012. [Google Scholar] [CrossRef]
- Mukai, K.; Hatano, N. Discrete-time quantum walk on complex networks for community detection. Phys. Rev. Res. 2020, 2, 023378. [Google Scholar] [CrossRef]
- Berry, D.W.; Childs, A.M. Black-Box Hamiltonian Simulation and Unitary Implementation. Quantum Info. Comput. 2012, 12, 29–62. [Google Scholar]
- Chandrashekar, C.M.; Banerjee, S.; Srikanth, R. Relationship between quantum walks and relativistic quantum mechanics. Phys. Rev. A 2010, 81, 062340. [Google Scholar] [CrossRef]
- Di Molfetta, G.; Brachet, M.; Debbasch, F. Quantum walks as massless Dirac fermions in curved space-time. Phys. Rev. A 2013, 88, 042301. [Google Scholar] [CrossRef]
- Arrighi, P.; Facchini, S.; Forets, M. Quantum walking in curved spacetime. Quantum Inf. Process. 2016, 15, 3467–3486. [Google Scholar] [CrossRef]
- Molfetta, G.D.; Pérez, A. Quantum walks as simulators of neutrino oscillations in a vacuum and matter. New J. Phys. 2016, 18, 103038. [Google Scholar] [CrossRef]
- Zhan, X.; Qin, H.; Bian, Z.h.; Li, J.; Xue, P. Perfect state transfer and efficient quantum routing: A discrete-time quantum-walk approach. Phys. Rev. A 2014, 90, 012331. [Google Scholar] [CrossRef]
- Yalçınkaya, İ.; Gedik, Z. Qubit state transfer via discrete-time quantum walks. J. Phys. A Math. Theor. 2015, 48, 225302. [Google Scholar] [CrossRef]
- Wang, Y.; Shang, Y.; Xue, P. Generalized teleportation by quantum walks. Quantum Inf. Process. 2017, 16, 221. [Google Scholar] [CrossRef]
- Shang, Y.; Wang, Y.; Li, M.; Lu, R. Quantum communication protocols by quantum walks with two coins. Europhys. Lett. 2019, 124, 60009. [Google Scholar] [CrossRef]
- Srikara, S.; Chandrashekar, C.M. Quantum direct communication protocols using discrete-time quantum walk. Quantum Inf. Process. 2020, 19, 295. [Google Scholar] [CrossRef]
- Panda, S.S.; Yasir, P.A.A.; Chandrashekar, C.M. Quantum direct communication protocol using recurrence in k-cycle quantum walks. Phys. Rev. A 2023, 107, 022611. [Google Scholar] [CrossRef]
- Bottarelli, A.; Frigerio, M.; Paris, M.G.A. Quantum routing of information using chiral quantum walks. AVS Quantum Sci. 2023, 5, 025001. [Google Scholar] [CrossRef]
- Vlachou, C.; Krawec, W.; Mateus, P.; Paunković, N.; Souto, A. Quantum key distribution with quantum walks. Quantum Inf. Process. 2018, 17, 288. [Google Scholar] [CrossRef]
- Abd El-Latif, A.A.; Abd-El-Atty, B.; Amin, M.; Iliyasu, A.M. Quantum-inspired cascaded discrete-time quantum walks with induced chaotic dynamics and cryptographic applications. Sci. Rep. 2020, 10, 1930. [Google Scholar] [CrossRef]
- Venegas-Andraca, S.E. Quantum walks: A comprehensive review. Quantum Inf. Process. 2012, 11, 1015–1106. [Google Scholar] [CrossRef]
- Portugal, R. Quantum Walks and Search Algorithms, 2nd ed.; Springer Nature: Cham, Switzerland, 2018. [Google Scholar]
- Kadian, K.; Garhwal, S.; Kumar, A. Quantum walk and its application domains: A systematic review. Comput. Sci. Rev. 2021, 41, 100419. [Google Scholar] [CrossRef]
- Wang, J.; Manouchehri, K. Physical Implementation of Quantum Walks; Springer: New York, NY, USA, 2013. [Google Scholar]
- Gräfe, M.; Heilmann, R.; Lebugle, M.; Guzman-Silva, D.; Perez-Leija, A.; Szameit, A. Integrated photonic quantum walks. J. Opt. 2016, 18, 103002. [Google Scholar] [CrossRef]
- Neves, L.; Puentes, G. Photonic Discrete-time Quantum Walks and Applications. Entropy 2018, 20, 731. [Google Scholar] [CrossRef]
- Loke, T.; Wang, J.B. Efficient quantum circuits for continuous-time quantum walks on composite graphs. J. Phys. A Math. Theor. 2017, 50, 055303. [Google Scholar] [CrossRef]
- Ryan, C.A.; Laforest, M.; Boileau, J.C.; Laflamme, R. Experimental implementation of a discrete-time quantum random walk on an NMR quantum-information processor. Phys. Rev. A 2005, 72, 062317. [Google Scholar] [CrossRef]
- Douglas, B.L.; Wang, J.B. Efficient quantum circuit implementation of quantum walks. Phys. Rev. A 2009, 79, 052335. [Google Scholar] [CrossRef]
- Jordan, S.P.; Wocjan, P. Efficient quantum circuits for arbitrary sparse unitaries. Phys. Rev. A 2009, 80, 062301. [Google Scholar] [CrossRef]
- Loke, T.; Wang, J.B. Efficient circuit implementation of quantum walks on non-degree-regular graphs. Phys. Rev. A 2012, 86, 042338. [Google Scholar] [CrossRef]
- Wing-Bocanegra, A.; Venegas-Andraca, S.E. Circuit implementation of discrete-time quantum walks via the shunt decomposition method. Quantum Inf. Process. 2023, 22, 146. [Google Scholar] [CrossRef]
- Nzongani, U.; Zylberman, J.; Doncecchi, C.E.; Pérez, A.; Debbasch, F.; Arnault, P. Quantum circuits for discrete-time quantum walks with position-dependent coin operator. Quantum Inf. Process. 2023, 22, 270. [Google Scholar] [CrossRef]
- Acasiete, F.; Agostini, F.P.; Moqadam, J.K.; Portugal, R. Implementation of quantum walks on IBM quantum computers. Quantum Inf. Process. 2020, 19, 426. [Google Scholar] [CrossRef]
- Slimen, I.B.; Gueddana, A.; Lakshminarayanan, V. Discrete-time quantum walk on circular graph: Simulations and effect of gate depth and errors. Int. J. Quantum Inf. 2021, 19, 2150008. [Google Scholar] [CrossRef]
- Olivieri, P.; Askarpour, M.; di Nitto, E. Experimental Implementation of Discrete Time Quantum Walk with the IBM Qiskit Library. In Proceedings of the 2021 IEEE/ACM 2nd International Workshop on Quantum Software Engineering (Q-SE), Madrid, Spain, 1–2 June 2021; pp. 33–38. [Google Scholar] [CrossRef]
- Georgopoulos, K.; Emary, C.; Zuliani, P. Comparison of quantum-walk implementations on noisy intermediate-scale quantum computers. Phys. Rev. A 2021, 103, 022408. [Google Scholar] [CrossRef]
- Wadhia, V.; Chancellor, N.; Kendon, V. Cycle discrete-time quantum walks on a noisy quantum computer. Eur. Phys. J. D 2024, 78, 29. [Google Scholar] [CrossRef]
- Shakeel, A. Efficient and scalable quantum walk algorithms via the quantum Fourier transform. Quantum Inf. Process. 2020, 19, 323. [Google Scholar] [CrossRef]
- Panda, D.K.; Benjamin, C. Recurrent generation of maximally entangled single-particle states via quantum walks on cyclic graphs. Phys. Rev. A 2023, 108, L020401. [Google Scholar] [CrossRef]
- Singh, S.; Alderete, C.H.; Balu, R.; Monroe, C.; Linke, N.M.; Chandrashekar, C.M. Quantum circuits for the realization of equivalent forms of one-dimensional discrete-time quantum walks on near-term quantum hardware. Phys. Rev. A 2021, 104, 062401. [Google Scholar] [CrossRef]
- Saeedi, M.; Pedram, M. Linear-depth quantum circuits for n-qubit Toffoli gates with no ancilla. Phys. Rev. A 2013, 87, 062318. [Google Scholar] [CrossRef]
- Barenco, A.; Bennett, C.H.; Cleve, R.; DiVincenzo, D.P.; Margolus, N.; Shor, P.; Sleator, T.; Smolin, J.A.; Weinfurter, H. Elementary gates for quantum computation. Phys. Rev. A 1995, 52, 3457–3467. [Google Scholar] [CrossRef]
- IBM Quantum. 2021. Available online: https://quantum.ibm.com/ (accessed on 18 October 2023).
- Qiskit Contributors. Qiskit: An Open-source Framework for Quantum Computing. 2023. Available online: https://www.ibm.com/quantum/qiskit (accessed on 18 October 2023). [CrossRef]
- Dukes, P.R. Quantum state revivals in quantum walks on cycles. Results Phys. 2014, 4, 189–197. [Google Scholar] [CrossRef]
- Trevisan, D. Lecture Notes on Mathematical Aspects of Quantum Information Theory. 2023. Available online: https://people.cs.dm.unipi.it/trevisan/teaching/PhD/2022-qinfo/2022-Qinfo-notes.pdf (accessed on 20 December 2023).
- Azzini, S.; Mazzucchi, S.; Moretti, V.; Pastorello, D.; Pavesi, L. Single-Particle Entanglement. Adv. Quantum Technol. 2020, 3, 2000014. [Google Scholar] [CrossRef]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865–942. [Google Scholar] [CrossRef]
- Brydges, T.; Elben, A.; Jurcevic, P.; Vermersch, B.; Maier, C.; Lanyon, B.P.; Zoller, P.; Blatt, R.; Roos, C.F. Probing Rényi entanglement entropy via randomized measurements. Science 2019, 364, 260–263. [Google Scholar] [CrossRef] [PubMed]
- Thew, R.T.; Nemoto, K.; White, A.G.; Munro, W.J. Qudit quantum-state tomography. Phys. Rev. A 2002, 66, 012303. [Google Scholar] [CrossRef]
- Preskill, J. Quantum computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Córcoles, A.D.; Kandala, A.; Javadi-Abhari, A.; McClure, D.T.; Cross, A.W.; Temme, K.; Nation, P.D.; Steffen, M.; Gambetta, J.M. Challenges and Opportunities of Near-Term Quantum Computing Systems. Proc. IEEE 2020, 108, 1338–1352. [Google Scholar] [CrossRef]
- Bharti, K.; Cervera-Lierta, A.; Kyaw, T.H.; Haug, T.; Alperin-Lea, S.; Anand, A.; Degroote, M.; Heimonen, H.; Kottmann, J.S.; Menke, T.; et al. Noisy intermediate-scale quantum algorithms. Rev. Mod. Phys. 2022, 94, 015004. [Google Scholar] [CrossRef]
- Kim, T.; Choi, B.S. Efficient decomposition methods for controlled-Rn using a single ancillary qubit. Sci. Rep. 2018, 8, 5445. [Google Scholar] [CrossRef]
- Yamamoto, T.; Ohira, R. Error suppression by a virtual two-qubit gate. J. Appl. Phys. 2023, 133, 174401. [Google Scholar] [CrossRef]
- Linke, N.M.; Maslov, D.; Roetteler, M.; Debnath, S.; Figgatt, C.; Landsman, K.A.; Wright, K.; Monroe, C. Experimental comparison of two quantum computing architectures. Proc. Natl. Acad. Sci. USA 2017, 114, 3305–3310. [Google Scholar] [CrossRef] [PubMed]
- Murali, P.; Debroy, D.M.; Brown, K.R.; Martonosi, M. Architecting Noisy Intermediate-Scale Trapped Ion Quantum Computers. In Proceedings of the 2020 ACM/IEEE 47th Annual International Symposium on Computer Architecture (ISCA), Valencia, Spain, 30 May–3 June 2020; pp. 529–542. [Google Scholar] [CrossRef]
- Ramette, J.; Sinclair, J.; Vendeiro, Z.; Rudelis, A.; Cetina, M.; Vuletić, V. Any-To-Any Connected Cavity-Mediated Architecture for Quantum Computing with Trapped Ions or Rydberg Arrays. PRX Quantum 2022, 3, 010344. [Google Scholar] [CrossRef]
- Walczak, Z.; Bauer, J.H. Parrondo’s paradox in quantum walks with deterministic aperiodic sequence of coins. Phys. Rev. E 2021, 104, 064209. [Google Scholar] [CrossRef]
- Panda, A.; Benjamin, C. Order from chaos in quantum walks on cyclic graphs. Phys. Rev. A 2021, 104, 012204. [Google Scholar] [CrossRef]
- Lai, J.W.; Cheong, K.H. Parrondo’s paradox from classical to quantum: A review. Nonlinear Dyn. 2020, 100, 849–861. [Google Scholar] [CrossRef]
- Qiang, X.; Loke, T.; Montanaro, A.; Aungskunsiri, K.; Zhou, X.; O’Brien, J.L.; Wang, J.B.; Matthews, J.C.F. Efficient quantum walk on a quantum processor. Nat. Commun. 2016, 7, 11511. [Google Scholar] [CrossRef] [PubMed]
- Aharonov, D.; Ambainis, A.; Kempe, J.; Vazirani, U. Quantum Walks on Graphs. In Proceedings of the Thirty-Third Annual ACM Symposium on Theory of Computing, STOC ’01, Hersonissos, Greece, 6–8 July 2001; pp. 50–59. [Google Scholar] [CrossRef]
- Tregenna, B.; Flanagan, W.; Maile, R.; Kendon, V. Controlling discrete quantum walks: Coins and initial states. New J. Phys. 2003, 5, 83. [Google Scholar] [CrossRef]
- Gray, R.M. Toeplitz and Circulant Matrices: A Review. Found. Trends® Commun. Inf. Theory 2006, 2, 155–239. [Google Scholar] [CrossRef]
- Benenti, G.; Casati, G.; Rossini, D.; Strini, G. Principles of Quantum Computation and Information; World Scientific: Singapore, 2018. [Google Scholar] [CrossRef]

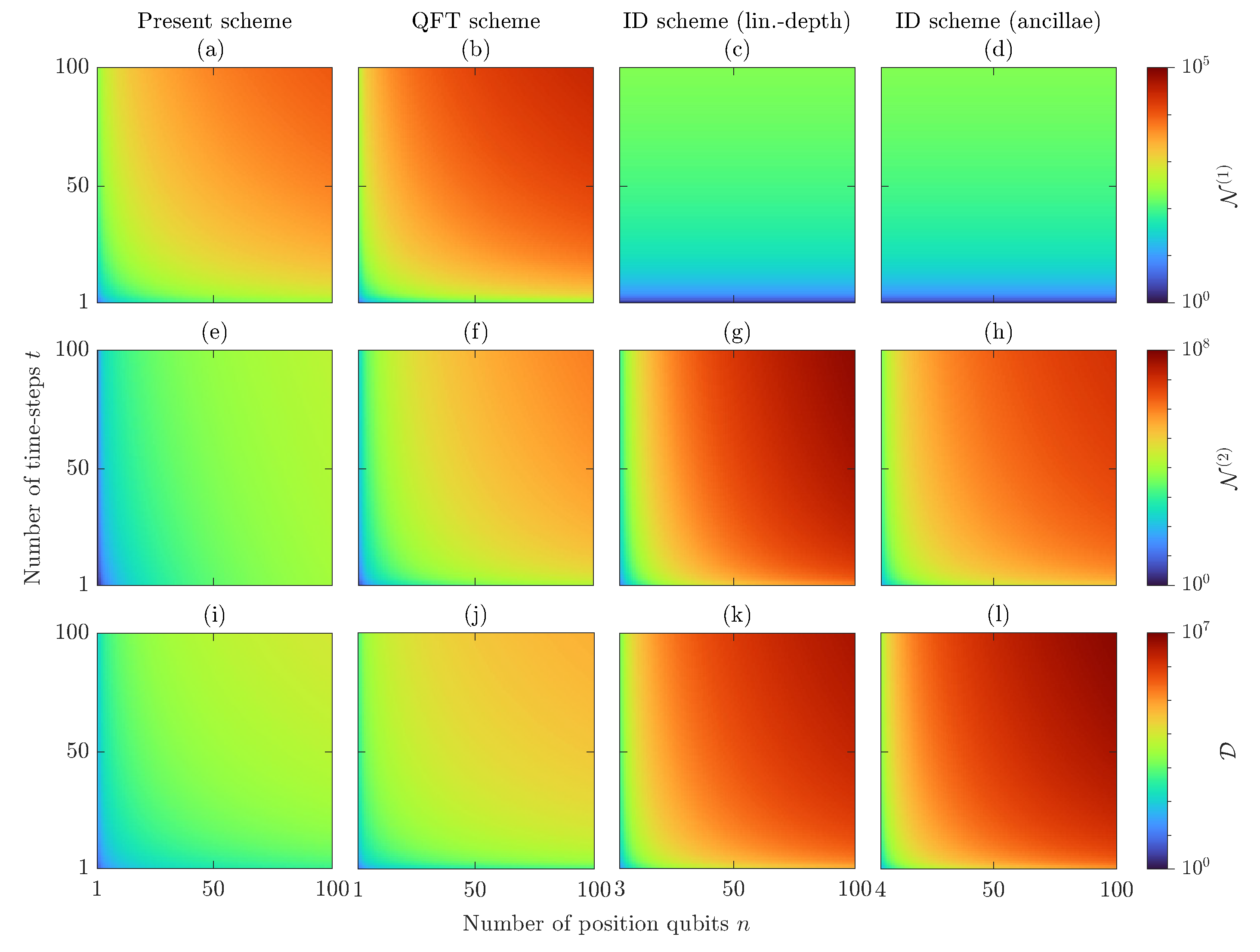

| Scheme | Figure | One-Qubit | Two-Qubit | Depth | Ancillae |
|---|---|---|---|---|---|
| Present work | 4 | 0 | |||
| QFT [58] | 3 | 0 | |||
| ID * [48] (lin.-depth q.c. [61], ) | 2d | 0 | |||
| ID * [48] (ancillae [62], ) | 2d |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Razzoli, L.; Cenedese, G.; Bondani, M.; Benenti, G. Efficient Implementation of Discrete-Time Quantum Walks on Quantum Computers. Entropy 2024, 26, 313. https://doi.org/10.3390/e26040313
Razzoli L, Cenedese G, Bondani M, Benenti G. Efficient Implementation of Discrete-Time Quantum Walks on Quantum Computers. Entropy. 2024; 26(4):313. https://doi.org/10.3390/e26040313
Chicago/Turabian StyleRazzoli, Luca, Gabriele Cenedese, Maria Bondani, and Giuliano Benenti. 2024. "Efficient Implementation of Discrete-Time Quantum Walks on Quantum Computers" Entropy 26, no. 4: 313. https://doi.org/10.3390/e26040313
APA StyleRazzoli, L., Cenedese, G., Bondani, M., & Benenti, G. (2024). Efficient Implementation of Discrete-Time Quantum Walks on Quantum Computers. Entropy, 26(4), 313. https://doi.org/10.3390/e26040313









