Robust Free-Space Optical Communication Utilizing Polarization for the Advancement of Quantum Communication
Abstract
1. Introduction
2. Materials and Methods
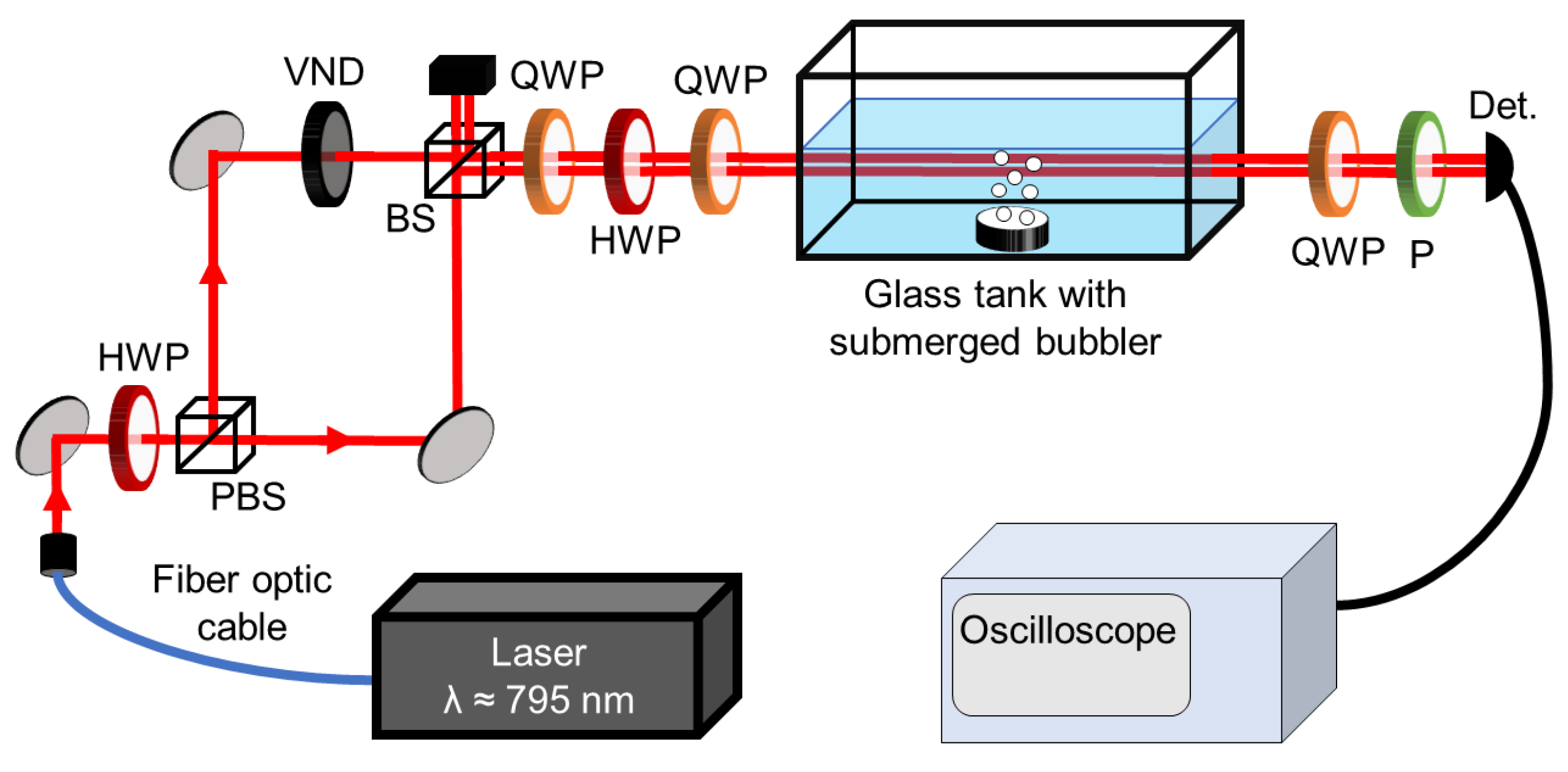
2.1. Experiment
2.2. Simulation
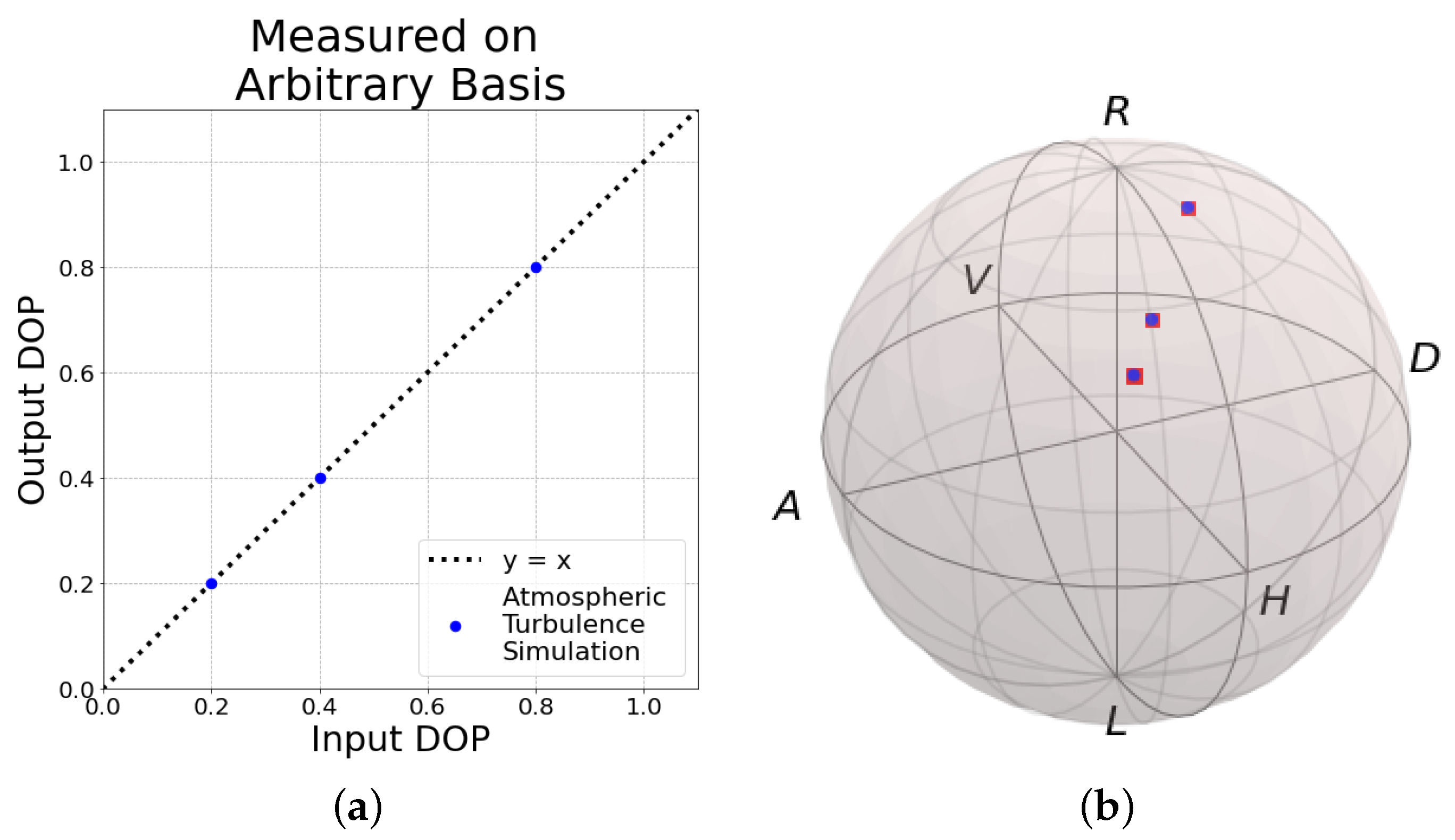
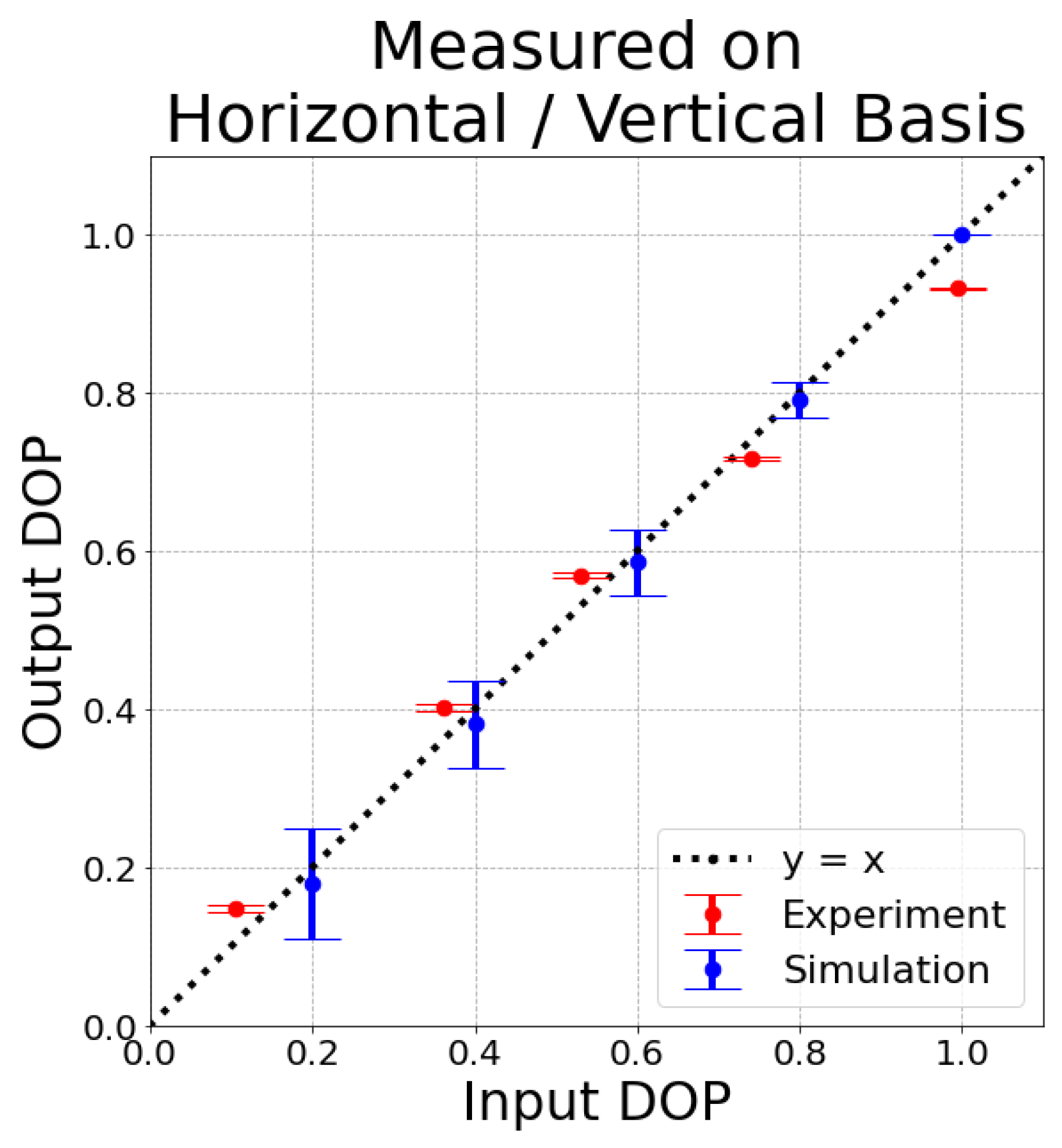
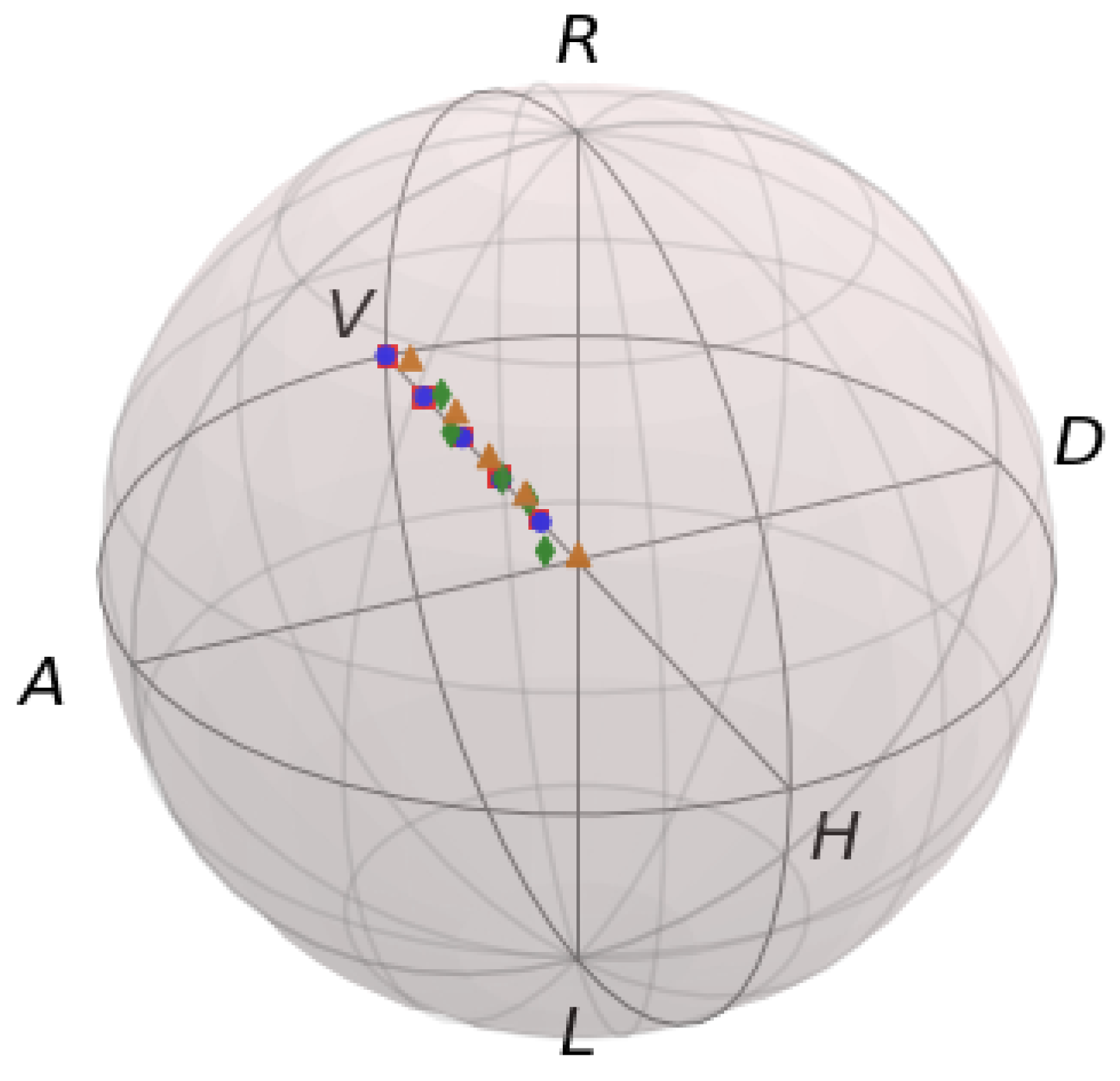
3. Results
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DOP | Degree of polarization |
| FSO | Free-space optics |
| SOP | State of polarization |
| LP | Linear polarizer |
| BS | Beam splitter |
| QWP | Quarter wave plate |
| HWP | Half wave plate |
| Det. | Detector |
| VND | Variable neutral density |
Appendix A. Simulation of Atmospheric Turbulence
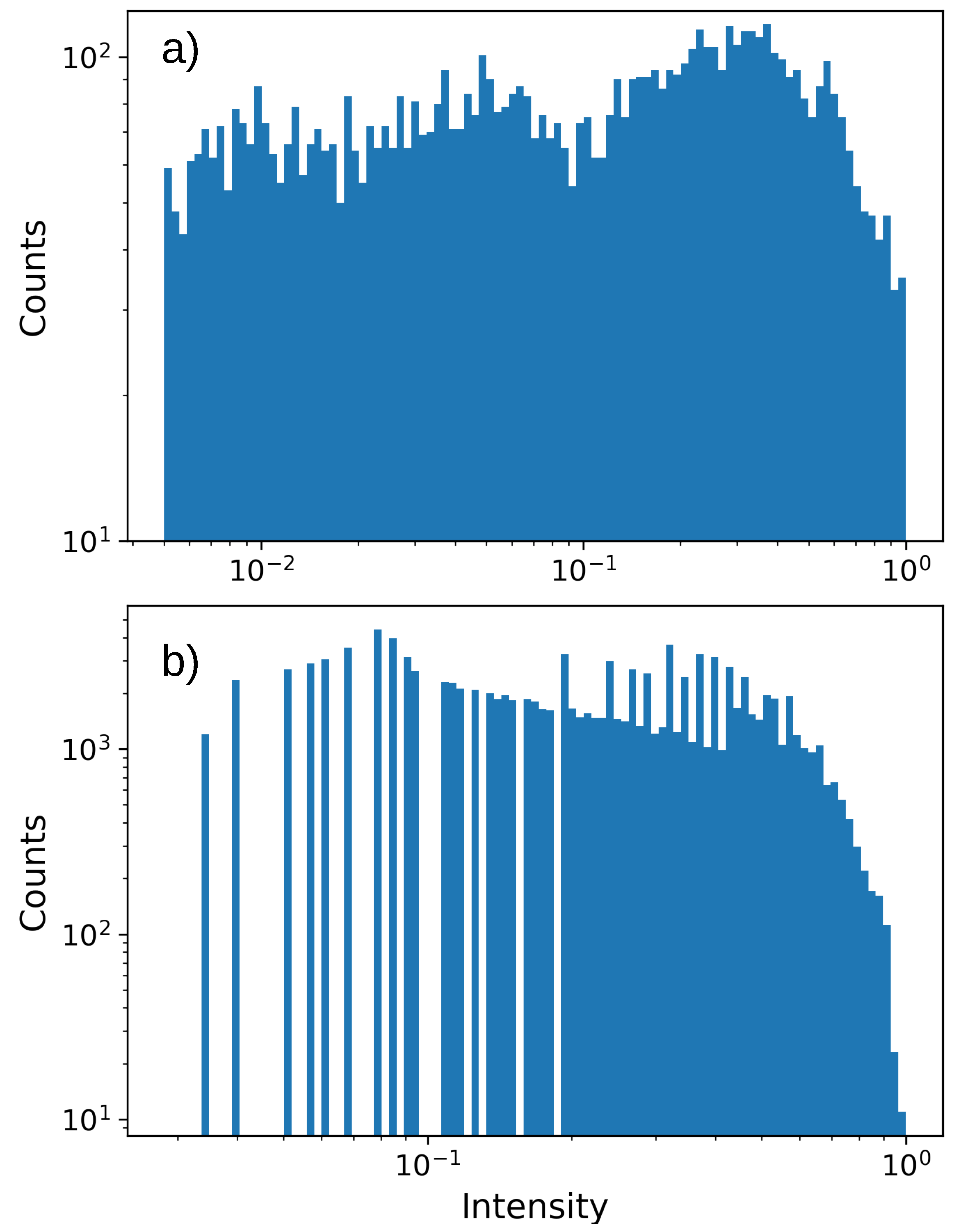
Appendix B. Intensity Distribution

References
- Malik, A.; Singh, P. Free space optics: Current applications and future challenges. Int. J. Opt. 2015, 2015, 945483. [Google Scholar] [CrossRef]
- Khalighi, M.A.; Uysal, M. Survey on Free Space Optical Communication: A Communication Theory Perspective. IEEE Commun. Surv. Tutor. 2014, 16, 2231–2258. [Google Scholar] [CrossRef]
- Willebrand, H.A.; Ghuman, B.S. Fiber optics without fiber. IEEE Spectr. 2001, 38, 40–45. [Google Scholar] [CrossRef]
- Yang, L.; Zhu, B.; Cheng, J.; Holzman, J.F. Free-Space Optical Communications Using on–off Keying and Source Information Transformation. J. Light. Technol. 2016, 34, 2601–2609. [Google Scholar] [CrossRef]
- Majumdar, A.K. Chapter 4—Fundamentals of Free-Space Optical Communications Systems, Optical Channels, Characterization, and Network/Access Technology. In Optical Wireless Communications for Broadband Global Internet Connectivity; Majumdar, A.K., Ed.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 55–116. [Google Scholar] [CrossRef]
- Andrews, L.C.; Phillips, R.L.; Young, C.Y. Laser Beam Scintillation with Applications; SPIE Press: Bellingham, WA, USA, 2001. [Google Scholar] [CrossRef]
- Oh, E.S.; Ricklin, J.C.; Gilbreath, G.C.; Vallestero, N.; Eaton, F. Optical turbulence model for laser propagation and Imaging Applications. In Free-Space Laser Communication and Active Laser Illumination III; SPIE Press: Bellingham, WA, USA, 2004. [Google Scholar] [CrossRef]
- Kon, A.I.; Tatarskii, V.I. On the theory of propagation of partially coherent light beams in a turbulent atmosphere. Radiophys. Quantum Electron. 1972, 15, 1187–1192. [Google Scholar] [CrossRef]
- Trichili, A.; Ragheb, A.; Briantcev, D.; Esmail, M.A.; Altamimi, M.; Ashry, I.; Ooi, B.S.; Alshebeili, S.; Alouini, M.S. Retrofitting FSO Systems in Existing RF Infrastructure: A Non-Zero Sum Game Technology. IEEE Open J. Commun. Soc. 2021, 2, 2597–2615. [Google Scholar] [CrossRef]
- Shen, C.; Guo, Y.; Oubei, H.; Ng, T.; Liu, G.; Park, K.; Ho, K.; Alouini, M.; Ooi, B. 20-meter underwater wireless optical communication link with 1.5 Gbps data rate. Opt. Express 2016, 24, 25502–25509. [Google Scholar] [CrossRef]
- Zhu, X.; Kahn, J. Free-space optical communication through atmospheric turbulence channels. IEEE Trans. Commun. 2002, 50, 1293–1300. [Google Scholar] [CrossRef]
- Lohani, S.; Glasser, R.T. Turbulence correction with artificial neural networks. Opt. Lett. 2018, 43, 2611–2614. [Google Scholar] [CrossRef]
- Lohani, S.; Knutson, E.M.; O’Donnell, M.; Huver, S.D.; Glasser, R.T. On the use of deep neural networks in optical communications. Appl. Opt. 2018, 57, 4180–4190. [Google Scholar] [CrossRef]
- Arnon, S.; Kopeika, N. Effect of particulate on performance of optical communication in space and an adaptive method to minimize such effects. Appl. Opt. 1994, 33, 4930–4937. [Google Scholar] [CrossRef]
- Lohani, S.; Knutson, E.; Glasser, R. Generative machine learning for robust free-space communication. Commun. Phys. 2020, 3, 177. [Google Scholar] [CrossRef]
- Toyoshima, M.; Takenaka, H.; Shoji, Y.; Takayama, Y.; Koyama, Y.; Kunimori, H. Polarization measurements through space-to-ground atmospheric propagation paths by using a highly polarized laser source in space. Opt. Express 2009, 17, 22333–22340. [Google Scholar] [CrossRef]
- Peranic, M.; Clark, M.; Wang, R.; Bahrani, S.; Obada Alia, S.W.; Radman, A.; Loncaric, M.; Stipcevic, M.; Rarity, J.; Nejabati, R.; et al. A study of polarization compensation for quantum networks. EPJ Quantum Technol. 2023, 10, 30. [Google Scholar] [CrossRef]
- Goodman, J.; Skrockij, G.; Kokin, A. Statistical Optics; A Wiley-Interscience Publication; Wiley: Hoboken, NJ, USA, 1985. [Google Scholar]
- Clifford, S.F. The classical theory of wave propagation in a turbulent medium. In Laser Beam Propagation in the Atmosphere; Strohbehn, J.W., Ed.; Springer: Berlin/Heidelberg, Germany, 1978; pp. 9–43. [Google Scholar] [CrossRef]
- Strohbehn, J.; Clifford, S. Polarization and angle-of-arrival fluctuations for a plane wave propagated through a turbulent medium. IEEE Trans. Antennas Propag. 1967, 15, 416–421. [Google Scholar] [CrossRef]
- Zhang, W.; Saripalli, R.K.; Leamer, J.M.; Glasser, R.T.; Bondar, D.I. All-optical input-agnostic polarization transformer. arXiv 2021, arXiv:2103.05398. [Google Scholar]
- Cvijetic, N.; Qian, D.; Yu, J.; Huang, Y.K.; Wang, T. Polarization-Multiplexed Optical Wireless Transmission with Coherent Detection. J. Light. Technol. 2010, 28, 1218–1227. [Google Scholar] [CrossRef]
- Rosskopf, M.; Mohr, T.; Elsäßer, W. Ghost Polarization Communication. Phys. Rev. Appl. 2020, 13, 034062. [Google Scholar] [CrossRef]
- Zhang, J.; Li, R.; Dang, A. Experimental Studies on Characteristics of Polarization Parameters over Atmospheric Turbulence. In Proceedings of the ECOC 2016—42nd European Conference on Optical Communication, Dusseldorf, Germany, 18–22 September 2016; pp. 1–3. [Google Scholar]
- Tang, X.; Xu, Z.; Ghassemlooy, Z. Coherent Polarization Modulated Transmission through MIMO Atmospheric Optical Turbulence Channel. J. Light. Technol. 2013, 31, 3221–3228. [Google Scholar] [CrossRef]
- Yang, R.; Xue, Y.; Li, Y.; Shi, L.; Zhu, Y.; Zhu, Q. Influence of atmospheric turbulence on the quantum polarization state. In Young Scientists Forum 2017; Zhuang, S., Chu, J., Pan, J.W., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2018; Volume 10710, pp. 36–41. [Google Scholar] [CrossRef]
- Sait, M.; Sun, X.; Alkhazragi, O.; Alfaraj, N.; Kong, M.; Ng, T.K.; Ooi, B.S. The effect of turbulence on NLOS underwater wireless optical communication channels [Invited]. Chin. Opt. Lett. 2019, 17, 100013. [Google Scholar] [CrossRef]
- Zedini, E.; Oubei, H.M.; Kammoun, A.; Hamdi, M.; Ooi, B.S.; Alouini, M.S. Unified Statistical Channel Model for Turbulence-Induced Fading in Underwater Wireless Optical Communication Systems. IEEE Trans. Commun. 2019, 67, 2893–2907. [Google Scholar] [CrossRef]
- Jamali, M.V.; Mirani, A.; Parsay, A.; Abolhassani, B.; Nabavi, P.; Chizari, A.; Khorramshahi, P.; Abdollahramezani, S.; Salehi, J.A. Statistical Studies of Fading in Underwater Wireless Optical Channels in the Presence of Air Bubble, Temperature, and Salinity Random Variations. IEEE Trans. Commun. 2018, 66, 4706–4723. [Google Scholar] [CrossRef]
- Oubei, H.M.; ElAfandy, R.T.; Park, K.H.; Ng, T.K.; Alouini, M.S.; Ooi, B.S. Performance Evaluation of Underwater Wireless Optical Communications Links in the Presence of Different Air Bubble Populations. IEEE Photonics J. 2017, 9, 7903009. [Google Scholar] [CrossRef]
- Shin, M.; Park, K.H.; Alouini, M.S. Statistical Modeling of the Impact of Underwater Bubbles on an Optical Wireless Channel. IEEE Open J. Commun. Soc. 2020, 1, 808–818. [Google Scholar] [CrossRef]
- Barberena, D.; Gatti, G.; Zela, F.D. Experimental demonstration of a secondary source of partially polarized states. J. Opt. Soc. Am. A 2015, 32, 697–700. [Google Scholar] [CrossRef] [PubMed]
- Ijaz, M. Experimental Characterisation and Modelling of Atmospheric Fog and Turbulence in FSO. Ph.D. Thesis, Northumbria University, Newcastle upon Tyne, UK, 2013. [Google Scholar]
- van Vliet, V.; van der Heide, S.; van den Hout, M.; Okonkwo, C. Turbulence Characterisation for Free Space Optical Communication Using Off-Axis Digital Holography. In Signal Processing in Photonic Communications; Optica Publishing Group: Washington, DC, USA, 2022. [Google Scholar] [CrossRef]
- Leamer, J.M.; Zhang, W.; Saripalli, R.K.; Glasser, R.T.; Bondar, D.I. Robust polarimetry via convex optimization. Appl. Opt. 2020, 59, 8886–8894. [Google Scholar] [CrossRef] [PubMed]
- Schaefer, B.; Collett, E.; Smyth, R.; Barrett, D.; Fraher, B. Measuring the Stokes polarization parameters. Am. J. Phys. 2007, 75, 163–168. [Google Scholar] [CrossRef]
- COMSOL Multiphysics ®v. 6.0; COMSOL AB: Stockholm, Sweden; Available online: https://www.comsol.com/release/6.0 (accessed on 26 March 2024).
- Leamer, J.M. DOP Communication. 2020. Available online: https://github.com/jleamer/DOP_Comm (accessed on 26 March 2024).
- Son, I.K.; Mao, S. A survey of free space optical networks. Digit. Commun. Netw. 2017, 3, 67–77. [Google Scholar] [CrossRef]
- Kaushal, H.; Kaddoum, G. Underwater Optical Wireless Communication. IEEE Access 2016, 4, 1518–1547. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. Proc. IEEE Int. Conf. Comput. Syst. Signal Process. 1984, 175, 8. [Google Scholar] [CrossRef]
- Wu, H.W.; Lu, H.H.; Tsai, W.S.; Huang, Y.C.; Xie, J.Y.; Huang, Q.P.; Tu, S.C. A 448-Gb/s PAM4 FSO Communication with Polarization-Multiplexing Injection-Locked VCSELs through 600 M Free-Space Link. IEEE Access 2020, 8, 28859–28866. [Google Scholar] [CrossRef]
- Willner, A.; Ren, Y.; Xie, G.; Yan, Y.; Li, L.; Zhao, Z.; Wang, J.; Tur, M.; Molisch, A.; Ashrafi, S. Recent advances in high-capacity free-space optical and radio-frequency communications using orbital angular momentum multiplexing. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2017, 375, 20150439. [Google Scholar] [CrossRef] [PubMed]
- Takenaka, H.; Carrasco-Casado, A.; Fujiwara, M.; Kitamura, M.; Sasaki, M.; Toyoshima, M. Satellite-to-ground quantum-limited communication using a 50-kg-class microsatellite. Nat. Photonics 2017, 11, 502–508. [Google Scholar] [CrossRef]
- Zhang, D.; Hao, S.; Zhao, Q.; Zhang, M.; Fan, B. Atmospheric turbulence phase screen modeling method based on sub-bands division and multirate sampling. Optik 2018, 163, 72–80. [Google Scholar] [CrossRef]
- Martin, J.M.; Flatté, S.M. Intensity images and statistics from numerical simulation of wave propagation in 3-D random media. Appl. Opt. 1988, 27, 2111–2126. [Google Scholar] [CrossRef] [PubMed]
- Rampy, R.; Gavel, D.; Dillon, D.; Thomas, S. Production of phase screens for simulation of atmospheric turbulence. Appl. Opt. 2012, 51, 8769–8778. [Google Scholar] [CrossRef] [PubMed]
- Wild, A.J.; Hobbs, R.W.; Frenje, L. Modelling complex media: An introduction to the phase-screen method. Phys. Earth Planet. Inter. 2000, 120, 219–225. [Google Scholar] [CrossRef]
- Wu, R.S. Wide-angle elastic wave one-way propagation in heterogeneous media and an elastic wave complex-screen method. J. Geophys. Res. Solid Earth 1994, 99, 751–766. [Google Scholar] [CrossRef]
- Vorontsov, A.M.; Paramonov, P.V.; Valley, M.T.; Vorontsov, M.A. Generation of infinitely long phase screens for modeling of optical wave propagation in atmospheric turbulence. Waves Random Complex Media 2008, 18, 91–108. [Google Scholar] [CrossRef]
- Buckley, R. Diffraction by a random phase-changing screen: A numerical experiment. J. Atmos. Terr. Phys. 1975, 37, 1431–1446. [Google Scholar] [CrossRef]

| Parameter | Symbol | Value |
|---|---|---|
| Power transmitted | ≈24 dBm | |
| Transmitter gain | ≈0 dB | |
| Transmitter loss | ≈15 to 18 dB | |
| Free-space loss | ≈0 dB | |
| Turbulence related loss | ≈13 dB | |
| Receiver gain | ≈0 dB | |
| Receiver loss | ≈0 to 20 dB |
| State | DOP | |||||||
|---|---|---|---|---|---|---|---|---|
| Input | Output | Input | Output | Input | Output | Input | Output | |
| 0 | 0.09 | 0.14 | −0.04 | 0.01 | −0.04 | −0.05 | 0.11 | 0.15 |
| 1 | 0.36 | 0.39 | −0.05 | −0.07 | −0.03 | −0.07 | 0.36 | 0.40 |
| 2 | 0.53 | 0.55 | −0.04 | −0.08 | −0.02 | −0.10 | 0.53 | 0.57 |
| 3 | 0.74 | 0.71 | −0.05 | −0.03 | −0.02 | −0.06 | 0.74 | 0.72 |
| 4 | 0.99 | 0.92 | −0.06 | −0.10 | −0.02 | −0.08 | 0.99 | 0.93 |
| State | DOP | |||||||
|---|---|---|---|---|---|---|---|---|
| Input | Output | Input | Output | Input | Output | Input | Output | |
| 0 | 0.03 | 0.04 | 0.06 | −0.02 | 0.05 | 0.10 | 0.08 | 0.11 |
| 1 | 0.08 | 0.11 | −0.11 | −0.15 | 0.29 | 0.33 | 0.32 | 0.38 |
| 2 | 0.12 | 0.13 | −0.32 | −0.25 | 0.43 | 0.43 | 0.55 | 0.51 |
| 3 | 0.18 | 0.17 | −0.45 | −0.36 | 0.62 | 0.68 | 0.79 | 0.79 |
| 4 | 0.25 | 0.25 | −0.43 | −0.47 | 0.78 | 0.73 | 0.93 | 0.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Savino, N.; Leamer, J.; Saripalli, R.; Zhang, W.; Bondar, D.; Glasser, R. Robust Free-Space Optical Communication Utilizing Polarization for the Advancement of Quantum Communication. Entropy 2024, 26, 309. https://doi.org/10.3390/e26040309
Savino N, Leamer J, Saripalli R, Zhang W, Bondar D, Glasser R. Robust Free-Space Optical Communication Utilizing Polarization for the Advancement of Quantum Communication. Entropy. 2024; 26(4):309. https://doi.org/10.3390/e26040309
Chicago/Turabian StyleSavino, Nicholas, Jacob Leamer, Ravi Saripalli, Wenlei Zhang, Denys Bondar, and Ryan Glasser. 2024. "Robust Free-Space Optical Communication Utilizing Polarization for the Advancement of Quantum Communication" Entropy 26, no. 4: 309. https://doi.org/10.3390/e26040309
APA StyleSavino, N., Leamer, J., Saripalli, R., Zhang, W., Bondar, D., & Glasser, R. (2024). Robust Free-Space Optical Communication Utilizing Polarization for the Advancement of Quantum Communication. Entropy, 26(4), 309. https://doi.org/10.3390/e26040309







