Derivation of the Langevin Equation from the Microcanonical Ensemble
Abstract
1. Introduction
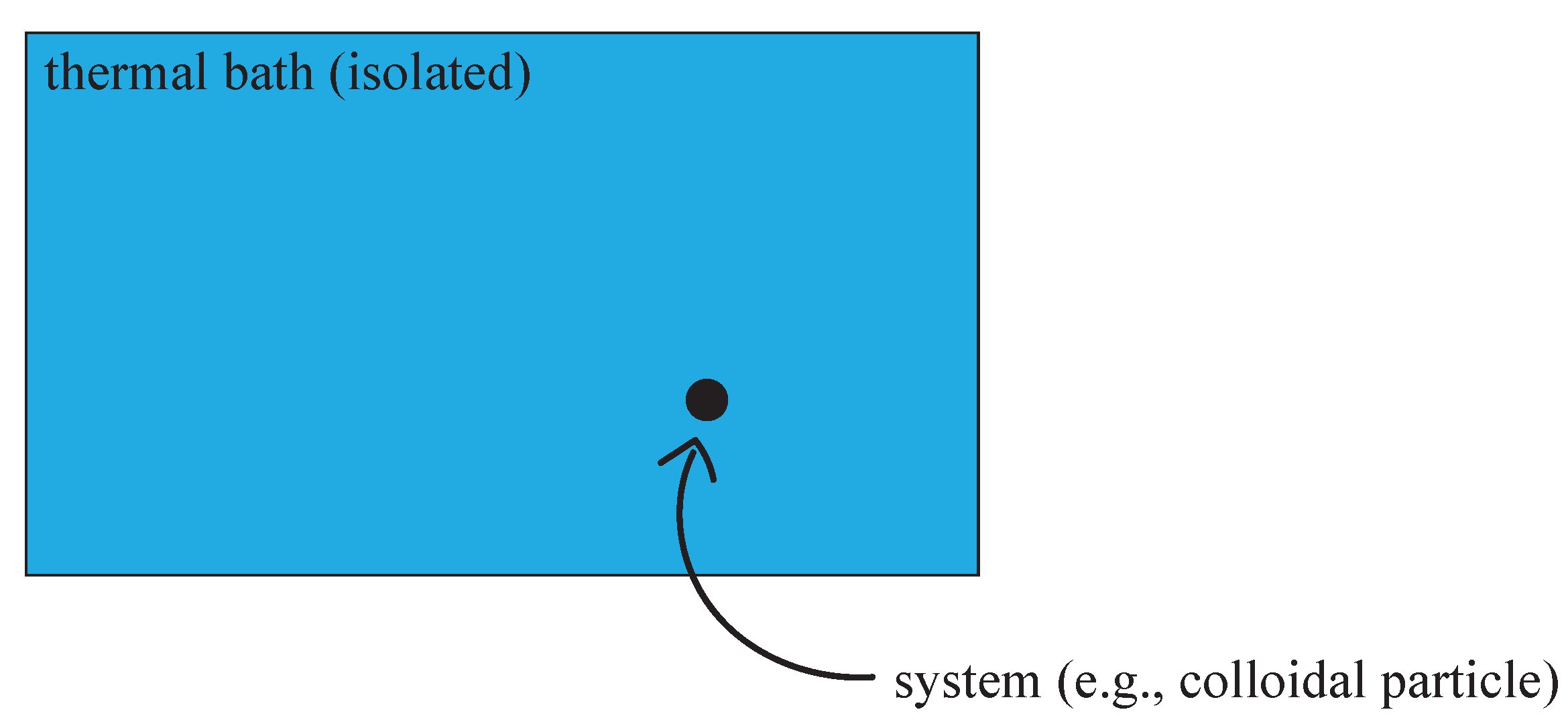
2. Model
2.1. Dynamics
2.2. Statistical Mechanics
3. Effective System Dynamics
3.1. Markov Property
3.2. Average System Behavior
3.2.1. Evaluation of
3.2.2. Evaluation of
Co-Moving Frame
Laboratory Frame
The Contribution in
3.2.3. Evaluation of
3.2.4. Evaluation of
3.2.5. Evaluation of
3.3. Summary
3.4. Rules of Calculus
3.5. Connection to the Fokker-Planck Equation
4. Discussion and Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Odd Averages Vanish
Appendix B. The Replacement δ’ (…)→δ (…)
Appendix C. The Different Representations for γij
References
- Snook, I. The Langevin and Generalized Langevin Approach to the Dynamics of Atomic, Polymeric and Colloidal Systems, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Mazo, R.M. Brownian Motion: Fluctuations, Dynamics and Applications, 1st ed.; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Gardiner, C.W. Handbook of Stochastic Methods, 2nd ed.; Springer: Berlin, Germany, 1985. [Google Scholar]
- van Kampen, N.G. Stochastic Processes in Physics and Chemistry, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Risken, H. The Fokker-Planck Equation, 2nd ed.; Springer: Berlin, Germany, 1989. [Google Scholar]
- Sekimoto, K. Stochastic Energetics, 1st ed.; Springer: Berlin, Germany, 2010. [Google Scholar]
- Goldstein, H.; Poole, C.P.; Safko, J.L. Classical Mechanics, Pearson new int. ed.; Pearson Education Limited: Edinburg, UK, 2013. [Google Scholar]
- Reif, F. Fundamentals of Statistical and Thermal Physics, Int. ed.; McGraw-Hill: Singapore, 1985. [Google Scholar]
- Zuckerman, D.M. Statistical Physics of Biomolecules, 1st ed.; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Zwanzig, R. Ensemble Method. J. Chem. Phys. 1960, 33, 1338–1341. [Google Scholar] [CrossRef]
- Mori, H. Transport, Collective Motion, and Brownian Motion. Prog. Theor. Phys. 1965, 33, 423–455. [Google Scholar] [CrossRef]
- Grabert, H.; Hänggi, P.; Talkner, P. Microdynamics and Nonlinear Stochastic Processes of Gross Variables. J. Stat. Phys. 1980, 22, 537–552. [Google Scholar] [CrossRef]
- Grabert, H. Projection Operator Techniques, 1st ed.; Springer: Berlin, Germany, 1982. [Google Scholar]
- te Vrugt, M.; Wittkowski, R. Projection operators in statistical mechanics: A pedagogical approach. Eur. J. Phys. 2020, 41, 045101. [Google Scholar] [CrossRef]
- Reimann, P. Brownian motors: Noisy transport far from equilibrium. Phys. Rep. 2002, 361, 57–265. [Google Scholar] [CrossRef]
- Zwanzig, R. Nonlinear Generalized Langevin Equations. J. Stat. Phys. 1973, 9, 215–220. [Google Scholar] [CrossRef]
- Miyazaki, K.; Seki, K. Brownian motion of spins revisited. J. Chem. Phys. 1998, 108, 7052–7059. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eichhorn, R. Derivation of the Langevin Equation from the Microcanonical Ensemble. Entropy 2024, 26, 277. https://doi.org/10.3390/e26040277
Eichhorn R. Derivation of the Langevin Equation from the Microcanonical Ensemble. Entropy. 2024; 26(4):277. https://doi.org/10.3390/e26040277
Chicago/Turabian StyleEichhorn, Ralf. 2024. "Derivation of the Langevin Equation from the Microcanonical Ensemble" Entropy 26, no. 4: 277. https://doi.org/10.3390/e26040277
APA StyleEichhorn, R. (2024). Derivation of the Langevin Equation from the Microcanonical Ensemble. Entropy, 26(4), 277. https://doi.org/10.3390/e26040277





