A Numerical Study of Quantum Entropy and Information in the Wigner–Fokker–Planck Equation for Open Quantum Systems
Abstract
1. Introduction
2. Materials and Methods
2.1. Monte-Carlo Solver: Euler–Maruyama Method
2.2. Pseudo-Code and Methodology Description
Algorithm Specifics for the Monte Carlo Solver of Wigner–Fokker–Planck
- Parameter Definitions
- L: Length of the domain in position space.
- and : Diagonal matrix elements of the covariance matrix of the Wigner function at the initial time.
- : Time step for the simulation.
- : Mean value vector for the initial distribution.
- and : Components of the mean value vector for the position and momentum, respectively.
- and : Diffusion coefficients for position and momentum, respectively.
- D: Diffusion matrix (assumed having zero off-diagonal terms).
- : Friction coefficient.
- Array Definitions
- q: Array to store position values for each particle at each time step.
- p: Array to store momentum values for each particle at each time step.
- Initial Conditions
- Gaussian Sampling: Initialize the position and momentum of each particle at the first time step using normal random number generation with mean components and standard deviations , .
- Time Evolution Loop
- Use nested loops to iterate over each time step i and each particle j.
- Generate random noise using a multivariate normal distribution with mean and as covariance matrix for position and momentum.
- Update the position and momentum of each particle using the Euler–Maruyama stochastic method.
- Simulation Output
- After the completion of the time evolution loop, the arrays q and p contain the simulated trajectories of position and momentum for each particle over time.
| Algorithm 1 Euler–Maruyama for the Wigner–Fokker–Planck equation (harmonic potential) |
|
3. Results
3.1. Wigner–Fokker–Planck Model: Gaussian States under Harmonic Potential
3.1.1. Husimi Transform of a Gaussian State (Gaussian Wigner Function)
3.1.2. Husimi Transform of Steady-State Solution for Harmonic Benchmark Problem
3.1.3. Husimi Transform of Harmonic Groundstate
3.1.4. Wehrl Entropy of a Gaussian State through Its Husimi Transform
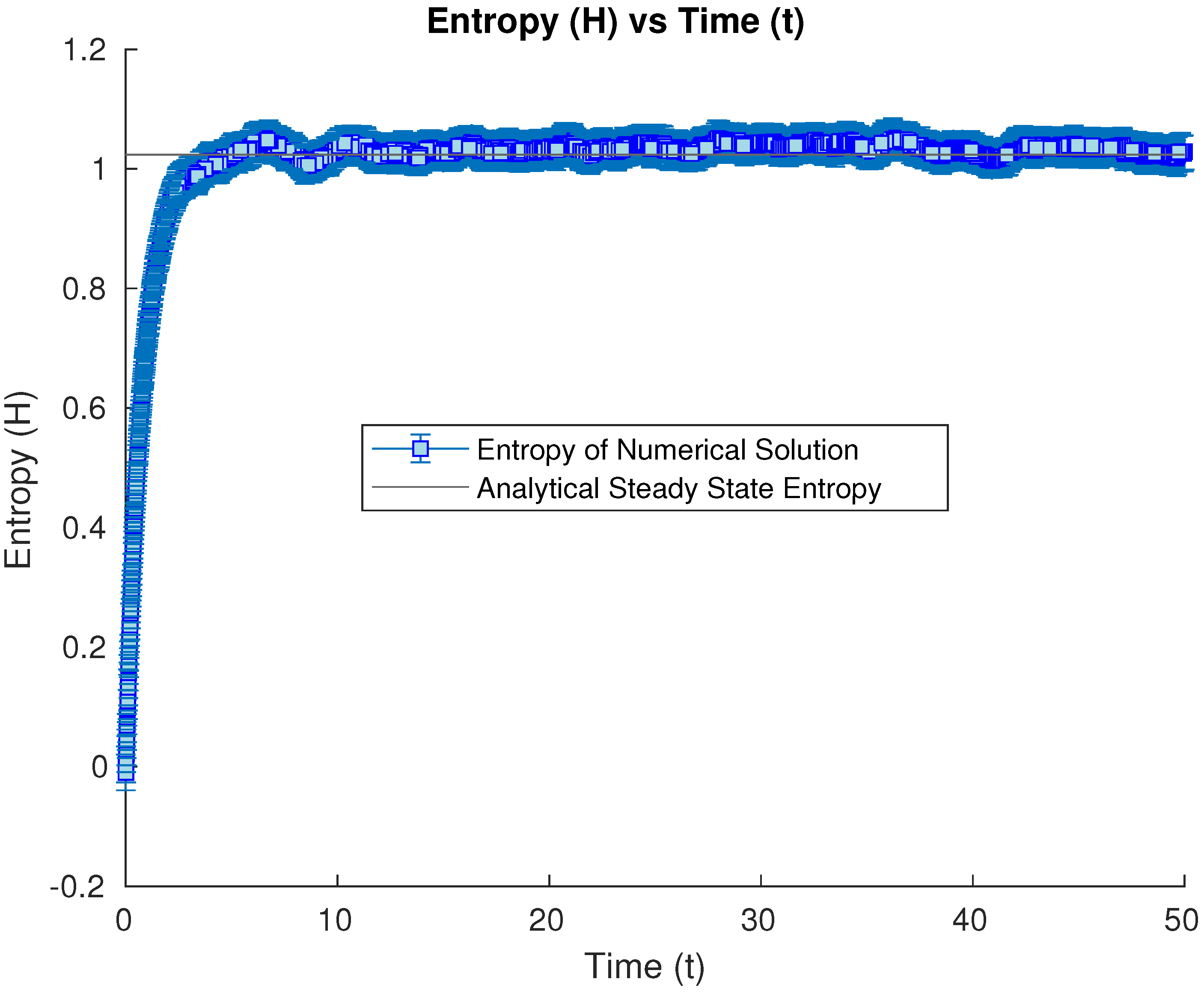
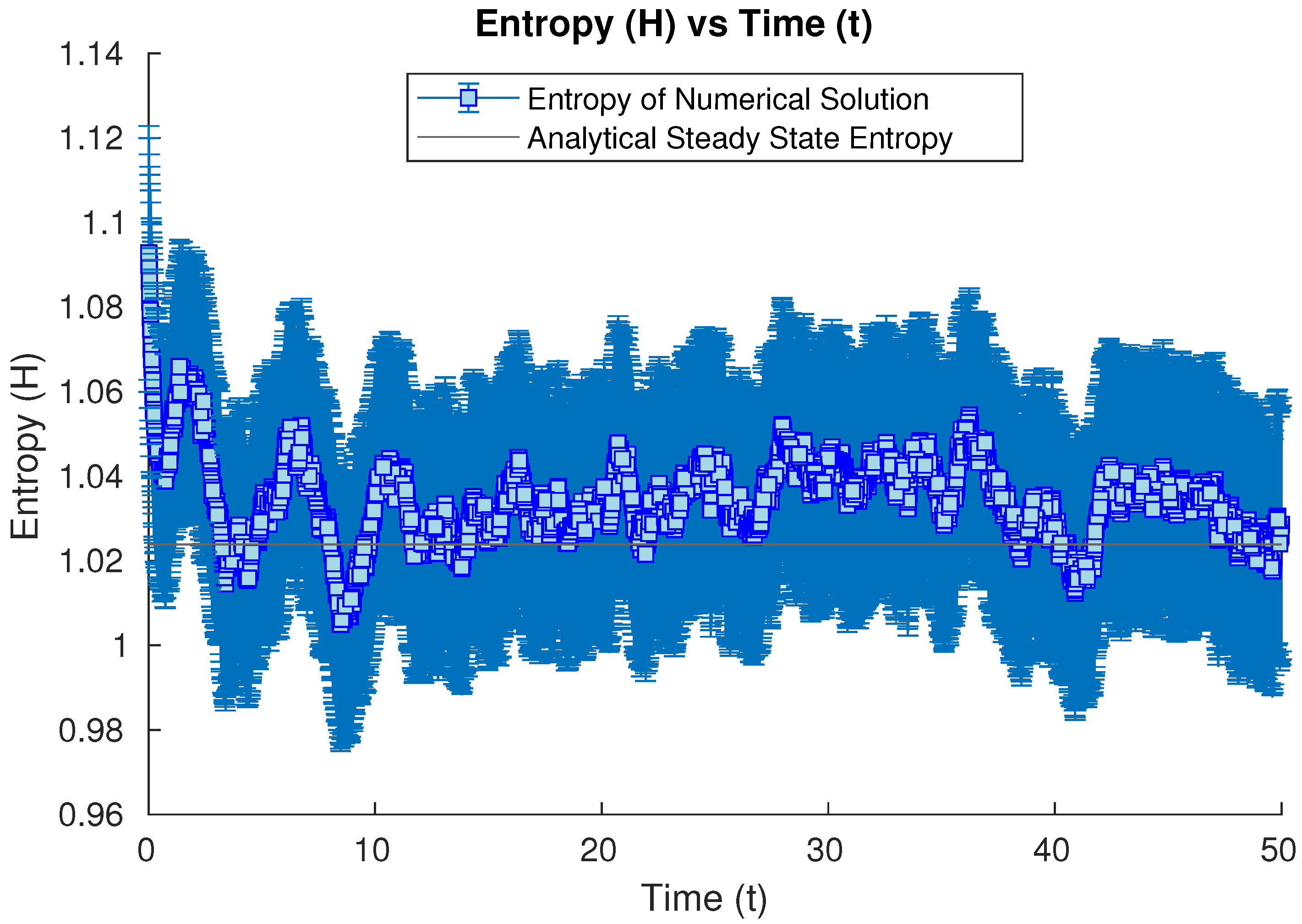
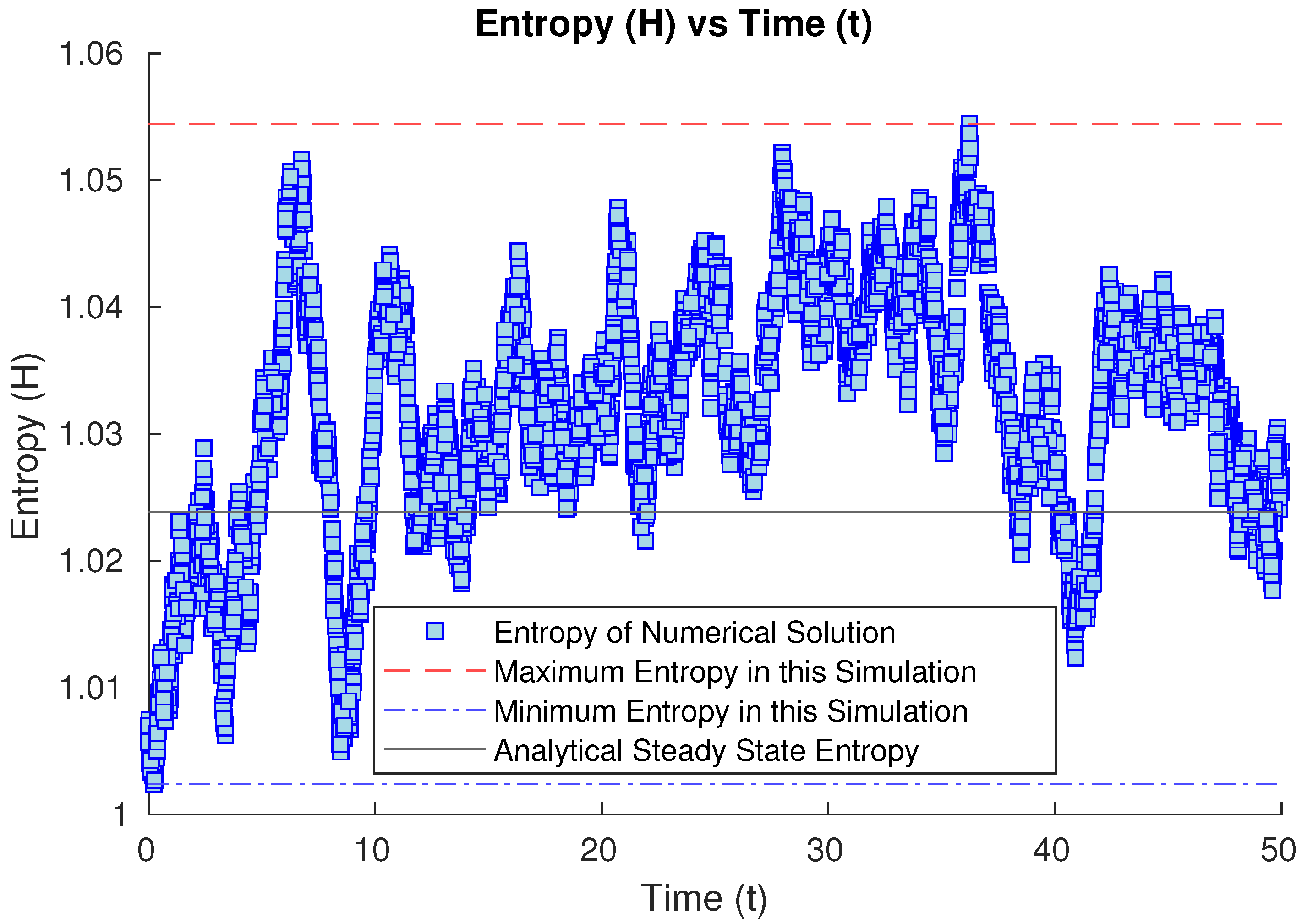
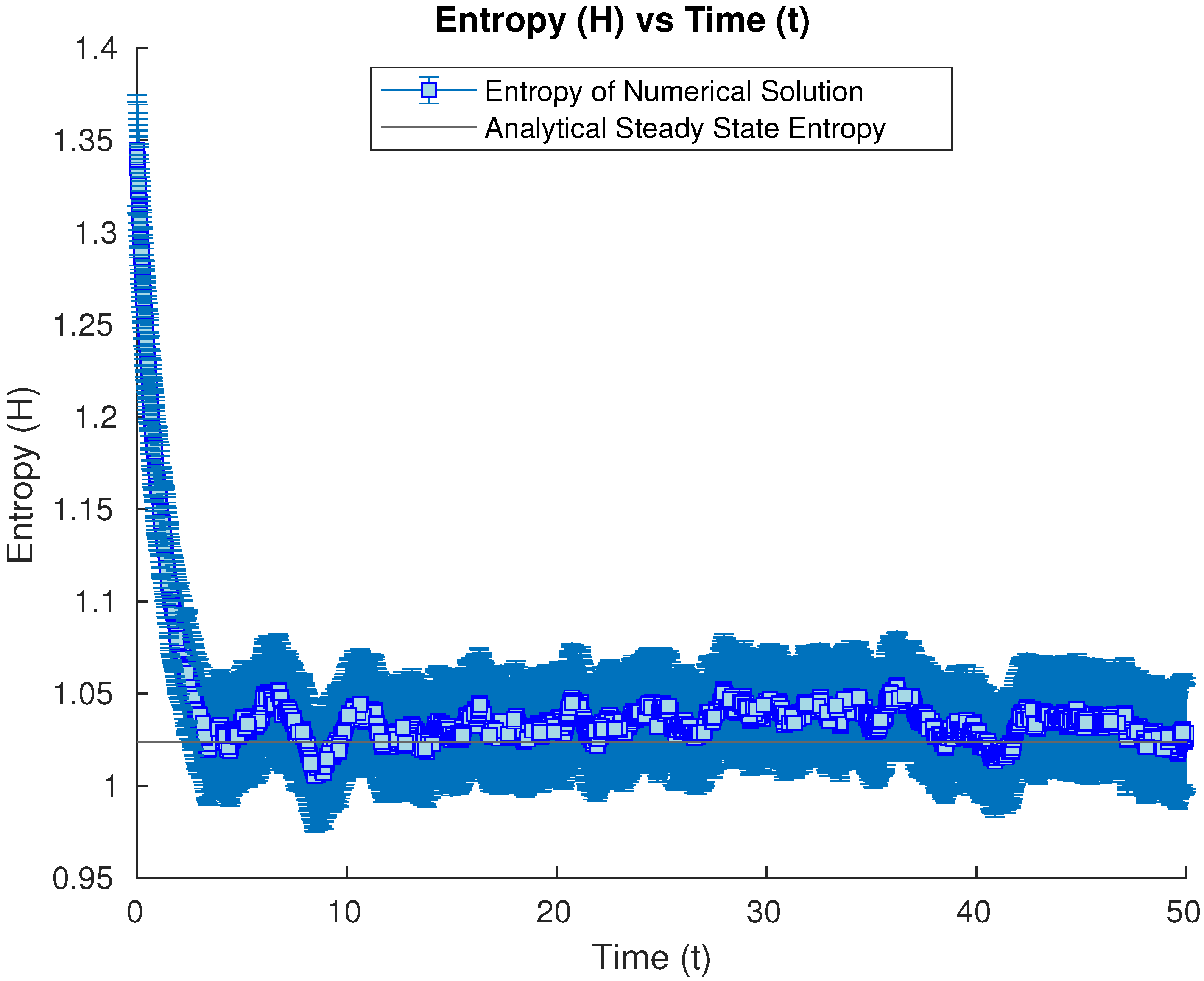
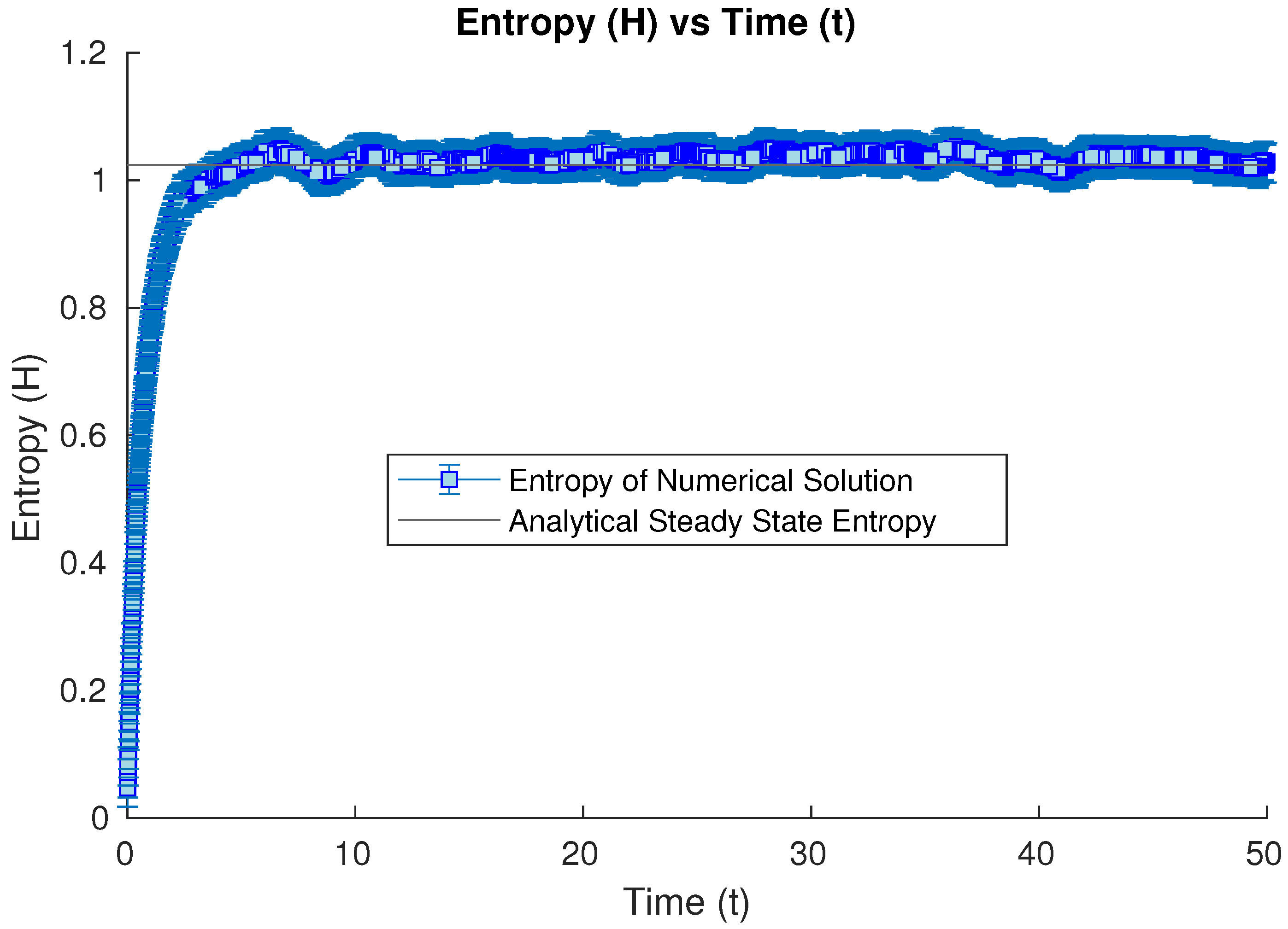
3.1.5. Numerical Results of Entropy Behavior
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Weighted L2-Distance between Wigner Function and Steady-State Solution for Harmonic Potential
References
- Ding, Z.; Chen, C.F.; Lin, L. Single-ancilla ground state preparation via Lindbladians. arXiv 2023, arXiv:2308.15676. [Google Scholar]
- Gamba, I.; Gualdani, M.P.; Sharp, R.W. An adaptable discontinuous Galerkin scheme for the Wigner-Fokker–Planck equation. Commun. Math. Sci. 2009, 7, 635–664. [Google Scholar] [CrossRef]
- Sparber, C.; Carrillo, J.; Dolbeault, J.; Markowich, P. On the Long Time Behavior of the Quantum Fokker–Planck Equation. Monatshefte Math. 2004, 141, 237–257. [Google Scholar] [CrossRef]
- D’ariano, G.; Macchiavello, C.; Moroni, S. On the Monte Carlo simulation approach to Fokker–Planck equations in quantum optics. Mod. Phys. Lett. B 1994, 08, 239–246. [Google Scholar] [CrossRef]
- Frensley, W.R. Boundary conditions for open quantum systems driven far from equilibrium. Rev. Mod. Phys. 1990, 62, 745–791. [Google Scholar] [CrossRef]
- Ringhofer, C. A Spectral Method for the Numerical Simulation of Quantum Tunneling Phenomena. SIAM J. Numer. Anal. 1990, 27, 32–50. [Google Scholar] [CrossRef]
- Arnold, A.; Ringhofer, C. An Operator Splitting Method for the Wigner–Poisson Problem. SIAM J. Numer. Anal. 1996, 33, 1622–1643. [Google Scholar] [CrossRef]
- Goudon, T. Analysis of a Semidiscrete Version of the Wigner Equation. SIAM J. Numer. Anal. 2002, 40, 2007–2025. [Google Scholar] [CrossRef]
- Keener, J. Biology in Time and Space: A Partial Differential Equation Modeling Approach; Pure and Applied Undergraduate Texts; American Mathematical Society: Providence, RI, USA, 2021. [Google Scholar]
- Nedjalkov, M.; Kosina, H.; Selberherr, S.; Ringhofer, C.; Ferry, D.K. Unified particle approach to Wigner-Boltzmann transport in small semiconductor devices. Phys. Rev. B 2004, 70, 115319. [Google Scholar] [CrossRef]
- Muscato, O. A benchmark study of the Signed-particle Monte Carlo algorithm for the Wigner equation. Commun. Appl. Ind. Math. 2017, 8, 237–250. [Google Scholar] [CrossRef][Green Version]
- Ganiu, V.; Schulz, D. Application of Discontinuous Galerkin Methods onto Quantum–Liouville type Equations. In Proceedings of the International Workshop on Computational Nanotechnology, Barcelona, Spain, 12–16 June 2023. [Google Scholar]
- Suh, N.D.; Feix, M.R.; Bertrand, P. Numerical simulation of the quantum Liouville–Poisson system. J. Comput. Phys. 1991, 94, 403–418. [Google Scholar] [CrossRef]
- Morales, J.; Boada-Gutierrez, M.G. Discontinuous Galerkin schemes for Master Equations Modeling Open Quantum Systems; NUMTA conference paper, Springer Lecture Notes in Computer Science; UTSA: San Antonio, TX, USA, 2024. [Google Scholar]
- Morales Escalante, J.A. NIPG-DG schemes for transformed master equations modeling open quantum systems. arXiv 2023, arXiv:2308.11580. [Google Scholar]
- Markowich, P.A.; Villani, C. On the trend to equilibrium for the Fokker–Planck equation: An interplay between physics and functional analysis. Mat. Contemp. (SBM) 2000, 19, 1–2. [Google Scholar]
- Jüngel, A. Entropy Methods for Diffusive Partial Differential Equations; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Wehrl, A. On the relation between classical and quantum-mechanical entropy. Rep. Math. Phys. 1979, 16, 353–358. [Google Scholar] [CrossRef]
- Arnold, A.; López, J.L.; Markowich, P.A.; Soler, J. An analysis of quantum Fokker–Planck models: A Wigner function approach. Rev. Matemática Iberoam. 2004, 20, 771–814. [Google Scholar] [CrossRef]
- Jordan, R.; Kinderlehrer, D.; Otto, F. The Variational Formulation of the Fokker–Planck Equation. SIAM J. Math. Anal. 1998, 29, 1–17. [Google Scholar] [CrossRef]
- Arnold, A.; Markowich, P.; Toscani, G.; Unterreiter, A. On convex sobolev inequalities and the rate of convergence to equilibrium for Fokker–Planck type equations. Commun. Partial. Differ. Equations 2001, 26, 43–100. [Google Scholar] [CrossRef]
- Temme, K.; Pastawski, F.; Kastoryano, M.J. Hypercontractivity of quasi-free quantum semigroups. J. Phys. A Math. Theor. 2014, 47, 405303. [Google Scholar] [CrossRef]
- Müller-Hermes, A.; Franca, D.S. Sandwiched Rényi Convergence for Quantum Evolutions. Quantum 2018, 2, 55. [Google Scholar] [CrossRef]
- Carlen, E.A.; Maas, J. Gradient flow and entropy inequalities for quantum Markov semigroups with detailed balance. J. Funct. Anal. 2017, 273, 1810–1869. [Google Scholar] [CrossRef]
- Maas, J. Gradient flows of the entropy for finite Markov chains. arXiv 2011, arXiv:1102.5238. [Google Scholar] [CrossRef]
- Cao, Y.; Lu, J.; Lu, Y. Exponential Decay of Rényi Divergence Under Fokker–Planck Equations. J. Stat. Phys. 2019, 176, 1172–1184. [Google Scholar] [CrossRef]
- Cheng, Y.; Gamba, I.; Proft, J. Positivity-preserving discontinuous Galerkin schemes for linear Vlasov-Boltzmann transport equations. Math. Comput. 2012, 81, 153–190. [Google Scholar] [CrossRef][Green Version]
- Heath, R.; Gamba, I.; Morrison, P.; Michler, C. A discontinuous Galerkin method for the Vlasov–Poisson system. J. Comput. Phys. 2012, 231, 1140–1174. [Google Scholar] [CrossRef]
- Pennie, C.A.; Gamba, I.M. Entropy Decay Rates for Conservative Spectral Schemes Modeling Fokker–Planck–Landau Type Flows in the Mean Field Limit. arXiv 2020, arXiv:1910.03110. [Google Scholar]
- Pennie, C.A.; Gamba, I.M. Decay of entropy from a conservative spectral method for Fokker–Planck–Landau type equations. AIP Conf. Proc. 2019, 2132, 020001. [Google Scholar] [CrossRef]
- Case, W.B. Wigner functions and Weyl transforms for pedestrians. Am. J. Phys. 2008, 76, 937–946. [Google Scholar] [CrossRef]
- Sellier, J.M.; Dimov, I. Wigner Functions, Signed Particles, and the Harmonic Oscillator. J. Comput. Electron. 2015, 14, 907–915. [Google Scholar] [CrossRef]
- Ferry, D.K.; Nedjalkov, M. The Wigner Function in Science and Technology; IoP Publishing: Bristol, UK, 2018. [Google Scholar]
- Benam, M.; Nedjalkov, M.; Selberherr, S. A Wigner Potential Decomposition in the Signed-Particle Monte Carlo Approach. In Numerical Methods and Applications; Nikolov, G., Kolkovska, N., Georgiev, K., Eds.; Springer: Cham, Switzerland, 2019; pp. 263–272. [Google Scholar]
- Serafini, A. Quantum Continuous Variables: A Primer of Theoretical Methods; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2017. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Edrisi, A.; Patwa, H.; Morales Escalante, J.A. A Numerical Study of Quantum Entropy and Information in the Wigner–Fokker–Planck Equation for Open Quantum Systems. Entropy 2024, 26, 263. https://doi.org/10.3390/e26030263
Edrisi A, Patwa H, Morales Escalante JA. A Numerical Study of Quantum Entropy and Information in the Wigner–Fokker–Planck Equation for Open Quantum Systems. Entropy. 2024; 26(3):263. https://doi.org/10.3390/e26030263
Chicago/Turabian StyleEdrisi, Arash, Hamza Patwa, and Jose A. Morales Escalante. 2024. "A Numerical Study of Quantum Entropy and Information in the Wigner–Fokker–Planck Equation for Open Quantum Systems" Entropy 26, no. 3: 263. https://doi.org/10.3390/e26030263
APA StyleEdrisi, A., Patwa, H., & Morales Escalante, J. A. (2024). A Numerical Study of Quantum Entropy and Information in the Wigner–Fokker–Planck Equation for Open Quantum Systems. Entropy, 26(3), 263. https://doi.org/10.3390/e26030263






