Constrained Reweighting of Distributions: An Optimal Transport Approach
Abstract
1. Introduction
2. General Framework
3. Semi-Parametric Inference in Complex Surveys
3.1. Related Works
3.2. Proposed Methodology
3.3. Experiments
3.4. National Health and Nutrition Examination Surveys (NHANES) Data Analysis
4. Demographic Parity
4.1. Proposed Methodology
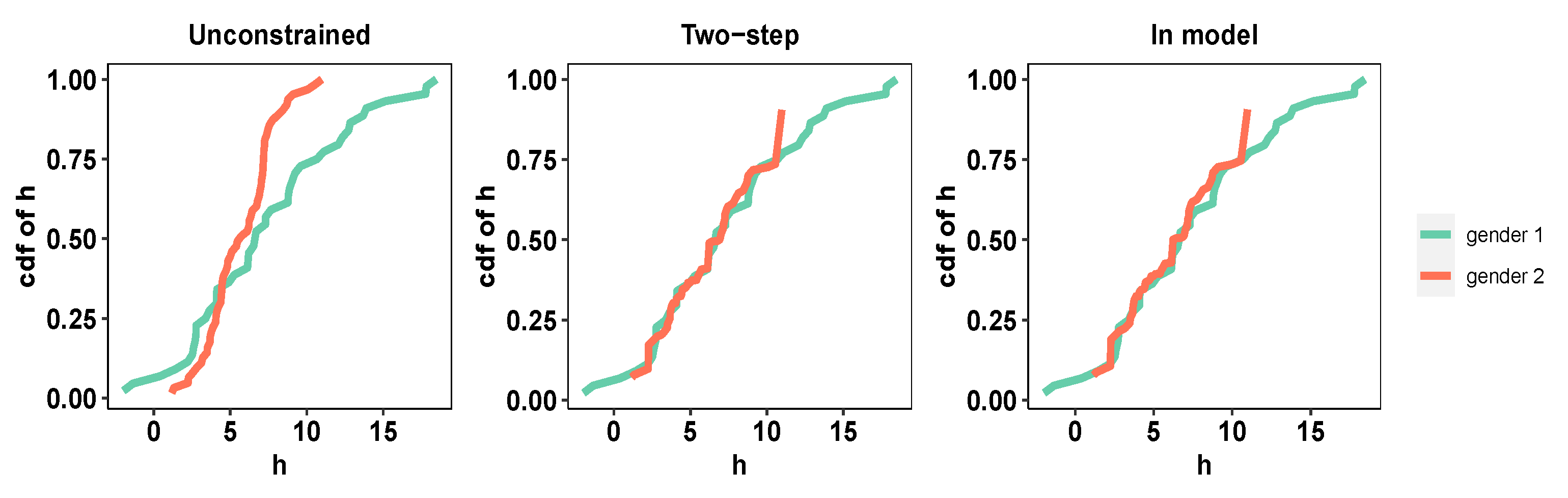
4.2. Distress Analysis Interview Corpus (DAIC)
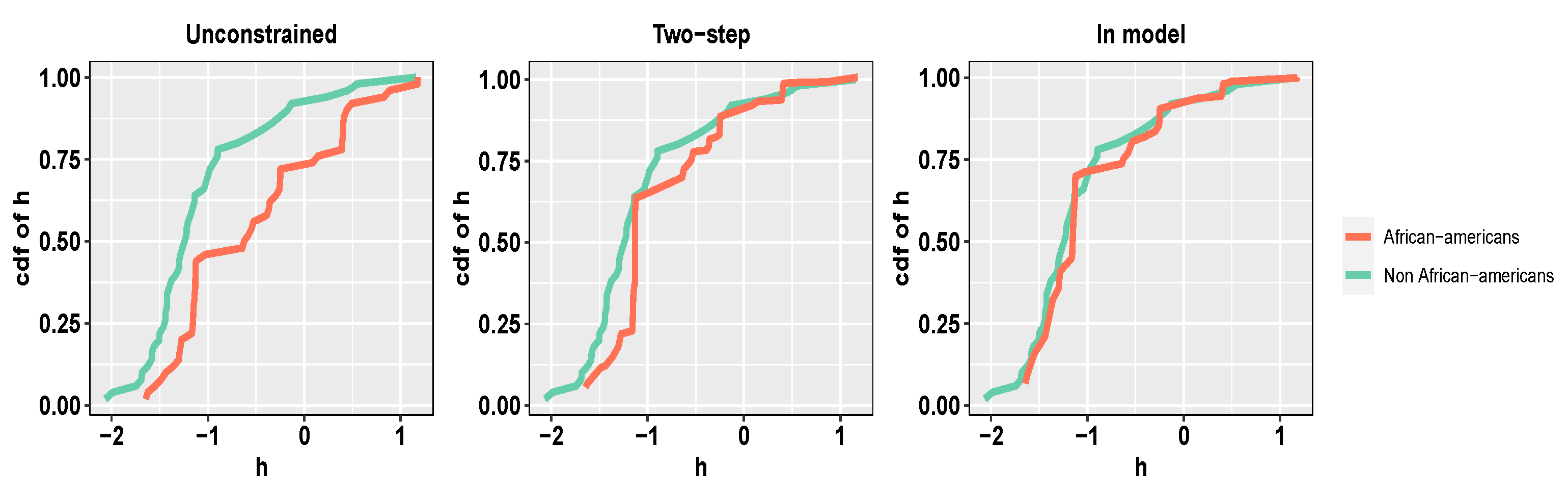
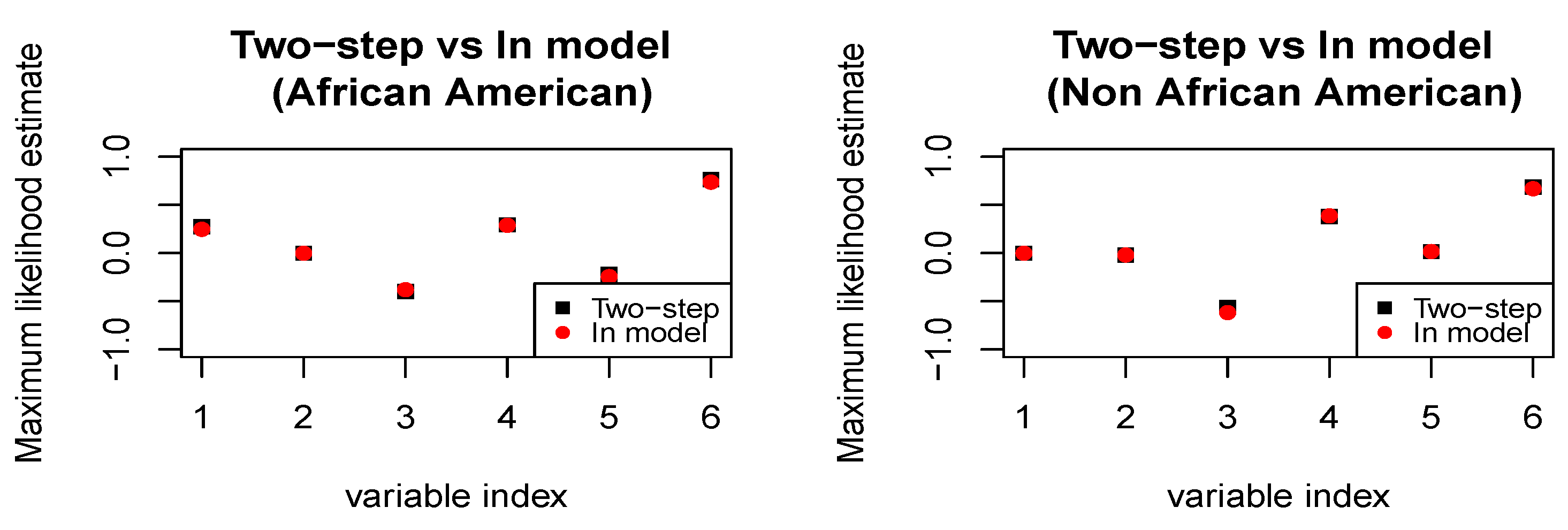
4.3. COMPAS Recidivism Data Analysis
5. Entropy-Based Portfolio Allocation
5.1. Related Works
5.2. Proposed Methodology
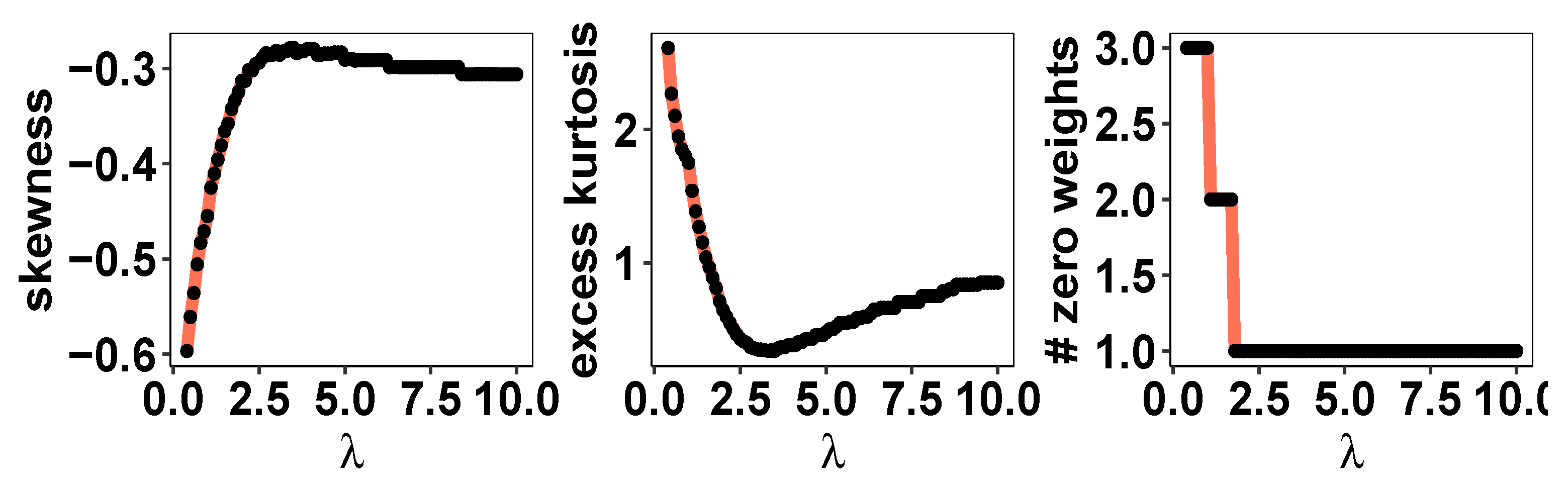
5.3. Historical Stock Returns Data Analysis
6. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev. Ser. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Skilling, J.; Bryan, R.K. Maximum entropy image reconstruction: General algorithm. Mon. Not. R. Astron. Soc. 1984, 211, 111–124. [Google Scholar] [CrossRef]
- Gamboa, F.; Gassiat, E. Bayesian methods and maximum entropy for ill-posed inverse problems. Ann. Stat. 1997, 25, 328–350. [Google Scholar] [CrossRef]
- Bera, A.K.; Park, S.Y. Optimal portfolio diversification using the maximum entropy principle. Econom. Rev. 2008, 27, 484–512. [Google Scholar] [CrossRef]
- Chib, S.; Shin, M.; Simoni, A. Bayesian estimation and comparison of moment condition models. J. Am. Stat. Assoc. 2018, 113, 1656–1668. [Google Scholar] [CrossRef]
- Gudivada, V.N. Computational analysis and understanding of natural languages: Principles, methods and applications. In Handbook of Statistics; Elsevier: Amstardam, The Netherlands, 2018. [Google Scholar]
- de Abril, I.M.; Yoshimoto, J.; Doya, K. Connectivity inference from neural recording data: Challenges, mathematical bases and research directions. Neural Netw. 2018, 102, 120–137. [Google Scholar]
- Eysenbach, B.; Levine, S. Maximum entropy RL (provably) solves some robust RL problems. CoRR. 2021. Available online: https://arxiv.org/abs/2103.06257 (accessed on 16 October 2023).
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Kardar, M. Statistical Physics of Particles; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Einmahl, J.H.J.; Krajina, A.; Segers, J. A method of moments estimator of tail dependence. Bernoulli 2008, 14, 1003–1026. [Google Scholar] [CrossRef]
- Chernozhukov, V.; Newey, W.K.; Santos, A. Constrained conditional moment restriction models. Econometrica 2023, 91, 709–736. [Google Scholar] [CrossRef]
- Chakraborty, A.; Bhattacharya, A.; Pati, D. Robust Probabilistic Inference via a Constrained Transport Metric. 2023. Available online: https://arxiv.org/abs/2303.10085 (accessed on 16 October 2023).
- Rachev, S.T.; Stoyanov, S.; Fabozzi, F.J. Advanced Stochastic Models, Risk Assessment, and Portfolio Optimization: The Ideal Risk, Uncertainty, and Performance Measures; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Santambrogio, F. Optimal Transport for Applied Mathematicians. Calculus of Variations, Pdes and Modeling. 2015. Available online: https://www.math.u-psud.fr/~filippo/OTAM-cvgmt.pdf (accessed on 16 October 2023).
- Villani, C. Topics in Optimal Transportation; American Mathematical Society. 2003. Available online: https://www.math.ucla.edu/~wgangbo/Cedric-Villani.pdf (accessed on 16 October 2023).
- Wang, Y.; Kucukelbir, A.; Blei, D.M. Robust probabilistic modeling with bayesian data reweighting. In Proceedings of the 34th International Conference on Machine Learning—Volume 70; JMLR. org: Sydney, Australia, 2017; pp. 3646–3655. [Google Scholar]
- Wen, J.; Yu, C.-N.J.; Greiner, R. Robust learning under uncertain test distributions: Relating covariate shift to model misspecification. In Proceedings of the International Conference on Machine Learning (ICML), Beijing, China, 21–26 June 2014. [Google Scholar]
- Yan, B.; Seto, S.; Apostoloff, N. Forml: Learning to Reweight Data for Fairness. 2022. Available online: https://arxiv.org/abs/2202.01719 (accessed on 16 October 2023).
- Ramas, J.G.; Le, T.; Chen, B.; Kumar, M.; Kay Rottmann, K. Unsupervised training data reweighting for natural language understanding with local distribution approximation. In Proceedings of the EMNLP 2022, Abu Dhabi, UAE, 7–11 December 2022; Available online: https://www.amazon.science/publications/unsupervised-training-data-reweighting-for-natural-language-understanding-with-local-distribution-approximation (accessed on 16 October 2023).
- Mandt, S.; McInerney, J.; Abrol, F.; Ranganath, R.; Blei, D. Variational tempering. In Artificial Intelligence and Statistics; Cadiz, Spain, 2016; pp. 704–712. [Google Scholar]
- White, H. Maximum likelihood estimation of misspecified models. Econometrica 1982, 50, 1–25. Available online: http://www.jstor.org/stable/1912526 (accessed on 16 October 2023). [CrossRef]
- Hall, A. Generalized Method of Moments; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Chib, S.; Shin, M.; Simoni, A. Bayesian estimation and comparison of conditional moment models. arXiv 2021, arXiv:2110.13531. [Google Scholar]
- Azzalini, A.; DALLA Valle, A. The multivariate skew-normal distribution. Biometrika 1996, 83, 715–726. [Google Scholar] [CrossRef]
- Panaretos, V.M.; Zemel, Y. Statistical aspects of Wasserstein distances. Annu. Rev. Stat. Its Appl. 2019, 6, 405–431. [Google Scholar] [CrossRef]
- Owen, A.B. Empirical likelihood ratio confidence intervals for a single functional. Biometrika 1988, 75, 237–249. [Google Scholar] [CrossRef]
- Owen, A.B. Empirical likelihood confidence regions. Ann. Stat. 1990, 18, 90–120. [Google Scholar] [CrossRef]
- Owen, A.B. Empirical likelihood for linear models. Ann. Stat. 1991, 19, 1725–1747. [Google Scholar] [CrossRef]
- Owen, A.B. Empirical Likelihood; Chapman and Hall/CRC: Boca Raton, FL, USA, 2001. [Google Scholar]
- Qin, J.; Lawless, J.L. Empirical likelihood and general estimating equations. Ann. Stat. 1994, 22, 300–325. [Google Scholar] [CrossRef]
- Nordman, D.J.; Lahiri, S.N. A review of empirical likelihood methods for time series. J. Stat. Plan. Inference 2014, 155, 1–18. [Google Scholar] [CrossRef]
- Newey, W.; Smith, R.J. Higher-order properties of gmm and generalized empirical likelihood estimators. Econometrica 2004, 72, 219–255. [Google Scholar] [CrossRef]
- Schennach, S.M. Point estimation with exponentially tilted empirical likelihood. Ann. Stat. 2007, 35, 634–672. [Google Scholar] [CrossRef]
- Brown, K.C.; Harlow, W.V.; Tinic, S.M. Risk aversion, uncertain information, and market efficiency. J. Financ. Econ. 1988, 22, 355–385. [Google Scholar] [CrossRef]
- De Luca, G.; Loperfido, N. A skew-in-mean garch model for financial returns. In Skew-Elliptical Distributions and Their Applications: A Journey beyond Normality; CRC/Chapman & Hall: Boca Raton, FL, USA, 2004; pp. 205–222. [Google Scholar]
- Peiro, A. Skewness in financial returns. J. Bank. Financ. 1999, 23, 847–862. [Google Scholar] [CrossRef]
- Birgin, E.G.; Martínez, J.M. Improving ultimate convergence of an augmented lagrangian method. Optim. Methods Softw. 2008, 23, 177–195. [Google Scholar] [CrossRef]
- Conn, A.R.; Gould, N.I.M.; Toint, P. A globally convergent augmented lagrangian algorithm for optimization with general constraints and simple bounds. Siam J. Numer. Anal. 1991, 28, 545–572. [Google Scholar] [CrossRef]
- Becker, S.R.; Candès, E.J.; Grant, M. Templates for convex cone problems with applications to sparse signal recovery. Math. Program. Comput. 2011, 3, 165–218. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022; Available online: https://www.R-project.org/ (accessed on 16 October 2023).
- Johnson, S.G. The Nlopt Nonlinear-Optimization Package; The Comprehensive R Archive Network; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]
- Grant, M.; Boyd, S. Graph implementations for nonsmooth convex programs. In Recent Advances in Learning and Control, Lecture Notes in Control and Information Sciences; Blondel, V., Boyd, S., Kimura, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 95–110. Available online: http://stanford.edu/~boyd/graph_dcp.html (accessed on 16 October 2023).
- Gunawan, D.; Panagiotelis, A.; Griffiths, W.; Chotikapanich, D. Bayesian weighted inference from surveys. Aust. N. Z. J. Stat. 2020, 62, 71–94. [Google Scholar] [CrossRef]
- Lumley, T. Complex Surveys: A Guide to Analysis Using R: A Guide to Analysis Using R; John Wiley and Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Cohen, M.P. The Bayesian Bootstrap and Multiple Imputation for Unequal Probability Sample Designs; Technical report; National Center for Education Statistics: New Jersey Avenue, NW, USA; Washington, DC, USA, 1997. [Google Scholar]
- Dong, Q.; Elliott, M.R.; Raghunathan, T.E. A nonparametric method to generate synthetic populations to adjust for complex sampling design features. Surv. Methodol. 2014, 40, 29–46. [Google Scholar]
- Lo, A.Y. A bayesian method for weighted sampling. Ann. Stat. 1993, 21, 2138–2148. [Google Scholar] [CrossRef]
- Agarwal, A.; Dudík, M.; Wu, Z.S. Fair regression: Quantitative definitions and reduction-based algorithms. In Proceedings of the 36th International Conference on Machine Learning, ICML 2019, Long Beach, CA, USA, 9–15 June 2019; International Machine Learning Society (IMLS): Bellevue, WA, USA, 2019; pp. 166–183. [Google Scholar]
- Gajane, P.; Pechenizkiy, M. On Formalizing Fairness in Prediction with Machine Learning. 2018. Available online: https://www.fatml.org/media/documents/formalizing_fairness_in_prediction_with_ml.pdf (accessed on 16 October 2023).
- Elton, E.J.; Gruber, M.J.; Brown, S.J.; Goetzmann, W.N. Modern Portfolio Theory and Investment Analysis; Wiley: Hoboken, NJ, USA, 2014; ISBN 978-1118469941. [Google Scholar]
- Markowitz, H. Portfolio selection. J. Financ. 1952, 7, 77–91. Available online: http://www.jstor.org/stable/2975974 (accessed on 16 October 2023).
- Wooldridge, J.M. Inverse probability weighted estimation for general missing data problems. J. Econom. 2007, 141, 1281–1301. Available online: https://www.sciencedirect.com/science/article/pii/S0304407607000437 (accessed on 16 October 2023). [CrossRef]
- Schennach, S.M. Bayesian exponentially tilted empirical likelihood. Biometrika 2005, 92, 31–46. [Google Scholar] [CrossRef]
- León-Novelo, L.G.; Savitsky, T.D. Fully Bayesian estimation under informative sampling. Electron. J. Statist. 2019, 13, 1608–1645. [Google Scholar] [CrossRef]
- Fitzsimons, J.; Al Ali, A.; Osborne, M.; Roberts, S. A general framework for fair regression. Entropy 2019, 21, 741. [Google Scholar] [CrossRef]
- Yang, D.; Lafferty, J.; Pollard, D. Fair Quantile Regression. 2019. Available online: https://arxiv.org/abs/1907.08646 (accessed on 16 October 2023).
- Jiang, R.; Pacchiano, A.; Stepleton, T.; Jiang, H.; Chiappa, S. Wasserstein fair classification. In Machine Learning Research, Proceedings of the 35th Uncertainty in Artificial Intelligence Conference, Tel Aviv, Israel, 22–25 July 2019; Adams., R.P., Gogate, V., Eds.; PMLR, Association for Uncertainty in Artificial, Intelligence: Pittsburg, PA, USA, 2020; Volume 115, pp. 862–872. Available online: https://proceedings.mlr.press/v115/jiang20a.html (accessed on 16 October 2023).
- Nandy, P.; DiCiccio, C.; Venugopalan, D.; Logan, H.; Basu, K.; El Karoui, N. Achieving fairness via post-processing in web-scale recommender systems. In Proceedings of the 2022 ACM Conference on Fairness, Accountability, and Transparency (FAccT ’22), Seoul, Republic of Korea, 21–24 June 2022; Association for Computing Machinery: New York, NY, USA, 2022; pp. 715–725. [Google Scholar] [CrossRef]
- Xian, R.; Yin, L.; Zhao, H. Fair and optimal classification via post-processing. In Machine Learning Research, Proceedings of the 40th International Conference on Machine Learning, Honolulu, HI, USA, 23–29 July 2023; Krause, A., Brunskill, E., Cho, K., Engelhardt, B., Sabato, S., Scarlett, J., Eds.; PMLR: Bellevue, WA, USA, 2023; Volume 202, pp. 37977–38012. Available online: https://proceedings.mlr.press/v202/xian23b.html (accessed on 16 October 2023).
- Gratch, J.; Artstein, R.; Lucas, G.; Stratou, G.; Scherer, S.; Nazarian, A.; Wood, R.; Boberg, J.; DeVault, D.; Marsella, S.; et al. The distress analysis interview corpus of human and computer interviews. In Proceedings of the Ninth International Conference on Language Resources and Evaluation (LREC’14), Reykjavik, Iceland, 26–31 May 2014; European Language Resources Association (ELRA): Paris, France, 2014; pp. 3123–3128. Available online: http://www.lrec-conf.org/proceedings/lrec2014/pdf/508_Paper.pdf (accessed on 16 October 2023).
- Aliverti, E.; Lum, K.; Johndrow, J.E.; Dunson, D.B. Removing the influence of group variables in high-dimensional predictive modelling. J. R. Stat. Soc. Ser. Stat. Soc. 2021, 184, 791–811. Available online: https://rss.onlinelibrary.wiley.com/doi/abs/10.1111/rssa.12613 (accessed on 16 October 2023). [CrossRef]
- Mills, T.C. Modelling skewness and kurtosis in the london stock exchange ft-se index return distributions. Statistician 1995, 44, 323–332. [Google Scholar] [CrossRef]
- Liechty, M.W.; Harvey, C.R.; Liechty, J.C.; Müller, P. Portfolio selection with higher moments. Quant. Financ. 2010, 10, 469–485. [Google Scholar] [CrossRef]
- Mehlawat, M.K.; Gupta, P.; Khan, A.Z. Portfolio optimization using higher moments in an uncertain random environment. Inf. Sci. 2021, 567, 348–374. Available online: https://www.sciencedirect.com/science/article/pii/S0020025521002565 (accessed on 16 October 2023). [CrossRef]
- Kang, Y.L.; Tian, J.-S.; Chen, C.; Zhao, G.-Y.; Li, Y.F.; Wei, Y. Entropy based robust portfolio. Phys. Stat. Mech. Its Appl. 2021, 583, 126260. Available online: https://www.sciencedirect.com/science/article/pii/S0378437121005331 (accessed on 16 October 2023). [CrossRef]
- Zhou, R.; Yang, Z.; Yu, M.; Ralescu, D.A. A portfolio optimization model based on information entropy and fuzzy time series. Fuzzy Optim. Decis. Mak. 2015, 14, 381–397. [Google Scholar] [CrossRef]
- Park, J. Finding Bayesian Optimal Portfolios with Skew-Normal Returns; Elsevier: Rochester, NY, USA, 2021; 48p. [Google Scholar] [CrossRef]
- Roberts, C. A correlation model useful in the study of twins. J. Am. Stat. Assoc. 1966, 61, 1184–1190. Available online: http://www.jstor.org/stable/2283207 (accessed on 16 October 2023). [CrossRef]
- Loperfido, N. Generalized skew-normal distributions. In Skew-Elliptical Distributions and Their Applications: A Journey beyond Normality; Chapman & Hall/CRC: Boca Raton, FL, USA, 2004; pp. 65–80. [Google Scholar]


| n | 0.1 | 0.5 | 0.8 | |
|---|---|---|---|---|
| 500 | MLE | 0.19 (0.91) | 0.68 (0.48) | 1.11 (0.45) |
| BPPE | 0.67 (0.82) | 0.65 (0.72) | 0.71 (0.78) | |
| PMLE | 0.16 (0.94) | 0.16 (0.91) | 0.16 (0.94) | |
| BDCM | 0.16 (0.92) | 0.16 (0.93) | 0.16 (0.95) | |
| 1000 | MLE | 0.16(0.87) | 0.69(0.48) | 1.11(0.42) |
| BPPE | 0.15 (0.92) | 0.18 (0.90) | 0.18(0.92) | |
| PMLE | 0.11 (0.94) | 0.10 (0.94) | 0.10 (0.92) | |
| BDCM | 0.11 (0.93) | 0.10 (0.94) | 0.10 (0.96) | |
| 1500 | MLE | 0.15(0.84) | 0.68(0.47) | 1.11(0.42) |
| BPPE | 0.12 (0.94) | 0.10 (0.89) | 0.12 (0.90) | |
| PMLE | 0.09(0.94) | 0.08(0.94) | 0.07 (0.93) | |
| BDCM | 0.09(0.94) | 0.08(0.93) | 0.08(0.94) | |
| 2000 | MLE | 0.15 (0.81) | 0.68 (0.48) | 1.10 (0.40) |
| BPPE | 0.09 (0.92) | 0.08 (0.92) | 0.07(0.92) | |
| PMLE | 0.07(0.95) | 0.07(0.95) | 0.06(0.92) | |
| BDCM | 0.07 (0.95) | 0.07 (0.97) | 0.07 (0.97) | |
| 2500 | MLE | 0.15 (0.75) | 0.68 (0.47) | 1.10 (0.39) |
| BPPE | 0.06(0.94) | 0.07(0.88) | 0.06 (0.92) | |
| PMLE | 0.06(0.96) | 0.07 (0.94) | 0.06 (0.92) | |
| BDCM | 0.06(0.97) | 0.06 (0.95) | 0.06 (0.94) |
| n | 250 | 500 | 1000 | 2000 |
| Coverage | 0.95 | 0.95 | 0.96 | 0.96 |
| Bias | 0.42 | 0.27 | 0.18 | 0.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chakraborty, A.; Bhattacharya, A.; Pati, D. Constrained Reweighting of Distributions: An Optimal Transport Approach. Entropy 2024, 26, 249. https://doi.org/10.3390/e26030249
Chakraborty A, Bhattacharya A, Pati D. Constrained Reweighting of Distributions: An Optimal Transport Approach. Entropy. 2024; 26(3):249. https://doi.org/10.3390/e26030249
Chicago/Turabian StyleChakraborty, Abhisek, Anirban Bhattacharya, and Debdeep Pati. 2024. "Constrained Reweighting of Distributions: An Optimal Transport Approach" Entropy 26, no. 3: 249. https://doi.org/10.3390/e26030249
APA StyleChakraborty, A., Bhattacharya, A., & Pati, D. (2024). Constrained Reweighting of Distributions: An Optimal Transport Approach. Entropy, 26(3), 249. https://doi.org/10.3390/e26030249





